Abstract
It is necessary to develop a health monitoring system (HMS) for complex systems to improve safety and reliability and prevent potential failures. Time-series signals are collected from multiple sensors installed on the equipment that can reflect the health condition of them. In this study, a novel interpretable recurrent variational state-space model (IRVSSM) is proposed for time-series modeling and anomaly detection. To be specific, the deterministic hidden state of a recursive neural network is used to capture the latent structure of sensor data, while the stochastic latent variables of a nonlinear deep state-space model capture the diversity of sensor data. Temporal dependencies are modeled through a nonlinear transition matrix; an automatic relevance determination network is introduced to selectively emphasize important sensor data. Experimental results demonstrate that the proposed algorithm effectively captures vital information within the sensor data and provides accurate and reliable fault diagnosis during the steady-state phase of liquid rocket engine operation.
1. Introduction
The liquid rocket engine, as the core component of a spacecraft, plays a crucial role in ensuring the safe launch and flight of a rocket. However, due to prolonged operation under harsh conditions such as high temperatures, high pressures, strong corrosion, and intense energy release, the engine is prone to malfunctions. If anomalies occur in the liquid rocket engine during ignition or flight, it often leads to rapid consequences such as explosions, resulting in significant financial losses and even jeopardizing human lives. Hence, it is imperative to conduct fault detection for liquid rocket engines. Engine fault detection essentially involves processing and analyzing multidimensional sensor time-series data, extracting features to obtain engine states. To detect the fault of LRE, statistical analysis methods such as red-line threshold algorithms [1] and autoregressive moving average (ARMA) algorithms [2] were initially applied due to their rapid and reliable computation. However, these methods often neglect the relationships between sensors, leading to false alarms due to the unstable threshold ranges and data of some sensors. With the advancement of deep learning techniques, an increasing number of deep neural models are employed in liquid rocket engine for fault detection, which aim to overcome the shortcomings of traditional machine learning methods such as artificial neural network (ANN) [3] and support vector machines (SVM) [4], which have inadequate feature extraction capabilities. Park et al. [3] integrated convolutional neural networks (CNN) and long short-term memory networks (LSTM) to identify transient faults during engine startup. Yan et al. [5] proposed a memory-enhanced skip-connection autoencoder for unsupervised anomaly detection in rocket engine operations. Feng et al. [6] employed a generative adversarial network (GAN) to achieve multi-source fusion for LRE anomaly detection. However, these approaches exhibit limited capacity in modeling long-term dependencies in multidimensional complex temporal data and are prone to overfitting issues due to sample imbalances and small sample sizes. Moreover, the multi-source data fusion strategies are relatively simple and lack interpretability, hindering the representation of the relationship between sensors and model performance.
Meanwhile, model-based fault detection methods are also investigated, utilizing mathematical analytical models of the engine combined with methods like Kalman filtering to achieve fault detection [7,8]. The effectiveness of this approach depends on the accuracy of the model, yet analytical models established often diverge from actual engine behavior. Similar to model-based methods, state-space models describe the evolution of system states over time through state equations and observation equations. By integrating deep learning, state-space models can leverage their multi-level representation capabilities to capture features across different scales, thus enabling a more precise understanding and prediction of complex time series data. In 2022, Shalini et al. [9] employed state-space models for currency price forecasting. Similarly, in the same year, Li et al. [10] utilized state-space models for anomaly detection in time-series data. However, state-space models typically assume a linear relationship between system states and observations, which may pose limitations when dealing with the complex nonlinear relationships in liquid rocket engine data. Therefore, state-space models require further improvement to accommodate these complex scenarios.
To tackle the aforementioned challenges, a novel approach named interpretable recurrent variational state-space model (IRVSSM) is proposed for fault diagnosis of liquid rocket engines, which leverages the recursive nonlinear state-space framework of deep neural networks. The nonlinear emission and transition matrices are designed to adeptly capture the intricate temporal dependencies and dynamic variations inherent among sequential signals. This adaptability bolsters the model’s resilience to complex data distributions. Additionally, an automatic relevance determination (ARD) network was employed to facilitate the identification of critical factors within sensor data, thereby enhancing the model’s interpretability. The contributions of this study are summarized as follows:
- (1).
- A novel interpretable recurrent variational state-space model (IRVSSM) is proposed for diagnosis of complex systems. Recurrent neural networks (RNNs) are utilized to capture long-term dependencies in sensor data, while the state-space model (SSM) captures dynamic changes in complex sensor data. The incorporation of nonlinear emission and transition matrices enables the model to flexibly adapt to various data distributions. Additionally, integrating a variational autoencoder (VAE) within the state-space framework not only enhances the model’s generalization capability but also helps alleviate overfitting issues.
- (2).
- To extract crucial information from sensor data, an automatic relevance determination (ARD) network is designed. By comparing sensor weights with actual fault information and conducting detailed analyses of the model’s decisions, the ARD network furnishes compelling explanations for engine fault classification.
- (3).
- Experiments were carried out on simulated and actual liquid rocket engine test data. The results demonstrate the fault diagnosis performance of the proposed methodology outperforms baseline models.
2. Related Works
2.1. State-Space Models
State-space models (SSMs) provide a versatile and flexible approach for modeling sequential data [11]. Stemming from Kalman’s pioneering work, SSMs were rapidly employed including estimating the trajectory of the spacecraft transporting humans to the moon [12]. SSMs primarily serve as generative models for sequential data, encompassing prediction modeling, state inference, and representation learning. As depicted in Formula (1), the state-space model consists of state transition equations and observation equations. The former describes the dynamics of hidden states over time , while the latter summarizes the conditional probability distribution of observations given the hidden states .
where the input vector, hidden state vector, and output vector are denoted as , and . The state transition equation includes the state transition matrix and the intensity of state transition noise , while the observation equation comprises the weight and bias of the observation model and , and the intensity of observation noise . Furthermore, and represent the effects of input on hidden variables and observations, respectively. The state vector follows a Gaussian distribution , and the noise follows a standard normal distribution .
2.2. Deep State-Space Model
The deep state-space model builds upon the foundation of the state-space model by incorporating stochastic latent variables from variational autoencoders (VAE) [13,14], thereby enabling scalable training through stochastic backpropagation and inference networks. The SSM model allows for modeling the temporal relationships of stochastic latent variables, extending the time dimension of VAEs. The integration of SSM and VAE permits the creation of flexible conditional distributions using neural networks, offering a viable approach to modeling uncertainty in latent variables. Deep state-space model primarily focus on unsupervised learning of complex temporal data probability distributions [9,15], with wide applications in areas such as speech, music, video, and text generation [16,17,18]. These applications face similar challenges, characterized by complex high-dimensional temporal distributions with uncertainty and variability. For instance, video generation necessitates sophisticated architectures capable of modeling high-dimensional observation data at each time step while capturing long-term temporal dependencies. Similarly, engine sensor data exhibit characteristics such as nonlinearity, high dimensionality, dynamics, and strong correlations. Modeling sensor data in high dimensions at each time step serves the purpose of fault detection and diagnosis. Hence, the deep state-space model aligns well with the requirements of liquid rocket engine fault diagnosis.
2.3. Variational Autoencoders
Variational autoencoders (VAEs) have great success in generative models for high-dimensional data [19], which introduce the probabilistic modeling and employ deep neural networks to parameterize the probability distribution of latent variables. Simultaneously, VAEs provide an effective approximate inference process that can be scaled to large datasets [20]. The variational autoencoder consists of a generative network and an inference network. The inference network is responsible for learning the latent representation of the data, while the generative network utilizes these latent representations to generate data samples. Together, they collaborate to achieve data dimensionality reduction and feature extraction, thereby maximizing the model’s performance.
3. Proposed Model
This section provides a detailed overview of the main framework of the proposed algorithm, as depicted in Figure 1. The model primarily comprises the following components: (1) A nonlinear recurrent variational state-space model, which utilizes RNNs to capture long-term dependencies and incorporates nonlinear transition and emission matrices to account for dynamic changes across different time steps. (2) An automatic relevance determination algorithm, which selects crucial information from sensor data, thereby enhancing the model’s classification performance and interpretability.
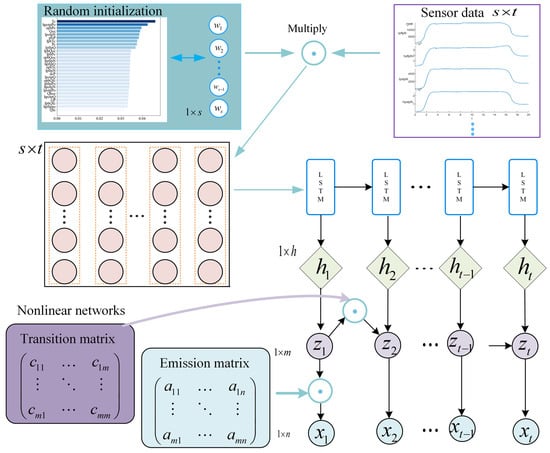
Figure 1.
Schematic diagram of recurrent variational state-space model.
3.1. Problem Formulation
When provided with a time series of sensor data originating from a liquid rocket engine , the operating state can be evaluated . In state-space form, our goal can be represented as in Equation (2). However, the state-space model constructed for this experiment does not account for input variables . This is because the control element of the liquid rocket engine is typically a valve, whose opening is used to regulate the oxygen-fuel mixture during engine startup. In steady-state operation, the valve’s opening remains constant and only changes when adjusting flow under varying operational conditions.
3.2. Recurrent Variational State-Space Model for Liquid Rocket Engines
We introduce a deep state-space model with two primary features: (1) using a recurrent neural network (RNN) to capture long-term dependencies in sensor data and (2) employing neural networks to nonlinearize the state-space transition and emission matrices.
The initial state-space model (SSM) is based on linear Gaussian models and hidden Markov models (HMM), which include linear transition and emission matrices [14]. However, liquid rocket engine sensor data exhibits complex nonlinear relationships and long-term dependencies. Traditional frameworks are insufficient for modeling these complexities. The interpretable recursive variational state-space model (IRVSSM) employs a recurrent neural network (RNN) to capture long-term dependencies in sensor data, relaxing the Markov assumption [20]. The RNN then extracts deterministic sensor states. The generative model for the state-space is illustrated in Figure 2a and can be expressed mathematically as follows:
where is the RNN function, and is a delta distribution. For stochastic latent states, mean and covariance functions for Gaussian distribution of state transitions, which are also parameterized by neural networks. is an arbitrary probability distribution, and its parameter is also parameterized by neural networks.
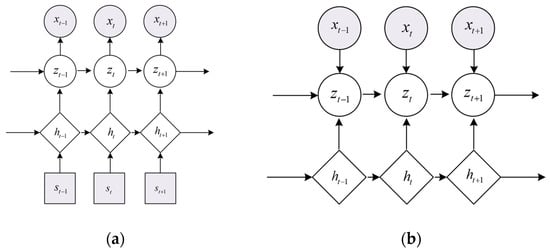
Figure 2.
Recurrent variational state-space model. (a) Generative model; (b) Inference network.
The deep state-space model represented in Equations (3)–(5) is parameterized as . The parameterization is implemented as follows: a long short-term memory (LSTM) network is employed to capture the temporal dependencies in the data, and the hidden state transition matrix is parameterized using the following method:
where and denote two neural networks parameterized by , and .
The parameterization of the emission matrix also uses neural networks to approximate arbitrary distributions [21].
3.3. Inference Network
Our objective is to maximize the log marginal likelihood . Owing to the nonlinear characteristics of parameterized deep neural networks, accurately calculating the data’s log likelihood in variational autoencoders (VAE) presents a challenge. Nevertheless, to optimize the parameters of the VAE through maximum likelihood estimation, we use variational inference to approximate challenging posterior distributions and select an efficient variational approximation , as shown in Figure 2. Specifically, the deep neural network takes data points as input and generates the corresponding mean and diagonal covariance matrix of the Gaussian variational approximation. The formula is as follows:
Then we maximize the variational evidence lower bound (ELBO); the maximization over in Equations (3)–(5) is actually a maximization over the parameters (use below the notation ). ELBO can be decomposed in two terms [22]:
The reconstruction term allows the likelihood and the inference network to accurately reconstruct data, thereby maximizing the autoencoding capability of VAEs. The regularization term, as a penalty, discourages posterior approximations that deviate significantly from the prior distribution. Given that both the generative and inference models are defined using neural networks, we can effectively compute gradients of and using the backpropagation algorithm [23]. To obtain low-variance, differentiable, and unbiased estimates of the lower bound, the reparameterization technique is also employed [24], which allows backpropagation to flow through latent variables and approximates complex expectations via Monte Carlo integration. Notably, due to the Gaussian nature of and , the KL divergence term can be analytically computed [25].
3.4. Automatic Relevance Determination Network
Given the variability in engine component failure probabilities, the likelihood and magnitude of responses from engine sensors differ. Some sensors demonstrate more pronounced changes, necessitating greater scrutiny. This study utilizes an automatic relevance determination (ARD) network to allocate priority weights to each sensor. These weights may be randomly initialized or determined based on the engine’s historical failure rates. Employing gradient descent within the network yields the sensors’ final posterior weights, indicative of the significance of each sensor’s data [26,27]. Conventional ARD approaches regard variables as governed by sparsity-induced priors. To circumvent intricate weight inference, constant inputs are parameterized via a neural network, and a Softmax function ensures their aggregate equals one [28].
where . The input vector , which corresponds to the dimensionality of the number of sensors, can be defined randomly or based on the engine’s prior probability of failure. As depicted in Figure 3, where denotes input sensor data, represents the number of sensors, and indicates the time step. The ARD network’s posterior weights can be efficiently determined through gradient descent on the parameters by training sensor data thereby avoiding the posterior inference issues of traditional Bayesian methods.
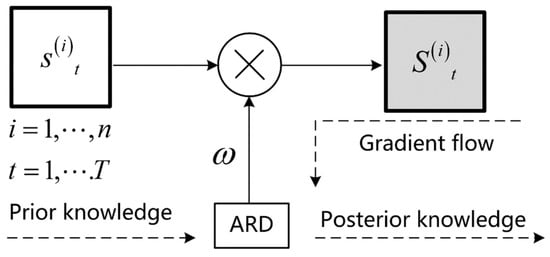
Figure 3.
Automatic relevance determination network.
4. Experiments
In this section, the proposed model is evaluated in two multi-source datasets and compared with baseline methods. The experiment results demonstrate the effectiveness and superiority of interpretable recurrent variational state-space model (IRVSSM).
4.1. Datasets
This investigation employs two principal datasets: steady-state simulated fault data and empirical rocket engine test data. The simulated dataset encompasses both normal operational states and four distinct fault scenarios; the empirical test data derives from measurements across multiple sensors, identified as LRE-1 and LRE-2. Table 1 furnishes an exhaustive delineation of the LRE datasets. In the course of model training and evaluation, signals are partitioned into subsequences with lengths of 25 and 20. These subsequences facilitate the categorization of engine states, each annotated with a label delineating the engine’s specific state. The dataset allocation for training follows an 80/20 partition, utilizing 80% for model training and the remaining 20% for validation. The loss function applied in the model is delineated in Equation (9). The model’s dimensionality is established at 80, while in the deep state-space model, the stochastic latent variables’ dimensionality is configured to 5 for the LRE-1 dataset and 8 for the LRE-2 dataset. Optimization of the model is conducted using the Adam algorithm. In experiments, all methods are implemented with Python 3.6. The working configurations are Intel Core i5-10400F CPU and NVIDIA GeForce GTX 1660Ti GPU.

Table 1.
Description of two LRE datasets.
4.2. Compared Methods
By introducing the ARD network into the deep state-space model, we aim to further capture critical information from sensor data and validate the model’s ability to capture data through weights. We refer to this model as the interpretable recurrent variational state-space model (IRVSSM), which can be categorized based on the presence of the ARD network and nonlinear layers: (1) the basic DSSM without the ARD network and nonlinear layers, (2) the DSSM-A with the added ARD network, and (3) the DSSM-NL with the additional nonlinear layers.
4.3. Results and Analysis
Figure 4a,b illustrate the classification performance of the model on datasets LRE-1 and LRE-2, respectively. The classification performance of the network is evaluated using the training epochs and corresponding accuracy. In the LRE-1 experiment, the baseline DSSM model exhibits poor classification performance, while the DSSM-A model, augmented with the ARD network, shows improvement in classification results after additional epochs. Furthermore, the classification performance of the DSSM-nl model, which includes nonlinear state-space transitions, surpasses that of the baseline DSSM model, indicating that nonlinear layers can better fit the data. The IRVSSM, which combines nonlinear state-space transitions and ARD network, demonstrates the best performance after a certain number of epochs, indicating that the combination of ARD network and nonlinear layers effectively enhances the model’s classification capability. Similar classification results are observed in the LRE-2 experiment, demonstrating the effectiveness of the model.
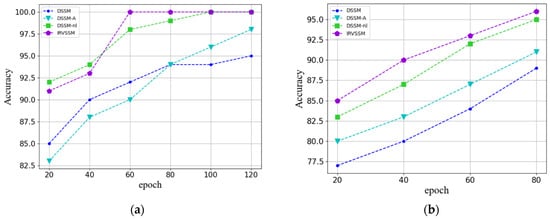
Figure 4.
(a) Classification accuracy of LRE-1; (b) Classification accuracy of LRE-2.
Figure 5 depicts the sensor weight diagram obtained after training the ARD network on the LRE-1 dataset. Sensors such as low-pressure oxygen turbine pump flow, high-pressure oxygen turbine pump flow, high-pressure oxygen turbine pump pressure, fuel preburner pump pressure, high-pressure hydrogen turbine pump flow, low-pressure hydrogen turbine pump flow, and fuel preburner pump pressure (lpotpQ, hpotpQ, hpotpPo, fpbQoc, hpoftpQ, lpftpQ) exhibit relatively high weights. In actual faults, such as oxygen turbine pump leaks, hydrogen turbine pump leaks, and cooling jacket leaks, changes in turbine pump flow and pressure occur. Therefore, the high weights of turbine pump flow and pressure correspond to actual fault patterns, demonstrating that the ARD network effectively captures crucial information from the data and verifies the interpretability of the model.
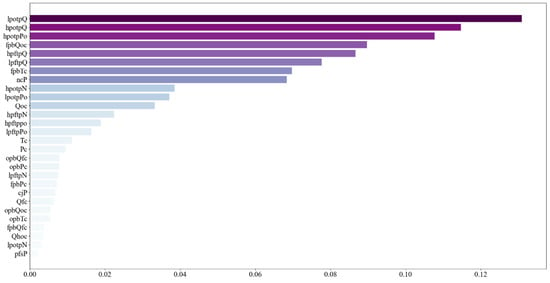
Figure 5.
Sensor weight graph.
5. Conclusions
This paper proposes a fault diagnosis method for liquid rocket engine based on an interpretable recursive variational state-space model. The method relies on a recursive nonlinear state-space model implemented using deep networks, allowing for nonlinear emission and transition matrices, which enables flexible adaptation to data distributions, thereby extracting and conveying the engine’s state and enhancing the model’s robustness. Additionally, the utilization of ARD networks facilitates the exploration of sensor importance, effectively identifying crucial factors within the data and enhancing the interpretability of the model. With the evolution of reusable rocket technology, the accurate diagnosis of liquid rocket engine malfunctions has become paramount. Swift and precise diagnostic algorithms are imperative for fault identification. While state-space models are adept at long-term fault modeling and monitoring in engines, data-driven diagnostic approaches are prone to sensor malfunction interference. Consequently, the development of a precise mathematical model of the engine, juxtaposed with real sensor data and deep neural networks, is essential for accurately differentiating between sensor and engine faults, preventing misdiagnosis, and will be a focal point of forthcoming research.
Author Contributions
Conceptualization, M.M. and J.Z.; methodology, M.M.; validation, M.M. and J.Z.; writing—original draft preparation, M.M.; writing—review and editing, M.M. and J.Z.; visualization, J.Z.; supervision, M.M.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research is financed by the National Natural Science Foundation of China (No. 52205124), the Basic Research Program of China (No. 2022-JCJQ-JJ-0643), the Basic Research Fund of Xi’an Jiaotong University (No. xxj032022011), and the High level innovation and entrepreneurship talent program (No. QCYRCXM-2022-315).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Acknowledgments
The authors look forward to the insightful comments and suggestions of the anonymous reviewers and editors, which will go a long way towards improving the quality of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hu, N.; Qin, G.; Hu, L.; Xie, G.; Hu, H. Real-time fault detection system for turbopump of liquid rocket engine based on vibration measurement signals. In Proceedings of the 6th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 11–13 September 2007. [Google Scholar]
- Norman, J.A.; Nemeth, E. Development of a health monitoring algorithm. In Proceedings of the 26th Joint Propulsion Conference, Orlando, FL, USA, 16–18 July 1990; p. 1991. [Google Scholar]
- Park, S.-Y.; Ahn, J. Deep neural network approach for fault detection and diagnosis during startup transient of liquid-propellant rocket engine. Acta Astronaut. 2020, 177, 714–730. [Google Scholar] [CrossRef]
- Zhu, X.; Cheng, Y.; Wu, J.; Hu, R.; Cui, X. Steady-state process fault detection for liquid rocket engines based on convolutional auto-encoder and one-class support vector machine. IEEE Access 2019, 8, 3144–3158. [Google Scholar] [CrossRef]
- Yan, H.; Liu, Z.; Chen, J.; Feng, Y.; Wang, J. Memory-augmented skip-connected autoencoder for unsupervised anomaly detection of rocket engines with multi-source fusion. ISA Trans. 2023, 133, 53–65. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Liu, Z.; Chen, J.; Lv, H.; Wang, J.; Yuan, J. Make the rocket intelligent at IoT edge: Stepwise GAN for anomaly detection of LRE with multisource fusion. IEEE Internet Things J. 2021, 9, 3135–3149. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, H.; Qi, C.; Liu, Y. Model-Based Leakage Estimation and Remaining Useful Life Prediction of Control Gas Cylinder. Int. J. Aerosp. Eng. 2023, 2023, 3606822. [Google Scholar] [CrossRef]
- Omata, N.; Tsutsumi, S.; Abe, M.; Satoh, D.; Hashimoto, T.; Sato, M.; Kimura, T.; IEEE. Model-based fault detection with uncertainties in a reusable rocket engine. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022. [Google Scholar]
- Sharma, S.; Majumdar, A. Deep state space model for predicting cryptocurrency price. Inf. Sci. 2022, 618, 417–433. [Google Scholar] [CrossRef]
- Li, L.; Yan, J.; Wen, Q.; Jin, Y.; Yang, X. Learning robust deep state space for unsupervised anomaly detection in contaminated time-series. IEEE Trans. Knowl. Data Eng. 2022, 35, 6. [Google Scholar] [CrossRef]
- Liu, Y.; Ajirak, M.; Djuric, P. Sequential Estimation of Gaussian Process-based Deep State-Space Models. IEEE Trans. Signal Process. 2023, 71, 14. [Google Scholar] [CrossRef]
- Lefferts, E.J.; Markley, F.L.; Shuster, M.D. Kalman Filtering for Spacecraft Attitude Estimation. J. Guid. Control. Dyn. 1982, 5, 536–542. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Rangapuram, S.S.; Seeger, M.; Gasthaus, J.; Stella, L.; Wang, Y.; Januschowski, T. Deep state space models for time series forecasting. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 7796–7805. [Google Scholar]
- Fraccaro, M. Deep Latent Variable Models for Sequential Data; DTU Compute: Lyngby, Denmark, 2018. [Google Scholar]
- Nugraha, A.A.; Sekiguchi, K.; Yoshii, K. A Flow-Based Deep Latent Variable Model for Speech Spectrogram Modeling and Enhancement. TechRxiv 2020, 28, 1104–1117. [Google Scholar] [CrossRef]
- Shen, X. Deep Latent-Variable Models for Text Generation. arXiv 2022, arXiv:2203.02055. [Google Scholar]
- Hai-Long, T.; Makoto, M.; Sophia, A. BioVAE: A pre-trained latent variable language model for biomedical text mining. Bioinformatics 2021, 38, 872–874. [Google Scholar]
- Chira, D.; Haralampiev, I.; Winther, O.; Dittadi, A.; Liévin, V. Image Super-Resolution with Deep Variational Autoencoders. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Krishnan, R.G.; Shalit, U.; Sontag, D.; Aaai. Structured Inference Networks for Nonlinear State Space Models. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2101–2109. [Google Scholar]
- Gedon, D.; Wahlstrm, N.; Schn, T.B.; Ljung, L. Deep State Space Models for Nonlinear System Identification; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Burda, Y.; Grosse, R.; Salakhutdinov, R. Importance Weighted Autoencoders. arXiv 2015, arXiv:1509.00519. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic Backpropagation and Approximate Inference in Deep Generative Models. In Proceedings of the International Conference on Machine Learning, Beijing, China, 22–24 June 2014; pp. 1278–1286. [Google Scholar]
- Kingma, D.P.; Rezende, D.J.; Mohamed, S.; Welling, M. Semi-supervised Learning with Deep Generative Models. In Proceedings of the 28th Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Wipf, D.; Nagarajan, S. A New View of Automatic Relevance Determination. Adv. Neural Inf. Process. Syst. 2007, 49, 641. [Google Scholar]
- Rudy, S.H.; Sapsis, T.P. Sparse methods for automatic relevance determination. Phys. D Nonlinear Phenom. 2021, 418, 132843. [Google Scholar] [CrossRef]
- Li, L.Y.; Yan, J.C.; Yang, X.K.; Jin, Y.H. Learning Interpretable Deep State Space Model for Probabilistic Time Series Forecasting. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 2901–2908. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).