AOSMA-MLP: A Novel Method for Hybrid Metaheuristics Artificial Neural Networks and a New Approach for Prediction of Geothermal Reservoir Temperature
Abstract
Featured Application
Abstract
1. Introduction
2. Material and Methods
2.1. Data Acquisition
2.2. Artificial Neural Network
Multi-Layer Perceptron Neural Networks
2.3. Whale Optimization Algorithm
2.4. Ant Lion Algorithm
2.4.1. Random Walks of Ants
2.4.2. Trapping in Antlion’s Pits
2.4.3. Building Trap
2.4.4. Sliding Ants towards Antlion
2.4.5. Sliding Ants towards Antlion
2.4.6. Elitism
2.5. Slime Mould Algorithm and Adaptive Opposition Slime Mould Algorithm
2.5.1. Opposition-Based Learning
2.5.2. Adaptive Decision Strategy
2.6. Metaheuristic Optimization Algorithms for Learning Mlp
2.7. Evaluation Metrics
2.8. Normalization
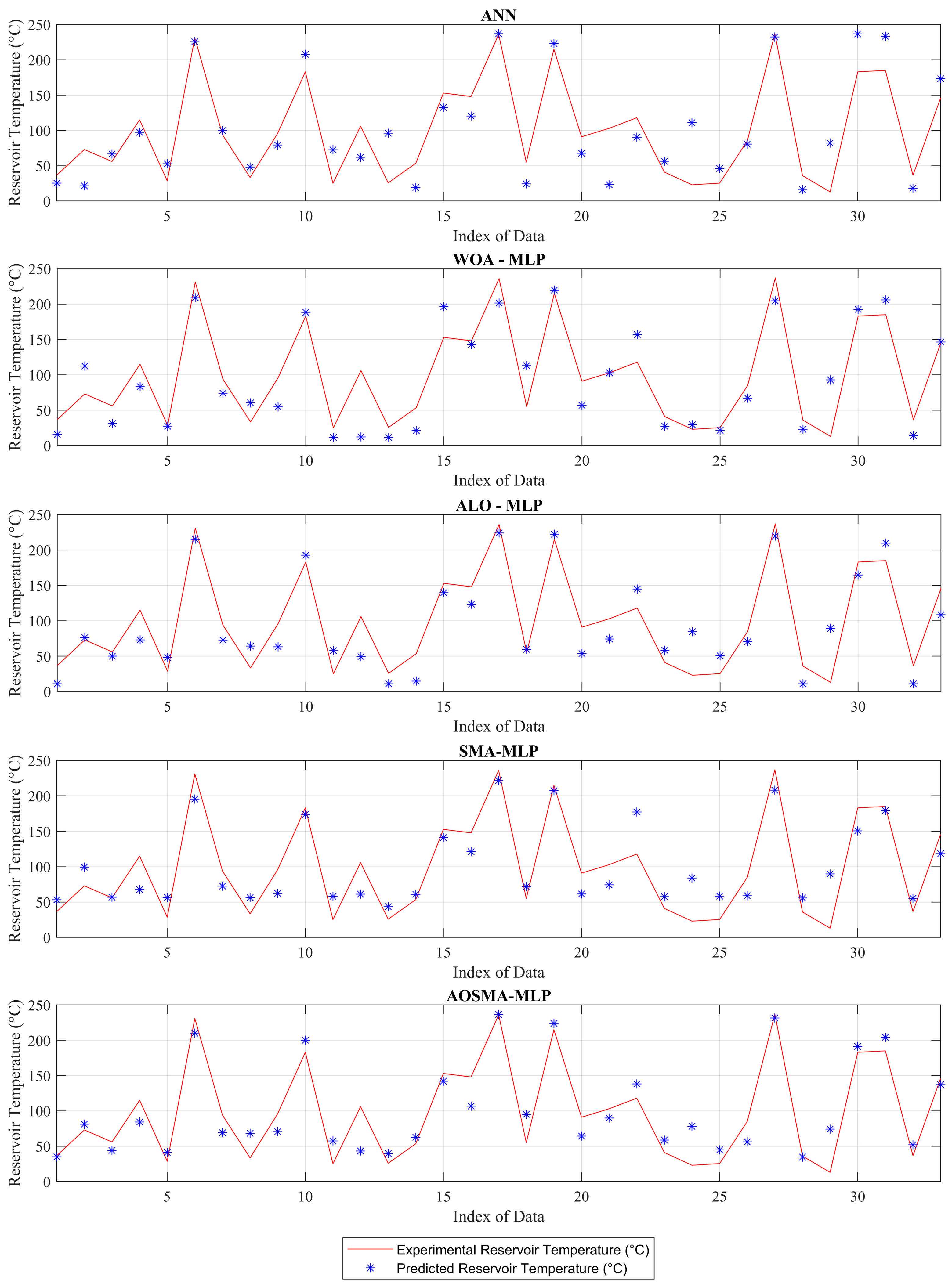
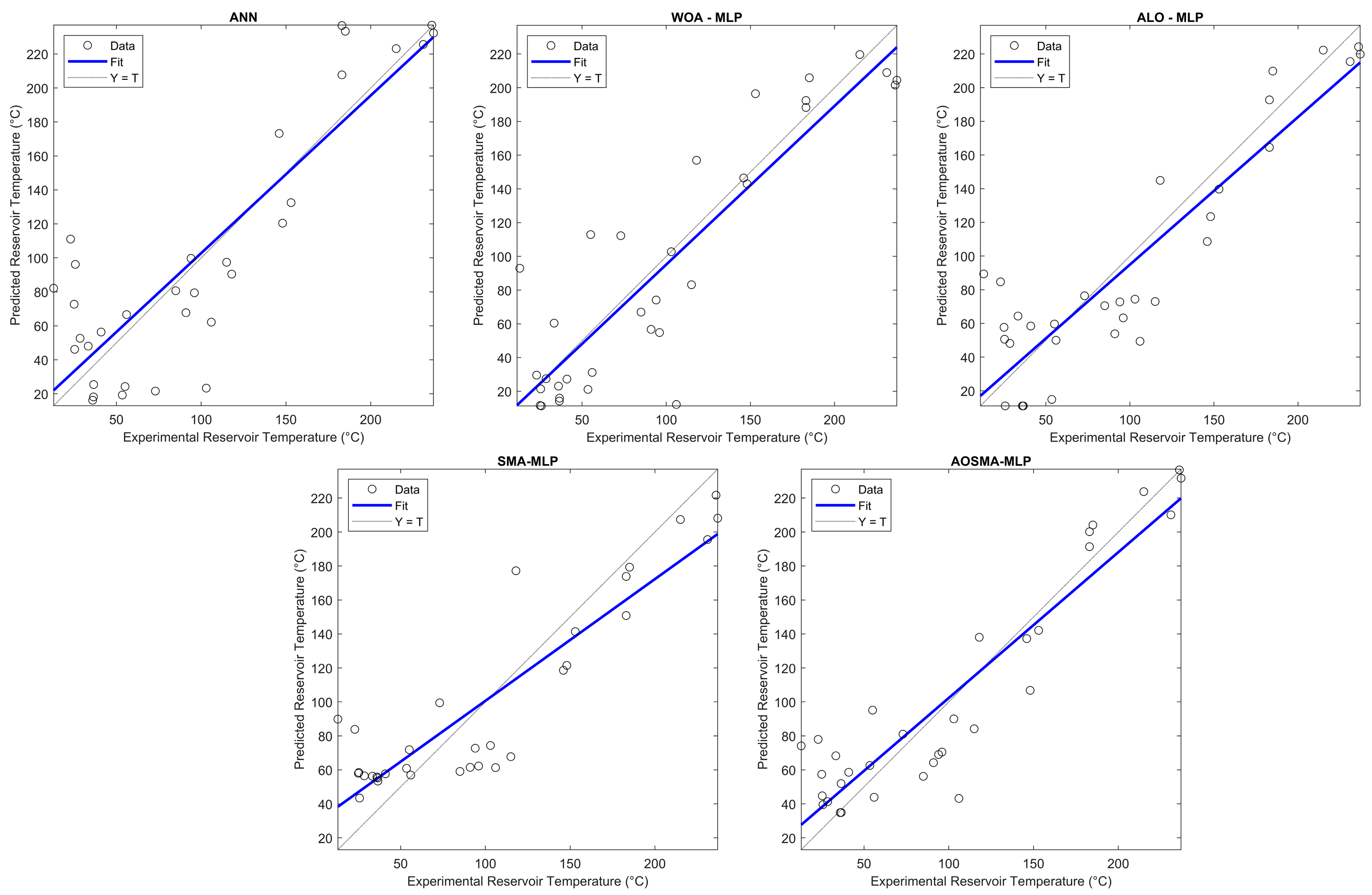
3. Results
4. Discussion
- R2 Value: The AOSMA-MLP algorithm outperformed the ANN, WOA-MLP, ALO-MLP, and SMA-MLP methods by 18.76%, 9.65%, 5.16%, and 7.03%, respectively, indicating a more accurate fit to the data.
- R Value: In terms of correlation, the AOSMA-MLP method exhibited superior performance by 6.11%, 2.94%, 2.03%, and 2.89% compared to the ANN, WOA-MLP, ALO-MLP, and SMA-MLP algorithms, respectively, suggesting stronger linear relationships between predicted and observed values.
- RMSE Value: The AOSMA-MLP model demonstrated a significant reduction in prediction error, showing improvements of 27.56%, 18.46%, 11.65%, and 14.75% over the ANN, WOA-MLP, ALO-MLP, and SMA-MLP algorithms, respectively.
- MAE: In terms of absolute errors, the AOSMA-MLP approach was found to be more precise, reducing errors by 26.74%, 15.08%, 16.44%, and 19.99% compared to the ANN, WOA-MLP, ALO-MLP, and SMA-MLP algorithms, respectively.
5. Conclusions
- The AOSMA-MLP demonstrated superior performance relative to the other metaheuristic optimization algorithms tested. By leveraging AOSMA for ANN training with hydrogeochemical and RT data derived from geothermal sources, it effectively addressed common limitations of alternative methods, such as susceptibility to local minima and constraints on global exploration capabilities.
- Across the board, AOSMA-MLP showcased a distinct advantage over competing methods across the four different evaluation metrics employed in this study. This underscores its efficacy and robustness in predicting RTs.
- In terms of accuracy of fit to the data, the AOSMA-MLP algorithm performed better than the ANN, WOA-MLP, ALO-MLP, and SMA-MLP approaches by 18.76%, 9.65%, 5.16%, and 7.03%, respectively.
- The promising outcomes achieved with AOSMA-MLP indicate its potential applicability across a broad spectrum of regression problems, extending beyond the scope of this study.
- The AOSMA-MLP model demonstrated a significant reduction in prediction error, showing improvements of 27.56%, 18.46%, 11.65%, and 14.75% over the ANN, WOA-MLP, ALO-MLP, and SMA-MLP algorithms, respectively.
- The application of the AOSMA-MLP model for predicting RTs in geothermal resources is projected to significantly aid engineers and project planners in identifying optimal drilling locations. Given the typically time-intensive, expensive, and complex nature of such determinations, this model can substantially reduce project costs and enhance flexibility within the investment and design phases of geothermal energy projects.
- Overall, the introduction and application of AOSMA-MLP represent a significant advancement in geothermal energy research, offering practical benefits for the planning and execution of geothermal projects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EU | European Union |
| RT | Reservoir temperature |
| ANN | Artificial Neural Network |
| FNNS | Feed-Forward Networks |
| MLP | Multilayer Perceptron |
| WOA-MLP | Whale Optimization |
| ALO-MLP | Ant Lion Optimizer |
| SMA-MLP | Slime Mould Algorithm |
| AOSMA | Adaptive Opposition SMA |
| EC | Electrical Conductivity |
| Cl− | Chloride ion |
| K+ | Potassium ion |
| B | Boron |
| Na+ | Sodium ion |
| SiO2 | Silicon dioxide |
References
- Luo, Z.; Wang, Y.; Zhou, S.; Wu, X. Simulation and prediction of conditions for effective development of shallow geothermal energy. Appl. Therm. Eng. 2015, 91, 370–376. [Google Scholar] [CrossRef]
- Çetin, T.H.; Zhu, J.; Ekici, E.; Kanoglu, M. Thermodynamic assessment of a geothermal power and cooling cogeneration system with cryogenic energy storage. Energy Convers. Manag. 2022, 260, 115616. [Google Scholar] [CrossRef]
- Ambriz-Díaz, V.M.; Rubio-Maya, C.; Chávez, O.; Ruiz-Casanova, E.; Pastor-Martínez, E. Thermodynamic performance and economic feasibility of Kalina, Goswami and Organic Rankine Cycles coupled to a polygeneration plant using geothermal energy of low-grade temperature. Energy Convers. Manag. 2021, 243, 114362. [Google Scholar] [CrossRef]
- Werner, S. International review of district heating and cooling. Energy 2017, 137, 617–631. [Google Scholar] [CrossRef]
- Gang, W.; Wang, S.; Xiao, F. District cooling systems and individual cooling systems: Comparative analysis and impacts of key factors. Sci. Technol. Built Environ. 2017, 23, 241–250. [Google Scholar] [CrossRef]
- Moya, D.; Aldás, C.; Kaparaju, P. Geothermal energy: Power plant technology and direct heat applications. Renew. Sustain. Energy Rev. 2018, 94, 889–901. [Google Scholar] [CrossRef]
- Inayat, A.; Raza, M. District cooling system via renewable energy sources: A review. Renew. Sustain. Energy Rev. 2019, 107, 360–373. [Google Scholar] [CrossRef]
- Kanoğlu, M.; Çengel, Y.A.; Cimbala, J.M. Fundamentals and Applications of Renewable Energy; McGraw-Hill Education: New York, NY, USA, 2020. [Google Scholar]
- Gang, W.; Wang, S.; Xiao, F.; Gao, D.-c. District cooling systems: Technology integration, system optimization, challenges and opportunities for applications. Renew. Sustain. Energy Rev. 2016, 53, 253–264. [Google Scholar] [CrossRef]
- Rostamzadeh, H.; Gargari, S.G.; Namin, A.S.; Ghaebi, H. A novel multigeneration system driven by a hybrid biogas-geothermal heat source, Part II: Multi-criteria optimization. Energy Convers. Manag. 2019, 180, 859–888. [Google Scholar] [CrossRef]
- Michaelides, E.E.S. Future directions and cycles for electricity production from geothermal resources. Energy Convers. Manag. 2016, 107, 3–9. [Google Scholar] [CrossRef]
- Tut Haklidir, F.S.; Haklidir, M. Prediction of reservoir temperatures using hydrogeochemical data, Western Anatolia geothermal systems (Turkey): A machine learning approach. Nat. Resour. Res. 2020, 29, 2333–2346. [Google Scholar] [CrossRef]
- Okan, Ö.Ö.; Kalender, L.; Çetindağ, B. Trace-element hydrogeochemistry of thermal waters of Karakoçan (Elazığ) and Mazgirt (Tunceli), Eastern Anatolia, Turkey. J. Geochem. Explor. 2018, 194, 29–43. [Google Scholar] [CrossRef]
- Haklidir, F.S.T.; Haklidir, M. The fluid temperature prediction with hydro-geochemical indicators using a deep learning model: A case study Western Anatolia (Turkey). In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 11–13 February 2019. [Google Scholar]
- Porkhial, S.; Salehpour, M.; Ashraf, H.; Jamali, A. Modeling and prediction of geothermal reservoir temperature behavior using evolutionary design of neural networks. Geoth 2015, 53, 320–327. [Google Scholar] [CrossRef]
- Alacali, M. Hydrogeochemical investigation of geothermal springs in Erzurum, East Anatolia (Turkey). Environ. Earth Sci. 2018, 77, 802. [Google Scholar] [CrossRef]
- Altay, E.V.; Gurgenc, E.; Altay, O.; Dikici, A. Hybrid artificial neural network based on a metaheuristic optimization algorithm for the prediction of reservoir temperature using hydrogeochemical data of different geothermal areas in Anatolia (Turkey). Geoth 2022, 104, 102476. [Google Scholar] [CrossRef]
- Bassam, A.; Santoyo, E.; Andaverde, J.; Hernández, J.; Espinoza-Ojeda, O. Estimation of static formation temperatures in geothermal wells by using an artificial neural network approach. Comput. Geosci. 2010, 36, 1191–1199. [Google Scholar] [CrossRef]
- Fannou, J.-L.C.; Rousseau, C.; Lamarche, L.; Kajl, S. Modeling of a direct expansion geothermal heat pump using artificial neural networks. Energy Build. 2014, 81, 381–390. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Florides, G.A.; Pouloupatis, P.D.; Panayides, I.; Joseph-Stylianou, J.; Zomeni, Z. Artificial neural networks for the generation of geothermal maps of ground temperature at various depths by considering land configuration. Energy 2012, 48, 233–240. [Google Scholar] [CrossRef]
- Bourhis, P.; Cousin, B.; Loria, A.F.R.; Laloui, L. Machine learning enhancement of thermal response tests for geothermal potential evaluations at site and regional scales. Geoth 2021, 95, 102132. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, E.; Liu, L.; Qi, C. Machine learning-based performance prediction for ground source heat pump systems. Geoth 2022, 105, 102509. [Google Scholar] [CrossRef]
- Rezvanbehbahani, S.; Stearns, L.A.; Kadivar, A.; Walker, J.D.; van der Veen, C.J. Predicting the geothermal heat flux in Greenland: A machine learning approach. GeoRL 2017, 44, 12271–12279. [Google Scholar] [CrossRef]
- Pérez-Zárate, D.; Santoyo, E.; Acevedo-Anicasio, A.; Díaz-González, L.; García-López, C. Evaluation of artificial neural networks for the prediction of deep reservoir temperatures using the gas-phase composition of geothermal fluids. Comput. Geosci. 2019, 129, 49–68. [Google Scholar] [CrossRef]
- Yang, J.; Ma, J. Feed-forward neural network training using sparse representation. Expert Syst. Appl. 2019, 116, 255–264. [Google Scholar] [CrossRef]
- Orr, M.J. Introduction to Radial Basis Function Networks; University of Edinburgh: Edinburgh, Scotland, 1996. [Google Scholar]
- Fekri-Ershad, S. Bark texture classification using improved local ternary patterns and multilayer neural network. Expert Syst. Appl. 2020, 158, 113509. [Google Scholar] [CrossRef]
- Altay, O.; Ulas, M.; Alyamac, K.E. DCS-ELM: A novel method for extreme learning machine for regression problems and a new approach for the SFRSCC. PeerJ Comput. Sci. 2021, 7, e411. [Google Scholar] [CrossRef] [PubMed]
- Aljarah, I.; Faris, H.; Mirjalili, S.; Al-Madi, N.; Sheta, A.; Mafarja, M. Evolving neural networks using bird swarm algorithm for data classification and regression applications. Clust. Comput. 2019, 22, 1317–1345. [Google Scholar] [CrossRef]
- Liao, J.; Asteris, P.G.; Cavaleri, L.; Mohammed, A.S.; Lemonis, M.E.; Tsoukalas, M.Z.; Skentou, A.D.; Maraveas, C.; Koopialipoor, M.; Armaghani, D.J. Novel fuzzy-based optimization approaches for the prediction of ultimate axial load of circular concrete-filled steel tubes. Buildings 2021, 11, 629. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Mirjalili, S.; Aljarah, I.; Mafarja, M. Ant lion optimizer: Theory, literature review, and application in multi-layer perceptron neural networks. In Nature-Inspired Optimizers; Springer: Cham, Switzerland, 2020; pp. 23–46. [Google Scholar]
- Zubaidi, S.L.; Abdulkareem, I.H.; Hashim, K.S.; Al-Bugharbee, H.; Ridha, H.M.; Gharghan, S.K.; Al-Qaim, F.F.; Muradov, M.; Kot, P.; Al-Khaddar, R. Hybridised artificial neural network model with slime mould algorithm: A novel methodology for prediction of urban stochastic water demand. Water 2020, 12, 2692. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R.; Abraham, A. Adaptive opposition slime mould algorithm. Soft Comput. 2021, 25, 14297–14313. [Google Scholar] [CrossRef]
- Pasvanoğlu, S.; Çelik, M. Hydrogeochemical characteristics and conceptual model of Çamlıdere low temperature geothermal prospect, northern Central Anatolia. Geoth 2019, 79, 82–104. [Google Scholar] [CrossRef]
- Aydin, H.; Karakuş, H.; Mutlu, H. Hydrogeochemistry of geothermal waters in eastern Turkey: Geochemical and isotopic constraints on water-rock interaction. J. Volcanol. Geotherm. Res. 2020, 390, 106708. [Google Scholar] [CrossRef]
- Pasvanoğlu, S.; Chandrasekharam, D. Hydrogeochemical and isotopic study of thermal and mineralized waters from the Nevşehir (Kozakli) area, Central Turkey. J. Volcanol. Geotherm. Res. 2011, 202, 241–250. [Google Scholar] [CrossRef]
- Pasvanoğlu, S.; Gültekin, F. Hydrogeochemical study of the Terme and Karakurt thermal and mineralized waters from Kirşehir Area, central Turkey. Environ. Earth Sci. 2012, 66, 169–182. [Google Scholar] [CrossRef]
- Bozdağ, A. Hydrogeochemical and isotopic characteristics of Kavak (Seydişehir-Konya) geothermal field, Turkey. J. Afr. Earth Sci. 2016, 121, 72–83. [Google Scholar] [CrossRef]
- Ulas, M.; Altay, O.; Gurgenc, T.; Özel, C. A new approach for prediction of the wear loss of PTA surface coatings using artificial neural network and basic, kernel-based, and weighted extreme learning machine. Friction 2020, 8, 1102–1116. [Google Scholar] [CrossRef]
- Asteris, P.G.; Maraveas, C.; Chountalas, A.T.; Sophianopoulos, D.S.; Alam, N. Fire resistance prediction of slim-floor asymmetric steel beams using single hidden layer ANN models that employ multiple activation functions. Steel Compos. Struct. 2022, 44, 769–788. [Google Scholar]
- Ren, H.; Ma, Z.; Lin, W.; Wang, S.; Li, W. Optimal design and size of a desiccant cooling system with onsite energy generation and thermal storage using a multilayer perceptron neural network and a genetic algorithm. Energy Convers. Manag. 2019, 180, 598–608. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Altay, E.V. Gerçek Dünya Mühendislik Tasarım Problemlerinin Çözümünde Kullanılan Metasezgisel Optimizasyon Algoritmalarının Performanslarının İncelenmesi. Int. J. Innov. Eng. Appl. 2022, 6, 65–74. [Google Scholar]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Altay, O. Chaotic slime mould optimization algorithm for global optimization. Artif. Intell. Rev. 2022, 55, 3979–4040. [Google Scholar] [CrossRef]
- Mostafa, M.; Rezk, H.; Aly, M.; Ahmed, E.M. A new strategy based on slime mould algorithm to extract the optimal model parameters of solar PV panel. Sustain. Energy Technol. Assess. 2020, 42, 100849. [Google Scholar] [CrossRef]
- Altay, O.; Gurgenc, T.; Ulas, M.; Özel, C. Prediction of wear loss quantities of ferro-alloy coating using different machine learning algorithms. Friction 2020, 8, 107–114. [Google Scholar] [CrossRef]
- Ibrahim, B.; Konduah, J.O.; Ahenkorah, I. Predicting reservoir temperature of geothermal systems in Western Anatolia, Turkey: A focus on predictive performance and explainability of machine learning models. Geoth 2023, 112, 102727. [Google Scholar] [CrossRef]
- Quan, Q.; Hao, Z.; Xifeng, H.; Jingchun, L. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2022, 34, 8501–8510. [Google Scholar] [CrossRef]
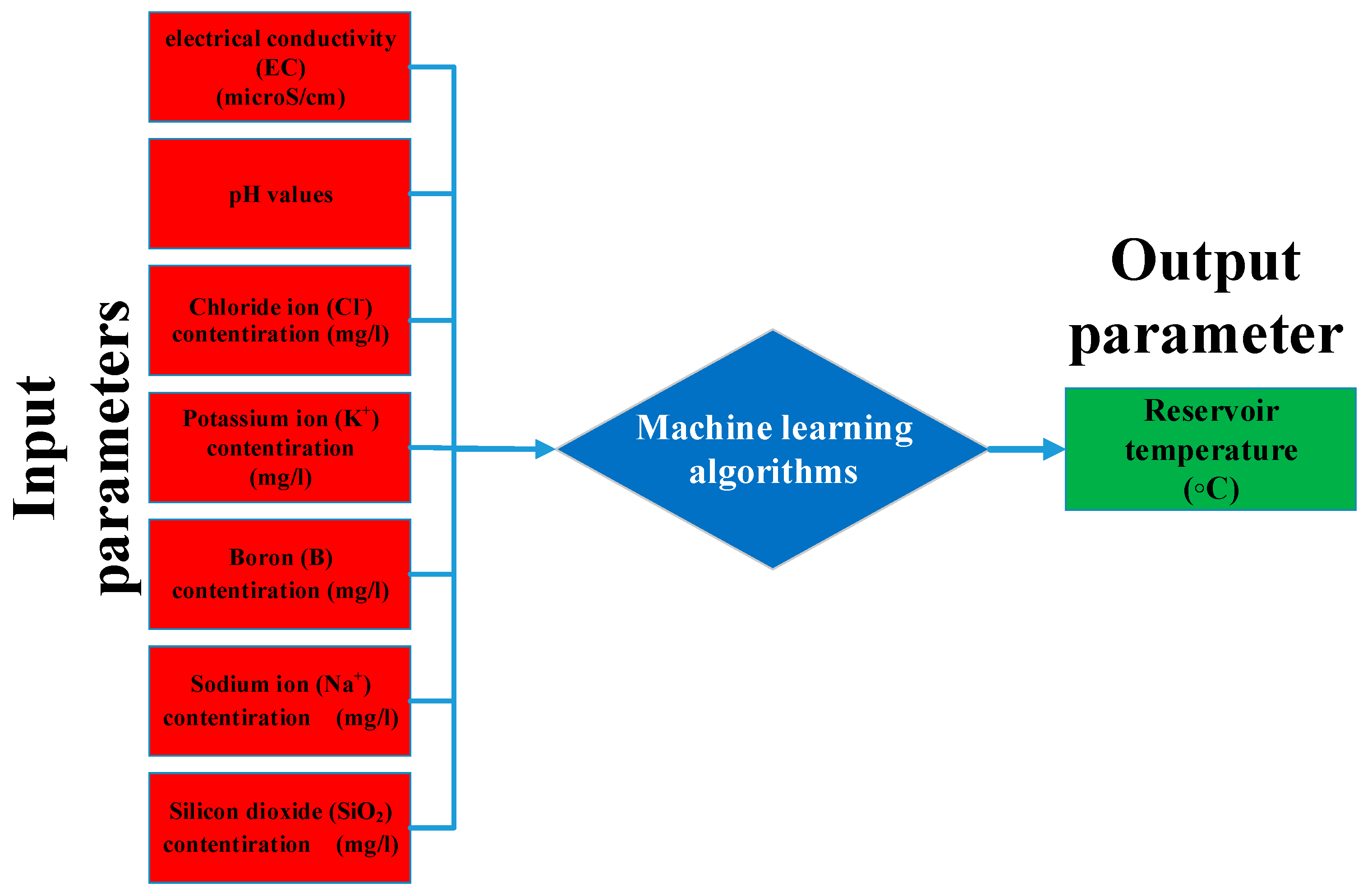


| Parameter | Unit | Value | |
|---|---|---|---|
| Input Data | pH | - | 2.4–9.7 |
| EC | microS/cm | 203–10,434 | |
| K+ | mg/L | 0.7–191 | |
| Na+ | 2.6–2600 | ||
| Boron | 0–38 | ||
| SiO2 | 11–650 | ||
| Cl− | 2.8–2500 | ||
| Output Data | RT | °C | 11–245 |
| NA | NS | NTRS | NTS | HNO | Dim | W | B | NNS |
|---|---|---|---|---|---|---|---|---|
| 7 | 161 | 128 | 33 | 15 | 136 | 120 | 16 | 7-15-1 |
| Algorithm | Parameters | Values |
|---|---|---|
| WOA | Shape of the logarithmic spiral () | Linearly decreased from 2 to 0 1 |
| SMA | 0.03 | |
| AOSMA | 0.03 |
| R2 | R | RMSE | MAE | |
|---|---|---|---|---|
| ANN | 0.7169 | 0.8701 | 36.94 | 29.28 |
| WOA-MLP | 0.7765 | 0.8969 | 32.82 | 25.26 |
| ALO-MLP | 0.8096 | 0.9049 | 30.29 | 25.67 |
| SMA-MLP | 0.7955 | 0.8974 | 31.39 | 26.81 |
| AOSMA-MLP | 0.8514 | 0.9233 | 26.76 | 21.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurgenc, E.; Altay, O.; Altay, E.V. AOSMA-MLP: A Novel Method for Hybrid Metaheuristics Artificial Neural Networks and a New Approach for Prediction of Geothermal Reservoir Temperature. Appl. Sci. 2024, 14, 3534. https://doi.org/10.3390/app14083534
Gurgenc E, Altay O, Altay EV. AOSMA-MLP: A Novel Method for Hybrid Metaheuristics Artificial Neural Networks and a New Approach for Prediction of Geothermal Reservoir Temperature. Applied Sciences. 2024; 14(8):3534. https://doi.org/10.3390/app14083534
Chicago/Turabian StyleGurgenc, Ezgi, Osman Altay, and Elif Varol Altay. 2024. "AOSMA-MLP: A Novel Method for Hybrid Metaheuristics Artificial Neural Networks and a New Approach for Prediction of Geothermal Reservoir Temperature" Applied Sciences 14, no. 8: 3534. https://doi.org/10.3390/app14083534
APA StyleGurgenc, E., Altay, O., & Altay, E. V. (2024). AOSMA-MLP: A Novel Method for Hybrid Metaheuristics Artificial Neural Networks and a New Approach for Prediction of Geothermal Reservoir Temperature. Applied Sciences, 14(8), 3534. https://doi.org/10.3390/app14083534







