Abstract
In crowd simulation, representing crowd behavior in complex dynamic environments is one of the biggest challenges. In this paper, we propose new algorithms to make crowds satisfy a given formation while they are moving towards a destination. For this, we apply the Position Based Dynamics (PBD) framework, but introduce a new formation constraint based on a so-called Short Range Destination (SRD). The SRD is a short-term goal to which an agent must move in formation. In addition, a grid structure that we use for neighbor search is also used for congestion control. Depending on the congestion value, the agents in the cell may break the formation and instead exhibit emergent behaviors such as collision avoidance, but must automatically restore the original formation once the situation is resolved. Smooth movement of agents is also achieved by adding special behaviors when they are moving along the path that the user specifies. From several experiments, we show that the proposed scheme is capable of exhibiting natural aggregate behavior of crowds in real time, even for a highly condensed environment.
1. Introduction
Crowd simulation is the virtual representation of the movement of a large number of objects or people. Various applications are possible, from the media industry, such as movies and games, to the urban industry, such as urban planning or evacuation simulations.
When we simulate crowds, controlling the movement of the crowd as the user wants is the most important requirement. Formation control is one example. Formation-controlled crowds can be used in various situations, such as tactical positioning in team sports training or rehearsals for large performances [1]. However, so far, not much research has been carried out on this problem.
In crowd simulation, the larger the crowd, the more expensive it is to compute the movement of each individual. However, because computing resources are limited, efficient methods must be proposed to represent the behavior of the crowd. For example, to represent the movement of large-scale dense crowds, Narain et al. proposed a control method based on the continuum crowd [2]. An extension of the original method is also proposed to compensate for the shortcomings of lack of representation in dense crowd environments [3]. However, since these methods are designed for dense crowds, they may not be suitable for representing sparse crowds where a highly detailed interaction mechanism is required [4]. Karamouzas et al., on the other hand, proposed the Power-Law model [5], which focused on the interaction between crowd members with a mechanistic and statistical way to control the crowd. This method is well-suited for the aggregate behavior of sparse crowds. However, although the Power-Law model can represent stable crowd behavior, it involves an explicit time integration that requires smaller time steps and, consequently, representing dense crowds would be computationally expensive [4]. In environments with dense agent populations, there has been a technique that has explored methods to assist agents in avoiding collisions with others by defining a personal space around each agent within which they can interact [6]. While this method can produce more realistic crowd representations, it may not be suitable for real-time simulation because of the high computational cost.
In this paper, we apply position-based dynamics (PBD) for crowd simulation [7]. The PBD was originally developed for the simulation of solid objects; furthermore, it has been applied to simulate complicated objects such as fluids and articulated rigid bodies [8]. Unlike classical dynamic simulations, which use the relationship between force and acceleration and update the position through numerical integration, the PBD uses a constraint-based approach to compute the position directly. Because it directly computes the position, the method is considered a highly controllable, easy to implement, and stable physical simulation method [7].
When we apply the PBD to the crowd simulation problem, we have an advantage: natural aggregate group movements at a reasonable computational cost regardless of the size of the crowd, although it may not show sophisticated individual movements [4]. However, even though the PBD is good for aggregate behavior, it still does not consider formation control because it focuses on designing collision-avoidance models. In this research, we address the problem of crowd formation control here.
Our hypothesis is that the PBD is also good for crowd formation control. Because the crowd formation should look like a specific shape, each agent should be placed at a particular position. This can be seen as enforcing position constraints for all agents, which can be naturally integrated within the current PBD framework.
In some prior research for crowd formation control, the start and finish positions of each individual must be set to satisfy the given formation. The crowd formation transformation technique with a least-effort pair assignment method [1,9] is one of the formation control research methods. In this study, the start and end positions of the crowd must be predefined for a particular formation, and the path between them must also be precalculated. Therefore, it is quite difficult to obtain collision-free paths when there are dynamically moving obstacles in the environment.
Basically, the PBD uses constraints to control the movement of objects. For example, a distance constraint between two objects allows them to remain a certain distance apart during the simulation. When we apply it to the crowd formation problem, we can set the obstacle avoidance and formation control constraints simultaneously, allowing flexible control of crowd formation in environments with dynamic obstacles. More specifically, we utilize distance constraints to control the distance between the current positions of agents and the so-called Short Range Destination (SRD). These are new constraints that make agents satisfy a given formation. If we set the short-range destination constraint to zero, then all agents start moving to their final goals to meet the constraint. If we are able to set all destinations to satisfy a formation and let agents move together, then we can make them move to the targets while keeping the formation.
In multi-agent simulations such as crowds, because all agents consider other agents as moving obstacles, it is not easy to make them maintain the formation while moving to their targets. This makes things worse when they encounter other agents with different formation constraints. That is, because there would be many conflicts among agents to make a decision regarding their respect formation, the algorithm must know when to maintain or break the constraints automatically. In our algorithms, we set the hard constraints on the interpenetration and collision avoidance between agents and making agents arrive at the targets, and we set the soft constraints on formation. The soft constraints can be broken depending on the situation, but must be recovered as soon as the situations are resolved. These algorithms break the formation when they are in an inevitable situation, but restore the formation when they resolve the inevitable situations.
The proposed method has the following contributions:
- We propose a new algorithm that introduces a scheme called Short Range Destination (SRD) to help crowds move to a destination while satisfying a given shape;
- We propose a method of leveling constraints that allows the agent to determine for itself which constraints it should respond to in various situations;
- Our method grids the field in two dimensions and embeds local information, which is combined with the respective leveled constraints to influence the decisions of each agent.
A sample result of the proposed algorithm is presented in Figure 1. The red and blue spheres in the figure represent the crowd in different groups while maintaining a particular formation constraint. Note that the blue line is the path along which the blue crowd is moving, whereas the red line is the path along which the red crowds are moving. Both paths are given by scribble. The reason why the crowd moves along the path drawn by the user is to cause intentional collisions between different groups. Because the two paths are sufficiently close, many collisions happen between two groups, which breaks the formation constraint in the middle. However, as soon as they exit the jamming situation, they automatically recover the formation constraint and then eventually arrive at the target positions. The yellow arrow in Figure 1 is the direction of movement of the blue crowd, which forms a bird shape.

Figure 1.
Overview of controlling crowd formation using SRD. (a) There are two groups of agents, a red group and a blue group. Both groups are supposed to maintain a bird formation and are about to collide while moving to the opposite side. (b) The two groups are crossing and passing each other, losing their formation to avoid collisions. (c) After the two groups cross, the agents in each group restore the original formation automatically. (d) The blue group is moving to their destination with the formation restored.
The remainder of this work is structured as follows. Section 2 introduces related work, where we summarize all prior works and compare them with the proposed method. Section 3 describes the crowd simulations with formation constraints using this PBD technique in detail. Section 4 presents a set of experiments and the results. Finally, Section 5 concludes with a discussion and future research directions.
2. Related Work
2.1. Crowd Simulation
The dynamic formation control of the crowds based on PBD is influenced by various existing crowd simulation techniques. In this chapter, we review important prior research related to our work.
Historically, crowd simulation has been focused on various aspects of collective behavior [10]. A typical technique of these is to use rules based on physical laws [11].
The Social Force Model was a probabilistic model to predict pedestrian behavior proposed by Helbing and Molnar [12]. The idea behind the model is that pedestrian movements appear to be subject to social forces. In this model, pedestrians are influenced by several forces to reach their destination, including the force to move in the desired direction and the repulsive force when considering static obstacles.
Karamouzas et al. proposed the Power-Law technique to control pedestrian interactions. It controlled crowds by measuring the energy of interaction between pedestrians [5]. It also described and reproduced crowd interactions from different situations, speeds, and densities of the crowd. When applied to the movement of a large number of pedestrians, it can predict not only the physical distance between pedestrians but also potential future collisions.
Reynolds proposed a flocking technique in which flocks of animals, such as birds, schools of fish, etc., behave naturally based on local information about their dynamic environment [13]. In this algorithm, the flocks of animals behave in three states: separation, alignment, and aggregation. Reynolds extended this work and proposed the Steering Behavior technique [14]. Steering Behavior expands the three states by adding additional states, such as tracking specific neighbors and collision avoidance to avoid obstacles. In Steering Behavior, the crowd decides on an action through three stages: action selection, steering, and movement. This technique allows the crowd to move back and forth between different states, creating natural crowd behavior.
2.2. Dynamical Systems and PBD
One of the traditional techniques for controlling crowds is the application of the dynamical system. Basically, the dynamical system controls the movement of crowds by first setting the physical properties of individuals and then applying the appropriate forces and integrating their accelerations and velocities [7]. However, finding the force to move a user to a desired position is recognized as a difficult problem in dynamical systems.
Müller et al. introduced the PBD as an alternative to the dynamical system [7]. Unlike traditional dynamics models, the PBD does not use the relationship between force and acceleration to derive the velocity of an object, but instead focuses on an instantaneous position change, which has the advantage of being fast and controllable. It also avoids the overshooting problem that occurs during explicit time integration in conventional dynamical models, and it can completely solve the problem of penetrations between objects. These advantages further improve the stability of the simulation. In light of these advantages, T. Weiss et al. introduced a crowd simulation in real time using PBD [4]. The crowd simulation using PBD is redesigned to use the Power-Law technique [5] that expresses the movement of the crowd based on the existing explicit method as a constraint in the form of an implicit method. This redesigned constraint is defined as the long-range collision constraint. This algorithm works in an iterative fashion until agents arrive at their final destinations while avoiding collisions and penetrations. However, such crowd simulations using PBD only focus on crowd collision avoidance, not on controlling crowds that move in formation. In this paper, we extend the current method so that we can control the formation of a crowd while utilizing the advantages of PBD. Figure 2 compares the two methods.

Figure 2.
Comparison of processes in dynamical systems and PBD. The * symbol means multiplication.
2.3. Crowd Formation Control Methods
One of the challenges in crowd simulation is how to generate crowd behavior in specific situations, for example, simulating people evacuating through a narrow exit, standing in line, etc., in a virtual space. Similarly, making crowds move in groups or formations can be considered another specific situation.
Z. Ren et al. proposed a group modeling method for crowd formation with different sizes [15]. Group modeling was a unified solution to control the movement of a crowd in which the size of each group, the relationships among its members, and the goals of each group were considered. This solution introduced the idea of the velocity connection, which allowed the crowd to move together while avoiding collisions and achieving goals. This research is similar to our paper in that it uses the property of a group to represent crowd behavior in a specific situation, but there is a difference where we focus on representing crowd behavior under the constraint of formation.
Xu et al. proposed an optimized crowd formation transformation technique [1]. This work aimed to transform a crowd in a formation into another user-specified form of the formation. In this research, the focus was on transforming the crowd into an optimized movement. They used the Kuhn–Munkres algorithm [9] to determine the most efficient destination for each agent, where the destination was within another formation that the crowd would form. And they used a social force model [12] and mutual information to avoid collisions between moving agents and minimized confusion. Through this method, the crowd could transform the formation based on optimized directional decisions. However, when an agent encountered an obstacle while transforming, it did not consider collision avoidance, which meant that the crowd control method was somewhat limited in its ability to adapt to unpredictable obstacle crossing locations (such as dynamic obstacles) and to transform in real time.
There was another study related to multi-agent formation. This method, proposed by T. Weiss, combined PBD and the shape-matching constraint [16], and was able to move multiple agents in a formation while maintaining a given shape [17]. Agents in formation could be dynamically reconfigured. Agents could be assigned to closer positions based on a linear sum assignment approach [18]. As a result, this method allowed users to simulate crowds with a variety of group numbers and formation shapes in real time, but this method had the limitation that all agents had only a linear movement path and the same speed.
To overcome the shortcomings in these studies with respect to crowd formation, we propose a dynamic crowd formation control method based on PBD techniques that allows a formed crowd to move toward a goal while prioritizing collision avoidance when encountering dynamic obstacles, breaking up the crowd formation freely, but recovering its own formation when conditions are suitable.
3. Proposed Algorithms
3.1. Overview
The original PBD algorithm was first applied to crowd simulation by T. Weiss et al. [4]. Compared to other studies, this method has shown that it can avoid dynamic obstacles reliably and quickly, even in dense situations. However, because this crowd simulation focused on natural representations of agent collision avoidance, it did not consider the formation control problem. In this paper, we propose a new method that can handle collision avoidance and formation control. Figure 3 is an overview of our method, which expands the original crowd simulation using the PBD method. In this process, Computing the degree of congestion and Determining behavior phases were added and Determining the velocity phase was modified for this purpose. Each step in Figure 3 is described below.
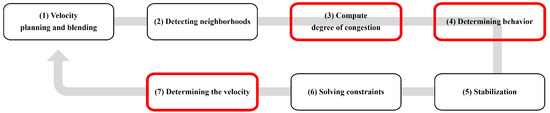
Figure 3.
A flowchart of the crowd formation control method expanded from the crowd simulation using PBD.
- 1.
- Velocity planning and blending: Given a planned velocity that leads the agent to the final destination, each agent blends the current velocity with the planned velocity together. Then, the future position is predicted from the blended velocity;
- 2.
- Detecting neighborhoods: This step updates the local information. It includes the presence or absence of agents in neighboring spaces, the number of neighboring agents, and the number of agents belonging to other groups. Each agent can detect neighborhoods using this local information;
- 3.
- Computing the degree of congestion: This step uses the local information explored in the previous step. The degree of congestion calculated with the local information is then mapped onto the grid space;
- 4.
- Determining behavior: In this step, the soft constraints, such as the formation constraint, are enforced. After that, the agent determines whether to follow the soft constraints or not;
- 5.
- Stabilization: Since agents are rigid bodies, interpenetration is not allowed. In this step, hard constraints are enforced so that neighboring agents are repositioned to prevent them from being penetrated by each other;
- 6.
- Solving constraints: This is a step to solve the constraints. Constraints are set to control the distance between neighboring agents and avoid obstacles in the previous steps. At this stage, it predicts the future position after solving the constraints;
- 7.
- Determining the velocity: The velocity is derived from the difference between the predicted future position and the current position in the constraint-solving step. The speed limit of the agent is set in advance to increase stability. Furthermore, this method applies the steering behavior technique to prevent sudden changes in the velocity of agents when moving along the path [14]. Through these processes, the agent is moved by the final velocity.
Algorithm 1 is a pseudocode representation of the flow chart above.
| Algorithm 1 Crowd formation control using SRD |
|
In Algorithm 1, each group of agents has a position , which is set by averaging all the positions of the agent in the group. From lines 2 to 3, the group position is planned and an SRD is updated for each group. An agent , in a group has a position , a velocity , a mass , and an SRD . And is the predicted position of the agent of the path planner, where is the time unit. From lines 4 to 7 of the code, the algorithm calculates the external forces on the agent and plans its velocity. Lines 8 and 9 focus on updating the local information; a grid space has a degree of congestion . From lines 10 to 13 of the code, we set the degree of congestion influenced by the agent’s position. In lines 14 to 18, soft and hard constraints that we have set are enforced and solved. Here, N is the number of iterations to solve the constraints. The larger the value of N, the more expensive it is to compute, but the higher its accuracy. Finally, in lines 19 through 23, the algorithm moves agents that satisfy the constraints and the steering behavior.
3.2. Setup for User-Specific Environment
3.2.1. Crowds, Groups, and Agents
In this article, a group is defined as a subset of the entire crowd. We consider a group as a set of agents who share the same purposes of movement. One of the purposes is to form a formation, and the other one is to move to a final destination together. That is, the final goal of a group is to move to a certain destination while maintaining formation.
Mathematically, suppose that the entire crowd G has a total of n agents. We divide G into m groups. In this case, the relationships between the crowd, agents, and groups are represented in Equation (1). Through the establishment of these relationships, we can have various groups and formations.
where is an agent and G is the complete set of agents. is a subset of G, which we use in the sense of a group. Figure 4 is a graphical representation of this.

Figure 4.
A group that is a subset of the entire crowd.
3.2.2. Crowd Formation Constraint: Forced Position Constraints for Agents
The crowd formation constraint means that agents should form a certain shape as a group. In other words, the meaning of satisfying the formation constraint is that agents within a group place a specific position for formation. These shapes can be a circle, a square, or a certain closed polygon. While there are many ways to sample positions for formation, we use a 3D mesh projection method where the vertices of a mesh are projected onto the 2D plane on the ground, and those projected points become targets that agents must move to. This method has the advantage because it allows the user to easily configure various formations. Figure 5 shows the formation of a crowd in this way.
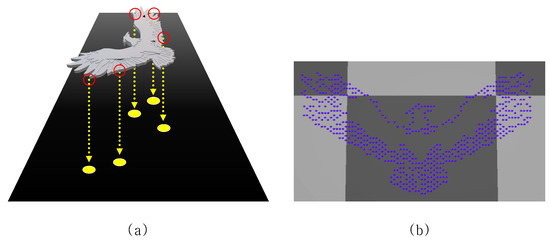
Figure 5.
A projection of the vertices of a 3D bird insignia model onto a 2D plane [19]. Red circles, yellow arrows, and yellow dots are represented to explain that the vertices of the model being projected onto a 2D plane. (a) A 3D model of bird insignia for crowd formation. (b) An example of a crowd formation formed by using the vertex positions of the model.
After the initial positions of all agents in the group are set, the position of the group is set. The group position is set by averaging all the positions of the agents inside. Equation (2) shows the calculation of the position of the group :
where is the a-th group, is the agent belonging to , is the current position of , is the group position of , and A is the number of agents belonging to .
3.2.3. User-Drawn Group Path
In a crowd simulation, the crowd does not stand still; it moves to the final destination. In this paper, we assume that the crowds are moving along a path that the user draws on the floor directly. The user-drawn path consists of a set of 2D points, and those points are connected while keeping the minimum distance between them. Note that we set a single path for each group instead of assigning a path to each individual agent. The 2D points of the path become the waypoints that the crowd follows. In Figure 6, a group is facing the waypoint at a particular time, which is the closest point to the group on the path. If the group approaches sufficiently closely, then will be the current target instead. This process is iterated until the crowd reaches the final destination. To move from P to W, which is the current target of the group, we have to calculate the group velocity . Equation (3) is the formula that calculates the velocity and the update of the group positions:
where is the direction vector from the current position of the group P to the current target W, is the group velocity, and is the new position of the group. is the preferred group speed, which is initially set as a constant speed and uses a weight value to adjust the velocity of a group. The computed group velocity affects the short-range destinations of each agent in the group collectively, and Equation (4) is a representation of this:
where is an SRD of the i-th agent in the group and is the new position of the SRD that moves from by the amount of translation of the position of the group.
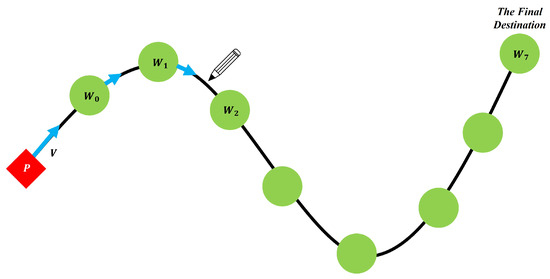
Figure 6.
A group moves to a final destination along the path drawn by the user.
3.3. Proposed Algorithms
3.3.1. Short Range Destination (SRD)
PBD was first introduced by Müller and is a constraint-based physics simulation technique [7]. The principle of this technique is to modify the position of an object by solving the constraints. This chapter briefly describes the basic principles of PBD.
The constraint solver finds the solution of the constraint equation. Equation (5) is an equation that expresses a distance constraint that keeps two objects a certain distance apart:
where is the scalar constraint function and are the positions of the two objects involved in the constraint of distance , in which d is the size of the distance to be maintained between the two points.
Solving the distance constraint forces the two objects to move the specific positions, and , appropriately to maintain a distance equal to d. Figure 7 is a graphical representation of Equation (5).

Figure 7.
Distance constraints between two objects.
In Figure 7, p is the position of an object in the distance constraint, and is a vector that p must move to satisfy the constraint.
To find , we need to first calculate the gradients of the constraint function. The gradient can be obtained by applying the derivative at a point in a scalar field and represents the direction of the maximum change at the point. Finally, Equations (6) and (7) show the generalized solution for finding :
where is a scaling factor that controls the magnitude of the direction in which the object should move. For more details on the derivation of this equation, see [7].
In this paper, we propose the Short Range Destination (SRD) to control crowd formation. An SRD is a single short-term goal position that is given to an agent to maintain the given formation, and the priority action of an agent is to reach this destination. After the initial positions of the agents are completely set, each SRD is generated in the same position of each agent at the beginning. Once the destinations are generated for all agents, the formation constraints, which are extensions of the distance constraints between the current position of the agent and the SRD, are added to the simulation loop. Equation (8) illustrates the formation constraint. Note that, since formation constraints are one of the soft constraints, they can be ignored during the simulation to avoid emergent situations such as collision with other agents. That is, although the SRD is the ideal position for an agent to satisfy the formation, the agent may not go there directly if the situation does not allow it. However, agents are able to return to the formation using the positions of the SRDs that are kept in the group once they exit the emergent situation.
where is for the formation constraint, is the current position of the i-th agent, is the position of the SRD that needs to chase, and d is the distance that and should maintain. The distance between the agent and the destination to be chased can be adjusted according to d. In this paper, we set d to 0, so that the agent always moves to the exact position of the SRD. If the agent is far away from the SRD, then the agent will take the action of chasing to the destination to reduce the distance. The formation constraint is maintained throughout the simulation in this way.
In the original distance constraint of the PBD, if two moving objects have a distance constraint, both objects move to satisfy the distance constraint. However, in our formation constraint, which is set between an agent and the SRD, only the agent is allowed to move. Figure 8 compares the distance constraint with the formation constraint.

Figure 8.
Comparison of traditional distance constraint and formation constraint: (a) traditional distance constraint, (b) formation constraint.
Figure 8a shows when two objects are moving together to satisfy a distance constraint. Figure 8b shows when an agent moves to reach an SRD to satisfy a formation constraint. Here, the SRD and the position of the agent are expressed as and , respectively. In Figure 8b, the is not changed by constraint for formation. That is, only the agent moves to satisfy the constraints when the distance between and has increased to more than d. This ensures that, even if an agent leaves the formation, it can still regain the formation by returning to the original SRD.
Figure 9 illustrates the movement of two blue agents that chase their SRDs to form a formation. Note that the blue agents are in the same group as the white ones.
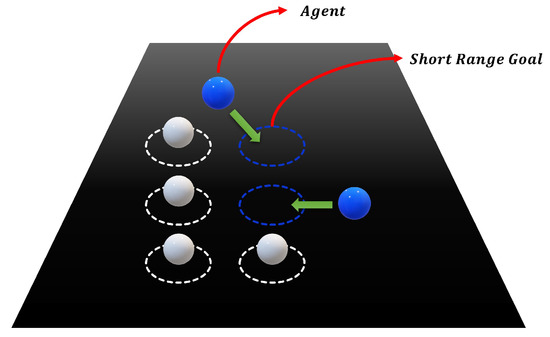
Figure 9.
Movement of agents to reach their SRD. Agents away from their SRD are colored blue.
Additionally, the positions of the SRDs, which relate to the formation constraint, are based on the group position. When the group position is moving, the SRDs are moving as well. The amount of translation of the SRDs is decided by the amount of movement in group positions. Equation (4) shows the changes in the positions of the SRDs, and Figure 10 is a graphical representation of this chain rule. Note that the frame time goes from 0 to 1 in Figure 10.

Figure 10.
The movement of SRDs as a result of the group’s movement and each agent tracking each target. The SRDs move as much as the group has moved.
In addition to these schemes, to enhance the realism of the simulation, it was necessary to consider agent-specific characteristics. To represent the different behaviors of the agents, each agent can have the following different parameters: speed, agility, and reaction time. Agent-specific parameters can be easily seen when they are not under a formation constraint because they can go to their targets independently. However, when they are under formation constraint, all agents must consider their neighboring agents to keep the formation, which requires agents to adjust their given parameters. We define agility as a factor that determines how quickly an agent can perform avoidance behavior. The higher the value of agility, the faster it can avoid obstacles. Finally, the reaction time is defined as how quickly the agent reacts to dynamic obstacles. A high reaction time value means that the agent sees an obstacle in the distance and reacts quickly to leave the formation, or quickly determines that there is no obstacle and returns to the formation. Figure 11 shows that the agent slowly loses formation as they move at different speeds in the absence of formation constraints. More details can be found in the result video (result video is Video S1 in the Supplementary Materials).
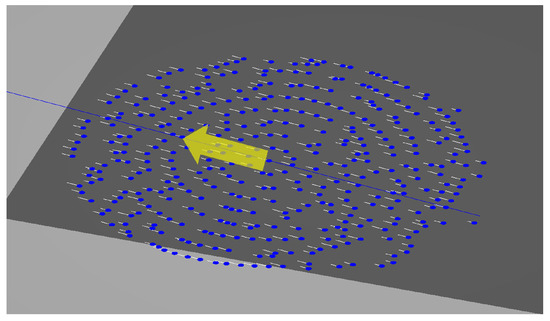
Figure 11.
The movement of agents without formation constraints. The white lines attached to each agent are not visible in the actual simulation, but are drawn for illustration purposes. These lines represent the speed magnitude of the agent, with longer lines being faster and shorter lines being slower.
3.3.2. Degree of Congestion
Many techniques have been proposed to optimize crowd simulations. Among them, discretizing the space is one of the effective methods to speed up neighbor search [20]. For example, a two-dimensional space can be partitioned into a grid structure [21], called the bin/spatial grid, and partitioned cells are indexed and used to find the neighbor. In our approach, we apply this technique for searching the neighbors, and also embed extra information in each cell for congestion control. Each cell maintains the list of agents when they are in the cell. This list is dynamically updated as the agents pass through the cell. When we need a list of neighbors for a particular agent, we can restrict the search area to the cell of the agent, which improves overall performance.
In this paper, we also use the grid structure to control congestion. Since each cell has a list of agents inside, we can easily know how many of them belong to other groups. Mathematically, let us denote the congestion value as . Then, the value of the cell m can be calculated using Equation (9):
where is a grid cell, is the congestion of that grid space, is the identifier of a group, and and are constants.
takes the value if there are no agents in the cell , takes if there are more than two different groups in the cell, and takes if there is only one group of agents. Practically, we set to −2 and to −1. For example, in Figure 12, is because different groups of agents share space . The space and is empty, so and are .

Figure 12.
Neighborhood detection of agents in a grid space. Space 6 is shared by different agents and they perceive each other as obstacles.
Agents would think that other agents belonging to different groups as moving obstacles. They must avoid these obstacles, if they are aware of the obstacles, using the congestion value in the neighbor detection step. However, because the agents are connected by the formation constraint, it is difficult for them to make a decision to break the formation constraint. Nevertheless, the formation constraint is the soft constraint that can be broken temporally for an emergency situation. In our work, we let the agent determine whether to break the formation constraint or not by checking the congestion value. If an agent decides to break the soft constraint, it stops to maintain the formation and then performs collision avoidance instead. When the agent finds that there are no dynamic obstacles in the neighboring space, as shown in in Figure 12, the formation constraint is recovered, and they are trying to move to their SRDs. Note that this decision is quite local because it only works for agents in a particular cell. That is, the behavioral changes of the agents are limited to the cell in which the agents are located. This makes the aggregate behavior of whole crowds natural, even if agents are in a highly congested area. This is one of the advantages over other algorithms.
In terms of dealing with agents in the same group, when an agent meets other agents in the same group, it will not take an action to avoid them if they are under a formation constraint. Even if they are not under the formation constraint, they would not avoid each other but perform the cohesive movement, which is the natural motion for real crowds. This cohesive movement results in collective avoidance between groups.
3.3.3. Steering Behavior for Control Inertia
When the crowd suddenly has to turn or stop, the inertial force of the crowd makes it difficult for them to do it smoothly. To overcome this problem, we add the seek behavior [14] to the velocity of the final agents so that the crowd can move smoothly along the path or stop at the particular position. Basically, steering behaviors apply the steering forces to adjust the velocity of the moving agent. Among the various types of steering behavior proposed in [14], the seek behavior first detects the target and then applies a steering force so that the agent does not suddenly change its velocity when the distance to the target becomes short. Equation (10) explains the seek behavior applied to our algorithm. By adding the steering behavior, , to the agent’s velocity, we can prevent rapid changes in velocity.
where is the current position of the agent, is the SRD which is the position of the target, is the current velocity of the agent, is the desired velocity to the target, and is a constant, which is the maximum speed for . Figure 13 shows the seek behavior.

Figure 13.
An agent changes direction of travel smoothly through steering force.
4. Experiments
To verify the proposed algorithms, we performed a series of experiments. The system we built was based on the following hardware and software specifications:
- CPU: Intel i7-8700 with 32 G main memory;
- GPU: NVIDIA RTX3080;
- IDE: Visual Studio 2019;
- Graphic Library: OpenGL 4.3.
Before starting the experiment, we examined frames per second (FPS) as a method of measuring the number of agents in the crowd to check whether our method was capable of simulating crowds in real time, as shown in Table 1 (please see the accompanying Video S2 in Supplementary Materials for better understanding).

Table 1.
Minimum and average FPS values based on crowd size.
We performed the experiment in two stages. The first stage was to verify that our algorithm works correctly to control the crowd formation in a dynamic environment. The second stage was the comparison between our method and two other known methods to evaluate ours.
4.1. Formation Control on a Dynamic Environment
First, we showed that our algorithms are effective in a situation where the formation needs to be controlled in a dynamic environment. To prove that our algorithms are independent of the shape of the formation and the number of agents, we set up two scenarios. In the first scenario, we used a 3D mesh model to form a crowd formation. We divided the whole crowd into two groups and let each group have the same formation. The 3D mesh that we used was a bird-shaped insignia model. The number of agents in each group was 585. Figure 14a,b show the 3D mesh model and the initial arrangement of the crowds in the model.
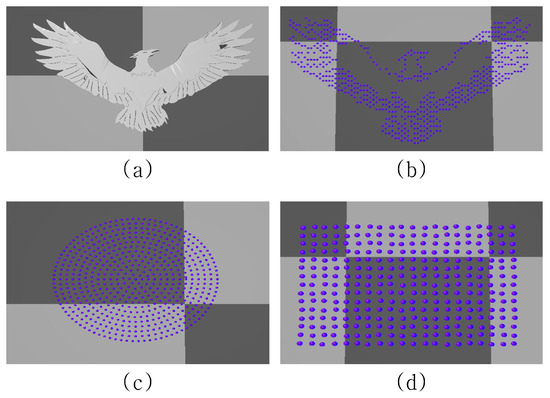
Figure 14.
Crowd formation in different ways (a) A 3D mesh for formation constraint; (b) Initial setup of crowds based on a 3D mesh; (c) Circle formation; (d) Rectangle formation.
In the second scenario, we used an analytical method to set up the formation. Similar to the first case, we created two groups and let each group have 375 agents. However, in the second case, one group had a circle formation, while the other group had a rectangle formation. Figure 14c,d show the initial set-up of the crowds based on the analytical method. To make it more interesting, we made two groups meet in the middle of the environment for both cases when they move. To do this, we drew paths on the environment so that two groups mixed in the middle. In the existing study [17], it was difficult to observe the crowd colliding from various sides because the crowd could only show linear movement. However, our method can show various situations more. Figure 15 shows a case where we used a 3D mesh for the formation and drawn paths for the groups. From this experiment, we saw that the crowds changed direction along the tangent of the path.

Figure 15.
Two groups with formation constraints are moving along the path set by user. Yellow arrows indicate the direction of travel for each group.
Figure 16 shows the simulation screenshots where two groups with different formation constraints were met in the middle. As we can see, the formations were broken to avoid collisions, but immediately recovered when the emergency situation was resolved. A key point in this simulation was that breaking of the formation constraints was limited to particular cells. Therefore, most of the agents kept the formations while they were moving. This feature creates a natural movement of the crowds. Figure 17 shows another simulation of different formations and different numbers of agents. From these experiments, we knew that the proposed algorithm worked in a highly dynamic environment. The formation of the crowd and its breakdown were convincing (please see the accompanying Video S3 in the Supplementary Materials for a better understanding).

Figure 16.
The simulations are shown in order from (a–f), two groups with a different formation constraints are crossing each other. There is a breakdown of the formation on the both groups in the middle, but they regain the formation automatically and then reach their respective final destinations.
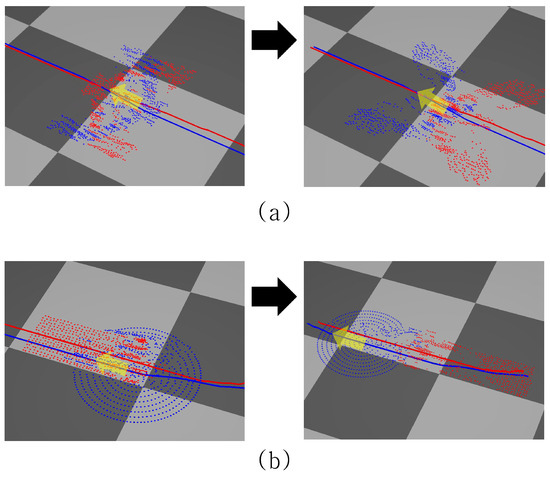
Figure 17.
Experiments in which various shapes of the crowd formations are crossed. (a) Two groups with the same shape formations. (b) Two groups with different shapes of formations from each other.
4.2. Comparison with Other Methods
Second, we compared the proposed method with two prior methods. The first prior method was the crowd control technique based on PBD proposed by T. Weiss et al. [4], and the second was the method that transforms crowd formation focusing on a least-effort pair assignment proposed by M. Xu et al. [1].
Figure 18 shows an observation of crowd behavior after obstacle avoidance. Figure 18a shows the result of using the method proposed in [4] where the crowd avoided obstacles and then simply moved to destinations without hesitation. Since there was no formation constraint in this method, the crowds did not consider any other target except their final destinations. On the other hand, Figure 18b shows the result of applying the proposed method, and we could see that the crowd, after avoiding the obstacle, restored the original formation, a bird formation, while still moving toward the destination.
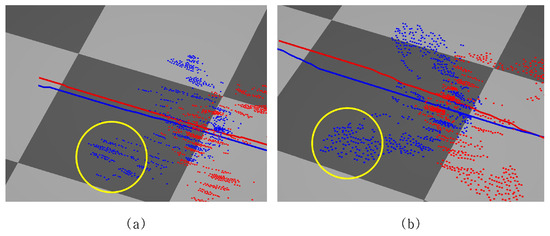
Figure 18.
Comparisonof crowd behaviour after obstacle avoidance behaviour. (a) The algorithm from [4] applied, with no recovery after formation breakdown. (b) Proposed algorithm applied, with recovery after formation breakdown.
To check the overall performance, we calculated the FPS (Frames Per Second) as we increased the number of agents. Since the proposed method was an extension of an existing method, it required additional computations compared to existing methods, and it was expected that this would result in performance degradation. Figure 19 shows a graph comparing the FPS between the proposed method and the original crowd method based on PBD as we increased the number of agents to 1500. The chart shows that there is no significant performance drop.

Figure 19.
Performance comparison between the original PBD-based crowds and the proposed method.
We also compared our method with other formation control methods. M. Xu et al. proposed an algorithm that transforms crowd formation with least-effort pair assignment [1]. Figure 20a shows the behavior of two groups of crowds crossing each other to reach their destination based on [1]. One of the limitations of this algorithm is that it could not handle an environment with dynamic obstacles, as shown in Figure 20a [1]. Figure 20a shows what happens when the crowd encounters a dynamic obstacle such as another group during the transformation of the formation. Instead of avoiding it, the crowd collides with it and slides past it.

Figure 20.
A situation where two groups of agents, which regard each other as obstacles, encounter each other in proximity. (a) Screenshot of observation from a simulation of the method proposed by M. Xu et al. [22]. (b) Observation of our method. The black and white lines are the paths of travel for the blue and red groups, respectively.
On the other hand, Figure 20b shows the result of the proposed method for the same scenario. The proposed method shows that the agents detected obstacles and then escaped from the given formation for the obstacle avoidance behavior. This demonstrates that the proposed method can handle the dynamic environment more naturally.
5. Conclusions
Crowd simulation has been used in a variety of fields that require the movement of large numbers of people, including games, films, and urban industries. In particular, war movies, sports, and other fields that require the strategic movement of crowds require the crowd to move in a particular formation.
In this paper, we propose a new method for controlling crowds to satisfy a given formation while avoiding collisions by introducing a new concept called Short Range Destinations (SRD) based on the PBD framework. SRD is a short-term goal toward which an agent moves in order to satisfy the formation. This goal works as a constraint and makes each agent move to maintain formation. We also let a group be a subset of the entire crowd. Each group can also have its own properties, such as position and velocity. These properties are used to make agents move along the path. To make the path, we applied an easy-to-use scribble interface that allowed the user to specify the path on the environment directly. During the simulation, the SRDs of the agents in a group were translated by the amount of displacement of the group position, and then the agents moved to the SRDs accordingly. In addition, the crowd performed a neighbor search during the simulation to find out where the dynamic obstacles were in the near space, and, based on the presence of obstacles, it decided whether or not to abandon the formation constraint and then avoid urgent collisions. Smooth movement of the crowd is also achieved by adding a special behavior.
In contrast to traditional crowd formation methods, which did not show natural avoidance behavior in the presence of dynamic obstacles, the proposed method showed that crowds moved toward their destinations while breaking and restoring the formation constraint naturally.
However, our method has limitations. Our current method depends only on the CPU power. Therefore, the number of agents running at a real-time rate is limited. In the future, we would like to redesign our current method in a parallel computing framework such as CUDA or Compute Shader. We believe that our algorithms can run faster, more accurately, and handle a larger number of crowds. The second limitation is that the proposed algorithm does not consider static obstacles, such as walls, in the environment. Therefore, collisions between crowds and static obstacles are not prevented. We believe in the future that we can integrate well-known path-planning algorithms with the proposed method to obtain a collision-free path with obstacles. The third limitation is that the formation is not allowed to change during simulation. In the future, we would like to extend the current algorithms to have dynamically changing formation constraints. If it is possible to change the formation during the simulation, then it will be possible to better express the appearance of a flexible, strategic, and varied crowd. The fourth limitation of our simulation is that it does not support the dynamic environment. We assume that the environment has a flat surface. In future work, we would like to expand our work to explore scenarios with highly dynamic terrain or varying weather conditions, which show more complex and dynamic behavior for agents for given formation constraints. In order to do this, we would like to expand our 2D grid space to a 3D grid space and embed more information into each cell to support 3D behaviors of agents. We believe that this would enhance the adaptability and robustness of crowd simulation systems.
Supplementary Materials
Video S1: Position-based Formation Control Scheme for Crowd Simulation using Short Range Distance (SRD) (https://youtu.be/io3nZNFIZKo?si=zSzwK6vlVzw795Qs, accessed on 12 January 2024); Video S2: Position-based Formation Control Scheme—Real-time Test. (https://youtu.be/HpPRs7drIM8?si=mScixTIGVgaoaAu9, accessed on 5 April 2024). Video S3: Position-based Formation Control Scheme—Agents Parameters Experiment. (https://youtu.be/QPQdxc4mhww?si=xUfHkxcl00rKjslW, accessed on 5 April 2024).
Author Contributions
Conceptualization and methodology, J.H.S. and M.K.S.; software, J.H.S.; validation, J.H.S. and M.K.S.; formal analysis, J.H.S. and M.K.S.; investigation, J.H.S.; resources, J.H.S. and M.K.S.; data curation, J.H.S.; writing—original draft preparation, J.H.S. and M.K.S.; writing—review and editing, J.H.S. and M.K.S.; visualization, J.H.S.; supervision, M.K.S.; project administration, M.K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2021R1A2C1012316).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article and Supplementary Materials.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, M.; Wu, Y.; Ye, Y.; Farkas, I.; Jiang, H.; Deng, Z. Collective crowd formation transform with mutual information–based runtime feedback. Comput. Graph. Forum 2015, 34, 60–73. [Google Scholar] [CrossRef]
- Treuille, A.; Cooper, S.; Popović, Z. Continuum crowds. ACM Trans. Graph. (TOG) 2006, 25, 1160–1168. [Google Scholar] [CrossRef]
- Narain, R.; Golas, A.; Curtis, S.; Lin, M.C. Aggregate dynamics for dense crowd simulation. In Proceedings of the ACM SIGGRAPH Asia 2009 Papers, Yokohama, Japan, 16–19 December 2009; pp. 1–8. [Google Scholar]
- Weiss, T.; Litteneker, A.; Jiang, C.; Terzopoulos, D. Position-based multi-agent dynamics for real-time crowd simulation. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 28–30 July 2017; pp. 1–2. [Google Scholar]
- Karamouzas, I.; Skinner, B.; Guy, S.J. Universal power law governing pedestrian interactions. Phys. Rev. Lett. 2014, 113, 238701. [Google Scholar] [CrossRef] [PubMed]
- Hesham, O.; Wainer, G. Advanced models for centroidal particle dynamics: Short-range collision avoidance in dense crowds. Simulation 2021, 97, 529–543. [Google Scholar] [CrossRef] [PubMed]
- Müller, M.; Heidelberger, B.; Hennix, M.; Ratcliff, J. Position based dynamics. J. Vis. Commun. Image Represent. 2007, 18, 109–118. [Google Scholar] [CrossRef]
- Bender, J.; Müller, M.; Macklin, M. Position-Based Simulation Methods in Computer Graphics. In Proceedings of the Eurographics (Tutorials), Zurich, Switzerland, 4–8 May 2015; p. 8. [Google Scholar]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Thalmann, D.; Musse, S.R. Crowd Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hosoi, R.; Ishijima, S.; Kojima, A. Dynamical Model of a Pedestrian in a Crowd. In Proceedings of the 5th IEEE International Workshop on Robot and Human Communication, RO-MAN’96 TSUKUBA, Tsukuba, Japan, 11–14 November 1996; pp. 44–49. [Google Scholar]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- Reynolds, C.W. Steering behaviors for autonomous characters. In Proceedings of the Game Developers Conference, Citeseer, San Jose, CA, USA, 17–19 March 1999; Volume 1999, pp. 763–782. [Google Scholar]
- Ren, Z.; Charalambous, P.; Bruneau, J.; Peng, Q.; Pettré, J. Group Modeling: A Unified Velocity-Based Approach. Comput. Graph. Forum 2017, 36, 45–56. [Google Scholar] [CrossRef]
- Müller, M.; Heidelberger, B.; Teschner, M.; Gross, M. Meshless deformations based on shape matching. ACM Trans. Graph. (TOG) 2005, 24, 471–478. [Google Scholar] [CrossRef]
- Weiss, T. Fast Position-based Multi-Agent Group Dynamics. Proc. ACM Comput. Graph. Interact. Tech. 2023, 6, 1–15. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. Fundamental algorithms for scientific computing in python and SciPy 1.0 contributors. SciPy 1.0. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Ridwan. Bird Pendant. 2016. Available online: https://www.cgtrader.com/free-3d-print-models/jewelry/pendants/bird-pendant-a5a9da70-4192-433f-b596-e12ae7982ba6 (accessed on 2 September 2016).
- Green, S. Particle simulation using cuda. NVIDIA Whitepaper 2010, 6, 121–128. [Google Scholar]
- Ericson, C. Real-Time Collision Detection; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- VisComp2006. Collective Crowd Formation Transform with Mutual Information–Based Runtime Feedback. 2017. Available online: https://youtu.be/sS2IryxpL3U (accessed on 5 March 2017).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).