A Lightweight Image Cryptosystem for Cloud-Assisted Internet of Things

Abstract

Cloud computing and the increasing popularity of 5G have greatly increased the application of images on Internet of Things (IoT) devices. The storage of images on an untrusted cloud has high security and privacy risks. Several lightweight cryptosystems have been proposed in the literature as appropriate for resource-constrained IoT devices. These existing lightweight cryptosystems are, however, not only at the risk of compromising the integrity and security of the data but also, due to the use of substitution boxes (S-boxes), require more memory space for their implementation. In this paper, a secure lightweight cryptography algorithm, that eliminates the use of an S-box, has been proposed. An algorithm termed Enc, that accepts a block of size n divides the block into L n R bits of equal length and outputs the encrypted block as follows: $E=\left(L⨂R\right)⨁R,$ where $⨂$ and $⨁$ are exclusive-or and concatenation operators, respectively, was created. A hash result, $hasR=SHA256\left(P⨁K\right),$ was obtained, where SHA256, P, and K are the Secure Hash Algorithm (SHA−256), the encryption key, and plain image, respectively. A seed, S, generated from $enchash=Enc\left(hashenc,K\right),$ where hashenc is the first n bits of hasR, was used to generate a random image, Rim. An intermediate image, $intimage=Rim⨂P$, and cipher image, $C=Enc\left(intimage,K\right),$ were obtained. The proposed scheme was evaluated for encryption quality, decryption quality, system sensitivity, and statistical analyses using various security metrics. The results of the evaluation showed that the proposed scheme has excellent encryption and decryption qualities that are very sensitive to changes in both key and plain images, and resistance to various statistical attacks alongside other security attacks. Based on the result of the security evaluation of the proposed cryptosystem termed Hash XOR Permutation (HXP), the study concluded that the security of the cryptography algorithm can still be maintained without the use of a substitution box.

1. Introduction

Internet of things (IoT) amalgamates diverse devices running on different platforms, communicate with different caliber of devices, and employ internet to send and receive messages [1]. Despite the wide acceptability of IoT, standardization, energy management, IPv6 adoption, and security are fundamental issues of its applications [2]. These problems of IoT applications emanated from the fact that most IoT devices have limited processing power, memory, and storage space [3]. These constraints of IoT devices led to the adoption of edge computing [4], and the need to have access to data and computing resources anytime and anywhere on demand led to the adoption of cloud computing [5]. IoT applications employ a cloud to store and sense readings. A computationally costly security program can easily run in a cloud server and also ensures user privacy and security without having trouble managing these applications on the device [6]. The fact that a cloud provider has a huge processing power [7], and the capability of the cloud to make data accessible to IoT devices anytime and anywhere [8], make cloud computing a very suitable technology in IoT applications which are, though resource constrained, needed in real-time applications, where quick and precise responses with vital security are required [9]. These capabilities, provided by cloud computing to IoT applications, make IoT applicable to almost all works of life [10]. Hence, the integration of IoT and cloud computing technology is referred to as cloud-assisted IoT (CIoT) [11], which was called cloudIoT by the authors of [12].

Cloud-enabled IoT frameworks have recently become prominent [13]. However, connecting different remotely operated IoT devices to the cloud via the internet raises security and privacy concerns for users [14,15]. Both the IoT and the cloud sides of the CIoT are vulnerable to security attacks; hence, the need for security of the data on both sides. The growing awareness of data security during transmission, or when it is stored on the cloud, explains the reason for the high demand for cryptography algorithms [16]. Conventional cryptography algorithms, due to their high demand for computing resources for storage and processing, are not suitable for resource-starved IoT devices [10]. Resource-starved IoT applications, such as wireless sensor nodes (WSNs) [17,18], radio-frequency identification (RFID) networks [19], and secure robotic communications [20], require the area-optimized implementation of the cryptographic algorithm [21]. A lighter version of the cryptography scheme that requires a low computational storage and power will be more appropriate for these resource-starved IoT devices [22].

CIoT utilizes prevailing data processing proficiencies of the cloud platform to resolve massive Internet of Things (IoT) data [23]. A typical CIoT stores its data on the cloud storage to reduce the problem of data processing, as depicted in Figure 1.

Existing lightweight cryptosystems have proven to be highly efficient in terms of their memory and energy consumption. However, they are more suitable for text and binary data than for multimedia data [24]. As IoT applications are pivoting towards multimedia-oriented data, such as videoconferencing, surveillance sensors in the environment or military fields, and medical sensors and applications, a lightweight image cryptosystem will be more appropriate. In this study, a new lightweight image cryptosystem, that is suitable for resource-starved IoT applications that eliminates the use of an S-Box in its design in order to conserve its resources during the implementation of the cryptosystem, has been proposed.

1.1. Motivation

Confusion and diffusion constitute the two vital features of cryptography techniques [25,26]. Researchers use substitution boxes (S-boxes) to achieve the confusion property [27], while the bit permutation technique is normally used to achieve the diffusion property [28]. However, the use of an S-box increases the demands for memory (for storage) and computing power (for production) [29]. A cryptography algorithm that is capable of replacing an S-box with other less memory and less power-intensive techniques to achieve the same or higher level of security (which is still an open research problem) will be more appropriate for securing information in these resource-constrained IoT applications [29].

1.2. Contribution

In this paper, a lightweight image cryptosystem named Hash XOR Permutation (HXP) has been proposed. The use of an S-box is eliminated in HXP by applying a hash algorithm, exclusive-or (XOR) operation, and bit permutation. Through this approach, non-linearity, confusion, and diffusion properties were built into the HXP. Specifically, the following have been contributed to the existing knowledge:

i.

The use of an S-box and bit permutation techniques to achieve the confusion and diffusion properties of the cryptography algorithm was replaced with the use of the XOR function and bit permutation.

ii.

A hash algorithm was introduced to make the cryptosystem sensitive to both changes in the key and plain image bits.

iii.

The innovations (i) and (ii) were applied to design a new lightweight image cryptosystem.

The rest of this paper is prepared as follows. Section 2 presents a literature review. Section 3 explains the materials and methods employed in this study, while Section 4 presents the results and discussion of the results. Section 5 justifies the suitability of the proposed lightweight cryptography algorithm on resource-starved devices. Finally, the conclusion and suggestions for future work are presented in Section 6.

2. Literature Review

Security challenges militating against the wide acceptability of cloud computing technology range from vulnerability to security attacks [14], and breach of confidentiality [30] to privacy intrusion [16]. In the same vein, IoT applications increase the security and privacy risk [31] of their users. Luckily, researchers have put up measures, such as cryptography, steganography, watermarking, and a host of other measures, to secure and protect the privacy of data on transit or storage mediums.

Cryptography is an effective technique that guarantees data confidentiality, integrity, authentication, and authorization [32]. However, conventional cryptography algorithms require enormous memory, processing power, and physical areas for their implementation. This higher demand for resources makes the conventional cryptography algorithms unsuitable [33] for implementation on resource-starved IoT devices. An alternative approach is the use of hardware crypto processors, such as IBM 4758, SafeNet security processors, smartcards, and Atmel Crypto Authentication devices. It is important to note that these crypto-processors are also not immune to security attacks [34]. Recently, lightweight symmetric cryptography algorithms, such as PRESENT, an improved version of PRESENT—GIFT, RECTANGLE, TWINE, etc., have been developed. Lightweight hash functions and message authentication codes (MACs), such as SPONGENT, PHOTON, Quark, and Marvin, which can be efficiently implemented into IoT devices, have been reported in the literature. Lightweight asymmetric cryptography algorithms that can be used for IoT, such as elliptic curve cryptography (ECC), as well as post-quantum cryptography lattices and codes, have also been developed. A typical lightweight cryptography algorithm requires a small RAM for implementation and is very efficient at processing short messages. However, short key and short block messages make lightweight cryptography algorithms vulnerable to different attacks. The short key, for example, can increase vulnerability to key-related attacks [35], while the short block can also cause problems, such as cipher block chaining (CBC) eroding faster than other parts when the total quantity of n-bit blocks encrypted approaches 2 ^n/2 [36].

Although the authors of [28,29,30,31,32,33,34,35,36,37] roughly classified lightweight cryptography (LWC) algorithms into four categories based on their internal structure, the authors of [29] accurately categorized LWC algorithms into six groups. The six categories are as follows: substitution–permutation networks (SPNs), Addition/AND-Rotation-XOR (ARX), Feistel networks (FNs), generalized Feistel networks (GFNs), non-linear-feedback shift register (NLFSR), and hybrid. These internal structures are adopted to ensure the security of LWC algorithms. SPNs use S-boxes to achieve non-linearity; however, hardware implementation is resource-intensive; hence, it is not appropriate for resource-starved IoT devices. The same mechanism is used for encryption and decryption in the Feistel structure; therefore, the Feistel structure is less resource-intensive and more appropriate for resource-starved devices [38]. ARX structure-based cryptosystems combine addition/AND, rotation, and XOR operations to achieve non-linearity, diffusion, and confusion properties. The ARX structure is very simple, and its simplicity makes it more appropriate for lightweight block ciphers. However, in order to correctly generate plaintext images from cipher images through the decryption process, the round function of ARX is required to be built on either a Feistel structure or a generalized Feistel structure [39].

TEA, HIGHT, KATAN, and KLEIN, four of the most popular lightweight cryptography algorithms, were implemented and evaluated by the authors of [40] based on their memory efficiency, energy consumption, and the degree of confusion and diffusion. The results of the analysis revealed that KATAN is more memory efficient than HIGHT, TEA, and KLEIN, and consumed the least power among the ciphers. In terms of security, KLEIN had the lowest degree of diffusion and the highest degree of confusion. This behavior of KLEIN was believed to be related to its SPN structure.

A multiplatform Feistel structure-based lightweight cryptosystem called TWINE was developed by the authors of [41]. TWINE has a well-organized embedded software, a small hardware size, a block size of 64 bits, 36 rounds, and a key length of 80 or 128 bits. TWINE’s rounds have unpredictable four-bit S-boxes and four-bit block permutations as substitution and permutation layers, respectively. RECTANGLE is another lightweight multiplatform cryptosystem created by the authors of [42]. RECTANGLE has a block size of 64 bits, a key length of 80 or 128 bits, and runs on only 25 rounds. It is a bit-slice block encryption algorithm, requires a small hardware area for its implementation, and achieves an outstanding software performance. A lightweight image cryptography algorithm that employed the techniques of message passing and a two-dimensional logistic chaotic map, consumes a low memory space, is highly secure, and has a high running performance was designed by the authors of [43]. The algorithm was tested and evaluated. The scheme’s evaluation results demonstrated that the cryptosystem can withstand key sensitivity analysis even when its key space is insufficiently large. The results additionally showed that the encryption system is immune to statistical, differential, known-plaintext, and brute-force cryptanalysis attacks while consuming little time and space.

Table 1. Summary of existing work on lightweight cryptography algorithms.

Author	Title	Algorithm used	Strength	Weakness
[41]	Lightweight cryptography Algorithm for Multiple platforms	Generalized Feistel structure (GFS)	Less resources-intensive. The same program code can be used for encryption and decryption	It is vulnerable to related key attacks
[44]	An Ultra-Lightweight Block Cipher	Feistel structure	Conserves memory	Susceptible to related key attacks, and requires more rounds to ensure security
[45]	The Noekeon Block Cipher	SPN structure	Consumes less power and has better performance than the software on legacy sensors	It is resource-intensive
[46]	PRINCE—A low-latency block cipher for pervasive computing applications	Feistel structure	It conserves computational resources	It is susceptible to key-related attacks and requires more rounds to ensure security
[47]	A New Family of Lightweight Block Ciphers	SPN structure	Consumes low power and exhibits high diffusion	Hardware implementation is resource-intensive
[48]	New Lightweight DES Variants	Feistel structure	It uses only one S-Box	S-Box consumes memory and requires more rounds to ensure security
[49]	mCrypton—A Lightweight Block Cipher for the Security of Low-Cost RFID Tags and Sensors	Crypton architecture [50] (SPN structure)	Compact implementation in both hardware and software	Hardware implementation is resource-intensive

summarizes the various lightweight cryptography algorithms that are used today.

From the reviewed literature, it appears that SPNs and FNs are more common structures adopted by researchers to ensure the security of LWC.

3. Materials and Methods

In this section, a detailed description of the algorithms of the proposed cryptosystem has been provided. The description of the metrics used for the evaluation and the method of evaluation of the proposed cryptosystem have also been discussed.

Table 2. Description of the notations used in this research paper.

Symbol	Description
XOR	Exclusive-or
HXP	Hash, XOR, and bit permutation
$⨁$	Concatenation operator
$\otimes$	XOR operator
SHA−256	Secure Hash Algorithm 256
$P$	Input image
C	Cipher image
${\sigma }_p$	Contrast of P/standard deviation of pixels in P
${\mu }_p$	Luminance of P/mean of pixel in P
${\sigma }_C$	Contrast of C/standard deviation of pixels in C
${\mu }_P$	Luminance of C/mean of pixel in C
${var}_P$	Variance of P
${var}_C$	Variance of C

is a symbol table that outlines the description of the notations used in the description of the algorithms and the rest of this paper.

3.1. Proposed Lightweight Image Cryptography Algorithm

The proposed lightweight image cryptosystem (HXP) algorithm is a block cipher designed for low area overhead. The cipher features bit grouping, the XOR function, and bit permutation layers. The cipher accommodates a variable block size; hence, it can also be used with rich-resource IoTs, like conventional cryptography algorithms. There is no need for an S-box in the proposed image algorithm; hence, it conserves memory. The architectural design of HXP is shown in Figure 2. Figure 2a depicts the encryption module of HXP. The encryption module takes the permutation key and all the pixels in a single row of the image to be encrypted at a time. The array of pixels is converted into an array A of n bits.

The layers making up the HXP cryptosystem are outlined as follows:

i.

Bit grouping layer: The bits in A are grouped into two equal parts, L and R, each of size (n/2) bits.

$$L=A\left[0\dots \frac{n}{2}-1\right]$$

(1)

$$R=A\left[\frac{n}{2}\dots n-1\right]$$

(2)

ii.

XOR operation layer: A bitwise XOR operation is carried out on L and R, according to Equation (3), to form an array of xorbit and the bits in R is concatenated to xorbit to form xorbitR, which has n bits. The symbol $⨁$represents concatenation in Equation (4).

$$xorbit\left[i\right]=L\left[i\right]\otimes R\left[i\right] for 0\le i<\frac{n}{2}$$

(3)

$$xorbitR=xorbit \oplus R$$

(4)

iii.

Bit permutation: This layer takes the permutation key, permkey, and xorbitR as inputs. Permkey contains an array of random integers with size n. The value of integers in permkey ranges between 0 and n − 1. Each bit of xorbitR is rewritten according to Equation (5).

$$encbits\left[i\right]=xorbitR\left[permkey\left[i\right]\right] for 0\le i<n$$

(5)

The pseudocode in Algorithm 1 outlines the design of the encryption module.

Algorithm 1: Encryption module (block, permkey)

Output: encblock   1. $START$   2. $L=block\left[0\dots \frac{n}{2}-1\right]$  //a block contains n bits   3 $R=A\left[\frac{n}{2}\dots n-1\right]$   4. FOR I = 0 TO $\frac{n}{2}-1$   a. $xorbit\left[i\right]=L\left[i\right]\otimes R\left[i\right]$   5. $xorbitR=CONCATENATE(xorbit,R)$   6. encbits = CALL encreshufflement(xorbitR, permkey) //Algorithm 2   7. encblock = CONVERT encbits to pixels   8. STOP

Algorithm 2: encreshufflement (blockbits, permkey)

Output: rblockbit 1. START 2. FOR i = 0 TO n − 1 //blockbits has n bits   a. $rblockbit\left[i\right]=blockbit\left[permkey\left[i\right]\right]$ 3. STOP

Figure 2b depicts the encryption process where the encryption module of HXP is used. The image to be encrypted, pimage, and the encryption key, K, are the two inputs for the encryption process. The encryption process involves random key generation, random image generation, and generation of cipher images, which are detailed as follows:

• Random key generation: An array of random integer, PERMkey, is generated using the key. Given an image A with dimension $(a\times b\times c)$, the image A is converted into a grayscale image, grayA, of dimension $(a\times b)$. If a > b, the size of PERMkey will be a; otherwise, the size of PERMkey will be b.

ii.

Random image generation: the bytes of grayA and that of the key are combined together to form Cbyte. Cbyte is made to pass through SHA−256. The first k bits of the output of SHA−256, where k is the block size, is selected as the shavalue. The shavalue is encrypted using the encryption module and the output is used as the seed to generate the pixels of a random image, Randimage. The size of Randimage is equal to the size of grayA. A bitwise XOR operation is carried out between Randimage and grayA to form interimage.

iii.

Cipher image generation: The generation of cipherimage is carried according to Equations (6) and (7), where nrows and ncols represent the quantity of rows and columns in the interimage, respectively. Equations (6) and (7) outline the description of how the bits of interimage are manipulated along the rows and columns of the image, respectively, to form an encrypted image.

$$\begin{array}{l}cipherimage\left[row,:\right]\\ =Encryptionmodule\left(interimage\left[row,;\right], PERMkey\left[row\right] \right)for 0\le row\\ <nrrows\end{array}$$

(6)

$$\begin{array}{l}cipherimage\left[:,col\right]\\ =Encryptionmodule\left(cipherimage\left[:,col\right], PERMkey\left[col\right] \right)for 0\le col\\ <ncols \end{array}$$

(7)

The pseudocode in Algorithm 3 represents the design of the encryption process in HXP.

Algorithm 3: Encryption process (pimage, K)

Output: encimage   1. START   2. grayA = CONVERT pimage to gray image of dimension h and w   3. cbyte = CONCATENATE (grayA, K)   4. randseed = CALL generaterandomseed(key) // Algorithm 7   5. blocksize = MAXIMUM (h, w)   6. permkey [1…blocksize] = GENERATE array of random integers using randseed as seed   7. hashvalue = HASH (cbyte)   8. hashvalue = hashvalue [1…blocksize]   9. enchashvalue = CALL EncryptionModule(hashvalue,permkey) // Algorithm 1   10. rseed = CALL generaterandomseed(enchashvalue) // Algorithm 7   11. randimage = Generate random image of size (h × w) using rseed as seed   12. interimage = XOR (randimage, grayA)   13. FOR i = 0 TO h − 1   a. encimage[i, :] = CALL EncryptionModule(interimage[i, :], permkey) //Algorithm 1   14. FOR j = 0 TO w − 1   a. encimage[:,j] = CALL EncryptionModule(encimage[:,j], permkey) // Algorithm 1   15. STOP

The decryption procedure converses the steps in the encryption procedure to recover the plain image from the cipher image. Algorithms 4 and 5 outline the design of the decryption module and the decryption process in HXP, respectively.

Algorithm 4: Decryption module (encblock, permkey)

Output: decblock   1. START   2. ecbits = CALL decreshufflement(encblock, permkey) //Algorithm 6   3. $L=decbits\left[0\dots \frac{n}{2}-1\right]$  //a block contains n bits   4. $R=decbits\left[\frac{n}{2}\dots n-1\right]$   5. FOR i = 0 TO $\frac{n}{2}-1$   a. $dxorbit\left[i\right]=L\left[i\right]\otimes R\left[i\right]$   6. $dxorbitR=CONCATENATE(dxorbit,R)$   7. decblock = CONVERT dxorbitR to pixels   8. STOP

Algorithm 5: Decryption process (cimage, hasvalue, key)

Output: decimage   1. START   2. h, w = SIZEOF(cimage)   3. rseed = CALL generaterandomseed(key)//Algorithm 7   4. blocksize = MAXIMUM (h, w)   5. permkey [1…blocksize] = random integers obtained from using rseed as seed   6. hashvalue = hashvalue [1…blocksize]   7. enchashvalue = CALL EncryptionModule(hashvalue,permkey)//Algorithm 4   8. rseed = CALL generaterandomseed(enchashvalue)//Algorithm 7   9. randimage = Generate random image of size (h x w) using rseed as seed   10. interimage = XOR (randimage, grayA)   11. FOR j = 0 TO w − 1   a. dimage[:,j] = CALL DecryptionModule(cimage[:,j], permkey)//Algorithm 4   12. FOR i = 0 TO h − 1   a. decimage[i, :] = CALL DecryptionModule(dimage[i, :], permkey)//Algorithm 4   13. STOP

Algorithm 6: Decreshufflement (blockbits, permkey)

Output: im   1. START   2. m = LENGTH (permkey)   3. im [1…m] = empty 1 dimensional array of length m   4. FOR i = 1 TO m   a. $im\left[permkey\left[i\right]\right]=blockbit\left[i\right]$   5. STOP

Algorithm 7: Generate random seed (key)

Output: randomseed   1. START   2. binkey = key in its binary form   3. LET mstr = ‘10101010′   4. LET b = LENGTH (binkey)   5. LET m = b/8   6. LET mstr = DUPLICATE mstr IN m TIMES such that LENGTH (mstr) = LENGTH (binkey)   7. LET mstr1 = XOR (mstr,binkey)   8. LET m = COUNT number of 1′s in mstr1   9. LET confusionkey = random integers obtained by using m as seed   10. LET mstr = reshuffleforencryption(confusionkey,mstr)   11. mstr2 = XOR (mstr1, mstr)   12. k = mstr2[m:]   13. randseed = CONVER k TO an integer   14. IF randseed = 0 THEN   a. k = mstr2[:m2]   b. randseed = CONVER k TO an integer ENDIF   15. IF randseed > $2^{32}$ − 1 THEN   a. randseed = MOD (randseed, $2^{32}$ − 1) ENDIF   5. STOP

3.2. Metrics and Methods of Analysis of the Proposed Lightweight Image Cryptosystem

This section begins with the discussion of the metrics used for the analysis, following which the procedures for carrying out the analysis are outlined.

3.2.1. Metrics Used for the Analysis of the Proposed Algorithm

The security of the cryptosystem and the quality of the image obtained are very important features to look for in any image cryptosystem. The security of HXP and the quality of the decrypted images were measured using the following metrics:

• Encryption quality (EQ): Given the plain image P and its equivalent cipher image C each with the equal size M × N, the gray values of pixel P(I,j) and C(i,j) in P and C range from 0…255. If $f_L\left(P\right)$ and $f_L\left(C\right)$ represent the occurrence of each gray value, L, in P and C, respectively, then, Equation (8) gives the encryption quality of the cryptosystem. The higher the value of EQ, the better the |EQ of the cryptosystem.

  $$EQ=\sum _{L=0}^{255}\frac{{\left(f_L\left(C\right)-f_L\left(P\right)\right)}^2}{256}$$

  (8)
• Mean square error (MSE): This metric measures the distance between the input P and the output C, where P and C represent the plain and cipher images of size MN, respectively. A cryptosystem with a high value of MSE indicates a better encryption quality. Mathematically, the MSE of images P and C with pixels $P\left(i,j\right)$ and $C\left(i,j\right)$ at grid location $\left(i,j\right)$ is outlined by the formula in Equation (9). When the MSE is used as a metric for measuring the quality of the decrypted image, the image C in Equation (9) is replaced with the decrypted image D. In this scenario, the value of the MSE should be low for a good decryption algorithm.

  $$MSE=\frac{1}{MN}\sum _{i=1}^M\sum _{j=1}^N{\left(P\left(i,j\right)-C\left(i,j\right)\right)}^2$$

  (9)
• Peak signal-to-noise ratio (PSNR): The PSNR is a standard way of measuring image fidelity. It compares the quality of the cipher image C with that of the plain image P. Mathematically, PSNR is defined by Equation (10), where $I_{max}$ represents the highest image pixel value. A secure cryptosystem is expected to produce low values of the PSNR; the low value indicates a great difference between P and C. In the case of comparing P and a decrypted image, the value of PSNR is expected to be infinity for a good cipher.

  $$PSNR={10\log }_2\left(\frac{{I^2}_{max}}{MSE}\right)$$

  (10)
• Structural similarity index measure (SSIM): SSIM values range from −1 to +1. A value of +1 signifies a similarity between two images, whereas a value of −1 implies a dissimilarity of the two images. The SSIM compares the two images based on their luminance, ${\mu }_p$, which represents the average of all the pixel values. In contrast, ${\sigma }_p$, which represents the standard deviation of all the pixel values, can be implemented to uncover the structural characteristics of the images, which are obtained by applying the following formula: $\frac{P-{\mu }_p}{{\sigma }_p},$ where P is the input image. The SSIM between images P and C can be found by applying the formula in Equation (11), where $D_1$ and $D_2$ are constant to steady division with the feeble denominator.

  $$SSIM\left(P,C\right)=\frac{\left(2{\mu }_p{\mu }_c+D_1\right)\left(2{\sigma }_{pc}+D_2\right)}{\left({{\mu }_p}^2+{{\mu }_c}^2+D_1\right)\left({{\sigma }_p}^2+{{\sigma }_c}^2+D_2\right)}$$

  (11)

For a secure cryptosystem with good decryption quality, the SSIM between the plain image P and the cipher image C is expected to be low and close to −1; meanwhile, the SSIM between P and the decrypted image Di is expected to high and close to 1.

v.

Normalized cross-correlation (NCC): NCC is a widely accepted metric for measuring similarity between the two images P and C. The value of NCC ranges from −1 to 1. The value −1 implies that there is strong correlation between P and C, while the value 1 indicates that there is no strong correlation between P and C. NCC is also used in measuring image quality in image processing. Pixels of plain image P and that of the cipher image C should lack a correlation. Hence, it is expected that the NCC between P and C should be close to 1 for a good cipher. There should be a strong correlation between the pixels of P and that of the decrypted image D obtained from the decryption of C. Hence, the NCC value obtained when P and D are used as the inputs should be close to −1. Equation (12) details the mathematical description of NCC:

$$NCC=\frac{1}{M\times N}\times \frac{\sum _{i,j}^{M,N}{(P}_{i,j}-{\mu }_p)\times {(C}_{i,j}-{\mu }_c)}{\sqrt{{var}_P\times {var}_C}}$$

(12)

where M and N represent the height and width of the images P and C (the two images should have the same size), $P_{i,j}$ represents the pixel of image P at row i, column j, ${\mu }_p$ and ${\mu }_c$ represent the mean of the pixels in images P and C, respectively, and ${var}_P and {var}_C$ represent the variance of images P and C, respectively.

vi.

Mean absolute error (MAE): The MAE can be used in the determination of an image’s quality and the resistance of an image cryptosystem to differential attacks. An image cryptosystem is considered secure if the value of MAE is greater than 75; otherwise, the cryptosystem is said to be insecure. When comparing cryptosystems, a cryptosystem that has a higher value of MAE is said to be more secure. When considering the quality of the plain image and decrypted image obtained from the decryption of the cipher image, a cryptosystem that has the lower value of MAE is said to produce a higher quality image than the one with a higher value of MAE. Equation (13) represents the formula for determining the MAE of a cryptosystem:

$$MAE=\frac{1}{MN}\sum _{i=1}^M\sum _{j=1}^N\left|P\left(i,j\right)-C\left(i,j\right)\right|$$

(13)

where $P\left(i,j\right)$, and $C\left(i,j\right)$are the pixels in P and C at grid location $\left(i,j\right)$, respectively.

vii.

Normalized absolute error (NAE): NAE is a metric that can be used to compare the quality of an image with that of a reference image. If the value of NAE is high, it means that the image quality is low. A low value of NAE implies a higher quality of the image. Equation (14) represents the formula for calculating the NAE between the reference image P and image C.

$$\frac{\sum _{i,j=1}^{M,N}\left(\left|P\left(i,j\right)-C\left(i,j\right)\right|\right)}{\sum _{i,j=1}^{M,N}P\left(i,j\right)}$$

(14)

viii.

Maximum difference (MD): The MD is determined by obtaining the maximum value when corresponding pixels at grid location (i,j) of plain image P and the cipher image C are subtracted from each other, as shown in Equation (15). A higher value of the MD indicates a significant difference between P and C. Hence, a cryptosystem with a higher value of MD is said to be more secure than the one with a lower value. In the case of consideration of P and the decrypted image D obtained from the decryption of C, a lower value of the MD is desirable. A cryptosystem with a lower value of the MD between the plain image and the decrypted image is said to be better, as a lower value indicates that there is no substantial alteration between the two images. The formula for finding the MD is outlined by Equation (15).

$$MD=MAX\left(P\left(i,j\right)-C\left(i,j\right)\right)$$

(15)

ix.

Average difference (AD): A higher value of the AD, that can be obtained when the plain image P and the cipher image C are used for the computation, signifies that the image cryptosystem is secure, while a low value implies a less secure cryptosystem. In the case of the computation of the AD between P and the decrypted image D, which can be obtained when C undergoes the decryption process, a lower value of AD implies a better quality of the decrypted image, while a high value indicates that the decryption process cannot obtain an image that is similar to P from C. Equation (16) represents the formula for determining the AD between the two images P and C, where $P\left(i,j\right)$ and $C\left(i,j\right)$ represent the pixels at grid location (i,j) of P and C, respectively.

$$AD=\frac{1}{MN}\sum _{i=1}^M\sum _{j=1}^N\left(P\left(i,j\right)-C\left(i,j\right)\right)$$

(16)

x.

Structural content (SC): SC is another metric that can be used to measure the image quality. The image quality of a processed image, Pm, is a measure of the degradation of pm when compared to an ideal image, P. Achieving a value of 1 for the SC indicates a high quality of Pm, while a higher value indicates a low quality of Pm. For a good cryptosystem, when the cipher image Pm is compared with the original image P, it is expected that the value of SC should be high for the cipher to be regarded as secure. When the decrypted image D is compared to P, it is expected that a good cryptosystem should provide a SC of 1 in order for the cipher to be rated as being able to retrieve the exact copy of P from the cipher image Pm. Equation (17) represents the formula for calculating the SC between the original image P and the processed image (cipher/decrypted) Pm.

$$SC=\frac{\sum _{i,j}^{M,N}{\left(P_{i,j}\right)}^2}{\sum _{i,j}^{M,N}{\left({Pm}_{i,j}\right)}^2}$$

(17)

xi.

Two-dimensional correlation coefficient (2DCC): The 2DCC can be used to calculate the similarity or difference between two images. If the value of the 2DCC is small (or zero), the two images are said to be different. A large value of the 2DCC implies that the two images are similar. Equation (18) represents the formular for finding the 2DCC between two images P and C.

$$2DCC=\frac{\sum _{i,j}^{M,N}{(P}_{i,j}-{\mu }_p)\times {(C}_{i,j}-{\mu }_c)}{\sqrt{\left(\left(\sum _{i,j}^{M,N}{{(P}_{i,j}-{\mu }_p)}^2\right)\times \left(\sum _{i,j}^{M,N}{{(C}_{i,j}-{\mu }_c)}^2\right)\right)}}$$

(18)

where $P_{i,j}$, $C_{i,j}$, ${\mu }_p$, and ${\mu }_c$ are the pixels at grid location (i,j) of P and C, and the averages of the pixels in P and C, respectively.

xii.

Differential cryptanalysis: The net pixel change rate (NPCR) [51] and the unified average change intensity (UACI) [52] are the commonly used metrics for measuring the resistance of a cipher to cryptanalysis attack between two images P and C. The ideal values of the NPCR and UACI, according to the authors of [53], are 99.6093% and 33.4635%, respectively, for the differential cryptanalysis-resistant cipher. The formulae for determining the NPCR and UACI are given in Equations (19) and (20), respectively:

$$NPCR=\frac{\sum _{i,j}D\left(i,j\right)}{M\times N}$$

(19)

$$UACI=\frac{\sum _{i,j}\frac{E\left(i,j\right)}{255}}{M\times N}$$

(20)

where D(i,j) = 0 if $P\left(i,j\right)=C\left(i,j\right);$ otherwise, $D\left(i,j\right)=1$ and $E\left(i,j\right)=abs(P\left(i,j\right)-C\left(i,j\right)$.

xiii.

Histograms are graphical representations of the distribution of gray levels in the pixels of images [54]. Ciphertext images always have a uniform distribution of pixels; in the case of a plaintext image, these pixels are jerky. A uniform histogram of a cipher image therefore indicates a secure encryption scheme [55]. A Chi-square test was carried out to validate the histogram’s uniformity. The formula for calculating the uniformity of histograms is given by Equation (21):

$${\mathit{\chi }}^2=\sum _{i=1}^{256}\frac{{\left(O_i-E\right)}^2}{E}$$

(21)

where i is the pixel value in the interval (0….255), $O_i$ is the observed frequency of each i, and for a grayscale image with height M and width N, the expected frequency $E=\frac{M\times N}{256}$. The significance level $\propto$ was set to 0.05. A Chi-square test was carried out and the p-value was obtained. If the p-value <$=\propto$, the histogram is not uniform. If the p value > $\propto ,$ then the histogram is uniform.

xiv.

Adjacent pixels correlation coefficient: The correlation coefficient of adjacent pixels in an image can be calculated by applying Equation (22) [56]:

$$\left\{\begin{array}{c}\mathrm{E}\left(\mathrm{x}\right)=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\mathrm{x}}_{\mathrm{i}}, \mathrm{D}\left(\mathrm{x}\right)=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{{(\mathrm{x}}_{\mathrm{i}}-\mathrm{E}\left(\mathrm{x}\right))}^2\\ {\mathsf{\gamma }}_{\mathrm{x},\mathrm{y}}=\frac{\mathrm{c}\mathrm{o}\mathrm{v}\left(\mathrm{x},\mathrm{y}\right)}{\left(\sqrt{\mathrm{D}\left(\mathrm{x}\right)}\right)\left(\sqrt{\mathrm{D}\left(\mathrm{y}\right)}\right)},\mathrm{D}\left(\mathrm{x}\right)\ne 0 \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{D}\left(\mathrm{y}\right)\ne 0\\ \mathrm{c}\mathrm{o}\mathrm{v}\left(\mathrm{x},\mathrm{y}\right)=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{(\mathrm{x}}_{\mathrm{i}}-\mathrm{E}\left(\mathrm{x}\right)){(\mathrm{y}}_{\mathrm{i}}-\mathrm{E}(\mathrm{y}\left)\right)\end{array}\right.$$

(22)

where $x_i$ is the grayscale value of a pixel, n is the number of pairs ($x_i$, $y_i$), and E(x) and E(y) are the mean values of $x_i$ and $y_i$, respectively. It is expected that the results of an adjacent pixel correlation coefficient of a good encryption scheme should be close to zero [50].

xv.

The statistical measure that was used to test the entropy of the proposed image cryptosystem is given by the formula in Equation (23):

$$H\left(m\right)=\sum _{i=0}^{2^N-1}P\left(m_i\right){\log }_2\left(\frac{1}{P\left(m_i\right)}\right)$$

(23)

where m represents the image, $2^N$ represents the pixel sample space, $m_i$ represents the pixel i of image m, and $P\left(m_i\right)$ represents the probability of $m_i$. The entropy H(m) of an image, encrypted with a $2^N$ pixel sample space, is N. The pixel space was 256; hence, $2^N=256=2^8$. The maximum value of N was 8. In order for an image cryptosystem to be rated as resistant to an entropy attack, the result of the entropy analysis of the encrypted image should be close to 8. A cryptosystem that has an information entropy H(m) very close to 8 is said to be resistant to an entropy attack.

3.2.2. Methods of Analysis

In this section, the details of the analysis carried out on the proposed lightweight image cryptosystem are discussed. The following analyses were carried out: simulation, system sensitivity, statistical, and required resources analyses.

i.

Procedure for simulation analysis: ‘airplane.tiff’,’baboon.tiff’,’boat.tiff’,’lena.tiff’, and ‘pepper.tiff’ were retrieved from the USC-SIPI image database (http://sipi.usc.edu/database/) for simulation purposes. Each of the images was converted into a grayscale image. Each of the grayscale images was made to pass through an encryption algorithm of the proposed image cryptosystem to obtain a cipher image. Each of the obtained cipher images was also made to pass through the decryption algorithm of the proposed image cryptosystem to ascertain whether or not the decryption process is able to recover the original image from the cipher image.

ii.

Procedure for encryption/decryption quality analysis: In order to justify the claim as per the quality of the images produced by the encryption and decryption processes and the security of the proposed cryptosystem, metrics 1–10 were used. For EQ, the images produced by the encryption process were compared with the original images. For DQ, the images produced by the decryption process were compared with the original images.

iii.

Procedure for system sensitivity analysis: Key sensitivity and plain image sensitivity were used to test the system’s sensitivity via the following statistical procedures:

a.

Key sensitivity: A key, K, was randomly generated. A single bit at a random location within the bits of K was flipped to obtain another key, K1. The keys K and K1 were used in turns to encrypt the image P to obtain the cipher images C and C1, respectively. Metrics 3–11 were used to compare C and C1. This procedure was repeated for each of the test images.

b.

Plain image sensitivity: A key, K, was randomly generated. A single bit within the bits of an image P at a random location was flipped to obtain another image, P1. Both the P and P1 images were encrypted using key K to obtain the cipher images C and C1, respectively. Metrics 3–11 were used to compare C and C1. This procedure was repeated for each of the test images.

c.

Cipher image sensitivity: A key, K, was randomly generated. A plain image, P, was encrypted using the proposed image encryption algorithm to form the cipher image, C. A single bit within the bits of image C was flipped at a randomly selected location within the bits of image C to obtain another cipher image, C1. Both C and C1 were decrypted using the decryption algorithm of the proposed image cryptosystem and key K to obtain the decrypted images D and D1, respectively. Metrics 3–11 were used to compare D and D1. This procedure was repeated for each of the test images.

iv.

Statistical analysis procedure: The purpose of statistical analysis is to test the algorithm in order to ascertain its resistance to statistical attacks. Histograms, the adjacent pixel correlation coefficient, and entropy analysis were employed in this case as follows:

a.

Histogram analysis procedure: For each of the test images, histograms of the plain image and that of the cipher image were taken and the Chi-square test was used to verify the uniformity of each histogram.

b.

The adjacent pixel correlation coefficient: A thousand randomly selected pixels along the horizontal, vertical, and diagonal directions of each of the test images were plotted on scatter graphs for each direction. The same was conducted for each of the cipher images obtained from each test image. The correlation coefficient, in each case, was also calculated to verify the resistance of the cryptosystem against correlation coefficient attacks.

c.

Entropy analysis: Each of the test images were encrypted using the proposed encryption scheme. Entropy analysis, as specified by Equation (23), of both the plain and cipher images were measured.

4. Results and Discussions

In this section, the experimental results and the results of comparison of HXP with the existing algorithms are discussed. Implementation of the HXP was carried out on a laptop with the following configuration:

Processor	AMD E1−1200 APU with Radeon(tm) HD Graphics 1.40 GHz
Installed RAM	4.00 GB (3.59 GB usable)
Device ID	E4C0446D−57F5−4475−8A60-F1D4A41F6048
Product ID	00331−10000−00001-AA508
System type	64-bit operating system, x64-based processor

4.1. Discussion of Experimental Results

i.

Simulation results: Figure 3 shows the simulation results. The input images are shown in Figure 3a–e. The outputs of these images following their conversion into grayscale images are shown in Figure 3f–j. The resulting images when the images in Figure 3f–j are subjected to the encryption process are shown in Figure 3k–o, and Figure 3p–t represent the images recovered from the decryption of the images in Figure 3k–o. By visual inspection, the images in Figure 3k–o are very different from the images in Figure 3f–j. Comparing the images through visual inspection also shows that Figure 3f–j and Figure 3p–t are identical. These results reveal that HXP is capable of securing images and that the recovered images from the cipher images are of a high quality, such that mere visual inspection cannot detect any difference between the original image and the decrypted images.

ii.

Encryption quality of the HXP algorithm: The encryption quality of HXP was analyzed using the metrics one to eleven. Each cipher image C, in Figure 3k–o, was compared with their corresponding original image P, in Figure 3f–j, based on these metrics.

Table 3. Results of the encryption quality analysis of HXP.

Image	EQ	PSNR	SC	SSIM	NCC	DCC	MSE	MAE	NAE	MD	AD
airplane.tiff	2,869,083	8.0041	1.1062	0.0095	−0.0016	−0.0016	10,296.2	82.9506	0.4629	227	67.3335
baboon.tiff	750,867.4	9.5204	0.9773	0.0087	0	0	7261.71	71.0481	0.5481	221	36.4318
boat.tiff	1,533,181	9.2952	1.0287	0.009	0.0009	0.0009	7648.14	72.5083	0.559	248	37.4054
lena.tiff	623,642.2	9.2399	1.0012	0.0096	0.0022	0.0022	7746.15	72.895	0.5876	235	34.6345
pepper.tiff	2,610,186	8.8704	1.0452	0.0097	−0.002	−0.002	8434.09	75.6136	0.629	222	34.1703

shows the results that were obtained. The high values of EQ, MSE, MAE, NAE, MD, and AD indicate that C is very different from P. Furthermore, the low values of the metrics PSNR, SSIM, NCC, and DCC establish the fact that C is very different from P. The inability of the algorithm to produce a value of one for the metric SC is also an indication that C is different from P. Overall, these results showed that the quality of C produced by the HXP algorithm is not of the same quality as that of P. This is an indication of a secure image encryption algorithm.

iii.

Decryption quality of HXP: Metrics two to ten were used to measure the decryption quality of HXP. The values of these metrics were compared with the ideal values of these metrics in order to ascertain the quality of the decrypted images.

Table 4. Results of the decryption quality analysis of HXP.

Image	PSNR	SC	SSIM	NCC	DCC	MSE	MAE	NAE	MD	AD
Ideal values	Inf	1	1	1	1	0	0	0	0	0
airplane.tiff	inf	1	1	1	1	0	0	0	0	0
baboon.tiff	inf	1	1	1	1	0	0	0	0	0
boat.tiff	inf	1	1	1	1	0	0	0	0	0
lena.tiff	inf	1	1	1	1	0	0	0	0	0
pepper.tiff	inf	1	1	1	1	0	0	0	0	0

shows the results of the evaluation. The first row shows the ideal value of each metric in the heading of the table, while the subsequent rows show the obtained value for each metric in the headings of the columns of the table when the images in Figure 3p–t were compared with the images in Figure 3f–j. From the results in Table 4, it is clear that the obtained values for all the tests images are just the same as the ideal value. These results show that the recovered images from the encrypted images have the same quality as the original images. Hence, the HXP algorithm has an excellent decryption quality.

iv.

System Sensitivity Analysis Results

Measuring the system’s sensitivity involves the analysis of the degree of changes in the cipher image when a slight change is made on either a key or plain image and the degree of changes in the plain image when a slight change is made on a cipher image. The three dimensions of sensitivity, namely the key, plain image, and cipher image sensitivity, of the proposed image cryptosystem were carried out. In each case, metrics two to twelve, described above, were employed in the system sensitivity analysis.

• i.

  Key Sensitivity Analysis Results

  The results of the key sensitivity analysis are shown in Table 5. As shown in Table 5, the values of PSNR, SSIM, NCC, and DCC were greatly reduced when compared to the ideal values when two images that were of the same quality were compared. These results show that the obtained cipher images are different and are not of the same quality. The high values of MSE, MAE, MD, and AD are indicators that the cipher images are very different. The values of the NPCR and UACI were very close to the ideal values expected of a cryptosystem that is resistant to differential cryptanalysis. These results show that a small change in the key causes an enormous change in the cipher images. Hence, HXP is key sensitive.

  Table 5. Results of key sensitivity analysis.

  Image	PSNR	SC	SSIM	NCC	DCC	MSE	MAE	NAE	MD	AD	NPCR	UACI
  airplane.tiff	7.7493	1.0012	0.0055	0.0001	0.0001	10,918.08	85.2896	0.6693	255	42.6	99.6078	33.4469
  baboon.tiff	7.7494	0.9982	0.0068	0.0013	0.0013	10,917.94	85.3712	0.6698	255	42.7691	99.6178	33.4789
  boat.tiff	7.7504	1.0028	0.0073	0.0021	0.0021	10,915.36	85.3001	0.669	255	42.7253	99.6208	33.451
  lena.tiff	7.7413	0.9995	0.0045	−0.001	−0.001	10,938.39	85.4321	0.6715	255	42.5178	99.6143	33.5028
  pepper.tiff	7.7512	1.0012	0.0063	0.0013	0.0013	10,913.51	85.3219	0.6696	255	42.6955	99.6426	33.4596

  Table 5. Results of key sensitivity analysis.

  Image	PSNR	SC	SSIM	NCC	DCC	MSE	MAE	NAE	MD	AD	NPCR	UACI
  airplane.tiff	7.7493	1.0012	0.0055	0.0001	0.0001	10,918.08	85.2896	0.6693	255	42.6	99.6078	33.4469
  baboon.tiff	7.7494	0.9982	0.0068	0.0013	0.0013	10,917.94	85.3712	0.6698	255	42.7691	99.6178	33.4789
  boat.tiff	7.7504	1.0028	0.0073	0.0021	0.0021	10,915.36	85.3001	0.669	255	42.7253	99.6208	33.451
  lena.tiff	7.7413	0.9995	0.0045	−0.001	−0.001	10,938.39	85.4321	0.6715	255	42.5178	99.6143	33.5028
  pepper.tiff	7.7512	1.0012	0.0063	0.0013	0.0013	10,913.51	85.3219	0.6696	255	42.6955	99.6426	33.4596

  ii.

  Plaintext Sensitivity analysis and Results and Results

  The results shown in Table 6 are the obtained results when the proposed cryptosystem was subjected to plaintext sensitivity analysis. As can be seen, the obtained results resembles the results that were obtained during the key sensitivity analysis. These results reveal that HXP is very sensitive to a slight change in the plain image.

  Table 6. Plain image sensitivity analysis results.

  Image	PSNR	SC	SSIM	NCC	DCC	MSE	MAE	NAE	MD	AD	NPCR	UACI
  airplane.tiff	7.7561	0.9993	0.0075	0.0019	0.0019	10,901.08	85.2592	0.6679	255	42.6426	99.6025	33.435
  baboon.tiff	7.7637	1.0024	0.0081	0.0028	0.0028	10,882.12	85.1354	0.667	255	42.6557	99.593	33.3864
  boat.tiff	7.7586	0.9979	0.0078	0.0024	0.0024	10,894.76	85.1562	0.668	255	42.5446	99.5953	33.3946
  lena.tiff	7.7697	0.9987	0.0094	0.0041	0.0041	10,867.12	84.9817	0.6671	255	42.4845	99.6162	33.3262
  pepper.tiff	7.7388	1	0.0037	−0.0016	−0.0016	10,944.68	85.4524	0.6706	255	42.6269	99.6231	33.5107

  Table 6. Plain image sensitivity analysis results.

  Image	PSNR	SC	SSIM	NCC	DCC	MSE	MAE	NAE	MD	AD	NPCR	UACI
  airplane.tiff	7.7561	0.9993	0.0075	0.0019	0.0019	10,901.08	85.2592	0.6679	255	42.6426	99.6025	33.435
  baboon.tiff	7.7637	1.0024	0.0081	0.0028	0.0028	10,882.12	85.1354	0.667	255	42.6557	99.593	33.3864
  boat.tiff	7.7586	0.9979	0.0078	0.0024	0.0024	10,894.76	85.1562	0.668	255	42.5446	99.5953	33.3946
  lena.tiff	7.7697	0.9987	0.0094	0.0041	0.0041	10,867.12	84.9817	0.6671	255	42.4845	99.6162	33.3262
  pepper.tiff	7.7388	1	0.0037	−0.0016	−0.0016	10,944.68	85.4524	0.6706	255	42.6269	99.6231	33.5107

  iii.

  Cipher Image Sensitivity Analysis

  From the results shown in Table 7, it is obvious that HXP has a poor cipher image sensitivity. This is revealed from the values of PSNR, SC, SSIM, NCC, DCC MSE, MAE, NAE, MD, and AD, that were very close to the ideal values when two images of a similar quality were compared. These results revealed that there was no significant difference between the cipher image and the altered cipher image. This means that the two cipher images are of a similar quality. The obtained results for the NPCR and UACI were very far from the ideal values for the images that were different. Hence, HXP has a poor cipher image sensitivity. However, this poor cipher image sensitivity should not be seen as a weakness, as cipher image sensitivity and a chosen cipher image attack are not related. On the contrary, a cryptosystem that has a poor cipher image sensitivity is capable of resisting against certain noise interference. Hence, it can be said by these results that the proposed lightweight cryptosystem is resistant to some noise interference.

  Table 7. Cipher image sensitivity analysis results.

  Image	PSNR	SC	SSIM	NCC	DCC	MSE	MAE	NAE	MD	AD	NPCR	UACI
  airplane.tiff	inf	1	1	1	1	0	0	0	0	0	0.0004	0
  baboon.tiff	inf	1	1	1	1	0	0	0	0	0	0.0004	0
  boat.tiff	inf	1	1	1	1	0	0	0	0	0	0.0008	0
  lena.tiff	inf	1	1	1	1	0	0	0	0	0	0.0008	0
  pepper.tiff	inf	1	1	1	1	0	0	0	0	0	0.0004	0

  Table 7. Cipher image sensitivity analysis results.

  Image	PSNR	SC	SSIM	NCC	DCC	MSE	MAE	NAE	MD	AD	NPCR	UACI
  airplane.tiff	inf	1	1	1	1	0	0	0	0	0	0.0004	0
  baboon.tiff	inf	1	1	1	1	0	0	0	0	0	0.0004	0
  boat.tiff	inf	1	1	1	1	0	0	0	0	0	0.0008	0
  lena.tiff	inf	1	1	1	1	0	0	0	0	0	0.0008	0
  pepper.tiff	inf	1	1	1	1	0	0	0	0	0	0.0004	0

v.

Statistical Analysis and Results

i.

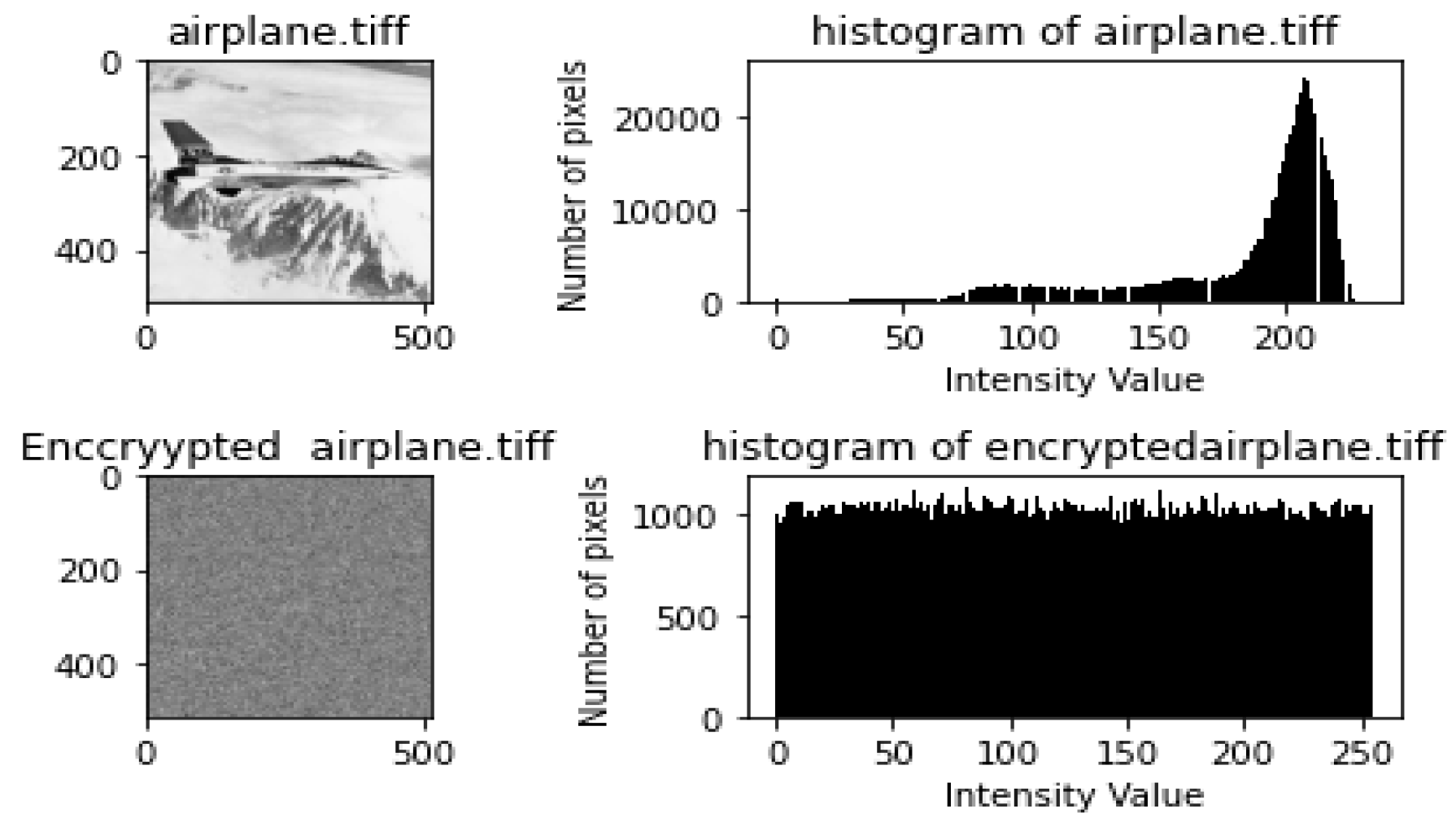
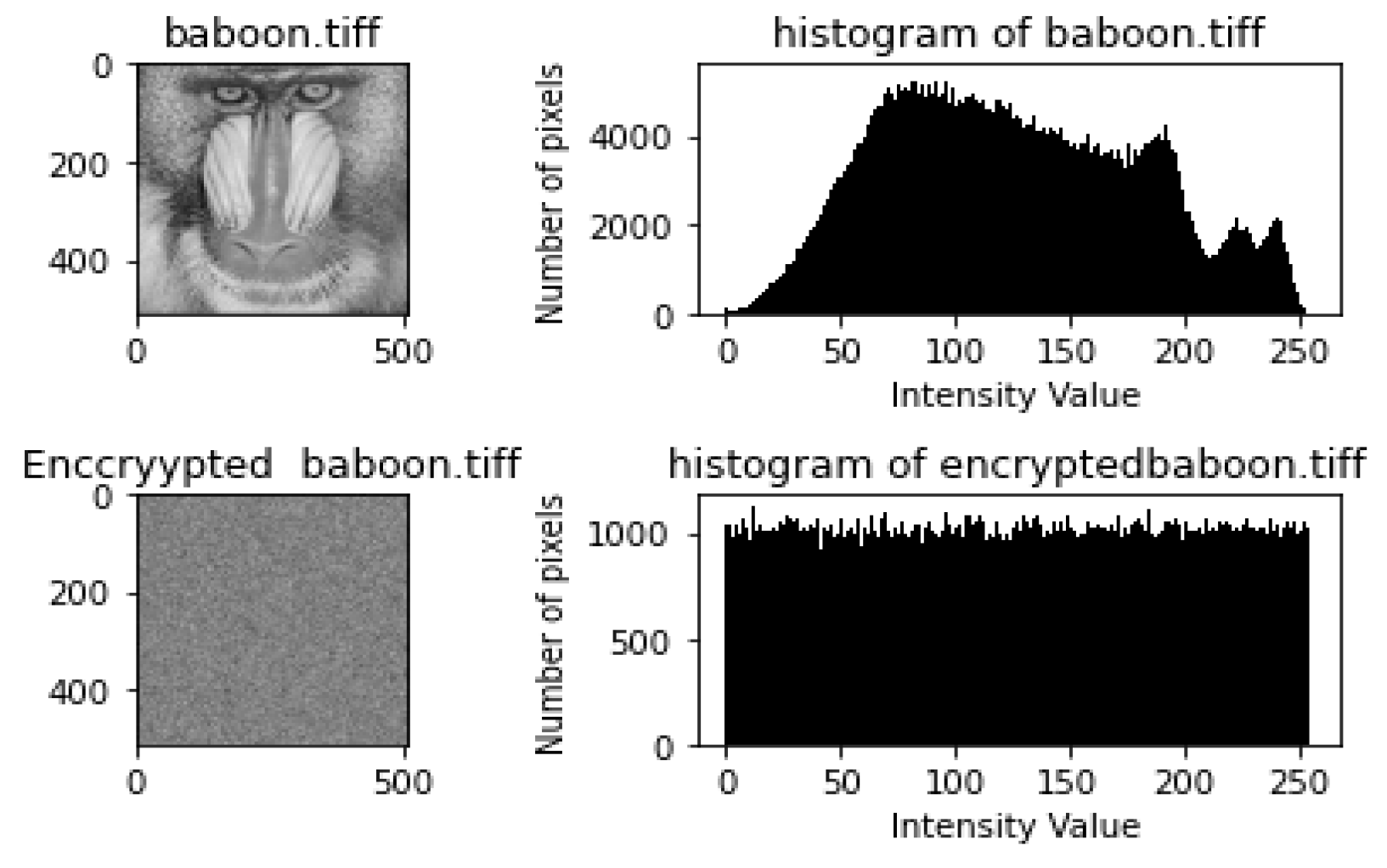
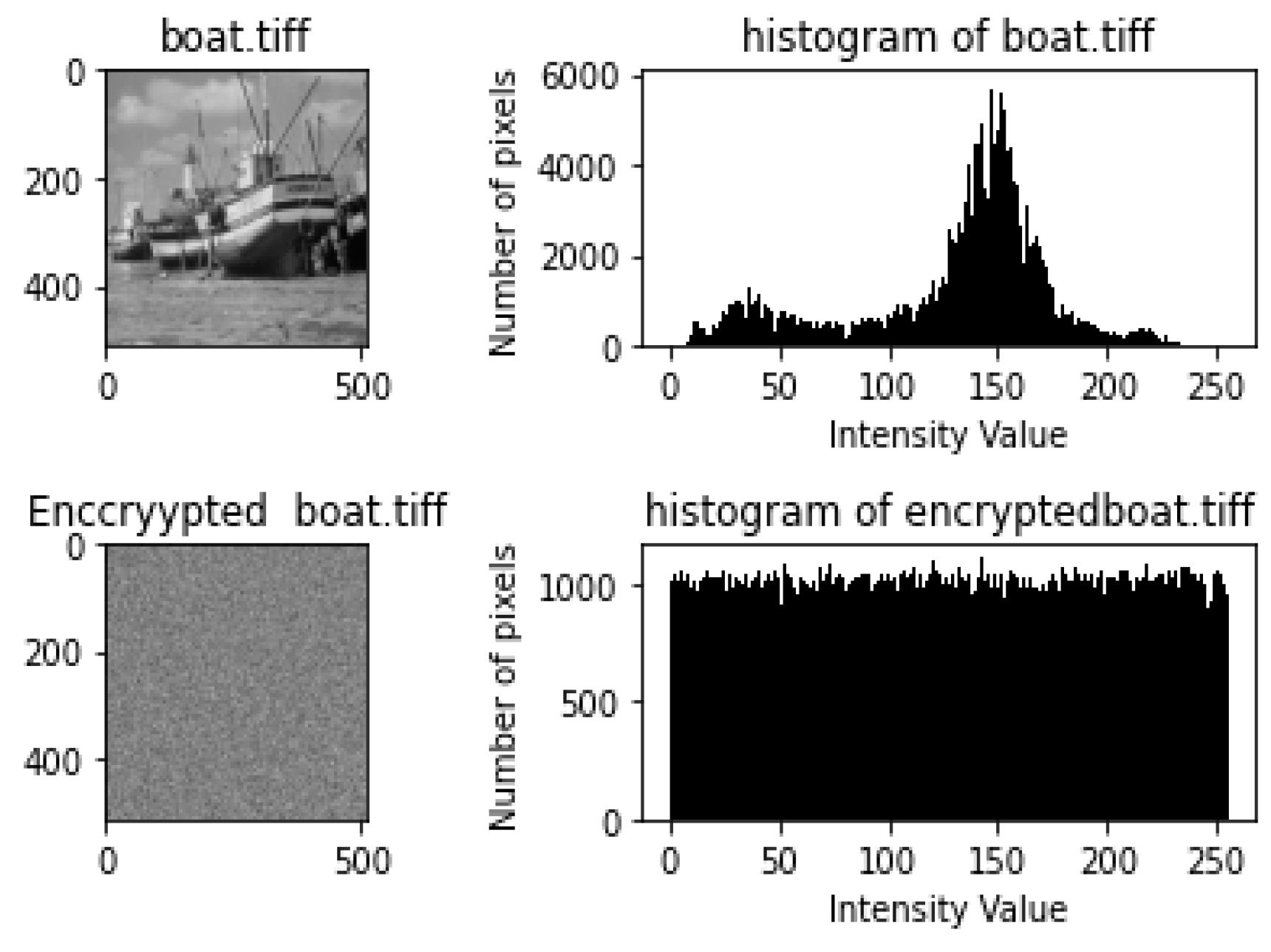
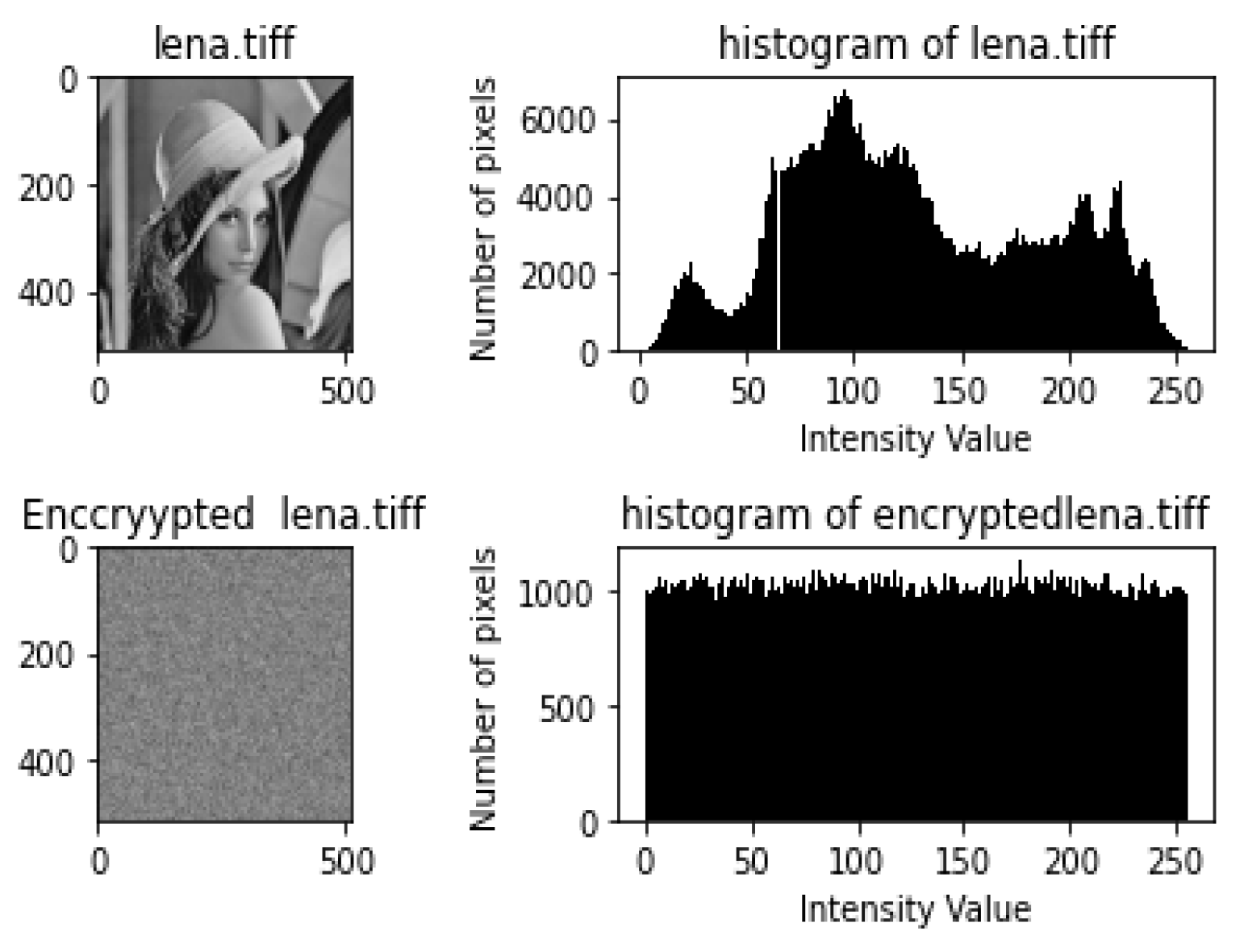
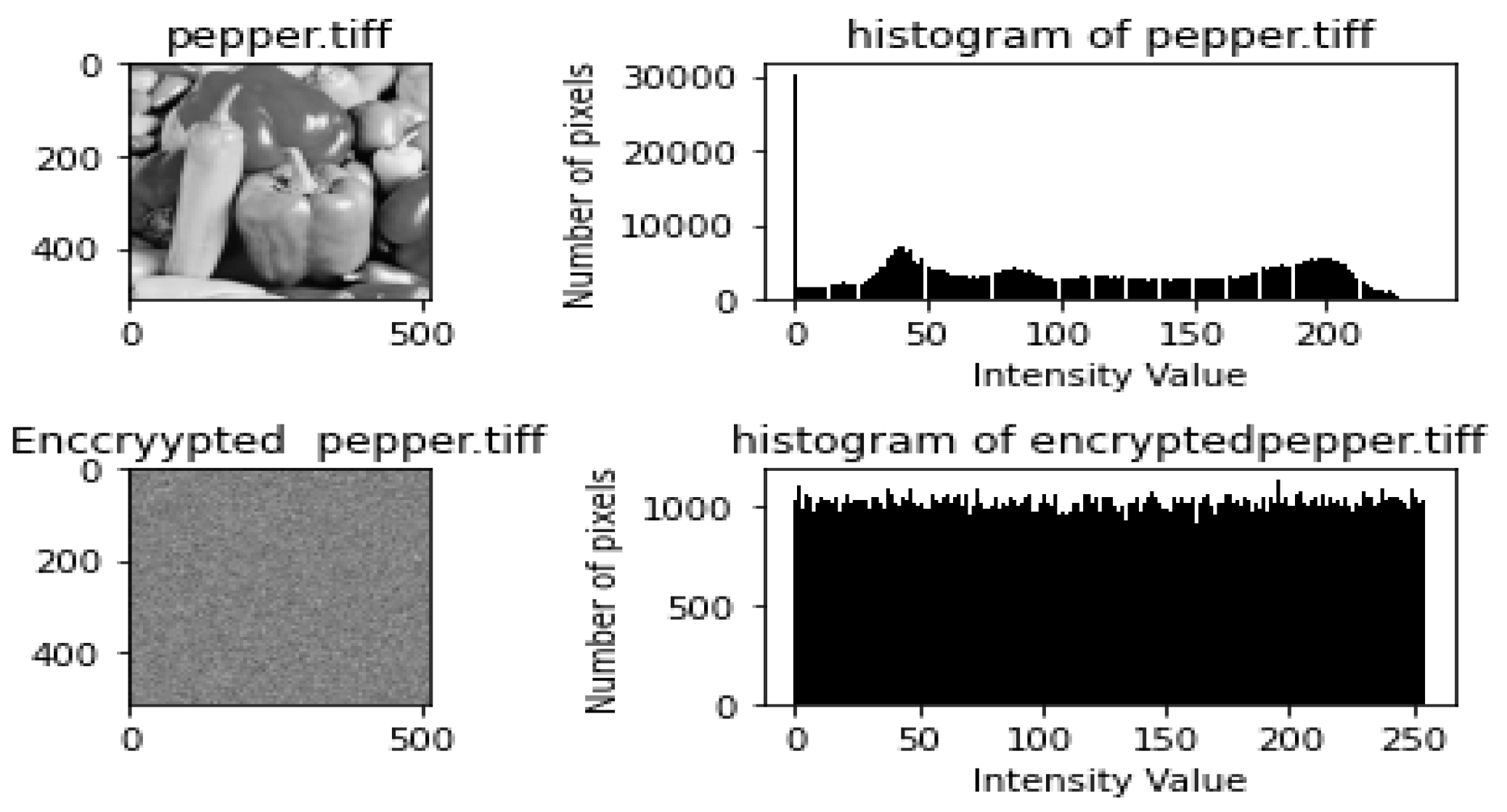
Histogram and Chi-Square Analysis Results

Each of the figures in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 shows the plain image, histogram of the plain image, the cipher image, and histogram of the cipher image, respectively. By visual inspection, the histograms of the plain images are not uniform, while those of the encrypted images appear uniform. The results from the chi-square tests carried out on the histograms are shown in

Table 8. Results of Chi-square analysis for Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

Plain image				Encrypted image
Image	Chi-square	p-Value	Remark	Chi-square	p-Value	Remark
airplane.tiff	564,672.6	0	not uniform	216.5977	0.961	Uniform
baboon.tiff	134,688.4	0	not uniform	225.127	0.911	Uniform
boat.tiff	381,445.8	0	not uniform	280.6582	0.129	Uniform
lena.tiff	91,011.39	0	not uniform	209.1113	0.984	Uniform
pepper.tiff	79,851.4	0	not uniform	289.3418	0.069	Uniform

. As shown in Table 8, the chi-square values for the plain images were very high, while the chi-square values of the encrypted images were very low. The lower the value of chi-square, the more uniform the histogram.

All the p-values of the plain images were found to be less than the significance value; hence, their histogram is not uniform. In contrast, all the p-values of the encrypted images were greater than the significance value of 0.05; hence, they are uniform. These results prove that HXP is resistant to histogram analysis.

ii.

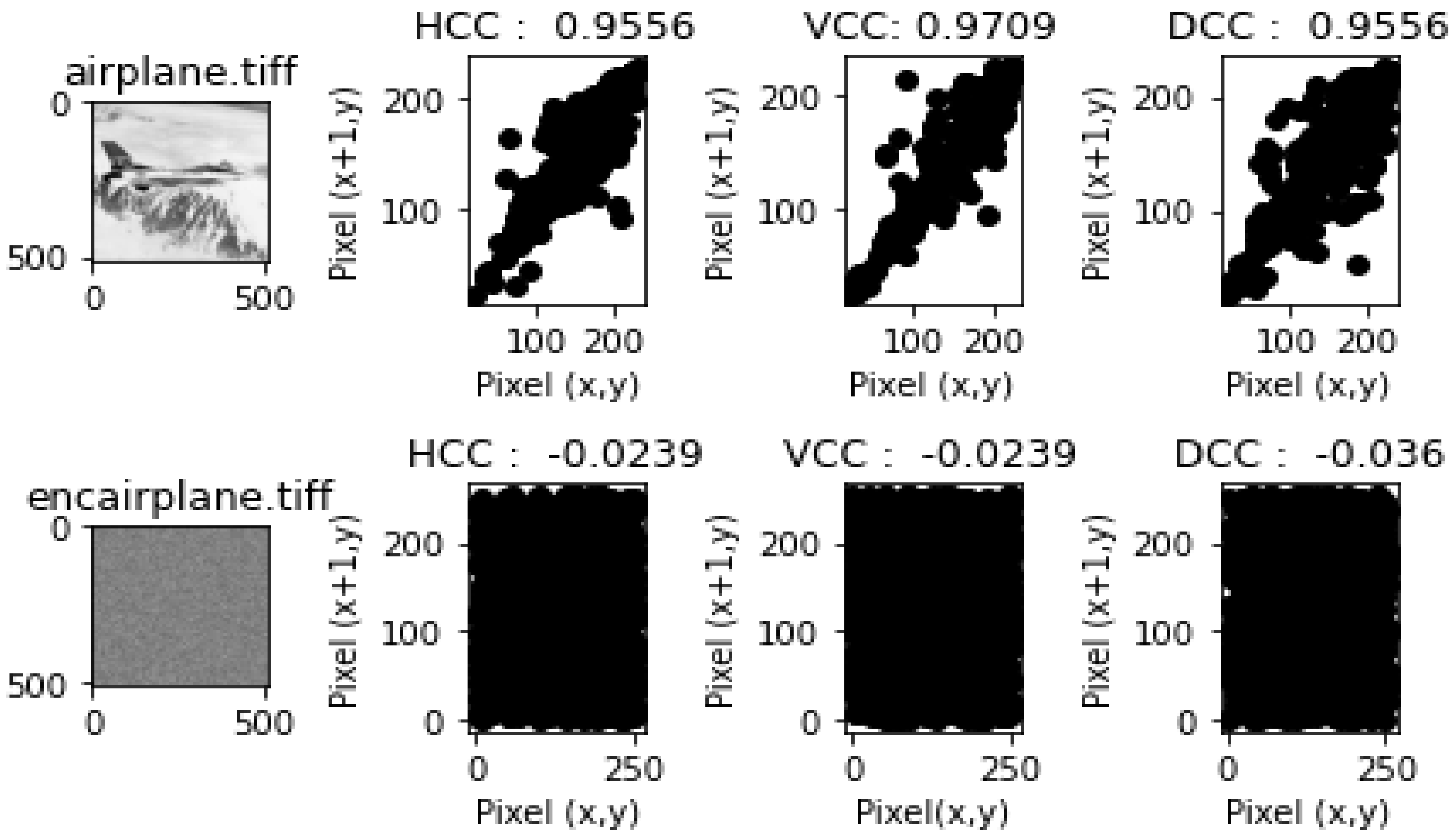
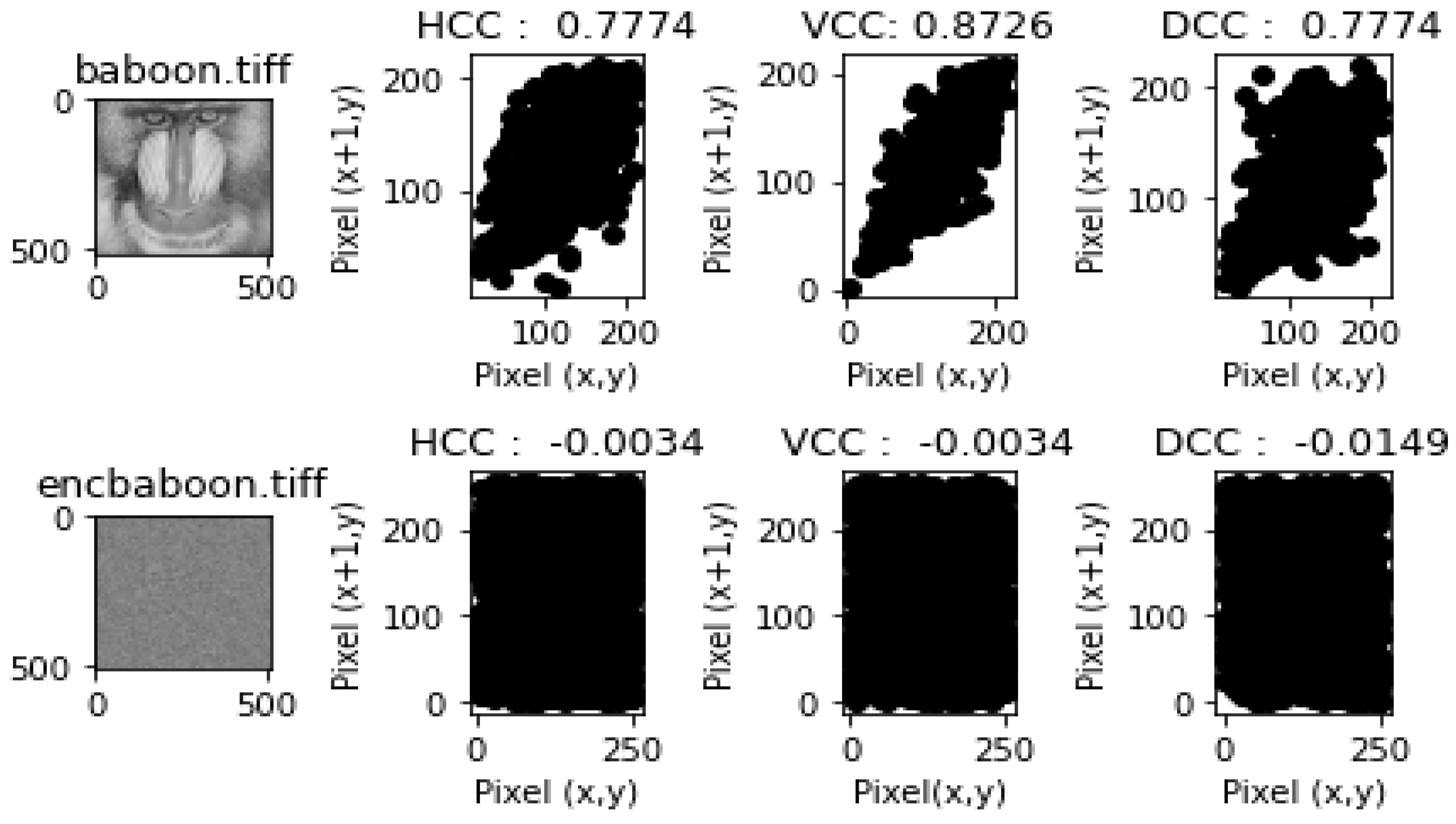
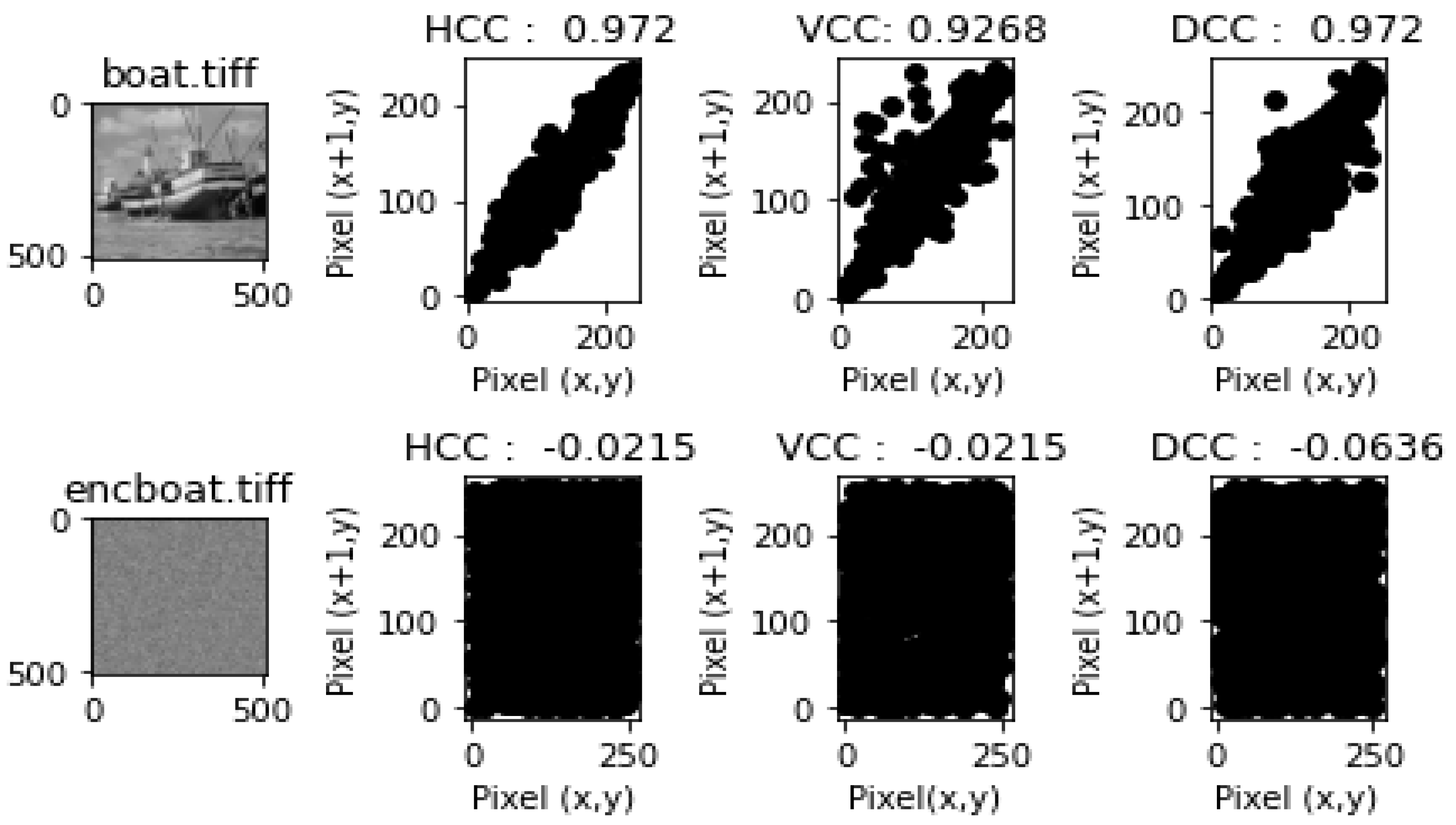
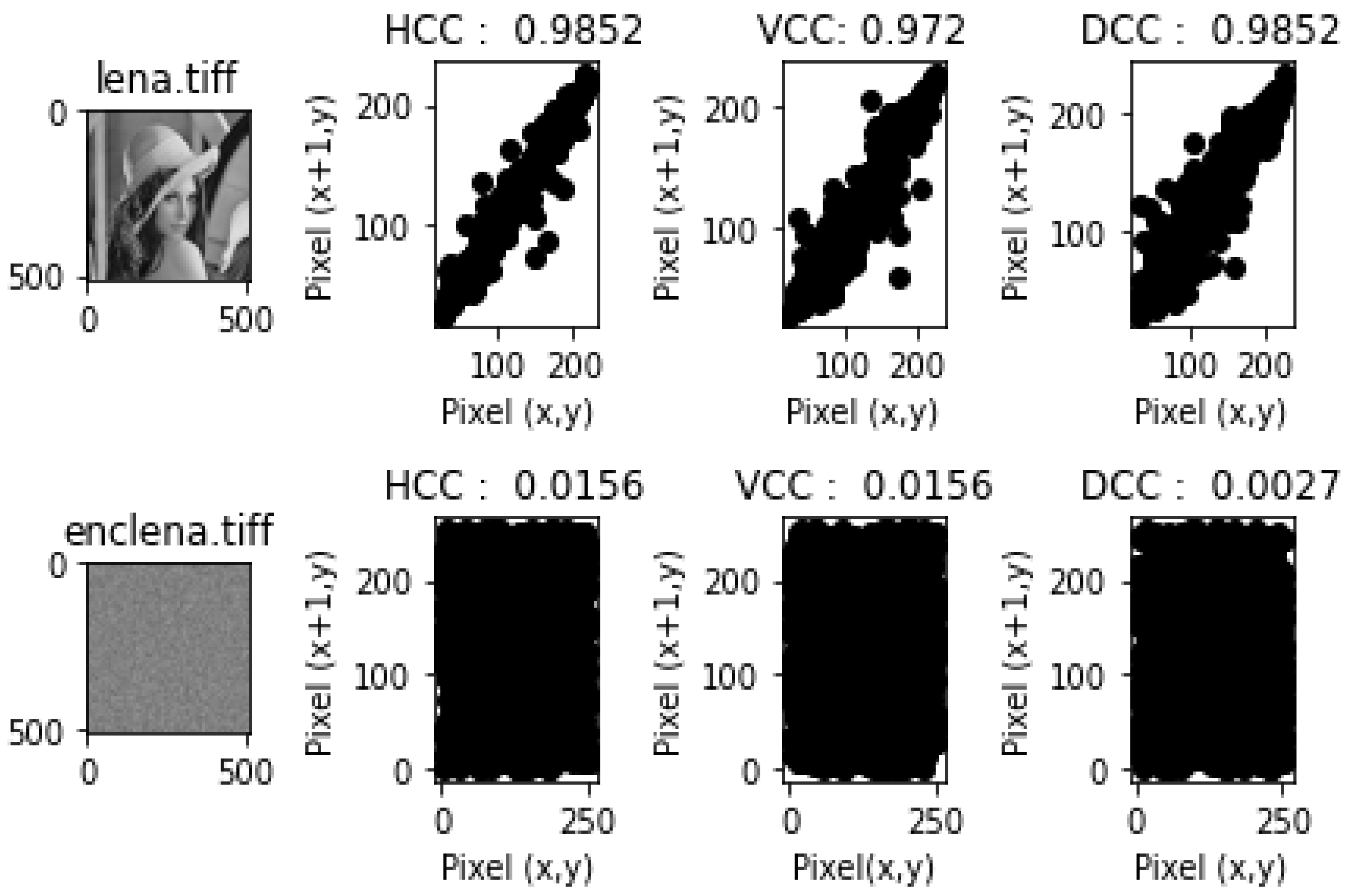
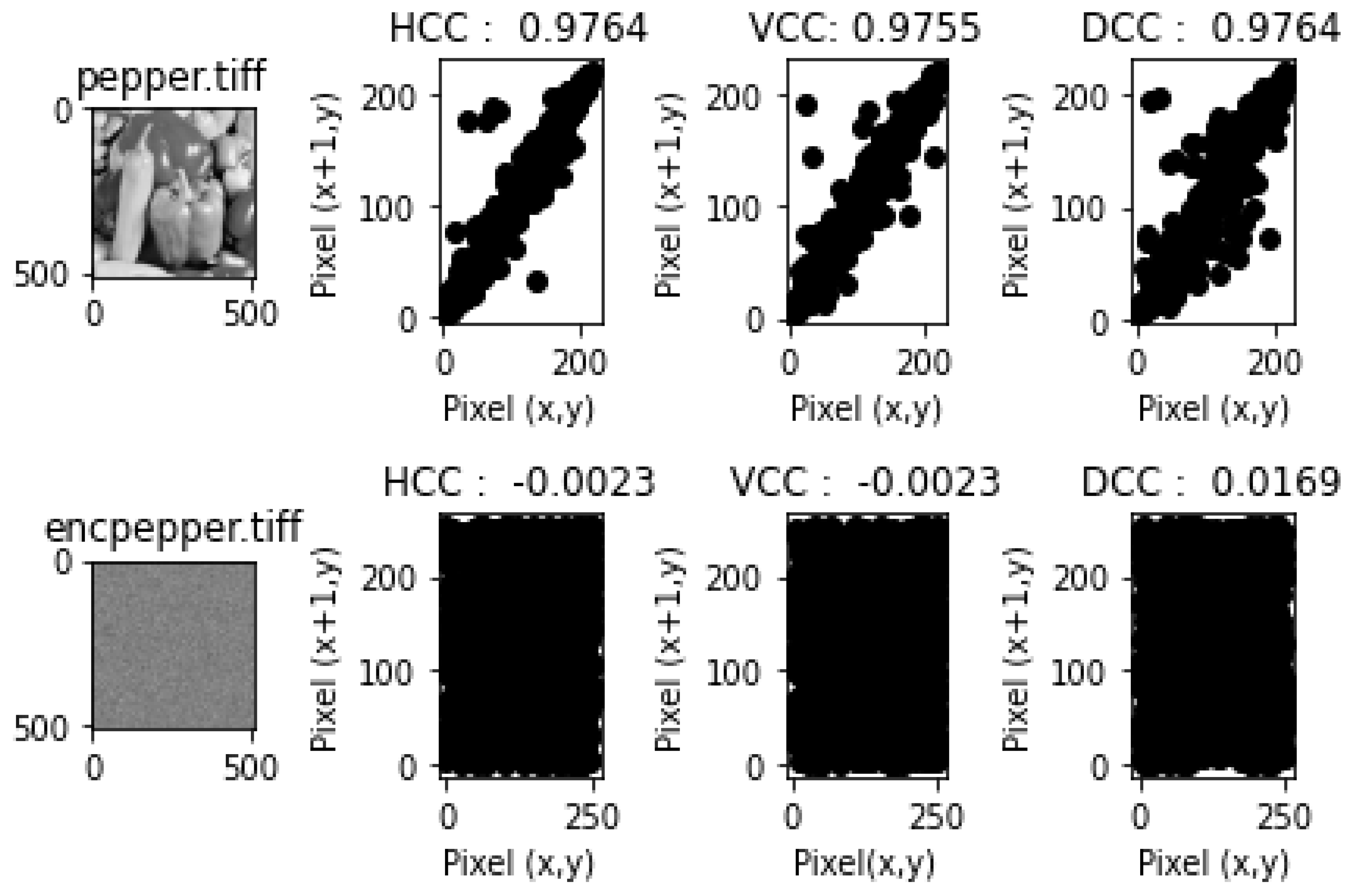
Correlation Coefficient Analysis and Results

Each of the figures in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show the plain image, the graphs of the horizontal correlation coefficient (HCC), the vertical correlation coefficient (VCC), and the diagonal correlation coefficient of the adjacent pixels of the plain image in the first row, and the encrypted image, the graphs of the HCC, VCC, and DCC of the encrypted image in the second row, respectively.

Table 9. Correlation coefficient of the adjacent pixels of the plain and encrypted images in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

	Plain image			Encrypted image
Image	Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal
airplane.tiff	0.9556	0.9709	0.9556	−0.0239	−0.0239	−0.036
baboon.tiff	0.7774	0.8726	0.7774	−0.0034	−0.0034	−0.0149
boat.tiff	0.972	0.9268	0.972	−0.0215	−0.0215	−0.0636
lena.tiff	0.9852	0.972	0.9852	0.0156	0.0156	0.0027
pepper.tiff	0.9764	0.9755	0.9764	−0.0023	−0.0023	0.0169

shows the HCC, VCC, and DCC of the plain and encrypted images in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. As shown in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, the correlation between the adjacent pixels of the plain images was very high for the HCC, VCC, and DCC, while those of the encrypted images appeared to be very low. These results reveal that the proposed lightweight image encryption system can successfully destroy the correlation between the adjacent pixels of the images. Hence, HXP is resistant to correlation coefficient analysis.

iii.

Entropy Analysis Results

Table 10. Entropies of the plain images in Figure 3f–j and the encrypted images in Figure 3k−o.

Image	Plain image	Encrypted image
airplane.tiff	6.66391	7.99934
baboon.tiff	7.76244	7.99941
boat.tiff	7.19137	7.99932
lena.tiff	7.7502	7.99941
pepper.tiff	7.66983	7.99927

shows the information entropies of the plain and encrypted images in Figure 3f–j and Figure 3k–o, respectively. The entropies of the plain images were low (meaning not close to the expected value of eight), while the entropies of the encrypted images were high (close to eight). These results show that HXP introduces enough confusion into the encrypted image; therefore, the encryption system is immune to entropy analysis.

Analysis of Memory Utilization during the Encryption and Decryption Processes of the HXP

Table 11. Memory utilization of the encryption module (Figure 2a) during python implementation.

Line #	Mem usage	Increment	Occurrences	Line contents
92	168.8 MiB	168.8 MiB	1	@ profile
93				def bitmodification(encseed, encryptedtext, bsize):
94	168.8 MiB	0.0 MiB	1	encryptedtext = bytestobinary(encryptedtext)
95	168.8 MiB	0.0 MiB	1	confusionkey = randgen(encseed,len(encryptedtext))
96	168.8 MiB	0.0 MiB	1	lnibble = encryptedtext [0: len(encryptedtext)//2]
97	168.8 MiB	0.0MiB	1	rnibble = encryptedtext[len(encryptedtext)//2: len(encryptedtext)]
98	168.8 MiB	0.0 MiB	2051	xornibble = [str(int(lnibble[i])^int(rnibble[i])) for i in range(len(lnibble))]
99	168.8 MiB			Xornibble = ‘‘.join(xornibble)
100	168.8 MiB	0.0MiB	1	fullbyte = ‘‘.join([xornibble, rnibble])
101	168.8 MiB	0.0MiB	1	fullbyte = reshuffleforencryption(confusionkey,fullbyte)
102	168.8 MiB	0.0MiB	1	encryptedtext = ‘‘.join(fullbyte)
103				#encryptedtext = ‘‘.join(reshuffleforencryption(confusionkey,fullbyte))
104				#encryptedtext = binarytobytes(encryptedtext)
105	168.8 MiB	0.0MiB	1	encryptedtext = list(binarytobytes(encryptedtext))
106	168.8 MiB	0.0MiB	1	return encryptedtext

and

Table 12. Memory utilization of the decryption module during python implementation.

Line #	Mem usage	Increment	Occurrences	Line contents
107	55.0 MiB	55.0 MiB	1	@ profile
108				def reversebitmodification(encseed, ciphertext, bsize):
109	55.0 MiB	0.0 MiB	1	reversebinX = bytestobinary(ciphertext)
110	55.0 MiB	0.0 MiB	1	confusionkey = randgen(encseed,len(reversebinX))
111	55.0 MiB	0.0 MiB	1	reversebinX = reshufflefordecryption(confusionkey, reversebinX)
112	55.0 MiB	0.0 MiB	1	lnibble = reversebinX [0: len(reversebinX)//2]
113	55.0 MiB	0.0 MiB	1	rnibble = reversebinX[len(reversebinX)//2: len(reversebinX)]
114	55.0 MiB	0.0 MiB	2051	Xornibble = [str(int(lnibble[j])^int(rnibble[j])) for j in range(len(lnibble))]
115	55.0 MiB	0.0 MiB	1	Xornibble = ‘‘.join(xornibble)
116	55.0 MiB	0.0 MiB	1	rnibble = ‘‘.join(rnibble)
117	55.0 MiB	0.0 MiB	1	reversebinX = xornibble + rnibble
118	55.0 MiB	0.0 MiB	1	revtext = list (binarytobytes(reversebinX))
119	55.0 MiB	0.0 MiB	1	return revtext

show the memory utilization by each line in the code when the encryption and decryption modules were implemented in python, respectively.

4.2. Comparative Security Analysis of HXP with the Existing Cryptosystems

Table 13. Comparative security analysis of HXP with existing systems.

Metrics	Algorithm	airplane.tiff	baboon.tiff	boat.tiff	lena.tiff	pepper.tiff
PSNR	HXP	8.0041	9.5204	9.2952	9.2399	8.8704
	[57]	7.9804	9.4722	-	8.55	8.8807
	[58]		9.5466		9.2322	8.9914
	[59]	-	9.400680	9.312557	9.287804	-
	[60]	-	9.4474	9.2653	8.5731	8.9603
NCC	HXP	−0.0016	0	0.0009	0.0022	−0.002
	[57]	−0.000004	0.00257	-	−0.0023	−0.011567
	[58]		−0.006632		0.002851	−0.001650
	[60]	-	−0.00070284	−0.00302940	0.003389097	0.002385462
MSE	HXP	10,296.1584	7261.712	7648.1358	7746.154	8434.092
	[57]	10352	7343	-	9080	8414
	[60]	-	7385	7701	9032	8261
	[61]	9980	6583	-	7510	8298
${\chi }^2$	HXP	216.5977	225.127	280.6582	209.1113	289.3418
	[57]	246	259	-	184	270
	[59]	-	274.7051	216.3223	254.5176	-
	[61]	265	266	-	263	274
	[62]	244.65	-	256.31	284.81	281.41
Entropy	HXP	7.99934	7.99941	7.99932	7.99941	7.99927
	[57]	7.9973	7.9972	-	7.9980	7.9970
	[58]	-	7.9970	-	7.9977	7.9973
	[59]	-	7.99924	7.99940	7.99930	-
	[63]	-	7.997436	-	7.997466	7.997355
EQ	HXP	2,869,083.01	750,867.4	1,533,181.18	623,642.2	261,0186
	[57]	259.17	189.78	-	147.20	155.67
	[60]	-	190.76	209.95	146.84	153.52

compares the security of HXP with the existing cryptosystems. The values EQ and entropy of HXP were found to be higher than what was obtainable in other algorithms. These result show that HXP has a better encryption quality and higher diffusion and confusion properties compared to other algorithms under consideration. The lower values of PSNR and NCC are desirable between the plain and encrypted image pixels. From Table 13, the PSNR and NCC values obtained from the analysis of HXP were found to be higher in some images than the PSNR and NCC values produced from the analysis of the existing algorithms. However, the differences observed were within the experimental error limits. These results also attest to the good encryption quality of HXP. The higher values of the MSE were desirable. However, in most of the cases, HXP produced a lower value of MSE than the algorithm proposed by the authors of [57]. These results showed that the algorithm outlined by the authors of [57] has a better MSE than the HXP algorithm. Lower values of chi-square are desirable. From Table 12, it can be seen that the HXP algorithm has a lower value of chi-square in most cases than the existing algorithms. These results are proof that HXP is more resistant to histogram analysis attacks. Generally, the comparative analysis of HXP revealed that HXP performs better than the existing algorithms in terms of security in most cases. It can therefore be said that HXP is more secure than the existing algorithms.

5. Justification of The Suitability of HXP on Resource-Staved IOT Devices

HXP takes after ARX. In ARX, AND, rotation, and XOR operations are used alongside the Feistel structure to achieve non-linearity, diffusion, and confusion properties, which ensure the security of the LWC algorithm. In HXP, the Secure Hash Algorithm (SHA), XOR, and bit permutation operations are used in conjunction with the Feistel structure to achieve non-linearity, diffusion, and confusion properties. Variants of SHA for LWC exist [64]; bit permutations are inexpensive operations that are commonly used to achieve diffusion [65], and of course XOR operations can easily be executed on resource-constrained IoT devices. Hence, HXP can be used on resource-constrained devices. HXP has an advantage over the existing ARX structure, because while ARX can only diffuse half of the block in one round [39], HXP has the capability of diffusing an entire block in a single round. This is achieved through the permutation of the bits that follow the XOR operation.

6. Conclusions and Future Works

In this paper, efforts have been made to implement a lightweight cryptosystem (HXP) that does not make use of a substitution box. Security analysis of the scheme revealed that it has good security and performs better than the existing schemes in terms of its encryption quality (EQ), entropy, and NCC. This scheme has a good plain image and key sensitivity; hence, it is resistant to known plaintext, known ciphertext, chosen plaintext, chosen ciphertext, and differential cryptanalysis attacks. It can therefore be inferred that security of the cryptography algorithm can still be maintained without the use of a substitution box, as demonstrated in this research paper. There is the need to evaluate whether this approach actually led to the reduction in memory usage. In the future, comparative analyses of the proposed scheme in terms of its memory usage, execution time, throughput, as well as power consumption will be carried out.