High-Precision Calculation Using the Method of Analytical Regularization for the Cut-Off Wave Numbers for Waveguides of Arbitrary Cross Sections with Inner Conductors
Abstract
1. Introduction
2. Theoretical Background
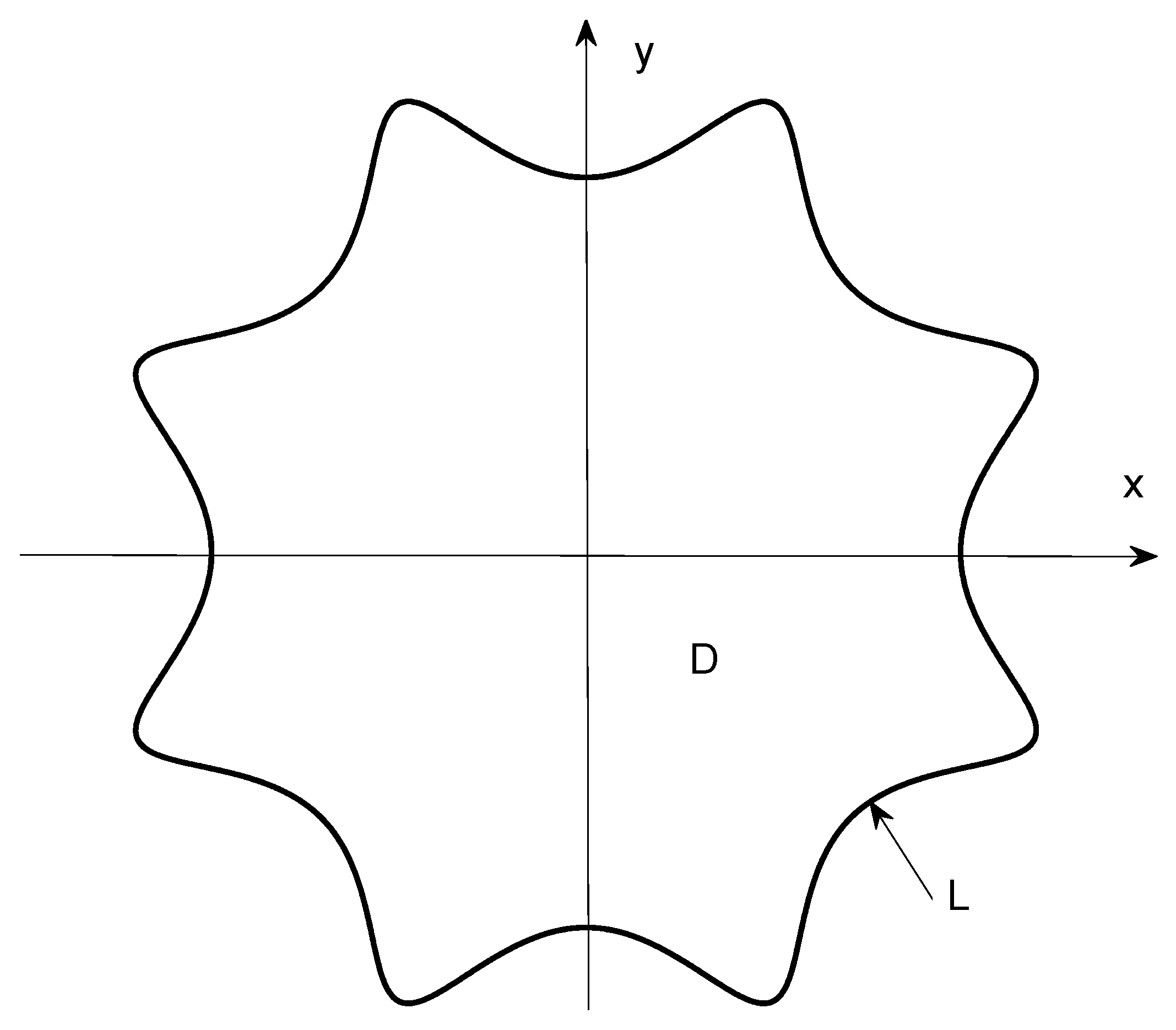
2.1. Hollow Waveguide of Arbitrary Cross Section
2.2. Waveguides of Arbitrary Cross Section Filled by M Metallic Conductors
3. Some Aspects of the Numerical Implementation of the MAR and Cross-Validation with Results Obtained by Other Methods
3.1. Cut-Off Wavenumbers of an Elliptical Waveguide
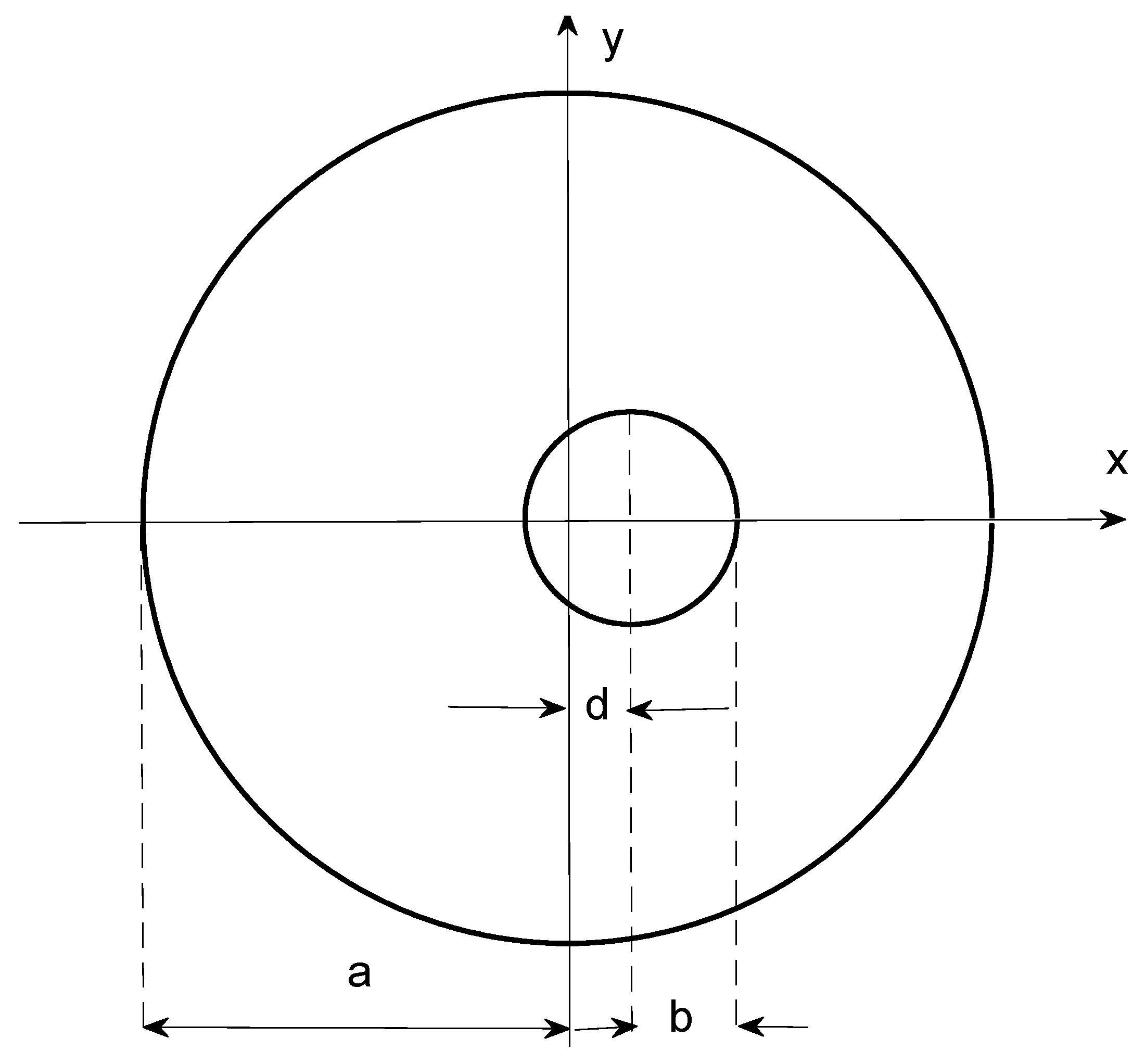
3.2. Waveguides with Circular Outer Conductors and Eccentric Circular Inner Conductors
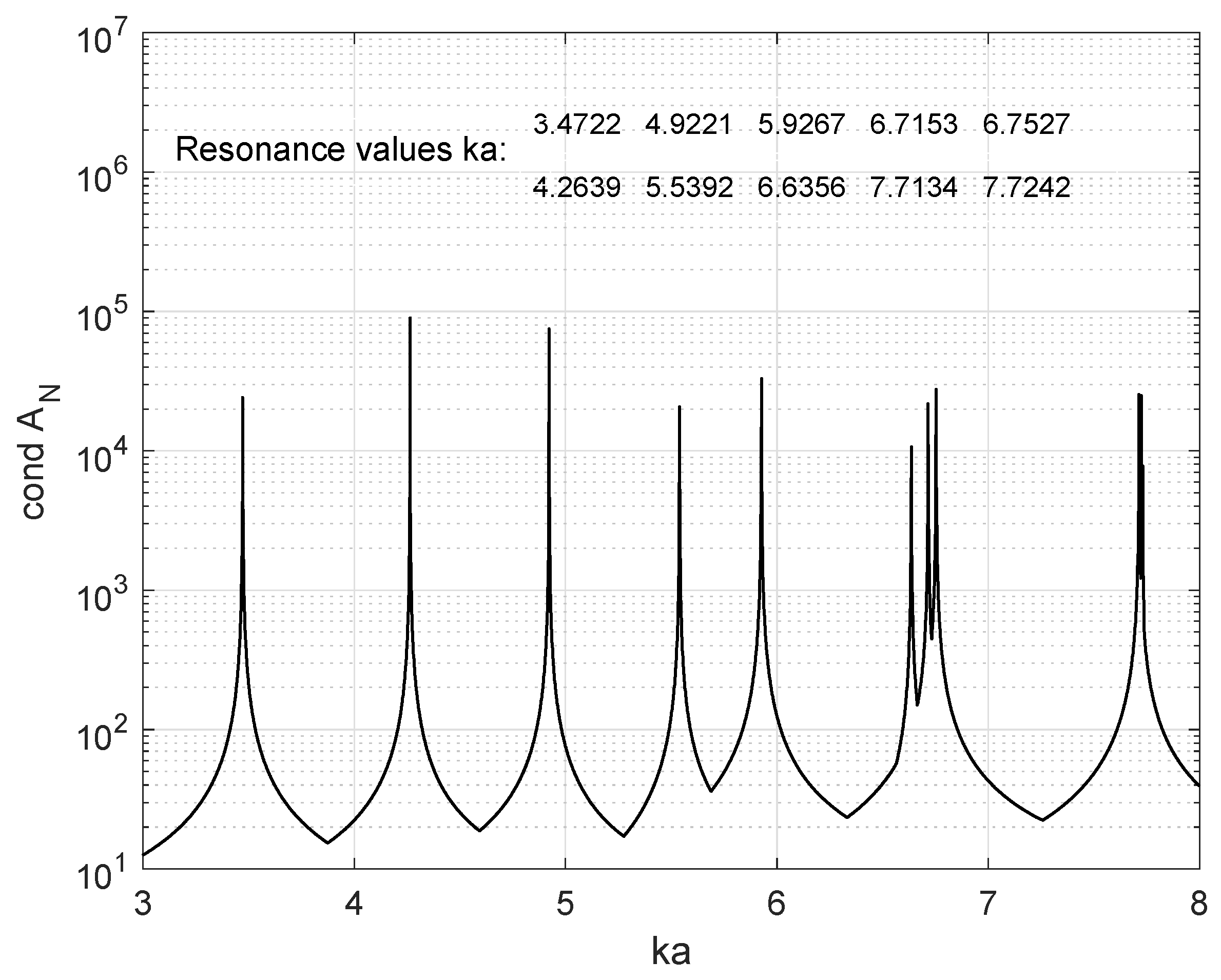
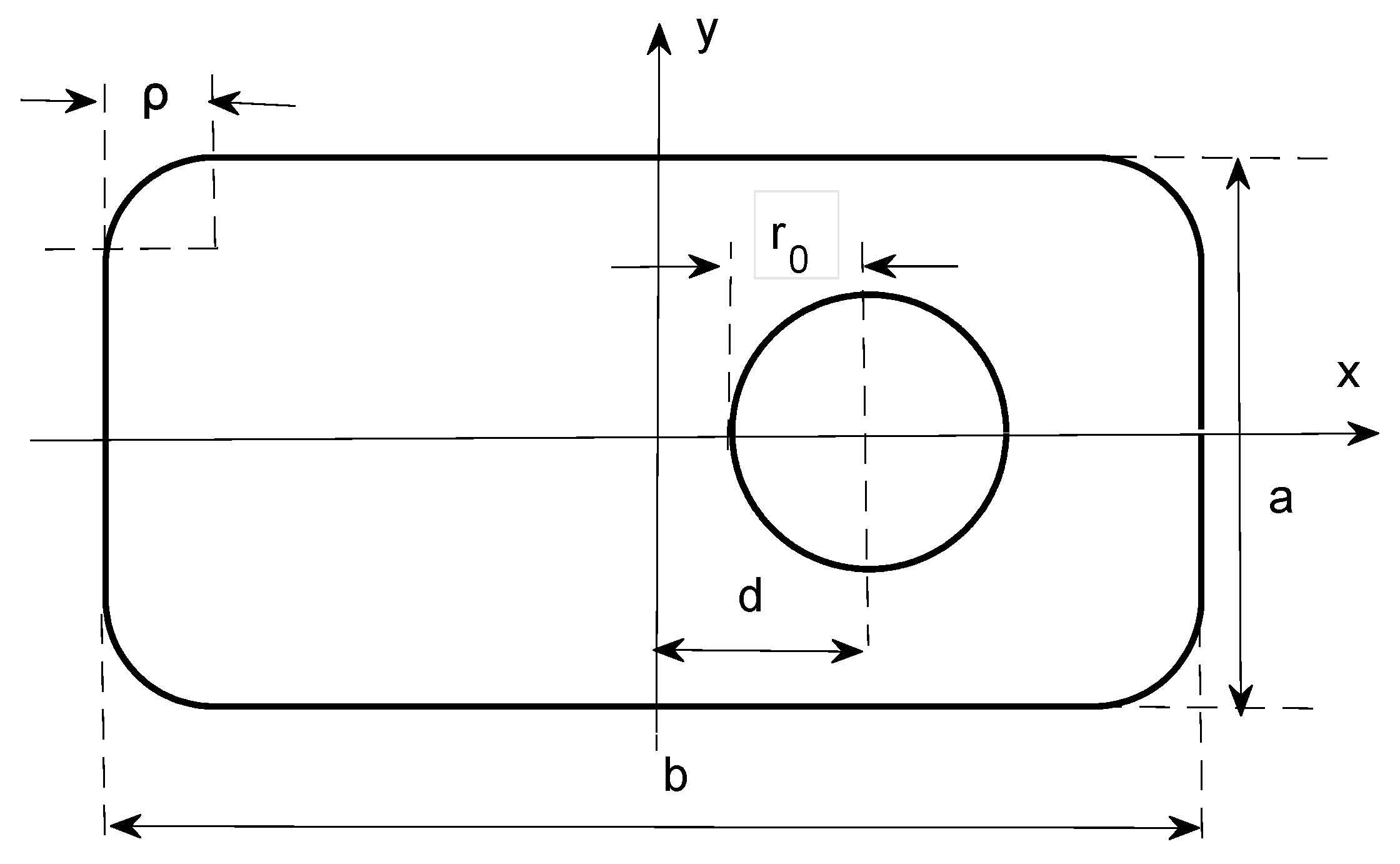
3.3. Analysis of a Circular–Rectangular Waveguide
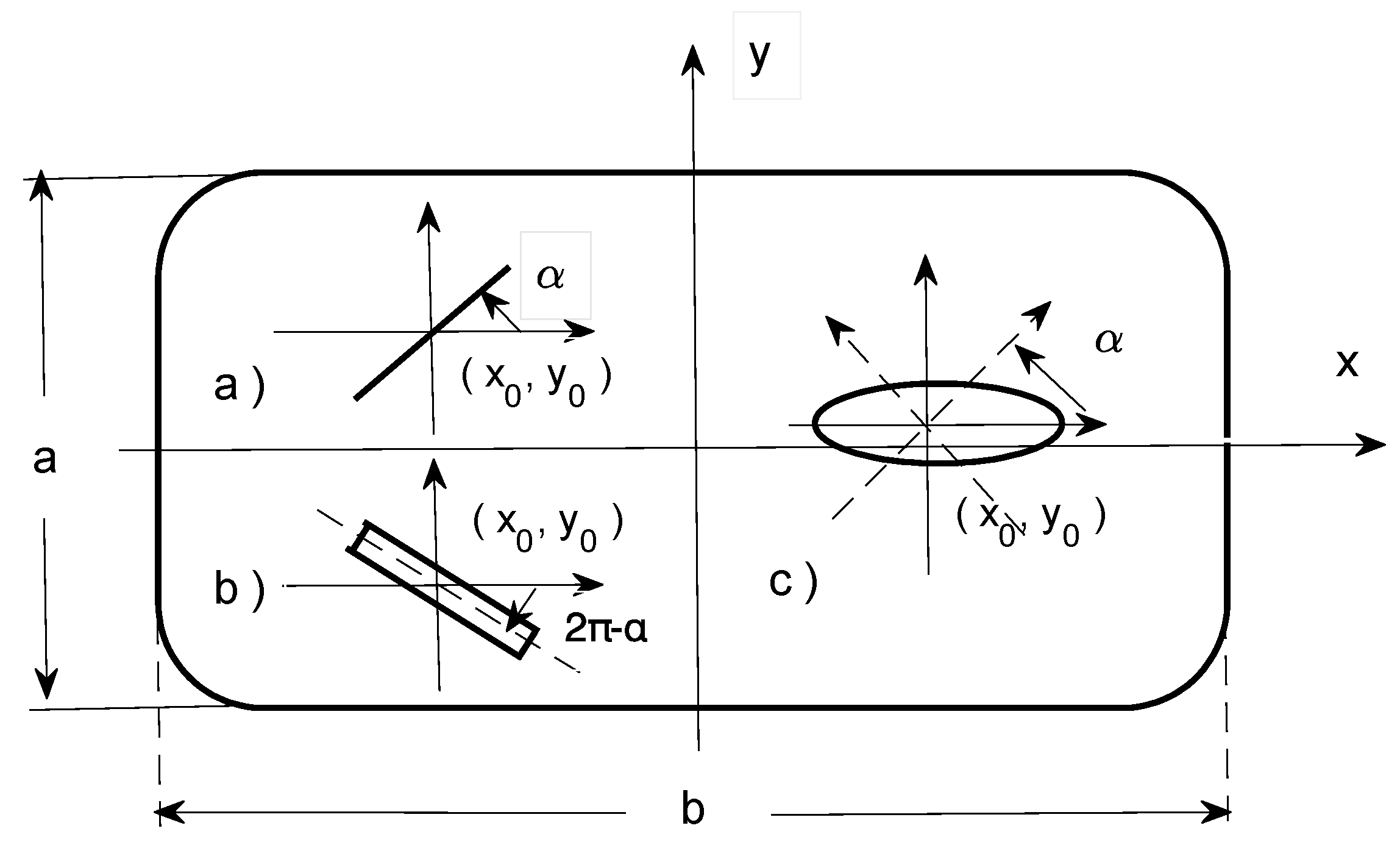
4. Air-Filled Rectangular Waveguides with Arbitrary Located Inner Conductors: Metallic Strips and Strip-like Elliptic Cylinders
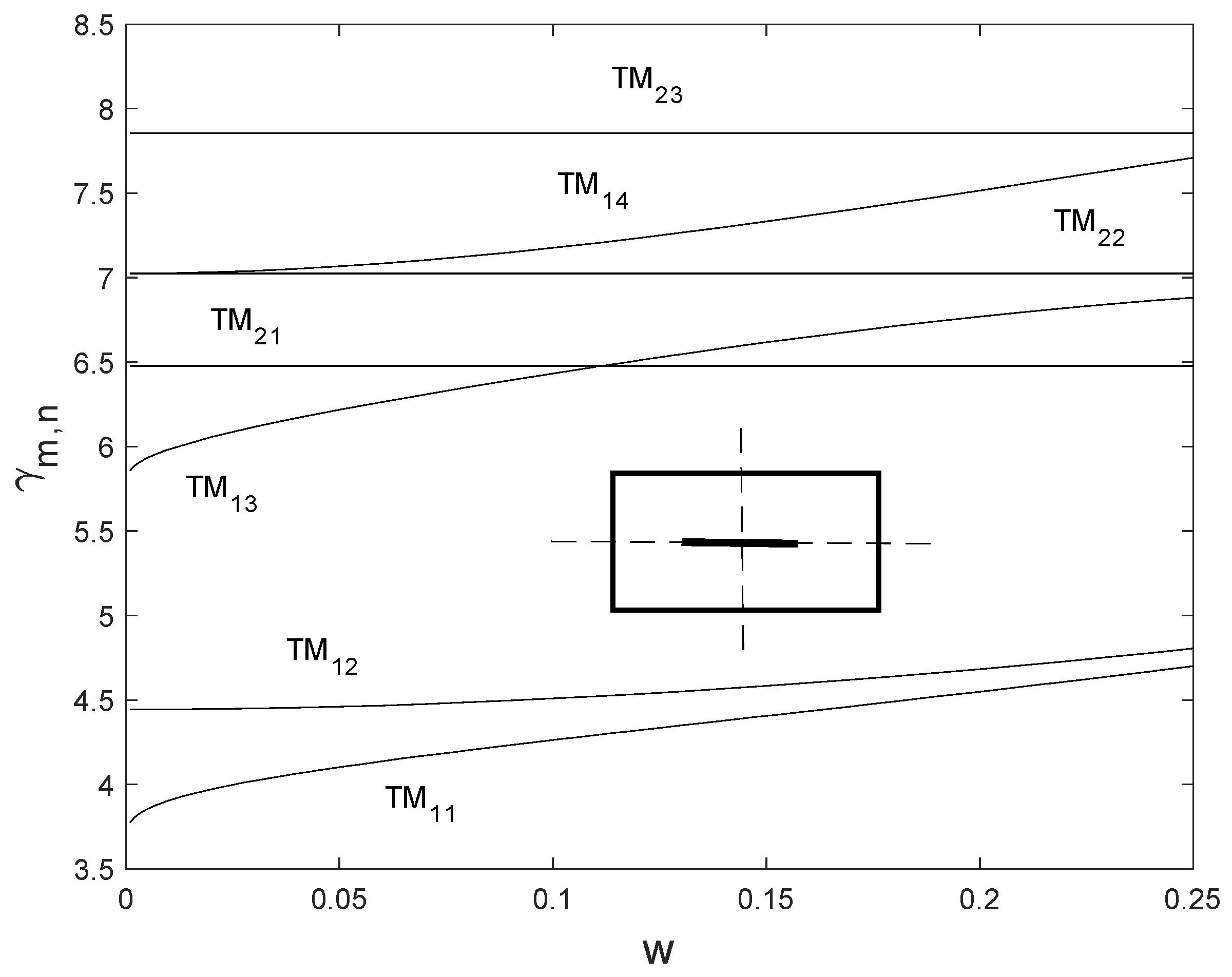
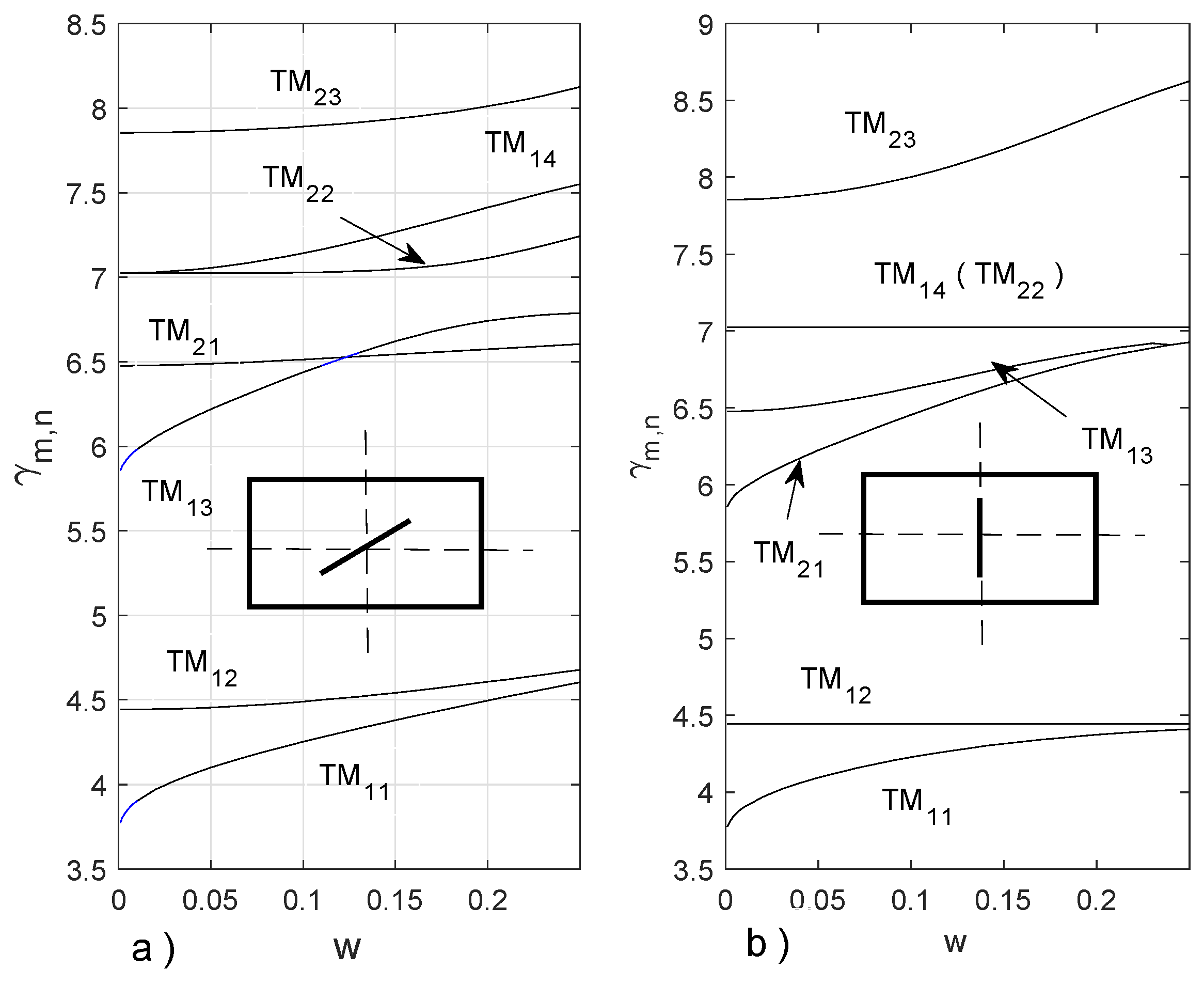
4.1. Waveguide with an Infinitesimally Thin Strip Placed Inside at Varying Locations
4.2. What Is the Difference in Cut-Off Wavenumbers between a Strip of Small but Non-Zero Thickness and an Infinitesimally Thin Strip?
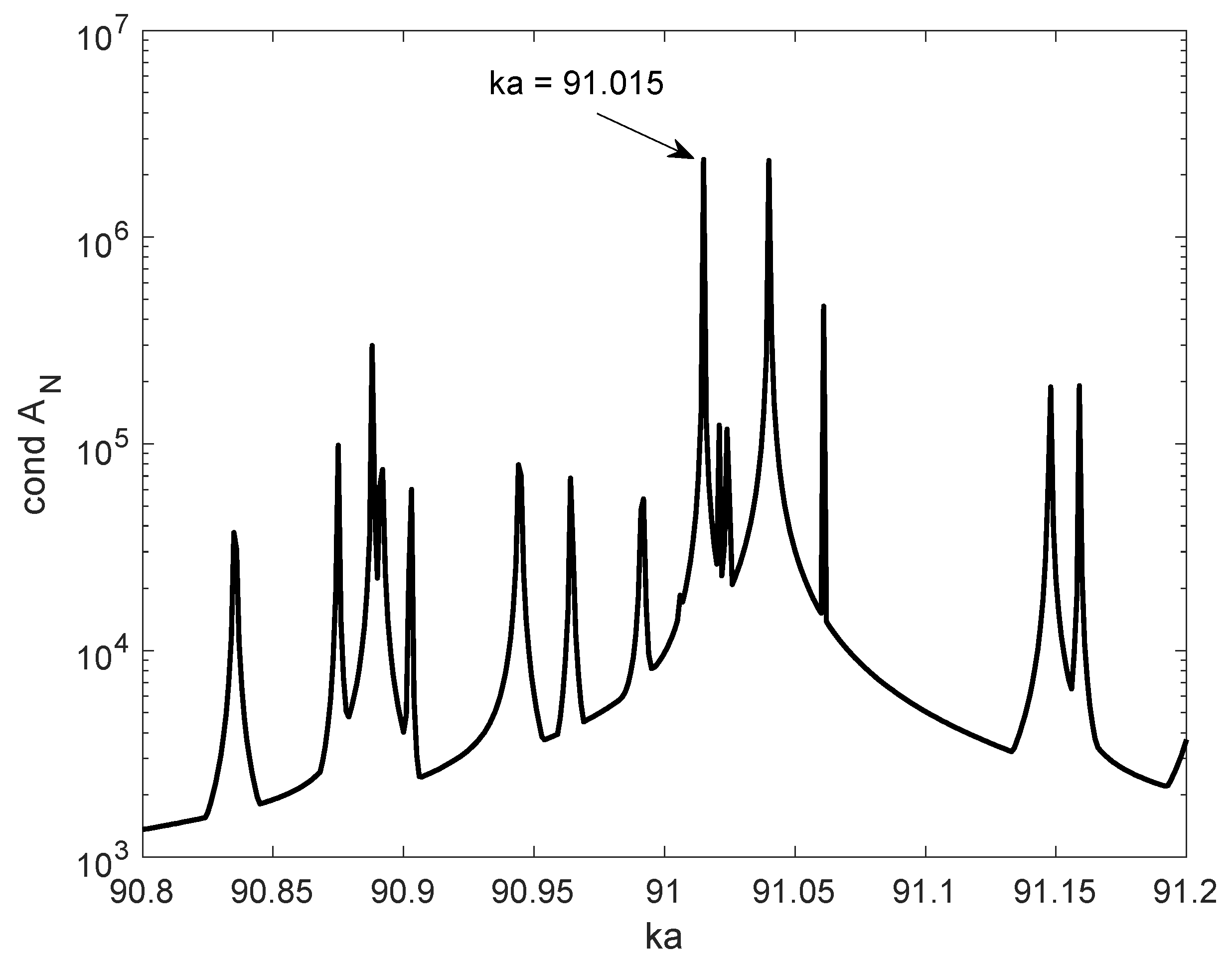
5. Electrically Large Structures
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shestopalov, V.P.; Shestopalov, Y.V. Spectral Theory and Excitation of Open Structures; The Institution of Electrical Engineers: London, UK, 1995. [Google Scholar]
- Shestopalov, Y. Resonance Frequencies of Arbitrarily Shaped Dielectric Cylinders. Appl. Anal. 2021, 102, 1618–1632. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.; Wang, W. Correct Determination of TE and TM Cut-off Wavenumbers in Transmission Lines with Circular Outer Conductors and Eccentric Circular Inner Conductors. IEEE Trans. Microw. Theory Tech. 1991, 39, 1416–1420. [Google Scholar] [CrossRef]
- Roumeliotis, J.A.; Savaidis, S.P. Cut-off Frequencies of Eccentric Circular-Elliptic Metallic Waveguides. IEEE Trans. Microw. Theory Tech. 1994, 42, 2128–2138. [Google Scholar] [CrossRef]
- de la Rubia, V.; Zapata, J. An Efficient Method for Determining TE and TM Modes in Closed Waveguides Made Up of N Cylindrical Conductors. IEEE Trans. Microw. Theory Tech. 2005, 53, 670–678. [Google Scholar] [CrossRef]
- Lee, J.-W.; Chen, J.-T. A Semi-analytical Approach for a Nonconfocal Suspended Strip in an Elliptical Waveguide. IEEE Trans. Microw. Theory Tech. 2012, 60, 3642–3655. [Google Scholar] [CrossRef]
- Omar, A.; Schunemann, K. Application of the Generalized Spectral-Domain Technique to the Analysis of Rectangular Waveguides with Rectangular and Circular Metal Inserts. IEEE Trans. Microw. Theory Tech. 1991, 39, 944–952. [Google Scholar] [CrossRef]
- Chi, M.; Laura, P.A. Approximate Method of Determining the Cut-off Frequencies of Waveguides of Arbitrary Cross Section. IEEE Trans. Microw. Theory Tech. 1964, 12, 248–249. [Google Scholar] [CrossRef]
- Navarro, E.; Such, V. Study of TE and TM Modes in Waveguides of Arbitrary Cross-Section Using an FD-TD Formulation. IEE Proc. H Microw. Antennas Propag. 1993, 139, 491–494. [Google Scholar] [CrossRef]
- Komarov, V.V. Dominant Mode Wave Impedance of Regular Polygonal Waveguides. Int. J. Microw. Sci. Technol. 2014, 2014, 485794. [Google Scholar] [CrossRef][Green Version]
- Gruner, L. Lower and Upper Bounds of Cut-off Frequencies in Metallic Waveguides. IEEE Trans. Microw. Theory Tech. 1992, 40, 995–999. [Google Scholar] [CrossRef]
- Abaka, E.; Baier, W. TE and TM modes in transmission lines with circular outer conductor and eccentric circular inner conductor. Electron. Lett. 1969, 5, 251–252. [Google Scholar] [CrossRef]
- Kuttler, J.R. Cut-off Frequencies of Uniform Waveguides with Lunar or Eccentric Annular Cross Section. IEEE Trans. Microw. Theory Tech. 1984, 32, 348–354. [Google Scholar] [CrossRef]
- Costamagna, E.; Fanni, A. Analysis of rectangular coaxial structures by numerical inversion of the Schwarz-Christoffel transformation. IEEE Trans. Magn. 1992, 28, 1454–1457. [Google Scholar] [CrossRef]
- Lee, C.; Christian, R.; Laura, P. High-order modes in a square coaxial waveguide. Proc. IEEE 1973, 61, 1754–1755. [Google Scholar] [CrossRef]
- Lee, W. Natural mode analysis of an acoustic cavity with multiple elliptical boundaries by using the collocation multipole method. J. Sound Vib. 2011, 330, 4915–4929. [Google Scholar] [CrossRef]
- Nagaya, K.; Poltorak, K. Method for solving eigenvalue problems of the Helmholtz equation with a circular outer and a number of eccentric circular inner boundaries. J. Acoust. Soc. Am. 1989, 85, 576–581. [Google Scholar] [CrossRef]
- Mehl, J.B.; Hill, R.N. Acoustic eigenfrequencies of cavities with an internal obstacle: A modified perturbation theory. J. Acoust. Soc. Am. 1989, 85, 1841–1851. [Google Scholar] [CrossRef]
- Nagaya, K.; Yamaguchi, T. Method for solving eigenvalue problems of the Helmholtz equation with an arbitrarily shaped outer boundary and a number of eccentric inner boundaries of arbitrary shape. J. Acoust. Soc. Am. 1991, 90, 2146–2153. [Google Scholar] [CrossRef]
- Fenech, B.; Jacobsen, F. Predicting the eigenmodes of a cavity containing an array of circular pipes. J. Acoust. Soc. Am. 2005, 117, 63–67. [Google Scholar] [CrossRef]
- Swaminatham, M.; Arvas, E.; Sarkar, T.K.; Djordjevich, A.R. Computation of Cut-off Wavenumbers of TE and TM modes in Waveguides of Arbitrary Cross Sections Using a Surface Integral Formulation. IEEE Trans. Microw. Theory Tech. 1990, 38, 154–159. [Google Scholar] [CrossRef]
- Haq, T.; Koziel, S.; Pietrenko-Dabrowska, A. Resonator-Loaded Waveguide Notch Filters with Broad Tuning Range and Additive-Manufacturing-Based Operating Frequency Adjustment Procedure. Electronics 2023, 12, 4486. [Google Scholar] [CrossRef]
- Vinogradov, S.S.; Smith, P.D.; Vinogradova, E.D. Canonical Problems in Scattering and Potential Theory. Part 1: Canonical Structures in Potential Theory, Part 2: Acoustic and Electromagnetic Diffraction by Canonical Structures; Chapman & Hall/CRC: Boca Raton, FL, USA; New York, NY, USA; Washington, DC, USA, 2002. [Google Scholar]
- Tuchkin, Y.A. Wave scattering by open cylindrical screens of arbitrary profile with Dirichlet boundary conditions. Sov. Phys. Dokl. 1985, 30, 1027–1029. [Google Scholar]
- Tuchkin, Y.A. A New Method in Wave Diffraction Theory by Thin Screens. Electromagnetics 1993, 13, 319–338. [Google Scholar] [CrossRef]
- Safonova, G.; Vinogradova, E.; Tuchkin, Y. Accurate impedance calculations for transmission lines with adjustable inner conductor. Microw. Opt. Technol. Lett. 2014, 56, 2066–2070. [Google Scholar] [CrossRef]
- Vinogradova, E. Electromagnetic plane wave scattering by arbitrary two-dimensional cavities: Rigorous approach. Wave Motion 2017, 70, 47–64. [Google Scholar] [CrossRef]
- Vinogradova, E.D. Complex eigenvalues of slotted arbitrary cylindrical cavities: Sound-soft elliptic cavity with variably placed longitudinal slit. J. Acoust. Soc. Am. 2018, 144, 1146–1153. [Google Scholar] [CrossRef] [PubMed]
- Safonova, G.; Vinogradova, E. Accurate backscattering studies for double-layered array of infinitely long cylinders. Microw. Opt. Technol. Lett. 2013, 55, 2127–2131. [Google Scholar] [CrossRef]
- Shestopalov, Y.V.; Smirnov, Y.G.; Chernokozhin, E.V. Logarithmic Integral Equations in Electromagnetics; Walter de Gruyter GmbH: Berlin, Germany, 2000; ISBN 9783110942057. [Google Scholar]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Wang, H.; Wu, K.-L.; Litva, J. The Higher Order Modal Characteristics of Circular-Rectangular Coaxial Waveguides. IEEE Trans. Microw. Theory Tech. 1997, 45, 414–419. [Google Scholar] [CrossRef][Green Version]
- Smith, P.D.; Markowskei, A.J. Rounding the Corners of Scatterers: A Perturbation Analysis of Far-Field Changes. URSI Radio Sci. Lett. 2021, 3, 1–3. [Google Scholar] [CrossRef]



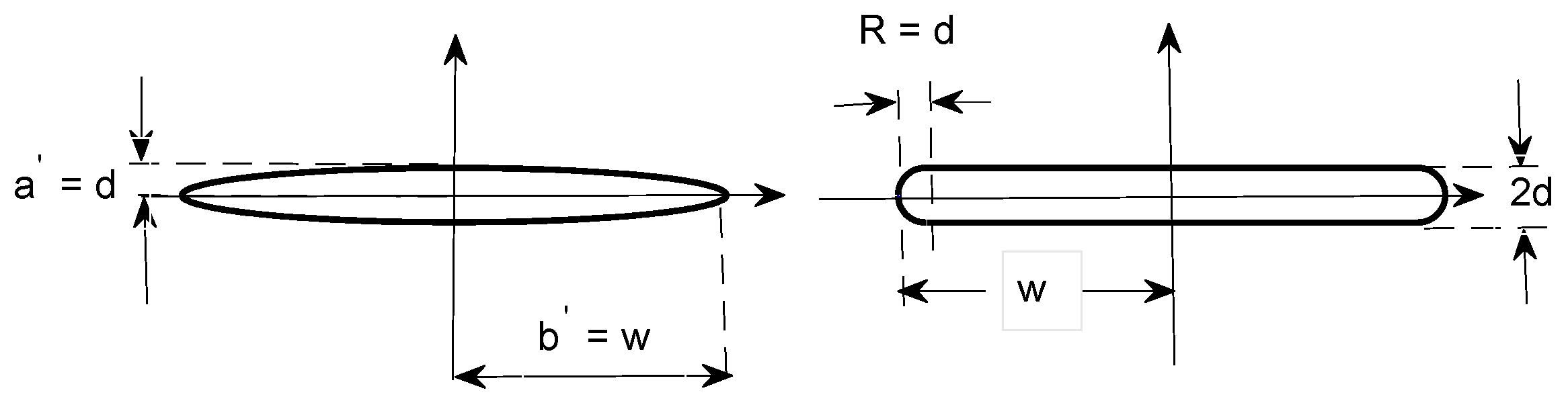
| Truncation Number N | Computed Value of |
|---|---|
| 32 | 2.410633039187760 − i · 0.000000066967616 |
| 64 | 2.410857871457190 − i · 0.000000001040154 |
| 128 | 2.410885878808779 − i · 0.000000000016227 |
| 256 | 2.410889376581807 − i · 0.000000000000253 |
| 512 | 2.410889813714743 − i · 0.000000000000004 |
| 1024 | 2.410889868251958 − i · 0.000000000000000 |
| 2048 | 2.410889875181512 − i · 0.000000000000000 |
| 4096 | 2.410889876035204 − i · 0.000000000000000 |
| Method | MAR | [28] | MAR | [28] | MAR | [28] |
|---|---|---|---|---|---|---|
| e = 0.1 | 2.41088987 | 2.41088987 | 3.83653893 | 3.83653893 | 3.84619062 | 3.84619061 |
| e = 0.5 | 2.59677924 | 2.59677924 | 3.98640797 | 3.98640797 | 4.28221524 | 4.28221523 |
| e = 0.9 | 4.21513438 | 4.21513437 | 5.41326079 | 5.41326080 | 7.76364414 | 7.76364415 |
| Symmetric Modes | Anti-Symmetric Modes | ||
|---|---|---|---|
| L. Zhang et al. [3] | MAR | L. Zhang et al. [3] | MAR |
| 3.4723 | 3.47226067 | 4.2640 | 4.26396049 |
| 4.9221 | 4.92212067 | 5.5393 | 5.53930291 |
| 5.9268 | 5.92681068 | 6.6357 | 6.63570629 |
| 6.7154 | 6.71544084 | 7.7135 | 7.71353358 |
| 6.7527 | 6.75275190 | 7.7243 | 7.72430654 |
| Truncation Number N | Computed Cut-Off Wavenumber of the Lowest Symmetric Mode | Time (Seconds) |
|---|---|---|
| 64 | 3.472157345180335 − i · 0.000000009781369 | 1.796 |
| 128 | 3.472247785036224 − i · 0.000000000152295 | 3.121 |
| 256 | 3.472259067569722 − i · 0.000000000002378 | 10.515 |
| 512 | 3.472260477172100 − i · 0.000000000000037 | 10.515 |
| 1024 | 3.472260653349862 − i · 0.000000000000001 | 207.292 |
| 2048 | 3.472260675371377 − i · 0.000000000000000 | 1340.219 |
| 4096 | 3.472260678124045 − i · 0.000000000000000 |
| TM-Mode | MAR, ϱ = 0.1 cm | MAR, ϱ = 0.02 cm | MAR, ϱ = 0.005 cm | H. Wang et al. [30] |
|---|---|---|---|---|
| TM11 | 1.9948124 | 1.9948058 | 1.9948058 | 1.9948099 |
| TM21 | 1.9953724 | 1.9953659 | 1.9953659 | 1.9953650 |
| TM12 | 2.8694972 | 2.8694828 | 2.8694828 | 2.8694867 |
| TM22 | 2.8721943 | 2.8721798 | 2.87217979 | 2.8721777 |
| TM31 | 3.3197479 | 3.3197356 | 3.3197356 | 3.3197216 |
| TM41 | 3.3265163 | 3.3265037 | 3.3265037 | 3.3264943 |
| TM32 | 3.7716492 | 3.7716114 | 3.7716117 | 3.7715987 |
| TM42 | 3.7941610 | 3.7941210 | 3.7941210 | 3.7941012 |
| TM51 | 3.9730566 | 3.9730249 | 3.9730250 | 3.9728472 |
| TM23 | 3.9844121 | 3.9843794 | 3.9843793 | 3.9843494 |
| Truncation Number N | TM11 | TM22 | TM23 |
|---|---|---|---|
| 128 | 1.99478678 | 2.87210785 | 3.98418755 |
| 512 | 1.99480566 | 2.87217868 | 3.98437637 |
| 1024 | 1.99480584 | 2.87217966 | 3.98437902 |
| 2048 | 1.99480588 | 2.87217979 | 3.98437935 |
| 4096 | 2.87217980 | 3.98437939 |
| w = 0.25 | w = 0.3 | w = 0.4 | w = 0.48 | ||||
|---|---|---|---|---|---|---|---|
| 7.02480 | 7.024814 | 6.98625 | 6.986267 | 7.02256 | 7.022578 | 7.02480 | 7.024814 |
| 6.99220 | 6.992208 | 7.02266 | 7.022682 | ||||
| 7.02480 | 7.024814 | 7.02480 | 7.024814 | ||||
| TM1,1 | TM1,2 | TM1.3 | TM2,1 | TM2,2 | TM1,4 | TM2,3 | ||
|---|---|---|---|---|---|---|---|---|
| Thin strip | 0.000 | 4.699720 | 4.804192 | 6.475592 | 6.880896 | 7.024814 | 7.710194 | 7.853981 |
| Elliptic strips | 0.005 | 4.702703 | 4.805858 | 6.482328 | 6.888568 | 7.025587 | 7.713700 | 7.857580 |
| 0.000635 | 0.000347 | 0.001040 | 0.001115 | 0.000110 | 0.000455 | 0.000458 | ||
| 0.01 | 4.705672 | 4.807522 | 6.488118 | 6.896279 | 7.026372 | 7.717212 | 7.861226 | |
| 0.001266 | 0.000693 | 0.001934 | 0.002236 | 0.000222 | 0.000910 | 0.000922 | ||
| 0.02 | 4.711575 | 4.810844 | 6.499754 | 6.911824 | 7.027974 | 7.724254 | 7.868661 | |
| 0.002522 | 0.001385 | 0.003731 | 0.004495 | 0.000450 | 0.001824 | 0.001869 | ||
| 0.05 | 4.728984 | 4.820755 | 6.535065 | 6.959426 | 7.033045 | 7.745534 | 7.892164 | |
| 0.006227 | 0.003448 | 0.009184 | 0.011413 | 0.001172 | 0.004584 | 0.004862 |
| TM1,1 | TM1,2 | TM1.3 | TM2,1 | TM2,2 | TM1,4 | TM2,3 | ||
|---|---|---|---|---|---|---|---|---|
| Thin strip | 0.000 | 4.699720 | 4.804192 | 6.475592 | 6.880896 | 7.024814 | 7.710194 | 7.853981 |
| Thick strips | 0.01 | 4.730638 | 4.826366 | 6.506220 | 6.928066 | 7.030347 | 7.749254 | 7.870873 |
| 0.006579 | 0.004616 | 0.004730 | 0.006855 | 0.000788 | 0.005066 | 0.002151 | ||
| 0.02 | 4.754750 | 4.843135 | 6.536790 | 6.972584 | 7.036501 | 7.780812 | 7.888865 | |
| 0.011709 | 0.008106 | 0.009451 | 0.013325 | 0.001664 | 0.009159 | 0.004442 | ||
| 0.05 | 4.816639 | 4.886328 | 6.631948 | 7.058027 | 7.107963 | 7.867458 | 7.950136 | |
| 0.024878 | 0.017097 | 0.024145 | 0.025742 | 0.011836 | 0.020397 | 0.012243 |
| Truncation Number N | Computed Value of γ |
|---|---|
| 128 | 91.026520534035598 − i · 0.000032228513004 |
| 256 | 91.022057188386270 − i · 0.001314350150315 |
| 512 | 91.020887459853000 − i · 0.000012035120209 |
| 1024 | 91.018051214398398 − i · 0.000000181342561 |
| 2048 | 91.018431876293164 − i · 0.000000002809210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinogradova, E.; Smith, P.; Shestopalov, Y. High-Precision Calculation Using the Method of Analytical Regularization for the Cut-Off Wave Numbers for Waveguides of Arbitrary Cross Sections with Inner Conductors. Appl. Sci. 2024, 14, 2265. https://doi.org/10.3390/app14062265
Vinogradova E, Smith P, Shestopalov Y. High-Precision Calculation Using the Method of Analytical Regularization for the Cut-Off Wave Numbers for Waveguides of Arbitrary Cross Sections with Inner Conductors. Applied Sciences. 2024; 14(6):2265. https://doi.org/10.3390/app14062265
Chicago/Turabian StyleVinogradova, Elena, Paul Smith, and Yury Shestopalov. 2024. "High-Precision Calculation Using the Method of Analytical Regularization for the Cut-Off Wave Numbers for Waveguides of Arbitrary Cross Sections with Inner Conductors" Applied Sciences 14, no. 6: 2265. https://doi.org/10.3390/app14062265
APA StyleVinogradova, E., Smith, P., & Shestopalov, Y. (2024). High-Precision Calculation Using the Method of Analytical Regularization for the Cut-Off Wave Numbers for Waveguides of Arbitrary Cross Sections with Inner Conductors. Applied Sciences, 14(6), 2265. https://doi.org/10.3390/app14062265








