Single-Shot Full Characterization of the Spatial Wavefunction of Light Fields via Stokes Tomography
Abstract
1. Introduction
2. Principle and Methods
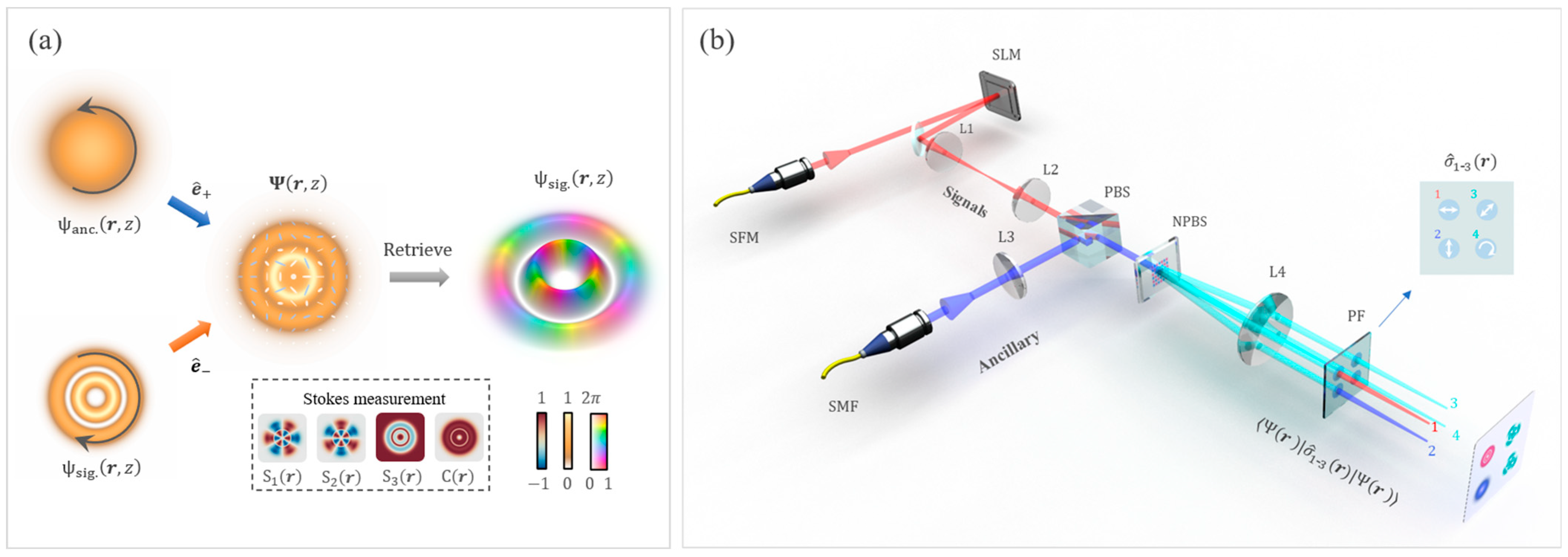
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Hermite–Laguerre–Gaussian Modes
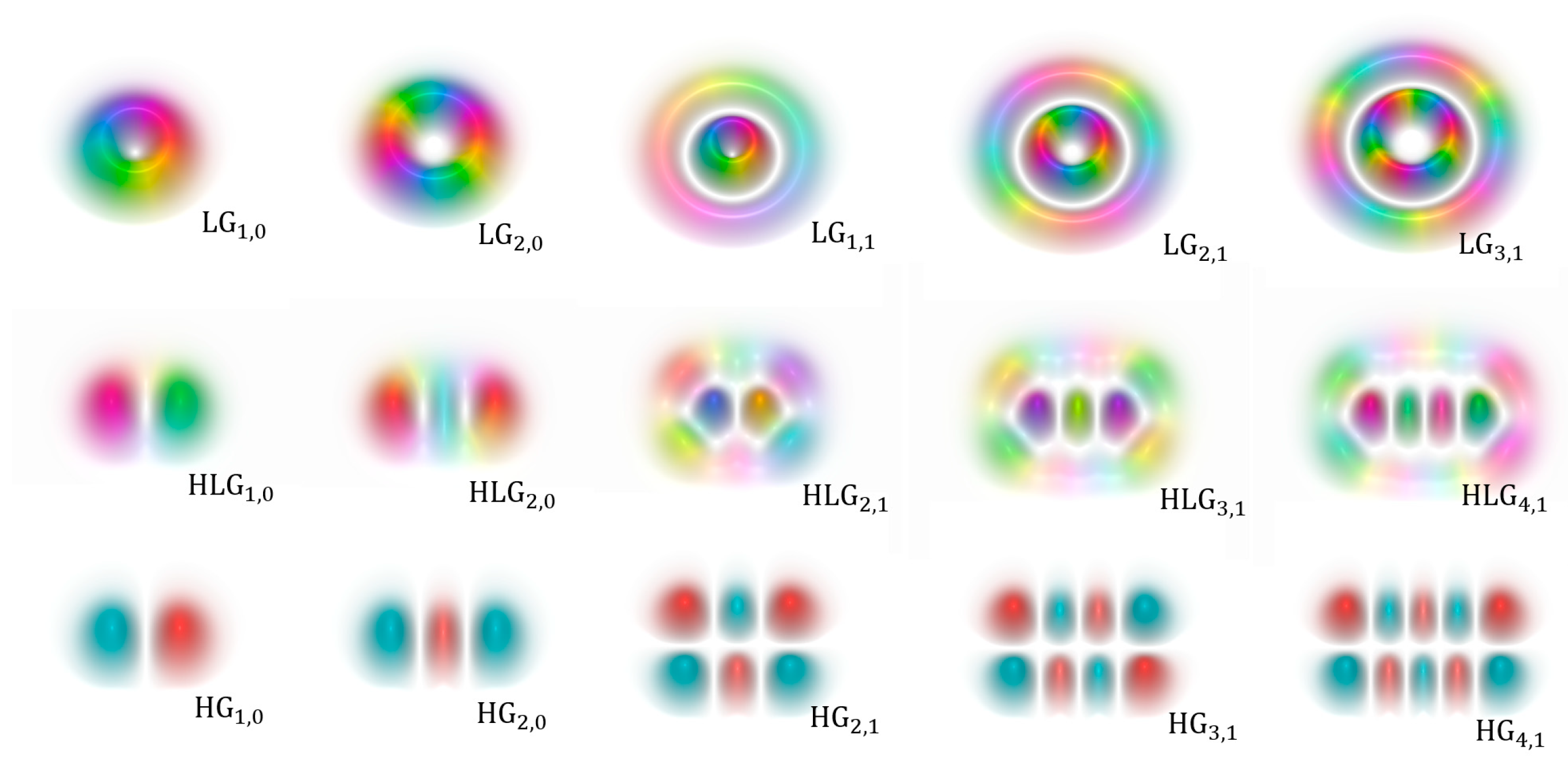
Appendix B. Spatial-Mode Projection Measurements Enabled by Spatial Complex Amplitude Observation
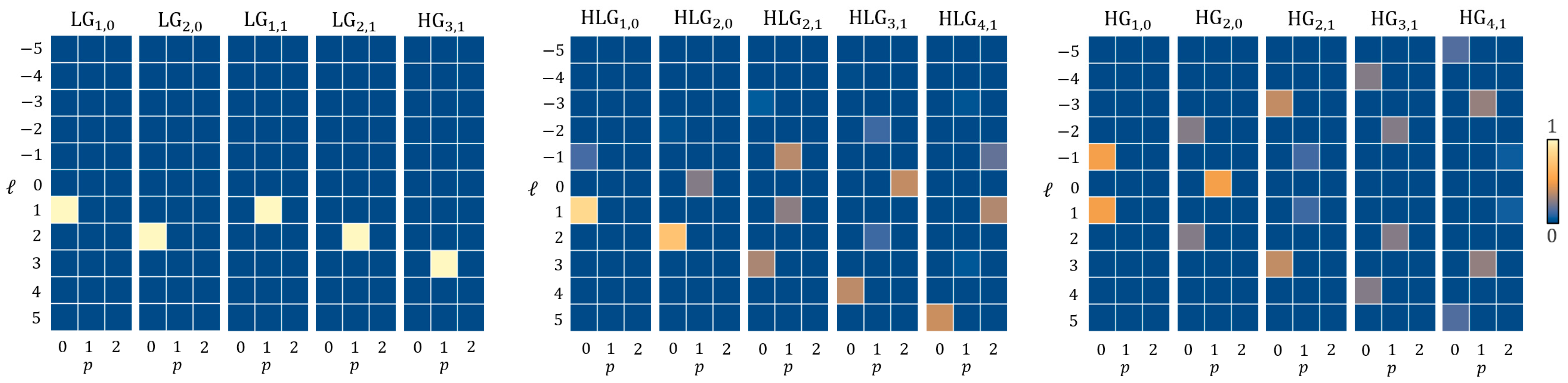
Appendix C. Spatial Stokes Tomography for Vector Modes
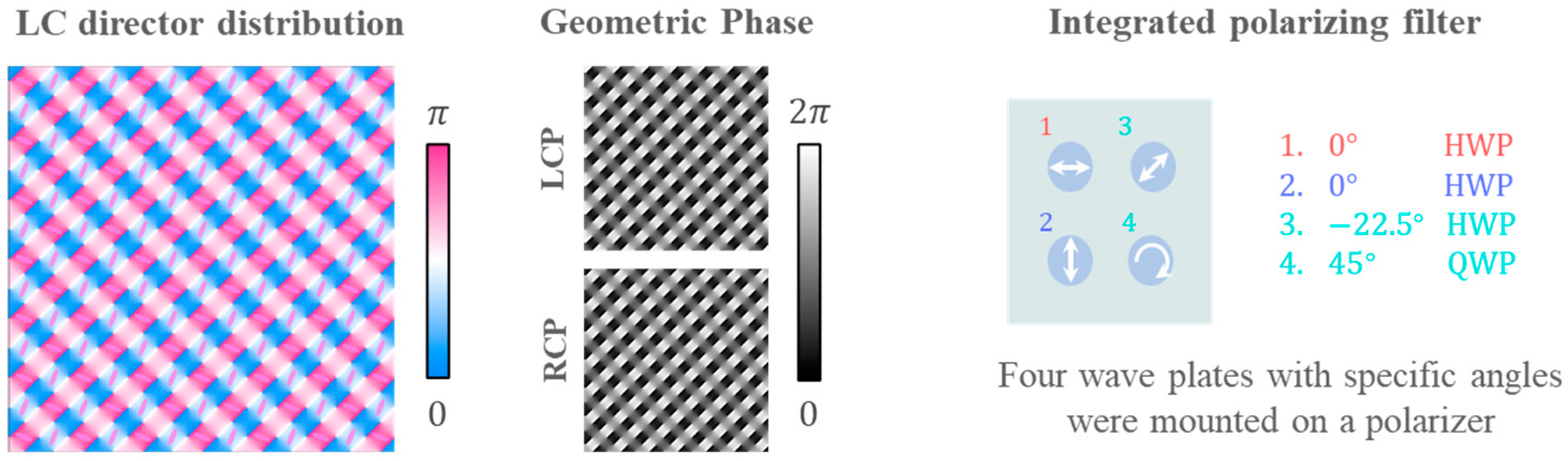
References
- Wheeler, J.-A.; Zurek, W.-H. Quantum Theory and Measurement; Princeton University Press: Princeton, NJ, USA, 1983; pp. 9–49. [Google Scholar]
- D’Ariano, G.M.; Matteo, G.A. Paris, and Massimiliano F. Sacchi, Quantum Tomography. arXiv 2003, arXiv:quant-ph/0302028. [Google Scholar]
- Max, B. Principles of Optics-Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Pergamon Press: Oxford, UK, 1999. [Google Scholar]
- Platt, B.-C.; Shack, R.-V. History and principles of Shack-Hartmann wavefront sensing. J. Refract. Surg. 2001, 17, S573. [Google Scholar] [CrossRef]
- Roddier, F. Curvature sensing and compensation: A new concept in adaptive optics. Appl. Opt. 1988, 27, 1223–1225. [Google Scholar] [CrossRef]
- Velghe, S.; Primot, J.; Guérineau, N.; Cohen, M.; Wattellier, B. Wave-front reconstruction from multidirectional phase derivatives generated by multilateral shearing interferometers. Opt. Lett. 2005, 30, 245–247. [Google Scholar] [CrossRef]
- Andersen, G.-P.; Dussan, L. Holographic wavefront sensor. Opt. Eng. 2009, 48, 085801. [Google Scholar]
- Dudley, A.; Milione, G.; Alfano, R.-R.; Forbes, A. All-digital wavefront sensing for structured light beams. Opt. Express 2014, 22, 14031–14040. [Google Scholar] [CrossRef]
- Norris, B.; Wei, J.; Betters, C.-H.; Wong, A.; Leon-Saval, S.-G. An all-photonic focal-plane wavefront sensor. Nat. Commun. 2020, 11, 5335. [Google Scholar] [CrossRef]
- Park, T.; Depeursinge, C.; Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photonics 2018, 12, 578–589. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- ISO 11146-1; Lasers and Laser Related Equipment-Test Methods for Laser Beam Widths, Divergence Angles and Beam Propagation Ratios. Part 1: Stigmatic and Simple Astigmatic Beams. International Organization for Standardization: Geneva, Switzerland, 2005.
- ISO 11146-2; Lasers and Laser Related Equipment-Test Methods for Laser Beam Widths, Divergence Angles and Beam Propagation Ratios. Part 2: General Astigmatic Beams. International Organization for Standardization: Geneva, Switzerland, 2005.
- Dennis, M.-R.; Alonso, M.-A. Swings and roundabouts: Optical Poincaré spheres for polarization and Gaussian beams. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20150441. [Google Scholar] [CrossRef] [PubMed]
- Collins, S.-A. Lens-System Diffraction Integral Written in Terms of Matrix Optics. J. Opt. Soc. Am. 1970, 60, 1168–1177. [Google Scholar] [CrossRef]
- Zhan, Q.-W. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Pereira, L.-J.; Khoury, A.-Z.; Dechoum, K. Quantum and classical separability of spin-orbit laser modes. Phys. Rev. A 2014, 90, 053842. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Ndagano, B.; Forbes, A. A review of complex vector light fields and their applications. J. Opt. 2018, 20, 31. [Google Scholar] [CrossRef]
- Toninelli, E.; Ndagano, B.; Vallés, A.; Sephton, B.; Forbes, A. Concepts in quantum state tomography and classical implementation with intense light: A tutorial. Adv. Opt. Photonics 2019, 11, 67–134. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Paris, M.G.; Sacchi, M.F. Quantum Tomography. Adv. Imaging Electron Phys. 2003, 128, 205–308. [Google Scholar]
- Forbes, A.; Oliveira, M.D.; Dennis, M.-R. Structured light. Nat. Photonics 2021, 15, 253. [Google Scholar] [CrossRef]
- Wang, J.; Castellucci, F.; Franke-Arnold, S. Vectorial light-matter interaction: Exploring spatially structured complex light fields. AVS Quantum Sci. 2020, 2, 031702. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, X.-B.; Rodríguez-Fajardo, V.; Zhu, Z.-H.; Rosales-Guzmán, C. Real-time Stokes polarimetry using a digital micromirror device. Opt. Express 2019, 27, 31087. [Google Scholar] [CrossRef]
- Li, C.-Y.; Liu, S.-J.; Yu, B.-S.; Wu, H.-J.; Rosales-Guzmán, C.; Shen, Y.; Chen, P.; Zhu, Z.-H.; Lu, Y.-Q. Toward Arbitrary Spin-Orbit Flat Optics Via Structured Geometric Phase Gratings. In Laser Photonics Reviews; Wiley: Hoboken, NJ, USA, 2023; p. 2200800. [Google Scholar]
- Rosales-Guzmán, C.; Forbes, A. How to Shape Light with Spatial Light Modulators; SPIE Press: Bellingham, WA, USA, 2017. [Google Scholar]
- Abramochkin, E.-G.; Volostnikov, V.-G. Generalized Gaussian beams. J. Opt. A Pure Appl. Opt. 2014, 6, S157. [Google Scholar] [CrossRef]
- Gutiérrez-Cuevas, R.; Dennis, M.-R.; Alonso, M.-A. Generalized Gaussian beams in terms of Jones vectors. J. Opt. 2019, 21, 084001. [Google Scholar] [CrossRef]
- Beijersbergen, M.-W.; Allen, L.; Veen, H.E.L.O.V.D.; Woerdman, J.-P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Wu, H.-J.; Yu, B.-S.; Jiang, J.-Q.; Li, C.-Y.; Rosales-Guzmán, C.; Liu, S.-L.; Zhu, Z.-H.; Shi, B.-S. Observation of anomalous orbital angular momentum transfer in parametric nonlinearity. Phys. Rev. Lett. 2023, 130, 153803. [Google Scholar] [CrossRef] [PubMed]
- Zhong, R.-Y.; Zhu, Z.-H.; Wu, H.-J.; Rosales-Guzman, C.; Song, S.-W.; Shi, B.-S. Gouy-phase-mediated propagation variations and revivals of transverse structure in vectorially structured light. Phys. Rev. A 2021, 103, 053520. [Google Scholar] [CrossRef]
- da Silva, B.P.; Pinillos, V.-A.; Tasca, D.-S.; Oxman, L.-E.; Khoury, A.-Z. Pattern revivals from fractional Gouy phases in structured light. Phys. Rev. Lett. 2020, 124, 033902. [Google Scholar] [CrossRef] [PubMed]
- da Silva, B.P.; Tasca, D.S.; Galvão, E.F.; Khoury, A.Z. Astigmatic tomography of orbital-angular-momentum superpositions. Phys. Rev. A 2019, 99, 043820. [Google Scholar] [CrossRef]
- da Silva, B.P.; Marques, B.A.D.; Rodrigues, R.B.; Ribeiro, P.H.S.; Khoury, A.Z. Machine-learning recognition of light orbital-angular-momentum superpositions. Phys. Rev. A 2021, 103, 063704. [Google Scholar] [CrossRef]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed]
- Ndagano, B.; Nape, I.; Cox, M.A.; Rosales-Guzman, C.; Forbes, A. Creation and Detection of Vector Vortex Modes for Classical and Quantum Communication. Light. Technol. 2018, 36, 292–301. [Google Scholar] [CrossRef]
- Sugic, D.; Droop, R.; Otte, E.; Ehrmanntraut, D.; Nori, F.; Ruostekoski, J.; Denz, C.; Dennis, M.-R. Particle-like topologies in light. Nat. Commun. 2021, 12, 6785. [Google Scholar] [CrossRef]
- Salakhutdinov, V.; Eliel, E.; Löffler, W. Full-field quantum correlations of spatially entangled photons. Phys. Rev. Lett. 2012, 108, 173604. [Google Scholar] [CrossRef] [PubMed]
- Brandt, F.; Hiekkamäki, M.; Bouchard, F.; Huber, M.; Fickler, R. High-dimensional quantum gates using full-field spatial modes of photons. Optica 2020, 7, 98–107. [Google Scholar] [CrossRef]
- Yu, B.-S.; Li, C.-Y.; Yang, Y.-J.; Rosales-Guzmán, C.; Zhu, Z.-H. Directly determining orbital angular momentum of ultrashort Laguerre-Gauss pulses via autocorrelation measurement. Laser Photonics Rev. 2022, 16, 2200260. [Google Scholar] [CrossRef]
- Courtial, J.; Dholakia, K.; Allen, L.; Padgett, M.-J. Second-harmonic generation and the conservation of orbital angular momentum with high-order Laguerre-Gaussian modes. Phys. Rev. A 1997, 56, 4193–4196. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Wu, H.-J.; Yu, B.-S.; Rosales-Guzmán, C.; Zhu, Z.-H.; Hu, X.-P.; Shi, B.-S.; Zhu, S.-N. Real-time superresolution interferometric measurement enabled by structured nonlinear optics. In Laser & Photonics Reviews; Wiley: Hoboken, NJ, USA, 2023; p. 202200967. [Google Scholar]
- Abdollahramezani, S.; Hemmatyar, O.; Adibi, A. Meta-optics for spatial optical analog computing. Nanophotonics 2020, 9, 4075–4095. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Li, C.; Jiang, J.; Wu, H.; Zhao, B.; Rosales-Guzmán, C.; Shi, B.; Zhu, Z. Single-Shot Full Characterization of the Spatial Wavefunction of Light Fields via Stokes Tomography. Appl. Sci. 2024, 14, 2067. https://doi.org/10.3390/app14052067
Yu B, Li C, Jiang J, Wu H, Zhao B, Rosales-Guzmán C, Shi B, Zhu Z. Single-Shot Full Characterization of the Spatial Wavefunction of Light Fields via Stokes Tomography. Applied Sciences. 2024; 14(5):2067. https://doi.org/10.3390/app14052067
Chicago/Turabian StyleYu, Bingshi, Chunyu Li, Jiaqi Jiang, Haijun Wu, Bo Zhao, Carmelo Rosales-Guzmán, Baosen Shi, and Zhihan Zhu. 2024. "Single-Shot Full Characterization of the Spatial Wavefunction of Light Fields via Stokes Tomography" Applied Sciences 14, no. 5: 2067. https://doi.org/10.3390/app14052067
APA StyleYu, B., Li, C., Jiang, J., Wu, H., Zhao, B., Rosales-Guzmán, C., Shi, B., & Zhu, Z. (2024). Single-Shot Full Characterization of the Spatial Wavefunction of Light Fields via Stokes Tomography. Applied Sciences, 14(5), 2067. https://doi.org/10.3390/app14052067








