Finite Element Model of Canine-Specific Vertebrae Incorporating Biomechanical Tissue Nonlinearity

Abstract

As dogs are considered valuable members of many families, ensuring their health and well-being is essential. This study introduces a numerical nonlinear model that explores the complexities of canine vertebrae, with a specific focus on their experimentally observed mechanical properties. The model underwent rigorous testing, and its results were compared with actual data on the compression of canine lumbar vertebrae. The numerical results and experimental data comparison had a 12% RRMSE. This research enhances our understanding of canine bone health and lays the groundwork for future initiatives aimed at treating and mitigating bone-related diseases in dogs.

1. Introduction

We studied dogs because they play an important role in people’s lives [1], and their health is important. Dogs are now studied not only in the laboratory animal context but also with the same consideration as humans in terms of clinical research. According to [2], in 2013, there were over 700 million dogs worldwide. We believe that research into diseases affecting canines should be conducted in the same manner as human research. Our focus on canine bone health stems from dogs’ importance in human lives and the need for in-depth research paralleling human clinical studies. This research underpins the development of a detailed numerical model to understand and evaluate bone disorders in canines.

Dogs can suffer from osteopenia, and other metabolic bone disorders can affect humans as well as dogs [3]. Dogs are at risk of developing pathological fractures in their bones as a result of steroidal anti-inflammatory drugs [4]. There are additional metabolic disorders such as hyperparathyroidism and kidney disease [5], which also make a dog’s bone tissue more fragile.

Rats are only used as models to investigate osteoporosis in humans [6,7,8]. Thus, animal health receives minimal consideration.

Fractures are common in dogs [9], and the risk of a fracture occurring or recurring in the future must be evaluated in addition to the secondary cause of the fracture—for example, osteoporosis. Treating fractures becomes complicated when dogs have bone conditions like osteoporosis. For example, in 2022, Marshall and his team pointed out that, after surgery, dogs often limp or, in severe cases, might even need an amputation [10]. This shows how complex it can be to manage fractures in dogs, especially if they have other bone problems.

When determining how likely dogs are to obtain fractures, it is essential to evaluate BMD. In 2021, Woods and colleagues used a special type of CT scan to measure BMD in dogs and found that heavier dogs might have a lower BMD, placing them at a greater risk for fractures [11].

In addition, some bone issues can make certain dog breeds more prone to fractures. Tamburro’s group found that spaniels and labradors, for example, often have a condition wherein part of their elbow bone does not form properly [12]. This study showed that when assessing fracture risks, it is important to consider the dog’s breed.

Additionally, there has been research into how treatments like bisphosphonates, which are usually used for osteoporosis, affect dog bones. In 2009, Tang and his team discovered that giving dogs a high dose of bisphosphonates can make their bones more brittle, which could lead to further fractures [13].

Individual animals vary, like humans, and using them in scientific research can be considered unethical. Spine research can typically be conducted post-mortem, and it is crucial to note that no animal has a spinal configuration identical to that of humans. Nevertheless, conducting experiments to construct and evaluate digital models is advantageous. Various animal models are used to research osteoporosis, with the choice of animal species depending on the disease’s underlying aetiology. One book [14] details the osteoporosis research that has been conducted using animal models.

Vertebral fractures were simulated in an earlier investigation using sheep cervical (C2–C7) and pig lumbar (Th14–L6) vertebrae from cadaveric animals. The MTS 858 Mini Bionix testing system was used for each test. Tests of the axial compression, extension, and flexion were conducted, and the resultant hysteresis loops were analyzed [15]. In addition, we have examined the mechanical properties of the three lumbar vertebrae, concentrating specifically on the hysteresis loops discovered in the aforementioned paper [16].

The bone volume per trabecular volume can determine the proportion of bone in the trabecular (or cancellous) structure, often referred to as BV/TV, a key morphological characteristic. This measure is instrumental in standardizing the ultimate stress, elastic modulus, and durability of the trabecular bone [17].

A rodent model study revealed that type 2 diabetes mellitus increases the risk of hip fracture by decreasing the microarchitecture and bone mass of the trabecular bone [18]. Another experiment on ovariectomized sleep-deprived rats showed a negative effect on the trabecular structure of the femoral head, increasing the hip fracture rate [19].

In our opinion, the main application of a canine vertebra model would be fraction risk evaluation for easier model verification, which allows the obtained knowledge to be adopted in understanding human bones’ fracture risk. Therefore, this study aimed to develop a numerical nonlinear model of canine vertebrae, comparing it with the experimentally observed biomechanical properties of vertebra tissue in compression tests.

2. Materials and Methods

The model’s development was anchored in real-time experimental data, crucial for an authentic representation of canine lumbar vertebrae. We incorporated a refined stress–strain curve within the model, mirroring the material properties of canine vertebrae observed in experimental settings. The application of vertical compressive forces and detailed observation of vertebral responses provided a comprehensive understanding of vertebral behavior under stress.

2.1. Real-Time Experiment

An animal carcass was used following the same principle applied in our previous experiment [16]. A short overview is provided below. The data were obtained from a real-time experiment, which was necessary to create the numerical model.

2.1.1. Specimen Guidelines

In our study, we carefully followed the requirements for the selection of the dogs, which are described in detail in

Table 1. Requirements for the sample.

Animal Species	Dog
Sex	Female
Weight	15–25 kg
Age	Not specified
Reproductive Status	Spayed
Breed	Any
Nutrition	Poor or average
Muscle Development	Not prone to muscle atrophy
Joint Damage	Any (but, if present, must be noted)
Medical History	The animal should not have suffered from metabolic diseases; thyroid disorders; diseases such as rickets, osteomalacia, osteomyelitis, bone tumors, osteochondritis, dysplasias, spinal hernias, discospondylosis, or discospondylitis; and other osteopathies. Suitable: If there is a recorded bone fracture, except in cases where the required bone samples are damaged.
Required Bones	Lumbar vertebrae (L1–L5)

. The selection criteria were based on the strict parameters established in our previously published paper [20], thus ensuring a high degree of consistency in our methodology. Given the difficulty of obtaining suitable subjects meeting these criteria, our study was conducted using a single dog. This subject was carefully selected for compliance with all the specified requirements, ensuring that our study was based on a representative and appropriate model.

In our case study, we used lumbar vertebrae samples from an 8-year-old 32 kg spayed mongrel. The dog was diagnosed with pulmonary thromboembolism, and the owner decided to euthanize. All consent forms were completed and signed by the animal’s owner.

2.1.2. Sample Preparation

The entire spine lumbar segment was removed from the carcass for processing. The lumbar vertebrae were separated from one another by severing the intervertebral discs and removing the spinal cord, muscles, ligaments, and adipose connective tissue surrounding each vertebra. We safely disposed of all animal byproducts. Each lumbar vertebra was numbered and stored at a constant temperature of $-{20}^{\circ }$ degrees Celsius. It was crucial to keep the specimen moist during the mechanical compression experiment since the mechanical properties change as it dries; thus, a 0.9% NaCl saline solution was used. A few days before the test, the sample was transferred from the freezer to the refrigerator and progressively thawed to a temperature of 4 °C.

2.1.3. Equipment Used in the Experiment

Compression testing is a widely used experimental technique in determining the mechanical properties of bones [21]. The external load was applied only to the body of the lumbar vertebrae. The costal (rib), caudal articular, and cranial articular processes of the lumbar vertebrae were excised before the compression experiment to prevent their interference with the compression.

The standard compression test traditionally involves compressing the bone specimen between two parallel stainless-steel plates with the lower plate fixed. A universal tensile testing machine 2055 P-5 (Tochpribor, Ivanovo, Russia), with a compression test tool, was utilized. In this study, vertical compressive loads were applied to canine lumbar vertebrae using the mechanical loading apparatus, controlled by “LabVIEW version 16” (National Instruments, Austin, TX, USA). The vertebrae were oriented with their longitudinal axes perpendicular to the load direction, ensuring the precise and vertical application of force for our biomechanical analysis. The PXI system hardware (chassis NI PXIe-1073, Austin, TX, USA and controller PXIe-4330, Austin, TX, USA) was also employed for the compression tests. An S-type tension/compression load cell up to 1 kN was used. A testing strain rate below 0.1 ${\mathrm{s}}^{-1}$ was used, which minimizes creep while being low enough to be considered quasistatic. The most common method of storing and preserving bone specimens prior to testing is freezing and subsequent thawing before testing; thus, thawed wet specimens were used.

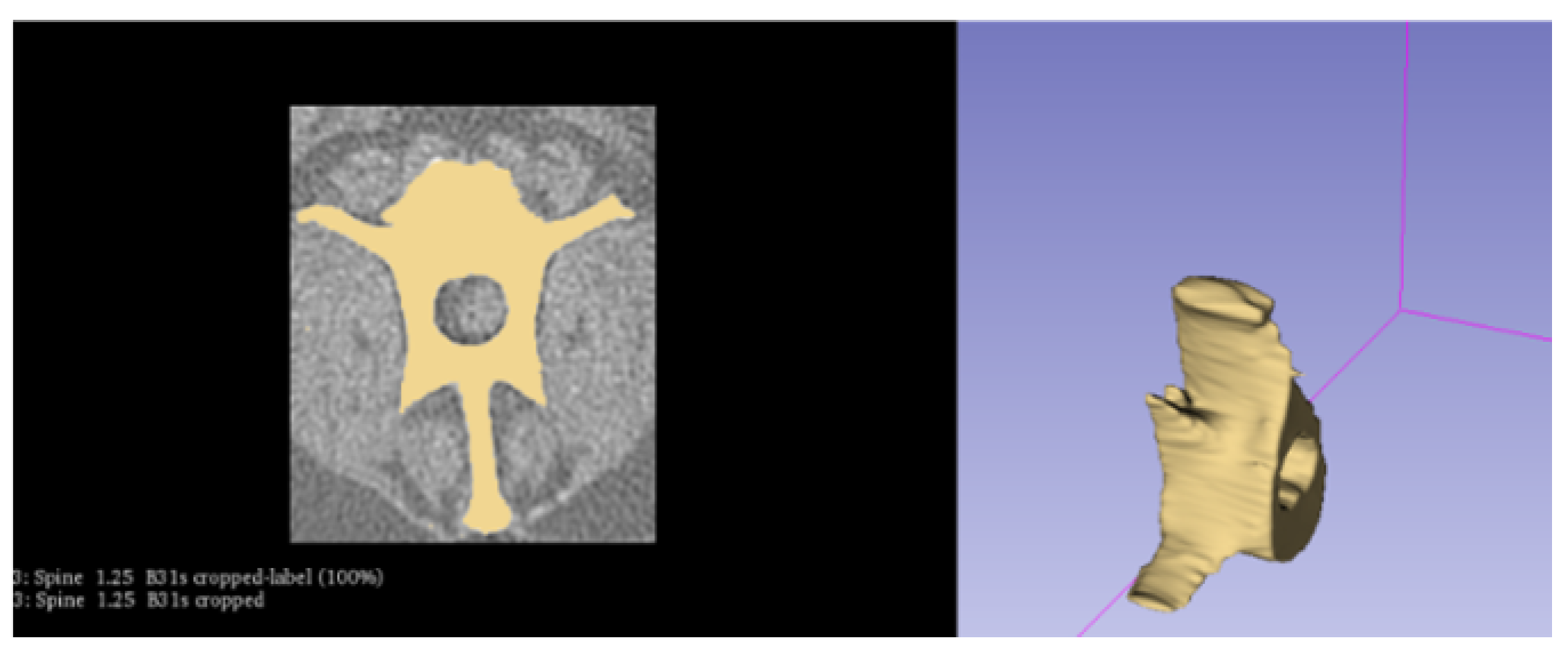
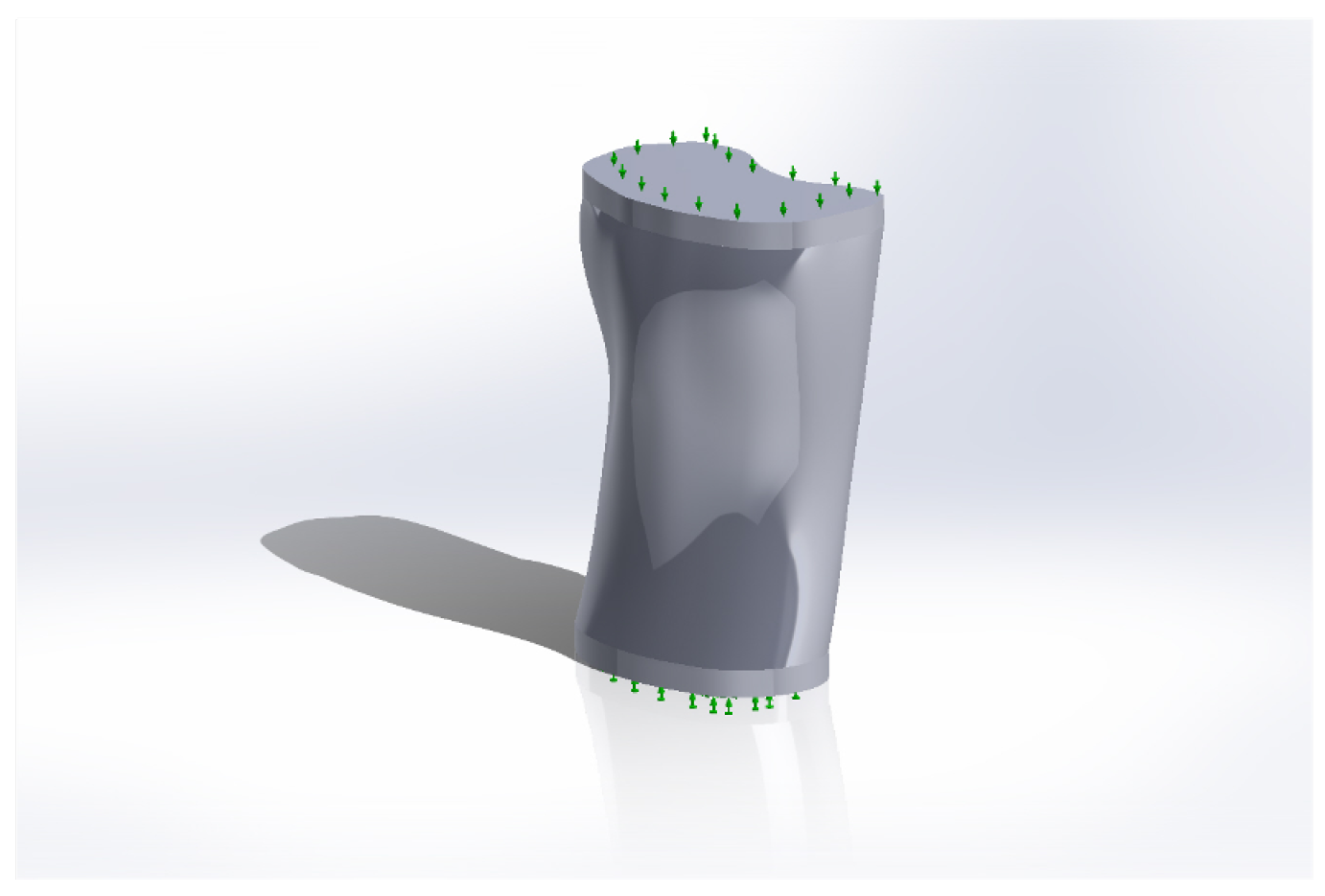
2.2. Creating the Geometry

Our numerical model’s construction began with a detailed CT scan analysis using “Siemens SOMATOM syngo CT 2007P” of software version Somaris/5.5. The segmentation of the lumbar spine vertebra was meticulously processed through “3D Slicer 5.2.2”, followed by simplification in “Meshlab 2023.12 release version” to optimize the computational efficiency. The final geometry, analyzed in “Solidworks 2022”, was pivotal in establishing a robust model foundation, incorporating varying cortical layer thicknesses and accurately simulating the vertebral trabeculae.

CT scan data were used for the geometry, surface area, and vertebral height calculations. Three separate software applications were used, “Osirix Lite” 13.0, “3D Slicer” 5.2.2, and “Fiji” 2.15.0. A confidence interval was also calculated.

The scan was performed using a Siemens CT scanner, with a slice thickness of 1.25 mm, using the B31s protocol. This protocol was designed for high-resolution imaging. A specialized bone reconstruction algorithm was used. This algorithm is designed to enhance the visibility and definition of bone structures in the scanned images. It optimizes the contrast and sharpness to accurately delineate the bone from other tissues, which is crucial for the precise 3D modeling and analysis of the bone anatomy.

In particular, “3D Slicer” is an open-source software program that allows the segmentation and analysis of medical images acquired from MRI or CT scans [22]. Here, the CT DICOM images were processed by the “3D Slicer” program to isolate the lumbar spine vertebra. Figure 1 illustrates the whole segmentation procedure. All the necessary vertebra parts were removed.

The segmented vertebral body was simplified using the “Meshlab” software, and the number of surface area components was decreased to 10,000. This simplification was conducted to reduce the computer resources required while retaining the model’s original shape.

The resultant geometry was analyzed using the “Solidworks” software and imported for theoretical calculations.

Subsequently, four distinct models were constructed. Three of these models varied in the cortical layer thicknesses, specifically 0.2, 0.25, and 0.3 millimeters. Instead of using nonlinear analysis, these models were evaluated using a linear approach paired with a simplified method designed for the analysis of nonlinear lumbar vertebra behavior. A key observation from this study was the necessity to model the trabeculae as ellipses to achieve the target porosity. Additionally, in the simplified vertebra geometry, trabeculae were approached as a continuum material.

The model was initially subjected to a linear static analysis in “Solidworks”. Although our primary focus was on the nonlinear characteristics of the model, a linear analysis was performed to ensure the model’s fundamental stability and structural integrity under typical loading conditions. The study ensured the veracity of the geometric model, boundary conditions, and loading parameters as a crucial first stage in the comparison procedure.

Intervertebral discs were treated as linear material. This important component is situated between each vertebra and functions to reduce friction and provide a damping system. Its mechanical properties were determined on the basis of the results of a literature review.

Table 2. Mechanical properties of the vertebral body model.

Cortical layer thickness, mm [23]	0.32
Surface area, ${\mathrm{mm}}^2$	415.0
Intervertebral disc thickness, mm [24]	2
Total vertebral volume, ${\mathrm{mm}}^3$	7240.75
Experimental loading rate, mm/min	7

shows the mechanical properties of the vertebral body.

We imported the geometry into the finite element analysis program “Solidworks”, which also supports finite element analysis for studies. It was necessary to specify that the current model was a three-dimensional (3D) solid body model, and, after selecting these settings, a nonlinear dynamic model was chosen for the calculations.

Not only are these characteristics necessary in predicting the likelihood of lumbar spine fractures in canines, but they also have the potential to contribute to the development of fracture prevention and treatment strategies.

2.2.1. Simplification of the Model

A technique that emphasizes experimental modeling and simulation was employed for the calculations. In this nonlinear study, a solid vertebra was analyzed.

The lumbar spine model was simplified by removing all vertebral spinous and transversal processes, since, as in the real experiment, these processes would interfere with the compression simulation. Figure 2 shows the simplified model. Only the vertebral body was retained. Removing the growths reduced the computational time required.

2.2.2. Mechanical Properties

A stress–strain curve was incorporated into the vertebra’s numerical model to ensure that the simulation faithfully reflected the material properties of the vertebra. The data originated from a legitimate experiment involving the lumbar vertebrae of canines. In Figure 3, the curve demonstrates the vertebra’s response to varying loads, which helped to establish the material’s elastic and plastic boundaries.

Table 3. Damping coefficients.

Type	Rayleigh Damping
Alpha Coefficient	0.01
Beta Coefficient	0.01

shows the damping factor values, which needed to be summed. The damping coefficients used to reduce the vibration and friction during the simulated experiment are depicted in the table below. These coefficients must be integrated into the model because they are essential in resolving a nonlinear dynamic problem.

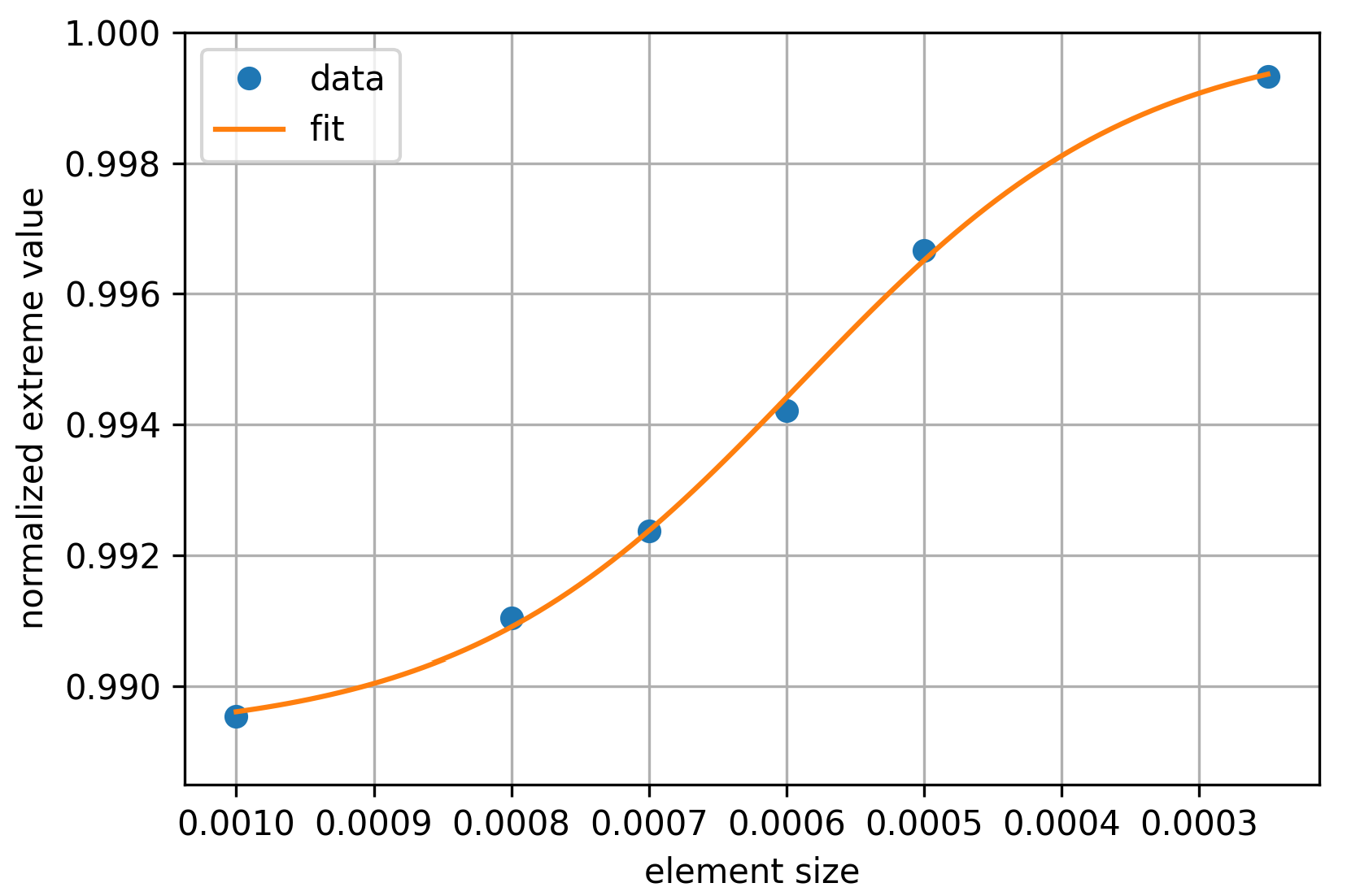
2.2.3. Convergence Analysis

The FEM problem convergence analysis was conducted as follows. Extreme values of the reaction force on the vertebra were calculated for element sizes of 0.001, 0.0008, 0.0007, 0.0006, 0.0005, and 0.00025. The obtained extreme reaction force values are presented in Figure 4 as blue dots. Additionally, curve fitting was applied using the following equation (shown as a continuous curve in Figure 4):

$$y=\frac{L_1}{(1+exp(-A·(x-B\left)\right))}+L.$$

(1)

The curve fitting parameters $L_1$, L, A, and B were determined using the Python scikit-learn library [25]. The convergence analysis showed that the error value of the FEM method results was within $\pm 1\%$ and converged to the exact values as the initial finite element size decreased.

The y-axis in Figure 4 represents the normalized extreme value of the vertebra reaction force and equals $N=L_1+L$, while the x-axis labels are sorted in descending order.

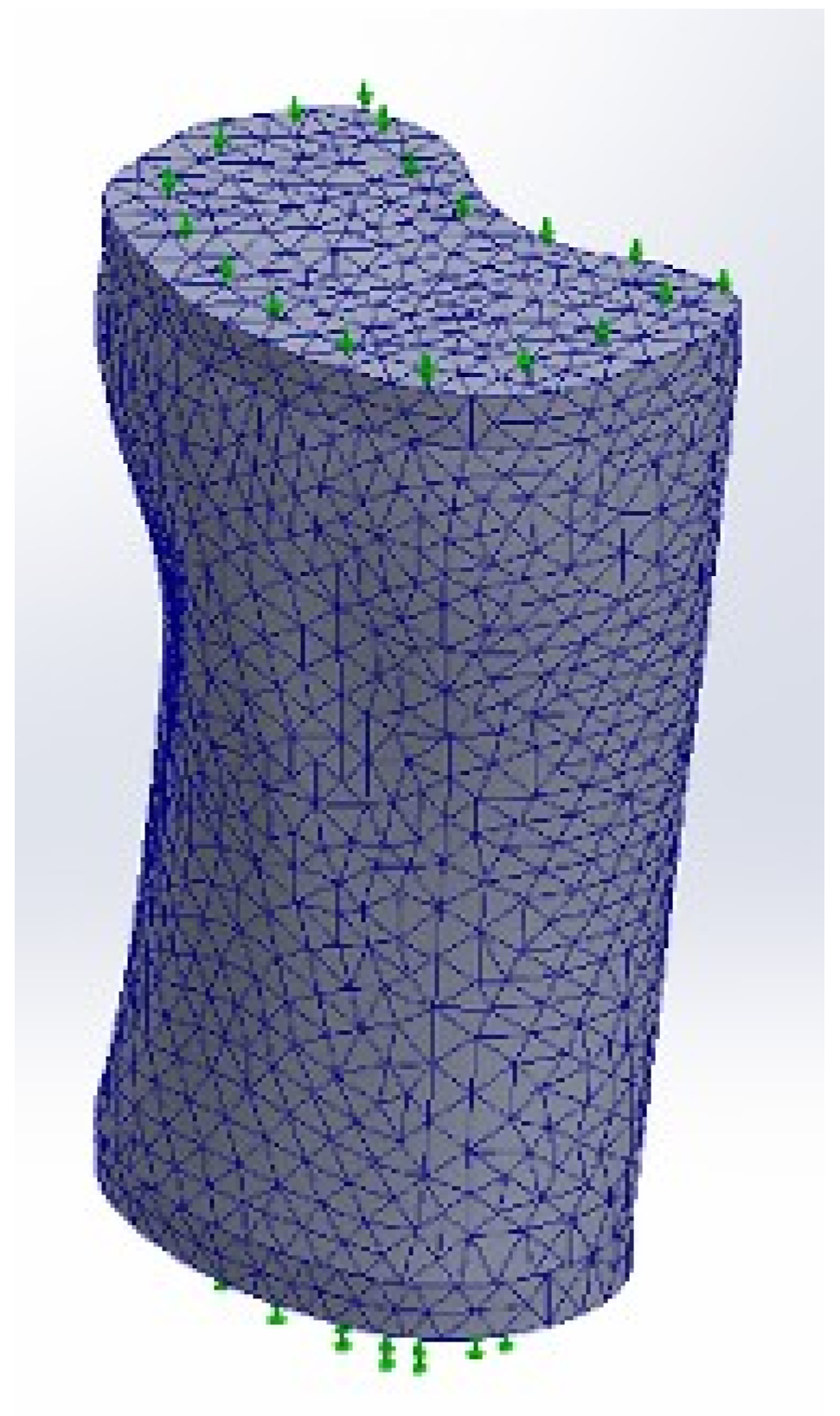
2.2.4. Meshing

Figure 5 displays the resulting finite element mesh, specifically designed to assume a tetrahedral shape, comprising over 371,000 finite elements.

Table 4. Finite element mesh.

Maximum Element Size	0.7 mm
Minimum Element Size	0.35 mm
Mesh Quality	High
Total Nodes	642,003
Total Elements	371,706

shows the dimensions of the smallest and the largest finite element in our current model.

2.3. Theoretical Background

The calculations were performed by applying a vertical compressive force to one side of the vertebral body while maintaining the original position of the opposite side. The behavior of the vertebra was observed and recorded following the completion of the calculations using this technique.

A comparison was made between the experimental data and the results of the theoretical calculation to verify the accuracy of the numerical model. The software packages “MATLAB 2023” and “Microsoft Excel 2016” were utilized throughout the data processing procedure, including optimizing the received data.

According to the developers of the “Solidworks” software [26], the calculation of a nonlinear dynamic model can be described by the equation as follows:

$${\left[M\right]}^{t+\Delta t}{\left\{U^{″}\right\}}^{\left(i\right)}+{\left[C\right]}^{t+\Delta t}{\left\{U^{\prime }\right\}}^{\left(i\right)}+{}^{t+\Delta t}\left[K\right]^{\left(i\right)t+\Delta t^t}{[\Delta U]}^{\left(i\right)}={}^{t+\Delta t}\left\{R\right\}-{}^{t+\Delta t}\left\{F\right\}^{(i-1)},$$

(2)

where ${\left[M\right]}^{t+\Delta t}$ is the mass matrix at the time $t+\Delta t$; ${\left\{U^{″}\right\}}^{\left(i\right)}$, which is the displacement vector; ${\left[C\right]}^{t+\Delta t}$, which is the damping matrix at the time $t+\Delta t$; ${\left[C\right]}^{t+\Delta t}$, which is the velocity vector; ${}^{t+\Delta t}\left[K\right]^{\left(i\right)t+\Delta t^t}$, which is the stiffness matrix at the time $t+\Delta t$; ${[\Delta U]}^{\left(i\right)}$, which is the displacement vector; ${}^{t+\Delta t}\left\{R\right\}$, which is the external load vector at the time $t+\Delta t$; and ${}^{t+\Delta t}\left\{F\right\}^{(i-1)}$, which is the internal force vector.

This equation is founded on FEM analysis, which is widely used in the fields of mechanics, engineering, and science to analyze the behavior of complex structures in various situations.

This equation can be used for many purposes—for example, determining the effect of various factors on the structure and function of the lumbar vertebrae in dogs, understanding how various loads (external and internal forces) influence the vertebra’s deformation (displacement vector), and examining how various vertebral properties (such as mass, damping, and rigidity) influence these deformations.

It can be argued that this equation can also be used to study and comprehend injuries, pathologies, and diseases of the canine lumbar spine, such as osteoporosis, and how they may respond to treatment, along with assessing the efficacy of different spinal implants and prostheses.

2.4. Statistical Approach

The relative root mean square error (RRMSE) is a normalized version of the root mean square error (RMSE), used to assess the accuracy of predictions relative to the scale of the data. It is calculated as the RMSE divided by a normalization factor, often the mean or range of the observed values, to provide a scale-independent measure of the prediction accuracy. The analytical expression of the RRMSE can be written as follows:

$$\mathrm{RRMSE}=\frac{\sqrt{\frac{1}{n}{\sum }_{i=1}^n{(y_i-{\overline{y}}_i)}^2}}{\mathrm{Normalization}\mathrm{Factor}},$$

(3)

where n is the number of observations, $y_i$ is the actual value of the ii-th observation, and ${\overline{y}}_i)$ is the predicted value for the ii-th observation. The normalization factor could be the mean of the observed values $\overline{y}=\frac{1}{n}{\sum }_{i=1}^n{y}_i$ or another relevant measure depending on the context, such as the range of yy values (i.e., $\mathrm{Normalization}\mathrm{Factor}\left(\mathrm{Range}\right)=max\left(y_i\right)-min\left(y_i\right)$).

The choice of normalization factor affects the interpretation of the RRMSE, making it versatile for different applications and allowing comparisons across datasets with different scales.

3. Results

This section presents the model’s verification, contrasting the model’s outputs with the actual experimental results. This critical evaluation underscores the model’s accuracy and reliability in simulating real-world scenarios, particularly in stress distribution and displacement analyses.

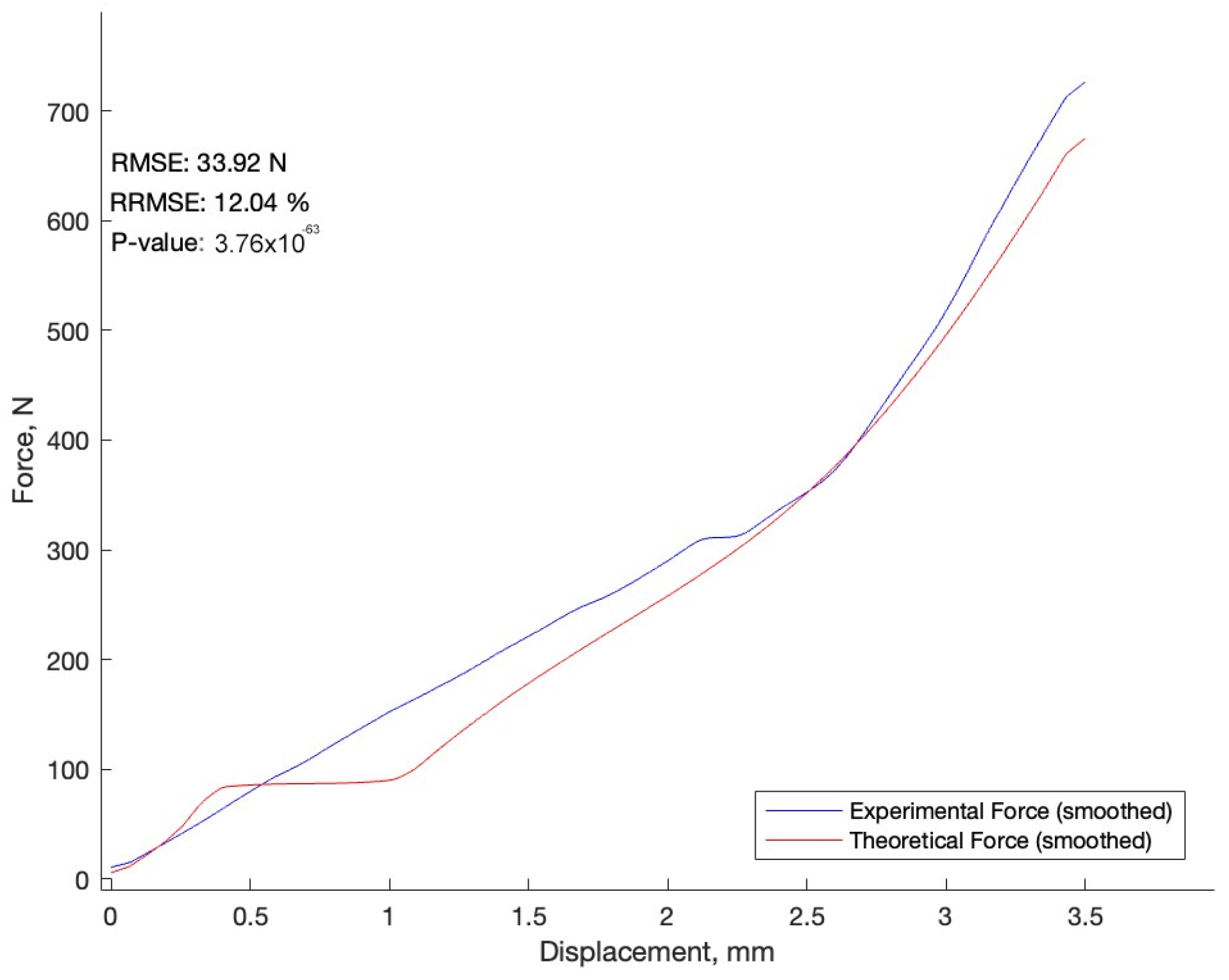
3.1. Comparison of the Experiment and the Numerical Model

The last phase to be completed was the numerical model’s comparison with the experiment, which is commonly regarded as one of the most crucial stages in any numerical model investigation. Demonstrating the simulation’s trustworthiness and ability to accurately reflect the real-world scenario is beneficial. Here, a comparison was made between the actual experimental results and those of the numerical model used to simulate the experiment. The outcomes of this comparison are depicted in Figure 6.

The calculated relative root mean square error (RRMSE) of 12.04%, based on the mean normal factor calculation, indicates the similarity of the two datasets, revealing that the numerical model is accurate and can be used to investigate canine lumbar spine biomechanics.

3.2. Stress Results

Through analyzing the tension variations across the vertebral structure, we can gain insights into its mechanical resistance. While Von Mises stress criteria are typically associated with ductile materials, their application in our nonlinear study is justified. Von Mises stress provides a stress value for comparison, which is crucial in identifying potential injury risks or pathological conditions in bone tissue, which often exhibits nonlinear and anisotropic characteristics. We acknowledge, however, that this criterion has its limitations in fully capturing the complex failure mechanisms of bone tissue. Advanced criteria, better suited for anisotropic materials, could be explored in future research. Figure 7 illustrates the stress distribution obtained.

3.3. Displacement Results

During our analysis, we meticulously mapped the displacement distribution across the vertebral body. Identifying regions with significant displacement is crucial, as these areas are prone to structural changes that could compromise vertebral function. The detailed mapping of these displacements, as depicted in Figure 8, provides a comprehensive view of the vertebral response to mechanical stress and its potential implications.

4. Discussion

A review of the scientific literature revealed that canines are sometimes used to evaluate the mechanical properties of various implants [27] or additional materials used in spinal vertebroplasty [28]. Studies have also been conducted to construct 3D models of canine bone to assess fracture risk. The purpose of this study was to simulate vertebral compression fractures [29]; however, it is essential to evaluate all possible risk factors to predict fractures.

4.1. Role and Significance of the Nonlinear Study

Due to the nonlinear characteristics of vertebral deformation and bone fracture phenomena, our main focus was on the nonlinear study, which served as a preliminary investigation. A nonlinear analysis permits a more precise representation of complex real-world situations, such as those involving large deformations, nonlinear material behavior, or complex contact interactions. Therefore, the verification of the model through a nonlinear investigation represents a significant advance in our understanding and ability to predict bone fracture mechanisms in canines.

4.2. Bipedal and Quadrupedal Locomotion Mechanical Aspects

Different laws of mechanics apply to four-legged animals, and the burdens are distributed not only to the vertebral body but also to the vertebral body processes that were not subjected to the simulated load. In real life, the stresses on the vertebrae would also be distributed to the muscles surrounding the vertebrae, the subcutaneous tissue beneath the vertebrae, and the abdominal muscles [30].

4.3. Limitations

The main limitation of our study is that only one dog was used. This was primarily due to the considerable difficulties encountered in finding a suitable sample. The specific and narrow criteria set for the study, combined with the limited resources and the prevailing practice of handling animal remains among pet owners, significantly limited our ability to obtain a larger sample. Most pet owners prefer cremation or prefer to take their pet’s remains with them, which limited the number of suitable subjects for the study. While this limitation may be considered a disadvantage, it also highlights the unique nature of our study. The detailed analysis carried out on one dog allowed us to gain a concentrated picture of the factors influencing canine bone health and fracture risk and provided a focused but comprehensive insight that offers valuable knowledge for the field of veterinary orthopedics.

Gong et al. highlighted the significance of bone tissue’s nonlinear material properties, emphasizing the role of Von Mises stress in determining the mechanical parameters of trabecular bone [31]. Likewise, Schwiedrzik et al. presented a generalized anisotropic quadric yield criterion, which includes Von Mises stress as a fundamental component [32].

Furthermore, the lumbar vertebra can be characterized as strongly anisotropic plastic biological tissue. Therefore, the yield criterion is based on the yield surface, which can be expressed as Taylor expansion [33] and is as follows:

$${\left(\sum _{ik}{a}_{ik}{\sigma }_{ik}\right)}^{\alpha }+{\left(\sum _{pqmn}{a}_{pqmn}{\sigma }_{pq}{\sigma }_{mn}\right)}^{\beta }+{\left(\sum _{rstlmn}{a}_{rstlmn}{\sigma }_{rs}{\sigma }_{tl}{\sigma }_{mn}\right)}^{\gamma }\le 1$$

(4)

where $a_{ik},a_{pqmn},a_{rstlmn}$ are strength tensors of different order. The yield criterion for isotropic materials was initially proposed by Von Mises [34]. This was extended to anisotropic materials by Hill [35], furthering the applicability of the Von Mises criterion. Tsai [36] expanded these concepts specifically for a unidirectional lamina within anisotropic materials. It can be demonstrated that both the Von Mises and Tsai–Hill failure criteria are derivations of the Goldenblatt–Kopnov failure criteria. In their simulation study of two-dimensional failure propagation, Korenczuk et al. [37] found that the Von Mises criterion inadequately represented the failure type, location, or propagation direction when compared to the Tsai–Hill criterion. Furthermore, both criteria significantly underestimated the displacement required to initiate failure in porcine abdominal aortas, suggesting that a reliance on the Von Mises or Tsai–Hill criteria might lead to the overestimation of the risk of lumbar vertebra fracture. Our study did not explore the failure of canine vertebrae specifically. Thus, the application of the Von Mises stress criterion in our study should be considered as an initial approximation of the yield under initial loading conditions, rather than a definitive analysis.

4.4. Implications of Breed, Age, and Other Risk Factors’ Variability in Canine Spinal Research

The results provide initial insights into the biomechanics of the canine lumbar spine, but they also show that the canine population is more diverse. Differences in spinal mechanics between different breeds and ages of dogs suggest that an individualized approach is necessary when applying these results in a clinical setting.

This study provides a basis for future studies that should include a more diverse canine population. Extending studies to include a wider range of breeds and age groups and other risk factors will be essential for a more comprehensive understanding of canine spinal health. Our study, although targeted in scope, highlights the importance of recognizing and exploring the diversity of the physiological characteristics of dogs to achieve more effective and targeted veterinary interventions.

5. Conclusions

Using the “Solidworks” software, we conducted a comprehensive analysis that yielded valuable information regarding the biomechanics and behavior of the lumbar vertebrae. When combined with experimental data, this information allows a greater understanding of the function of the canine’s lumbar vertebrae, the resistance of the vertebrae to loads, and the likelihood of fracture.

Based on the nonlinear model of the canine lumbar vertebrae obtained from a real experiment and the observed material properties, the following conclusions can be drawn.

-

This study’s findings can be applied to research on osteoporosis in dogs to obtain a better understanding of the role that biomechanical factors play in determining fracture risk.

-

A displacement of 3.5 mm was observed between the actual experiment and the numerical model. Nevertheless, the maximum force calculated by the numerical model was 690 N, while that of the actual experiment was 740 N.

-

The RRMSE of 12.11% indicates that the results are credible, and the investigation into the canine lumbar vertebrae and the numerical model yielded biomechanical insights.

-

The study’s findings will enable the development of methods for the prevention and treatment of osteoporosis, reducing the likelihood of fractures, enhancing quality of life, and strengthening numerical models for use in other contexts.

-

The analysis of convergence indicates that as the initial size of the finite elements reduces, the error margin of the finite element method (FEM) results is confined within $\pm 1$% and approaches the precise values.