Method for Sparse Representation of Complex Data Based on Overcomplete Basis, l1 Norm, and Neural MFNN-like Network
Abstract
1. Introduction
- represents the basic components,
- represents the overcomplete dictionary matrix.
- formed dictionary, where is the component of the basis with indexes
| Algorithm 1: BP |
| Start: ). fordo , end for return Sequence |
| Algorithm 2: SL0 |
|
- (1)
- Minimizing the loss function leads to minimizing the number of non-zero components in vector x.
- (2)
- Based on the perturbation theory, the l1 norm is more robust compared to the l2 norm, which affects the quality of processing of non-stationary signals that contain sections of transient processes.
- (3)
- From a computational point of view, the problem belongs to the LP problem (linear programming, the class of optimization problems).
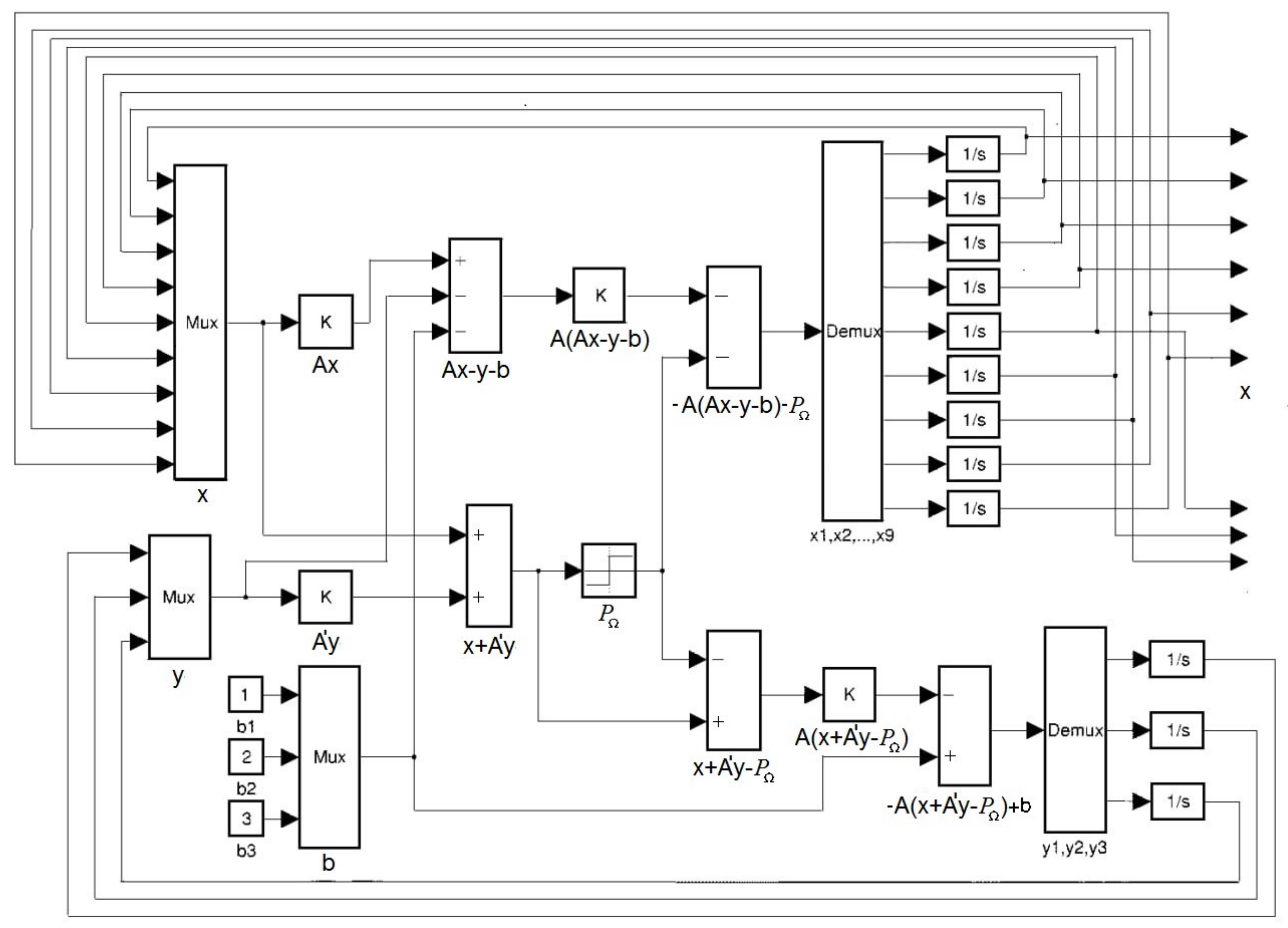
2. Minimum Fuel Neural Network for Complex Data
- (1)
- A grid of angular directions to the source can be formed with a uniform step both in wave numbers and in the angle , where i = 1, 2, …, N is the total number of angular directions. In the first case, it turns out to be denser in the vicinity of the zero-angle value.
- (2)
- For an m-channel receiving system, two parts of the dictionary are formed in the following ways:
- (3)
- The formed parts are combined into a common dictionary, according to the rule:
3. Activation Function to Implement the Algorithm in Real Form
4. Activation Function to Implement the Algorithm in Complex Form
5. Numerical Modeling
5.1. The Case of a Single External Source with a Varying Initial Phase

5.2. The Case of Two Sources with Different Initial Signal Phases
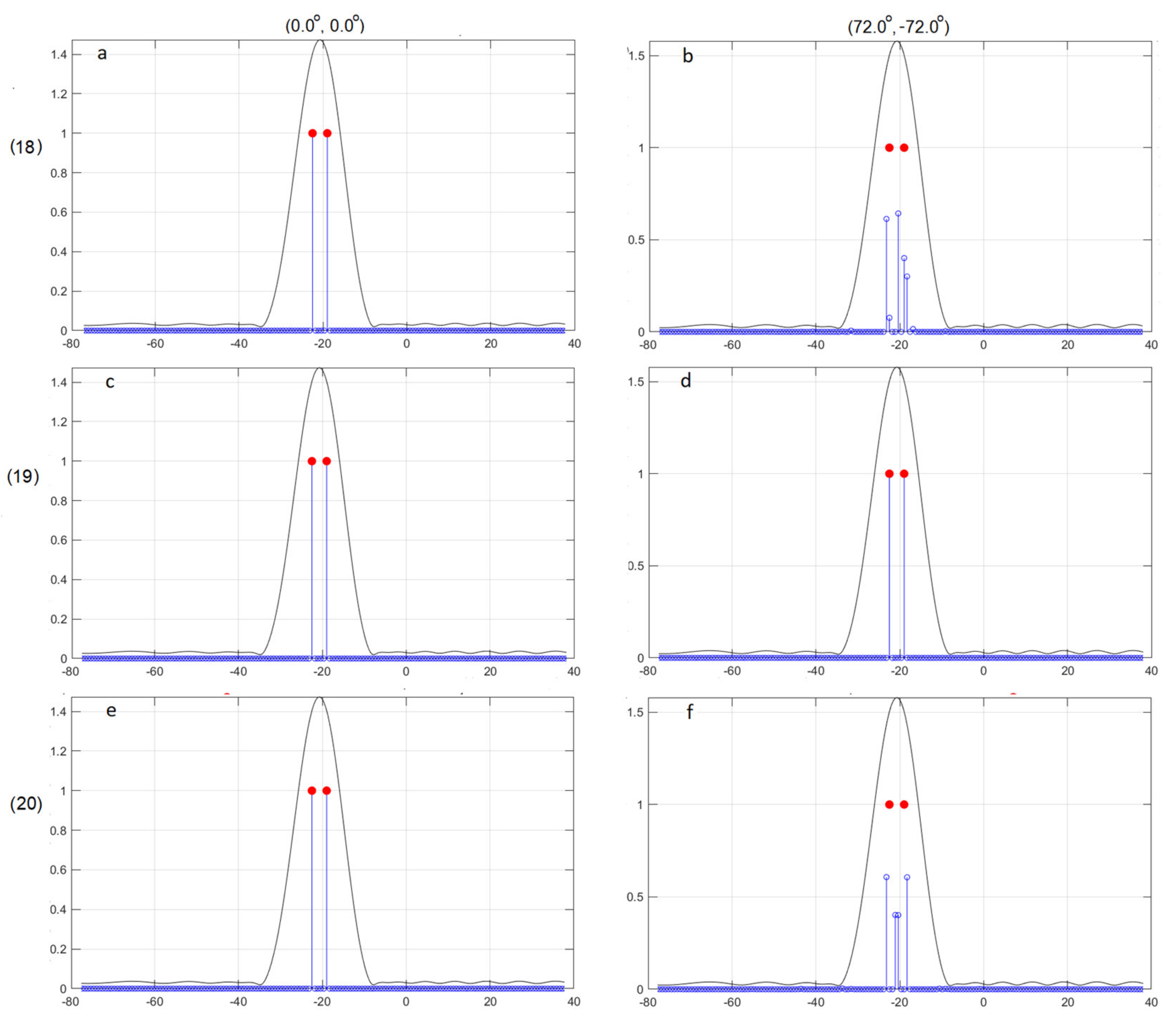
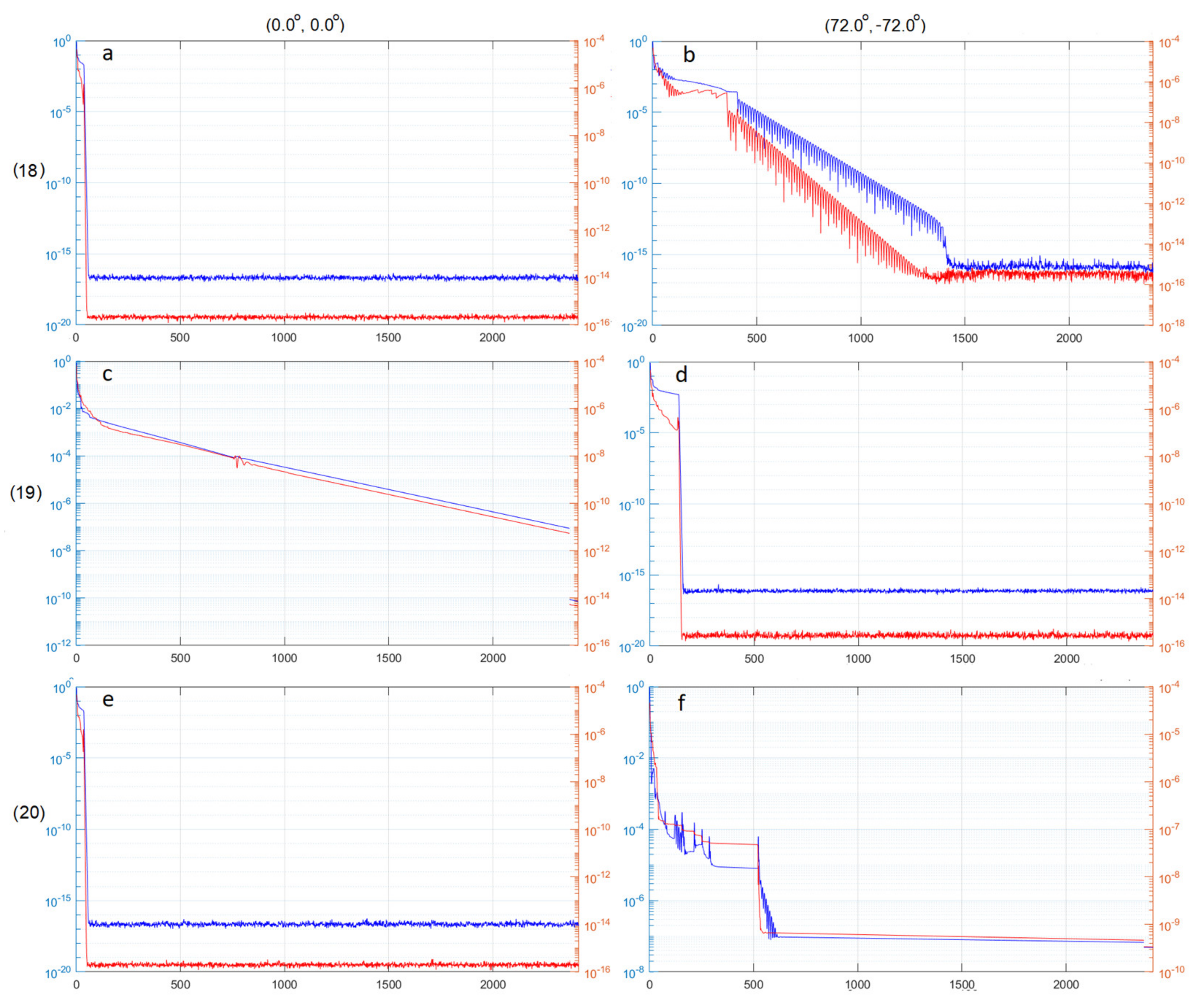
5.3. A Large Number of Sources
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schmidt, R.O. Multiple Emitter Location and Signal Parameter Estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Rao, B.D.; Hari, K.V.S. Performance analysis of root-MUSIC. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1939–1949. [Google Scholar] [CrossRef]
- Zala, C.A.; Barrodale, I.; Kennedy, J.S. High-resolution signal and noise field estimation using the L1 (least absolute values) norm. IEEE J. Ocean. Eng. 1987, 12, 253–264. [Google Scholar] [CrossRef]
- Bandler, J.W.; Kellerman, W.; Madsen, K. A nonlinear L1 optimization algorithm for design, modeling, and diagnosis of networks. IEEE Trans. Circuits Syst. 1987, 34, 174–181. [Google Scholar] [CrossRef]
- Abdelmalek, N.N. Solutions of minimum time problem and minimum fuel problem for discrete linear admissible control systems. Int. J. Syst. Sci. 1978, 8, 849–859. [Google Scholar] [CrossRef]
- Levy, S.; Walker, C.; Ulrych, T.J.; Fullagar, P.K. A linear programming approach to the estimation of the power spectra of harmonic processes. IEEE Trans. Acoust. Speech Signal Process. 1992, 30, 675–679. [Google Scholar] [CrossRef]
- Stanković, L.; Sejdić, E.; Stanković, S.; Daković, M.; Orović, I. A Tutorial on Sparse Signal Reconstruction and Its Applications in Signal Processing. Circuits Syst. Signal Process. 2019, 38, 1206–1263. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, S.; Huang, D.; Sun, D.; Liu, L.; Cui, H. L0-norm penalized shrinkage linear and widely linear LMS algorithms for sparse system identification. IET Signal Process. 2017, 11, 86–94. [Google Scholar] [CrossRef]
- Ishii, Y.; Koide, S.; Hayakawa, K. L0-norm Constrained Autoencoders for Unsupervised Outlier Detection. In Advances in Knowledge Discovery and Data Mining. PAKDD 2020; Lauw, H., Wong, R.W., Ntoulas, A., Lim, E.P., Ng, S.K., Pan, S., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12085. [Google Scholar] [CrossRef]
- Marquardt, D.W.; Snee, R.D. Ridge regression in practice. Am. Stat. 1975, 29, 3–20. [Google Scholar] [CrossRef]
- Rajko, R. Studies on the adaptability of different Borgen norms applied in selfmodeling curve resolution (SMCR) method. J. Chemom. 2009, 23, 265–274. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Schmidt, R.O. A Signal Subspace Approach to Multiple Emitter Location and Spectral Estimation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1981. [Google Scholar]
- Capon, J. High resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Sun, K.; Liu, Y.; Meng, H.; Wang, X. Adaptive Sparse Representation for Source Localization with Gain/Phase Errors. Sensors 2011, 11, 4780–4793. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L.; Huo, X. Uncertainty Principles and Ideal Atomic Decomposition. IEEE Trans. Inf. Theory 2001, 47, 2845–2862. [Google Scholar] [CrossRef]
- Malioutov, D.M.; Cetin, M.; Willsky, A.S. Optimal sparse representations in general overcomplete bases. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004. [Google Scholar] [CrossRef]
- Cichocki, A.; Unbehauen, R. Neural Networks for Solving Systems of Linear Equations and Related Problems. IEEE Trans. Circuits Syst. I Fund. Theory Appl. 1992, 39, 124–138. [Google Scholar] [CrossRef]
- Wang, Z.S.; Cheung, J.Y.; Xia, Y.S.; Chen, J.D.Z. Minimum fuel neural networks and their applications to overcomplete signal representations. IEEE Trans. Circuits Syst. I Fund. Theory Appl. 2000, 47, 1146–1159. [Google Scholar] [CrossRef]
- Kümmerle, C.; Verdun, C.M.; Stöger, D. Iteratively Reweighted Least Squares for Basis Pursuit with Global Linear Convergence Rate. In Proceedings of the Advances in Neural Information Processing Systems 34 (NeurIPS 2021), Online, 6–14 December 2021; Volume 34, pp. 2873–2886. [Google Scholar]
- Mohimani, G.H.; Babaie-Zadeh, M.; Jutten, C. Complex-valued sparse representation based on smoothed l0 norm. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3881–3884. [Google Scholar] [CrossRef]
- Mohimani, H.; Babaie-Zadeh, M.; Jutten, C. A fast approach for overcomplete sparse decomposition based on smoothed l0 norm. IEE Trans. Signal Process. 2009, 57, 289–301. [Google Scholar] [CrossRef]
- Wang, L.; Yin, X.; Yue, H.; Xiang, J. A regularized weighted smoothed L0 norm minimization method for underdetermined blind source separation. Sensors 2018, 12, 4260. [Google Scholar] [CrossRef] [PubMed]



| Activation Function | External Source Phase | Coefficients Quantity |
|---|---|---|
| (18) | 0° | 1 |
| (18) | 72° | 42 |
| (18) | −18.9° | 42 |
| (19) | 0° | 1 |
| (19) | 72° | 1 |
| (19) | −18.9° | 1 |
| (20) | 0° | 1 |
| (20) | 72° | 1 |
| (20) | −18.9° | 15 |
| Activation Function | Source Phase | Coefficients Quantity |
|---|---|---|
| (18) | (0°, 0°) | 2 |
| (18) | (72°, −72°) | 5 |
| (19) | (0°, 0°) | 2 |
| (19) | (72°, −72°) | 2 |
| (20) | (0°, 0°) | 4 |
| (20) | (72°, −72°) | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panokin, N.V.; Averin, A.V.; Kostin, I.A.; Karlovskiy, A.V.; Orelkina, D.I.; Nalivaiko, A.Y. Method for Sparse Representation of Complex Data Based on Overcomplete Basis, l1 Norm, and Neural MFNN-like Network. Appl. Sci. 2024, 14, 1959. https://doi.org/10.3390/app14051959
Panokin NV, Averin AV, Kostin IA, Karlovskiy AV, Orelkina DI, Nalivaiko AY. Method for Sparse Representation of Complex Data Based on Overcomplete Basis, l1 Norm, and Neural MFNN-like Network. Applied Sciences. 2024; 14(5):1959. https://doi.org/10.3390/app14051959
Chicago/Turabian StylePanokin, Nikolay V., Artem V. Averin, Ivan A. Kostin, Alexander V. Karlovskiy, Daria I. Orelkina, and Anton Yu. Nalivaiko. 2024. "Method for Sparse Representation of Complex Data Based on Overcomplete Basis, l1 Norm, and Neural MFNN-like Network" Applied Sciences 14, no. 5: 1959. https://doi.org/10.3390/app14051959
APA StylePanokin, N. V., Averin, A. V., Kostin, I. A., Karlovskiy, A. V., Orelkina, D. I., & Nalivaiko, A. Y. (2024). Method for Sparse Representation of Complex Data Based on Overcomplete Basis, l1 Norm, and Neural MFNN-like Network. Applied Sciences, 14(5), 1959. https://doi.org/10.3390/app14051959







