Intrinsic Mode-Based Network Approach to Examining Multiscale Characteristics of Sea Surface Temperature Variability
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Empirical Mode Decomposition (EMD)
- All the local extrema are identified for a given time series, .
- By interpolating all the local maxima and minima with cubic spline curves, respectively, we obtain the upper, , and lower, , envelops.
- An average envelop is obtained from the upper and lower envelops via .
- A proto-IMF is obtained via the following differences, .
- By checking if the proto-IMF satisfies two requirements, the definition of IMF and the stoppage criterion, the proto-IMF is determined to be an IMF.
- If the proto-IMF does not satisfy these requirements, steps 1 through 5 on are repeated until they are satisfied.
- When the requirements are satisfied, the proto-IMF, , is assigned as an IMF component, .
- For the next IMF, we repeat steps 1 through 7 on the residue, .
- All the iterations end when the final residue contains no more than one extremum.
2.3. Hilbert Spectrum
2.4. Complex Network Methodology
2.4.1. Network Construction
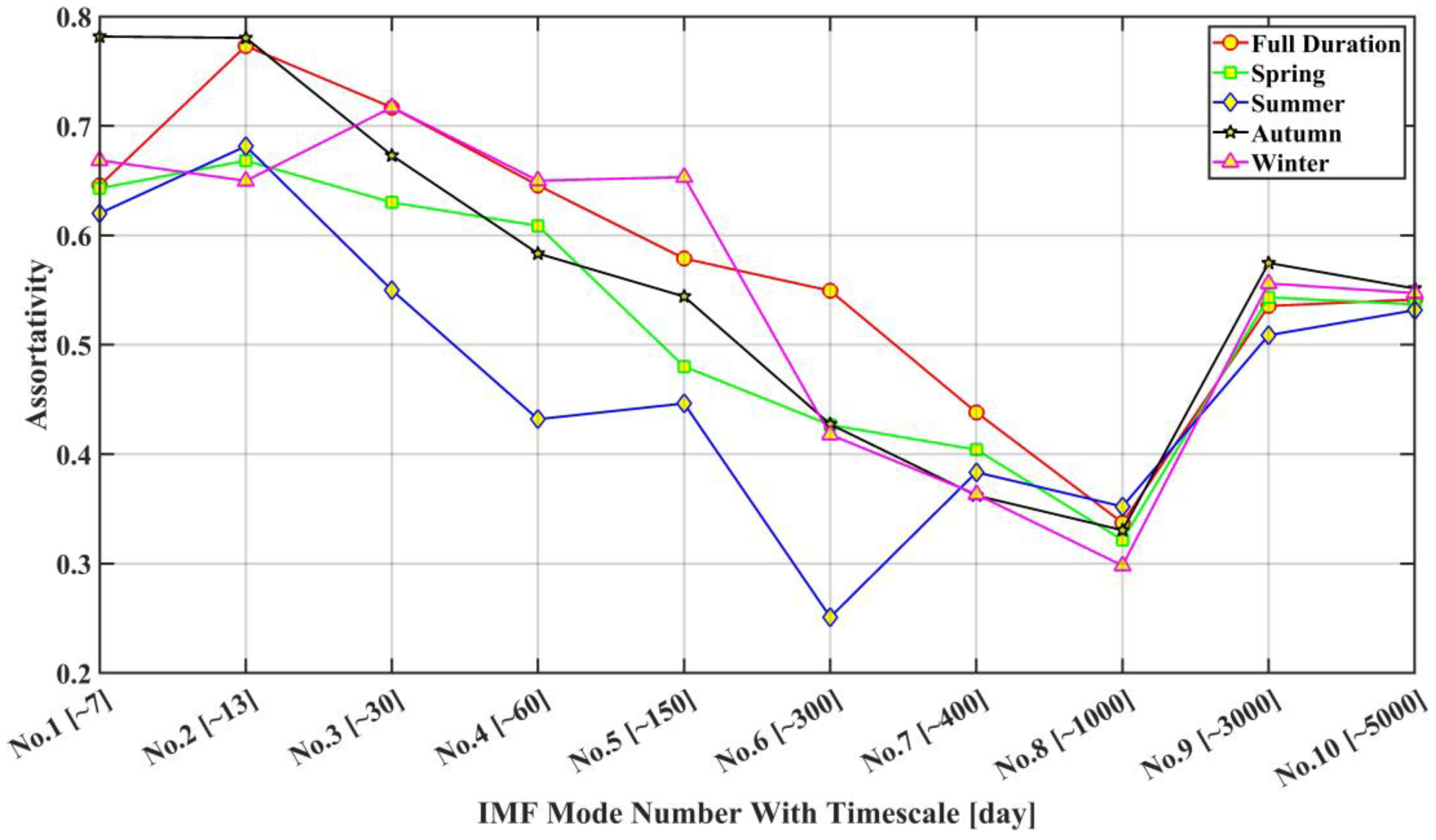
2.4.2. Network Metrics
- indicates an assortative network, characterized by a big clustered structure, robustness by multiple hubs, and stability in the network’s structure [41].
- indicates a disassortative network, characterized by a negative correlation between adjacent two nodes.
- implies that there is no correlation between two nodes of a network.
3. Analysis Results
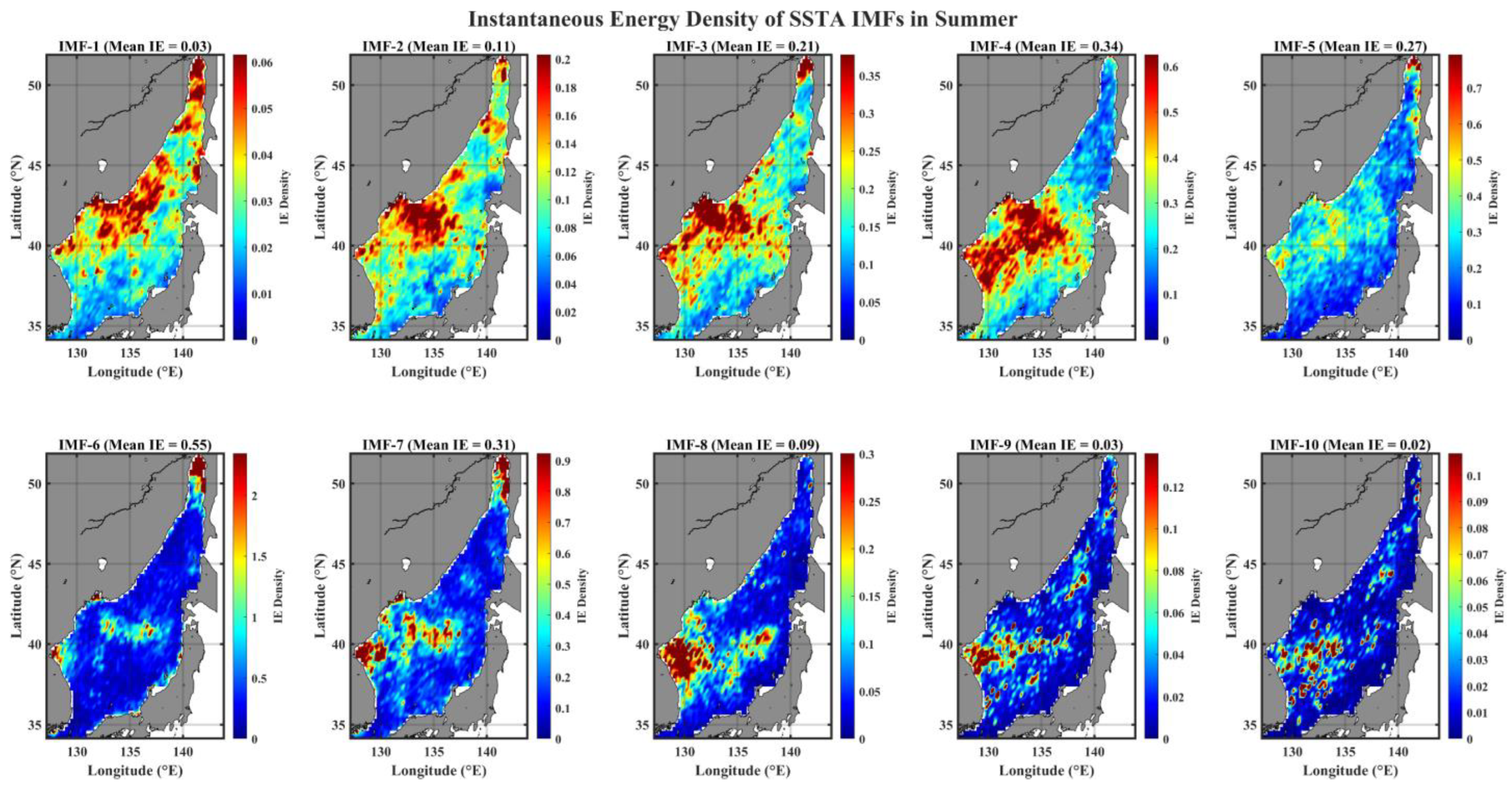
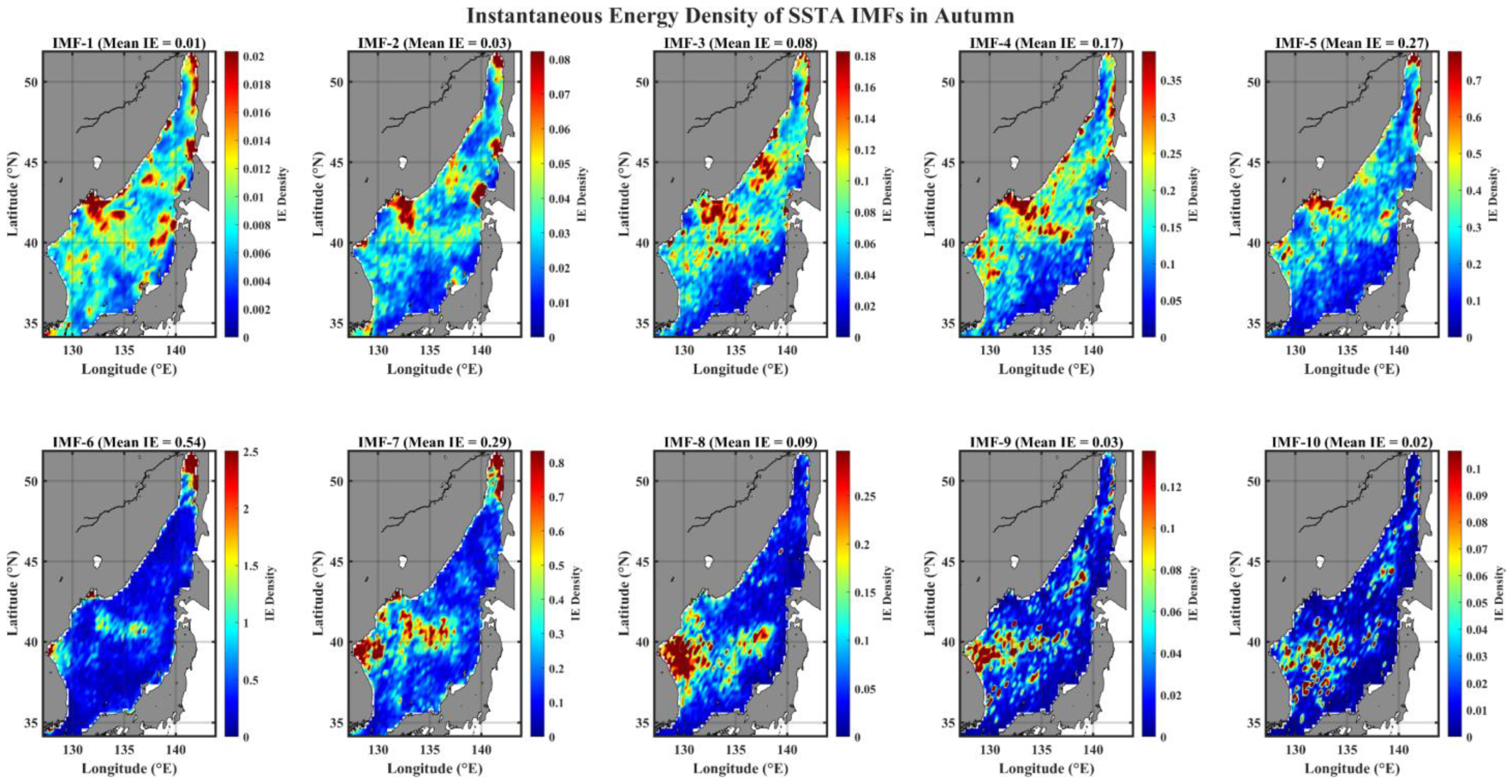
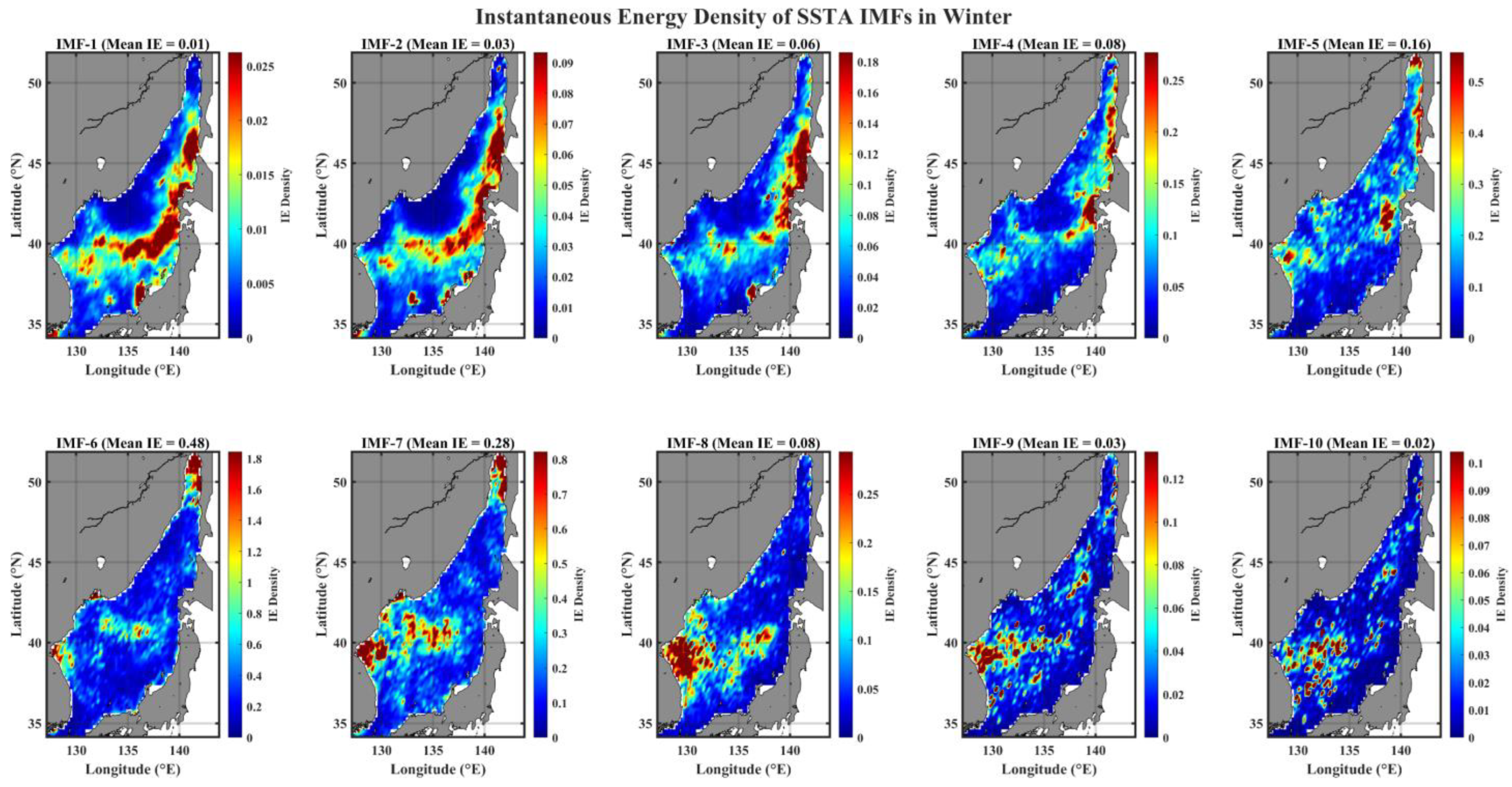
3.1. Spatial Pattern of Instantaneous Energy Level (IE) of IMFs
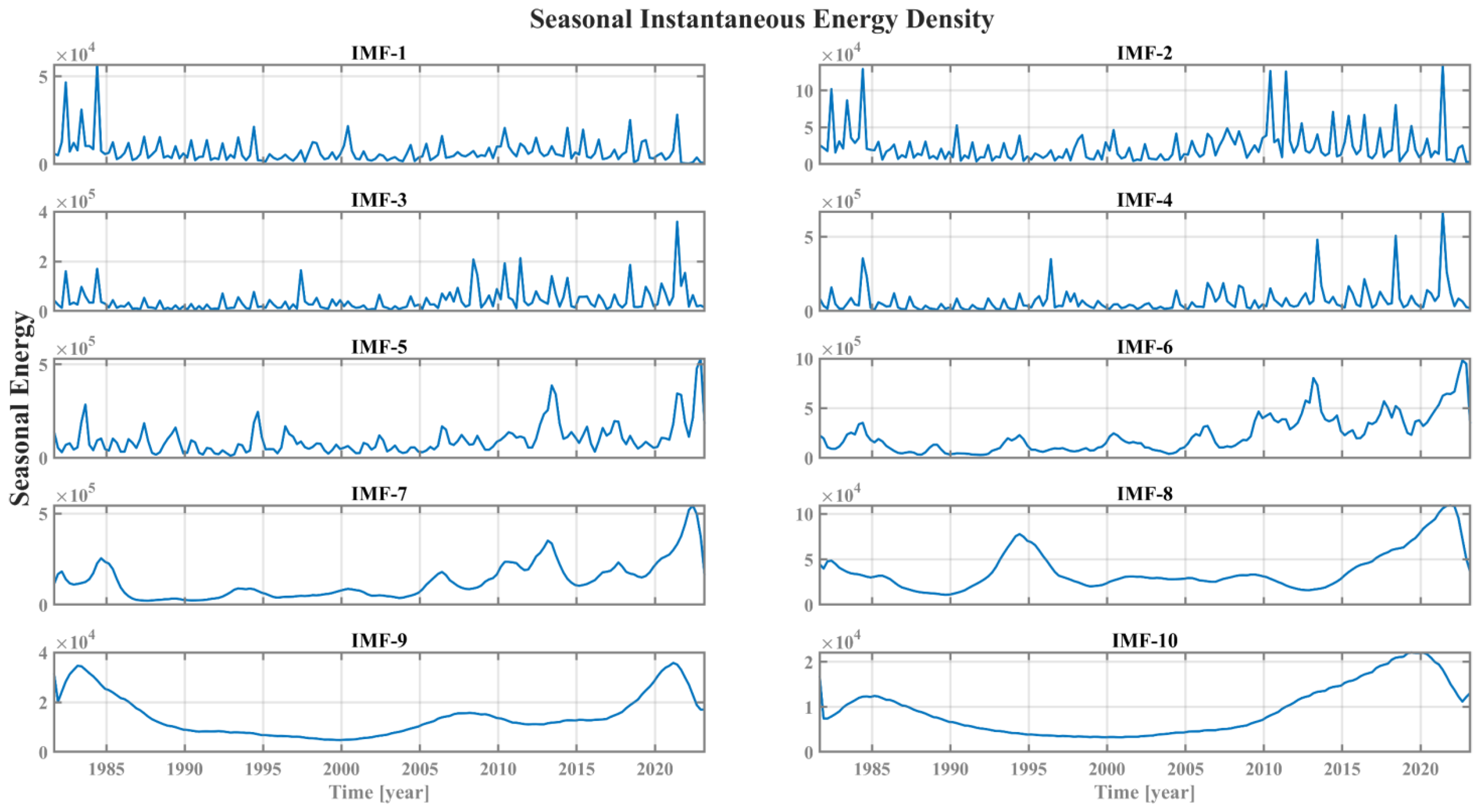
3.2. Temporal Evolution of the Instantaneous Energy Level (IE) of IMFs
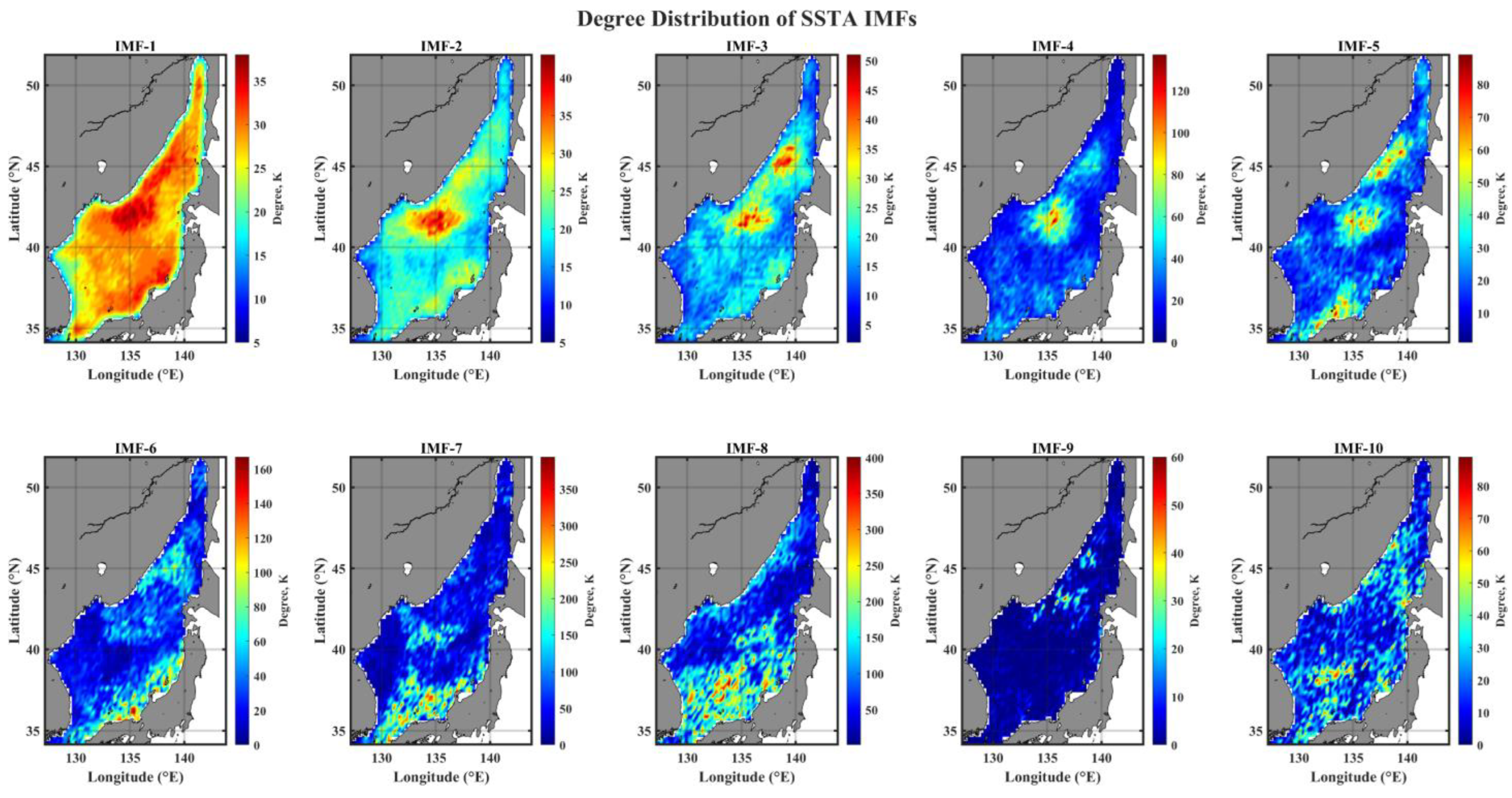
3.3. Spatial Pattern of Degree Distribution of IMF Networks
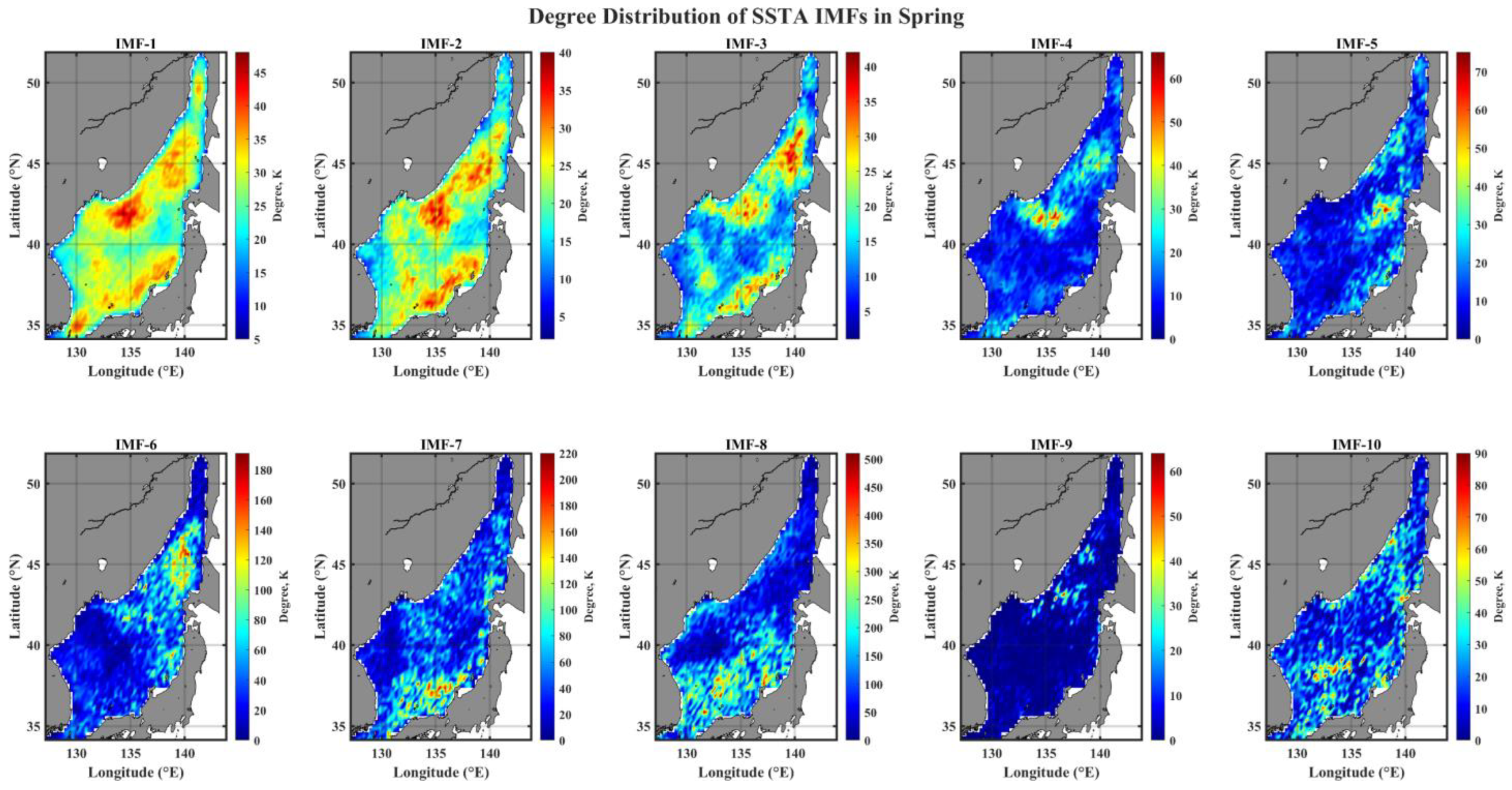

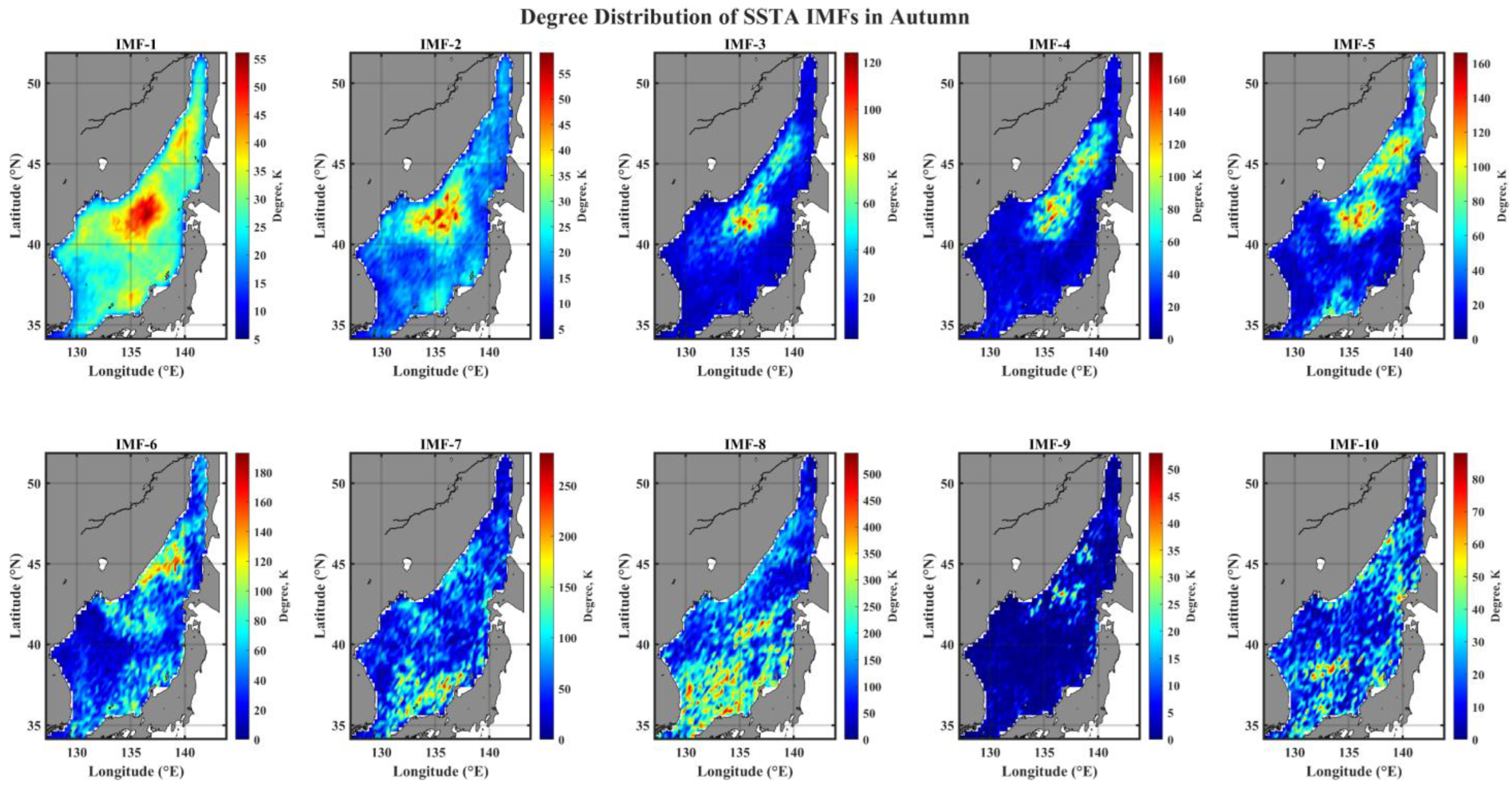
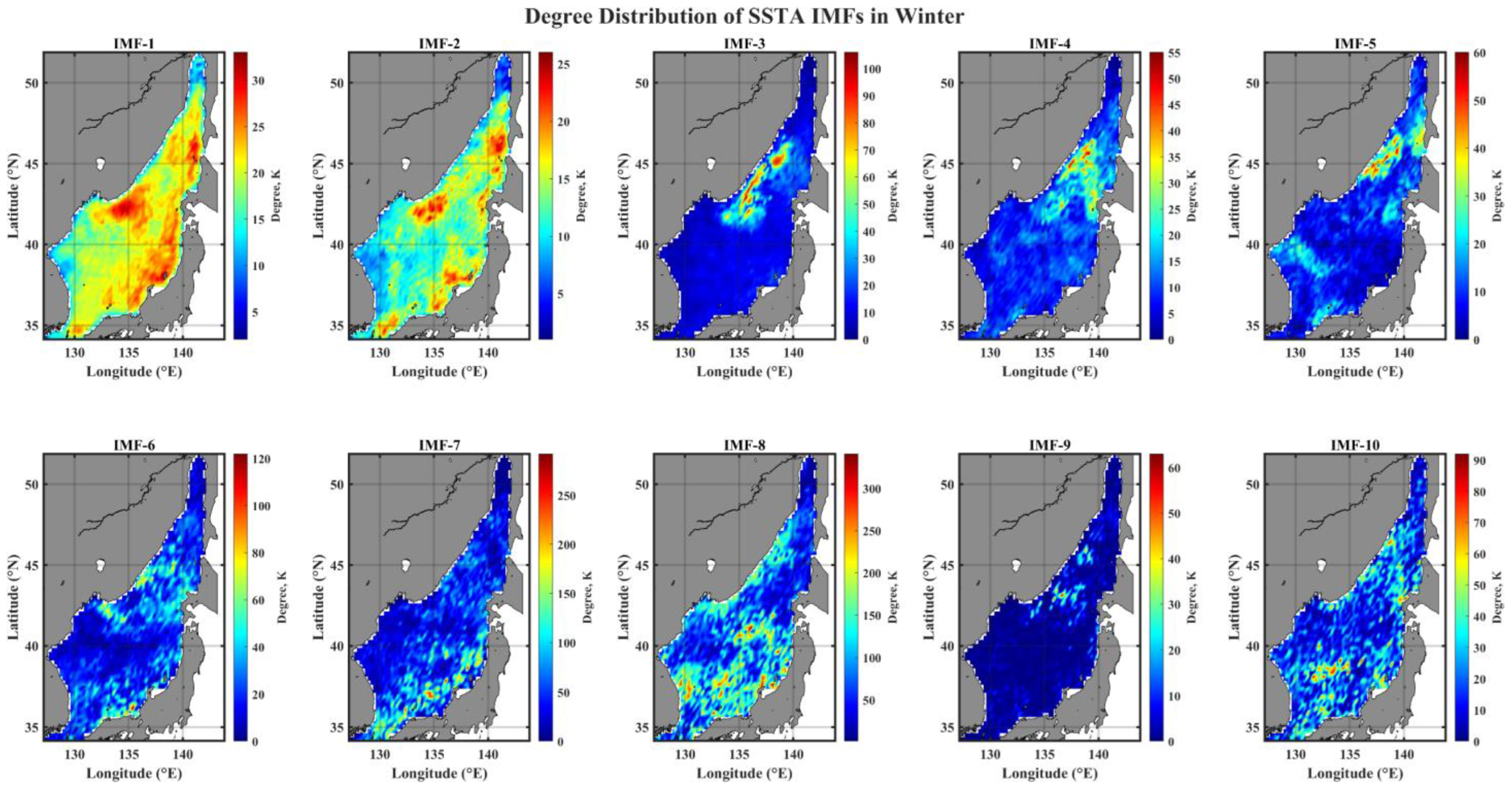
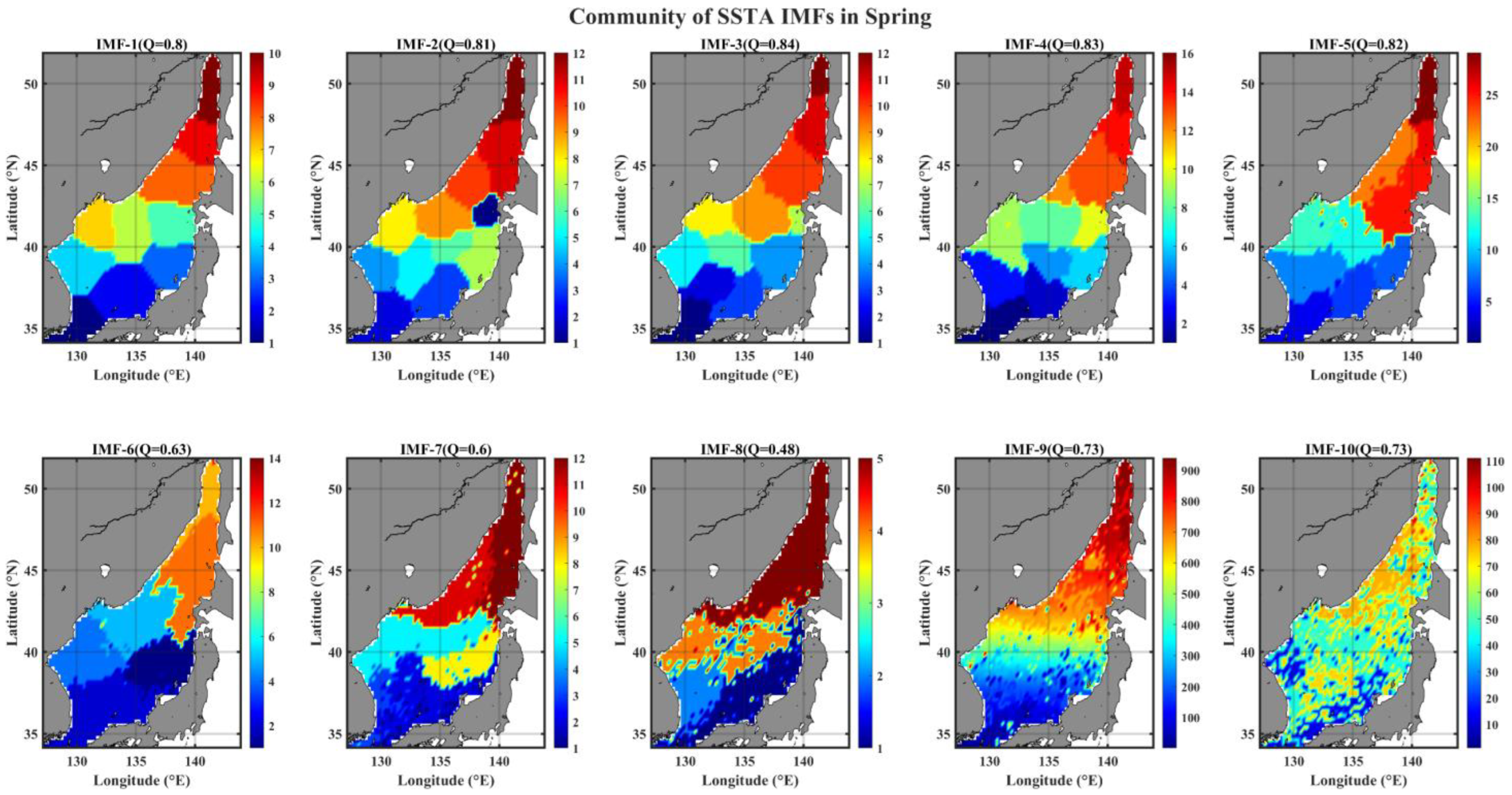
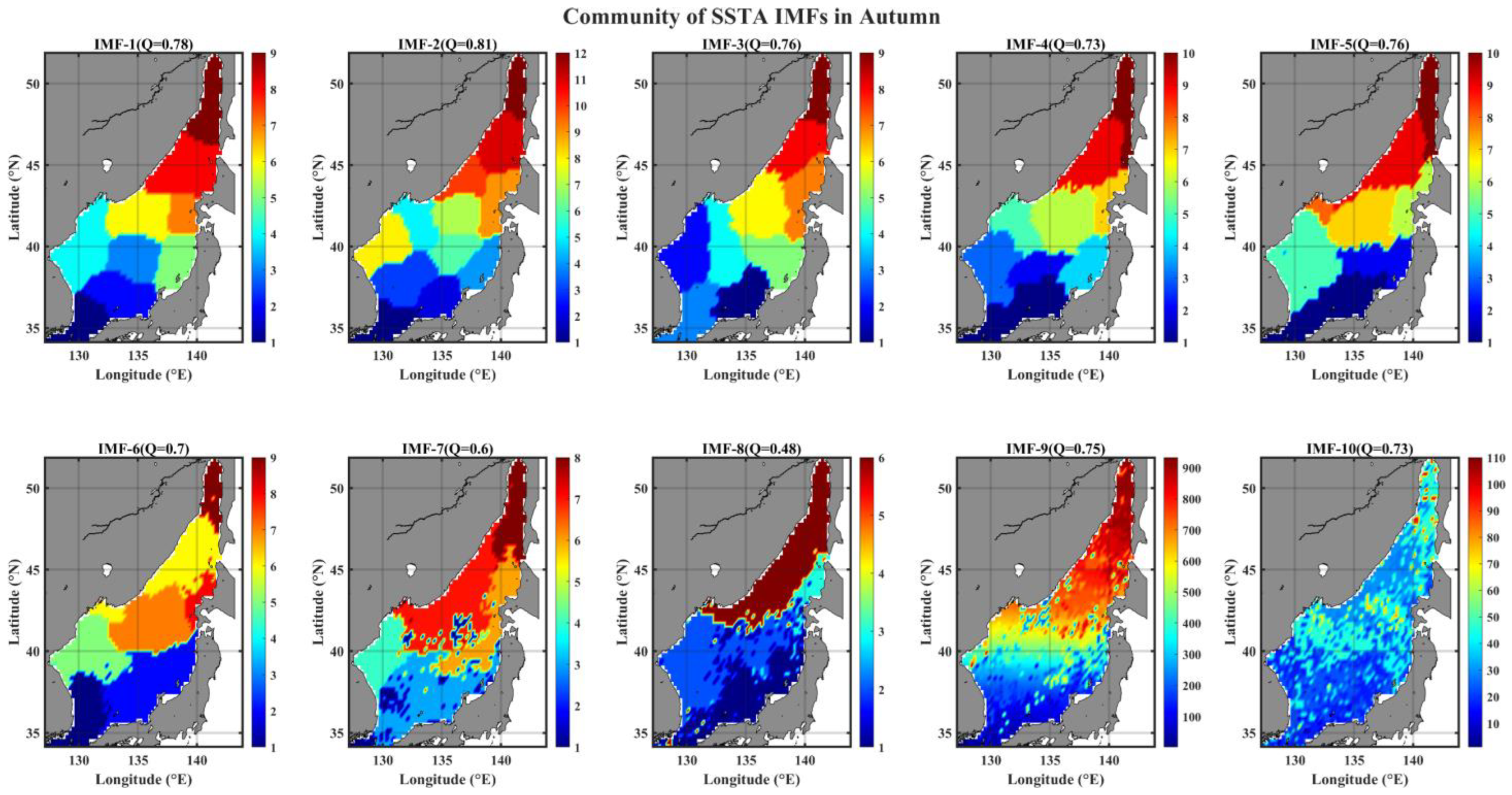
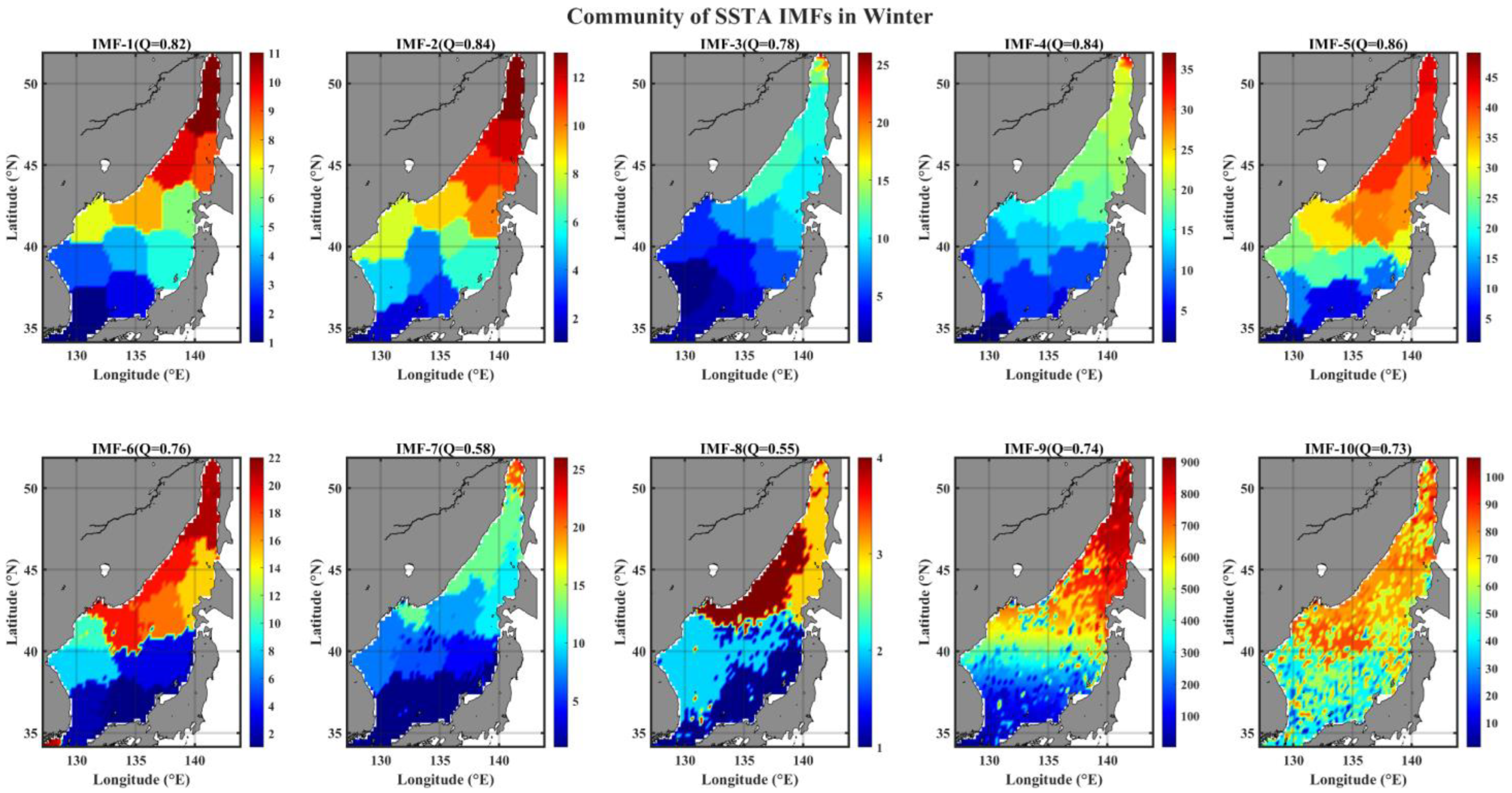
3.4. Spatial Pattern of Community in IMF Networks
4. Discussions
5. Conclusions
- Distinct spatial patterns of (amplitude) energy density distribution are greatly classified into two temporal scales, the weekly to semiannual timescales and the longer than annual timescales; the former reveals a strong seasonality with a high energy in the north-western (north-eastern) part of EJS during summer (winter), and the latter shows a persistent spatial structure of high energy distribution in a tongue-shape region from East Korea Bay (EKB) extending to Sub-Polar Front (SPF).
- There is an apparent seasonality in the temporal evolution of the basin-wide summed energy density, with a peak in the summer seasons, as well as an increasing energy level trend since the 2010s.
- The connectivity topological structure of IMF networks reveals season- and scale-specific features only for monthly to semiannual modes, in terms of nodes (hubs) with high connectivity; in summer, hubs are widely distributed in the southern EJS, while hubs occupy only small areas in the northern EJS during winter.
- The link-based community structure of IMF networks shows a region-specific feature only for weekly to seasonal modes and gradually expands its spatial extent to a basin-wide scale as the mode number (indicating the timescale of the mode) increases; in addition, there is qualitative information concerning the advection timescale of flowing-in waters with low salinity from the northern and southern ends of the EJS, known to be contributing to the ESIW formation at its formation site (40~43° N, 131~135° E) [31].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deser, C.; Alexander, M.A.; Xie, S.-P.; Phillips, A.S. Sea Surface Temperature Variability: Patterns and Mechanism. Annu. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef]
- Park, K.; Chung, J.Y. Spatial and temporal scale variations of sea surface temperature in the East Sea using NOAA/AVHRR data. J. Oceanogr. 1999, 55, 271–288. [Google Scholar] [CrossRef]
- Park, W.-S.; Oh, I.S. Interannual and interdecadal variations of sea surface temperature in the East Asian marginal seas. Prog. Oceanogr. 2000, 47, 191–204. [Google Scholar] [CrossRef]
- Minobe, S.; Sako, A.; Nakamura, M. Interannual to interdecadal variability in the Japan Sea based on a new gridded upper water temperature dataset. J. Phys. Oceanogr. 2004, 34, 2382–2397. [Google Scholar] [CrossRef]
- Jeong, Y.; Nam, S.; Kwon, J.-I.; Uppara, U.; Jo, Y.-H. Surface warming slowdown with continued subsurface warming in the East Sea (Japan Sea) over recent decades (2000–2014). Front. Mar. Sci. 2022, 9, 173. [Google Scholar] [CrossRef]
- Kawamura, H.; Wu, P. Formation mechanism of Japan sea proper water in the flux center off Vladivostok. J. Geophys. Res. 1998, 103, 21611–21622. [Google Scholar] [CrossRef]
- Hirose, N.; Ostrovskii, A.G. Quasi-biennial variability in the Japan Sea. J. Geophys. Res. 2000, 105, 14011–14027. [Google Scholar] [CrossRef]
- Watanabe, T.; Hanawa, K.; Toba, Y. Analyses of year-to-year variation of water temperature along the coast of Japan Sea. Prog. Oceanogr. 1986, 17, 337–357. [Google Scholar] [CrossRef]
- Isoda, Y. Interannual SST variations to the north and south of the Polar front in the Japan Sea. La Mer 1994, 32, 285–293. [Google Scholar]
- Isoda, Y.; Korematsu, H. Interannual variation of water temperature, salinity, and oxygen vertical distribution in the Tsushima current region. Umi Sora 1995, 71, 47–67. [Google Scholar]
- Watanabe, Y.W.; Wakita, M.; Maeda, N.; Ono, T.; Gamo, T. Synchronous bidecadal periodic changes of oxygen, phosphate and temperature between the Japan Sea deep water and the North Pacific intermediate water. Geophys. Res. Lett. 2003, 30, 2273. [Google Scholar] [CrossRef]
- Minobe, S. Interdecadal temperature variation of deep water in the Japan Sea (East Sea). In Proceedings of the Fourth Workshop CREAMS, R/V OKEAN, Vladivostok, Russia, 12–13 February 1996; pp. 81–88. [Google Scholar]
- Park, S.; Chu, P. Interannual SST variability in the Japan/East Sea and relationship with environmental variables. J. Oceanogr. 2006, 62, 115–132. [Google Scholar] [CrossRef]
- Ponomarev, V.I.; Dyakonova, I.; Palshin, N.; Rudykh, N.; Ishida, H. Multiscale Variability of oceanographic and meteorological characteristics in the Japan (East) Sea area. In Past, Present and Future Environments of Pan-Japan Sea Region; Hayakawa, K., Ed.; MARUZEN Co. Ltd.: Kanazawa, Japan, 2006; pp. 407–417. [Google Scholar]
- Park, K.-A.; Park, J.-E.; Choi, B.-J.; Byun, D.-S.; Lee, E.-I. An Oceanic Current Map of the East Sea for Science Textbooks Based on Scientific Knowledge Acquired from Oceanic Measurements. Sea J. Korean Soc. Oceanogr. 2013, 18, 234–265. [Google Scholar]
- Chen, S.; Wang, H.; Wang, N.; Wang, H.; Yu, P.; Yang, X.; Zhang, Y. Dominant modes of winter SST variability in the Japan Sea and their influences on atmosphere. J. Oceanogr. 2022, 78, 353–368. [Google Scholar] [CrossRef]
- Chu, P.C.; Chen, Y.; Lu, S. Temporal and spatial variabilities of Japan Sea surface temperature and atmospheric forcings. J. Oceanogr. 1998, 54, 273–284. [Google Scholar] [CrossRef]
- Dorman, C.E.; Friehe, C.A.; Khelif, D.; Scotti, A.; Edson, J.; Beardsley, R.C.; Limeburner, R.; Chen, S.S. Winter atmospheric conditions over the Japan/East Sea: The structure and impact of severe cold air outbreaks. Oceanography 2006, 19, 96–109. [Google Scholar] [CrossRef]
- Dorman, C.E.; Beardsley, R.C.; Dashko, N.A.; Friehe, C.A.; Kheilf, D.; Cho, K.; Limeburner, R.; Varlamov, S.M. Winter marine atmospheric conditions over the Japan Sea. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Trusenkova, O.O.; Lobanov, V.B.; Kaplunenko, D.D. Variability of sea surface temperature in the Japan Sea and its relationship to the wind-curl field. Izv. Atmos. Ocean. Phys. 2008, 44, 517. [Google Scholar] [CrossRef]
- Yoshikawa, Y.; Awaji, T.; Akitomo, K. Formation and circulation processes of intermediate water in the Japan Sea. J. Phys. Oceanogr. 1999, 29, 1701–1722. [Google Scholar]
- Yoon, J.-H.; Kawamura, H. The formation and circulation of the intermediate water in the Japan Sea. J. Oceanogr. 2002, 58, 197–211. [Google Scholar] [CrossRef]
- Park, K.-A.; Chung, J.Y.; Kim, K.; Cornillon, P.C. Wind and bathymetric forcing of the annual sea surface temperature signal in the East (Japan) Sea. Geophys. Res. Lett. 2005, 32, L05610. [Google Scholar] [CrossRef]
- Park, K.-A.; Ullman, D.S.; Kim, K.; Chung, J.Y.; Kim, K.-R. Spatial and temporal variability of satellite-observed Subpolar Front in the East/Japan Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2007, 54, 453–470. [Google Scholar] [CrossRef]
- Park, K.-A.; Lee, E.-Y. Semi-annual cycle of sea-surface temperature in the East/Japan Sea and cooling process. Int. J. Remote Sens. 2014, 35, 4287–4314. [Google Scholar] [CrossRef]
- Cui, Y.; Senjyu, T. Interdecadal oscillations in the Japan Sea proper water related to the arctic oscillation. J. Oceanogr. 2010, 66, 337–348. [Google Scholar] [CrossRef]
- Hong, C.-H.; Cho, K.-D.; Kim, H.-J. The relationship between ENSO events and sea surface temperature in the East (Japan) Sea. Prog. Oceanogr. 2001, 49, 21–40. [Google Scholar] [CrossRef]
- Isobe, A.; Beardsley, R.C. Atmosphere and marginal-sea interaction leading to an interannual variation in cold-air outbreak activity over the Japan Sea. J. Clim. 2007, 20, 5707–5714. [Google Scholar] [CrossRef][Green Version]
- Lee, E.-Y.; Park, K.-A. Change in the recent warming trend of sea surface temperature in the East Sea (Sea of Japan) over decades (1982–2018). Remote Sens. 2019, 11, 2613. [Google Scholar] [CrossRef]
- Min, H.-S.; Kim, C.-H. Interannual variability and long-term trend of coastal sea surface temperature in Korea. Ocean Polar Res. 2006, 28, 415–423. [Google Scholar] [CrossRef][Green Version]
- Kim, S.-Y.; Park, Y.-G.; Kim, Y.H.; Seo, S.; Jin, H.; Pak, G.; Lee, H.J. Origin, variability, and pathways of East Sea Intermediate Water in a high-resolution ocean reanalysis. J. Geophys. Res. Ocean. 2021, 126, e2020JC017158. [Google Scholar] [CrossRef]
- Ponomarev, V.; Rudykh, N.; Dmitrieva, E.; Ishida, H. Variability of Surface Water Properties in the Japan/East Sea on Different Time Scales. Ocean. Polar Res. 2009, 31, 177–187. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Liu, C.; Freeman, E.; Graham, G.; Smith, T.; Zhang, H.-M. Assessment and intercomparison of NOAA daily optimum interpolation sea surface temperature (DOISST) version 2.1. J. Clim. 2021, 34, 7421–7441. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Long, S.R.; Peng, C.K. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Chen, X.-Y.; Qiao, F.-L.; Wu, Z.; Huang, N.E. On Intrinsic Mode Function. Adv. Adapt. Data Anal. 2010, 02, 277–293. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Newman, M.E.J. Assortative Mixing in Networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef]
- Callaway, D.S.; Hopcroft, J.E.; Kleinberg, J.M.; Newman, M.E.J.; Strogatz, S.H. Are randomly grown graphs really random? Phys. Rev. E 2001, 64, 041902. [Google Scholar] [CrossRef]
- Song, S.-Y.; Kim, Y.-J.; Lee, E.-J.; Yeh, S.-W.; Park, J.-H.; Park, Y.-G. Wintertime sea surface temperature variability modulated by Arctic Oscillation in the northwestern part of the East/Japan Sea and its relationship with marine heatwaves. Front. Mar. Sci. 2023, 10, 1198418. [Google Scholar] [CrossRef]
- Wang, D.; Xu, T.; Fang, G.; Jiang, S.; Wang, G.; Wei, Z.; Wang, Y. Characteristics of Marine Heatwaves in the Japan/East Sea. Remote Sens. 2022, 14, 936. [Google Scholar] [CrossRef]
- Kraus, E.B.; Businger, J.A. Atmosphere-Ocean Interaction; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Choi, B.-J.; Cho, S.H.; Jung, H.S.; Lee, S.-H.; Byun, D.-S.; Kwon, K. Interannual variation of surface circulation in the Japan/East Sea due to external forcings and intrinsic variability. Ocean Sci. J. 2018, 53, 1–16. [Google Scholar] [CrossRef]
- Pak, G.; Kim, Y.H.; Park, Y.-G. Lagrangian Approach for a new separation index of the East Korea warm current. Ocean Sci. J. 2019, 54, 29–38. [Google Scholar] [CrossRef]
- Yeh, S.-W.; Park, Y.-G.; Min, H.; Kim, C.-H.; Lee, J.-H. Analysis of characteristics in the sea surface temperature variability in the East/Japan Sea. Prog. Oceanogr. 2010, 85, 213–223. [Google Scholar] [CrossRef]
- Park, J.; Lim, B. A new perspective on origin of the East Sea intermediate water: Observations of Argo floats. Prog. Oceanogr. 2018, 160, 213–224. [Google Scholar] [CrossRef]
- Lim, G.; Park, J.-J. Examining Modulations of Internal Tides within An Anticyclonic Eddy Using a Wavelet-Coherence Network Approach. Appl. Sci. 2024, 14, 1001. [Google Scholar] [CrossRef]
- Chen, X.; Tung, K.K. Global-mean surface temperature variability: Space–time perspective from rotated EOFs. Clim Dyn. 2018, 51, 1719–1732. [Google Scholar] [CrossRef]
- Borzelli, G.; Ligi, R. Empirical Orthogonal Function Analysis of SST Image Series: A Physical Interpretation. J. Atmos. Ocean. Technol. 1999, 16, 682–690. [Google Scholar] [CrossRef]
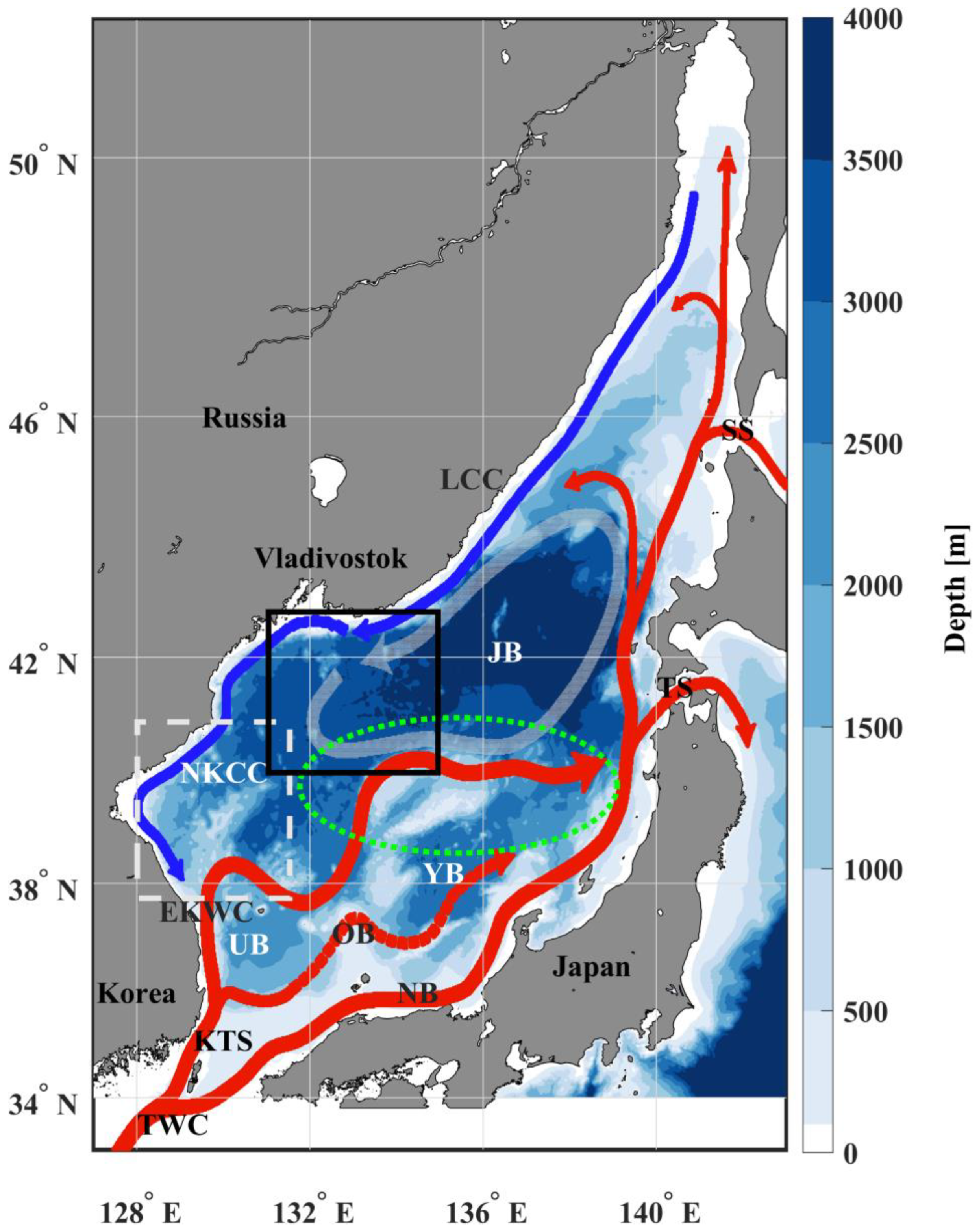
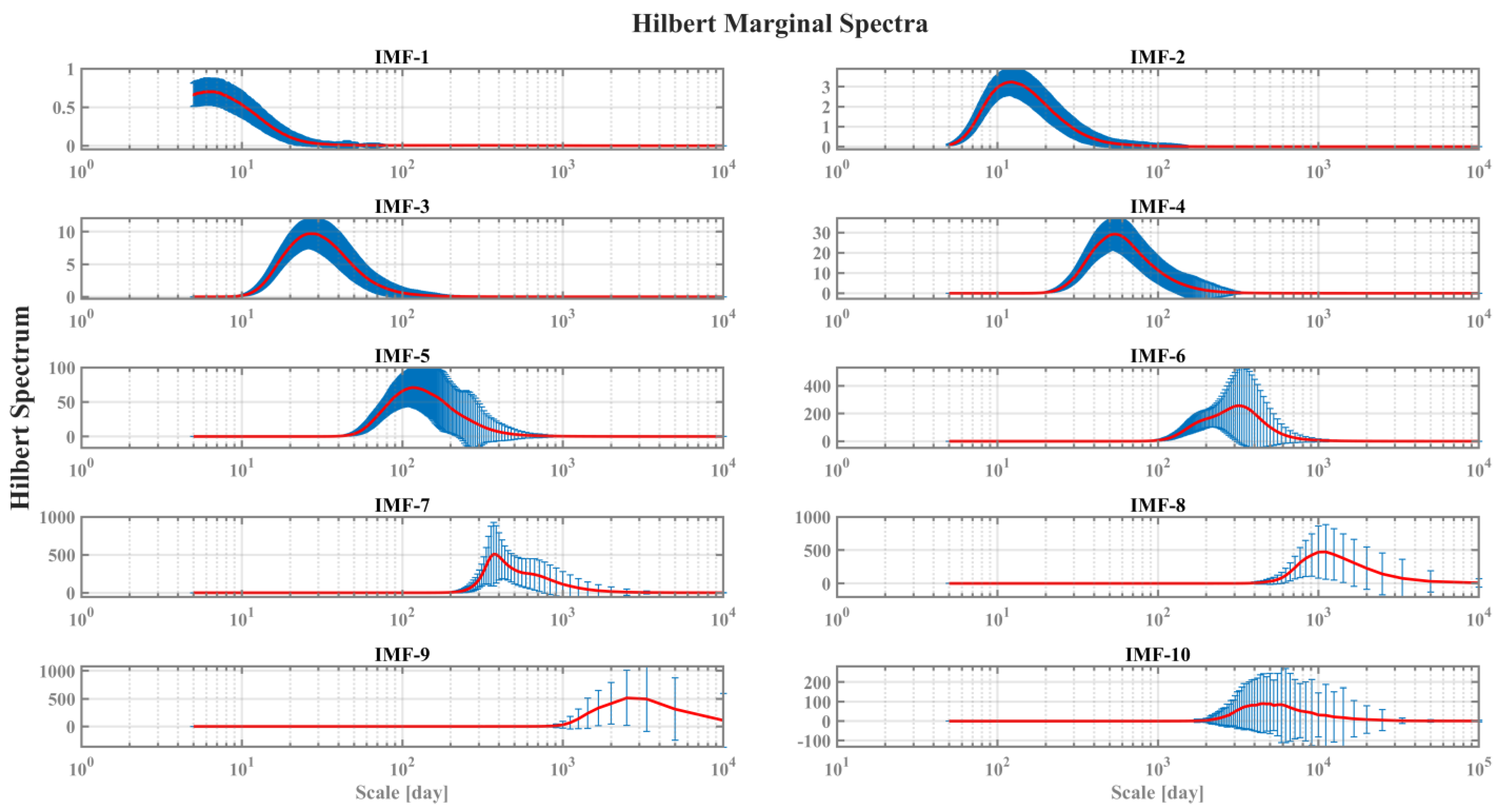
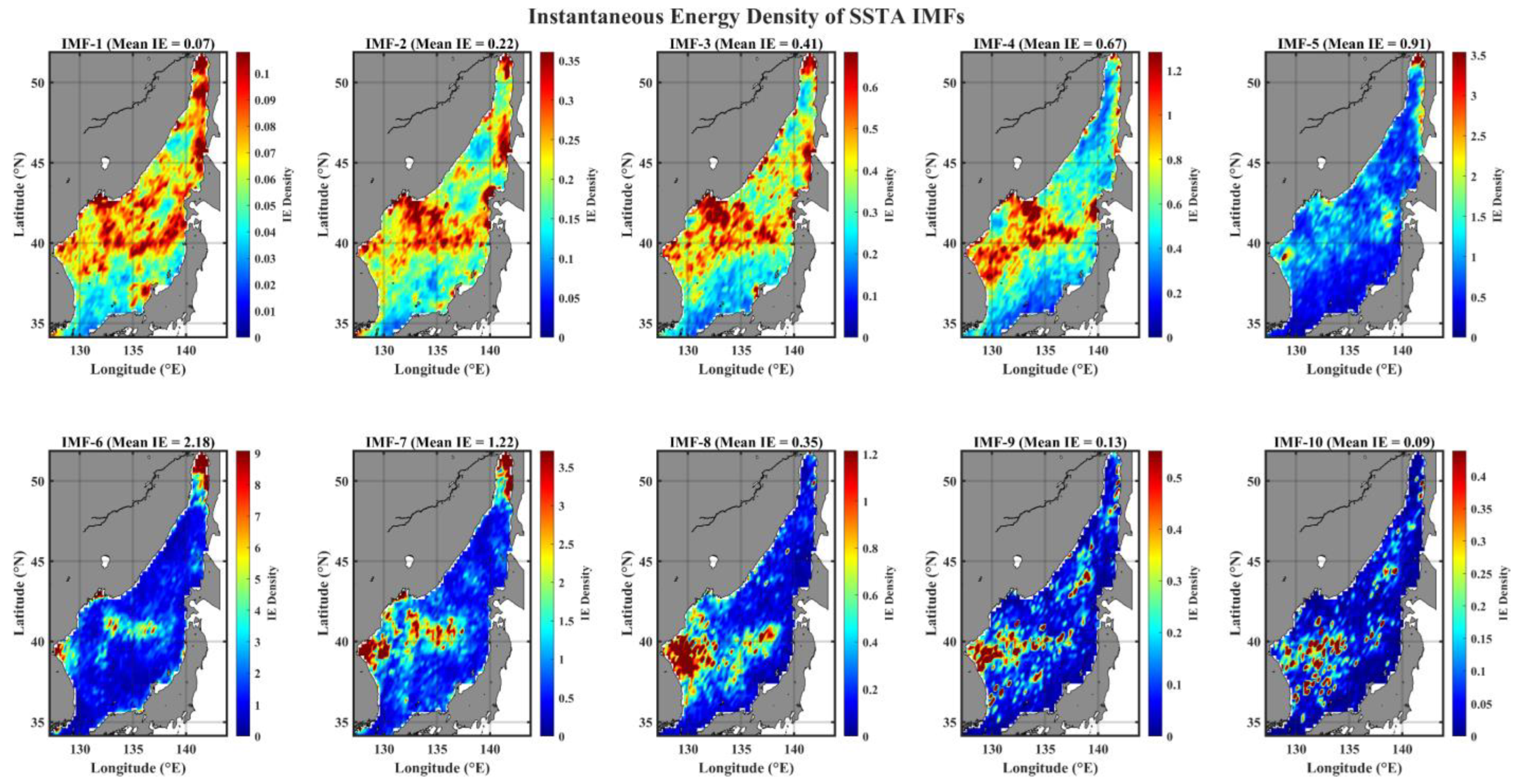
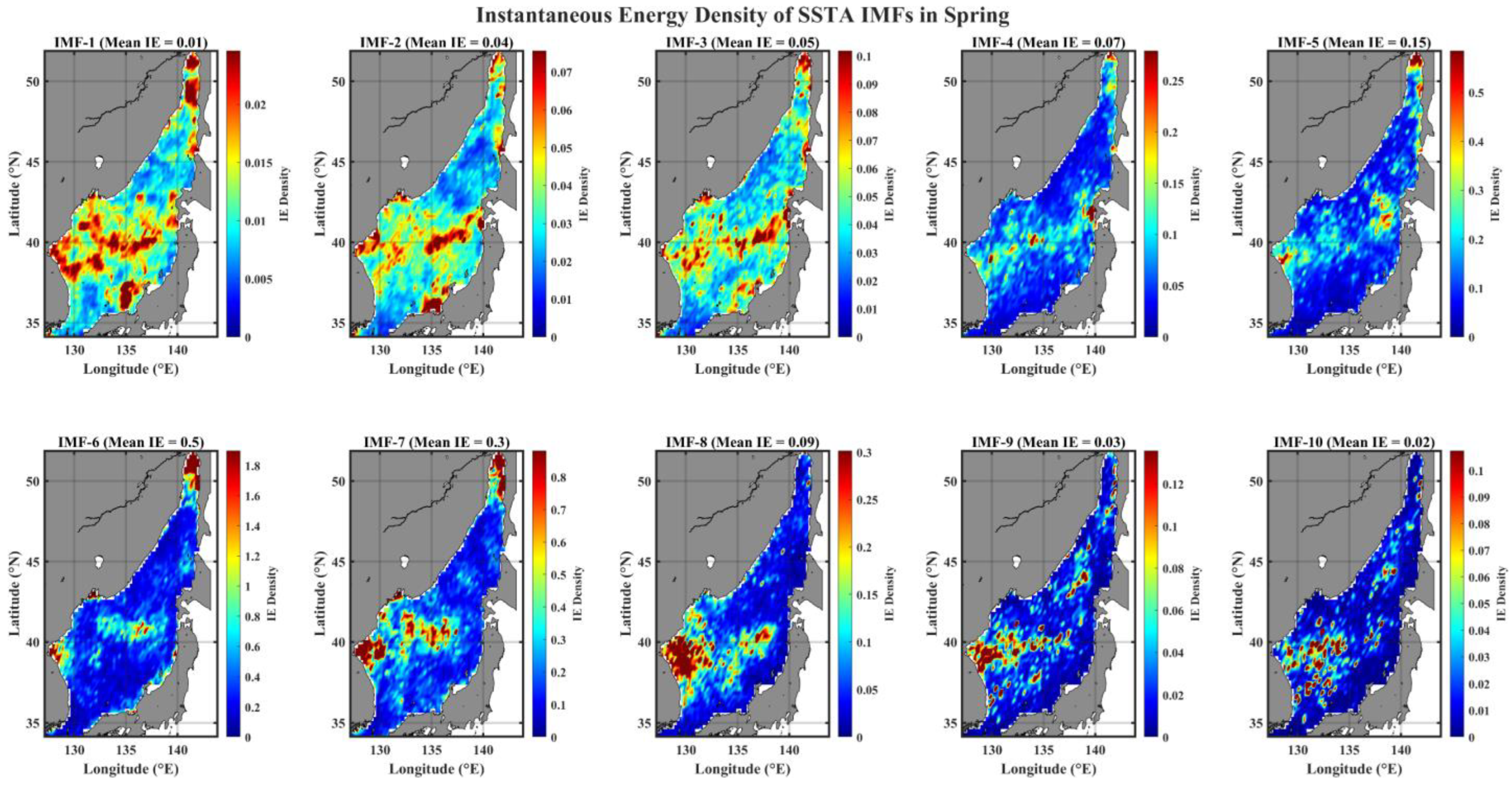


| IMF Mode No. | Peaked Timescale (Day) | Empirical Timescale |
|---|---|---|
| 1 | 6~7 | Atmospheric synoptic scale (5~18 days) |
| 2 | ~13 | Atmospheric synoptic scale |
| 3 | ~30 | Monthly scale |
| 4 | ~60 | Inter-monthly and seasonal scale |
| 5 | 100~200 | Seasonal and semi-annual scale |
| 6 | 300~400 | Semi-annual and intra-annual scale |
| 7 | 300~400 | Annual scale |
| 8 | ~1000 | Biennial scale (2~3 years) |
| 9 | 2500~3500 | Inter-annual scale (ENSO’s 3~7 years) |
| 10 | 4000~6000 | Decadal scale (8~15 years) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, G.; Park, J.-J. Intrinsic Mode-Based Network Approach to Examining Multiscale Characteristics of Sea Surface Temperature Variability. Appl. Sci. 2024, 14, 1752. https://doi.org/10.3390/app14051752
Lim G, Park J-J. Intrinsic Mode-Based Network Approach to Examining Multiscale Characteristics of Sea Surface Temperature Variability. Applied Sciences. 2024; 14(5):1752. https://doi.org/10.3390/app14051752
Chicago/Turabian StyleLim, Gyuchang, and Jong-Jin Park. 2024. "Intrinsic Mode-Based Network Approach to Examining Multiscale Characteristics of Sea Surface Temperature Variability" Applied Sciences 14, no. 5: 1752. https://doi.org/10.3390/app14051752
APA StyleLim, G., & Park, J.-J. (2024). Intrinsic Mode-Based Network Approach to Examining Multiscale Characteristics of Sea Surface Temperature Variability. Applied Sciences, 14(5), 1752. https://doi.org/10.3390/app14051752






