Stable Low-Rank CP Decomposition for Compression of Convolutional Neural Networks Based on Sensitivity
Abstract
1. Introduction
- The sensitivity of each convolutional layer is computed by Hessian trace to determine the amount of redundancy of each layer, and then select the optimal ranks for CP decomposition by considering the redundancy we obtained.
- In order to overcome the CP decomposition instability problem, an efficient optimization method is developed to quantify the sensitivity of CP decomposition and add sensitivity-constrained optimization during the process.
- Another potential approach is proposed to address the problem of instability in CP decomposition by using iterative fine-tuning techniques. The layer that exhibits more sensitivity should be prioritized for compression to minimize the accuracy degradation of the compressed model.
2. Related Work
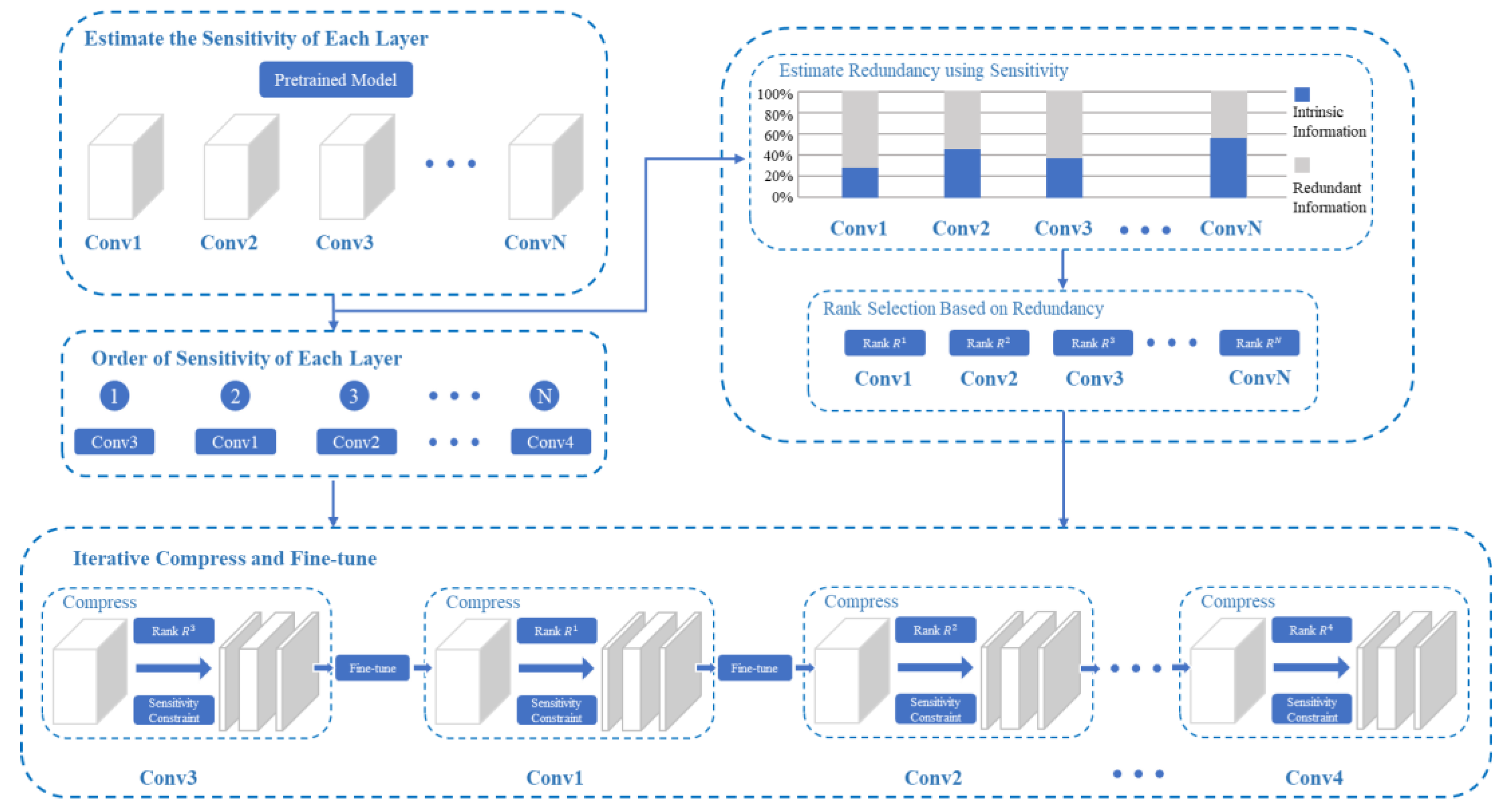
3. The Proposed Method
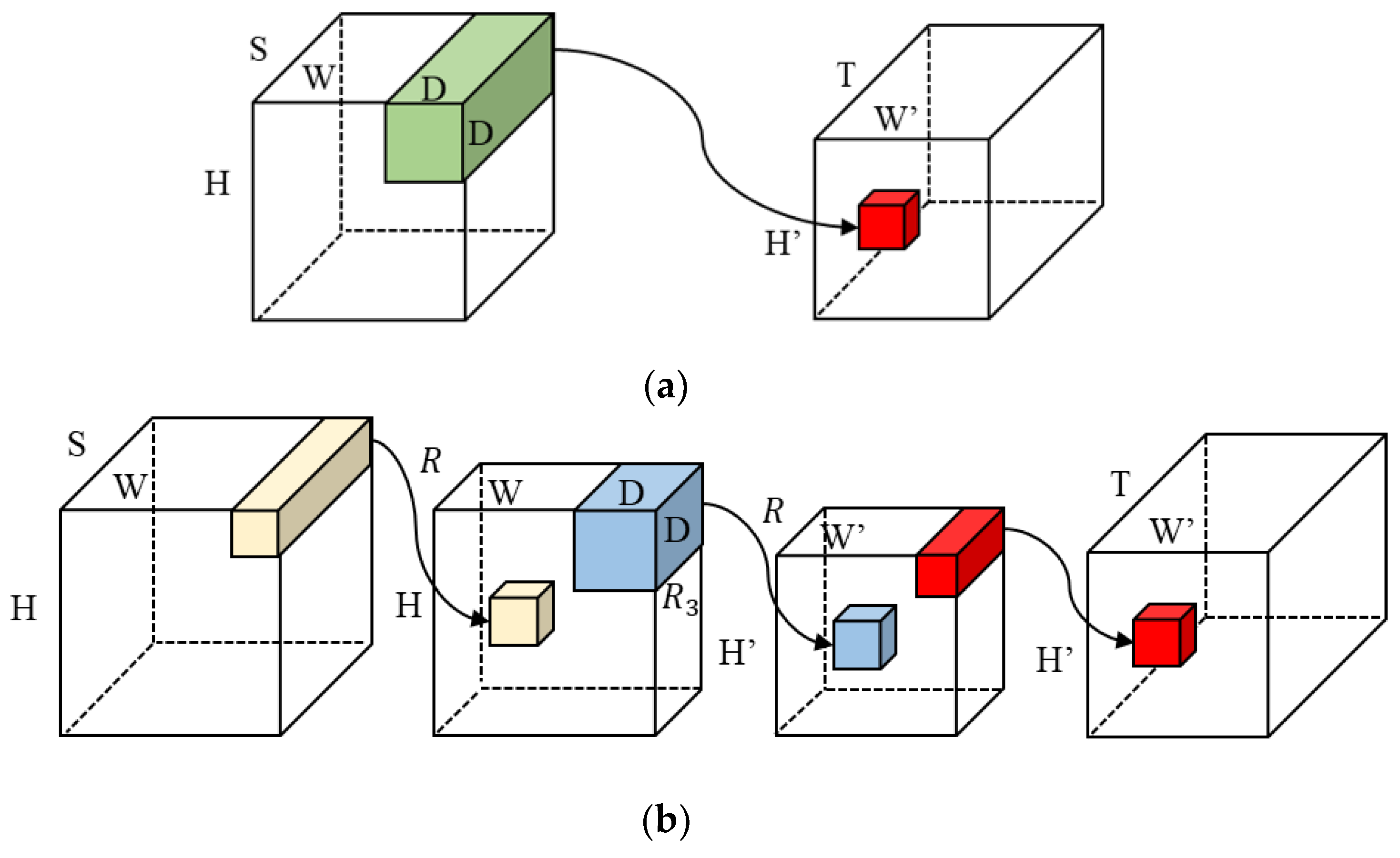
3.1. CP Decomposition for Convolutional Layers
3.2. Rank Selection Based on Sensitivity
3.3. Sensitivity-Constrained Optimization in CP Decomposition
3.4. Iterative Fine-Tuning Based on Sensitivity
- Estimating the sensitivity of each layer in the original model.
- Sorting each network layer according to the order of the sensitivity information content of each network layer from large to small.
- Determining the rank of each layer according to its sensitivity and an average rank we set in advance.
- Iterative compressing and fine-tuning based on the sensitivity of each layer. The sorting results obtained from the second step and the rank obtained from the third step are used to iteratively compress and fine-tune the network layer-by-layer.
4. Experimental Results
4.1. Experimental Results on CIFAR-10
4.2. Experimental Results on CIFAR-100
4.3. Experimental Results on ImageNet
| Model | Method | Compression Method | Top-5 Acc (%) | FLOPs Reduction |
|---|---|---|---|---|
| VGG-16 | AutoPruner [51] | Pruning | −1.49 | 3.79× |
| Standard Tucker [10] | Tucker | −0.50 | 4.93× | |
| HT-2 [52] | Tucker | −0.65 | 5.26× | |
| Ours | CP | −0.38 | 5.26× | |
| Resnet-18 | FPGM [53] | Pruning | −0.55 | 1.72× |
| DSA [54] | Pruning | −0.73 | 1.72× | |
| DACP [20] | Pruning | −1.48 | 1.89× | |
| Standard Tucker [10] | Tucker | −1.55 | 2.25× | |
| MUSCO [49] | Tucker | −0.30 | 2.42× | |
| TRP [50] | Low-Rank Matrix | −2.34 | 2.60× | |
| Ours | CP | −0.16 | 2.61× | |
| Resnet-50 | TRP [50] | Low-Rank Matrix | −0.80 | 1.80× |
| Standard Tucker [10] | Tucker | −1.75 | 2.04× | |
| AKECP [55] | Pruning | −2.30 | 2.62× | |
| HRANK [18] | Pruning | −1.86 | 2.64× | |
| HT-2 [52] | Tucker | −0.71 | 2.85× | |
| AutoPruner [51] | Pruning | −1.62 | 2.94× | |
| Ours | CP | −0.51 | 2.97× |
4.4. Discussion
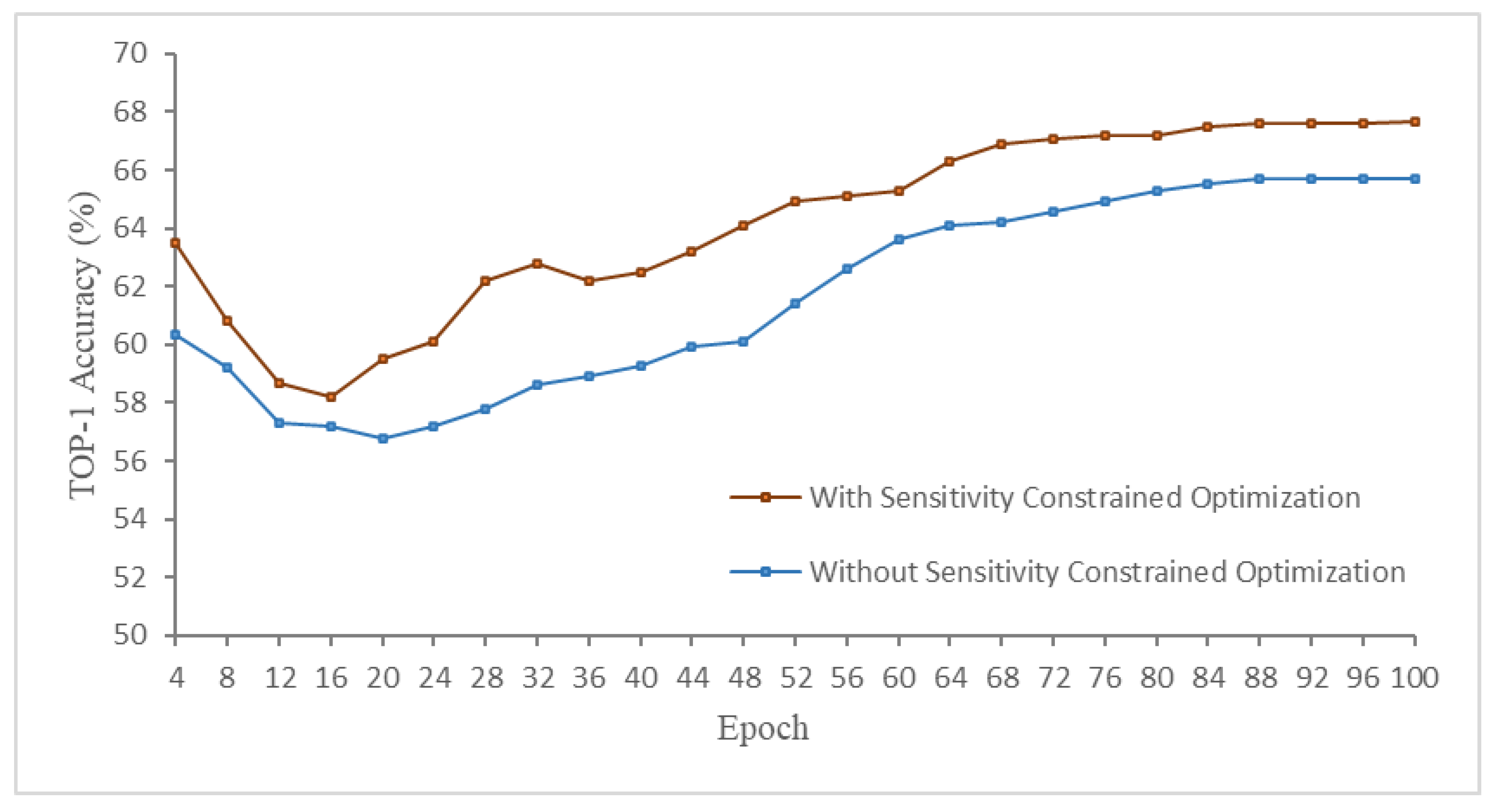
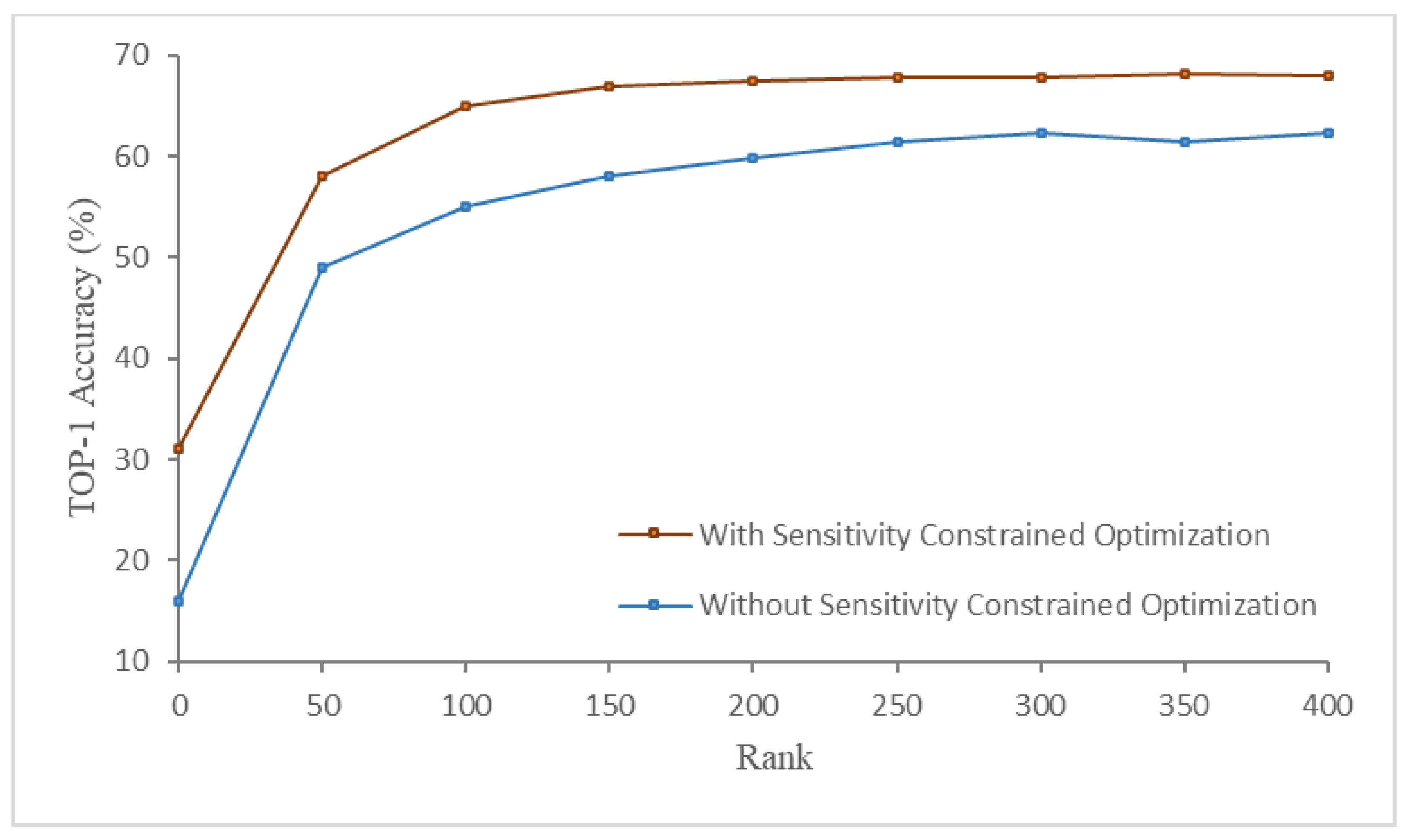
4.4.1. Sensitivity-Constrained Optimization
4.4.2. Iterative Fine-Tuning Based on Sensitivity Order
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, P.; Zhang, Z.; Dong, Z.; Yang, Y.; Pan, Z.; Deng, J. Axial and radial electromagnetic-vibration characteristics of converter transformer windings under current harmonics. High Volt. 2023, 8, 477–491. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, Z.; Yang, Y.; Xiao, J.; Chen, J. A Dynamic Monitoring Method of Temperature Distribution for Cable Joints Based on Thermal Knowledge and Conditional Generative Adversarial Network. IEEE Trans. Instrum. Meas. 2023, 72, 4507014. [Google Scholar] [CrossRef]
- Fang, G.; Ma, X.; Song, M.; Mi, M.B.; Wang, X. Depgraph: Towards any structural pruning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 16091–16101. [Google Scholar]
- Liu, Y.; Wu, D.; Zhou, W.; Fan, K.; Zhou, Z. EACP: An effective automatic channel pruning for neural networks. Neurocomputing 2023, 526, 131–142. [Google Scholar] [CrossRef]
- Molchanov, D.; Ashukha, A.; Vetrov, D. Variational Dropout Sparsifies Deep Neural Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; 2017; Volume 70, pp. 2498–2507. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning Both Weights and Connections for Efficient Neural Network. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28, pp. 1135–1143. [Google Scholar]
- Rokh, B.; Azarpeyvand, A.; Khanteymoori, A. A comprehensive survey on model quantization for deep neural networks in image classification. ACM Trans. Intell. Syst. Technol. 2023, 14, 1–50. [Google Scholar]
- Dong, Z.; Yao, Z.; Arfeen, D.; Gholami, A.; Mahoney, M.W.; Keutzer, K. HAWQ-V2: Hessian Aware Trace-Weighted Quantization of Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 18518–18529. [Google Scholar]
- Kossaifi, J.; Toisoul, A.; Bulat, A.; Panagakis, Y.; Hospedales, T.M.; Pantic, M. Factorized Higher-Order CNNs With an Application to Spatio-Temporal Emotion Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 6060–6069. [Google Scholar]
- Kim, Y.-D.; Park, E.; Yoo, S.; Choi, T.; Yang, L.; Shin, D. Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications. arXiv 2015, arXiv:1511.06530. [Google Scholar]
- Lebedev, V.; Ganin, Y.; Rakhuba, M.; Oseledets, I.; Lempitsky, V. Speeding-up Convolutional Neural Networks Using Finetuned CP-Decomposition. arXiv 2014, arXiv:1412.6553. [Google Scholar]
- Rayens, W.S.; Mitchell, B.C. Two-Factor Degeneracies and a Stabilization of PARAFAC. Chemom. Intell. Lab. Syst. 1997, 38, 173–181. [Google Scholar] [CrossRef]
- Krijnen, W.P.; Dijkstra, T.K.; Stegeman, A. On the Non-Existence of Optimal Solutions and the Occurrence of “Degeneracy” in the CANDECOMP/PARAFAC Model. Psychometrika 2008, 73, 431–439. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Li, B.; Fan, Y.; Bao, Y. A Novel Rank Selection Scheme in Tensor Ring Decomposition Based on Reinforcement Learning for Deep Neural Networks. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3292–3296. [Google Scholar]
- Dai, C.; Cheng, H.; Liu, X. A Tucker Decomposition Based on Adaptive Genetic Algorithm for Efficient Deep Model Compression. In Proceedings of the 2020 IEEE 22nd International Conference on High Performance Computing and Communications IEEE 18th International Conference on Smart City IEEE 6th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Yanuca Island, Cuvu, Fiji, 14–16 December 2020; pp. 507–512. [Google Scholar]
- Zhang, T.; Ye, S.; Zhang, K.; Tang, J.; Wen, W.; Fardad, M.; Wang, Y. A Systematic DNN Weight Pruning Framework Using Alternating Direction Method of Multipliers. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 184–199. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv 2015, arXiv:1510.00149. [Google Scholar] [CrossRef]
- Lin, M.; Ji, R.; Wang, Y.; Zhang, Y.; Zhang, B.; Tian, Y.; Shao, L. HRank: Filter Pruning Using High-Rank Feature Map. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 1529–1538. [Google Scholar]
- Luo, J.-H.; Wu, J.; Lin, W. Thinet: A Filter Level Pruning Method for Deep Neural Network Compression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5058–5066. [Google Scholar]
- Zhuang, Z.; Tan, M.; Zhuang, B.; Liu, J.; Guo, Y.; Wu, Q.; Huang, J.; Zhu, J. Discrimination-Aware Channel Pruning for Deep Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31, pp. 875–886. [Google Scholar]
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating Very Deep Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1389–1397. [Google Scholar]
- Bonetta, G.; Ribero, M.; Cancelliere, R. Regularization-Based Pruning of Irrelevant Weights in Deep Neural Architectures. Appl. Intell. 2022, 53, 17429–17443. [Google Scholar] [CrossRef]
- Mitsuno, K.; Kurita, T. Filter Pruning Using Hierarchical Group Sparse Regularization for Deep Convolutional Neural Networks. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021. [Google Scholar]
- Wang, Z.; Li, F.; Shi, G.; Xie, X.; Wang, F. Network Pruning Using Sparse Learning and Genetic Algorithm. Neurocomputing 2020, 404, 247–256. [Google Scholar] [CrossRef]
- Liu, B.; Wang, M.; Foroosh, H.; Tappen, M.; Pensky, M. Sparse Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 806–814. [Google Scholar]
- Lu, J.; Liu, D.; Cheng, X.; Wei, L.; Hu, A.; Zou, X. An Efficient Unstructured Sparse Convolutional Neural Network Accelerator for Wearable ECG Classification Device. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 4572–4582. [Google Scholar] [CrossRef]
- Han, S.; Liu, X.; Mao, H.; Pu, J.; Pedram, A.; Horowitz, M.A.; Dally, W.J. EIE: Efficient Inference Engine on Compressed Deep Neural Network. SIGARCH Comput. Archit. News 2016, 44, 243–254. [Google Scholar] [CrossRef]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning Structured Sparsity in Deep Neural Networks. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 5–10 December 2016; pp. 2082–2090. [Google Scholar]
- Chen, Y.-H.; Emer, J.; Sze, V. Eyeriss: A Spatial Architecture for Energy-Efficient Dataflow for Convolutional Neural Networks. SIGARCH Comput. Archit. News 2016, 44, 367–379. [Google Scholar] [CrossRef]
- Gong, R.; Liu, X.; Jiang, S.; Li, T.; Hu, P.; Lin, J.; Yu, F.; Yan, J. Differentiable Soft Quantization: Bridging Full-Precision and Low-Bit Neural Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27–28 October 2019; pp. 4852–4861. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 2704–2713. [Google Scholar]
- Courbariaux, M.; Bengio, Y.; David, J.-P. BinaryConnect: Training Deep Neural Networks with Binary Weights during Propagations. In Proceedings of the Advances in Neural Information Processing Systems; Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28, pp. 3123–3131. [Google Scholar]
- Pan, Y.; Xu, J.; Wang, M.; Ye, J.; Wang, F.; Bai, K.; Xu, Z. Compressing Recurrent Neural Networks with Tensor Ring for Action Recognition. Proc. AAAI Conf. Artif. Intell. 2019, 33, 4683–4690. [Google Scholar] [CrossRef]
- Yin, M.; Liao, S.; Liu, X.-Y.; Wang, X.; Yuan, B. Towards Extremely Compact RNNs for Video Recognition with Fully Decomposed Hierarchical Tucker Structure. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 12085–12094. [Google Scholar]
- Yang, Y.; Krompass, D.; Tresp, V. Tensor-Train Recurrent Neural Networks for Video Classification. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; 2017; Volume 70, pp. 3891–3900. [Google Scholar]
- Phan, A.-H.; Sobolev, K.; Sozykin, K.; Ermilov, D.; Gusak, J.; Tichavský, P.; Glukhov, V.; Oseledets, I.; Cichocki, A. Stable Low-Rank Tensor Decomposition for Compression of Convolutional Neural Network. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 522–539. [Google Scholar]
- Hillar, C.J.; Lim, L.-H. Most Tensor Problems Are NP-Hard. J. ACM 2013, 60, 1–39. [Google Scholar] [CrossRef]
- Avron, H.; Toledo, S. Randomized Algorithms for Estimating the Trace of an Implicit Symmetric Positive Semi-Definite Matrix. J. ACM 2011, 58, 1–34. [Google Scholar] [CrossRef]
- de Silva, V.; Lim, L.-H. Tensor Rank and the Ill-Posedness of the Best Low-Rank Approximation Problem. SIAM J. Matrix Anal. Appl. 2008, 30, 1084–1127. [Google Scholar] [CrossRef]
- Phan, A.-H.; Tichavský, P.; Cichocki, A. Error Preserving Correction: A Method for CP Decomposition at a Target Error Bound. IEEE Trans. Signal Process. 2019, 67, 1175–1190. [Google Scholar] [CrossRef]
- Phan, A.-H.; Yamagishi, M.; Mandic, D.; Cichocki, A. Quadratic Programming over Ellipsoids with Applications to Constrained Linear Regression and Tensor Decomposition. Neural Comput. Appl. 2020, 32, 7097–7120. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; Technical Report TR-2009; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Li, N.; Pan, Y.; Chen, Y.; Ding, Z.; Zhao, D.; Xu, Z. Heuristic Rank Selection with Progressively Searching Tensor Ring Network. Complex Intell. Syst. 2022, 8, 771–785. [Google Scholar] [CrossRef]
- Garipov, T.; Podoprikhin, D.; Novikov, A.; Vetrov, D. Ultimate Tensorization: Compressing Convolutional and Fc Layers Alike. arXiv 2016, arXiv:1611.03214. [Google Scholar]
- Wang, W.; Sun, Y.; Eriksson, B.; Wang, W.; Aggarwal, V. Wide Compression: Tensor Ring Nets. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 9329–9338. [Google Scholar]
- Gusak, J.; Kholiavchenko, M.; Ponomarev, E.; Markeeva, L.; Blagoveschensky, P.; Cichocki, A.; Oseledets, I. Automated Multi-Stage Compression of Neural Networks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; IEEE: Seoul, Republic of Korea, 2019; pp. 2501–2508. [Google Scholar]
- Xu, Y.; Li, Y.; Zhang, S.; Wen, W.; Wang, B.; Qi, Y.; Chen, Y.; Lin, W.; Xiong, H. TRP: Trained Rank Pruning for Efficient Deep Neural Networks. arXiv 2020, arXiv:2004.14566. [Google Scholar]
- Luo, J.-H.; Wu, J. AutoPruner: An End-to-End Trainable Filter Pruning Method for Efficient Deep Model Inference. Pattern Recognit. 2020, 107, 107461. [Google Scholar] [CrossRef]
- Gabor, M.; Zdunek, R. Compressing convolutional neural networks with hierarchical Tucker-2 decomposition. Appl. Soft Comput. 2023, 132, 109856. [Google Scholar] [CrossRef]
- He, Y.; Liu, P.; Wang, Z.; Hu, Z.; Yang, Y. Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4340–4349. [Google Scholar]
- Ning, X.; Zhao, T.; Li, W.; Lei, P.; Wang, Y.; Yang, H. DSA: More Efficient Budgeted Pruning via Differentiable Sparsity Allocation. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 592–607. [Google Scholar]
- Zhang, H.; Liu, L.; Zhou, H.; Hou, W.; Sun, H.; Zheng, N. AKECP: Adaptive Knowledge Extraction from Feature Maps for Fast and Efficient Channel Pruning. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual Event, China, 20–24 October 2021; ACM: New York, NY, USA, 2021; pp. 648–657. [Google Scholar]
| Model | Method | Compression Method | Top-1 Acc (%) | Compression Ratio |
|---|---|---|---|---|
| Resnet-20 | Standard Tucker [10] | Tucker | −3.84 | 2.6× |
| Standard Tensor Train [47] | Tensor Train | −4.55 | 5.4× | |
| Standard Tensor Ring [48] | Tensor Ring | −3.75 | 5.4× | |
| PSTR-S [46] | Tensor Ring | −0.45 | 2.5× | |
| PSTR-M [46] | Tensor Ring | −2.75 | 6.8× | |
| Ours | CP | −0.31 | 2.6× | |
| Ours | CP | −1.82 | 6.8× | |
| Resnet-32 | Standard Tucker [10] | Tucker | −4.79 | 5.1× |
| Standard Tensor Train [47] | Tensor Train | −4.19 | 4.8× | |
| Standard Tensor Ring [48] | Tensor Ring | −1.89 | 5.1× | |
| PSTR-S [46] | Tensor Ring | −1.05 | 2.7× | |
| PSTR-M [46] | Tensor Ring | −1.89 | 5.8× | |
| Ours | CP | −0.45 | 2.8× | |
| Ours | CP | −1.31 | 5.8× |
| Model | Method | Compression Method | Top-1 Acc (%) | Compression Ratio |
|---|---|---|---|---|
| Resnet-20 | Standard Tucker [10] | Tucker | −7.87 | 2.5× |
| Standard Tensor Train [47] | Tensor Train | −3.76 | 5.6× | |
| Standard Tensor Ring [48] | Tensor Ring | −1.85 | 4.7× | |
| PSTR-S [46] | Tensor Ring | +0.73 | 2.3× | |
| PSTR-M [46] | Tensor Ring | −1.78 | 4.7× | |
| Ours | CP | +1.05 | 2.6× | |
| Ours | CP | −1.32 | 4.7× | |
| Resnet-32 | Standard Tucker [10] | Tucker | −9.07 | 2.5× |
| Standard Tensor Train [47] | Tensor Train | −5.20 | 4.6× | |
| Standard Tensor Ring [48] | Tensor Ring | −1.40 | 4.8× | |
| PSTR-S [46] | Tensor Ring | −0.05 | 2.4× | |
| PSTR-M [46] | Tensor Ring | −1.33 | 5.2× | |
| Ours | CP | −0.25 | 2.5× | |
| Ours | CP | −0.81 | 5.2× |
| Model | Method | Top-1 Acc (%) | Top-5 Acc (%) | FLOPs Reduction |
|---|---|---|---|---|
| Resnet-18 | CP-one-shot | −4.09 | −2.57 | 2.61× |
| CP-random | −2.23 | −1.31 | 2.61× | |
| Ours | −1.28 | −0.16 | 2.61× | |
| Resnet-50 | CP-one-shot | −6.27 | −3.62 | 2.97× |
| CP-random | −4.07 | −1.86 | 2.97× | |
| Ours | −1.34 | −0.51 | 2.97× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Liu, H. Stable Low-Rank CP Decomposition for Compression of Convolutional Neural Networks Based on Sensitivity. Appl. Sci. 2024, 14, 1491. https://doi.org/10.3390/app14041491
Yang C, Liu H. Stable Low-Rank CP Decomposition for Compression of Convolutional Neural Networks Based on Sensitivity. Applied Sciences. 2024; 14(4):1491. https://doi.org/10.3390/app14041491
Chicago/Turabian StyleYang, Chenbin, and Huiyi Liu. 2024. "Stable Low-Rank CP Decomposition for Compression of Convolutional Neural Networks Based on Sensitivity" Applied Sciences 14, no. 4: 1491. https://doi.org/10.3390/app14041491
APA StyleYang, C., & Liu, H. (2024). Stable Low-Rank CP Decomposition for Compression of Convolutional Neural Networks Based on Sensitivity. Applied Sciences, 14(4), 1491. https://doi.org/10.3390/app14041491






