Segmental Regularized Constrained Inversion of Transient Electromagnetism Based on the Improved Sparrow Search Algorithm
Abstract
1. Introduction
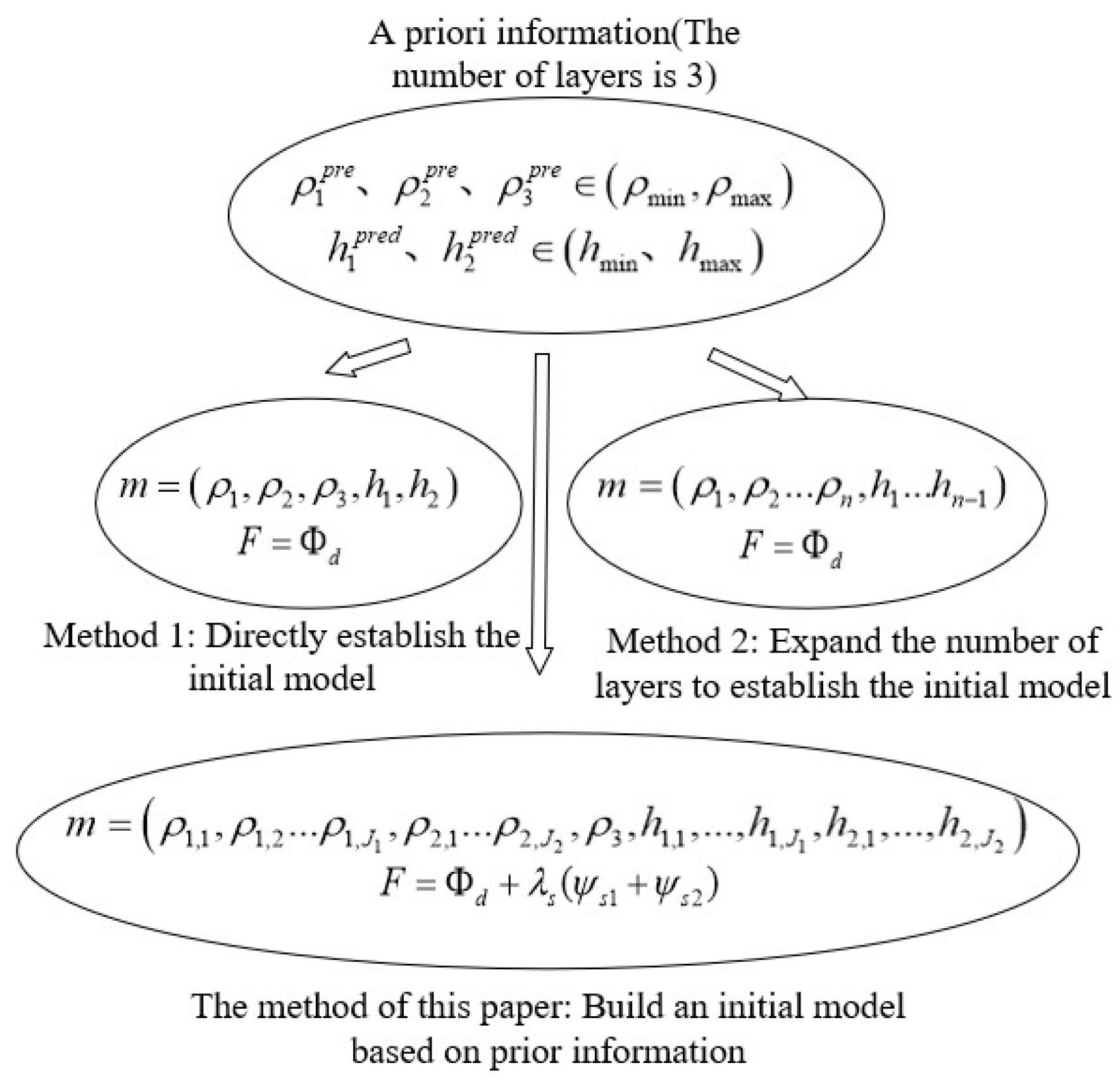
2. Piecewise Regularized Inversion Method
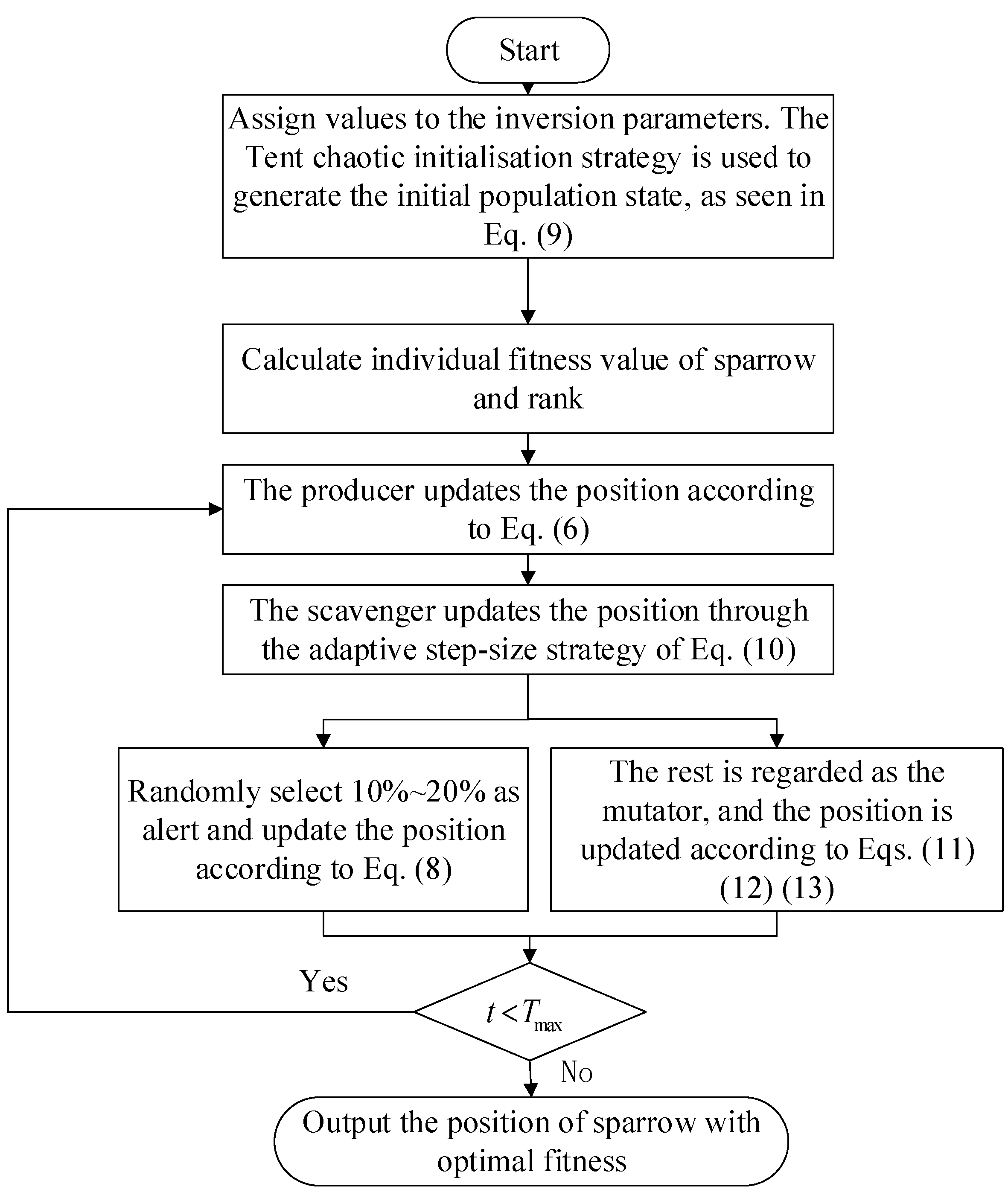
3. Improved Sparrow Search Algorithm
3.1. Sparrow Search Algorithm
- Step 1: The producer location update
- Step 2: Scroungers position update
- Step 3: Alert position update
3.2. Tent Chaotic Mapping
3.3. Adaptive Step-Size Adjustment Strategy for Scrounger Position Update
3.4. Differential Variational Operators
4. Function Test
5. Inversion Test of an Ideal Model
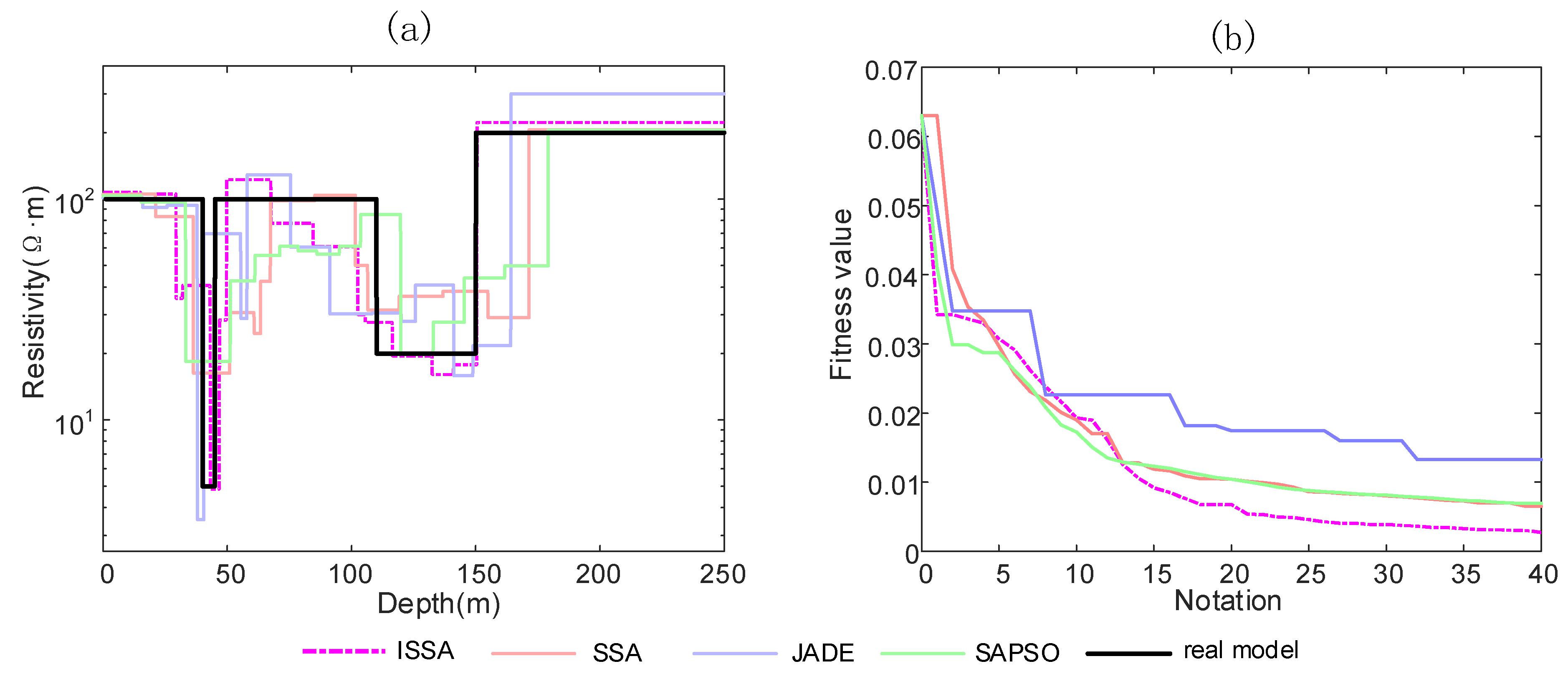
5.1. Inversion Performance Analysis of the Algorithm
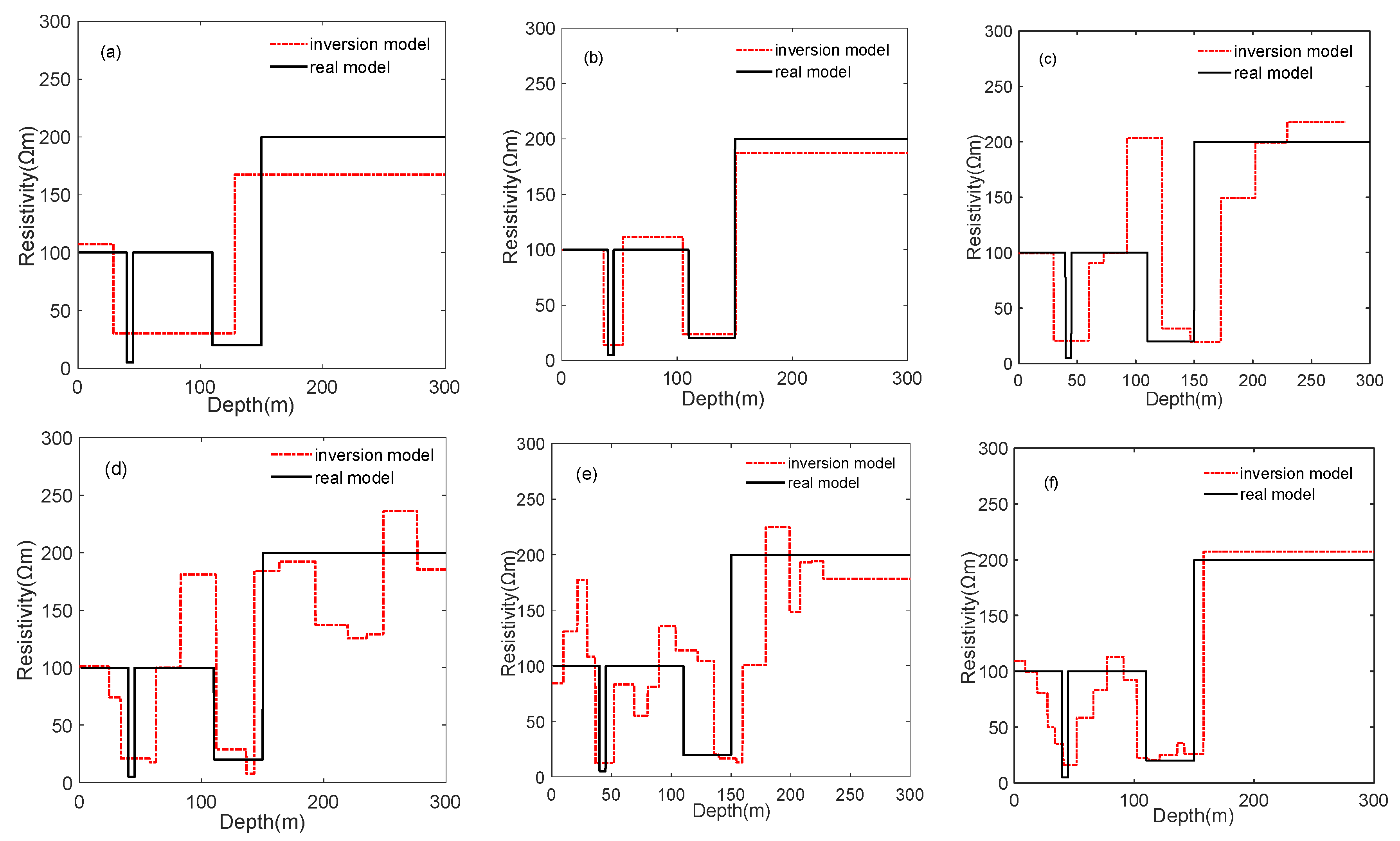
5.2. One-Dimensional Three-Layer Model Test
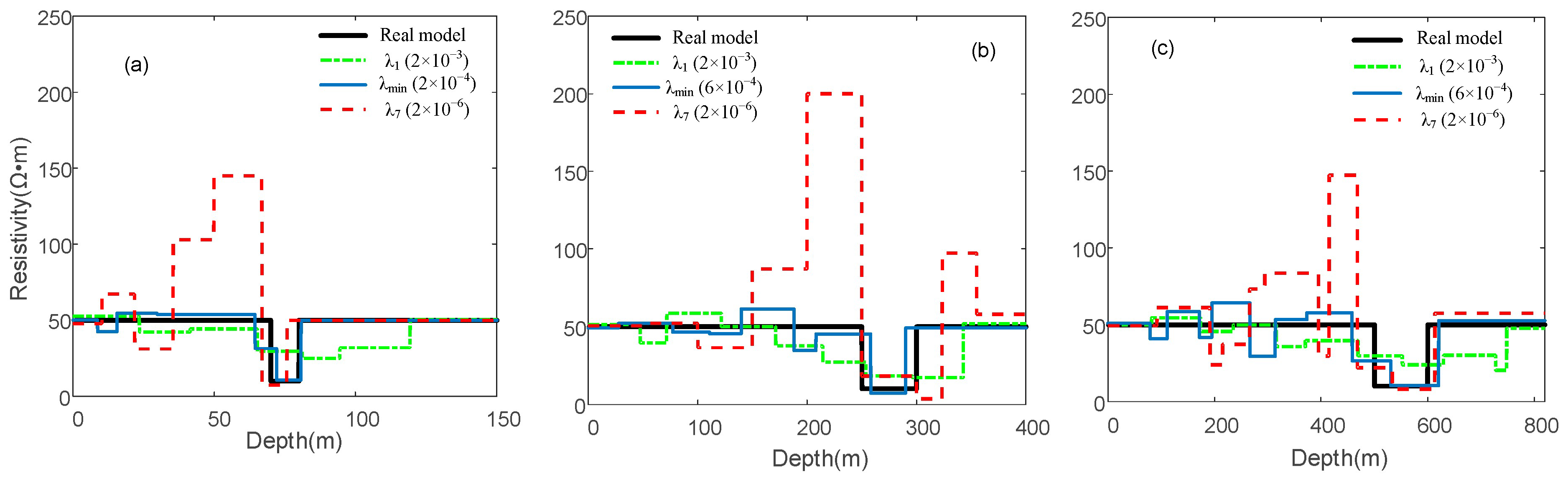
5.3. One-Dimensional Five-Layer Model Test
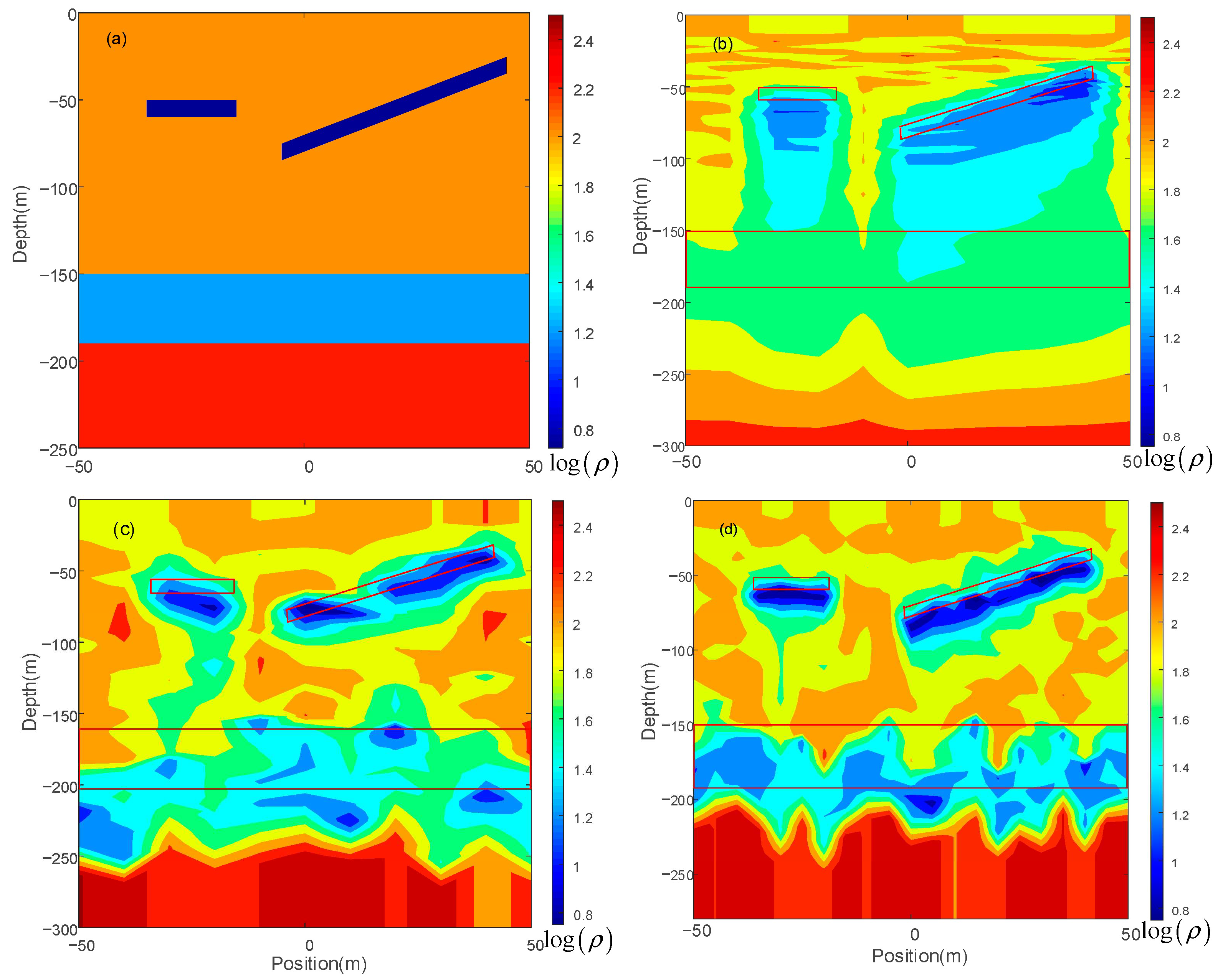
5.4. Two-Dimensional Model Inversion Test
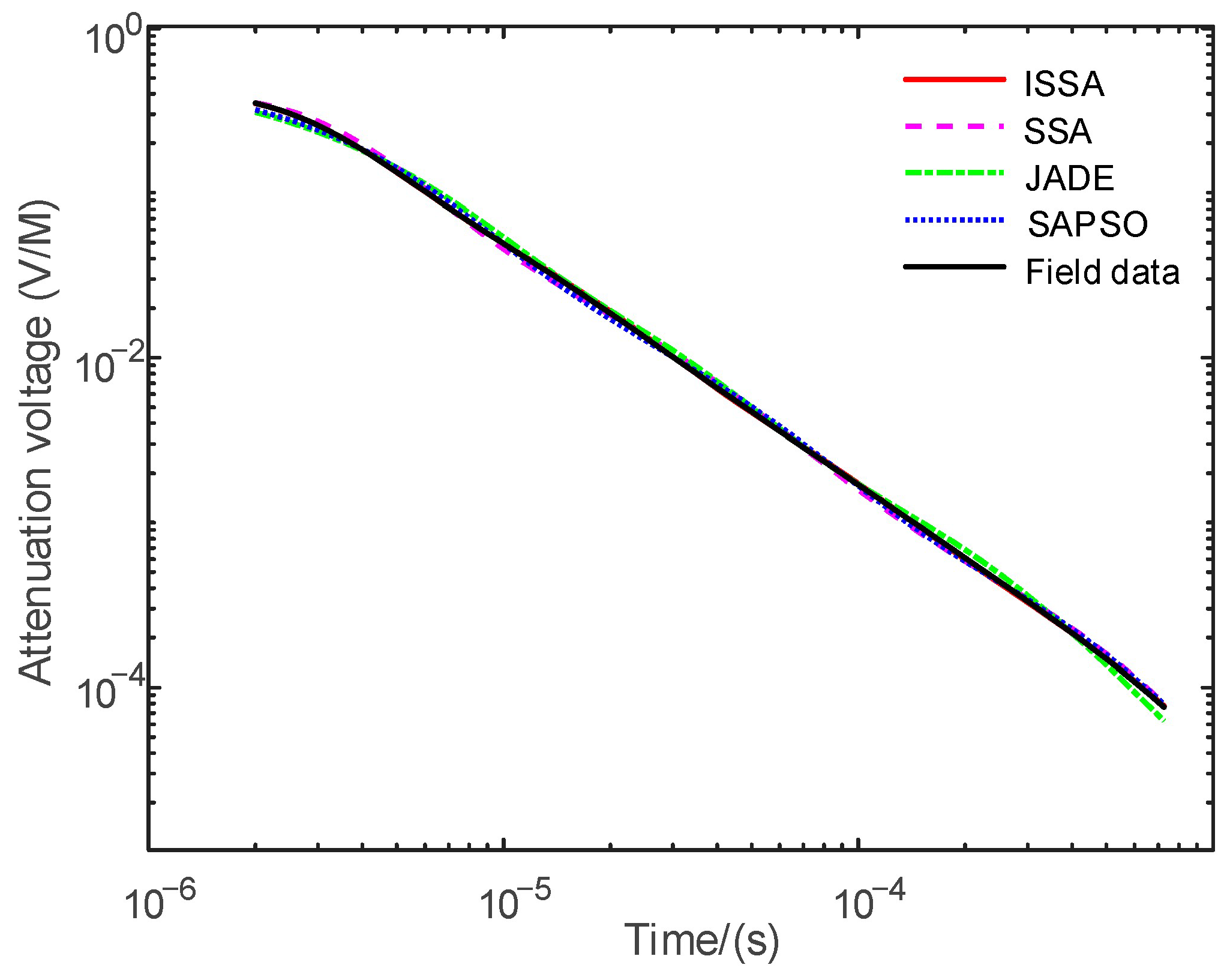
6. Field Data Inversion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McNeill, J.D. Application of Transient Electromagnetic Techniques; Geonics Limited: Missasauga, ON, Canada, 1980; 17p. [Google Scholar]
- Yang, D.; Oldenburg, D.W. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit. Geophysics 2012, 77, B23–B34. [Google Scholar] [CrossRef]
- Qian, W.; Xu, Y.; Gu, Z.; Xiang, Z.; Li, Z.; Liu, J.; Wu, J. Characterisation of transient electromagnetic signals during fixed interference sources in tunnel structure. Math. Biosci. Eng. 2021, 18, 6907–6925. [Google Scholar] [CrossRef]
- Ezersky, M.; Legchenko, A.; Al-Zoubi, A.; Levi, E.; Akkawi, E.; Chalikakis, K. TEM study of the geoelectrical structure and groundwater salinity of the nahal hever sinkhole site, dead sea shore, Israel. J. Appl. Geophys. 2011, 75, 99–112. [Google Scholar] [CrossRef]
- Su, B.; Yu, J.; Sheng, C.; Zhang, Y. Maxwell-equations based on mining transient electromagnetic method for coal mine-disaster water detection. Elektron. Ir. Elektrotechnika 2017, 23, 20–23. [Google Scholar] [CrossRef]
- Li, Z.; Huang, Q.; Xie, X.; Tang, X.; Chang, L. A Generic 1D Forward Modeling and Inversion Algorithm for TEM Sounding with an Arbitrary Horizontal Loop. Pure Appl. Geophys. 2016, 173, 2869–2883. [Google Scholar] [CrossRef]
- Haroon, A.; Adrian, J.; Bergers, R.; Gurk, M.; Tezkan, B.; Mammadov, A.L.; Novruzov, A.G. Joint inversion of long-offset and central-loop transient Electromagnetic Data: Application to a mud volcano exploration in Perekishkul, Azerbaijan. Geophys. Prospect. 2015, 63, 478–494. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Li, F.-P.; Chen, S.-E.; Yue, J.-H.; Guo, F.-S.; Chen, X.; Zhang, H. An inversion of transient electromagnetic data from a conical source. Appl. Geophys. 2018, 15, 545–555. [Google Scholar] [CrossRef]
- Wang, S.; Di, Q.; Xia, T.; Ren, Z.; Song, J.; Zou, G. Transient electromagnetic method inversion based on Lévy flight-particle swarm optimization. Chin. J. Geophys. 2022, 65, 1482–1493. (In Chinese) [Google Scholar] [CrossRef]
- Li, R.; Yu, N.; Li, R.; Zhuang, Q.; Zhang, H. Transient electromagnetic inversion based on particle swarm optimization and differential evolution algorithm. Near Surf. Geophys. 2021, 19, 59–71. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, N.; Liu, S.; Li, D.; Chen, C.; Ye, Q.; Xue, Y.; Yang, Y. L1-norm based nonlinear inversion of transient electromagnetic data. Chin. J. Geophys. 2019, 62, 4860–4873. (In Chinese) [Google Scholar] [CrossRef]
- Ai, H.; Essa, K.S.; Ekinci, Y.L.; Balkaya, Ç.; Li, H.; Géraud, Y. Magnetic anomaly inversion through the novel barnacles mating optimization algorithm. Sci. Rep. 2022, 12, 22578. [Google Scholar] [CrossRef]
- Cheng, J.; Li, M.; Xiao, Y.; Sun, X.; Chen, D. Study on particle swarm optimization inversion of mine transient electromagnetic method in whole-space. Chin. J. Geophys. -Chin. Ed. 2014, 57, 3478–3484. [Google Scholar] [CrossRef]
- Jiao, J.; Yang, H.; Chen, Z.; Gu, Y.; Liu, J. Inversion of Mine Transient Electromagnetic Data via the PSO-GIS Algorithm from a Conical Source. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5915512. [Google Scholar] [CrossRef]
- Liu, X.; Pan, C.; Zheng, F.; Sun, Y.; Gou, Q. Transient Electromagnetic 1-Dimensional Inversion Based on the Quantum Particle Swarms Optimization-Smooth Constrained Least Squares Joint Algorithm and Its Application in Karst Exploration. Adv. Civ. Eng. 2022, 2022, 1555877. [Google Scholar] [CrossRef]
- Xu, Z.; Fu, Z.; Fu, N. Firefly Algorithm for Transient Electromagnetic Inversion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5901312. [Google Scholar] [CrossRef]
- Ekinci Yunus Levent Şenol, Ö.; Petek, S.; Çaǧlayan, B.; Gökhan, G. Amplitude inversion of the 2D analytic signal of magnetic anomalies through the differential evolution algorithm. J. Geophys. Eng. 2017, 14, 1492–1508. [Google Scholar] [CrossRef]
- Askarzadeh, A. Comparison of particle swarm optimization and other metaheuristics on electricity demand estimation: A case study of Iran. Energy 2014, 72, 484–491. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, W.M. Design of RBF neural network based on SAPSO algorithm. Control Decis. 2021, 36, 2305–2312. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Yang, H.; Liu, H. Self-adaptive differential evolution algorithm with improved mutation strategy. Soft Comput. 2018, 22, 3433–3447. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Liu, G.G.; Zhang, L.Y.; Liu, D.; Liu, N.X.; Fu, Y.G.; Guo, W.Z.; Chen, G.L.; Jiang, W.J. Multi-strategy hybrid sparrow search algorithm for complex cons-trained optimization problems. Control Decis. 2023, 38, 3336–3344. [Google Scholar] [CrossRef]
- Zhang, Z.; Yi, G.; Wang, S.; Guo, M.; He, K.; Zhang, S.; Mao, L. Research on 1D forward modeling and inversion of ground-airborne transient electromagnetic method based on minimum structural model. Comput. Tech. Geophys. Geochem. Explor. 2021, 43, 352–359. [Google Scholar] [CrossRef]
- He, K.; Wang, X.; Guo, M.; Wang, S.; Yi, G.; Xie, X.; Guo, Y. Spatially constrained inversion of semi-airborne transient electromagnetic data based on a mixed norm. J. Appl. Geophys. 2022, 200, 104616. [Google Scholar] [CrossRef]
- Shan, L.; Qiang, H.; Li, J.; Wang, Z. Chaotic optimization algorithm based on Tent map. Control Decis. 2005, 20, 179–182. [Google Scholar] [CrossRef]
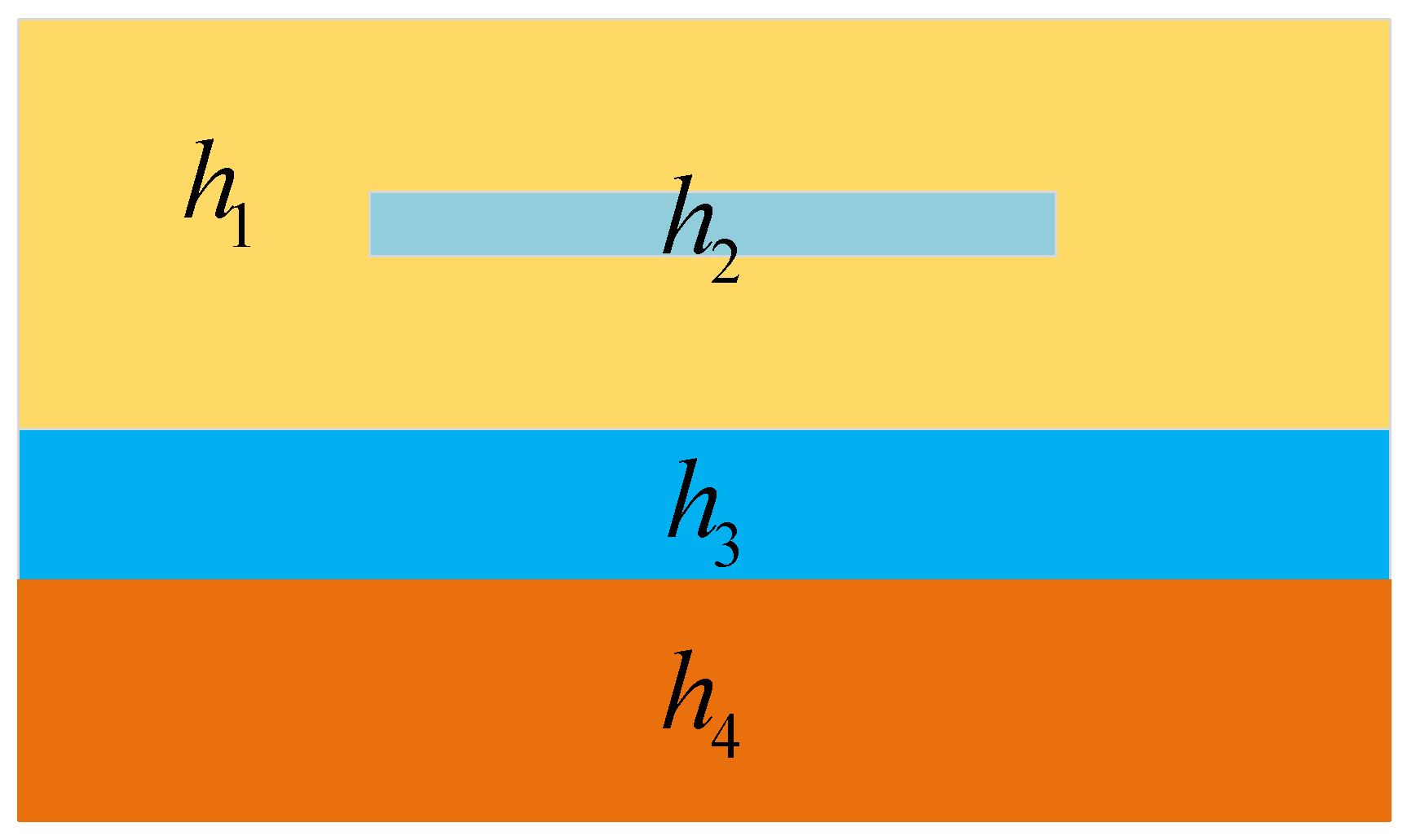

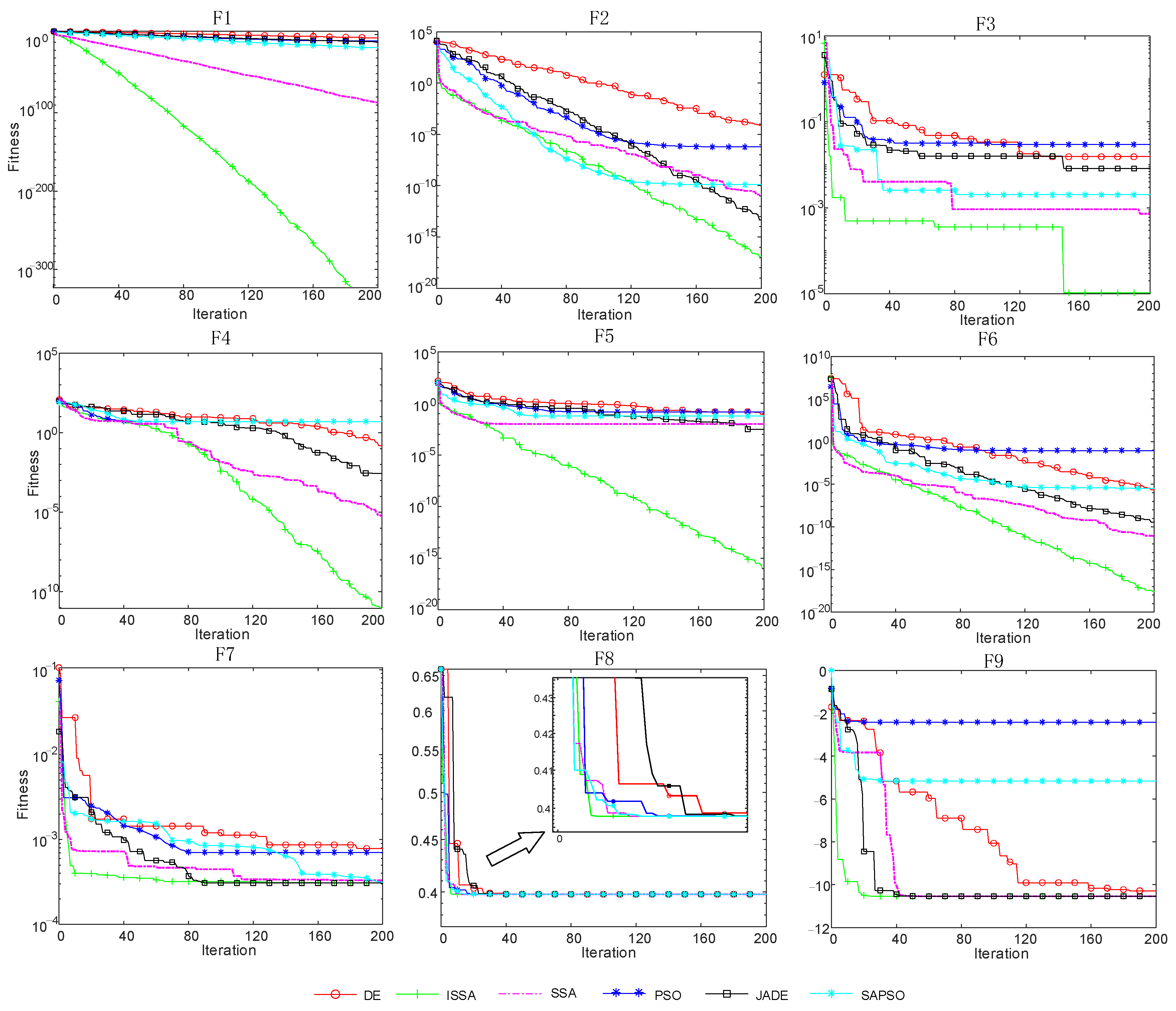


| Serial Number | Function | Dimension | Range | Theoretical Value | ISSA | SSA | DE | JADE | PSO | SAPSO |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Sphere | 30 | [−100, 100] | 0 | 0 × 100 | 4.5 × 10−87 | 4.8 × 10−5 | 1.8 × 10−10 | 8.4 × 10−9 | 1.3 × 10−17 |
| F2 | Step | 10 | [−100, 100] | 0 | 1.3 × 10−17 | 8.5 × 10−12 | 7.7 × 10−9 | 4.7 × 10−14 | 6.1 × 10−7 | 1.3 × 10−10 |
| F3 | Quartic | 10 | [−1.28, 1.28] | 0 | 1.1 × 10−5 | 6.3 × 10−4 | 1.6 × 10−2 | 8.2 × 10−3 | 3 × 10−2 | 2 × 10−3 |
| F4 | Generalized Rastrigin’s | 10 | [−5.12, 5.12] | 0 | 1.3 × 10−10 | 3.1 × 10−6 | 1.5 × 10−1 | 3 × 10−3 | 9.9 × 100 | 5 × 10−0 |
| F5 | Griewank’s | 10 | [−600, 600] | 0 | 1 × 10−16 | 7 × 10−3 | 9 × 10−2 | 3 × 10−3 | 1.5 × 10−1 | 6 × 10−2 |
| F6 | Generalized Penalized | 10 | [−50, 50] | 0 | 2.5 × 10−18 | 1.4 × 10−11 | 2.1 × 10−6 | 3.5 × 10−10 | 9 × 10−3 | 3.2 × 10−6 |
| F7 | Kowalik’s | 4 | [−5, 5] | 3 × 10−4 | 3 × 10−4 | 3.3 × 10−4 | 8 × 10−4 | 3 × 10−4 | 7.1 × 10−4 | 3.3 × 10−4 |
| F8 | Branin | [a, b] | [−5, 10], [0, 15] | 3.9 × 10−1 | 3.9 × 10−1 | 3.9 × 10−1 | 3.9 × 10−1 | 3.9 × 10−1 | 3.9 × 10−1 | 3.9 × 10−1 |
| F9 | Shekel’s Family | 4 | [0, 10] | −10 | −10 | −5.1 | −10 | −10 | −2.4 | −5.2 |
| Notation | Clarification | Value |
|---|---|---|
| n | Population size | 100 |
| M | Maximum number of iterations of the algorithm | 50 |
| ST | Safety threshold | 0.8 |
| P | Discoverers as a proportion of population size | 0.2 |
| F0 | Variance factor | 0.4 |
| CR | Cross-factor | 0.2 |
| Algorithm | Without Noise | 5% Noise | 10% Noise | |||
|---|---|---|---|---|---|---|
| Fitness Value | D-MSE | Fitness Value | D-MSE | Fitness Value | D-MSE | |
| ISSA | 0.0031 | 0.1182 | 0.0065 | 0.1298 | 0.0123 | 0.1893 |
| SSA | 0.0065 | 0.1966 | 0.0095 | 0.2255 | 0.0165 | 0.2563 |
| JADE | 0.0103 | 0.2299 | 0.01424 | 0.2177 | 0.0224 | 0.2388 |
| SAPSO | 0.0059 | 0.1945 | 0.0086 | 0.2013 | 0.0157 | 0.2255 |
| Layer Thickness Threshold | Resistivity Ratio | D-MSE | ||||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
| ||
| J1 | 0.1930 | 0.0833 | 0.0553 | 0.1052 | 0.1642 | 0.1264 | 0.4442 | |
| 0.2471 | 0.3109 | 0.2045 | 0.1874 | 0.1219 | 0.1096 | 0.2647 | ||
| J2 | 0.2020 | 0.0704 | 0.1149 | 0.1442 | 0.2062 | 0.2385 | 0.6767 | |
| 0.2784 | 0.1601 | 0.1952 | 0.1683 | 0.0673 | 0.1547 | 0.1881 | ||
| J3 | 0.2078 | 0.0937 | 0.0833 | 0.1079 | 0.1310 | 0.2041 | 0.3827 | |
| 0.2543 | 0.2178 | 0.1727 | 0.1614 | 0.1325 | 0.1863 | 0.2603 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, C.; Ou, X.; Tan, J.; Min, X.; Sun, Q. Segmental Regularized Constrained Inversion of Transient Electromagnetism Based on the Improved Sparrow Search Algorithm. Appl. Sci. 2024, 14, 1360. https://doi.org/10.3390/app14041360
Tan C, Ou X, Tan J, Min X, Sun Q. Segmental Regularized Constrained Inversion of Transient Electromagnetism Based on the Improved Sparrow Search Algorithm. Applied Sciences. 2024; 14(4):1360. https://doi.org/10.3390/app14041360
Chicago/Turabian StyleTan, Chao, Xingzuo Ou, Jiwei Tan, Xinyu Min, and Qihao Sun. 2024. "Segmental Regularized Constrained Inversion of Transient Electromagnetism Based on the Improved Sparrow Search Algorithm" Applied Sciences 14, no. 4: 1360. https://doi.org/10.3390/app14041360
APA StyleTan, C., Ou, X., Tan, J., Min, X., & Sun, Q. (2024). Segmental Regularized Constrained Inversion of Transient Electromagnetism Based on the Improved Sparrow Search Algorithm. Applied Sciences, 14(4), 1360. https://doi.org/10.3390/app14041360






