A Population-Based Search Approach to Solve Continuous Distributed Constraint Optimization Problems
Abstract
1. Introduction
- Motivation: The pseudo-tree is a communication structure commonly used in C-DCOP algorithms. The root agent can be aware of the aggregate utility according to the utility passing between all agents. We have two worries: (i) the root agent requires more computational and memory overhead. (ii) The privacy violation during utility passing, even if the privacy violation is minor [40].Contribution: Therefore, we use the graph structure in PLSA. The agent only passes its value assignments (instead of utilities received from other neighbors) to neighbors and optimizes the sum of local utilities through the neighbors’ value assignments. An important benefit is that each agent can guarantee equal overhead and privacy.
- Motivation: In distributed optimization, since none of the agents are aware of the quality of the aggregate utilities, the quality of aggregate utility fluctuates with the changes in value assignments. However, the sum of local utilities affects aggregate utility, so we consider that local stability promotes global stability to a certain extent.Contribution: Hence, we propose a STATE mechanism for each agent to control the changes in value assignments. Specifically, each agent changes its state (updates or holds values) based on historical values, which can make the current agent terminate the update early and keep local stability.
- Motivation: Falling into the local optimum is always an awkward problem in approximate optimization algorithms, which limits the exploration ability of the algorithm. Similarly, PLSA also faces the problem of falling into the local optimum as an approximate optimization algorithm.Contribution: With a simple idea, we introduce a classical mutation operator to jump out of the local optimum. The agent resets each value with probability to a random value from its domain.
2. Background
2.1. Distributed Constraint Optimization Problems
- is a set of agents; an agent can control one or more variables.
- is a set of discrete variables; each variable is controlled by one of the agents .
- is a set of discrete domains; each variable takes value from the domain .
- is a set of utility functions; each specifies the utility function assigned to each combination of , where the arity of the utility function is k. We consider that all utility functions are binary (thus ) in this paper.
- is a variable-to-agent mapping function that associates each variable to one agent . In this paper, we assume one agent controls only one variable (, thus the terms “agent” and “variable” could be used interchangeably).
2.2. Continuous Distributed Constraint Optimization Problems
- is the set of continuous variables and each variable is controlled by one of the agents .
- is the set of continuous domains and each continuous variable takes any value from the domain , where and represent the lower and upper bounds of the domain, respectively.
2.3. Distributed Population
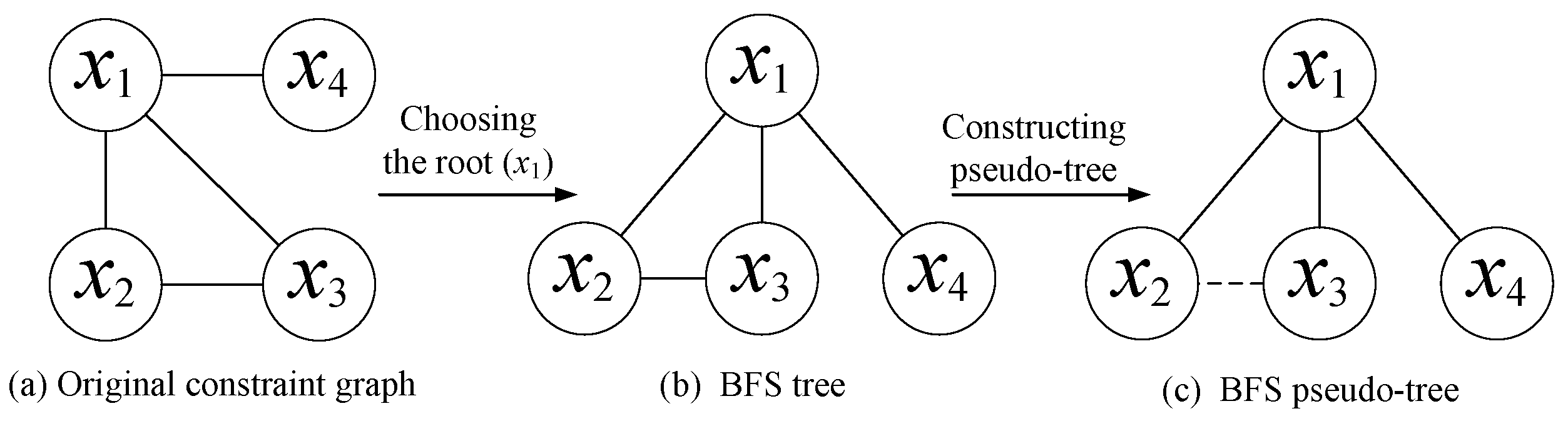
2.4. Breadth First Search Pseudo-tree
- —the tree edge, which connects and (e.g., is a tree edge in Figure 2).
- —the cross-edge, which directly connects node and in two different branches (e.g., is a cross-edge in Figure 2).
- — the parent of node , the single higher node directly connecting through a tree edge (e.g., in Figure 2).
- — the set of children of node , the lower nodes directly connecting through tree edges (e.g., in Figure 2).
- —the set of neighbors of node , the neighboring nodes that directly connect (e.g., in Figure 2).
- —the set of pseudo-neighbors of node , the neighboring nodes that directly connect through cross-edge edges (e.g., in Figure 2).
3. Our Algorithms
3.1. Population-Based Local Search Algorithm
| Algorithm 1: Population-based Local Search Algorithm |
 |
3.2. Population-Based Global Search Algorithm
| Algorithm 2: Population-based Global Search Algorithm |
 |
4. Theoretical Analysis
5. Experiment Results
5.1. Experimental Configuration
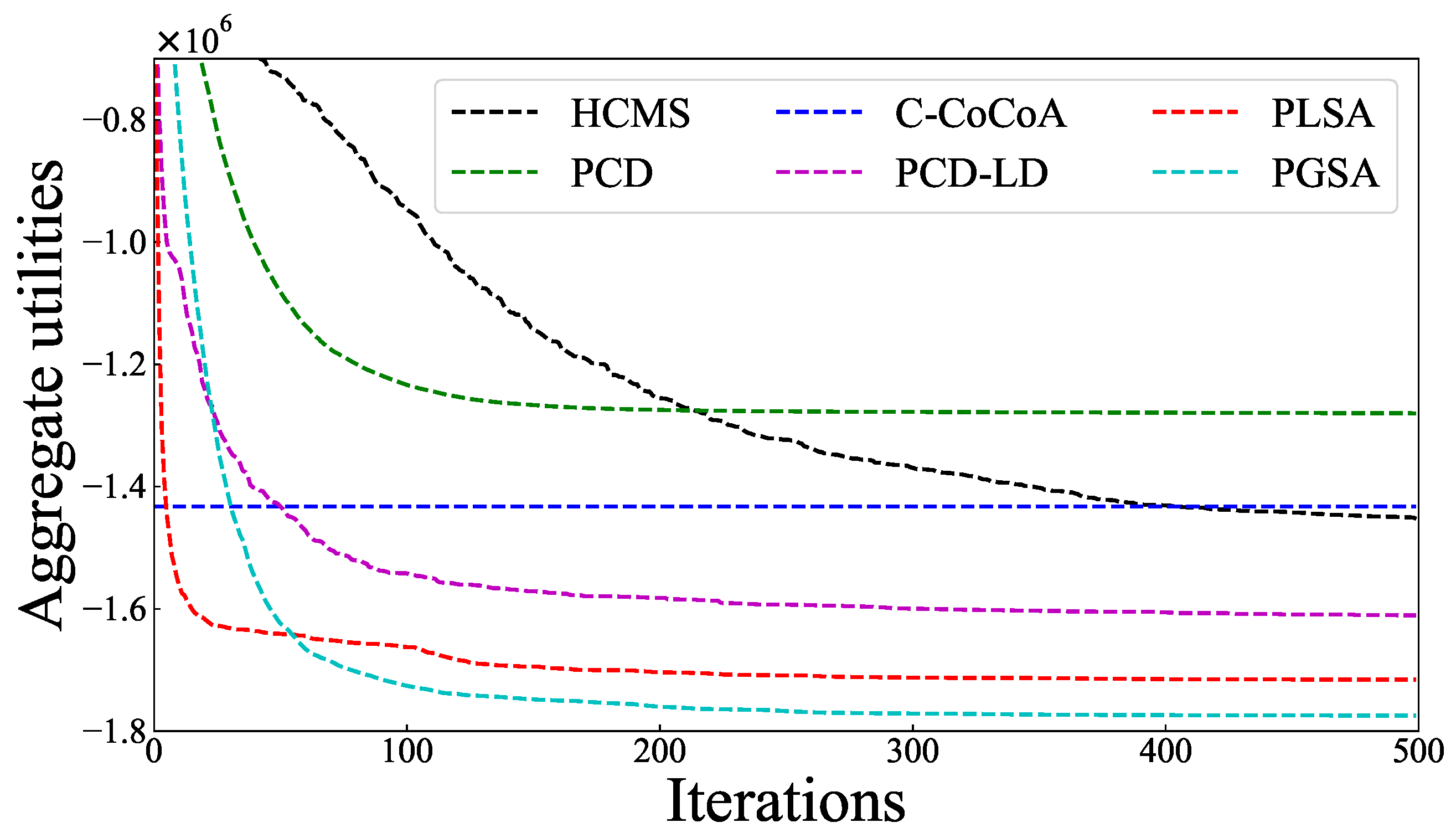
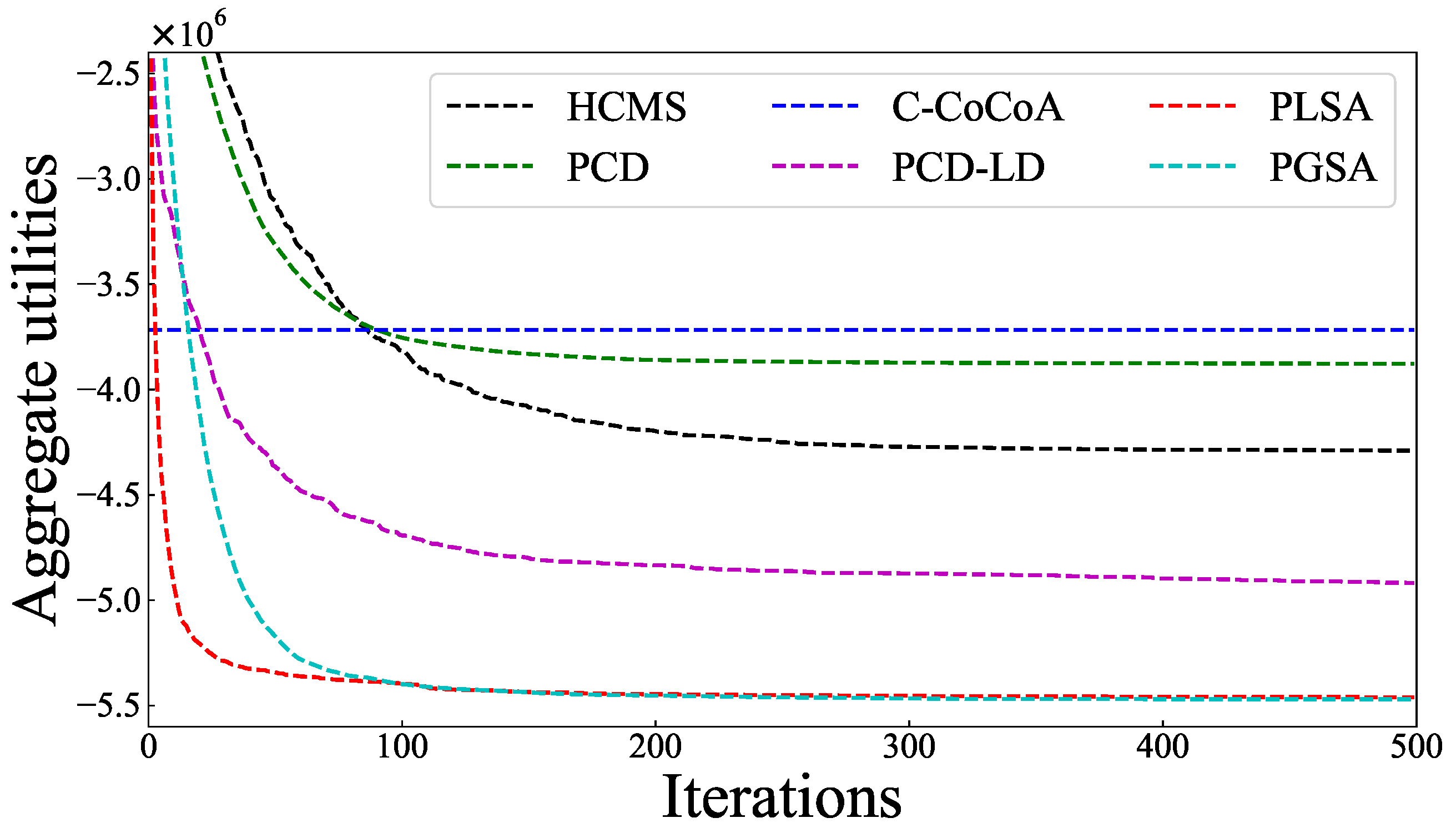
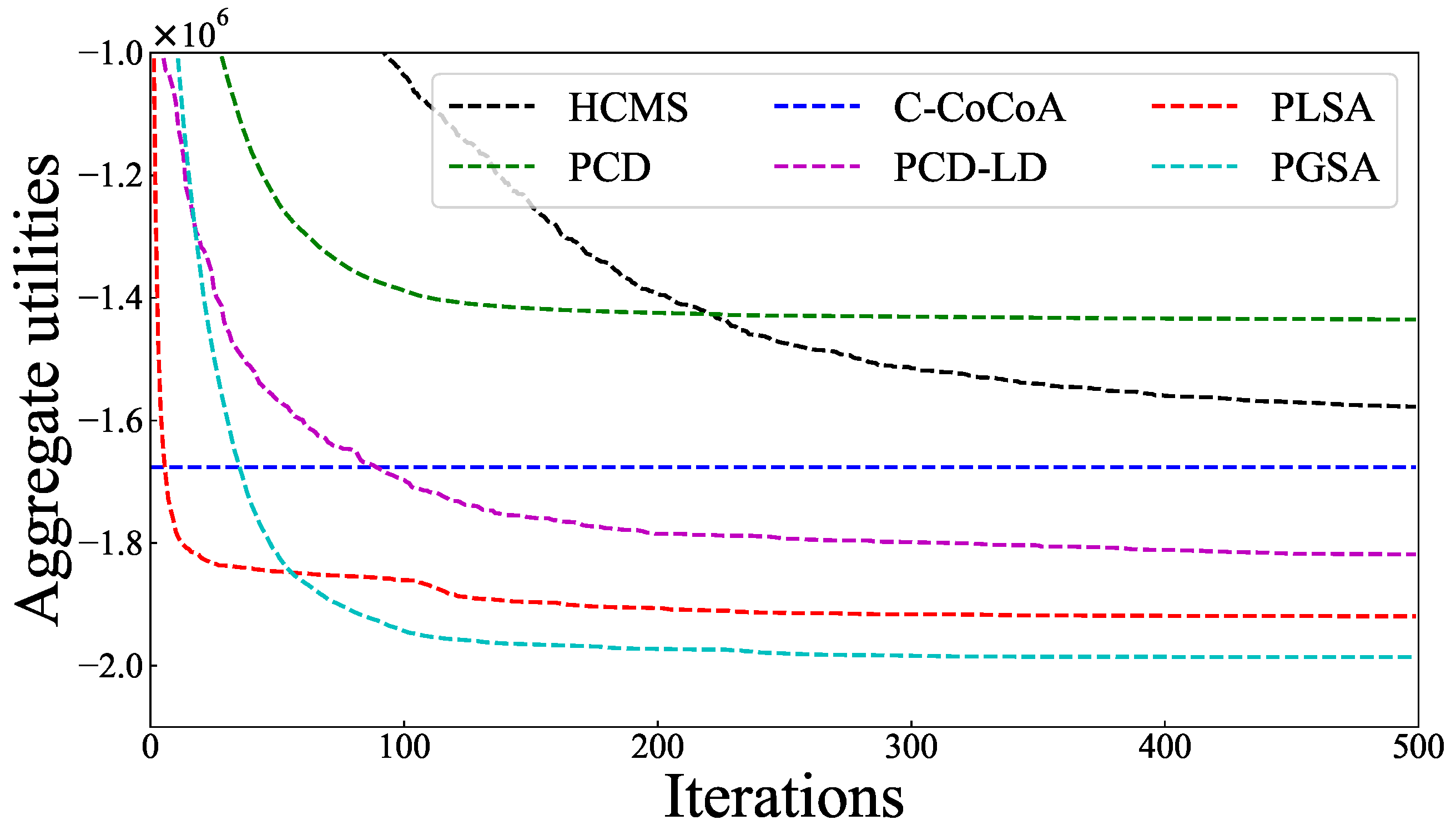
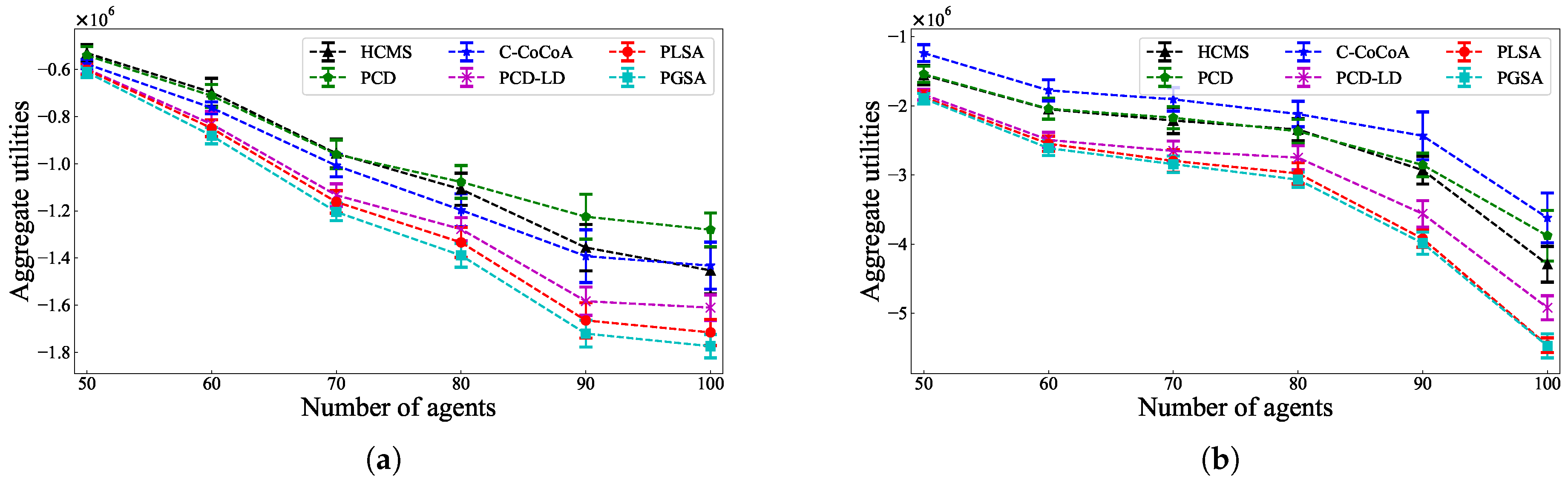
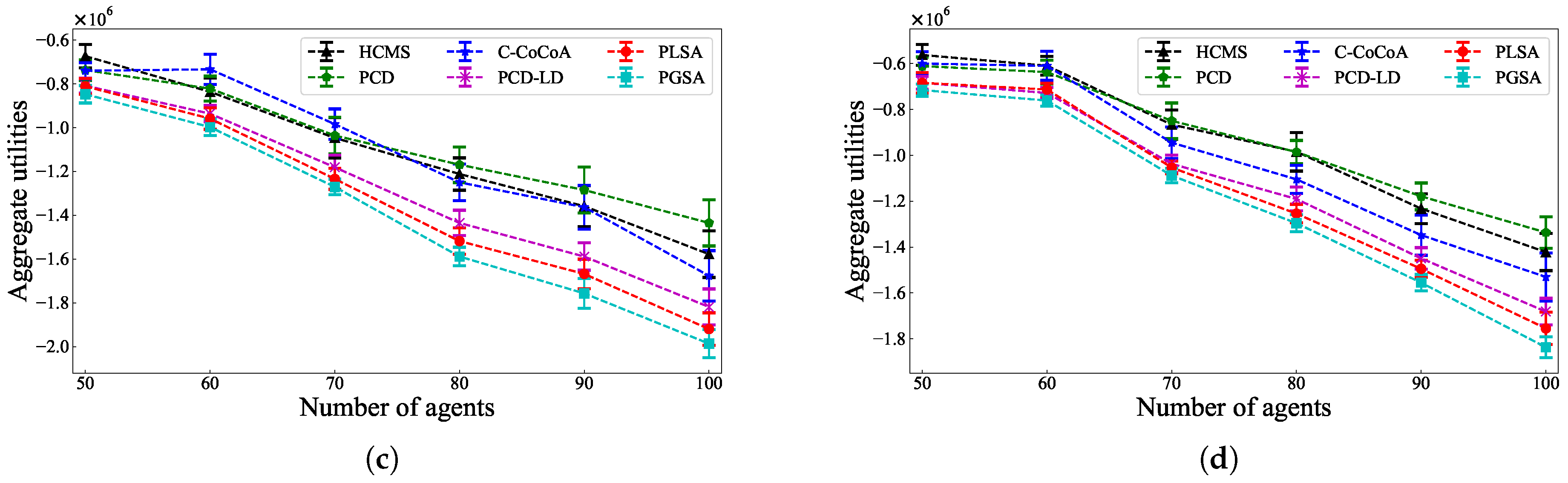
5.2. Comparison of Solution Quality
5.3. Statistical Analysis
6. Conclusions and Future Work
7. Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fioretto, F.; Pontelli, E.; Yeoh, W. Distributed constraint optimization problems and applications: A survey. J. Artif. Intell. Res. 2018, 61, 623–698. [Google Scholar] [CrossRef]
- Modi, P.; Shen, W.M.; Tambe, M.; Yokoo, M. ADOPT: Asynchronous distributed constraint optimization with quality guarantees. Artif. Intell. 2005, 161, 149–180. [Google Scholar] [CrossRef]
- Petcu, A.; Faltings, B. A scalable method for multiagent constraint optimization. In Proceedings of the 19th International Joint Conference on Artificial Intelligence, Edinburgh, Scotland, 28–30 July 2005; pp. 266–271. [Google Scholar]
- Hoang, K.D.; Fioretto, F.; Hou, P.; Yokoo, M.; Yeoh, W.; Zivan, R. Proactive dynamic distributed constraint optimization. In Proceedings of the 15th International Conference on Autonomous Agents and Multiagent Systems, Singapore, 9–13 May 2016; pp. 597–605. [Google Scholar]
- Maheswaran, R.T.; Tambe, M.; Bowring, E.; Pearce, J.P.; Varakantham, P. Taking DCOP to the real world: Efficient complete solutions for distributed multi-event scheduling. In Proceedings of the 3rd International Conference on Autonomous Agents and Multiagent Systems, New York, NY, USA, 19–23 July 2004; pp. 310–317. [Google Scholar]
- Enembreck, F.; Barthès, J.A. Distributed constraint optimization with MULBS: A case study on collaborative meeting scheduling. J. Netw. Comput. 2012, 35, 164–175. [Google Scholar] [CrossRef]
- Fioretto, F.; Yeoh, W.; Pontelli, E. A multiagent system approach to scheduling devices in smart homes. In Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems, São Paulo, Brazil, 8–12 May 2017; pp. 981–989. [Google Scholar]
- Rust, P.; Picard, G.; Ramparany, F. Using message-passing DCOP algorithms to solve energy-efficient smart environment configuration problems. In Proceedings of the 25th International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 468–474. [Google Scholar]
- Farinelli, A.; Rogers, A.; Petcu, A.; Jennings, N.R. Decentralised coordination of low-power embedded devices using the max-sum algorithm. In Proceedings of the 7th International Conference on Autonomous Agents and Multiagent Systems, Estoril, Portugal, 12–16 May 2008; pp. 639–646. [Google Scholar]
- Yeoh, W.; Yokoo, M. Distributed problem solving. AI Mag. 2012, 33, 53–65. [Google Scholar] [CrossRef]
- Zivan, R.; Yedidsion, H.; Okamoto, S.; Glinton, R.; Sycara, K.P. Distributed constraint optimization for teams of mobile sensing agents. Auton. Agent. Multi. Agent. Syst. 2015, 29, 495–536. [Google Scholar] [CrossRef]
- Yedidsion, H.; Zivan, R. Applying DCOP_MST to a team of mobile robots with directional sensing abilities. In Proceedings of the 15th International Conference on Autonomous Agents and Multiagent Systems, Singapore, 9–13 May 2016; pp. 1357–1358. [Google Scholar]
- Picard, G. Trajectory coordination based on distributed constraint optimization techniques in unmanned air traffic management. In Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems, Virtual Event, 9–13 May 2022; pp. 1065–1073. [Google Scholar]
- Chen, Z.; Deng, Y.; Wu, T. An iterative refined max-sum_ad algorithm via single-side value propagation and local search. In Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems, São Paulo, Brazil, 8–12 May 2017; pp. 195–202. [Google Scholar]
- Cohen, L.; Galiki, R.; Zivan, R. Governing convergence of max-sum on DCOPs through damping and splitting. Artif. Intell. 2020, 279, 103212. [Google Scholar] [CrossRef]
- Khan, M.M.; Tran-Thanh, L.; Jennings, N.R. A generic domain pruning technique for GDL-based DCOP algorithms in cooperative multi-agent systems. In Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 1595–1603. [Google Scholar]
- Khan, M.M.; Tran-Thanh, L.; Yeoh, W.; Jennings, N.R. A near-optimal node-to-agent mapping heuristic for GDL-based DCOP algorithms in multi-agent systems. In Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 1604–1612. [Google Scholar]
- Zivan, R.; Parash, T.; Cohen, L.; Peled, H.; Okamoto, S. Balancing exploration and exploitation in incomplete min/max-sum inference for distributed constraint optimization. Auton. Agent. Multi. Agent. Syst. 2017, 31, 1165–1207. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, Z.; Chen, D.; Zhang, W.; Jiang, X. AsymDPOP: Complete inference for asymmetric distributed constraint optimization problems. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 223–230. [Google Scholar]
- Leeuwen, C.J.; Pawelczak, P. CoCoA: A non-iterative approach to a local search (A)DCOP solver. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, 4–9 February 2017; pp. 3944–3950. [Google Scholar] [CrossRef]
- Zivan, R.; Parash, T.; Cohen-Lavi, L.; Naveh, Y. Applying max-sum to asymmetric distributed constraint optimization problems. Auton. Agent. Multi. Agent. Syst. 2020, 34, 1–29. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, Z.; Chen, D.; Jiang, X.; Li, Q. PT-ISABB: A hybrid tree-based complete algorithm to solve asymmetric distributed constraint optimization problems. In Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems, Montreal QC, Canada, 13–17 May 2019; pp. 1506–1514. [Google Scholar]
- Hoang, K.D.; Hou, P.; Fioretto, F.; Yeoh, W.; Zivan, R.; Yokoo, M. Infinite-horizon proactive dynamic DCOPs. In Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems, São Paulo, Brazil, 8–12 May 2017; pp. 212–220. [Google Scholar]
- Hoang, K.D.; Fioretto, F.; Hou, P.; Yeoh, W.; Yokoo, M.; Zivan, R. Proactive dynamic distributed constraint optimization problems. J. Artif. Intell. Res. 2022, 74, 179–225. [Google Scholar] [CrossRef]
- Hirayama, K.; Yokoo, M. Distributed partial constraint satisfaction problem. In Proceedings of the 3rd International Conference on Principles and Practice of Constraint Programming, Linz, Austria, 28–30 October 1997; pp. 222–236. [Google Scholar]
- Rashik, M.; Rahman, M.M.; Khan, M.M.; Mamun-Or-Rashid, M.; Tran-Thanh, L.; Jennings, N.R. Speeding up distributed pseudo-tree optimization procedures with cross edge consistency to solve DCOPs. Artif. Intell. 2021, 51, 1733–1746. [Google Scholar] [CrossRef]
- Litov, O.; Meisels, A. Forward bounding on pseudo-trees for DCOPs and ADCOPs. Artif. Intell. 2017, 252, 83–99. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, G.; Xing, Z.; Wittenburg, L. Distributed stochastic search and distributed breakout: Properties, comparison and applications to constraint optimization problems in sensor networks. Artif. Intell. 2005, 161, 55–87. [Google Scholar] [CrossRef]
- Maheswaran, R.T.; Pearce, J.P.; Tambe, M. Distributed algorithms for DCOP: A graphical-game-based approach. In Proceedings of the 17th International Conference on Parallel and Distributed Computing Systems, Newport Beach, CA, USA, 9–13 July 2004; pp. 432–439. [Google Scholar]
- Chen, Z.; Wu, T.; Deng, Y.; Zhang, C. An ant-based algorithm to solve distributed constraint optimization problems. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 4654–4661. [Google Scholar]
- Chen, Z.; Liu, L.; He, J.; Yu, Z. A genetic algorithm based framework for local search algorithms for distributed constraint optimization problems. Auton. Agent. Multi. Agent. Syst. 2020, 34, 1–31. [Google Scholar] [CrossRef]
- Stranders, R.; Farinelli, A.; Rogers, A.; Jennings, N.R. Decentralised coordination of continuously valued control parameters using the max-sum algorithm. In Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems, Budapest, Hungary, 10–15 May 2009; pp. 601–608. [Google Scholar]
- Voice, T.; Stranders, R.; Rogers, A.; Jennings, N.R. A hybrid continuous max-sum algorithm for decentralised coordination. In Proceedings of the 19th European Conference on Artificial Intelligence, Lisbon, Portugal, 8–12 August 2010; pp. 61–66. [Google Scholar]
- Fransman, J.; Sijs, J.; Dol, H.; Theunissen, E.; Schutter, B.D. Bayesian-DPOP for continuous distributed constraint optimization problems. In Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems, Montreal, QC, Canada, 13–17 May 2019; pp. 1961–1963. [Google Scholar]
- Choudhury, M.; Mahmud, S.; Khan, M.M. A particle swarm based algorithm for functional distributed constraint optimization problems. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 7111–7118. [Google Scholar]
- Hoang, K.D.; Yeoh, W.; Yokoo, M.; Rabinovich, Z. New algorithms for continuous distributed constraint optimization problems. In Proceedings of the 19th International Conference on Autonomous Agents and Multiagent Systems, Auckland, New Zealand, 9–13 May 2020; pp. 502–510. [Google Scholar]
- Sarker, A.; Choudhury, M.; Khan, M.M. A local search based approach to solve continuous DCOPs. In Proceedings of the 20th International Conference on Autonomous Agents and Multiagent Systems, Virtual Event, UK, 3–7 May 2021; pp. 1127–1135. [Google Scholar]
- Shi, M.; Liao, X.; Chen, Y. A particle swarm with local decision algorithm for functional distributed constraint optimization problems. Intern. J. Pattern. Recognit. Artif. Intell. 2022, 36, 2259025. [Google Scholar] [CrossRef]
- Abuhamdah, A.; Ayob, M.; Kendall, G.; Sabar, N.R. Population based Local search for university course timetabling problems. Appl. Intell. 2014, 40, 44–53. [Google Scholar] [CrossRef]
- Zivan, R.; Okamoto, S.; Peled, H. Explorative anytime local search for distributed constraint optimization. Artif. Intell. 2014, 212, 1–26. [Google Scholar] [CrossRef]
- Chen, Z.; He, Z.; He, C. An improved DPOP algorithm based on breadth first search pseudo-tree for distributed constraint optimization. Artif. Intell. 2017, 47, 607–623. [Google Scholar] [CrossRef]
- Paul, E.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung 1960, 5, 17–60. [Google Scholar] [CrossRef]
- Réka, A.; Albert-László, B. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ’small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Grinshpoun, T.; Grubshtein, A.; Zivan, R.; Netzer, A.; Meisels, A. Asymmetric distributed constraint optimization problems. J. Artif. Int. Res. 2013, 47, 613–647. [Google Scholar] [CrossRef]
- Delle Fave, F.M.; Stranders, R.; Rogers, A.; Jennings, N.R. Bounded decentralised coordination over multiple objectives. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems, Taipei, Taiwan, 2–6 May 2011; pp. 371–378. [Google Scholar]
- Hoang, K.D.; Yeoh, W. Dynamic continuous distributed constraint optimization problems. In Proceedings of the 24th International Conference on Principles and Practice of Multiagent Systems, Valencia, Spain, 16–18 November 2022; pp. 475–491. [Google Scholar]
- Nguyen, D.T.; Yeoh, W.; Lau, H.C. Stochastic dominance in stochastic DCOPs for risk-sensitive applications. In Proceedings of the 11th International Conference on Autonomous Agents and Multiagent Systems, Valencia, Spain, 4–8 June 2012; pp. 257–264. [Google Scholar]
- Chen, D.; Deng, Y.; Chen, Z.; He, Z.; Zhang, W. A hybrid tree-based algorithm to solve asymmetric distributed constraint optimization problems. Auton. Agent. Multi. Agent. Syst. 2020, 34, 1–42. [Google Scholar] [CrossRef]
- Chen, D.; Chen, Z.; Deng, Y.; He, Z.; Wang, L. Inference-based complete algorithms for asymmetric distributed constraint optimization problems. Artif. Intell. Rev. 2022, 56, 4491–4534. [Google Scholar] [CrossRef]
- Medi, A.; Okimoto, T.; Inoue, K. A two-phase complete algorithm for multi-objective distributed constraint optimization. J. Adv. Comput. Intell. Intell. Inform. 2014, 18, 573–580. [Google Scholar] [CrossRef]
- Matsui, T.; Silaghi, M.; Hirayama, K.; Yokoo, M.; Matsuo, H. Leximin multiple objective optimization for preferences of agents. In Proceedings of the 17th International Conference on Principles and Practice of Multiagent Systems, Gold Coast, QLD, Australia, 1–5 December 2014; pp. 423–438. [Google Scholar]
- Yeoh, W.; Varakantham, P.; Sun, X.; Koenig, S. Incremental DCOP search algorithms for solving dynamic DCOPs. In Proceedings of the 10th International Conference on Autonomous Agents and Multiagent Systems, Taipei, Taiwan, 2–6 May 2011; pp. 1069–1070. [Google Scholar]
- Shokoohi, M.; Afsharchi, M.; Shah-Hoseini, H. Dynamic distributed constraint optimization using multi-agent reinforcement learning. Soft Comput. 2022, 26, 360103629. [Google Scholar] [CrossRef]
- Léauté, T.; Faltings, B. Distributed constraint optimization under stochastic uncertainty. In Proceedings of the 25th AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011; pp. 68–73. [Google Scholar]
- Atlas, J.; Decker, K. Coordination for uncertain outcomes using distributed neighbor exchange. In Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems, Toronto, ON, Canada, 10–14 May 2010; pp. 1047–1054. [Google Scholar]
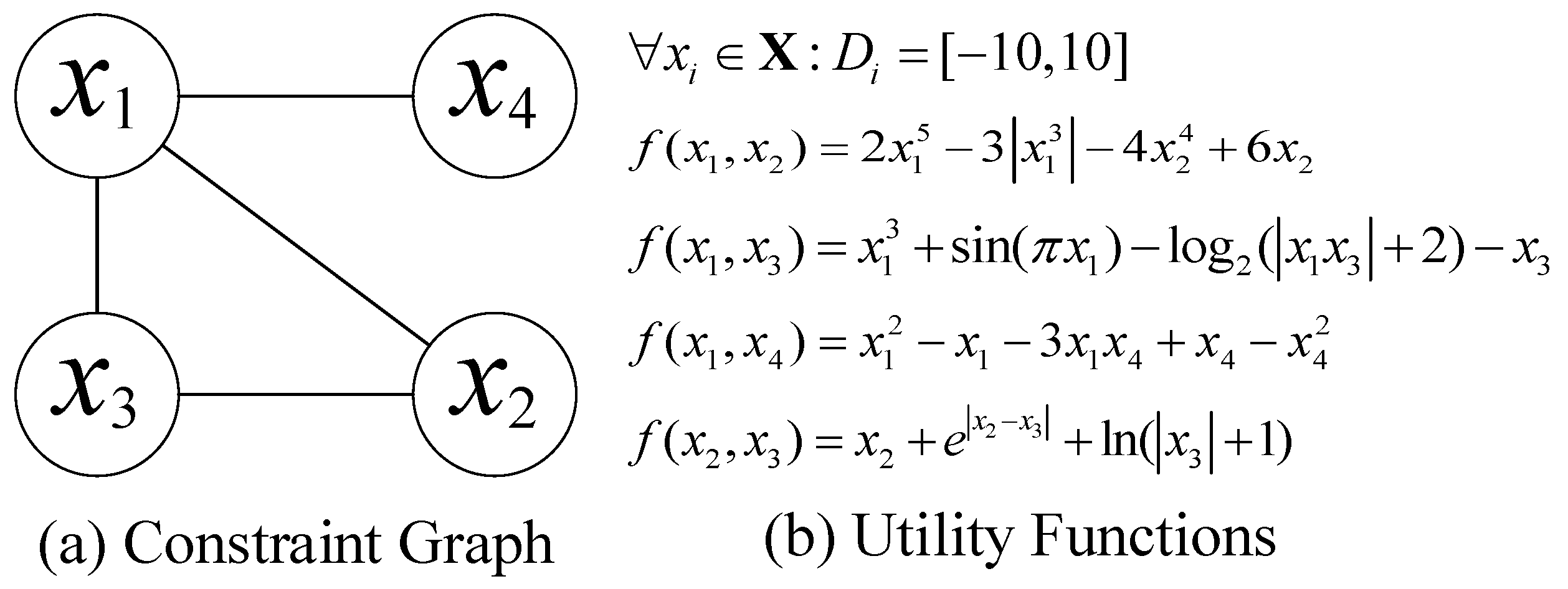


| Agent | Agent | … | Agent | |
|---|---|---|---|---|
| solution 1 | … | |||
| solution 2 | … | |||
| … | … | … | … | … |
| solution k | … | |||
| … | … | … | … | … |
| solution K | … |
| Type | Ours | HCMS | PCD | C-CoCoA | PCD-LD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | p | p | p | ||||||||||
| Sparse | PLSA | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 28/2 | 441/24 | 0.000 |
| PGSA | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 29/1 | 464/1 | 0.000 | |
| Dense | PLSA | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 |
| PGSA | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | |
| Scale-free | PLSA | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 28/2 | 462/3 | 0.000 | 25/5 | 414/51 | 0.000 |
| PGSA | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 29/1 | 464/1 | 0.000 | |
| Small-world | PLSA | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 29/1 | 463/2 | 0.000 | 22/8 | 375/90 | 0.003 |
| PGSA | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | 30/0 | 465/0 | 0.000 | |
| Graph Type | Our Algorithms | HCMS () | PCD () | C-CcCoA () | PCD-LD () |
|---|---|---|---|---|---|
| Sparse random graphs | PLSA | 19.68% (±3.17%) | 24.24% (±8.53%) | 13.61% (±5.40%) | 3.55% (±2.00%) |
| PGSA | 23.68% (±4.06%) | 28.41% (±9.25%) | 17.42% (±6.08%) | 7.01% (±2.58%) | |
| Dense random graphs | PLSA | 26.57% (±3.97%) | 29.83% (±6.94%) | 49.03% (±6.66%) | 6.52% (±3.56%) |
| PGSA | 28.70% (±4.26%) | 31.97% (±6.43%) | 51.50% (±6.13%) | 8.30% (±3.49%) | |
| Scale-free networks | PLSA | 20.43% (±3.42%) | 23.19% (±8.47%) | 20.65% (±6.90%) | 3.93% (±1.94%) |
| PGSA | 25.44% (±4.12%) | 28.31% (±9.02%) | 25.65% (±7.15%) | 8.23% (±2.14%) | |
| Small-world networks | PLSA | 20.03% (±3.08%) | 22.18% (±7.57%) | 13.57% (±1.99%) | 2.06% (±2.54%) |
| PGSA | 27.45% (±2.31%) | 27.57% (±7.16%) | 18.65% (±3.28%) | 6.59% (±1.98%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, X.; Hoang, K.D. A Population-Based Search Approach to Solve Continuous Distributed Constraint Optimization Problems. Appl. Sci. 2024, 14, 1290. https://doi.org/10.3390/app14031290
Liao X, Hoang KD. A Population-Based Search Approach to Solve Continuous Distributed Constraint Optimization Problems. Applied Sciences. 2024; 14(3):1290. https://doi.org/10.3390/app14031290
Chicago/Turabian StyleLiao, Xin, and Khoi D. Hoang. 2024. "A Population-Based Search Approach to Solve Continuous Distributed Constraint Optimization Problems" Applied Sciences 14, no. 3: 1290. https://doi.org/10.3390/app14031290
APA StyleLiao, X., & Hoang, K. D. (2024). A Population-Based Search Approach to Solve Continuous Distributed Constraint Optimization Problems. Applied Sciences, 14(3), 1290. https://doi.org/10.3390/app14031290






