Gear Integrated Error Determination Using the Gaussian Template Convolution-Facet Method
Abstract
1. Introduction
2. Theory of Gear Integrated Error
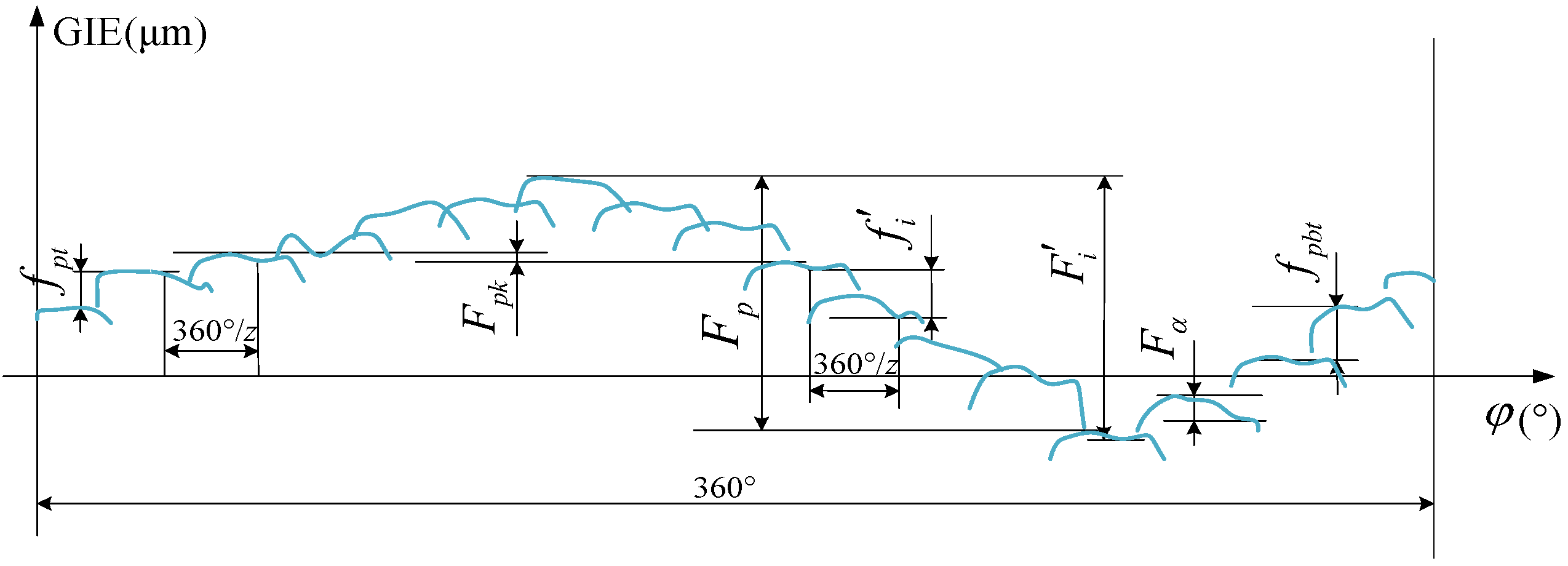
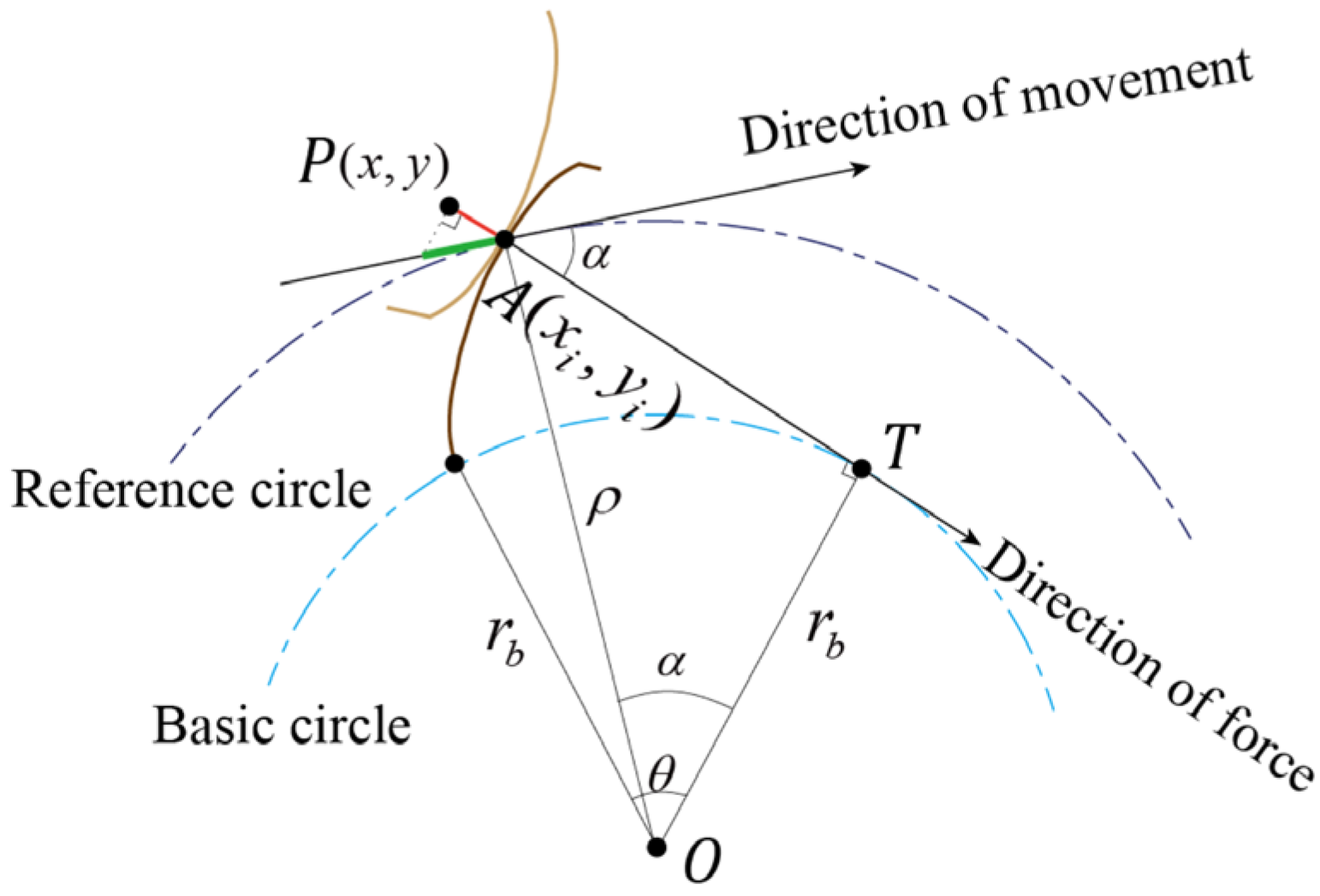
2.1. Gear Integrated Error Curve
2.2. Relationship between Integrated and Various Error Terms
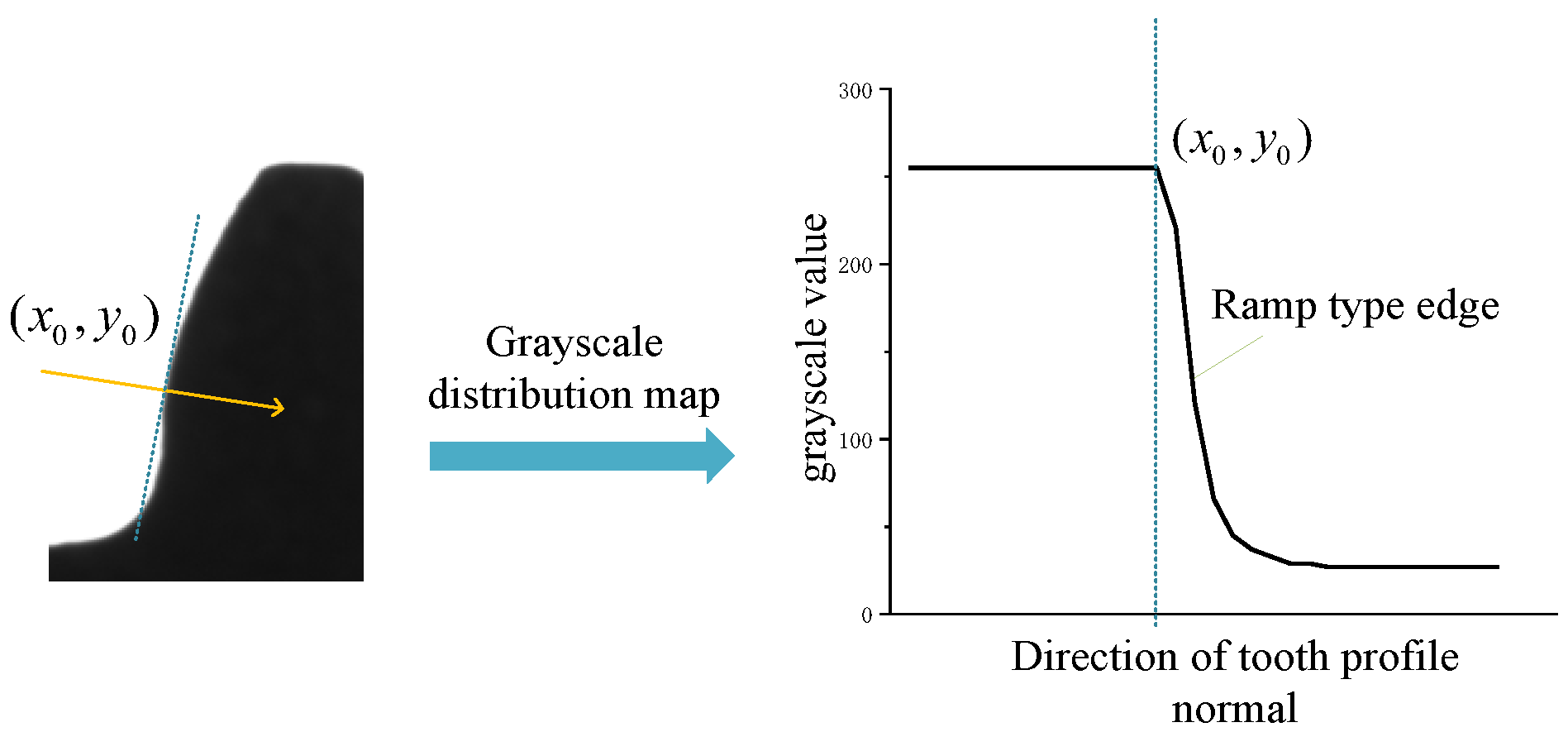
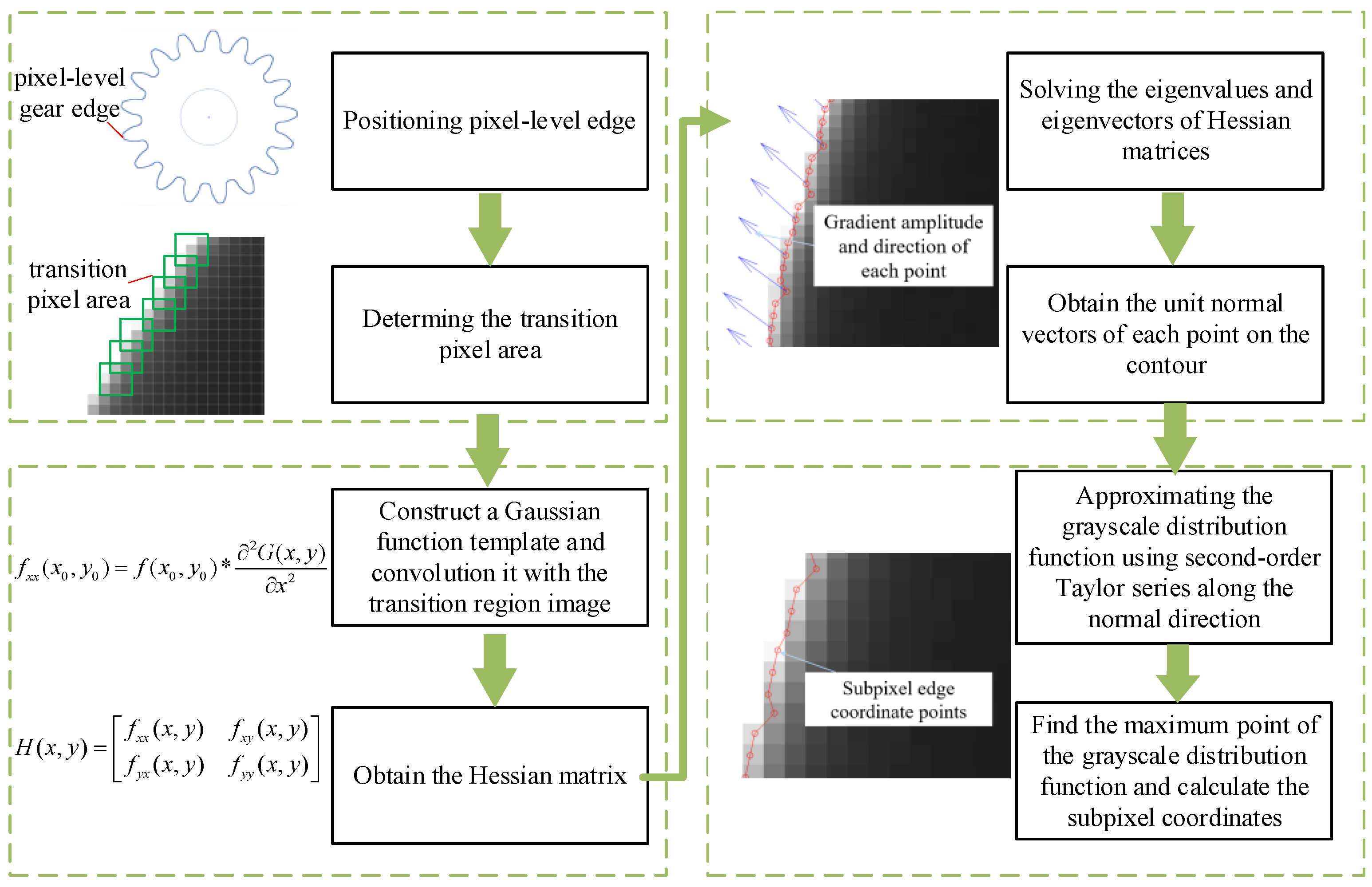
3. GTC−Facet Sub-Pixel Algorithm
4. Obtaining Gear Integrated Error Based on GTC−Facet
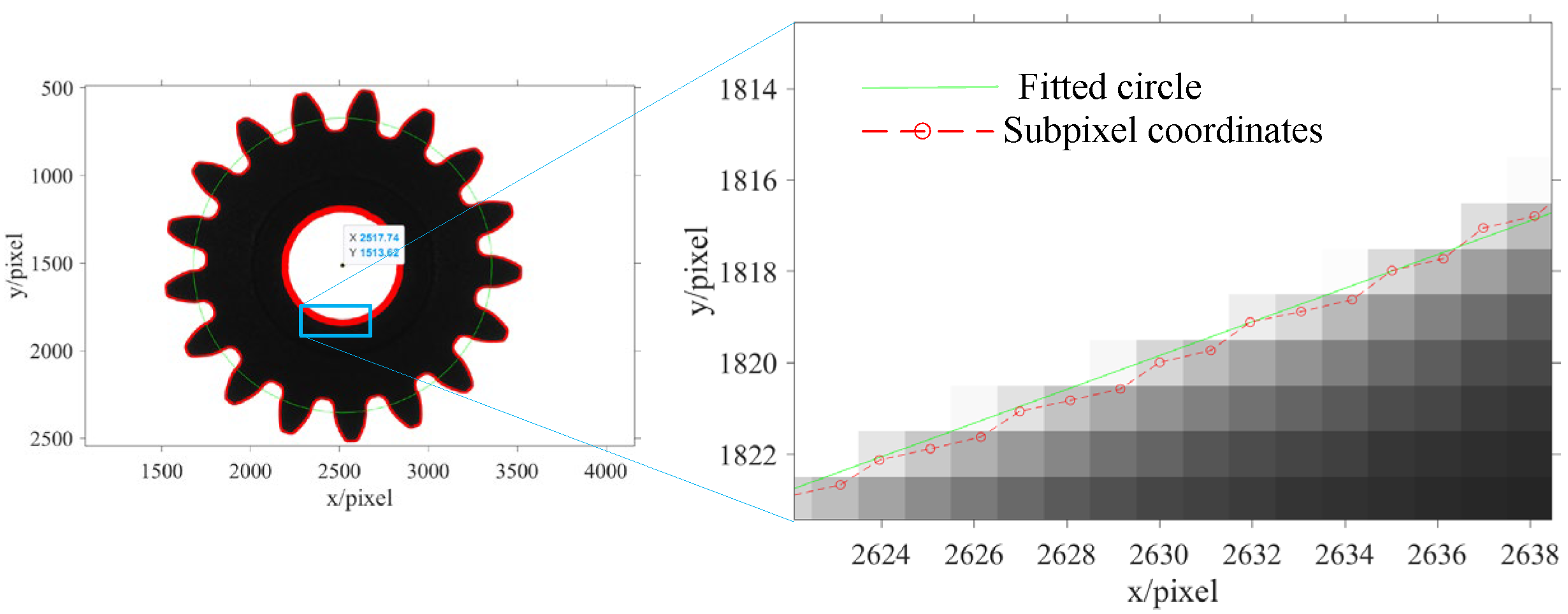
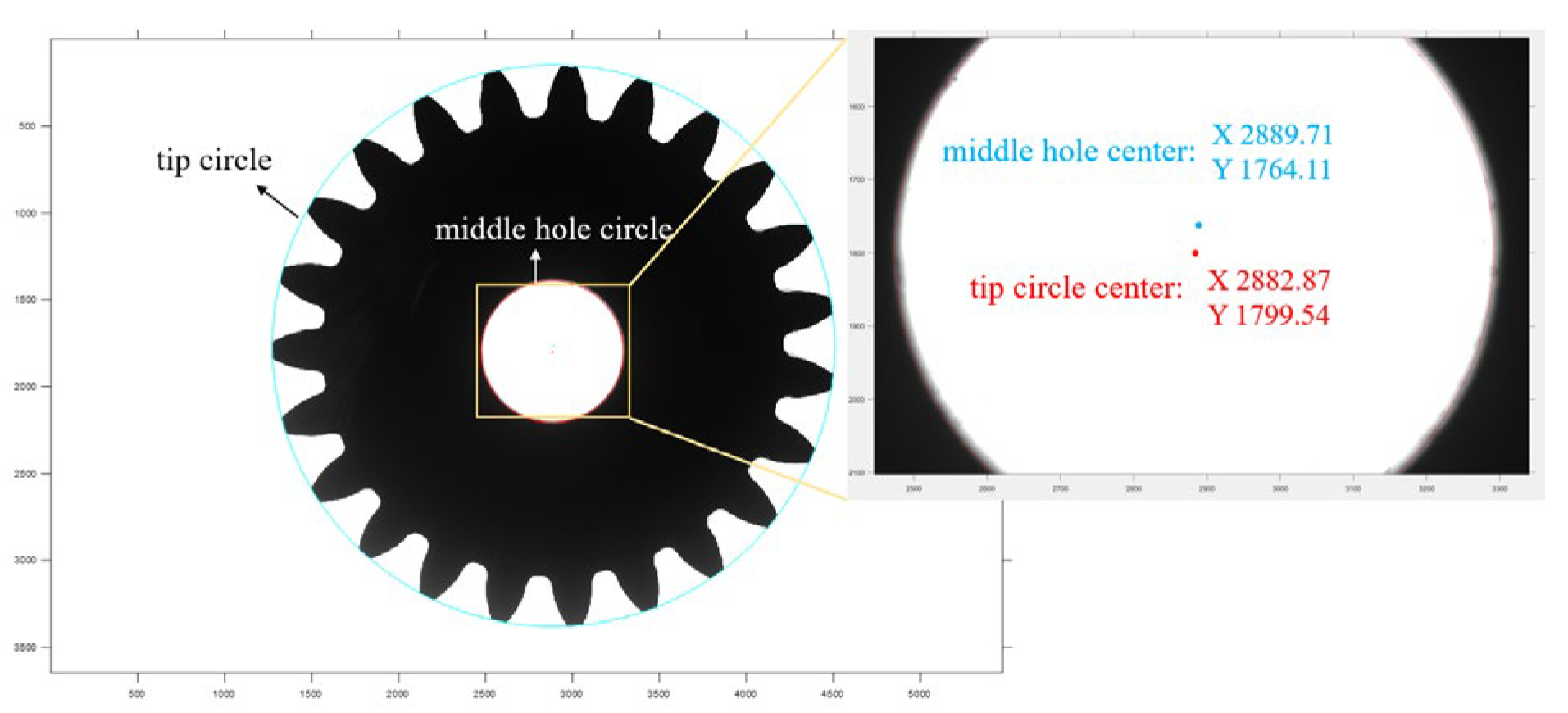
4.1. Accurate Positioning of the Center Point of the Gear End Face
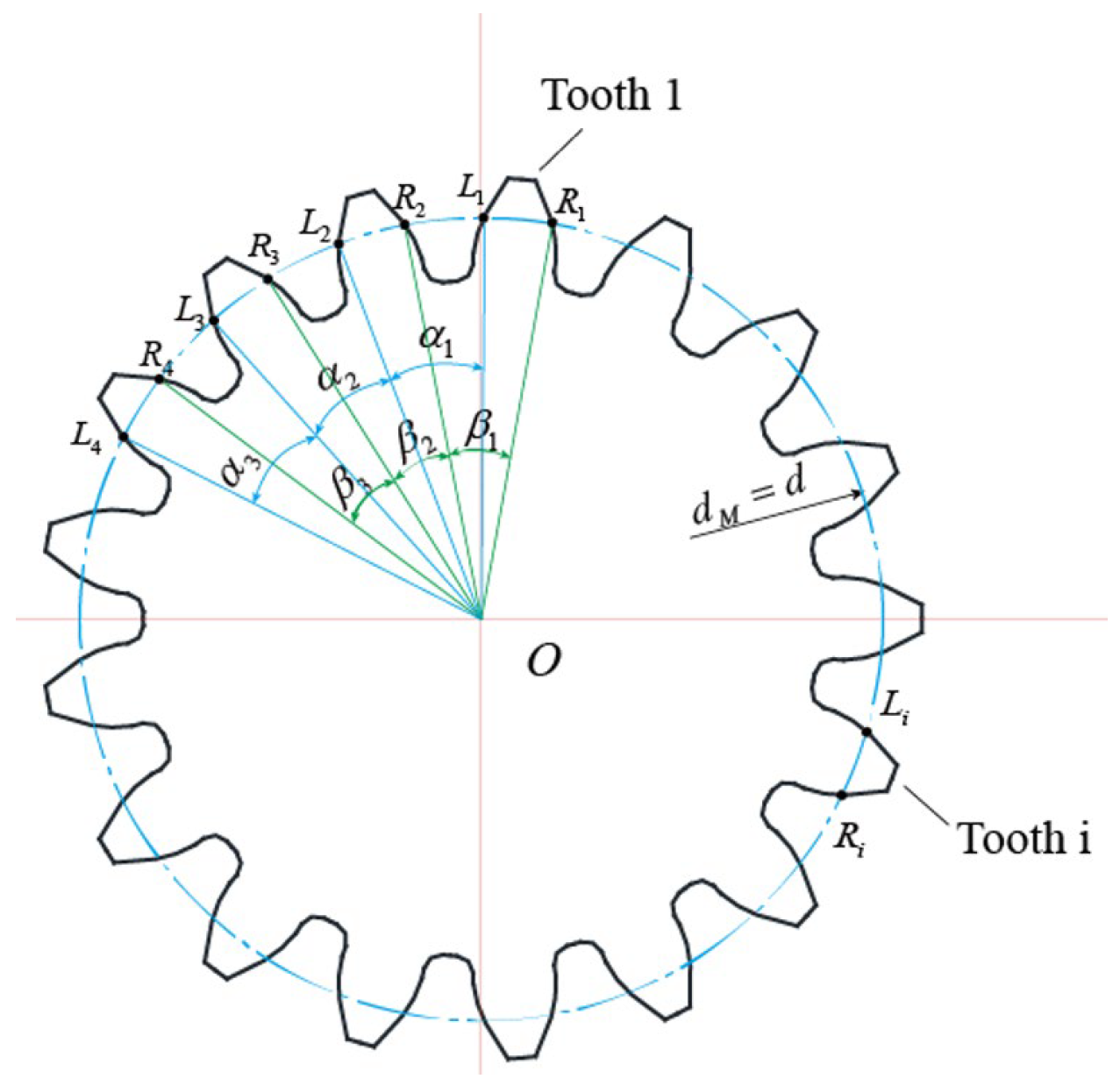
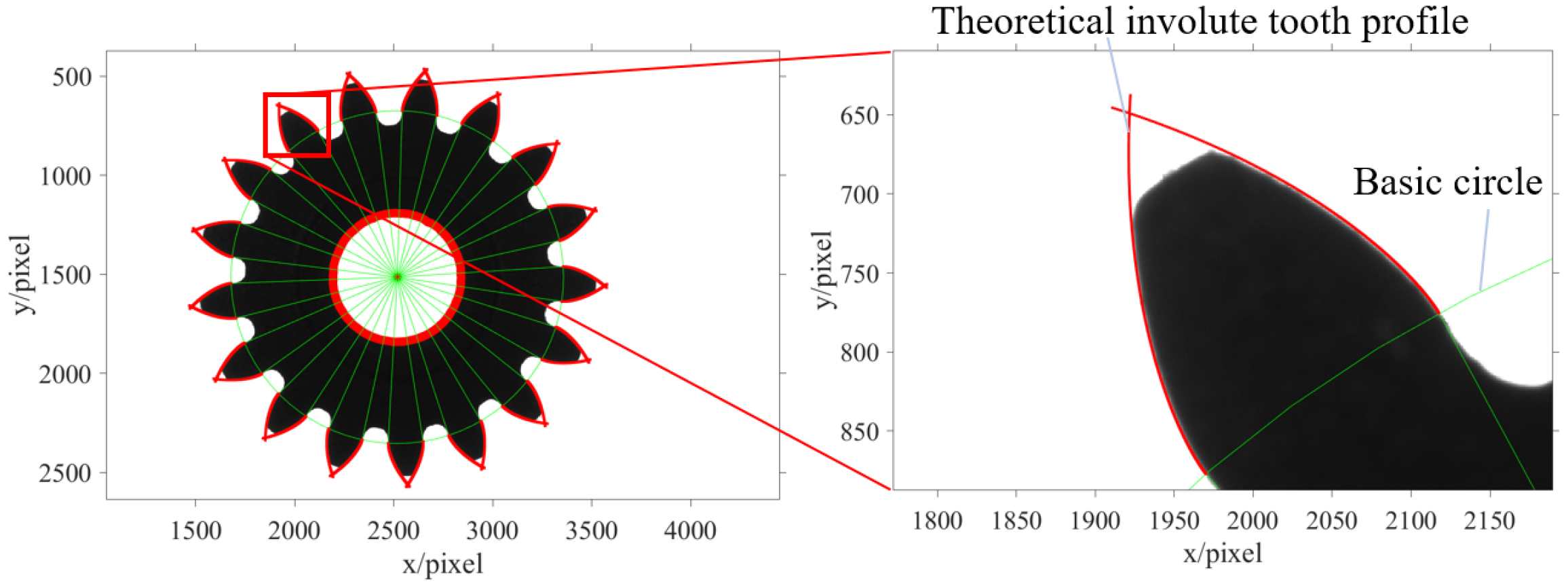
4.2. Calculation of Pitch Deviation and Profile Deviation
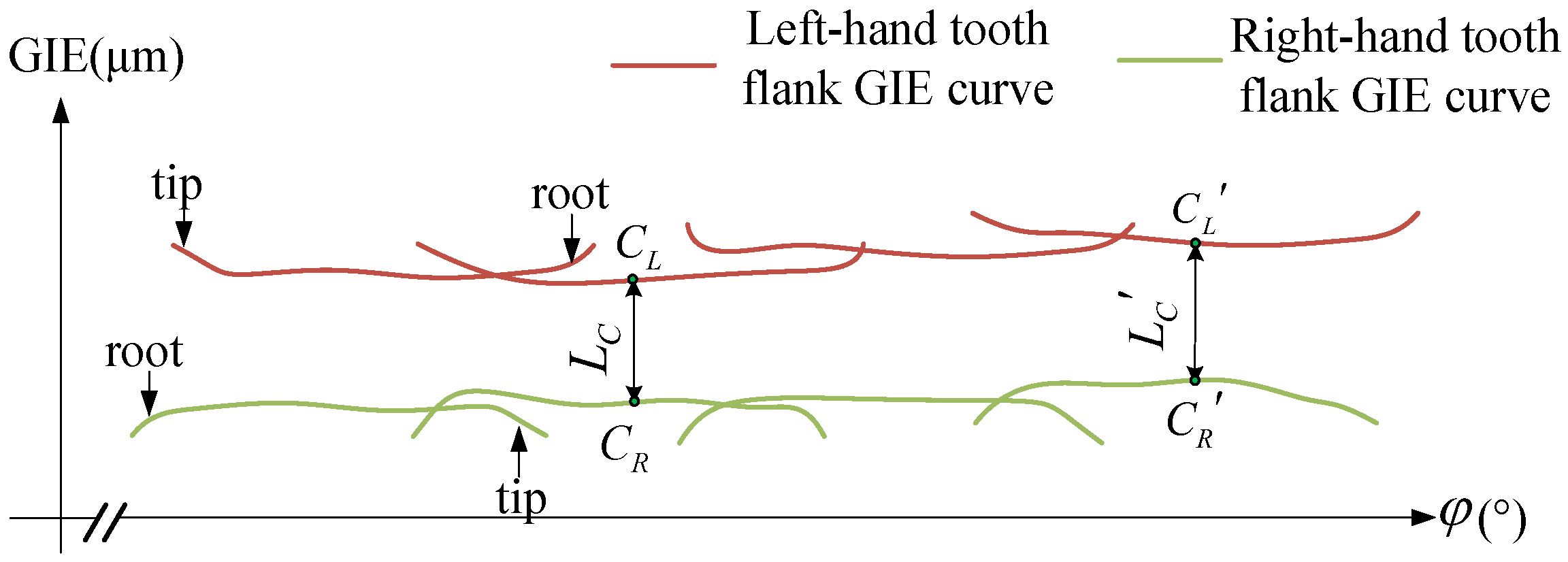
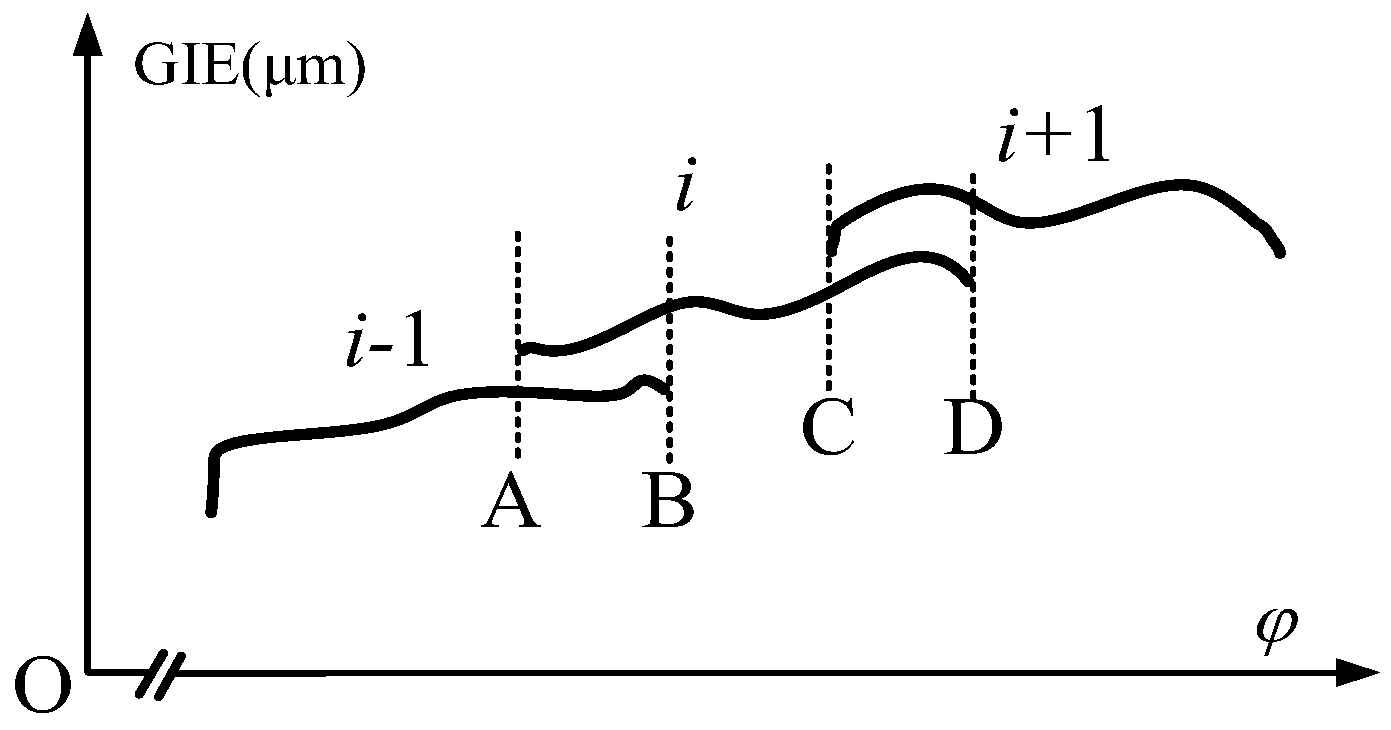
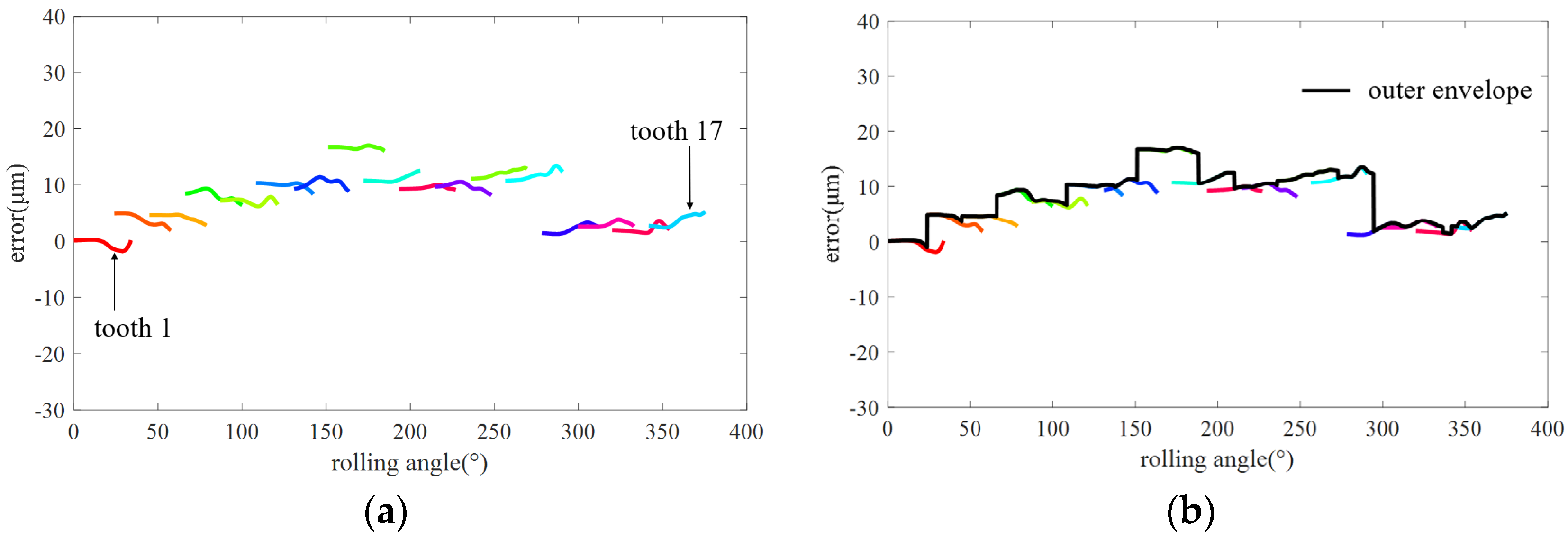
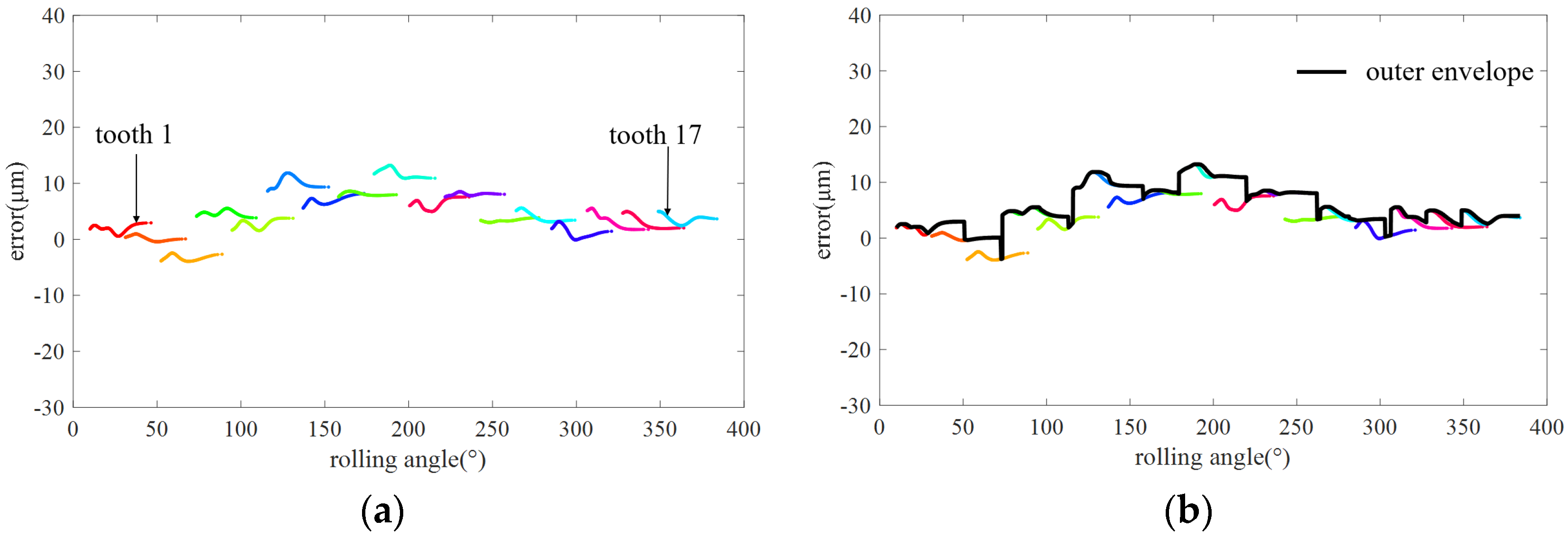
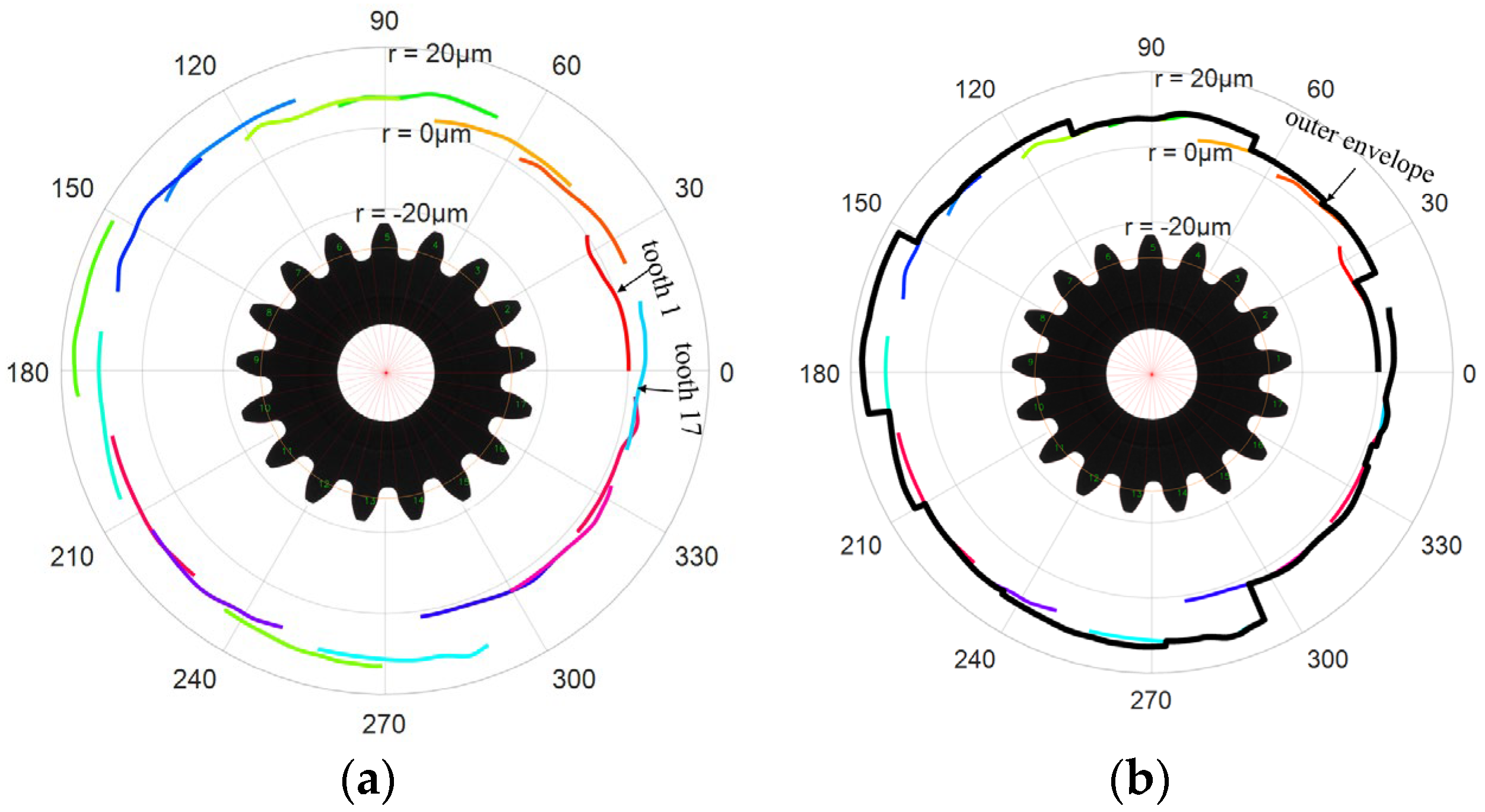
4.3. Synthesis of Gear Integrated Error Curve
5. Experiment and Discussion
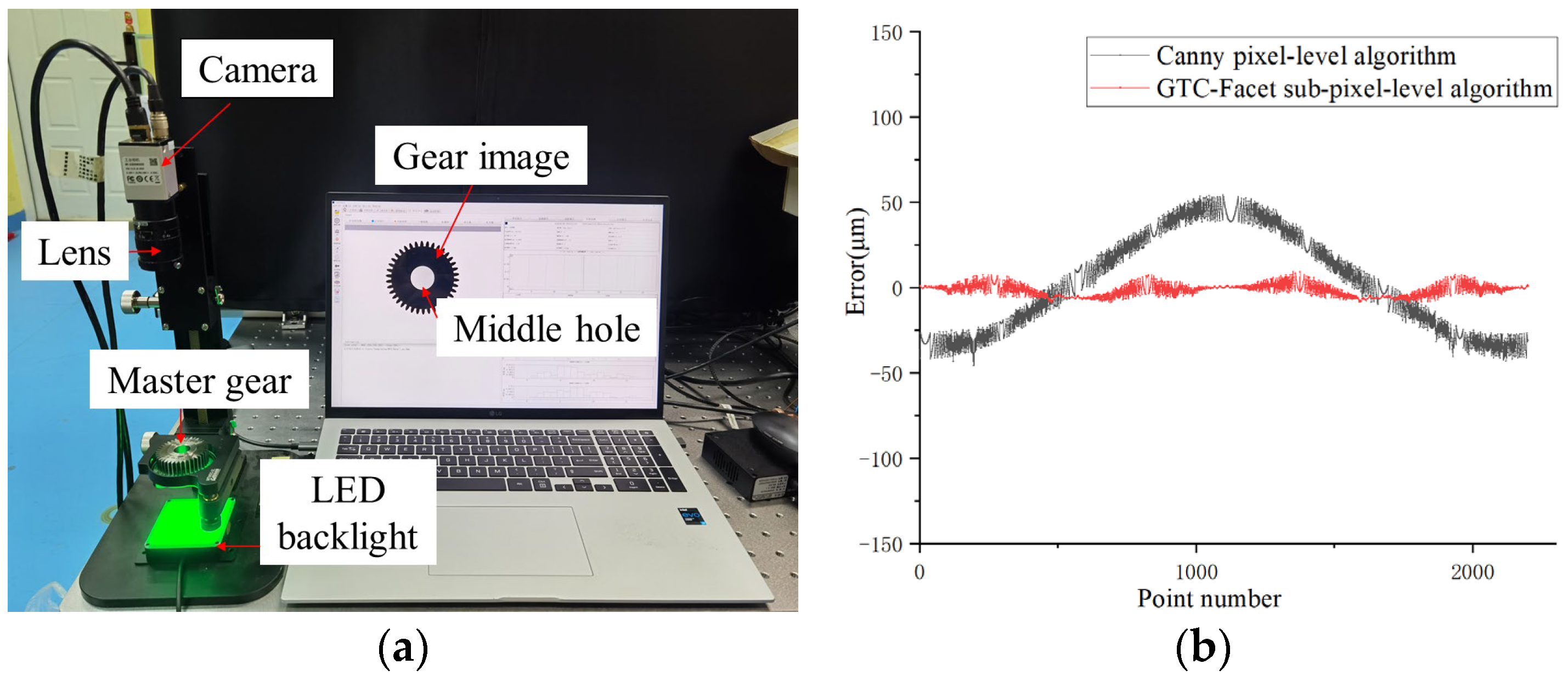
5.1. GTC−Facet Algorithm Positioning Accuracy
5.2. GVMS Integrated Measurement Experiment
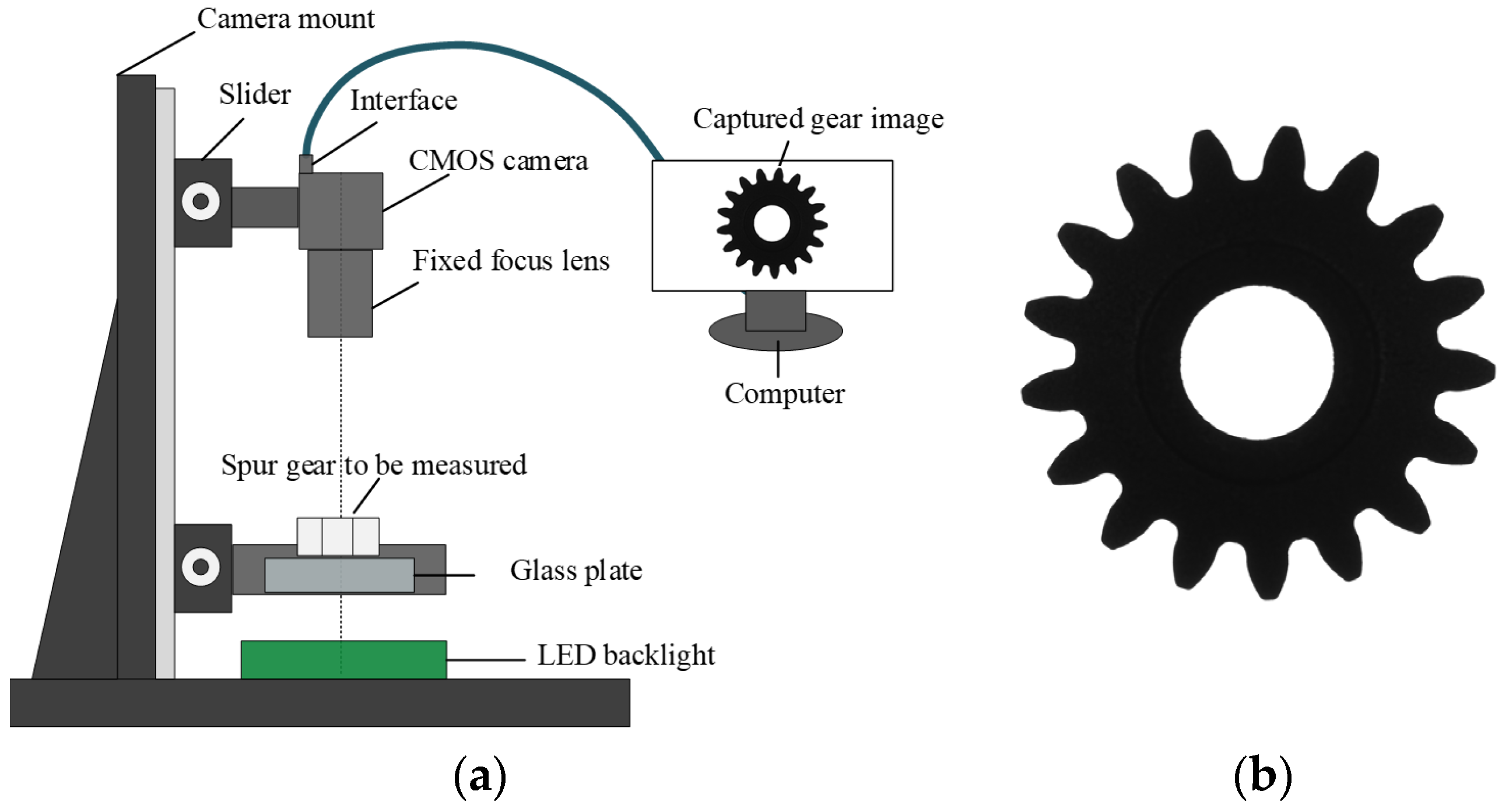
5.2.1. Experimental Setup
5.2.2. Measurement Results
5.3. Comparative Experiment between GVMS and P26
5.3.1. Comparison of Integrated Measurement Results
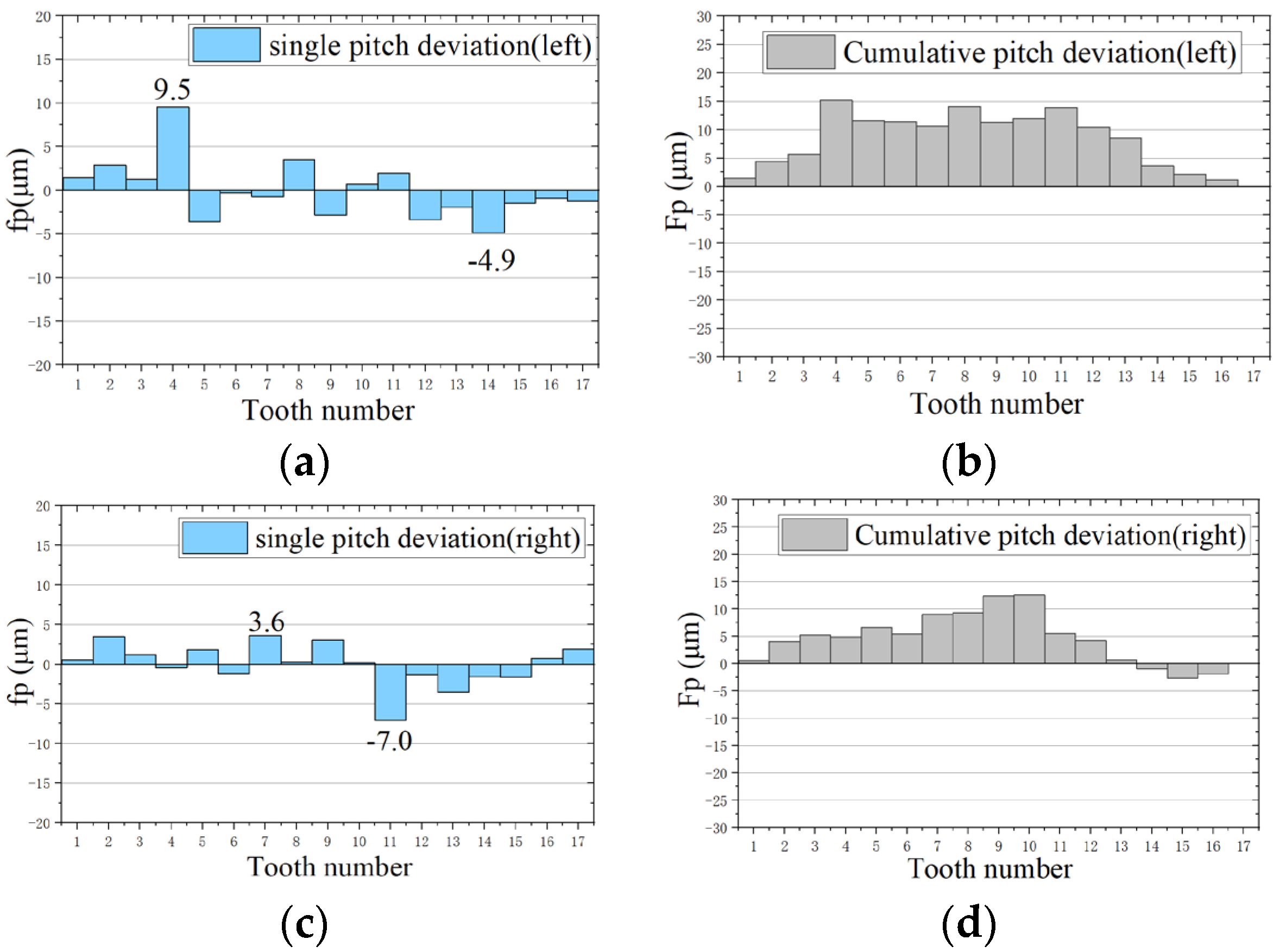
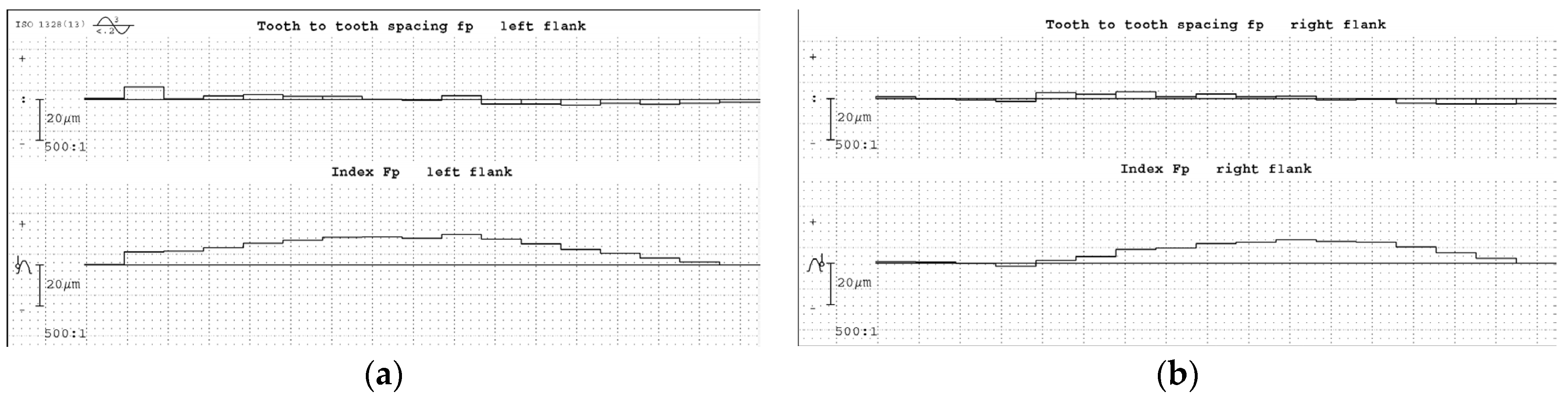
5.3.2. Comparison of Pitch Deviation Results
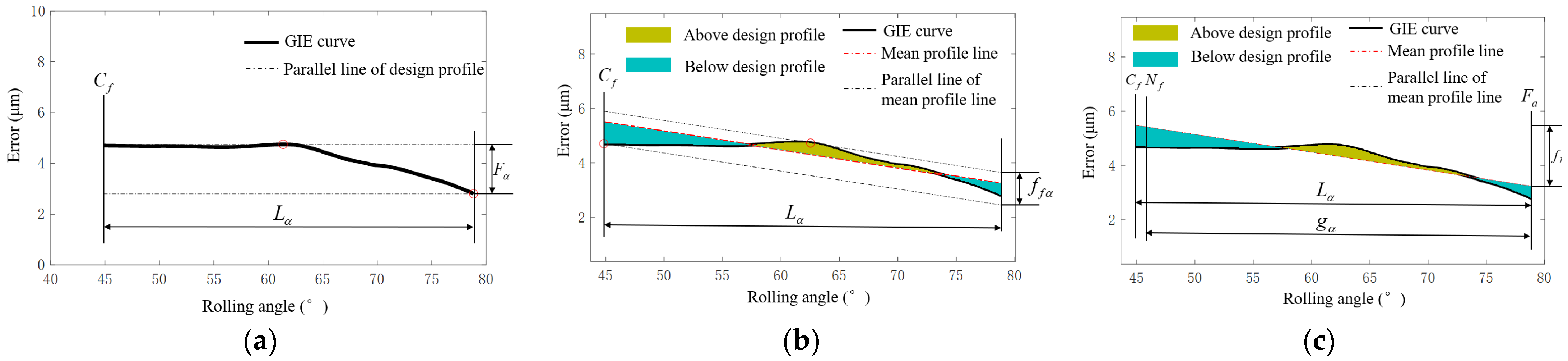
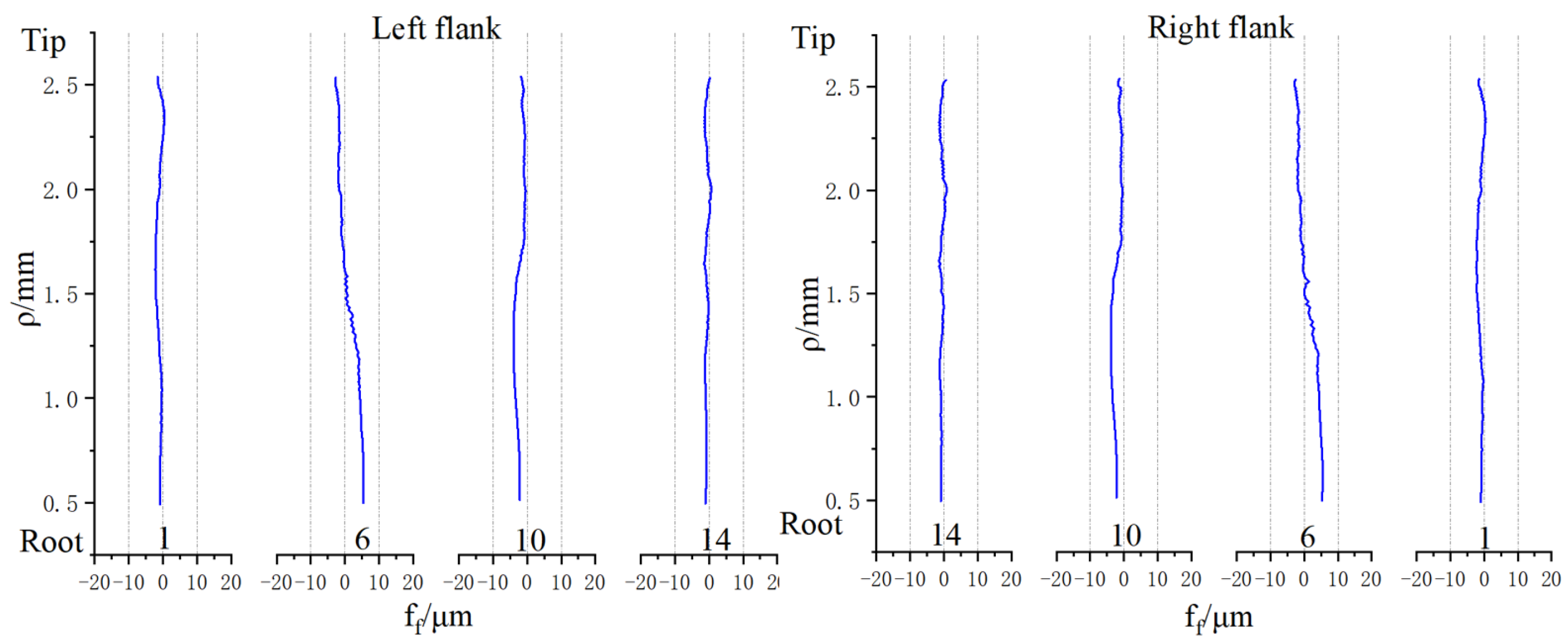
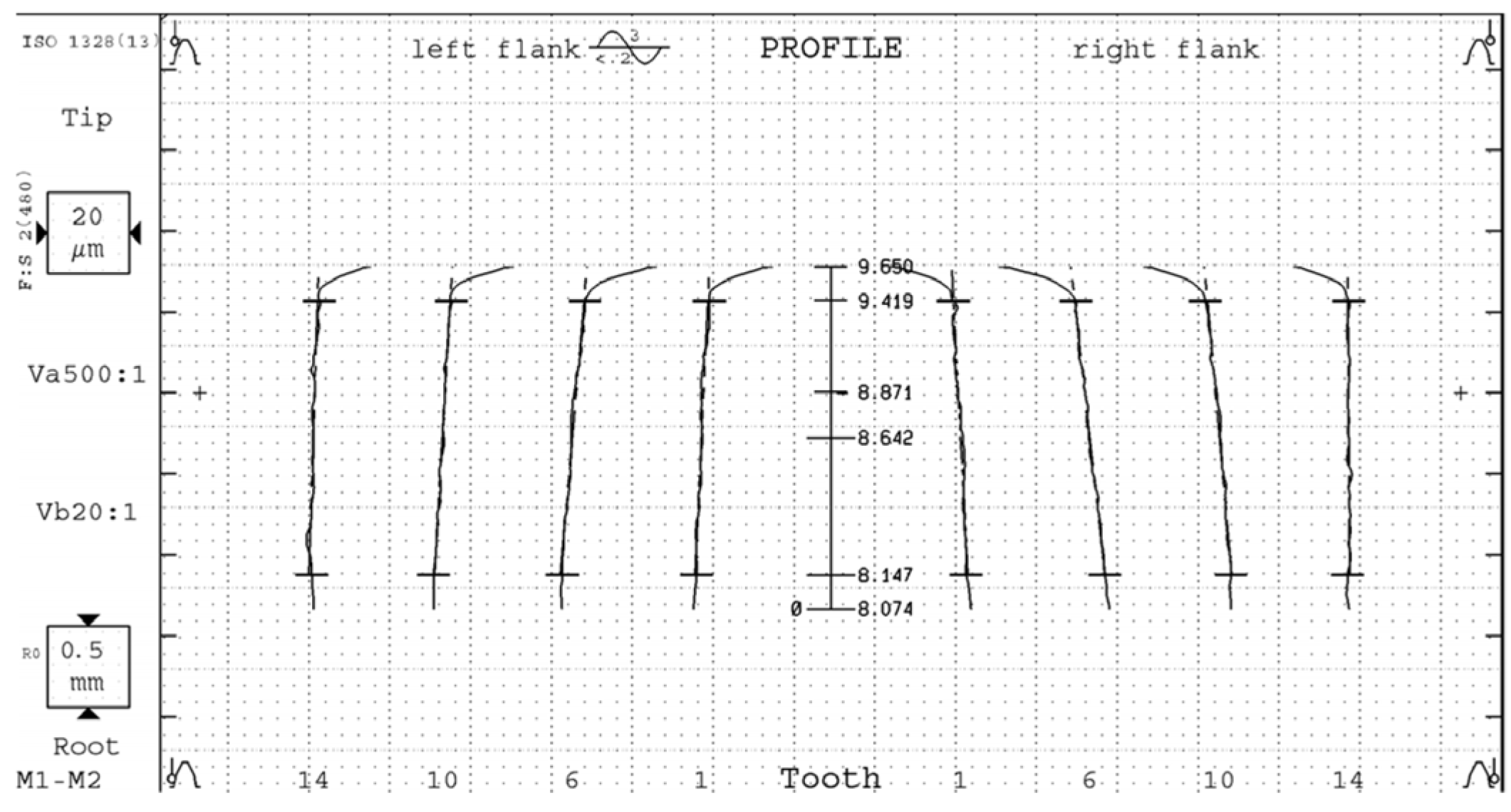
5.3.3. Comparison of Profile Deviation Results
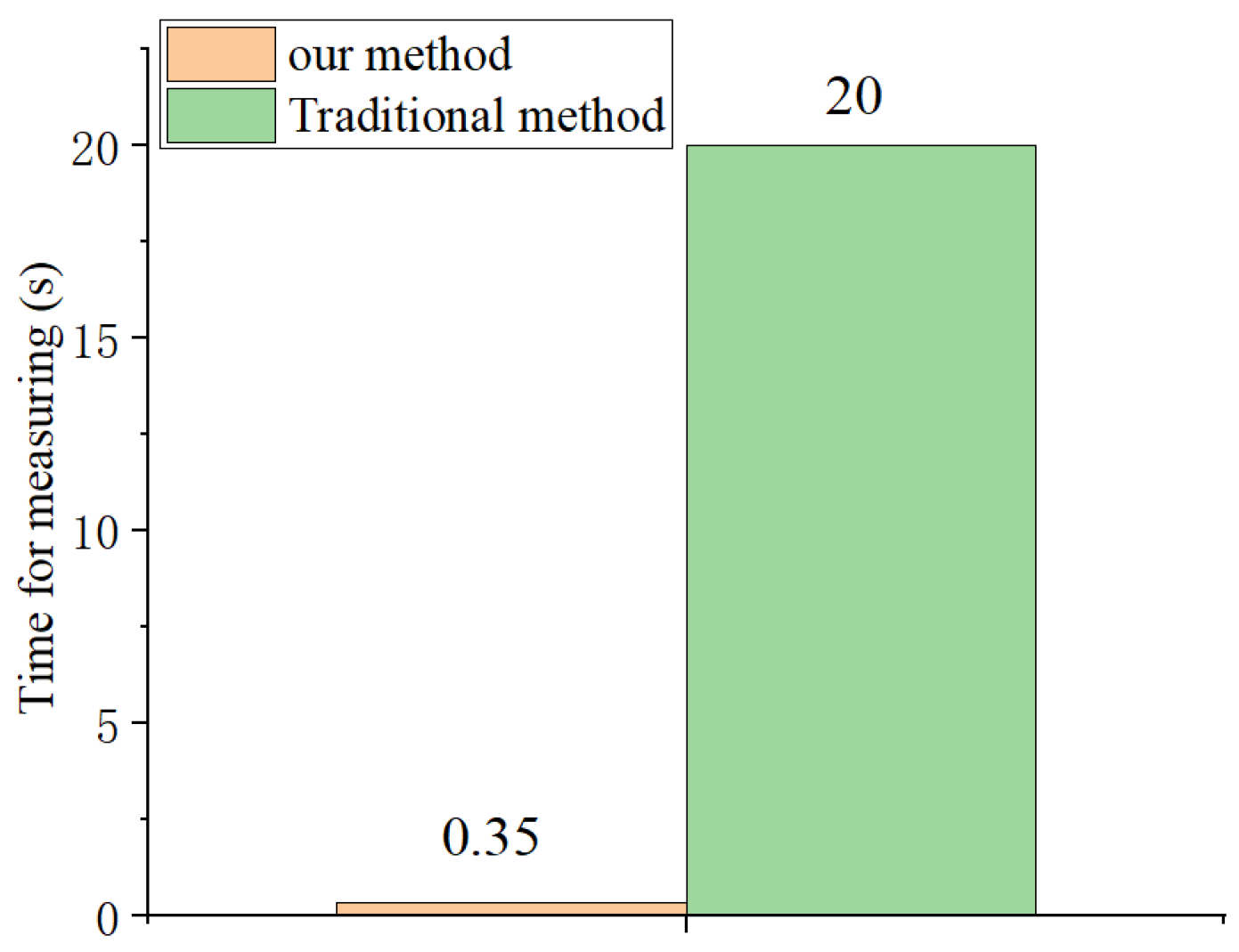
5.3.4. Measurement Speed Comparison
5.4. Application of Methods
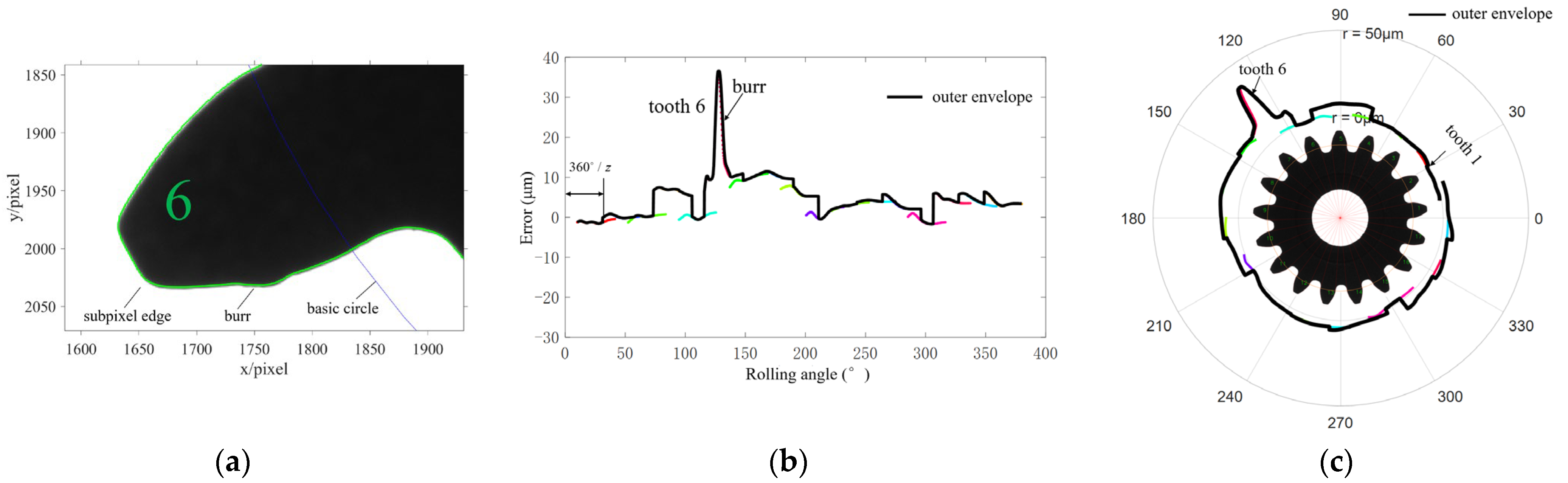
5.4.1. Detection of Tooth Face Burrs
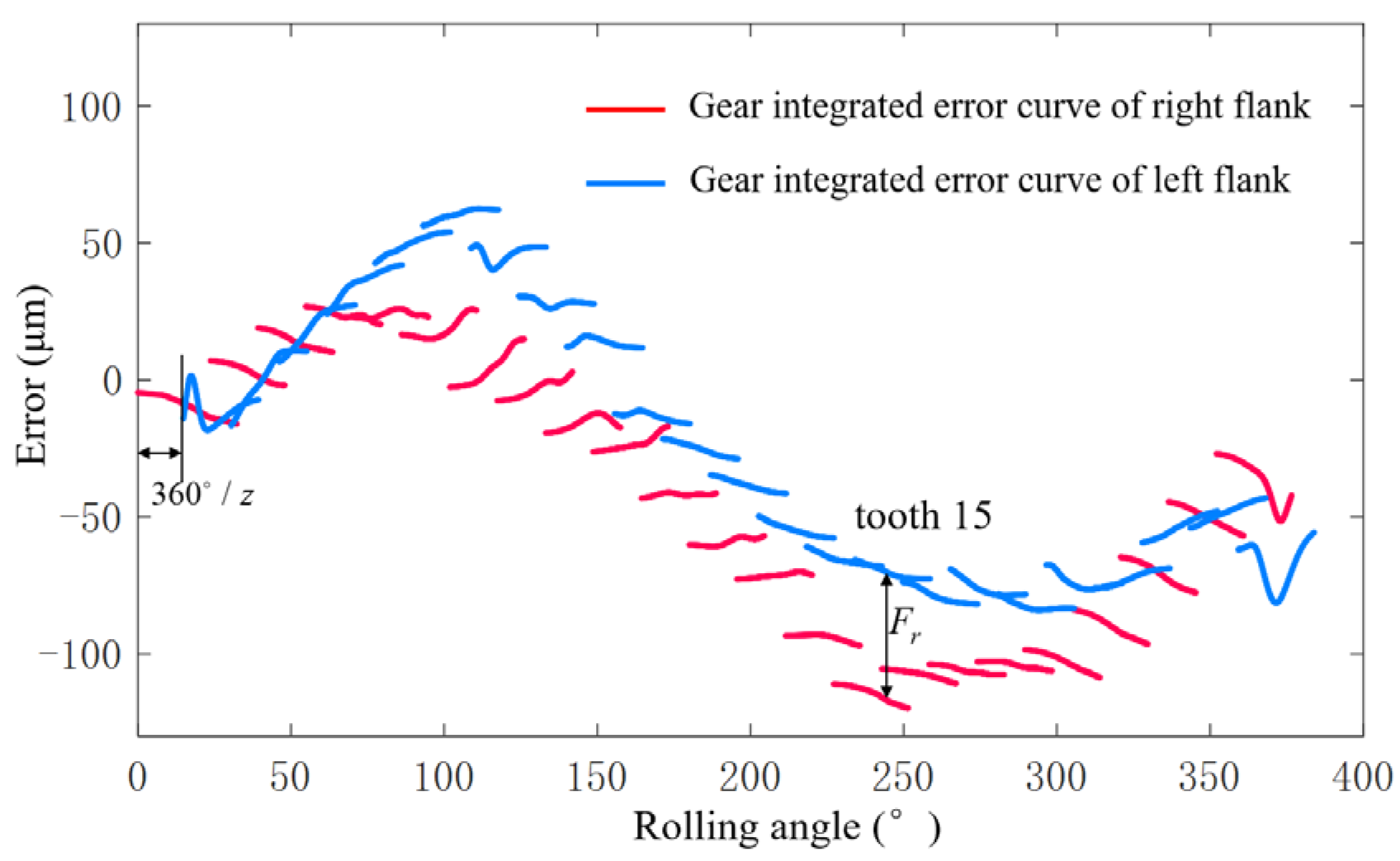
5.4.2. Detection of Gear Eccentricity
5.4.3. Analysis of Profile Modification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, Z.Y.; Yu, B.; Song, H.X.; Wang, X. Development of gear measurement technology in the last 20 years. China Mech. Eng. 2022, 33, 1009–1024. [Google Scholar]
- Goch, G.; Guenther, A.; Peng, Y.; Ni, K. Gear metrology—An update. CIRP Ann. Manuf. Technol. 2023, 72, 725–751. [Google Scholar] [CrossRef]
- Goch, G. Gear metrology. CIRP Ann. Manuf. Technol. 2023, 52, 659–695. [Google Scholar] [CrossRef]
- Goch, G.; Ni, K.; Peng, Y.; Guenther, A. Future gear metrology based on areal measurements and improved holistic evaluations. CIRP Ann. Manuf. Technol. 2017, 66, 469–474. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Wang, X.Y. Past, present and future of gear integrated error measurement technologies. Metrol. Meas. Technol. 2018, 38, 112–119. [Google Scholar]
- Wang, X.Y.; Shi, Z.Y.; Lin, J.C. Fast measurement method for pitch deviation based on full toothprofile information. Chin. J. Sci. Instrum. 2016, 37, 9. [Google Scholar]
- Wang, X.Y.; Shi, Z.Y.; Shu, Z.H. Different point contact error and correction method in gear integrated error measurement. J. Mech. Eng. 2017, 53, 166–175. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Fang, Y.M.; Wang, X.Y. Research progress of gear machine vision inspection instrument and technology. Laser Optoelectron. Prog. 2022, 59, 13. [Google Scholar]
- Wang, W.; Guan, F.; Ma, S.; Li, J. Measurement system of gear parameters based on machine vision. Meas. Control. 2015, 48, 242–248. [Google Scholar] [CrossRef]
- Irino, N.; Shimoike, M.; Mori, K.; Yamaji, I.; Mori, M. A vision-based machine accuracy measurement method. CIRP Ann. 2020, 69, 445–448. [Google Scholar] [CrossRef]
- Chen, M.J.; Wang, J.W. Research on the in-site measurement of spur gears based onmachine vision. J. Mach. Des. 2020, 37, 25–28. [Google Scholar]
- Moru, D.K.; Borro, D. A machine vision algorithm for quality control inspection of gears. Int. J. Adv. Manuf. Technol. 2020, 106, 105–123. [Google Scholar] [CrossRef]
- Duan, Z.Y.; Wang, N.; Zhao, W.Z.; Feng, B.Q. Sub-pixel edge location algorithm based on Gauss integral curved surface fitting. Chin. J. Sci. Instrum. 2017, 38, 219–225. [Google Scholar]
- 14. ISO 1328-1: 2013; Cylindrical Gears—ISO System of Flank Tolerance Classification—Part 1: Definitions and Allowable Values of Deviations Relevant to Flanks of Gear Teeth. ISO: Geneva, Switzerland, 2013.
- ISO/TR 10064-2:1996; Code of Inspection Practice—Part 2: Inspection Related to Radial Composite Deviations, Runout, Tooth Thickness and Backlash. ISO: Geneva, Switzerland, 1996.
- Shi, Z.Y.; Wang, X.Y.; Yu, B. New method to determine the profile evaluation area in gear integrated error measurement. J. Mech. Eng. 2017, 53, 34–42. [Google Scholar] [CrossRef]
- Haralick, R.M. Digital step edges from zero crossing of second directional derivatives. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 26, 211–229. [Google Scholar] [CrossRef] [PubMed]
- Canny, J. A Computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–697. [Google Scholar] [CrossRef] [PubMed]
- Steger, C. An unbiased detector of curvilinear structures. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 113–125. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Wang, X.Y. Research on Fundamental Theory & Its Practice of Gear Integrated Error Measurement; Beijing University of Technology: Beijing, China, 2017. [Google Scholar]





| Component | Parameters |
|---|---|
| Camera | CMOS, GigE interface, 5472 × 3648 px, 1″ target surface |
| Lens | Magnification: 0.5; distortion: <0.006%; resolution: 7.9 μm |
| Light source | LED surface light source |
| Pixel equivalent | 4.76 μm/pixel |
| Gear parameters | Powder metallurgy spur gears; number of teeth: 17; modulus: 0.5 mm; pressure angle: 20° |
| Items | Right-Hand Tooth Flank | Left-Hand Tooth Flank | ||||
|---|---|---|---|---|---|---|
| GVMS | P26 | Error | GVMS | P26 | Error | |
| 20.8 | 15.5 | 5.3 | 22.7 | 18.8 | 3.9 | |
| 4.5 | 3.3 | 1.2 | 6.3 | 3.4 | 2.9 | |
| 5.5 | 7.3 | −1.8 | 6.2 | 5.7 | 0.5 | |
| 2.5 | 1.5 | 1.0 | 2.9 | 1.2 | 1.7 | |
| 3.5 | −7.3 | −10.8 | 3.7 | −5.8 | 9.5 | |
| 15.1 | 12.9 | 2.2 | 15.2 | 14.9 | 0.3 | |
| 7.0 | 7.4 | −0.4 | 9.5 | 11.1 | −1.6 | |
| 0.2 | 0.1 | 0.1 | 0.3 | 0.1 | 0.2 | |
| 10.1 | 10.3 | −0.2 | 11.5 | 10.6 | 0.9 | |
| 0.3 | 0.1 | 0.2 | 0.2 | 0.1 | 0.1 | |
| Items | Tooth Flank | GVMS | P26 | Error |
|---|---|---|---|---|
| (μm) | left | 9.5 | 11.1 | −1.6 |
| right | 7.0 | 7.4 | −0.4 | |
| (μm) | left | 15.2 | 14.9 | 0.3 |
| right | 15.1 | 12.9 | 2.2 |
| Tooth Number | Tooth Flank | GVMS | P26 | Error |
|---|---|---|---|---|
| 1 | left | 2.4 | 3.5 | −1.1 |
| right | 2.0 | 3.4 | −1.4 | |
| 6 | left | 3.2 | 5.7 | −2.5 |
| right | 3.0 | 7.3 | −3.3 | |
| 10 | left | 2.6 | 4.5 | −1.9 |
| right | 2.8 | 6.4 | −3.6 | |
| 14 | left | 3.2 | 3.5 | −0.3 |
| right | 2.1 | 1.2 | 0.9 |
| Tooth Number | Tooth Flank | GVMS | P26 | Error |
|---|---|---|---|---|
| 1 | left | 2.5 | 1.5 | 1.0 |
| right | 2.3 | 1.5 | 0.8 | |
| 6 | left | 3.1 | 1.2 | 1.9 |
| right | 1.5 | 0.9 | 0.6 | |
| 10 | left | 2.2 | 1.1 | 1.1 |
| right | 0.9 | 1.2 | −0.3 | |
| 14 | left | 3.4 | 1.7 | 1.7 |
| right | 1.3 | 1.2 | 0.1 |
| Tooth Number | Tooth Flank | GVMS | P26 | Error |
|---|---|---|---|---|
| 1 | left | −0.3 | −3.1 | 2.8 |
| right | −2.2 | −3.6 | 1.4 | |
| 6 | left | 3.8 | −5.8 | 2.0 |
| right | −3.4 | −7.6 | 3.2 | |
| 10 | left | −1.2 | −3.9 | 2.7 |
| right | −2.1 | −6.0 | 3.9 | |
| 14 | left | −3.2 | −2.1 | −1.1 |
| right | 2.5 | −0.4 | 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Shi, Z.; Sun, Y.; Zhang, P. Gear Integrated Error Determination Using the Gaussian Template Convolution-Facet Method. Appl. Sci. 2024, 14, 1004. https://doi.org/10.3390/app14031004
Fang Y, Shi Z, Sun Y, Zhang P. Gear Integrated Error Determination Using the Gaussian Template Convolution-Facet Method. Applied Sciences. 2024; 14(3):1004. https://doi.org/10.3390/app14031004
Chicago/Turabian StyleFang, Yiming, Zhaoyao Shi, Yanqiang Sun, and Pan Zhang. 2024. "Gear Integrated Error Determination Using the Gaussian Template Convolution-Facet Method" Applied Sciences 14, no. 3: 1004. https://doi.org/10.3390/app14031004
APA StyleFang, Y., Shi, Z., Sun, Y., & Zhang, P. (2024). Gear Integrated Error Determination Using the Gaussian Template Convolution-Facet Method. Applied Sciences, 14(3), 1004. https://doi.org/10.3390/app14031004






