Carbon Quota Allocation Prediction for Power Grids Using PSO-Optimized Neural Networks
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Status of Carbon Emissions in the Power Sector
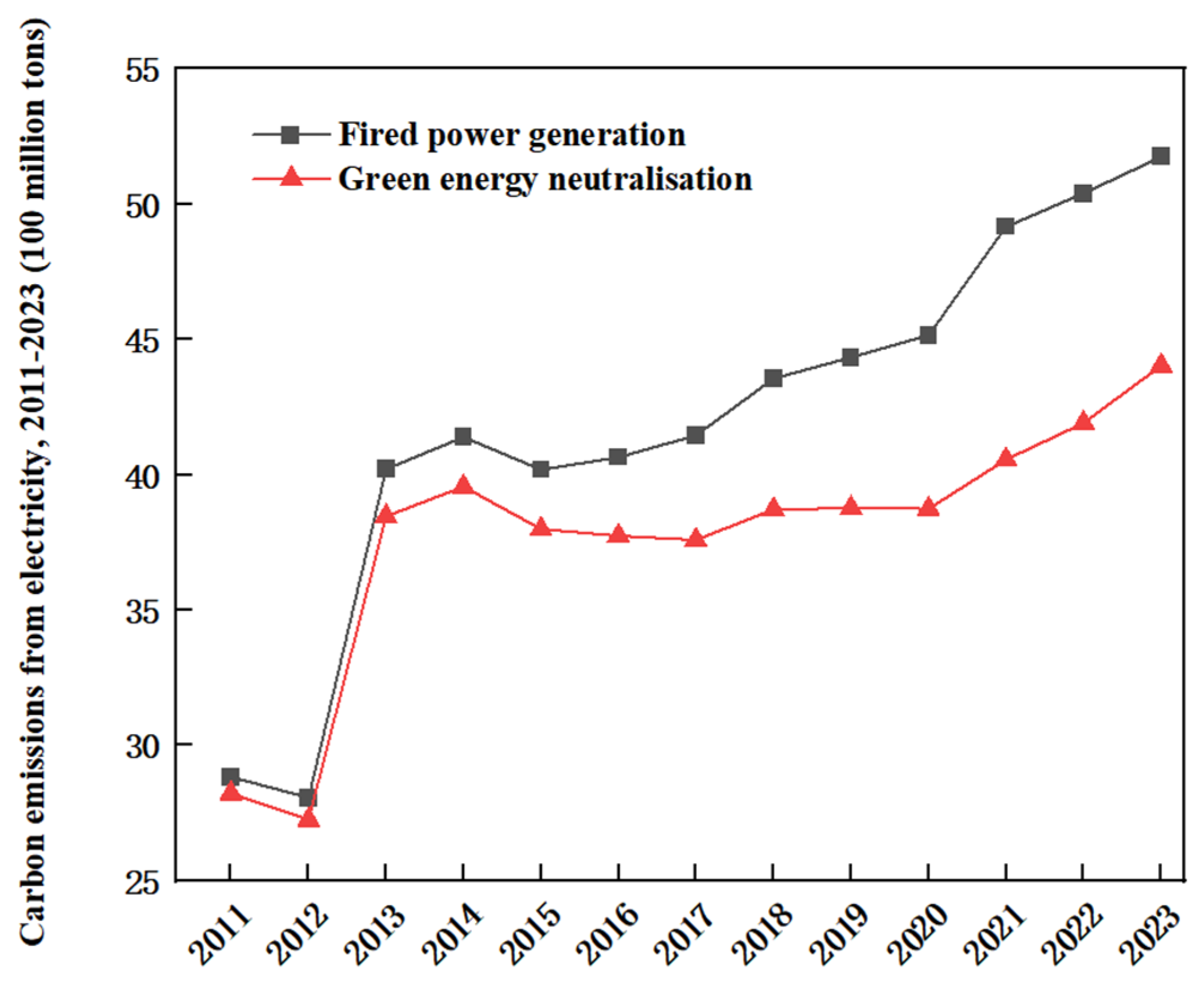
3.1.1. CO2 Emission Measurement in the Power Sector
- Thermal power generation CO2 emissions
- 2.
- Green energy neutralizes carbon emissions
3.1.2. Indicator Characteristics
3.2. Model Building and Optimization
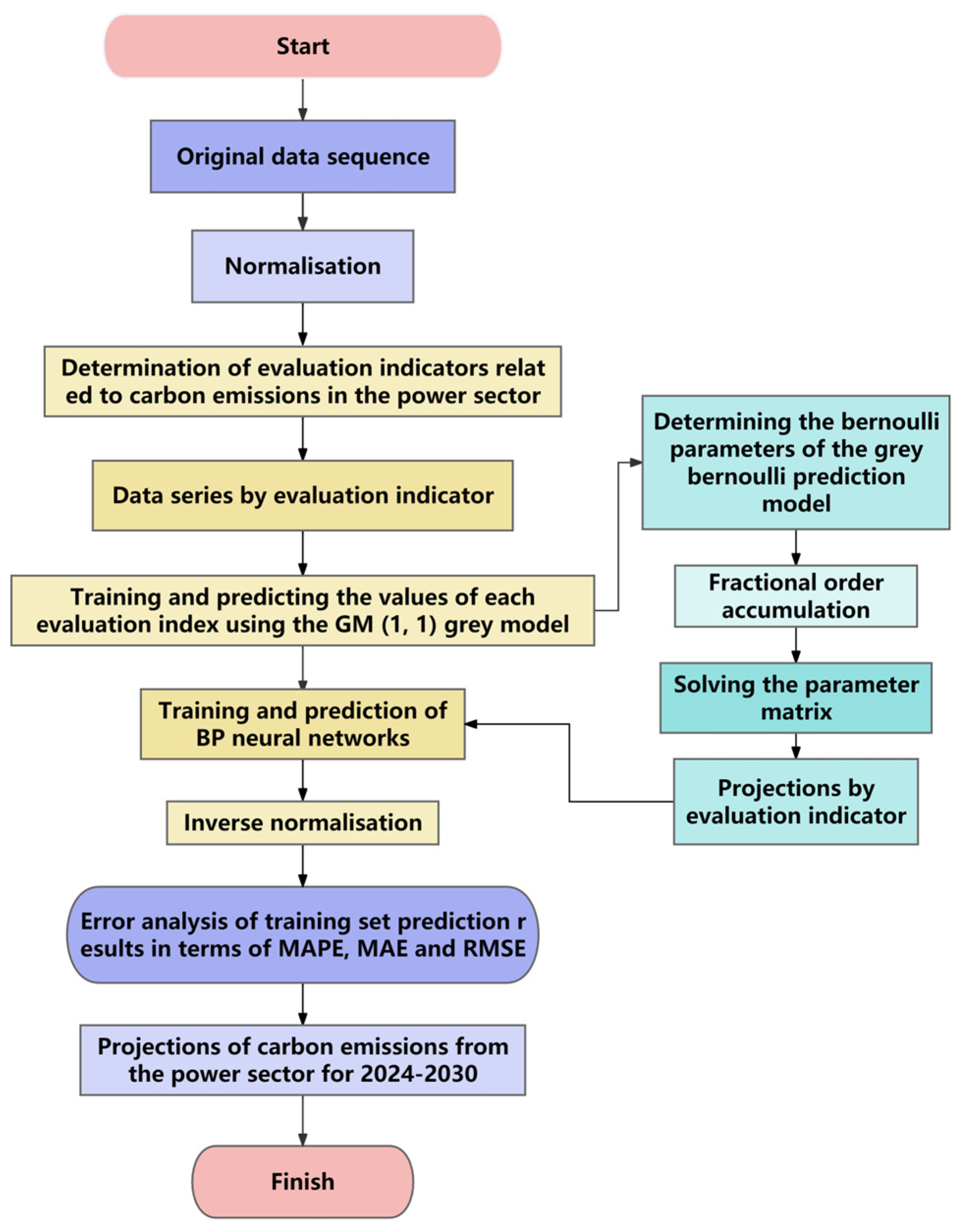
3.2.1. GM(1,1) Module
- Processing of raw carbon emissions data
- 2.
- Construction of GM(1,1) primitive form. Assuming that has an approximate exponential variation rule, then can be regarded as a function of time t , then, the whitened form of GM(1,1) is as follows:
- 3.
- Establishment of the data matrix and data vector of the grey Bernoulli prediction model for carbon emissions. In the calculation process, it is common to use and to represent the matrices.
- 4.
- Construct the time-response function and calculate the predicted values
- 5.
- Accuracy test of carbon emission projections
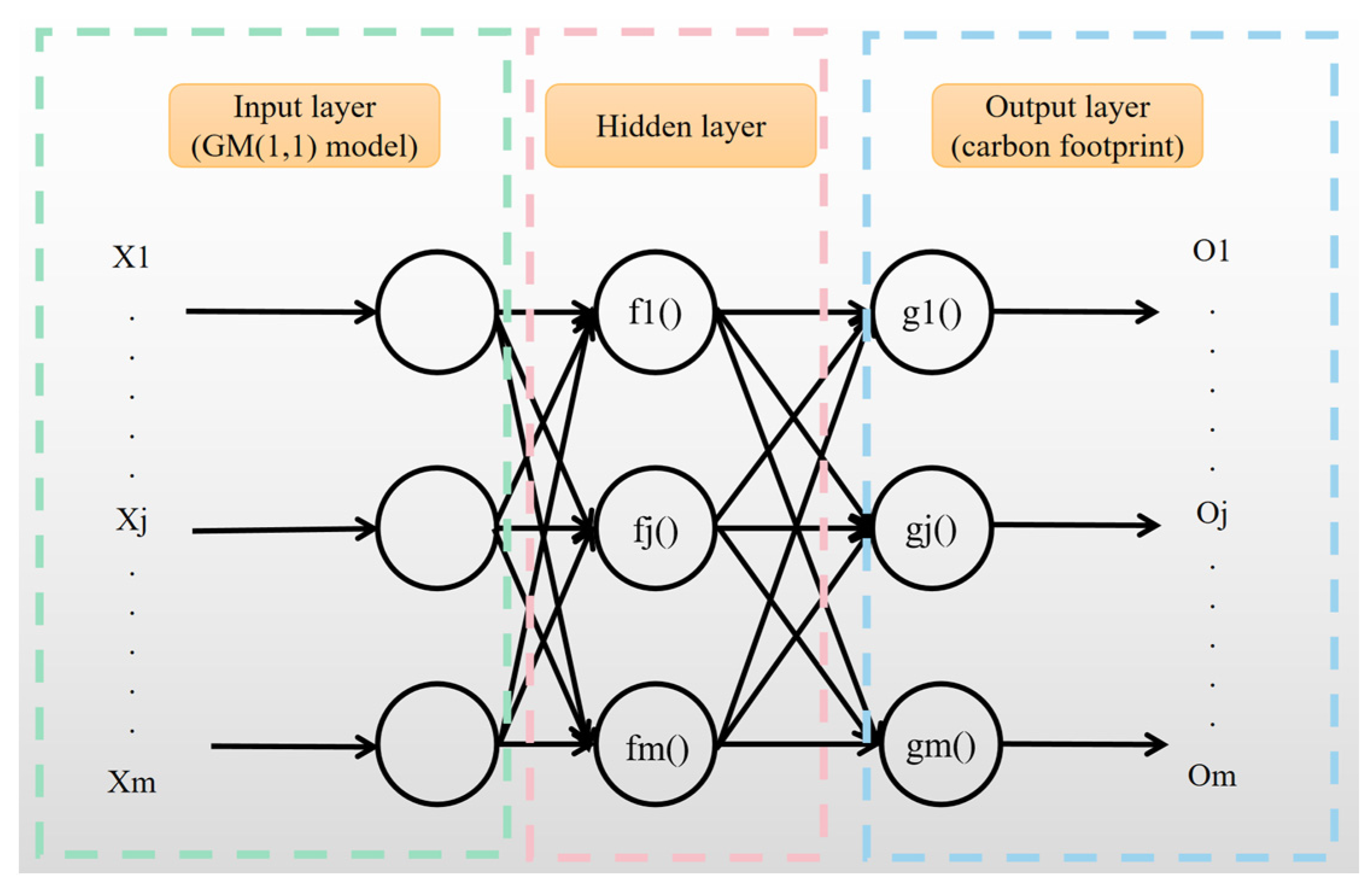
3.2.2. BPNN Module
- Neural network algorithm flow
- 2.
- PSO optimization algorithm
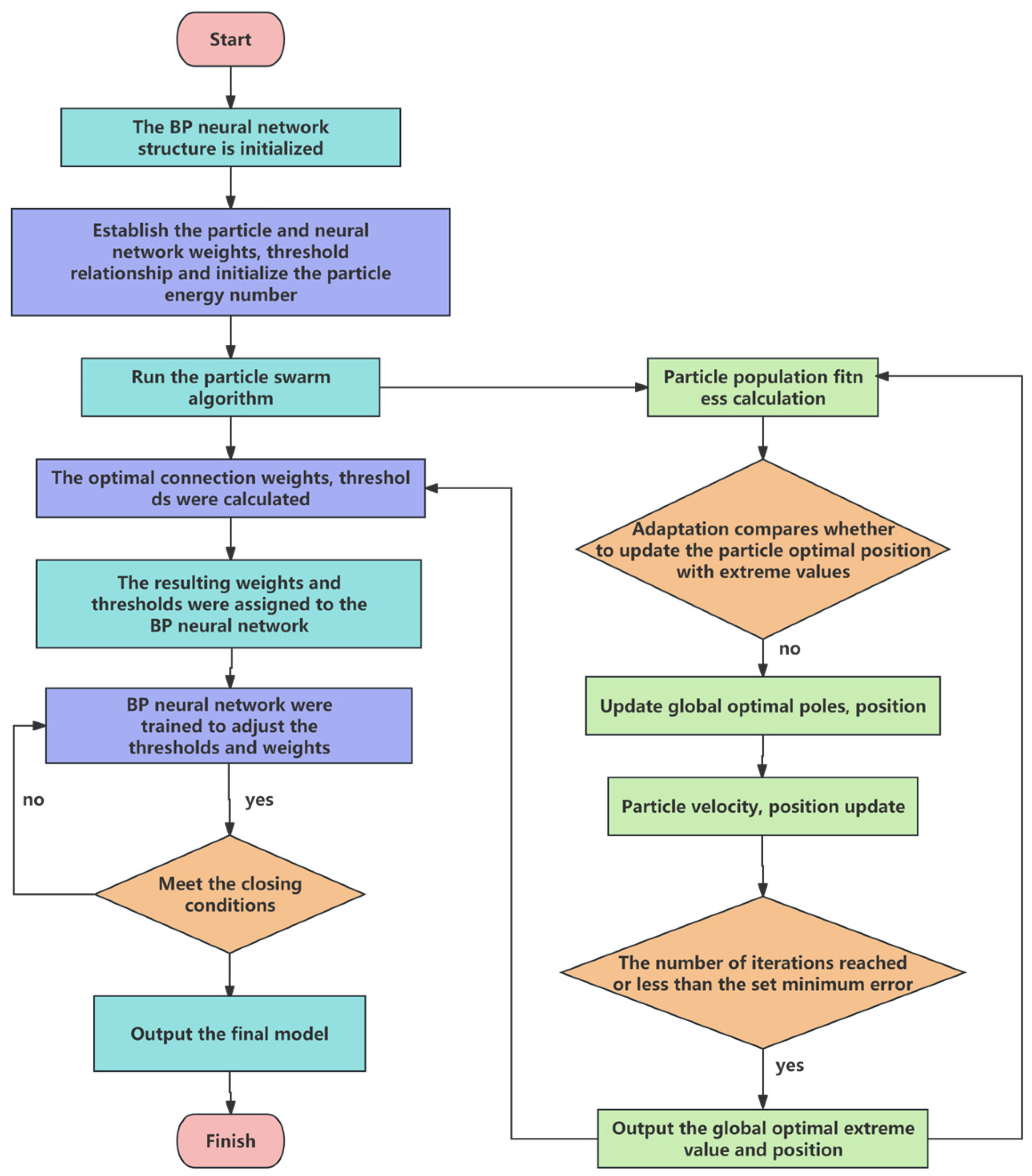
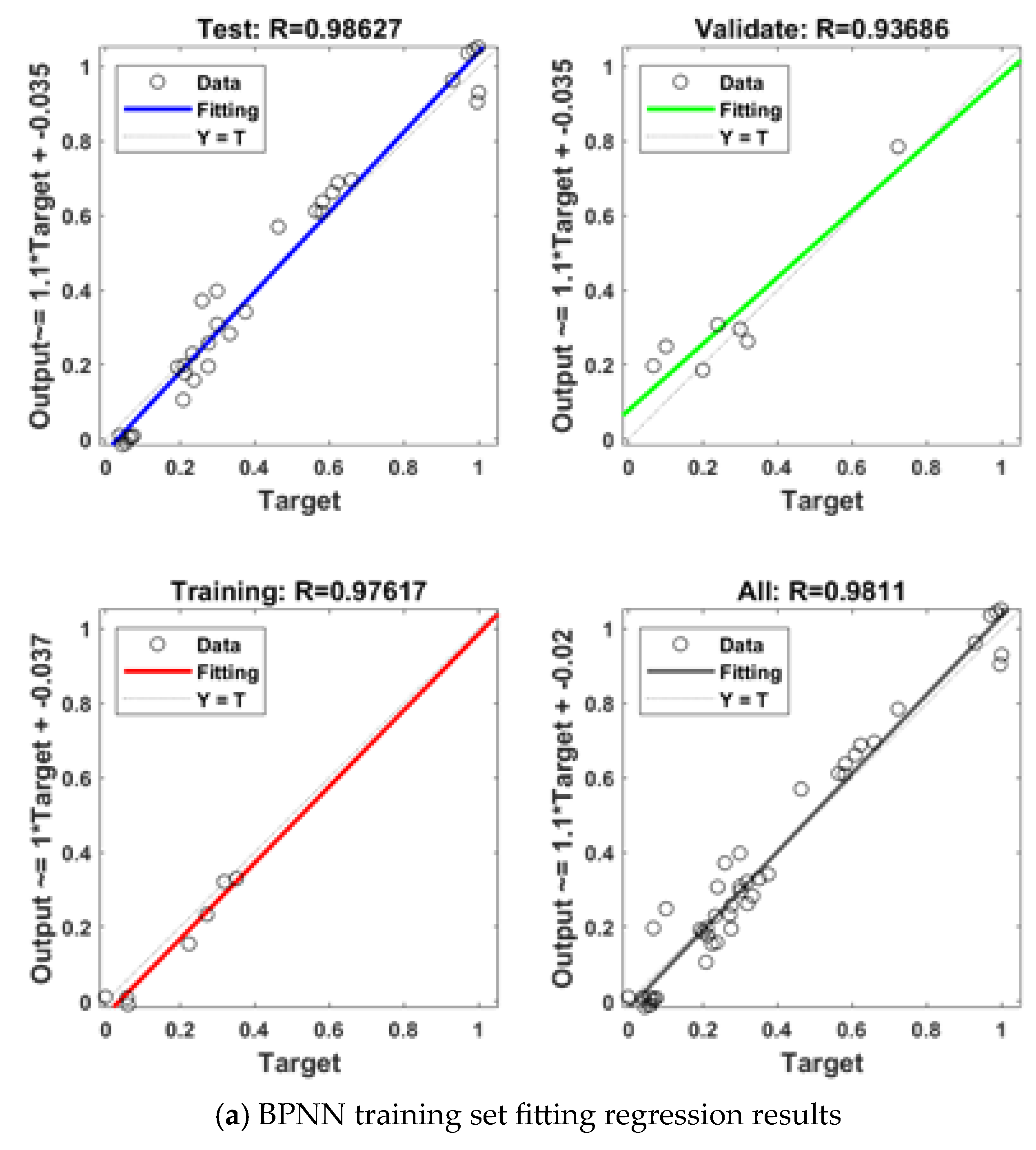
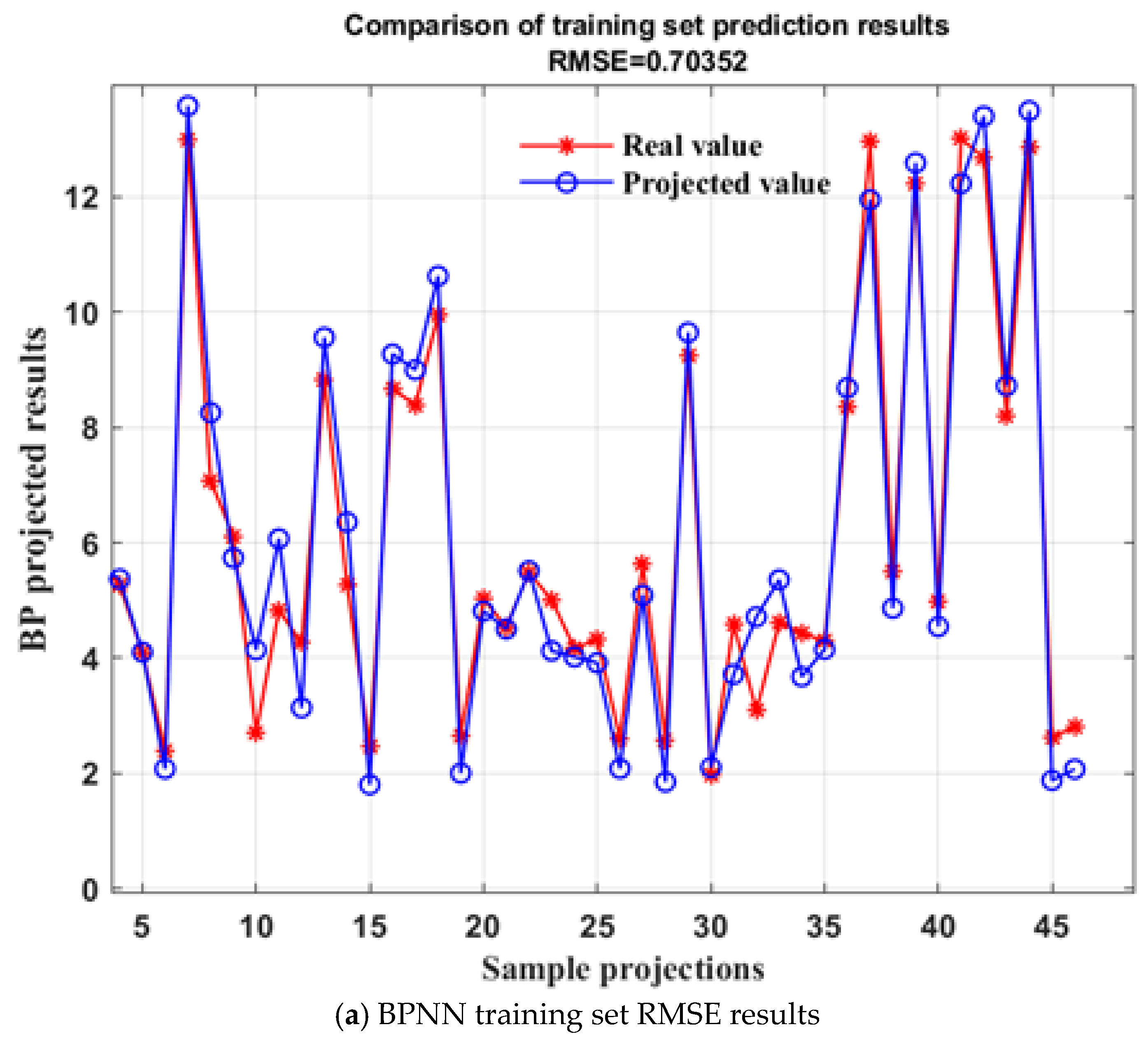
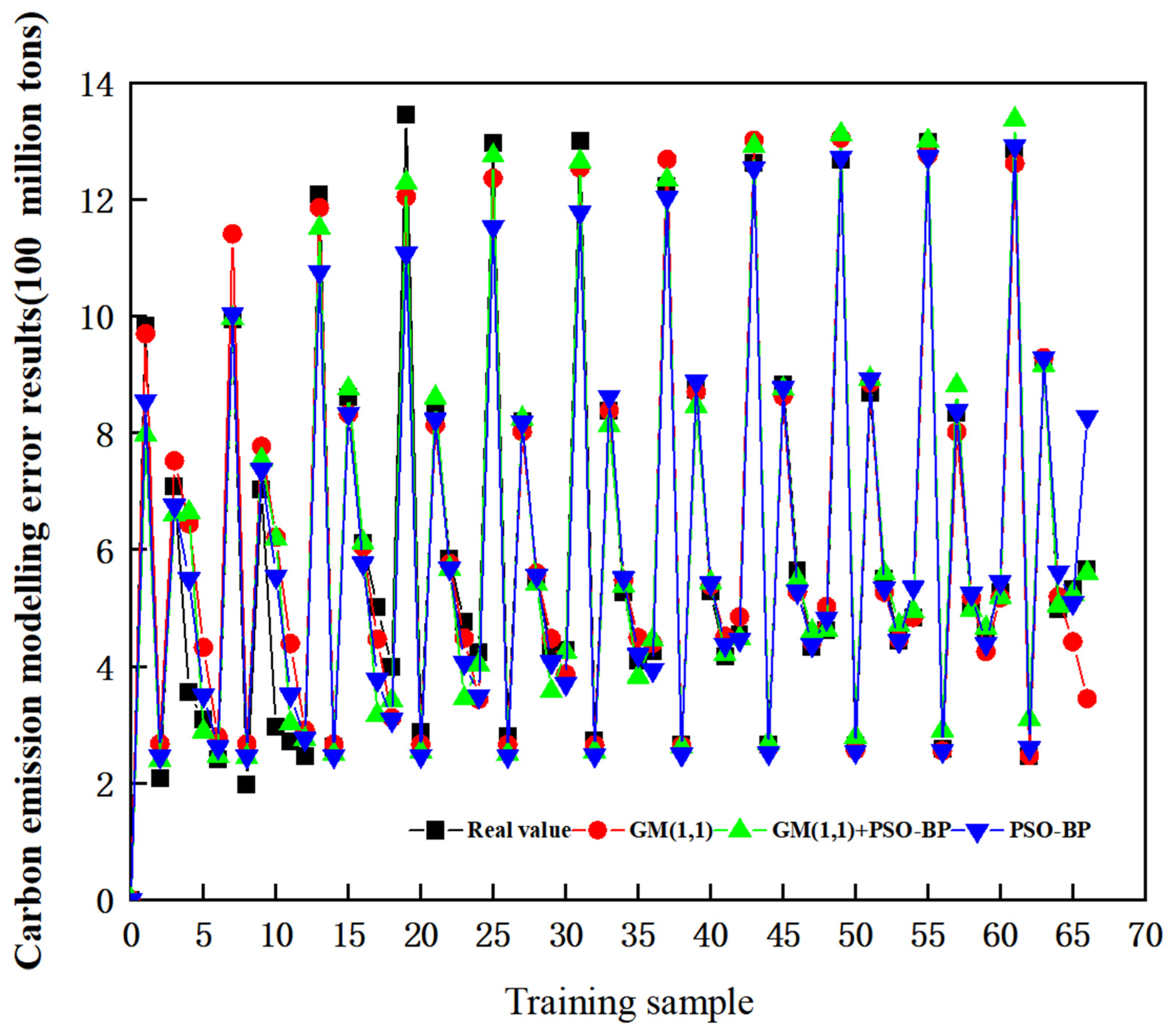
3.2.3. Combined Prediction Model Accuracy Test
- 1.
- GM(1,1) module accuracy test
- 2.
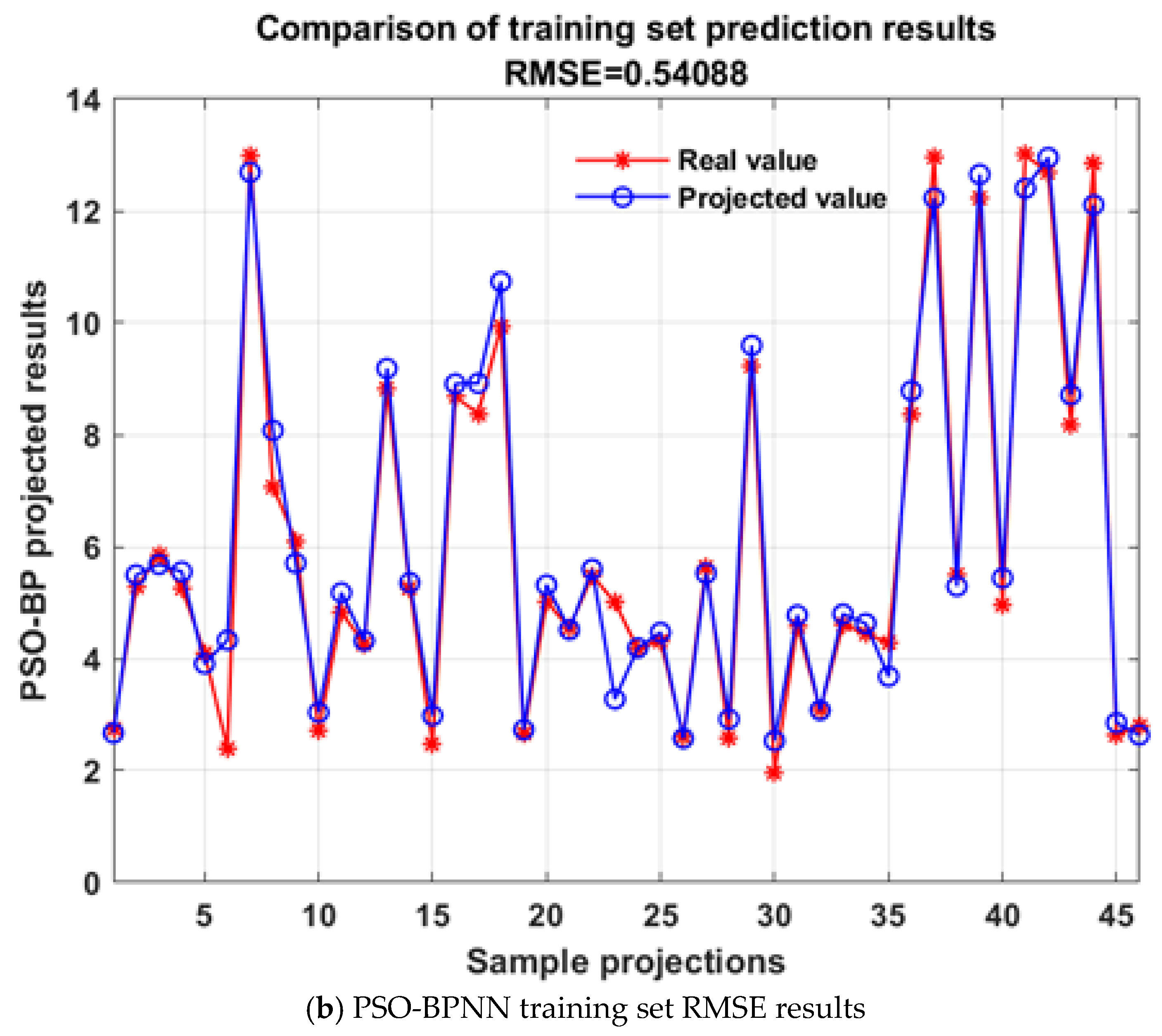
- Neural Network Module Accuracy Test
4. Result and Discussion
4.1. Projected Result Analysis
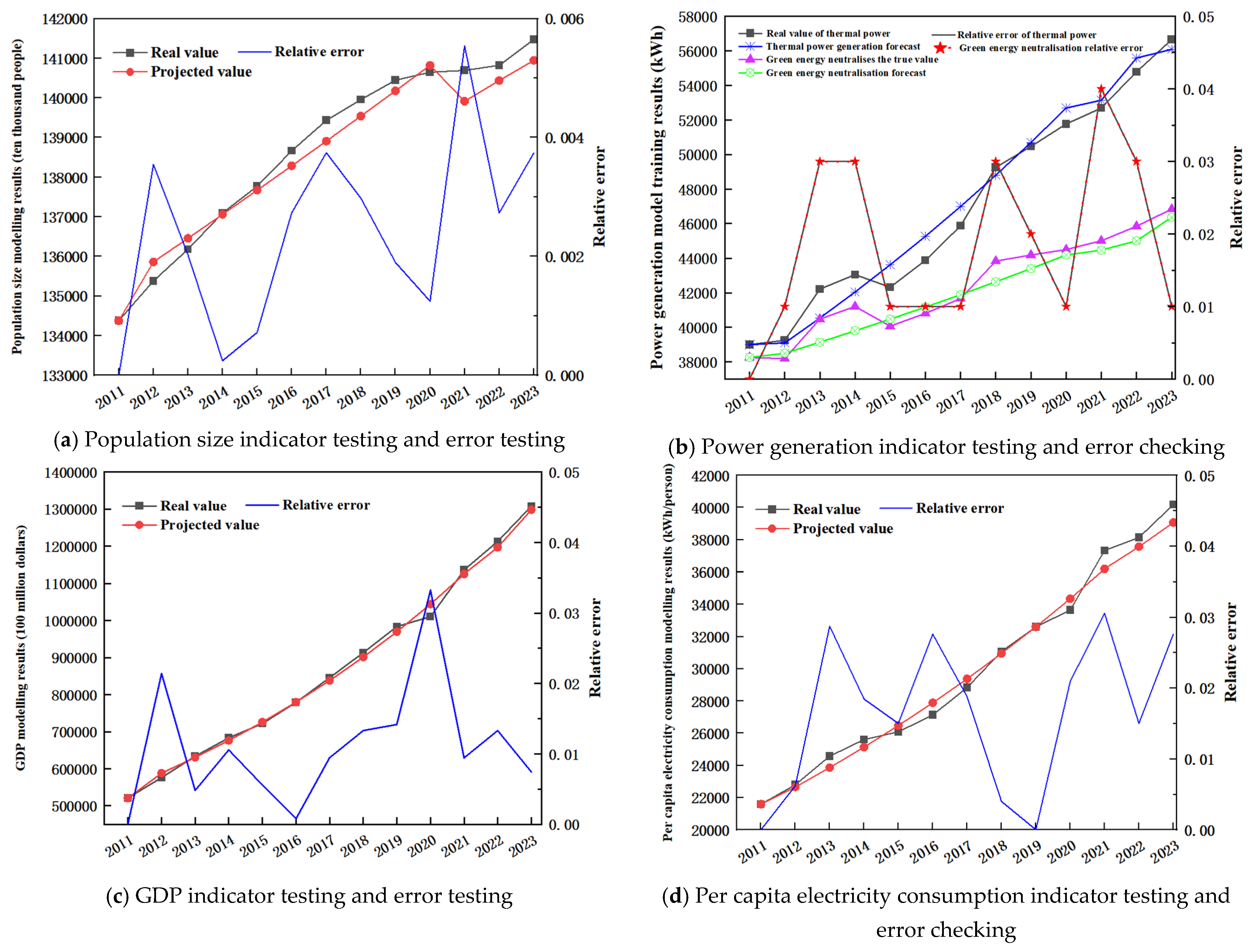
4.1.1. Projected Results of Indicators
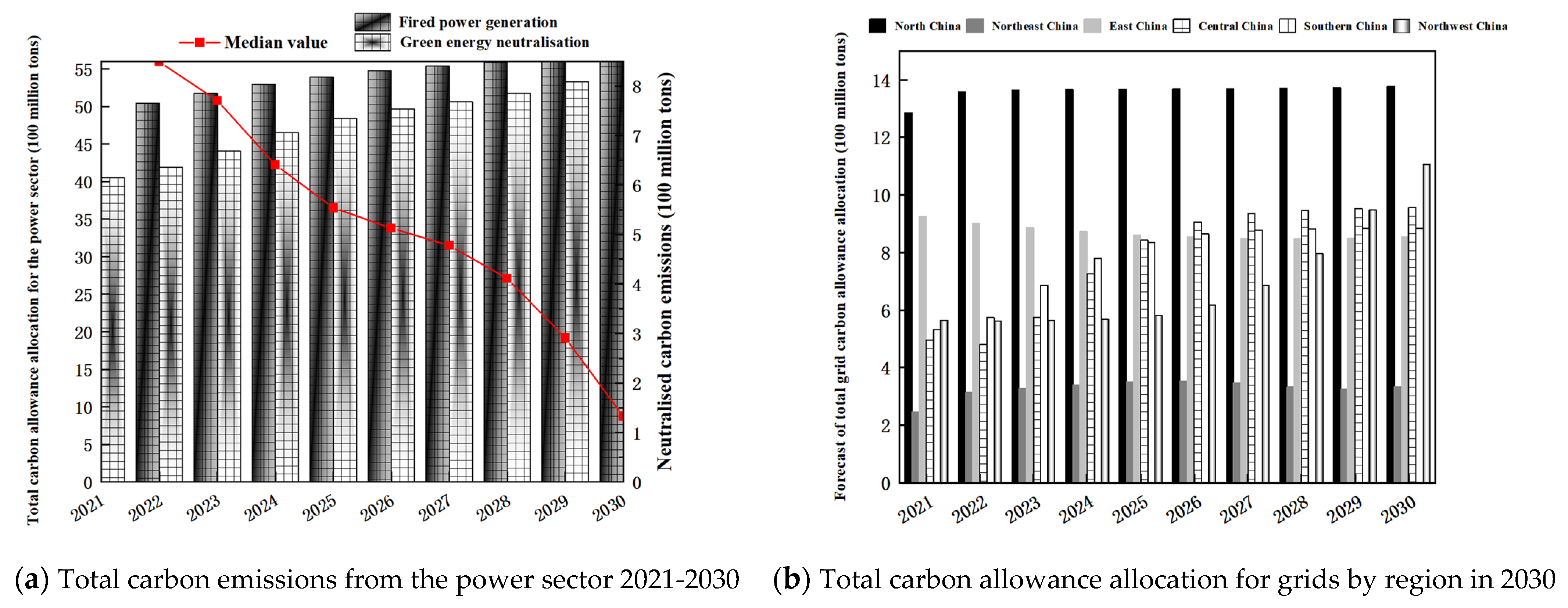
4.1.2. Results of Initial Quota Projections
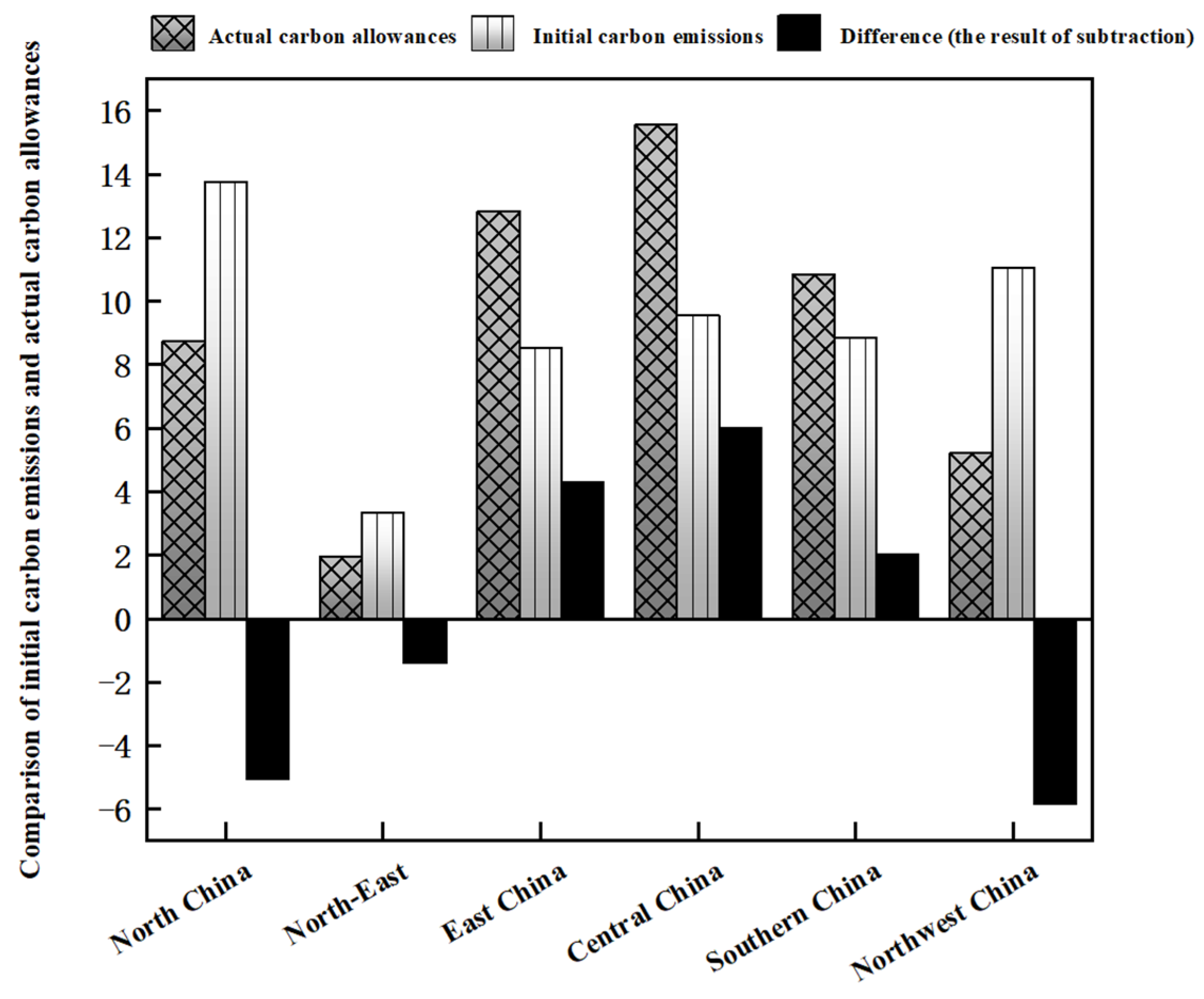
4.2. Carbon Allowance Reallocation Results
5. Conclusions
- 1.
- The PSO algorithm is integrated into the traditional BP neural network to perform a global optimization search for the initial weights and thresholds. This approach successfully helps the BP neural network escape local extrema. The performance metrics of the PSO-BPNN optimization algorithm are significantly higher than those of the traditional BP algorithm, and its overall fit surpasses that of other algorithms.
- 2.
- Given that carbon emissions are influenced by multiple factors, such as regional economic development, power structure, and technology level, rather than a single factor, the GM(1,1) algorithm is incorporated into the neural network. Testing revealed that the GM(1,1)-PSO-BPNN hybridized model achieves a prediction accuracy of 99.07% for CO2 emissions in the power industry, significantly surpassing the accuracy of single learning algorithms. Thus, the combined model can be effectively used as a carbon emission prediction tool for the power sector.
- 3.
- Based on the projections of the combined model, all four quantitative indicators related to carbon emissions are expected to show an upward trend from 2024 to 2030. While China’s power generation, per capita electricity consumption, and GDP are growing rapidly, population growth is slowing and gradually approaching saturation. The study on the influence of green energy on CO2 emissions indicates that China’s power sector can reduce its peak carbon emissions in 2030 by 133 million tons, lowering them to 5511.46 million tons during and after green energy generation.
- 4.
- Due to the complexity and variability of the internal structure of the power system, it is challenging for government departments to delineate the actual emission reduction responsibilities between power-generating and power-using regions. Therefore, shared responsibility coefficients are adopted to mitigate the risk of “carbon transfer” and to determine the actual emission reduction responsibility coefficients for each regional power grid. Based on model development and the adjustment of these responsibility coefficients, this paper proposes a fair and reasonable carbon quota allocated program for the power sector.
6. Research Shortcomings and Prospects
- 1.
- As this study adopts the GM(1,1) model to predict the carbon emission-related indicators of the electric power industry, the model itself adopts the exponential function growth, which grows too fast, leading to further research on whether the related indicators can reach that growth rate in the future.
- 2.
- In the carbon emissions measurement, taking into account the impact of green energy, due to regional differences, the adoption of green energy power generation technology level is limited in each region, making it difficult to obtain energy neutralization data, and has certain limitations in analyzing the impact of green energy on regional carbon emissions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Daaboul, J.; Moriarty, P.; Honnery, D. Net green energy potential of solar photovoltaic and wind energy generation systems. J. Clean. Prod. 2023, 415, 137806. [Google Scholar] [CrossRef]
- Buestán-Andrade, P.A.; Peñacoba-Yagüe, M.; Sierra-García, J.E.; Santos, M. Wind Power Forecasting with Machine Learning Algorithms in Low-Cost Devices. Electronics 2024, 13, 1541. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, P. Impact of Permit Allocation on Cap-and-trade System Performance under Market Power. Energy J. 2020, 41, 215–231. [Google Scholar] [CrossRef]
- Bai, M.R.; Li, C.B. Research on the allocation scheme of carbon emission allowances for China’s provincial power grids. Energy 2024, 299, 131551. [Google Scholar] [CrossRef]
- Groh, E.; Ziegler, A. On self-interested preferences for burden sharing rules: An econometric analysis for the costs of energy policy measures. Energy Econ. 2018, 74, 417–426. [Google Scholar] [CrossRef]
- Rose, A. Reducing conflict in global warming policy-the potential of equity as a unifying principle. Energy Policy 1990, 18, 927–935. [Google Scholar] [CrossRef]
- Pozo, C.; Galán-Martín, Á.; Reiner, D.M.; Mac Dowell, N.; Guillén-Gosálbez, G. Equity in allocating carbon dioxide removal quotas. Nat. Clim. Chang. 2020, 10, 640–646. [Google Scholar] [CrossRef]
- Tian, Y.; Chen, C. China’s Provincial Carbon Emission Reduction Reward and Punishment Programme Based on Carbon Emission Right Allocation. Chin. J. Popul. Resour. 2020, 30, 54–62. [Google Scholar]
- Jiang, M.X.; Zhu, B.Z.; Chevallier, J.; Xie, R. Allocating provincial CO2 quotas for the Chinese national carbon program. Aust. J. Agr. Resour. Ec. 2018, 62, 457–479. [Google Scholar] [CrossRef]
- Cai, W.G.; Ye, P.Y. A more scientific allocation scheme of carbon dioxide emissions allowances: The case from China. J. Clean. Prod. 2019, 215, 903–912. [Google Scholar] [CrossRef]
- Fang, M.Y.; Tan, K.S.; Wirjanto, T. Valuation of carbon emission allowance options under an open trading phase. Energy Econ. 2024, 131, 107351. [Google Scholar] [CrossRef]
- Li, J.J.; Tian, Y.J.; Zhang, Y.L.; Xie, K.C. Assessing spatially multistage carbon transfer in the life cycle of energy with a novel multi-flow and multi-node model: A case of China’s coal-to-electricity chain. J. Clean. Prod. 2022, 339, 130699. [Google Scholar] [CrossRef]
- Li, Y.W.; Yang, X.X.; Du, E.S.; Liu, Y.L.; Zhang, S.X.; Yang, C.; Zhang, N.; Liu, C. A review on carbon emission accounting approaches for the electricity power industry. Appl. Energy 2024, 359, 122681. [Google Scholar] [CrossRef]
- Von, W.G.; Cullenward, D.; Mastrandrea, M.D.; Weyant, J. Accounting for the greenhouse gas emission intensity of regional electricity transfers. Environ. Sci. Technol. 2021, 55, 6571–6579. [Google Scholar]
- Qu, S.; Li, Y.; Liang, S.; Yuan, J.H.; Xu, M. Virtual CO2 emission flows in the global electricity trade network. Environ. Sci. Technol. 2018, 52, 6666–6675. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.F.; Cai, W.Q.; Yao, M.T.; Wang, Z.Y.; Yang, L.Z.; Wei, W.D. Urban carbon emissions associated with electricity consumption in Beijing and the driving factors. Appl. Energy. 2020, 275, 115425. [Google Scholar] [CrossRef]
- Wei, W.D.; Zhang, P.F.; Yao, M.T.; Xue, M.; Miao, J.W.; Liu, B.; Wang, F. Multi-scope electricity-related carbon emissions accounting: A case study of Shanghai. J. Clean. Prod. 2020, 252, 119789. [Google Scholar] [CrossRef]
- Li, W.B.; Long, R.; Zhang, L.L.; He, Z.X.; Chen, F.Y.; Chen, H. Greenhouse Gas Emission Transfer of Inter-Provincial Electricity Trade in China. Int. J. Environ. Res. Public Health 2020, 17, 8375. [Google Scholar] [CrossRef] [PubMed]
- Eberle, A.L.; Heath, G. Estimating carbon dioxide emissions from electricity generation in the United States: How sectoral allocation may shift as the grid modernizes. Energy Policy 2020, 140, 111324. [Google Scholar] [CrossRef]
- Lopez, N.S.; Biona, J.B.M.; Chiu, A.F. Electricity trading and its effects on global carbon emissions: A decomposition analysis study. J. Clean. Prod. 2018, 195, 532–539. [Google Scholar] [CrossRef]
- Li, F.Y.; Xiao, X.L.; Xie, W.; Ma, D.W.; Song, Z.; Liu, K.P. Estimating air pollution transfer by interprovincial electricity transsions: The case study of the Yangtze River Delta Region of China. J. Clean. Prod. 2018, 183, 56–66. [Google Scholar] [CrossRef]
- Ehigiamusoe, K.U. A disaggregated approach to analyzing the effect of electricity on carbon emissions: Evidence from African countries. Energy Rep. 2020, 6, 1286–1296. [Google Scholar] [CrossRef]
- Xu, G.Q.; Feng, S.W. Spatial-temporal evolution characteristics of carbon emissions from energy consumption in China’s thermal power industry. Ecol. Econ. 2024, 40, 30–38. [Google Scholar]
- Wang, X.P.; Peng, W.K.; Lu, H.Y.; Yan, F. Forecast of cold chain logistics demand for agricultural products in Beijing based on neural network. GDAAS 2018, 45, 120–128. [Google Scholar]
- Zuo, Z.; Niu, Y.; Li, J.; Fu, H.; Zhou, M. Machine Learning for Advanced Emission Monitoring and Reduction Strategies in Fossil Fuel Power Plants. Appl. Sci. 2024, 14, 8442. [Google Scholar] [CrossRef]
- Jin, Y.K.; Sharifi, A.; Li, Z.S.; Chen, S.R.; Zeng, S.Z.; Zhao, S.L. Carbon emission prediction models: A review. Sci. Total. Environ. 2024, 927, 172319. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.X. Predicting China’s Energy Consumption and CO2 Emissions by Employing a Novel Grey Model. Energies 2024, 17, 5256. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Zhang, X.H.; Wang, T.; Liu, K.; Zhang, L.M. Predicting of carbon emission in the power industry based on the RFR model optimized by EABC algorithm. Shandong Electr. Power. 2024, 51, 77–84. [Google Scholar]
- Li, H.B.; Zhang, J.J. A new model for natural gas demand forecasting and its application—Takes Sichuan-Chongqing region as an example. Nat. Gas. Ind. 2021, 41, 935–951. [Google Scholar]
- He, X.; Wen, Y.; Zhang, D. A Fast Prediction Method for the Electromagnetic Response of the LTE-R System Based on a PSO-BP Cascade Neural Network Model. Appl. Sci. 2023, 13, 6640. [Google Scholar] [CrossRef]
- Mulumba, D.M.; Liu, J.; Hao, J.; Zheng, Y.; Liu, H. Application of an Optimized PSO-BP Neural Network to the Assessment and Prediction of Underground Coal Mine Safety Risk Factors. Appl. Sci. 2023, 13, 5317. [Google Scholar] [CrossRef]
- Hu, Y.C. Electricity Consumption Prediction Using a Neural-Network-Based Grey Forecasting Approach. J. Oper. Res. Soc. 2017, 68, 1259–1264. [Google Scholar] [CrossRef]
- Chiang, C.C.; Ho, M.C.; Chen, J.A. A Prediction Model for Shallow Groundwater Level in Harbin Based on GA-PSO-BP. Neural Comput. Appl. 2006, 15, 328–338. [Google Scholar] [CrossRef]
- Wang, X.L.; Dai, C.L.; Wen, J.W.; Qi, Y.; Zhang, Q.S. Shallow ground water level prediction model in Harbin city based on GA-PSO-BP. J. Zhejiang Univ. Water Resour. Hydropower Eng. 2023, 35, 27–31. [Google Scholar]
- Liu, H.J.; Shao, H.B. Research on prediction of aerospace panel clamping deformation based on SSA-PSO-BP neural network. Mach. Tool. Hydraul. 2023, 51, 114–120. [Google Scholar]
- Zheng, L.H.; Sun, Y.L.; Yu, Y. Carbon Peak Control Strategies and Pathway Selection in Dalian City: A Hybrid Approach with STIRPAT and GA-BP Neural Networks. Sustainability 2024, 16, 8657. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, X.; Liu, S.; Yang, X.; Li, S. Rolling Bearing Residual Useful Life Prediction Model Based on the Particle Swarm Optimization—Optimized Fusion of Convolutional Neural Network and Bidirectional Long–Short-Term Memory–Multihead Self-Attention. Electronics 2024, 13, 2120. [Google Scholar] [CrossRef]
- Ellahi, M.; Usman, M.R.; Arif, W.; Usman, H.F.; Khan, W.A.; Satrya, G.B.; Daniel, K.; Shabbir, N. Forecasting of Wind Speed and Power through FFNN and CFNN Using HPSOBA and MHPSO-BAACs Techniques. Electronics 2022, 11, 4193. [Google Scholar] [CrossRef]
- Zhang, X.L.; Liu, X.Q.; Zhang, Z.Y.; Tang, R.Y.; Zhang, T.; Yao, J. The Synergistic Effect of the Carbon Emission Trading Scheme on Pollution and Carbon Reduction in China’s Power Industry. Sustainability 2024, 16, 8681. [Google Scholar] [CrossRef]
- Jin, J.L.; Zhang, X.Y.; Xu, L.L.; Wen, Q.L.; Guo, X.J. Impacts of carbon trading and wind power integration on carbon emission in the power dispatching process. Energy Rep. 2021, 7, 3887–3897. [Google Scholar] [CrossRef]
- Wang, B.J.; Zhao, J.L.; Wei, Y.X. Carbon emission quota allocating on coal and electric power enterprises under carbon trading pilot in China: Mathematical formulation and solution technique. J. Clean. Prod. 2019, 239, 118104. [Google Scholar] [CrossRef]
- Meng, M.; Wang, L.X.; Chen, Q. Quota Allocation for Carbon Emissions in China’s Electric Power Industry Based Upon the Fairness Principle. Energies 2018, 11, 2256. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Qiu, J.; Tao, Y.C.; Zhao, J.H. Carbon—Oriented Operational Planning in Coupled Electricity and Emission Trading Markets. IEEE Trans. Power Syst. 2020, 35, 3145–3157. [Google Scholar] [CrossRef]
- Ma, C.Q.; Ren, Y.S.; Zhang, Y.J.; Sharp, B. The allocation of carbon emission quotas to five major power generation corporations in China. J. Clean. Prod. 2018, 189, 1–12. [Google Scholar] [CrossRef]
- Zhang, L.R.; Li, Y.K.; Jia, Z.J. Impact of carbon allowance allocation on power industry in China’s carbon trading market:Computable general equilibrium based analysis. Appl. Energy 2018, 229, 814–827. [Google Scholar] [CrossRef]
- Lyu, W.R.; Cui, Z.G.; Yuan, M.; Shan, E.F. Cooperation for trans-regional electricity trading from the perspective of carbon quota: A cooperative game approach. Int. J. Electr. Power. Energy Syst. 2024, 156, 109773. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Chen, X.F.; Song, M.L.; Li, X.C.; Shen, Z.Y. Impacts of renewable electricity standard and Renewable Energy Certificates on renewable energy investments and carbon emissions. J. Environ. Manag. 2022, 306, 114495. [Google Scholar] [CrossRef]
- Li, J.G.; Mao, T.; Huang, G.L.; Zhao, W.M.; Wang, T. Research on Day-Ahead Optimal Scheduling Considering Carbon Emission Allowance and Carbon Trading. Sustainability 2023, 15, 6108. [Google Scholar] [CrossRef]
- Wang, Y.X.; Huang, H.Q.; Chen, Y.; Dong, M.Q.; Li, S.W.; Yue, S.J.; Lu, Z.W. Analysis of carbon emission drivers in Chinese power consumption— Based on LMDI decomposition method. J. Hubei Univ. Econ. 2023, 20, 38–44. [Google Scholar]
- Wei, Y.M.; Wang, X.Y.; Ding, Y.H.; Zheng, J.; Shan, Z.J. Provincial carbon quota allocation for China’s electric power industry considering carbon transfer under the carbon peaking target. J. Arid. Land 2023, 37, 19–26. [Google Scholar]
- Tang, T.; Jiang, W.H.; Zhang, H.; Nie, J.T.; Xiong, Z.H.; Wu, X.G.; Feng, W.J. GM (1,1) based improved seasonal index model for monthly electricity consumption forecasting. Energy 2022, 252, 124041. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Wang, L.; Yi, S.; Yu, Y.; Gao, C.; Samali, B. Automated ultrasonic-based diagnosis of concrete compressive damage amidst temperature variations utilizing deep learning. Mech. Syst. Signal Process 2024, 221, 111719. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Xie, X.; Yousefi, A.M.; Zhang, G.; Li, J.; Samali, B. Compressive strength evaluation of cement-based materials in sulphate environment using optimized deep learning technology. Dev. Built Environ. 2023, 16, 100298. [Google Scholar] [CrossRef]
- Yu, Y.; Rashidi, M.; Dorafshan, S.; Samali, B.; Farsangi, E.N.; Yi, S.; Ding, Z. Ground penetrating radar-based automated defect identification of bridge decks: A hybrid approach. J. Civ. Struct. Health. Monit. 2024. [Google Scholar] [CrossRef]
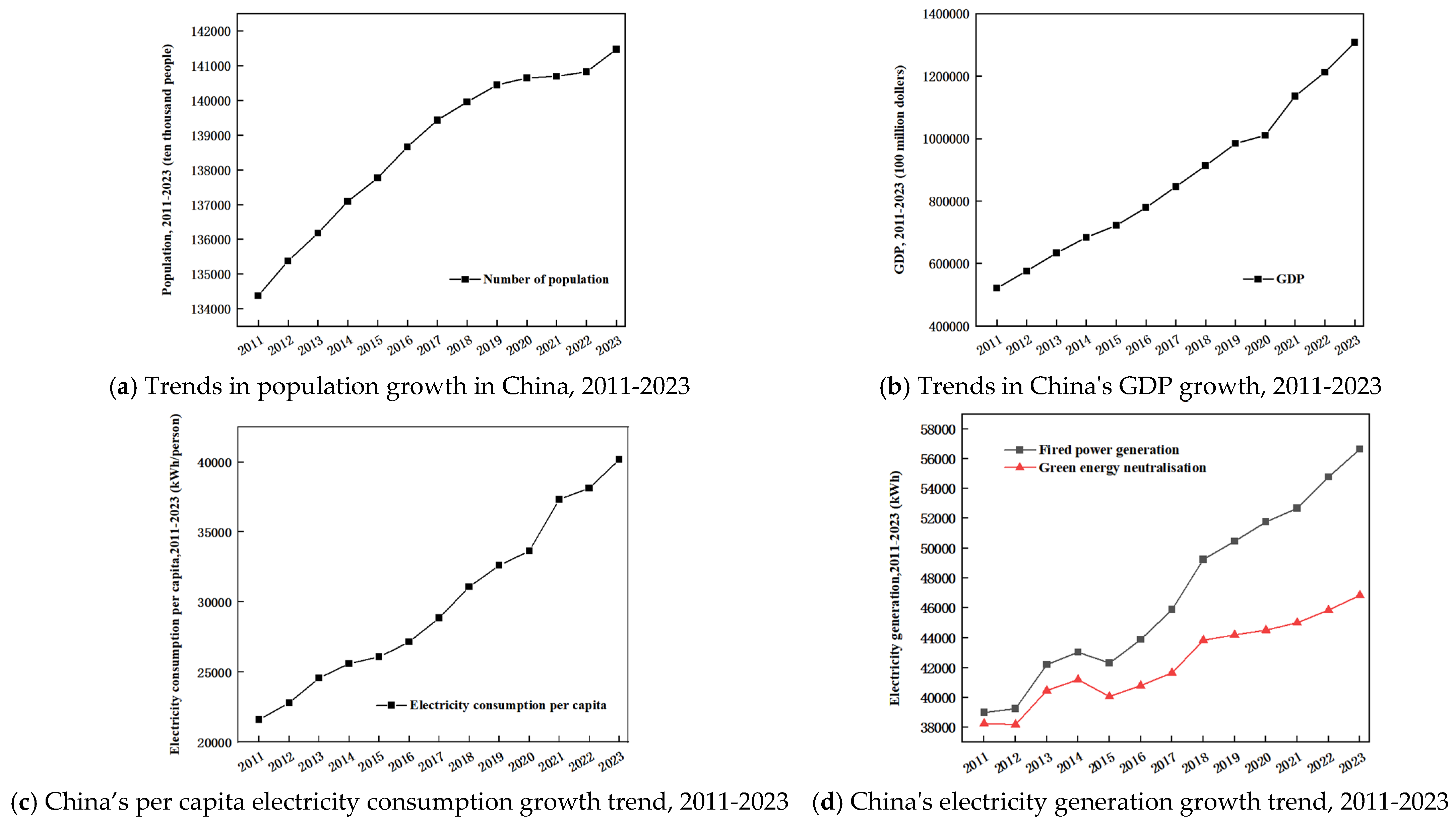

| First-Level Indicators | Second-Level Indicators |
|---|---|
| Emission reduction responsibility | Power generation (thermal power generation, Green energy neutralized power generation) |
| Emission reduction | Potential population |
| Per capita electricity consumption | |
| Emission reduction capacity | GDP |
| Training Set | BPNN | PSO-BPNN |
|---|---|---|
| RMSE | 0.70352 | 0.54088 |
| MAE | 0.59663 | 0.38247 |
| MAPE | 0.13158 | 0.08125 |
| R2 | 0.95388 | 0.97274 |
| Model | GM(1,1) | PSO-BP | GM(1,1) + PSO-BP |
|---|---|---|---|
| Average Error | 0.10713053 | 0.09673209 | 0.08855026 |
| Accuracy Rate | 0.98734 | 0.99368 | 0.99457 |
| Year | Population Number | GDP | Thermal Power Generation Capacity | Post-Neutralization Power Generation | Electricity Consumption per Capita |
|---|---|---|---|---|---|
| 2024 | 143,472.8 | 1,411,312 | 61,713.9 | 47,617.03 | 10,369.60 |
| 2025 | 144,153.1 | 1,523,631 | 64,268.0 | 48,546.84 | 11,033.36 |
| 2026 | 144,840.7 | 1,645,632 | 66,957.0 | 49,508.20 | 11,740.30 |
| 2027 | 145,536.6 | 1,778,178 | 69,790.8 | 50,505.61 | 12,492.39 |
| 2028 | 146,240.8 | 1,922,175 | 72,778.8 | 51,536.27 | 13,293.03 |
| 2029 | 146,950.2 | 2,078,684 | 75,930.2 | 52,602.23 | 14,145.05 |
| 2030 | 147,666.8 | 2,248,763 | 79,258.4 | 53,707.90 | 15,051.98 |
| Year | North China | Northeast China | East China | Central China | Southern China | Northwest China |
|---|---|---|---|---|---|---|
| 2024 | 0.67451 | 0.71388 | 1.21264 | 1.34472 | 1.03101 | 0.45959 |
| 2025 | 0.66767 | 0.68983 | 1.25675 | 1.38819 | 1.06131 | 0.46176 |
| 2026 | 0.66090 | 0.66658 | 1.30254 | 1.43302 | 1.09250 | 0.46390 |
| 2027 | 0.65419 | 0.64410 | 1.34992 | 1.47935 | 1.12460 | 0.46607 |
| 2028 | 0.64758 | 0.62241 | 1.39907 | 1.52711 | 1.15769 | 0.46820 |
| 2029 | 0.64102 | 0.60145 | 1.44995 | 1.57648 | 1.19173 | 0.47040 |
| 2030 | 0.63451 | 0.58117 | 1.50275 | 1.62743 | 1.22672 | 0.47256 |
| Year | North China | Northeast China | East China | Central China | Southern China | Northwest China | Nationwide |
|---|---|---|---|---|---|---|---|
| 2025 | 9.126 | 2.419 | 10.822 | 11.698 | 8.864 | 2.688 | 45.618 |
| 2026 | 9.035 | 2.357 | 11.111 | 12.983 | 9.440 | 2.863 | 47.790 |
| 2027 | 8.949 | 2.238 | 11.455 | 13.823 | 9.864 | 3.193 | 49.520 |
| 2028 | 8.869 | 2.082 | 11.858 | 14.453 | 10.214 | 3.728 | 51.204 |
| 2029 | 8.797 | 1.957 | 12.318 | 15.013 | 10.537 | 4.456 | 53.077 |
| 2030 | 8.733 | 1.941 | 12.832 | 15.564 | 10.854 | 5.227 | 55.151 |
| Area | Actual Carbon Quota (100 Million Tons) | Forecast Carbon Emissions (100 Million Tons) | Difference (100 Million Tons) |
|---|---|---|---|
| North China | 8.733 | 13.763 | −5.030 |
| Northeast China | 1.942 | 3.341 | −1.399 |
| East China | 12.832 | 8.539 | 4.293 |
| Central China | 15.564 | 9.564 | 6.001 |
| Southern China | 10.854 | 8.848 | 2.006 |
| Northwest China | 5.227 | 11.061 | −5.834 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Sun, Y.; Teng, Y.; Liu, S.; Ji, S.; Zou, Z.; Yu, Y. Carbon Quota Allocation Prediction for Power Grids Using PSO-Optimized Neural Networks. Appl. Sci. 2024, 14, 11996. https://doi.org/10.3390/app142411996
Xu Y, Sun Y, Teng Y, Liu S, Ji S, Zou Z, Yu Y. Carbon Quota Allocation Prediction for Power Grids Using PSO-Optimized Neural Networks. Applied Sciences. 2024; 14(24):11996. https://doi.org/10.3390/app142411996
Chicago/Turabian StyleXu, Yixin, Yanli Sun, Yina Teng, Shanglai Liu, Shiyu Ji, Zhen Zou, and Yang Yu. 2024. "Carbon Quota Allocation Prediction for Power Grids Using PSO-Optimized Neural Networks" Applied Sciences 14, no. 24: 11996. https://doi.org/10.3390/app142411996
APA StyleXu, Y., Sun, Y., Teng, Y., Liu, S., Ji, S., Zou, Z., & Yu, Y. (2024). Carbon Quota Allocation Prediction for Power Grids Using PSO-Optimized Neural Networks. Applied Sciences, 14(24), 11996. https://doi.org/10.3390/app142411996








