Autonomous Driving Decision-Making Method Based on Spatial-Temporal Fusion Trajectory Prediction
Abstract
1. Introduction
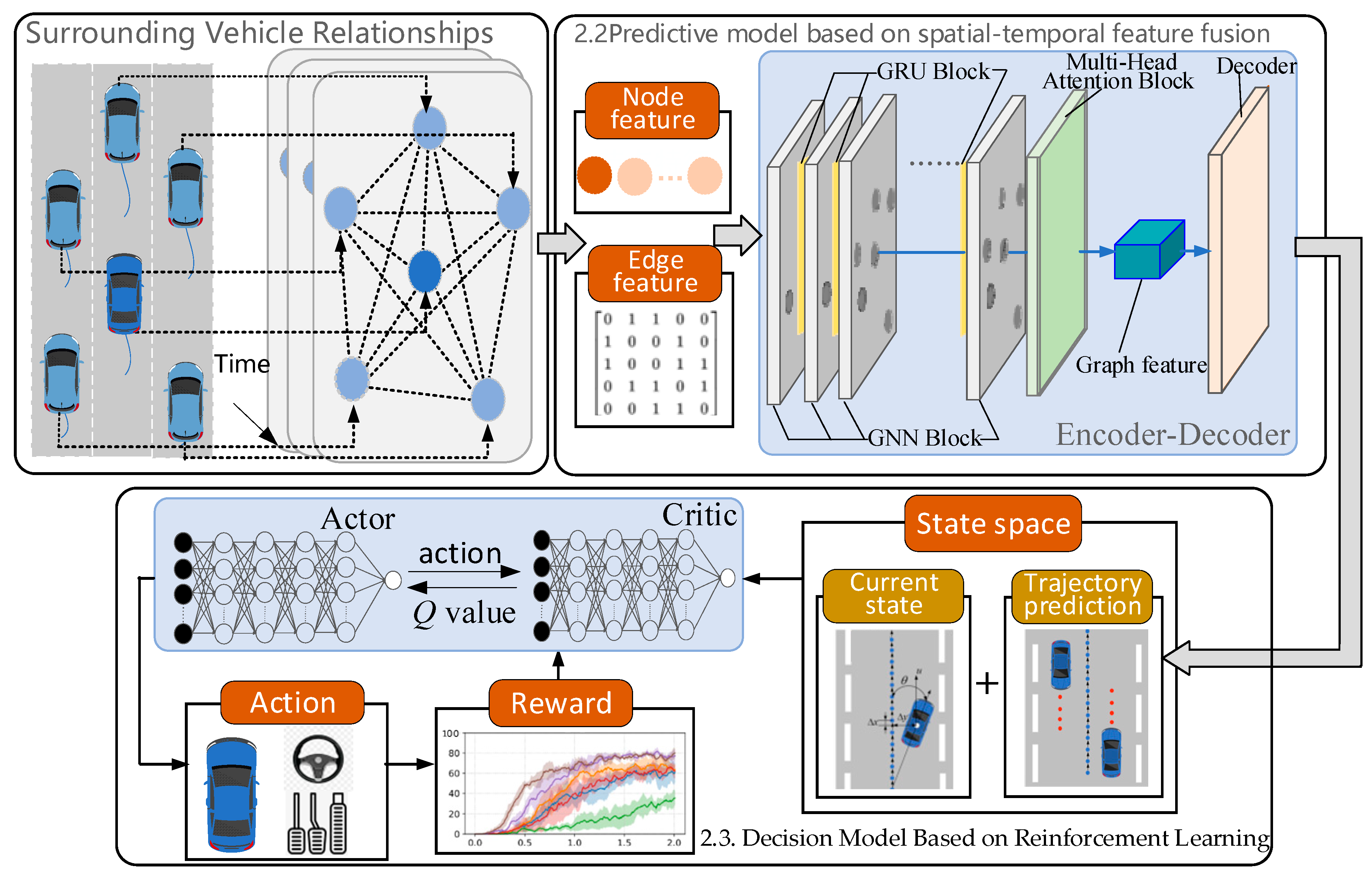
2. Method
2.1. Overall Structure
2.2. Predictive Model Based on Spatio-Temporal Feature Fusion
2.3. Decision Model Based on Reinforcement Learning
2.3.1. State Space Design
2.3.2. Reward Function Design
2.3.3. Action Space Design
3. Results and Analysis
3.1. Evaluation of Prediction Model
3.1.1. Experimental Details of Prediction Model
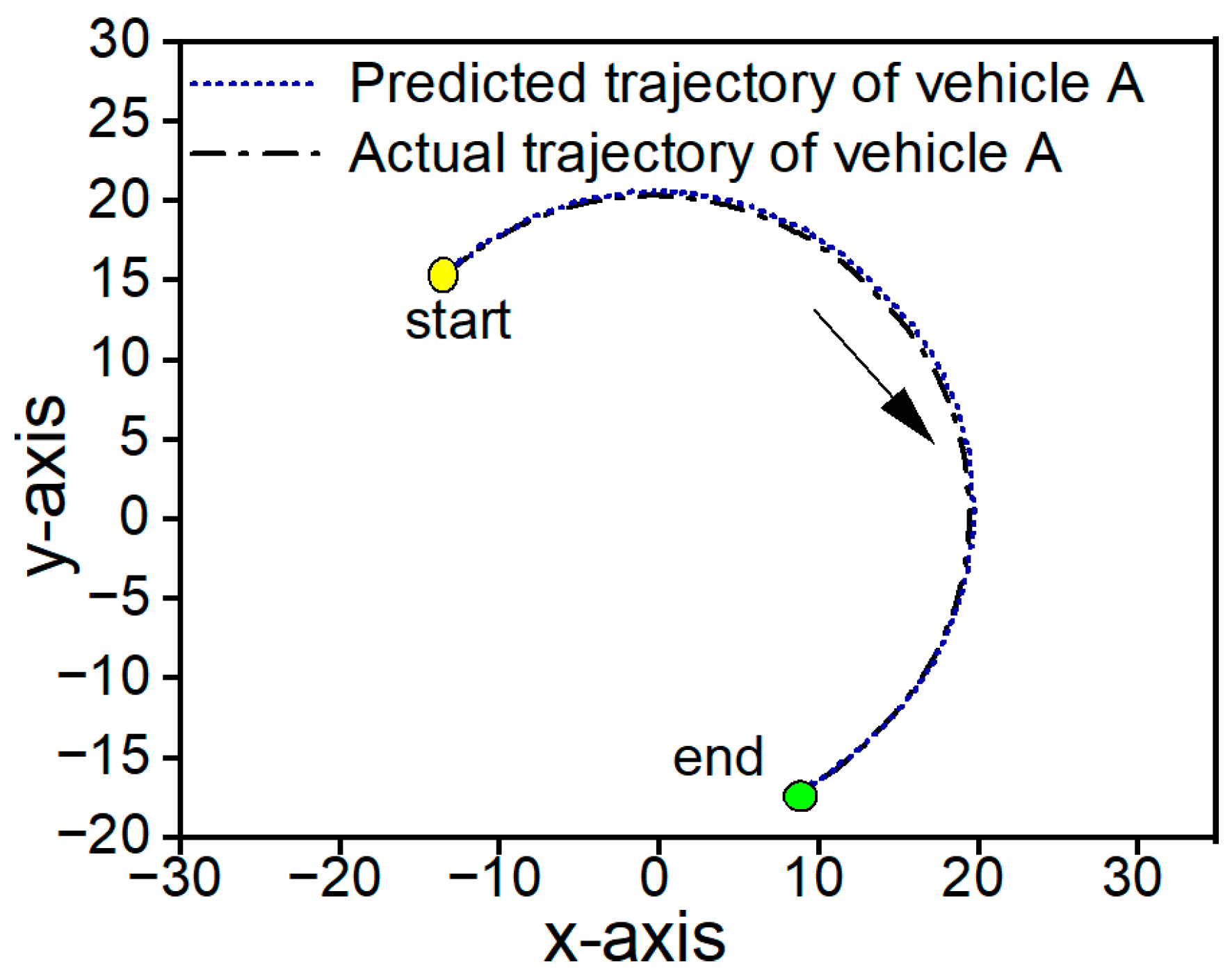
3.1.2. Experimental Results of Prediction Model
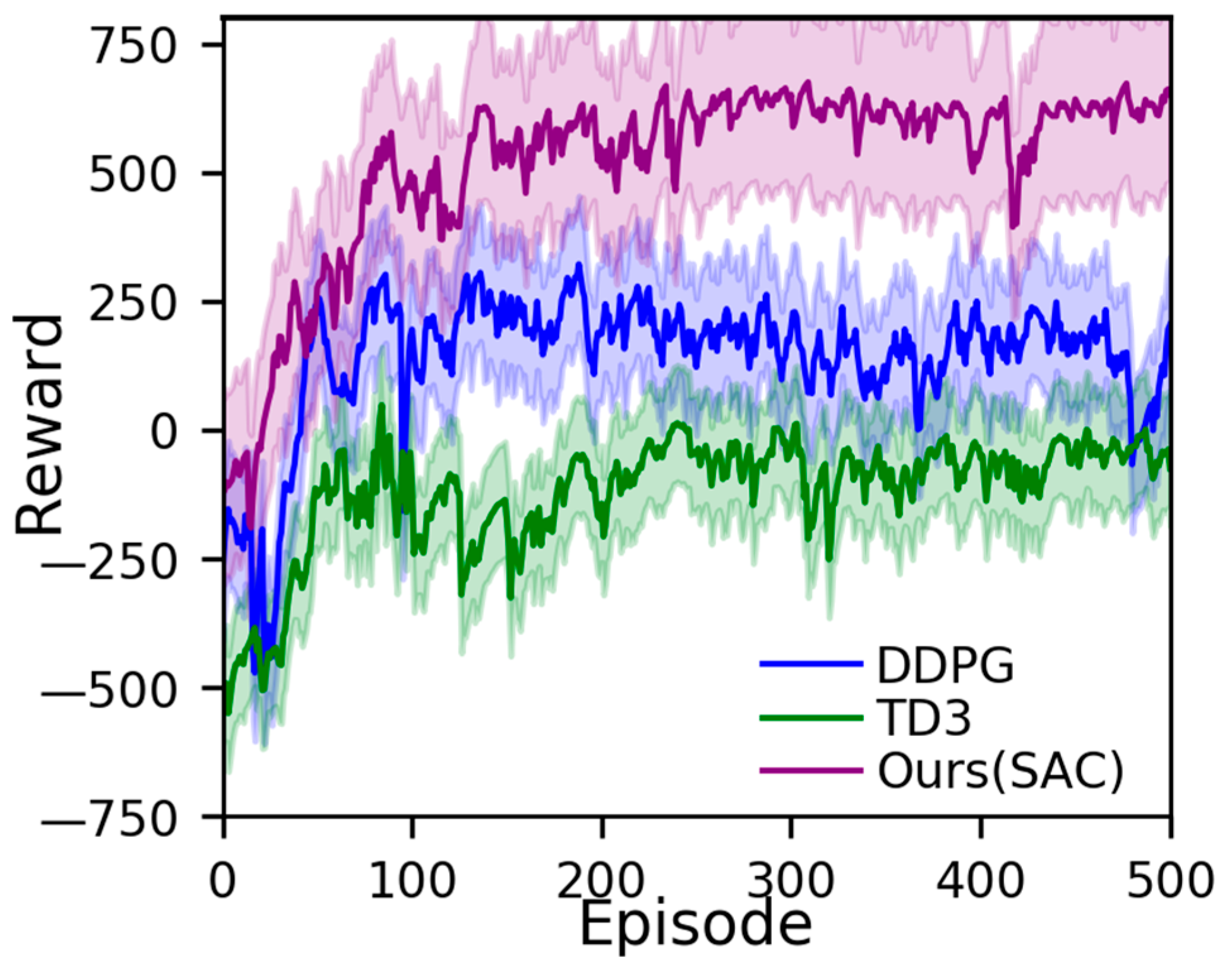
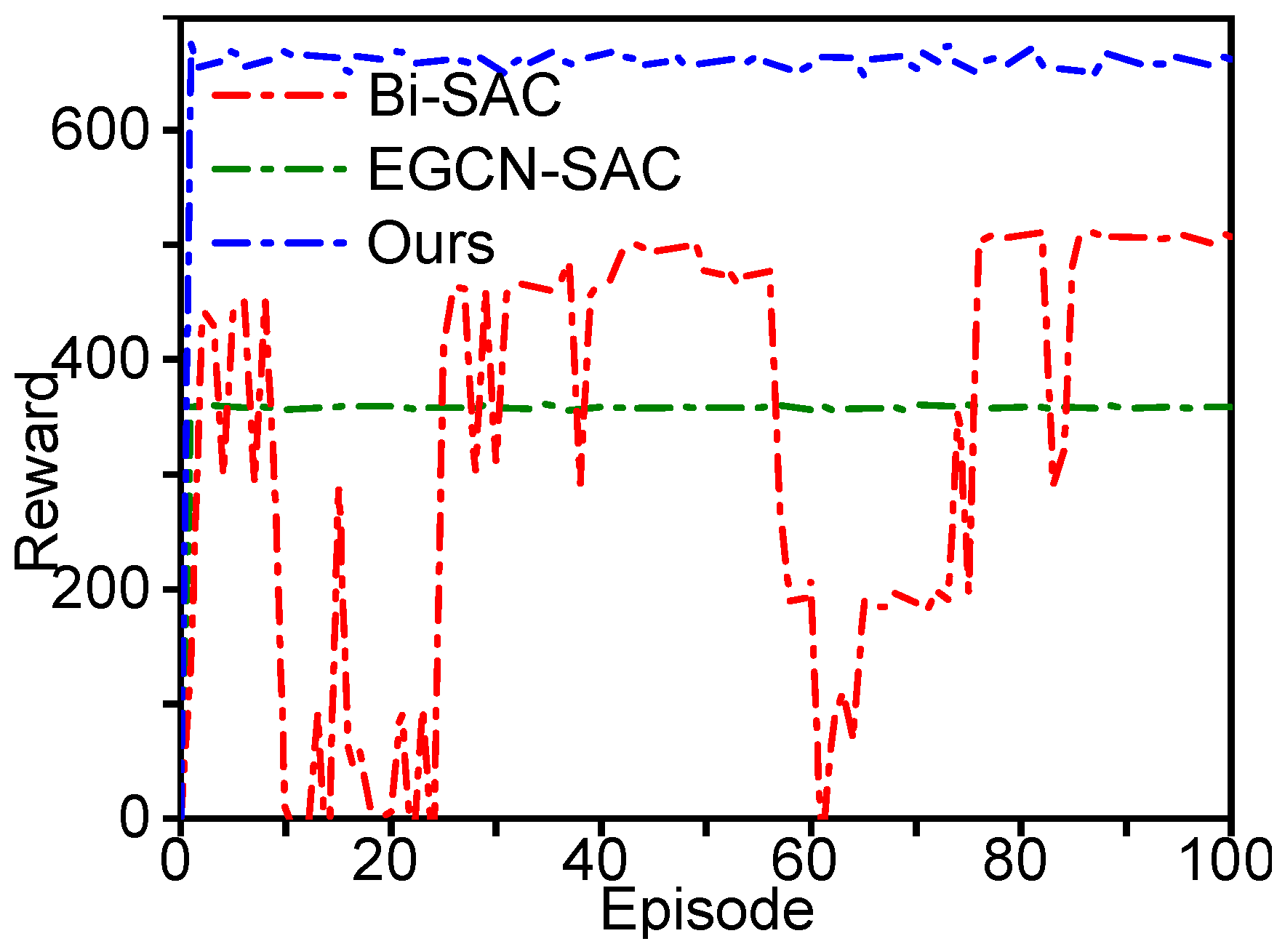
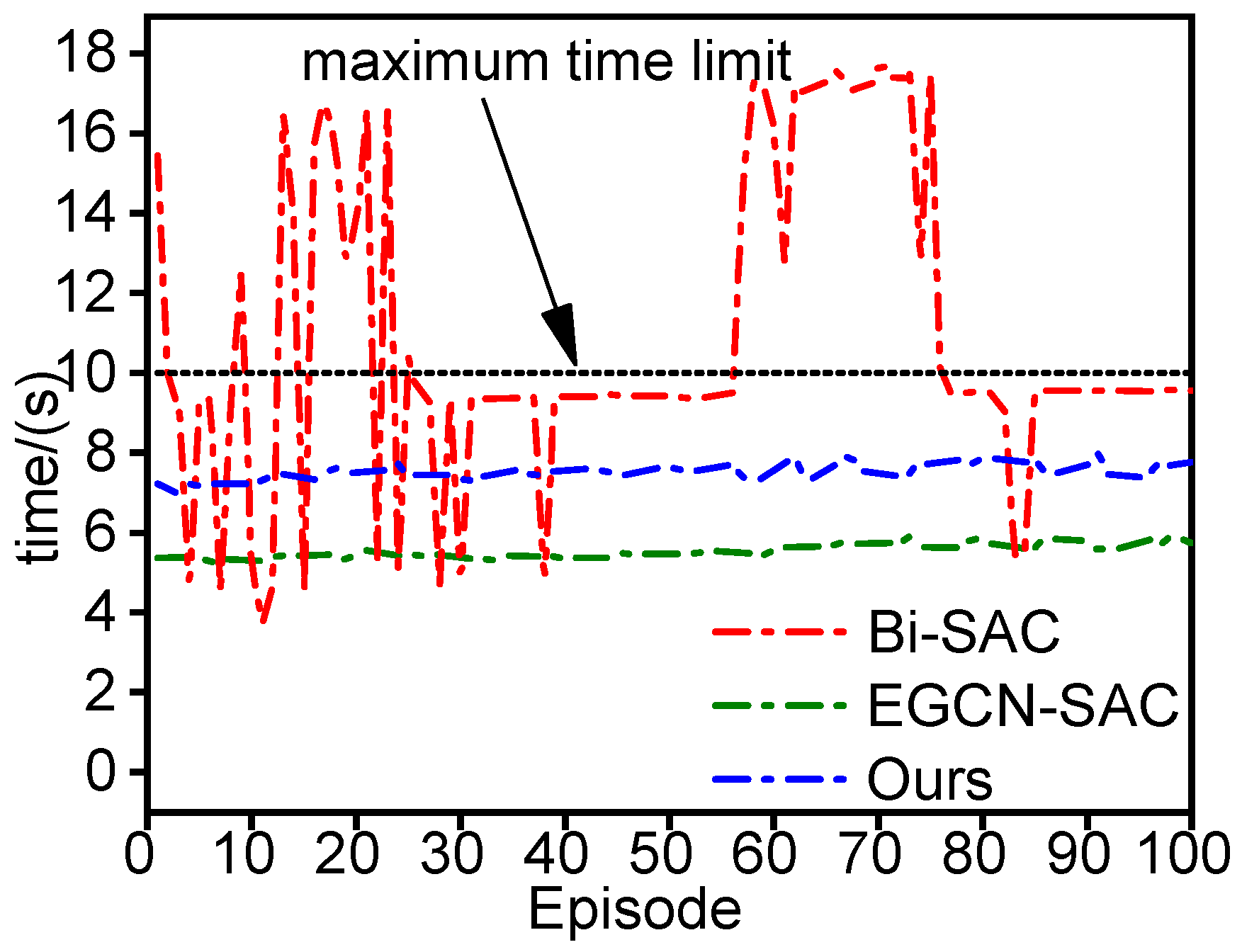
3.2. Evaluation of Decision Model
3.2.1. Experimental Details of Decision Model
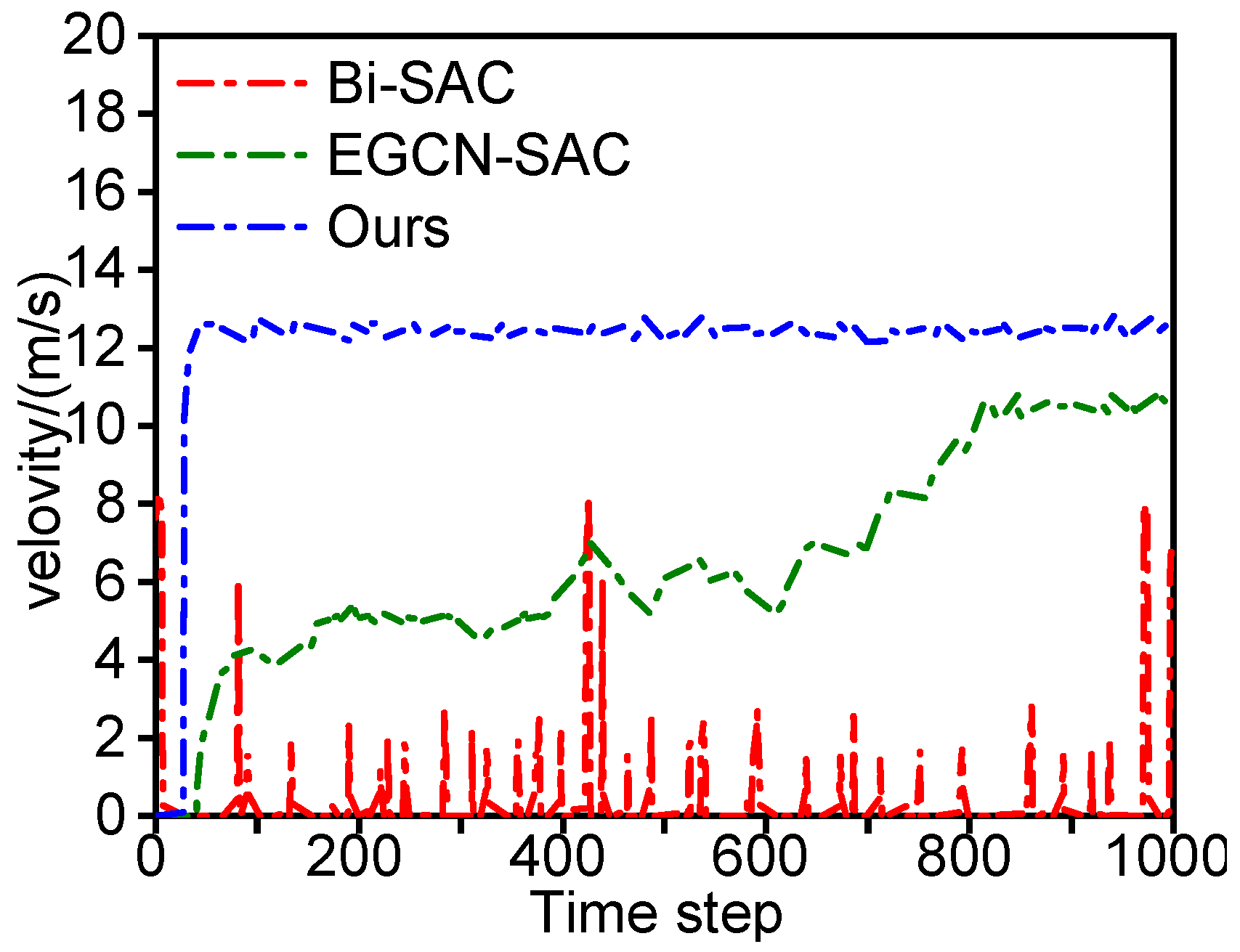
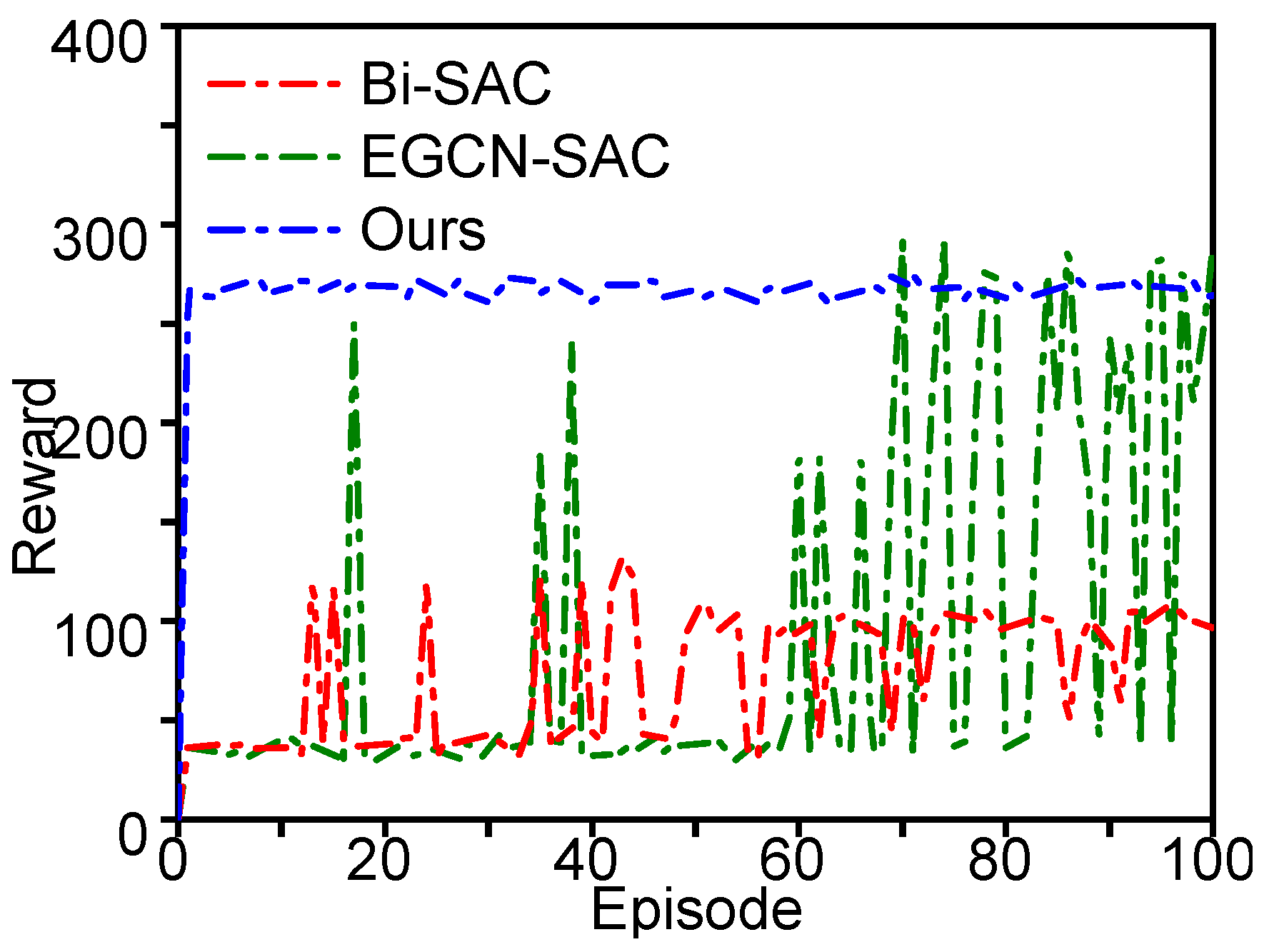
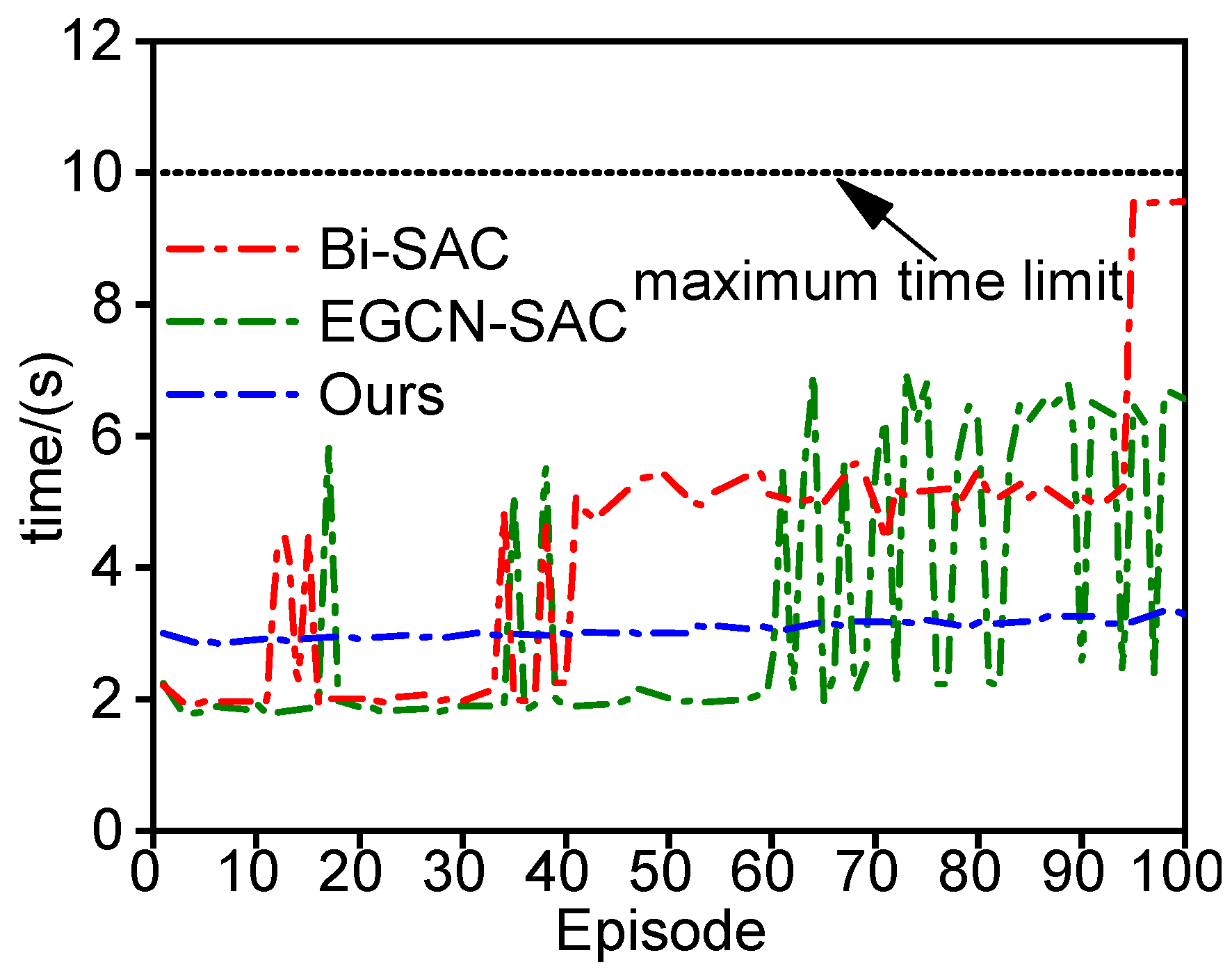
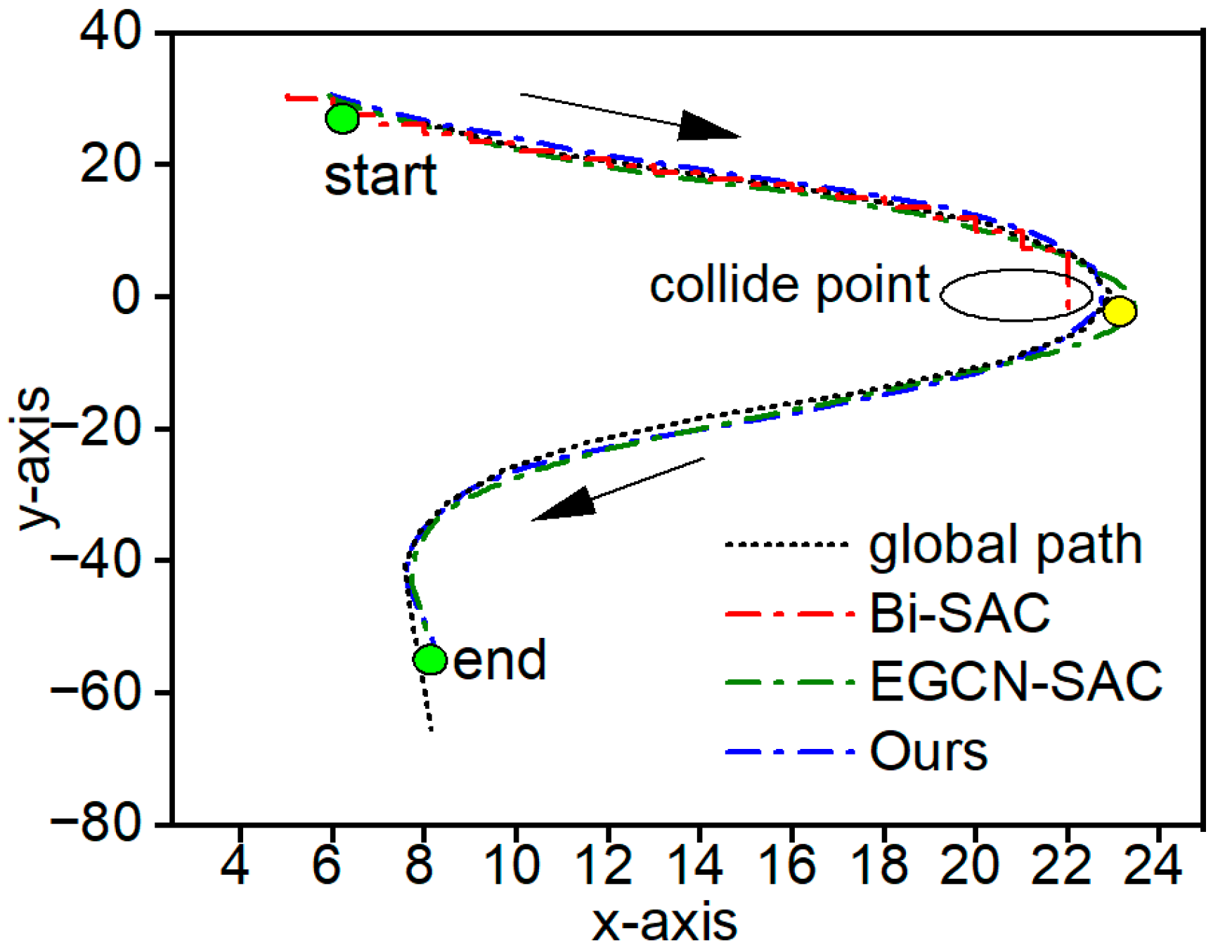
3.2.2. Experimental Results of Decision Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, G.T. Research on Dynamic Environment Cognition Method for Intelligent Vehicles Under Uncertainty Conditions. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2018. [Google Scholar]
- Xu, J.; Pei, X.; Fei, X.; Yang, B.; Fang, Z. Incorporating vehicle trajectory prediction for learning autonomous driving decision. J. Automot. Saf. Energy Conserv. 2022, 13, 317–324. [Google Scholar]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Gao, J.; Sun, C.; Zhao, H.; Shen, Y.; Anguelov, D.; Li, C.; Schmid, C. VectorNet: Encoding HD maps and agent dynamics from vectorized representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Fei, C.; He, X.; Liu, Y.; Liu, Y. Driving intention recognition and vehicle trajectory prediction based on LSTM network. Chin. J. Highway 2019, 32, 34–42. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, M.; Zhu, B. Research on multimodal vehicle trajectory prediction method considering multiple types of traffic participants in urban road scenarios. Automot. Eng. 2024, 46, 396–406. [Google Scholar] [CrossRef]
- Sheng, Z.; Xu, Y.; Xue, S.; Li, D. Graph-based spatial-temporal convolutional network for vehicle trajectory prediction in autonomous driving. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17654–17665. [Google Scholar] [CrossRef]
- Xiong, L.; Kang, Y.; Zhang, P.; Zhu, C.; Yu, Z. Research on behavioral decision-making system for driverless vehicles. Automot. Technol. 2018, 1–9. [Google Scholar] [CrossRef]
- Bansal, M.; Krizhevsky, A.; Ogale, A. Chauffeurnet: Learning to drive by imitating the best and synthesizing the worst. arXiv 2018, arXiv:1812.03079. [Google Scholar]
- Jin, L.; Han, G.; Xie, X.; Guo, B.; Liu, G.; Zhu, W. A review of research on automatic driving decision-making based on reinforcement learning. Automot. Eng. 2023, 45, 527–540. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, R.; Ouyang, M.; Wei, P.; Lin, J.; Su, J.; Lin, L. Deductive reinforcement learning for visual autonomous urban driving navigation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5379–5391. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Sun, T.; Xiao, H. Decision-making method for vehicle longitudinal automatic driving based on reinforcement Q-learning. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419853185. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, D.; Huang, C.; Wang, L.; Liu, J.; Chen, F.; Xu, H.; Gao, X.; Li, Q.; Zhou, Y.; et al. TD3 algorithm improvement and merging strategy learning for self-driving cars. J. Mech. Eng. 2023, 59, 224–234. [Google Scholar]
- Tinghan, W.; Yugong, L.; Jinxin, L.; Li, K. End-to-end autonomous driving strategy based on deep deterministic policy gradient algorithm considering state distribution. J. Tsinghua Univ. (Nat. Sci. Ed.) 2021, 61, 881–888. [Google Scholar] [CrossRef]
- Zhang, Z.; Liniger, A.; Dai, D.; Yu, F.; Van Gool, L. End-to-end urban driving by imitating a reinforcement learning coach. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Ghadi, N.; Deo, T.Y. Safe Navigation: Training Autonomous Vehicles using Deep Reinforcement Learning in CARLA. arXiv 2023, arXiv:2311.10735. [Google Scholar]
- Wang, M.; Tang, X.; Yang, K.; Li, G.; Hu, X. A motion planning method for self-driving vehicles considering predictive risk. Automot. Eng. 2023, 45, 1362–1372+1407. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Alexiadis, V.; Colyar, J.; Halkias, J.; Hranac, R.; McHale, G. The next generation simulation program. ITE J. 2004, 74, 22. [Google Scholar]
- Pareja, A.; Domeniconi, G.; Chen, J.; Ma, T.; Suzumura, T.; Kanezashi, H.; Kaler, T.; Schardl, T.B.; Leiserson, C.E. Evolvegcn: Evolving graph convolutional networks for dynamic graphs. Proc. AAAI Conf. Artif. Intell. 2020, 34, 2276–2283. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An open urban driving simulator. In Conference on Robot Learning; PMLR: Birmingham, UK, 2017. [Google Scholar]







| Typical Road Conditions | The Number of Lanes | Average Lane Width (m) | Average Speed (m/s) | Range of Interest Setting (m) |
|---|---|---|---|---|
| Straight sections of highways | Vertical 5 | 3.6 | 13.4 m/s | Horizontal ±4 m, vertical ±70 m |
| Arterial Road Intersection Section | Vertical 8, horizontal 6 | 3 | 7.23 m/s | Horizontal ±15 m, vertical ±10 m |
| Parameter Name | Parameter Value |
|---|---|
| Input Dimension | 4 |
| Number of nodes in the hidden layer of the encoder | 128 |
| Number of nodes in the hidden layer of the LSTM | 256 |
| GCN parameter learning rate | 5 × 10−3 |
| Model learning rate | 5 × 10−4 |
| Batchsize | 128 |
| Input Sequence Length | 10 |
| Output sequence length | 10 |
| Model | Number of Model Parameters | Dataset | ADE | FDE |
|---|---|---|---|---|
| Bilstm | 83,770 | US101 | 0.74 | 1.29 |
| Lankershim | 0.92 | 1.85 | ||
| Transformer Encoder | 3,987,373 | US101 | 1.68 | 3.46 |
| Lankershim | 2.73 | 4.60 | ||
| EGCN | 556,448 | US101 | 0.61 | 1.48 |
| Lankershim | 0.63 | 1.24 | ||
| Ours | 600,800 | US101 | 0.33 | 0.84 |
| Lankershim | 0.42 | 0.89 |
| Model | #FLOPs (M) | #Params (K) | Inference Time (ms) |
|---|---|---|---|
| Bilstm | 6.97 | 83.27 | 3.5 |
| Transformer Encoder | 16.73 | 42.17 | 7.14 |
| EGCN | 428.97 | 203.3 | 22.4 |
| Ours | 106.82 | 271.764 | 3.7 |
| Hyperparameterization | Parameter Value |
|---|---|
| Discount factor | 9.8 × 10−1 |
| Number of neurons in the hidden layer of the Actor network | 256 |
| Number of neurons in the hidden layer of the Critic network | 256 |
| Actor Network Learning Rate | 1 × 10−4 |
| Critic Network Learning Rate | 3 × 10−4 |
| batch volume | 256 |
| Experience pool capacity | 1 × 105 |
| Initial temperature coefficient value | −3 |
| Temperature coefficient learning rate | 3 × 10−4 |
| optimizer | Adam |
| Metrics | Explanation |
|---|---|
| Success rate | the percentage of autos successfully completing a prescribed route over multiple tests. |
| Crash rate | the percentage of crashes that occurred in multiple tests of the autocar. |
| Overtime rate | the percentage of autos exceeding the maximum time limit over multiple tests. |
| Model | Success Rate (%) | Crash Rate (%) | Overtime Rate (%) | Average Test Rewards | Average Test Time (s) |
|---|---|---|---|---|---|
| Ours | 100 | 0 | 0 | 654.29 | 5.54 |
| EGCN-SAC | 100 | 0 | 0 | 354.96 | 7.52 |
| Bi-SAC | 69 | 1 | 30 | 336.78 | 10.84 |
| Model | Success Rate (%) | Crash Rate (%) | Overtime Rate (%) | Average Test Rewards | Average Test Time (s) |
|---|---|---|---|---|---|
| Ours | 100 | 0 | 0 | 267.64 | 3.06 |
| EGCN-SAC | 60 | 40 | 0 | 92.83 | 3.26 |
| Bi-SAC | 30 | 70 | 0 | 73.01 | 4.29 |
| Obstacle Vehicle Setup | Model | Success Rate (%) | Crash Rate (%) | Overtime Rate (%) | Average Test Rewards | Average Test Time (s) |
|---|---|---|---|---|---|---|
| A, C | Ours | 99 | 1 | 0 | 419.71 | 6.37 |
| EGCN-SAC | 100 | 0 | 0 | 409.75 | 7.00 | |
| Bi-SAC | 97 | 3 | 0 | 228.68 | 8.56 | |
| A, C, D | Ours | 95 | 5 | 0 | 382.67 | 5.28 |
| EGCN-SAC | 90 | 10 | 0 | 251.11 | 2.93 | |
| Bi-SAC | 75 | 25 | 0 | 205.11 | 4.94 | |
| A, B, C, D | Ours | 76 | 24 | 0 | 286.36 | 7.00 |
| EGCN-SAC | 65 | 35 | 0 | 175.31 | 2.99 | |
| Bi-SAC | 54 | 30 | 16 | 122.62 | 3.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Sun, A.; Hong, J. Autonomous Driving Decision-Making Method Based on Spatial-Temporal Fusion Trajectory Prediction. Appl. Sci. 2024, 14, 11913. https://doi.org/10.3390/app142411913
Luo Y, Sun A, Hong J. Autonomous Driving Decision-Making Method Based on Spatial-Temporal Fusion Trajectory Prediction. Applied Sciences. 2024; 14(24):11913. https://doi.org/10.3390/app142411913
Chicago/Turabian StyleLuo, Yutao, Aining Sun, and Jiawei Hong. 2024. "Autonomous Driving Decision-Making Method Based on Spatial-Temporal Fusion Trajectory Prediction" Applied Sciences 14, no. 24: 11913. https://doi.org/10.3390/app142411913
APA StyleLuo, Y., Sun, A., & Hong, J. (2024). Autonomous Driving Decision-Making Method Based on Spatial-Temporal Fusion Trajectory Prediction. Applied Sciences, 14(24), 11913. https://doi.org/10.3390/app142411913






