An Electricity Sale Package Recommendation Method Based on Prospect Strengths and Weaknesses Degree and Choquet Integral
Abstract
1. Introduction
2. Methods
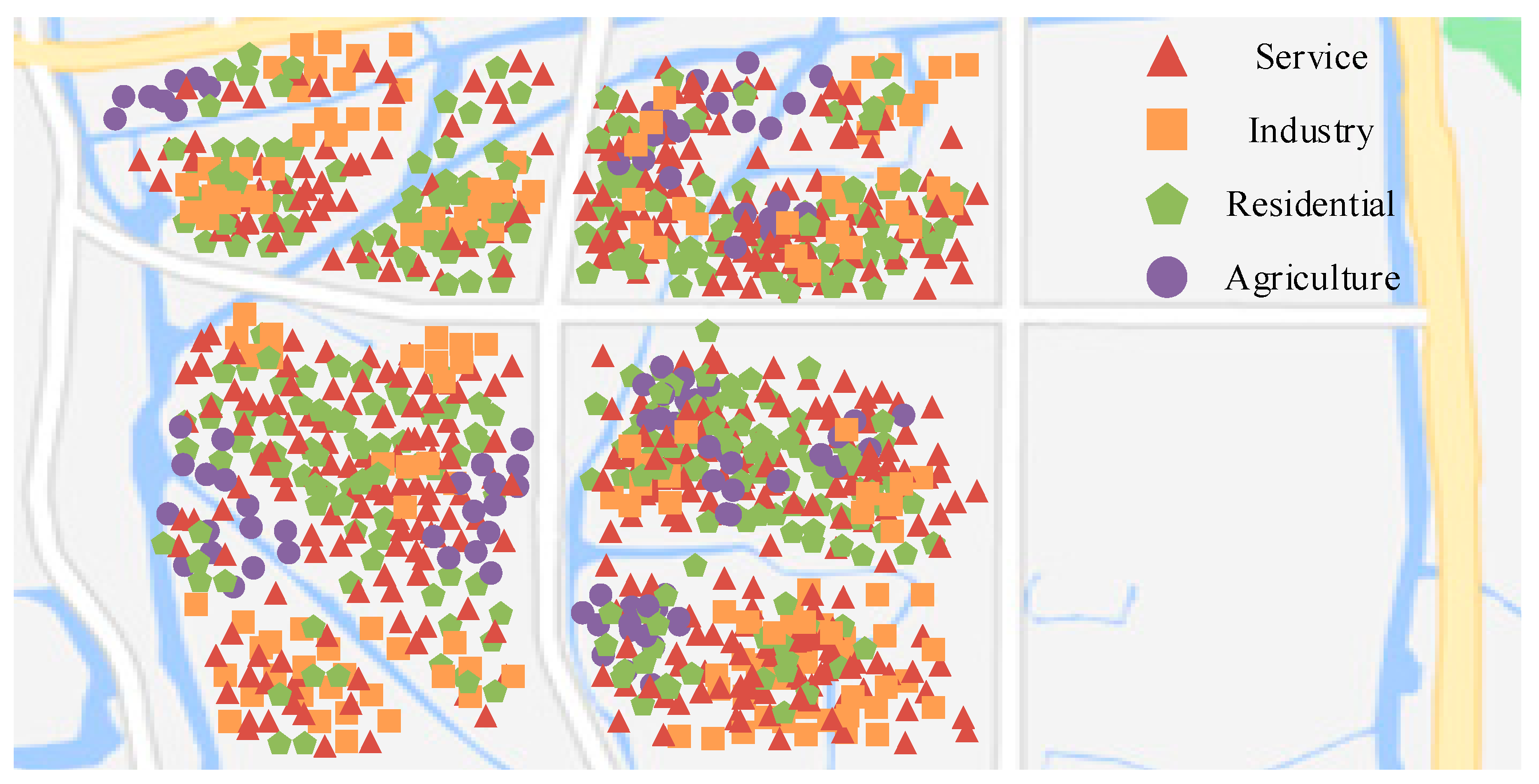
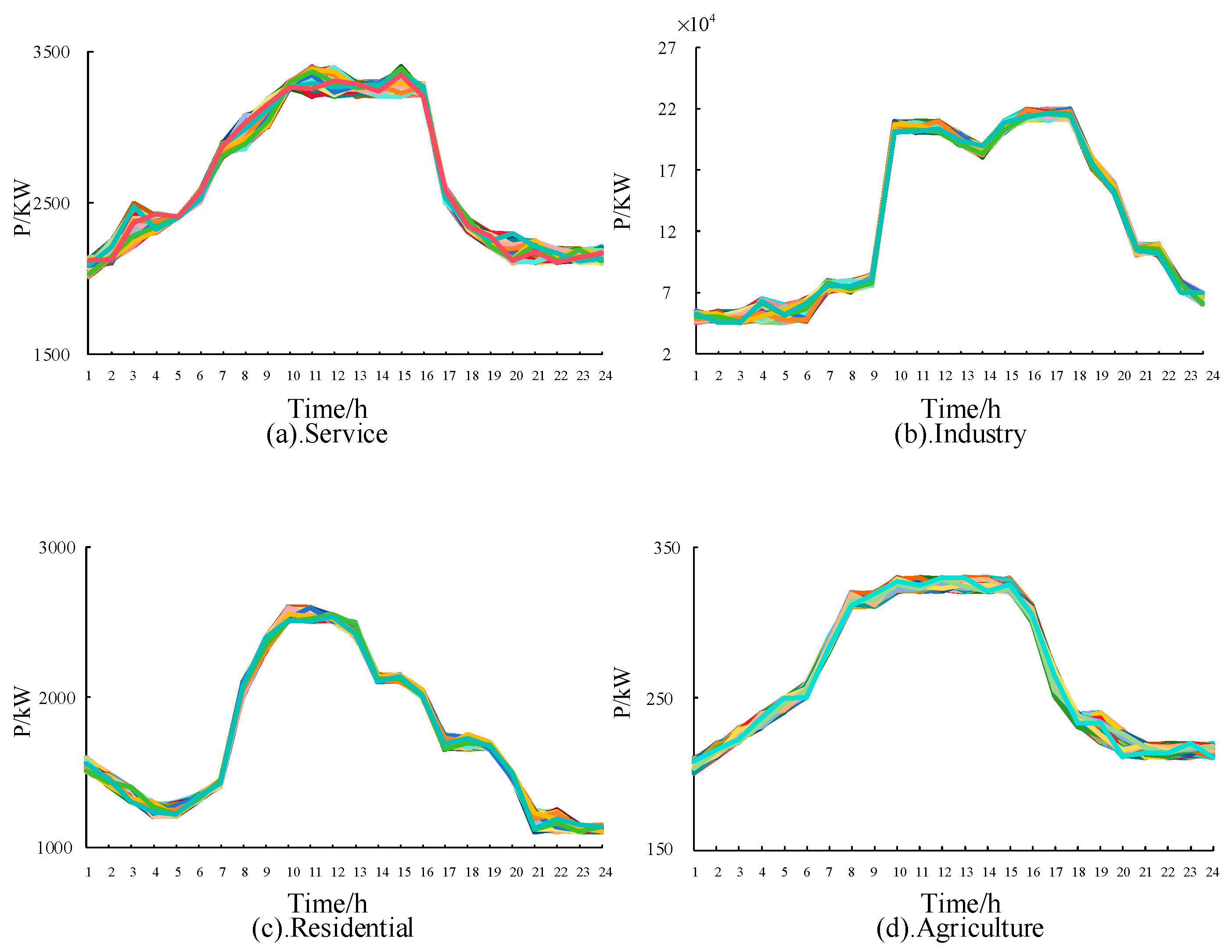
2.1. Survey Location and Dates
2.2. Multi-Attribute Customer Decision-Making System Establish
2.2.1. Establishment of Labeling System for Evaluation of Electricity Sale Packages
2.2.2. Sample Customer Clustering Division
2.3. Prospect Strengths and Weaknesses Degree and Choquet Integral Solution Methods
2.3.1. Prospect Theory and the SIR Method
2.3.2. Comprehensive Prospect Strengths and Weaknesses Degree
2.3.3. Choquet Integral
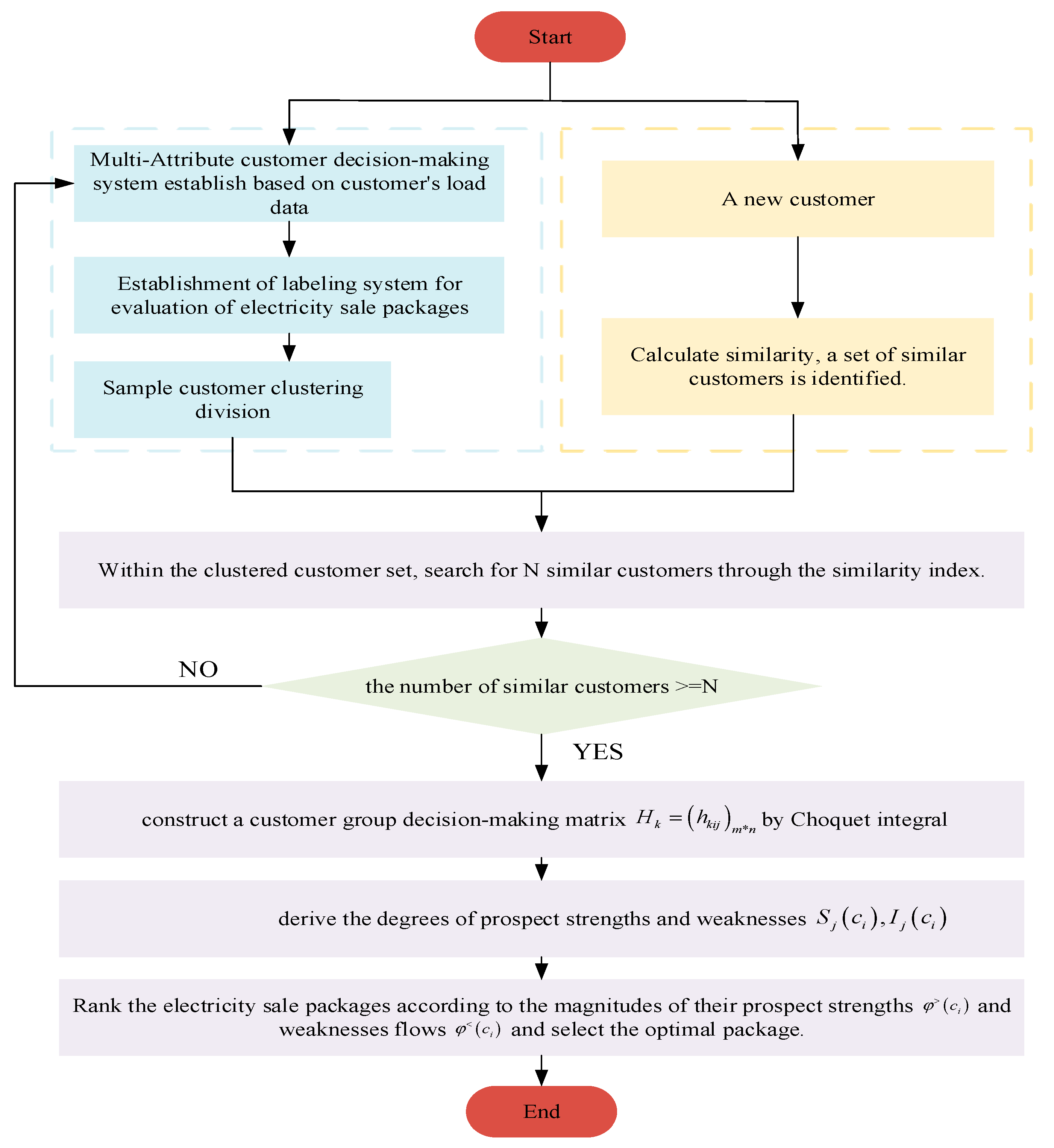
2.4. A Recommendation Method for Electricity Sale Package Based on Prospect Strengths and Weaknesses Degree and the Choquet Integral
2.4.1. New Customer Similarity Determination
2.4.2. Recommendations for Electricity Sale Package
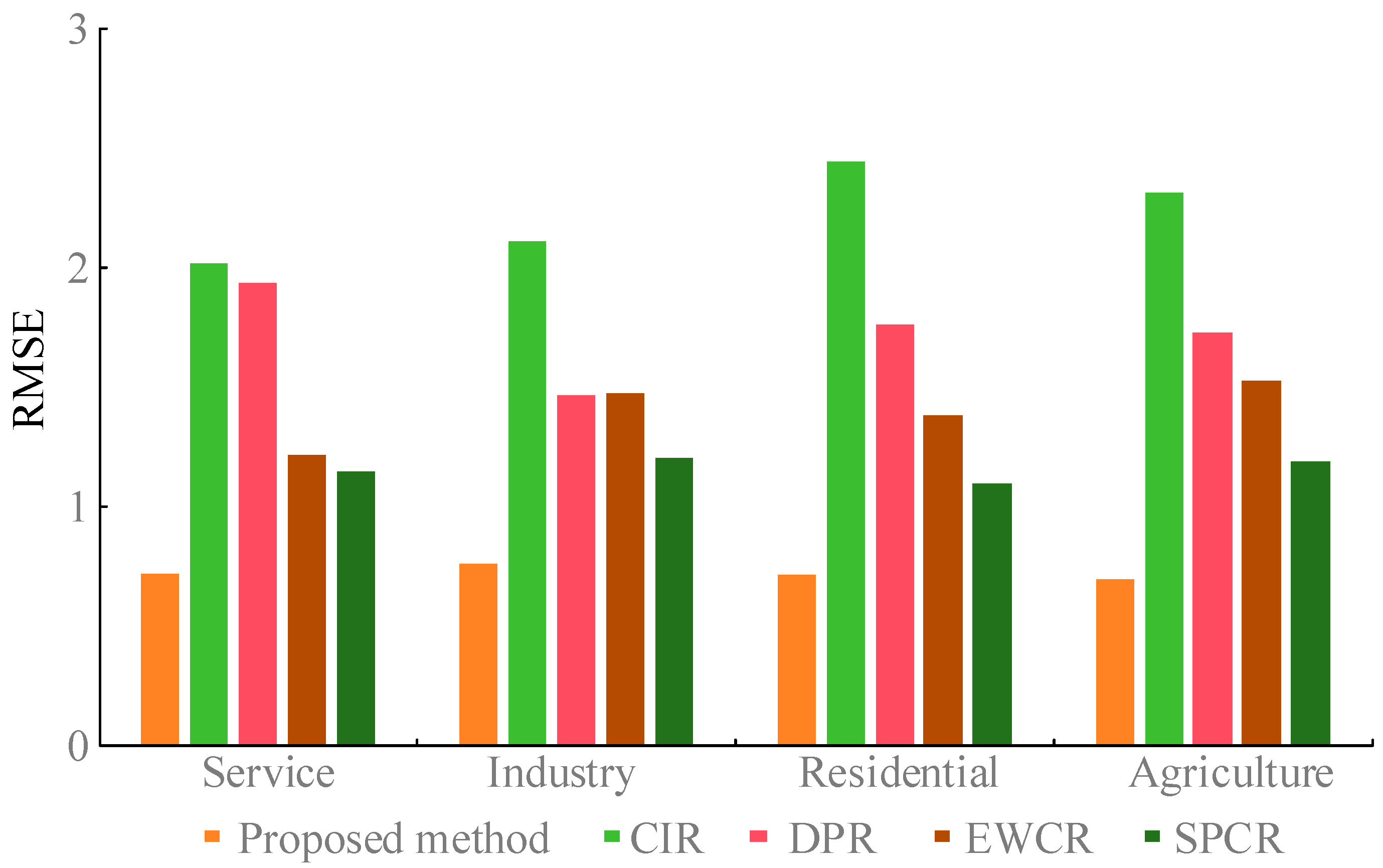
2.5. Research Contrast
3. Results
3.1. Introduction to the Arithmetic Example
3.2. Recommended Analysis of Electricity Sale Packages
3.2.1. Obtaining the Customer Decision Matrix
3.2.2. Aggregate Decision-Making Information from Different Customers
3.2.3. Identify the Prospect Strengths and Weaknesses Matrix of the Program
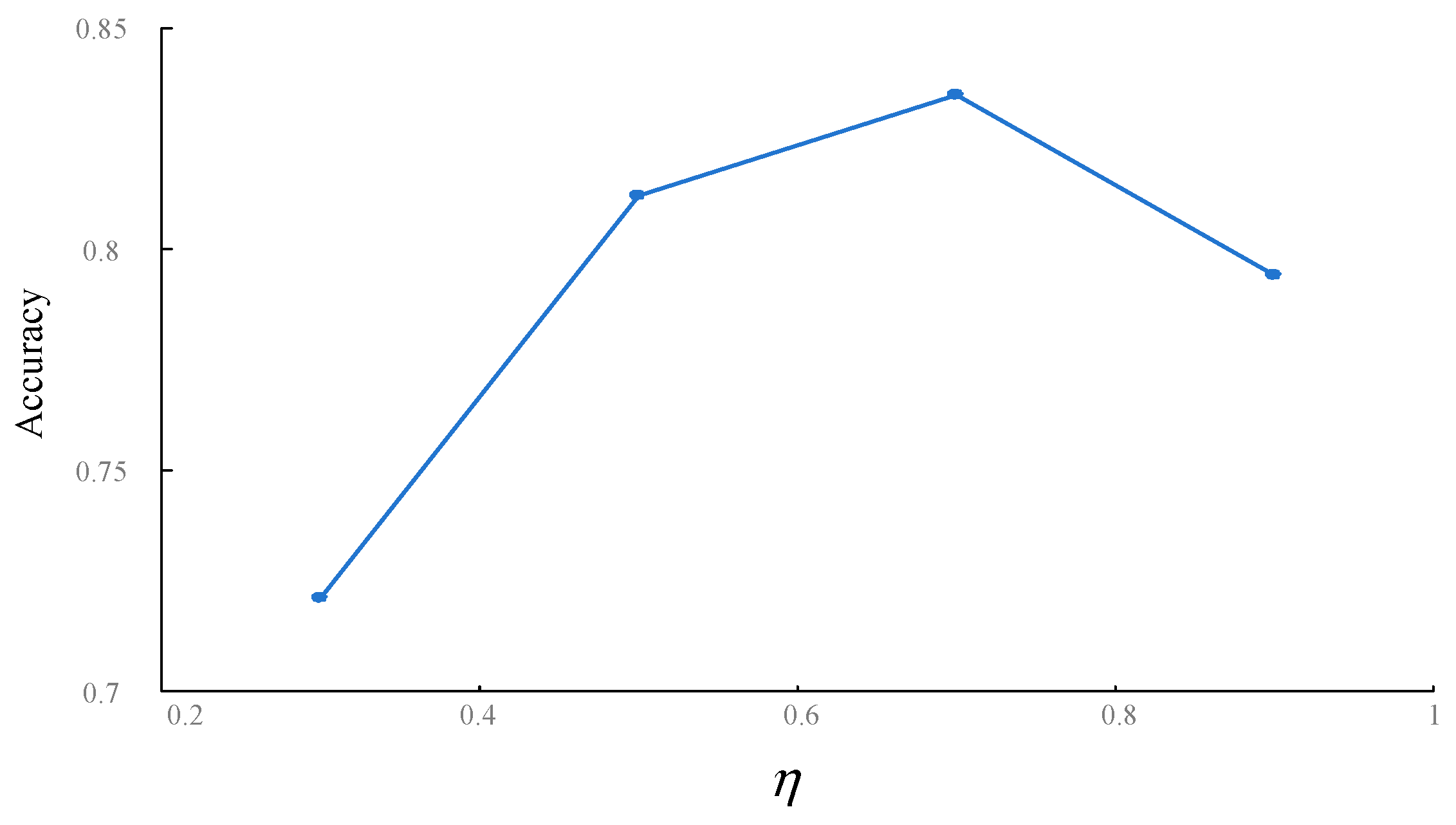
3.2.4. Calculate Fuzzy Measures for All Subsets of the Decision Information Set C
3.2.5. Full Sorting of Electricity Sale Packages
4. Discussion
5. Conclusions and Outlooks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| The sample customer | |
| Different sets of finite electricity sale packages | |
| Different sets of decision information | |
| The weights of each attribute based on the different decision information | |
| The similarity between the two key metrics of each customer. | |
| The optimal number of clusters. | |
| The yth image tag of Ui | |
| The mean value of image tags of Ui | |
| The clustering quality index for different pairs of clusters | |
| The prospect value function | |
| The risk attitude coefficients | |
| The risk attitude coefficients | |
| The loss aversion coefficient | |
| The mental weighting function | |
| Nonlinear weighting functions for gains | |
| Nonlinear weighting functions for losses | |
| The risk attitude coefficients for gains | |
| The risk attitude coefficients for losses | |
| Evaluation matrix | |
| A non-negative function on the set of electricity sale packages C | |
| Fuzzy measures of the customer | |
| The individual risk appetite | |
| Aversion coefficients | |
| The combined prospect superiority matrix | |
| The combined prospect inferiority matrix | |
| Fuzzy measure of the decision information set D | |
| The nth new customer | |
| The total number of new customers | |
| A symmetric linguistic term set |
Appendix A
- (U1) Monthly load factor
- (U2) Maximum monthly utilization hours
- (U3) Average weekday peak-to-valley differential rate
- (U4) Average non-working day peak-to-valley differential rate
- (U5) Peak load factor averages
- (U6) Mean flat-period load factor
- (U7) Mean value of valley load factor
Appendix B
- Step 1: Calculate the similarity between each customer portrait in U using Equation (A8)
- Step 2: Divide the customer set U into B parts and use the median customer portrait similarity as the customer self-similarity within each part, i.e., , where is the jth customer in .
- Step 3: Perform AP clustering for each segment of customers to obtain the set of cluster centers for each segment .
- Step 4: Form a new set of customers from the set of clustering centers for each part of the customers. If the number of customers in is greater than 400, return to Step 2; otherwise, go to Step 5.
- Step 5: Initialize the customer self-similarity in , where is the jth customer in and is the median value of the customer portrait similarity in .
- Step 6: Perform AP clustering on to obtain the number of stable clusters as , and determine whether customer Ui belongs to the clustering center based on Equation (A9):
- Step 7: Based on the clustering results obtained in Step 6, calculate the clustering quality indicator using Equation (A10).
- Step 8: Update the customer self-similarity using Equation (A11).
- Step 9: Determine whether the number of clusters satisfies . If so, the iteration ends and goes to step 10; otherwise, return to step 6 to continue the iteration.
- Step 10: Compare the corresponding clustering quality indicators under different number of clusters and determine the optimal number of clusters c* from Equation (2).
Appendix C
Appendix D
Appendix E
References
- China Energy Portal. Several Opinions of the Central Committee of the Communist Party of China and The State Council on Further Deepening the Reform of the Electric Power System. Pop. Util. Electr. 2016, 31, 6–7. [Google Scholar]
- Available online: https://www.gov.cn/xinwen/2015-12/01/content_5018612.htm (accessed on 7 November 2023).
- Cao, Q.; Zheng, M.; Ding, Y. Multi-attribute decision making model for customer evaluation and selection in electricity market. Power Syst. Technol. 2018, 42, 117–125. [Google Scholar]
- Ofgem. Available online: https://www.ofgem.gov.uk/energydata-and-research/data-portal/retail-market-indicators (accessed on 12 December 2023).
- Zhang, X.; Li, J.; Fu, H. UK retail electricity market reform and challenges. Autom. Electr. Power Syst. 2016, 40, 10–16. [Google Scholar] [CrossRef]
- iSelect. Available online: http://www.iselect.com.au/energy/ (accessed on 2 February 2023).
- He, Y.; Chen, F.; Ye, Y.; Liu, P.; Gao, X. Experience and enlightenment of electricity price package in australian retail market. Smart Power 2019, 47, 19–23+28. [Google Scholar]
- Lu, B.; Song, Y.; Wang, Y.; Wang, L. The operation mode and enlightenment of electricity sales company in Texas USA. Power Demand Side Manag. 2017, 19, 60–64. [Google Scholar]
- Wang, C.; Pang, M.; Chen, Y. Yunnan “to Amoy electricity” to explore the electricity side reform model. Econ. Inf. Dly. 2022, 005. Available online: https://link.cnki.net/doi/10.28419/n.cnki.njjck.2022.000171 (accessed on 12 December 2023). [CrossRef]
- Check24. Available online: http://www.check24.de/strom-gas/ (accessed on 2 February 2023).
- Power to Choose. 2019. Available online: https://www.powertochoose.org (accessed on 12 December 2023).
- Energy Made Easy. 2019. Available online: http://www.energymadeeasy.gov.au (accessed on 15 December 2023).
- Entega. 2023. Available online: https://www.entega.de/ (accessed on 7 January 2024).
- Eprimo. 2023. Available online: https://www.eprimo.de/ (accessed on 7 January 2024).
- Sun, Y.; Gu, W.; Li, B.; Cui, C.; Sun, C.; Zheng, A. Electricity-retail-market-reform oriented recommendation method of customer’s hierarchical clustering and pricing packages. Power Syst. Technol. 2018, 42, 447–454. [Google Scholar]
- Luo, F.; Ranzi, G.; Wang, X.; Dong, Z.Y. Social information filtering-based electricity retail plan recommender system for smart grid end customers. IEEE Trans. Smart Grid 2019, 10, 95–104. [Google Scholar] [CrossRef]
- Wang, M. The System and Price Designing Method Of Retail Electricity Price Package Under the Opening of Power Sale Side. Ph.D. Thesis, North China Electricity Power University, Beijing, China, 2021. [Google Scholar]
- Feng, R.; Hu, J.; Jiang, G.; Huang, C.; Tang, W.; Zhao, L.; Zhang, K.; Huang, X.; Zhu, W. Recommendation Pattern of Electricity Sales Package based on Improved Clustering and Spark Framework. In Proceedings of the 2022 IEEE International Conference on Advances in Electrical Engineering and Computer Applications, Dalian, China, 20–21 August 2022; pp. 293–299. [Google Scholar]
- Zhang, Z.; Wang, Y.; Lin, Z.; Ma, Y.; Lu, F.; Yang, L. Electricity plan recommendation method based on implicit score of electricity plan and customer portrait. Autom. Electr. Power Syst. 2023, 47, 91–101. [Google Scholar]
- Qu, Z.; Feng, R.; Qu, N. Recommendation method of electricity selling packages based on optimal feature subset of electricity trading customers. Power Syst. Technol. 2018, 42, 3298–3304. [Google Scholar]
- He, Y.; Wang, M.; Yu, J.; He, Q.; Sun, H.; Sun, F. Research on hybrid optimal selection of electricity price packages based on power customer characteristics and multi-attribute utility in China. Energies 2020, 13, 2693. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, K.; Kong, W.; Dong, Z.Y. Collaborative filtering-based electricity plan recommender system. IEEE Trans. Ind. Inform. 2019, 15, 1393–1404. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, K.; Kong, W.; Dong, Z.Y.; Qian, F. Bayesian hybrid collaborative filtering-based residential electricity plan recommender system. IEEE Trans. Ind. Inform. 2019, 15, 4731–4741. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Q.; Chen, H.; Zhang, Z.; Lin, Z.; Yang, Z. Recommendation method for electricity retail plan based on bi-level affinity propagation clustering and multigranular hesitant fuzzy sets. Autom. Electr. Power Syst. 2023, 47, 96–104. [Google Scholar]
- Fan, Z.; Chen, F.; Zhang, X. Method for hybrid multiple attribute decision making based on cumulative prospect theory. J. Syst. Eng. 2012, 27, 295–301. [Google Scholar]
- Chang, J.; Du, Y.; Liu, W. Pythagorean hesitant fuzzy risky multi-attribute decision making method based on cumulative prospect theory and vikor. Oper. Res. Manag. Sci. 2022, 31, 50–56. [Google Scholar]
- Cai, W.; Zhang, J.; Wu, X.; Wu, Z.; Yue, F.; Liu, D.; Rao, G. Comprehensive evaluation of carbon emission reduction technologies for thermal power generation enterprises based on hesitant huzzy set-prospect theory. Water Resour. Hydropower Eng. 2024, 1–14. Available online: http://kns.cnki.net/kcms/detail/10.1746.TV.20240924.1134.002.html (accessed on 12 December 2023).
- Zhang, X.; Fan, Z. A Method for Risky Interval Multiple Attribute Decision Making Based on Prospect Theory. Oper. Res. Manag. Sci. 2012, 21, 44–50. [Google Scholar]
- Ma, Q. Hesitant fuzzy multi-attribute group decision-making method based on prospect theory. Comput. Eng. Appl. 2015, 51, 249–253. [Google Scholar]
- Chou, J.-S.; Ongkowijoyo, C.S. Reliability-based decision making for selection of ready-mix concrete supply using stochastic superiority and inferiority ranking method. Reliab. Eng. Syst. Saf. 2015, 137, 29–39. [Google Scholar] [CrossRef]
- Xu, X. The sir method: A superiority and inferiority ranking method for multiple criteria decision making. Eur. J. Oper. Res. 2001, 131, 587–602. [Google Scholar] [CrossRef]
- Zhao, N.; Xu, Z.; Ren, Z. Hesitant fuzzy linguistic prioritized superiority and inferiority ranking method and its application in sustainable energy technology evaluation. Inf. Sci. 2019, 478, 239–257. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Zou, J.; Guo, Y.; Shang, Z.; Liu, H. Hybrid Multiple Attribute Group Decision Making Method in Equipment Suppliers Selection. J. Inf. Eng. Univ. 2017, 18, 458–463. [Google Scholar]
- Qin, J. Generalized Pythagorean Fuzzy Maclaurin Symmetric Means and Its Application to Multiple Attribute SIR Group Decision Model. Int. J. Fuzzy Syst. 2018, 20, 943–957. [Google Scholar] [CrossRef]
- Chan, J.W.K. Enhancing organisational resilience: Application of viable system model and MCDA in a small Hong Kong company. Int. J. Prod. Res. 2011, 49, 5545–5563. [Google Scholar] [CrossRef]
- Yang, J.; Li, D. Selection Method of Cooperative Innovation Partners with Dependent Attributes and Fuzzy Information. Oper. Reaseach Manag. Sci. 2016, 25, 53–58. [Google Scholar]
- Tian, G.; Hao, N.; Zhou, M.; Pedrycz, W.; Zhang, C.; Ma, F.; Li, Z. Fuzzy grey choquet integral for evaluation of multicriteria decision making problems with interactive and qualitative indices. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1855–1868. [Google Scholar] [CrossRef]
- Feng, Y.; Dang, Y.; Wang, J.; Yang, Z. Grey incidence decision-making method with mixed information based on 2-additive choquet integral and its application. Chin. J. Manag. Sci. 2023, 1–12. [Google Scholar] [CrossRef]
- Liu, N. Multi attribute group decision making method of intuitionistic linguistic todim based on choquet integral. Math. Pract. Theory 2020, 50, 10–19. [Google Scholar]
- Deva, K.; Mohanaselvi, S. Picture fuzzy choquet integral based geometric aggregation operators and its application to multi attribute decision-making. Math. Model. Eng. Probl. 2022, 9, 1043–1052. [Google Scholar] [CrossRef]
- Yang, J.; Cai, Z.; Zheng, Z.; Lai, L.; Xu, Z. A prospect theory and attribute association based probabilistic linguistic fuzzy sir method for multi-attribute group decision-making and its application. Chin. J. Manag. Sci. 2024, 1–15. [Google Scholar] [CrossRef]
- Hung, W.C.; Liu, Y.C.; Wu, Y.L.; Tang, C.Y.; Hor, M.K. Adaptive affinity propagation clustering in mapreduce environment. In Technologies and Applications of Artificial Intelligence; Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2014; Volume 8916, pp. 209–218. [Google Scholar]
- Chen, S.; Wang, J.; Wang, T. Cloud-based ERP system selection based on extended probabilistic linguistic MULTIMOORA method and Choquet integral operator. Comput. Appl. Math. 2019, 38. [Google Scholar] [CrossRef]
- Murofushi, T.; Sugeno, M. An interpretation of fuzzy measures and the choquet integral as an integral with respect to a fuzzy measure. Fuzzy Sets Syst. 1989, 29, 201–227. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Xu, M. Collaborative optimization of distributed energy resources in microgrid based on prospect theory under the framework of blockchain. Syst. Eng. Theory Pract. 2022, 42, 2551–2564. [Google Scholar]
- Ma, Y.; Ma, X.; Chen, H.; Lei, Y. Electricity sale package recommendation method based on unbalanced evaluation and incomplete weight multi - granularity fuzzy language set. Electr. Power Syst. Res. 2023, 221, 109382. [Google Scholar] [CrossRef]
- Ma, Y.; Zheng, R.; Lu, Y.; Zhang, Z.; Wang, Y.; Lin, Z.; Yang, L.; Liang, H.; Liu, P.X. Electricity retail plan recommendation method based on multigranular hesitant fuzzy sets and an improved non-negative latent factor model. IEEE Trans. Energy Mark. Policy Regul. 2024, 2, 146–161. [Google Scholar] [CrossRef]
- Zhang, Z. Research on Optimization of Operation Strategy of Power Selling Company Including Deviation Assessment and Demand Response. Ph.D. Thesis, Zhejiang University, Zhejiang, China, 2022. [Google Scholar]
| Key Attributes | Description |
|---|---|
| Monthly Load (kWh) | Average monthly electricity consumption of the customer. |
| Load Factor | Reflects the fluctuation of load change for the whole month. |
| Value-Added Services Pref. | Preference for value-added services such as power quality, energy management, etc. |
| Incentive Policy Pref. | Preference for incentive policies offered by electricity sale packages. |
| Renewable Energy Pref. | Preference for packages with a higher proportion of renewable energy sources. |
| Price Sensitivity | The influence of the price of electricity sale packages on the customer’s choice. |
| Category | Monthly Load (kWh) | Load Factor | Value-Added Services Pref. | Incentive Policy Pref. | Renewable Energy Pref. | Price Sensitivity | |
|---|---|---|---|---|---|---|---|
| Surveyed | Services | 2655.93 | 0.62 | 0.57 | 0.72 | 0.67 | 0.62 |
| Industry | 3,066,650.61 | 0.57 | 0.53 | 0.83 | 0.73 | 0.89 | |
| Residential | 1730.03 | 0.36 | 0.17 | 0.57 | 0.26 | 0.47 | |
| Agriculture | 264.96 | 0.37 | 0.39 | 0.47 | 0.52 | 0.53 | |
| Average | Services | 2500 | 0.60 | 0.55 | 0.75 | 0.65 | 0.60 |
| Industry | 3,000,000 | 0.60 | 0.50 | 0.80 | 0.70 | 0.90 | |
| Residential | 1500 | 0.35 | 0.20 | 0.55 | 0.30 | 0.50 | |
| Agriculture | 300 | 0.45 | 0.40 | 0.50 | 0.50 | 0.55 |
| Electricity Sale Packages | The Unit Price | Value-Added Service | Incentive Policy | Proportion of Renewable Energy/% | Whether It Is a Fixed Package |
|---|---|---|---|---|---|
| C1 | 0.59 (<500 kWh) 0.61 (500–1000 kWh) 0.87 (>1000 kWh) | Energy efficiency management | An 8% discount for on-time billing | 15 | be |
| C2 | 0.48 (<500 kWh) 0.67 (500–1000 kWh) 0.93 (>1000 kWh) | High electricity quality | Reward 10% of the battery percentage | 5 | be |
| C3 | 0.86 (Peak:10:00–12:00, 13:00–19:00) 0.60 (Flat: 06:00–10:00, 12:00–13:00, 19:00–22:00) 0.30 (Valley: 22:00–06:00 next day) | Energy efficiency management | 8%discount for on-time billing | 15 | clogged |
| C4 | 0.80 (Peak:10:00–12:00, 13:00–19:00) 0.63 (Flat: 06:00–10:00, 12:00–13:00, 19:00–22:00) 0.30 (Valley: 22:00–06:00 next day) | High electricity quality | Reward 10% of the battery percentage | 5 | clogged |
| Electricity Sale Packages | The Recommended Ranking in This Paper | Simulated Actual Ranking |
|---|---|---|
| C1 | 2 | 3 |
| C2 | 4 | 4 |
| C3 | 1 | 1 |
| C4 | 3 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Qiu, L.; Ma, Y. An Electricity Sale Package Recommendation Method Based on Prospect Strengths and Weaknesses Degree and Choquet Integral. Appl. Sci. 2024, 14, 11905. https://doi.org/10.3390/app142411905
Wu Y, Qiu L, Ma Y. An Electricity Sale Package Recommendation Method Based on Prospect Strengths and Weaknesses Degree and Choquet Integral. Applied Sciences. 2024; 14(24):11905. https://doi.org/10.3390/app142411905
Chicago/Turabian StyleWu, Yufei, Lifan Qiu, and Yuanqian Ma. 2024. "An Electricity Sale Package Recommendation Method Based on Prospect Strengths and Weaknesses Degree and Choquet Integral" Applied Sciences 14, no. 24: 11905. https://doi.org/10.3390/app142411905
APA StyleWu, Y., Qiu, L., & Ma, Y. (2024). An Electricity Sale Package Recommendation Method Based on Prospect Strengths and Weaknesses Degree and Choquet Integral. Applied Sciences, 14(24), 11905. https://doi.org/10.3390/app142411905





