A Robot Error Prediction and Compensation Method Using Joint Weights Optimization Within Configuration Space
Abstract
1. Introduction
2. Spatial Similarity Analysis and Sampling Method of Robot Errors in Configuration Space
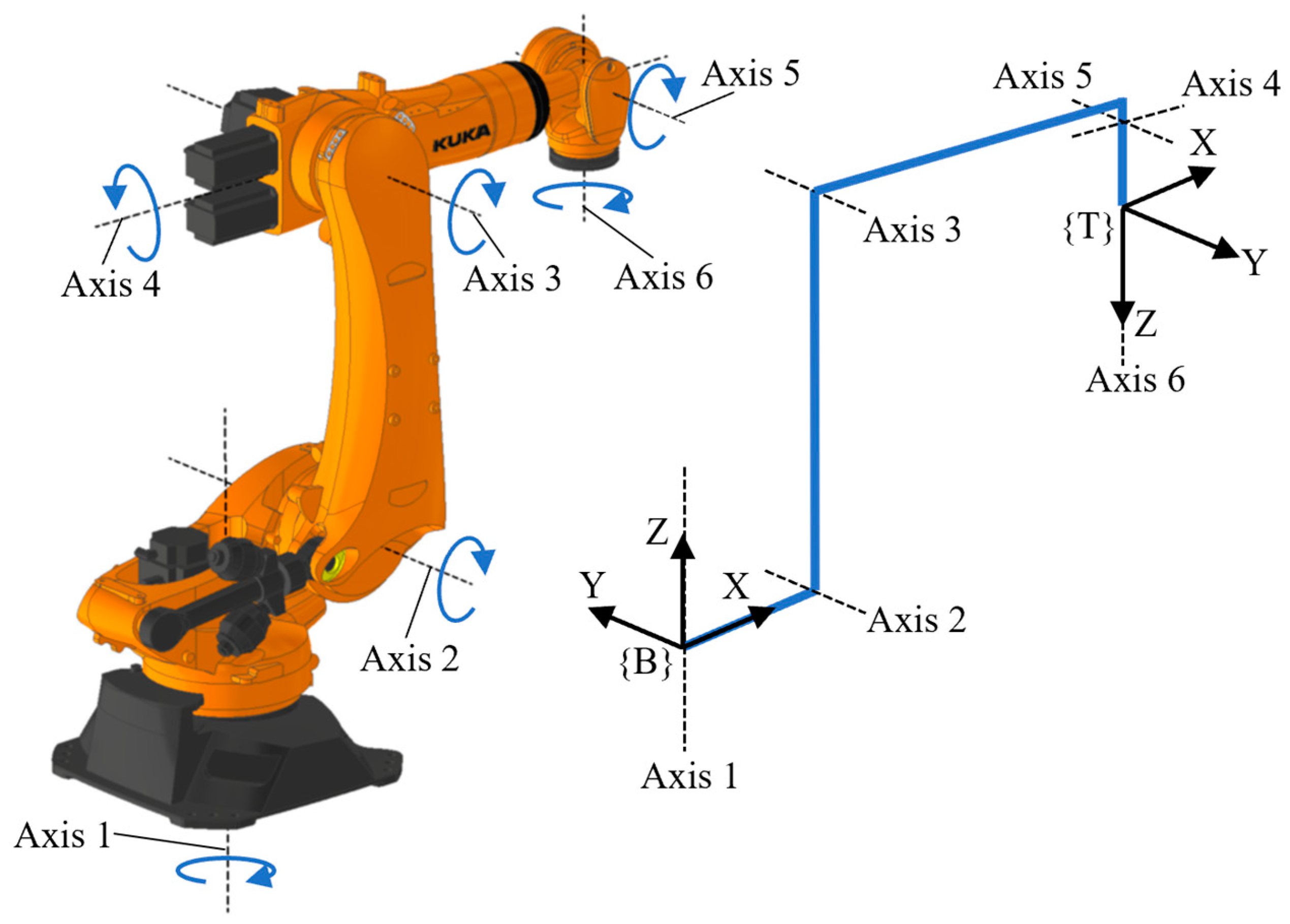
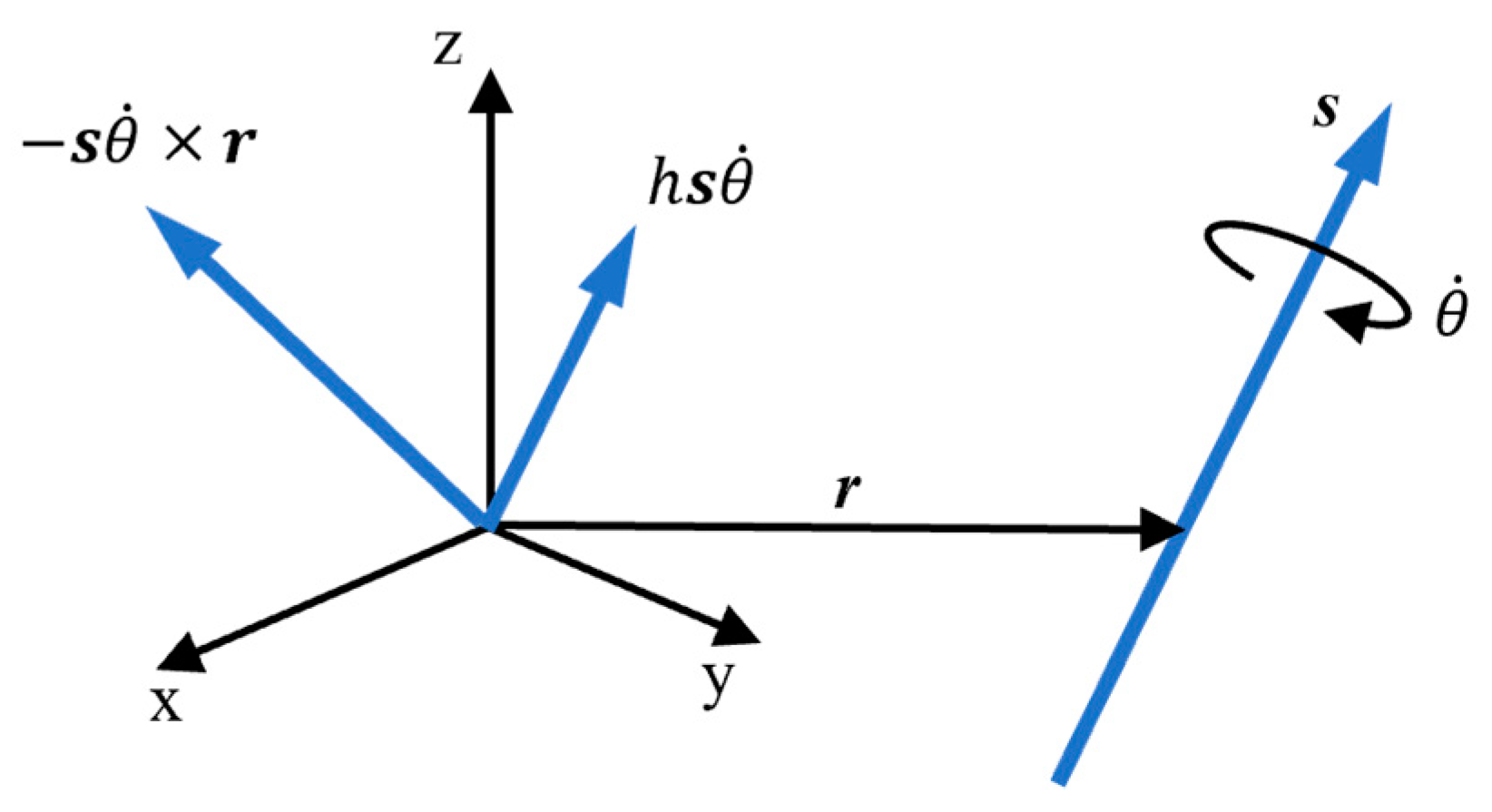
2.1. Robot Kinematics Model Construction
2.2. Spatial Distribution Patterns of Robot Errors in Configuration Space
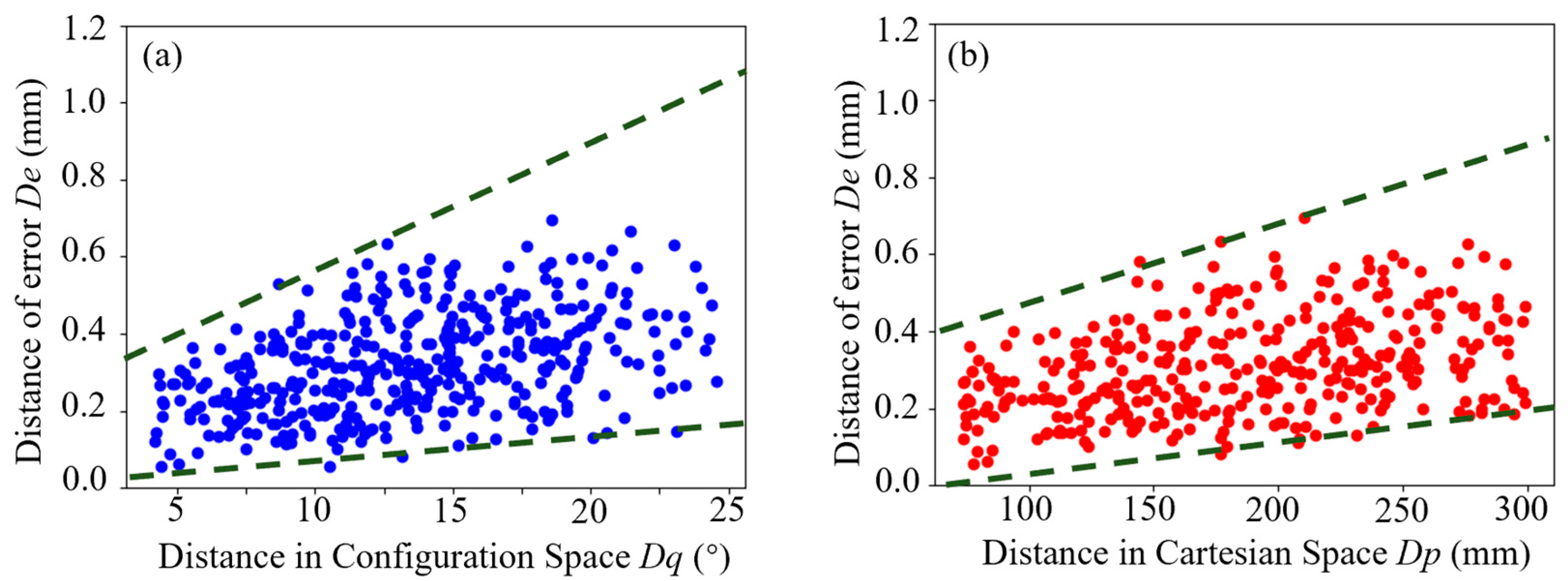
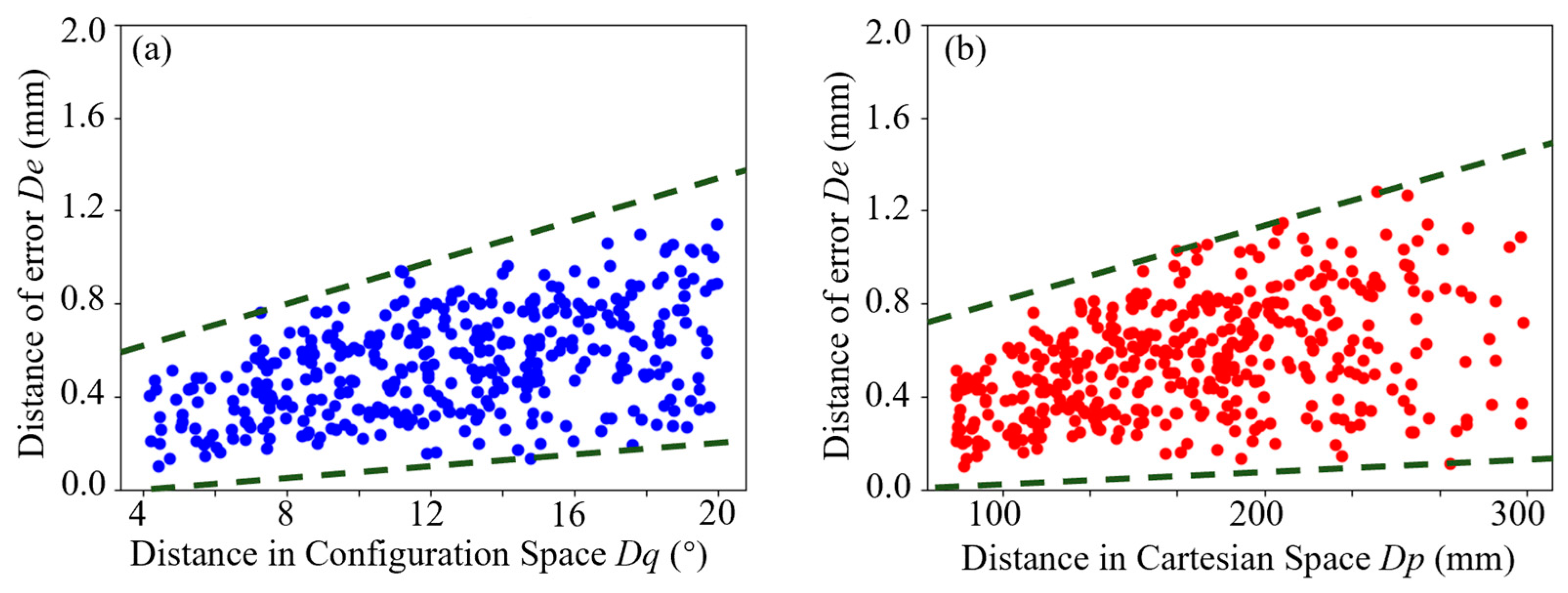
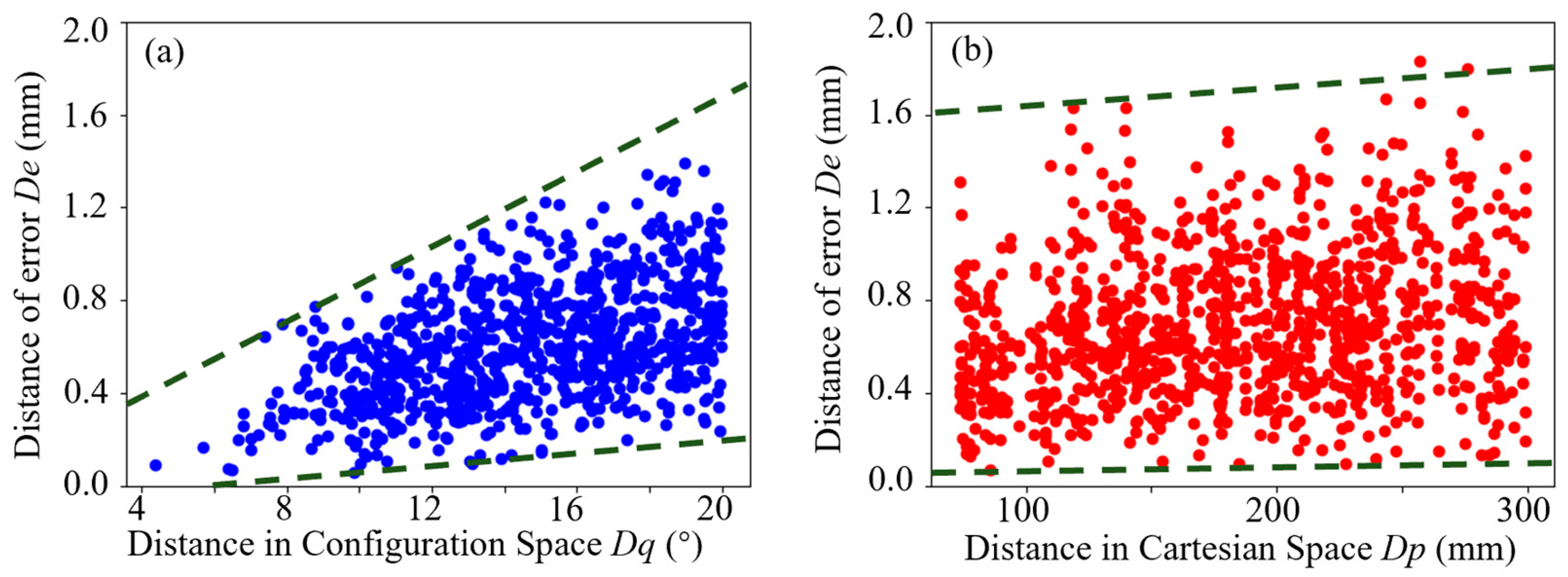
2.3. Experimental Analysis of Robot Error Spatial Similarity in Configuration Space
2.4. Sampling Method of Robot Task Workspace in Configuration Space
3. Robot Error Prediction and Accuracy Compensation Method
3.1. Anisotropy Analysis of Robot Positioning Error Distribution in Configuration Space
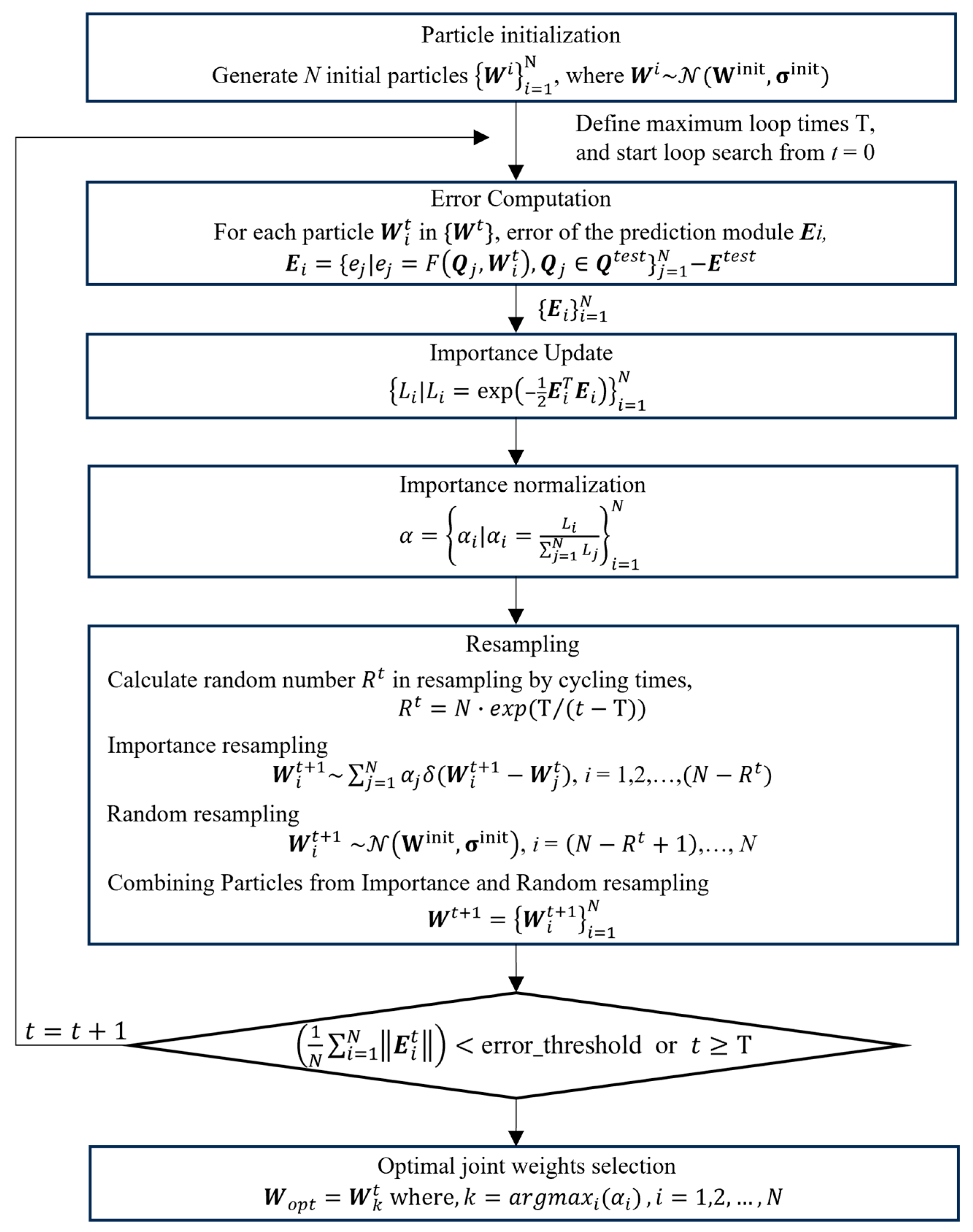
3.2. Spatial-Interpolation-Based Unbiased Error Estimation Method with Joint Weights Optimization
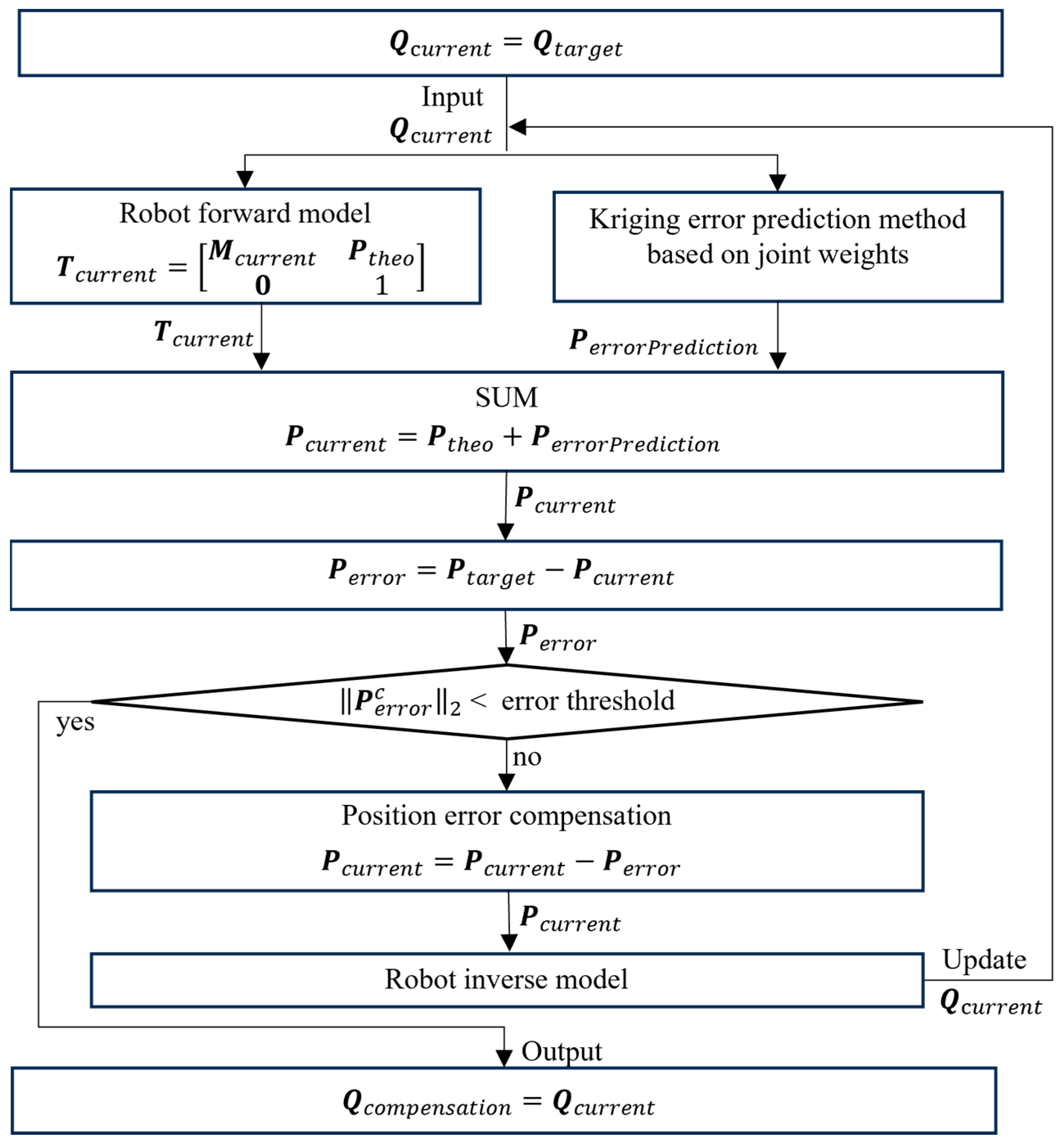
3.3. Cycling Search Method for Joint Angle Compensation
4. Experiments and Results
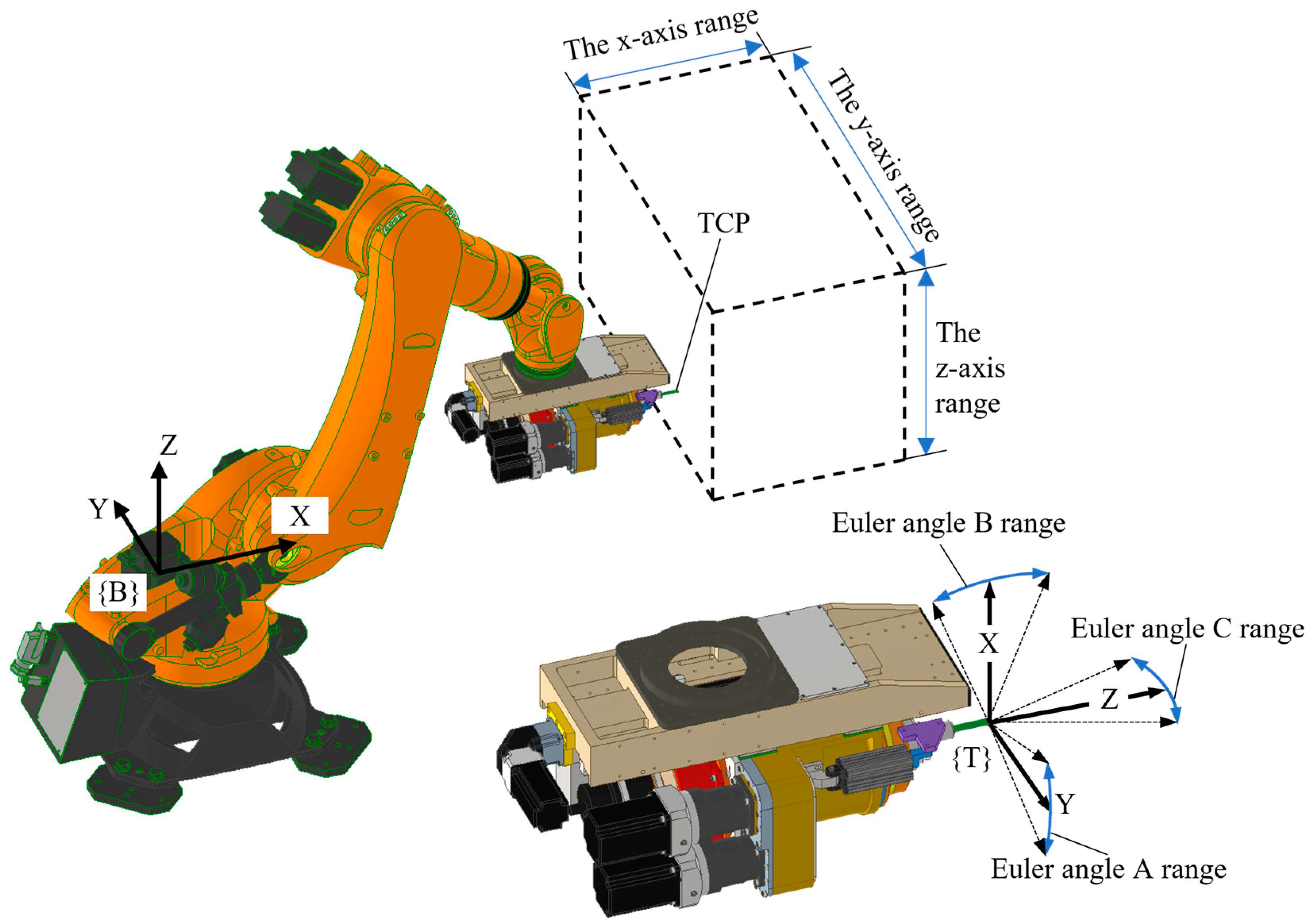
4.1. Establishment of Experimental Conditions
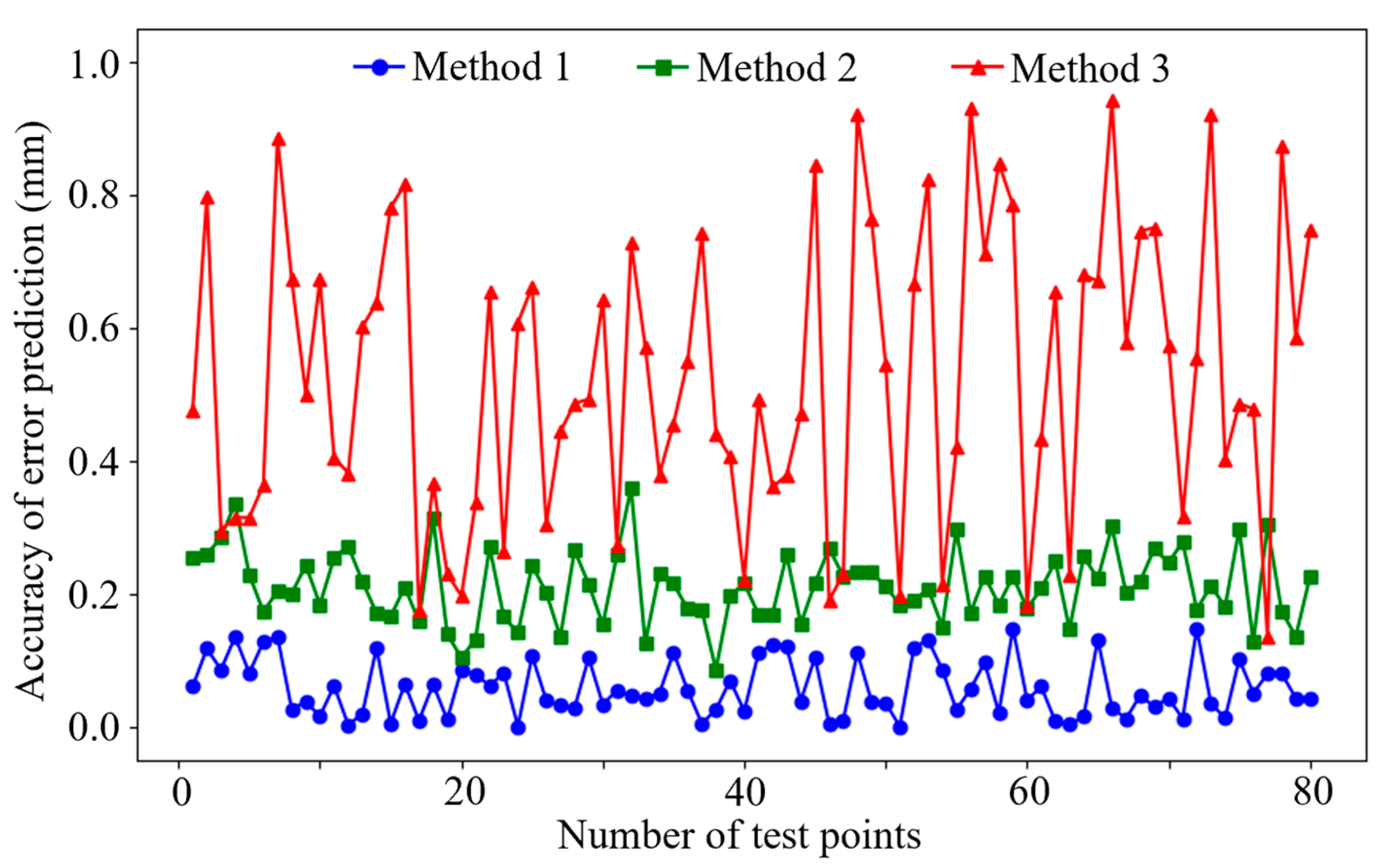
4.2. Experimental Results of Robot Error Prediction and Accuracy Compensation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Denavit, J.; Hartenberg, R.S. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices. J. Appl. Mech. 2021, 22, 215–221. [Google Scholar] [CrossRef]
- Hayati, S.; Mirmirani, M. Improving the absolute positioning accuracy of robot manipulators. J. Robot. Syst. 1985, 2, 397–413. [Google Scholar] [CrossRef]
- Okamura, K.; Park, F.C. Kinematic calibration using the product of exponentials formula. Robotica 1996, 14, 415–421. [Google Scholar] [CrossRef]
- Nubiola, A.; Bonev, I.A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker. Robot. Comput.-Integr. Manuf. 2013, 29, 236–245. [Google Scholar] [CrossRef]
- Chen, G.; Wang, H.; Lin, Z. Determination of the Identifiable Parameters in Robot Calibration Based on the POE Formula. IEEE Trans. Robot. 2014, 30, 1066–1077. [Google Scholar] [CrossRef]
- Qi, C.K.; Gao, F.; Zhao, X.C.; Wang, Q.; Sun, Q. Distortion Compensation for a Robotic Hardware-In-The-Loop Contact Simulator. IEEE Trans. Control. Syst. Technol. 2018, 26, 1170–1179. [Google Scholar] [CrossRef]
- Alam, M.M.; Ibaraki, S.; Fukuda, K.; Morita, S.; Usuki, H.; Otsuki, N.; Yoshioka, H. Inclusion of Bidirectional Angular Positioning Deviations in the Kinematic Model of a Six-DOF Articulated Robot for Static Volumetric Error Compensation. IEEE/ASME Trans. Mechatron. 2022, 27, 4339–4349. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, Q.J.; Sun, Y.L. Model-Based Compensation and Pareto-Optimal Trajectory Modification Method for Robotic Applications. Int. J. Precis. Eng. Manuf. 2019, 20, 1127–1137. [Google Scholar] [CrossRef]
- Bai, M.; Zhang, M.L.; Zhang, H.; Li, M.H.; Zhao, J.; Chen, Z.G. Calibration Method Based on Models and Least-Squares Support Vector Regression Enhancing Robot Position Accuracy. IEEE Access 2021, 9, 136060–136070. [Google Scholar] [CrossRef]
- Wan, H.Y.; Chen, S.L.; Liu, Y.S.; Jin, C.C.; Chen, F.R.; Wang, J.; Zhang, C.; Yang, G.L. A Hybrid Analytical and Data-driven Modeling Approach for Calibration of Heavy-duty Cartesian Robot. In Proceedings of the IEEE Advanced Intelligent Mechatronics, Boston, MA, USA, 6–9 July 2020; pp. 1286–1291. [Google Scholar]
- Li, L.; Chen, B.Y.; Wang, C.J. Positioning Accuracy and Numerical Analysis of the Main Casting Mechanism of the Hybrid Casting Robot. Math. Probl. Eng. 2022, 2022, 6140729. [Google Scholar] [CrossRef]
- Deng, K.N.; Gao, D.; Ma, S.D.; Zhao, C.; Lu, Y. Elasto-geometrical error and gravity model calibration of an industrial robot using the same optimized configuration set. Robot. Comput. Integr. Manuf. 2023, 83, 102558. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, H.; Ding, H. Real-time path correction of industrial robots in machining of large-scale components based on model and data hybrid drive. Robot. Comput. Integr. Manuf. 2023, 79, 102447. [Google Scholar] [CrossRef]
- Wang, Y.X.; Chen, Z.W.; Zu, H.F.; Zhang, X.; Mao, C.T.; Wang, Z.R. Improvement of Heavy Load Robot Positioning Accuracy by Combining a Model-Based Identification for Geometric Parameters and an Optimized Neural Network for the Compensation of Nongeometric Errors. Complexity 2020, 2020, 5896813. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, Z.; Hou, Z.C.; Yang, W.L.; Liang, J.M.; Yang, G.; Wang, J.; Wang, H.M.; Han, C. A Systematic Error Compensation Strategy Based on an Optimized Recurrent Neural Network for Collaborative Robot Dynamics. Appl. Sci. 2020, 10, 6743. [Google Scholar] [CrossRef]
- Peng, P.; Liu, Q.; Li, B.; Peng, W.; Wang, X.; Wang, J. A Model-Data Compound Driven Method for Compensating Robot Tracking Error. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Heilongjiang, China, 6–9 August 2023; pp. 979–985. [Google Scholar]
- Liao, Z.Y.; Wu, J.Z.; Wu, H.M.; Xie, H.L.; Wang, Q.H.; Zhou, X.F. Profile Error Estimation and Hierarchical Compensation Method for Robotic Surface Machining. IEEE Robot. Autom. Lett. 2024, 9, 3195–3202. [Google Scholar] [CrossRef]
- Zeng, Y.F.; Tian, W.; Liao, W.H. Positional error similarity analysis for error compensation of industrial robots. Robot. Comput. Integr. Manuf. 2016, 42, 113–120. [Google Scholar] [CrossRef]
- Jiao, J.C.; Tian, W.; Zhang, L.; Li, B.; Hu, J.S. Variable Parameters Stiffness Identification and Modeling for Positional Compensation of Industrial Robots. IOP J. Phys. Conf. Ser. 2020, 1487, 012046. [Google Scholar] [CrossRef]
- Cai, Y.; Yuan, P.J.; Chen, D.D. A flexible calibration method connecting the joint space and the working space of industrial robots. Ind. Robot. Int. J. Robot. Res. Appl. 2018, 45, 407–415. [Google Scholar] [CrossRef]
- Cao, S.; Cheng, Q.; Guo, Y.; Zhu, W.; Wang, H.; Ke, Y. Pose error compensation based on joint space division for 6-DOF robot manipulators. Precis. Eng. 2022, 74, 195–204. [Google Scholar] [CrossRef]
- Angelidis, A.; Vosniakos, G.C. Prediction and compensation of relative position error along industrial robot end-effector paths. Int. J. Precis. Eng. Manuf. 2014, 15, 63–73. [Google Scholar] [CrossRef]
- Yuan, P.J.; Chen, D.D.; Wang, T.M.; Cao, S.Q.; Cai, Y.; Xue, L. A compensation method based on extreme learning machine to enhance absolute position accuracy for aviation drilling robot. Adv. Mech. Eng. 2018, 10, 1687814018763411. [Google Scholar] [CrossRef]
- DChen, D.; Wang, T.M.; Yuan, P.J.; Sun, N.; Tang, H.Y. A positional error compensation method for industrial robots combining error similarity and radial basis function neural network. Meas. Sci. Technol. 2019, 30, 125010. [Google Scholar]
- Tiboni, M.; Legnani, G.; Pellegrini, N. Study of Neural-Kinematics Architectures for Model-Less Calibration of Industrial Robots. J. Robot. Mechatron. 2021, 33, 158–171. [Google Scholar] [CrossRef]
- Chen, G.; Yang, J.Z.; Xiang, H.; Ou, D.J. New positional accuracy calibration method for an autonomous robotic inspection system. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 177. [Google Scholar] [CrossRef]
- Xu, S.; Ding, D.W.; Huang, Z.R.; Xu, F.Y. Positioning Error Compensation of Bending Process Based on Improved Elman Neural Network. In Proceedings of the 2022 41st Chinese Control Conference (CCC) (2022), Hefei, China, 25–27 July 2022; pp. 1745–1750. [Google Scholar]
- Zhang, X.; Xu, Y.; Yang, Y.; Lin, C. Neural Network Based Friction Compensation for Joints in Robotic Motion Control. In Proceedings of the 2022 2nd International Conference on Computer, Control and Robotics (ICCCR) (2022), Shanghai, China, 18–20 March 2022; pp. 75–80. [Google Scholar]
- Tan, S.Z.; Yang, J.X.; Ding, H. A prediction and compensation method of robot tracking error considering pose-dependent load decomposition. Robot. Comput. Integr. Manuf. 2023, 80, 102476. [Google Scholar] [CrossRef]
- Li, G.H.; Zhu, W.D.; Dong, H.Y.; Ke, Y.L. Error compensation based on surface reconstruction for industrial robot on two-dimensional manifold. Ind. Robot. Int. J. Robot. Res. Appl. 2022, 49, 735–744. [Google Scholar] [CrossRef]
- Zeng, Y.F.; Tian, W.; Li, D.W.; He, X.X.; Liao, W.H. An error-similarity-based robot positional accuracy improvement method for a robotic drilling and riveting system. Int. J. Adv. Manuf. Technol. 2017, 88, 2745–2755. [Google Scholar] [CrossRef]
- Guo, Y.J.; Gao, X.H.; Liang, W.; Miao, L.; Zhao, S.B.; Dong, H.Y. Robot joint space grid error compensation based on three-dimensional discrete point space circular fitting. CIRP J. Manuf. Sci. Technol. 2024, 50, 140–150. [Google Scholar] [CrossRef]
- Dufera, A.G.; Liu, T.; Xu, J. Regression models of Pearson correlation coefficient. Stat. Theory Relat. Fields 2023, 7, 97–106. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]





| Load Status | Pose Variation Status | PCC | p-Value |
|---|---|---|---|
| 0 kg | Pose fixed | 0.469 | 1.236 × 10−22 |
| 120 kg | Pose fixed | 0.424 | 3.498 × 10−12 |
| 0 kg | Pose varied | 0.472 | 3.671 × 10−26 |
| 120 kg | Pose varied | 0.403 | 1.261 × 10−26 |
| Load Status | Pose Variation Status | PCC | p-Value |
|---|---|---|---|
| 0 kg | Pose fixed | 0.440 | 1.435 × 10−14 |
| 120 kg | Pose fixed | 0.381 | 1.854 × 10−12 |
| 0 kg | Pose varied | 0.214 | 1.021 × 10−12 |
| 120 kg | Pose varied | 0.226 | 1.414 × 10−14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, F.; Wei, J.; Feng, Q.; Dong, Z.; Kang, R.; Guo, D.; Yang, J. A Robot Error Prediction and Compensation Method Using Joint Weights Optimization Within Configuration Space. Appl. Sci. 2024, 14, 11682. https://doi.org/10.3390/app142411682
Meng F, Wei J, Feng Q, Dong Z, Kang R, Guo D, Yang J. A Robot Error Prediction and Compensation Method Using Joint Weights Optimization Within Configuration Space. Applied Sciences. 2024; 14(24):11682. https://doi.org/10.3390/app142411682
Chicago/Turabian StyleMeng, Fantong, Jinhua Wei, Qianyi Feng, Zhigang Dong, Renke Kang, Dongming Guo, and Jiankun Yang. 2024. "A Robot Error Prediction and Compensation Method Using Joint Weights Optimization Within Configuration Space" Applied Sciences 14, no. 24: 11682. https://doi.org/10.3390/app142411682
APA StyleMeng, F., Wei, J., Feng, Q., Dong, Z., Kang, R., Guo, D., & Yang, J. (2024). A Robot Error Prediction and Compensation Method Using Joint Weights Optimization Within Configuration Space. Applied Sciences, 14(24), 11682. https://doi.org/10.3390/app142411682






