Airwave Noise Identification from Seismic Data Using YOLOv5
Abstract
1. Introduction
2. Related Works
3. The Basic Principles of YOLOv5
3.1. Network Architecture
3.2. Output Layer and Loss Function
4. The Training of YOLOv5m
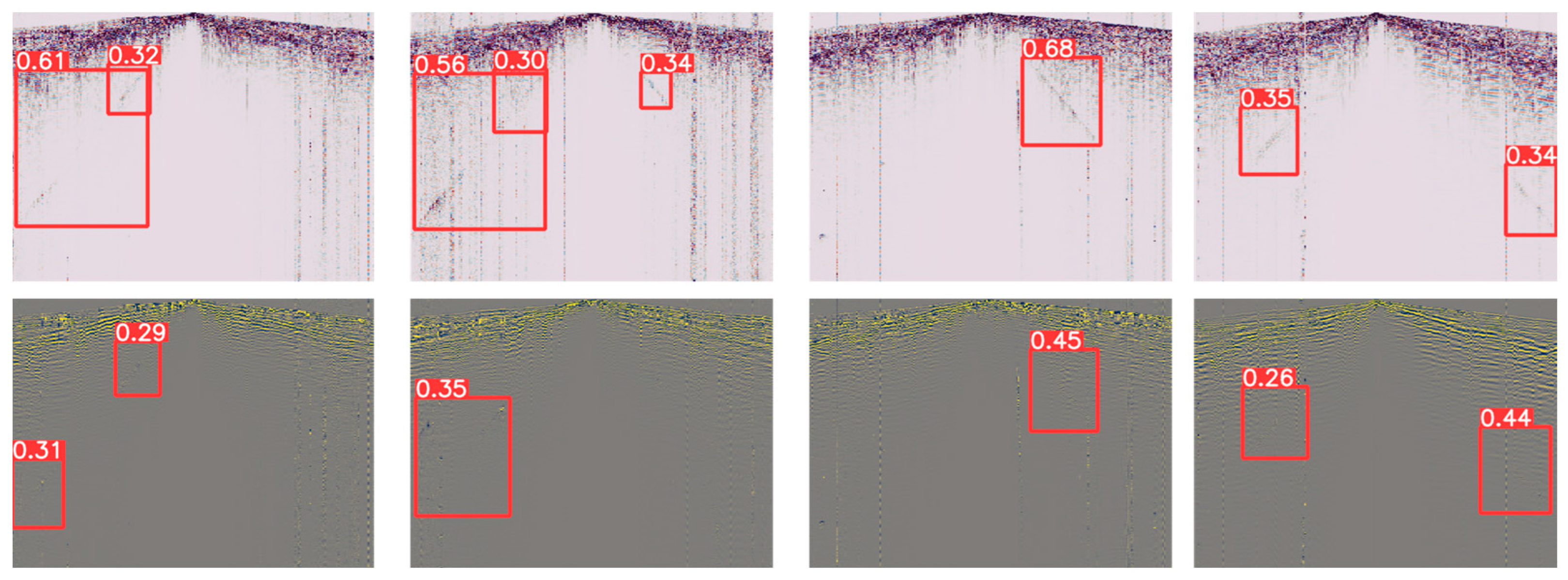
5. Results
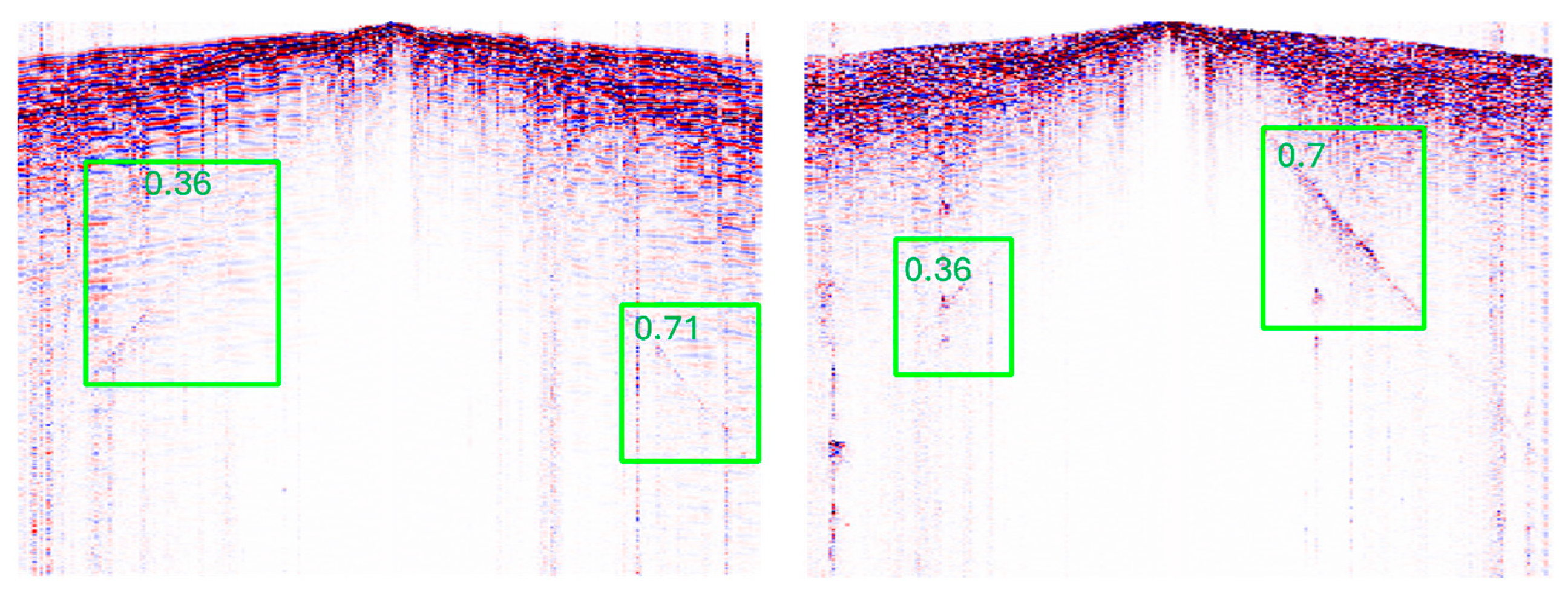
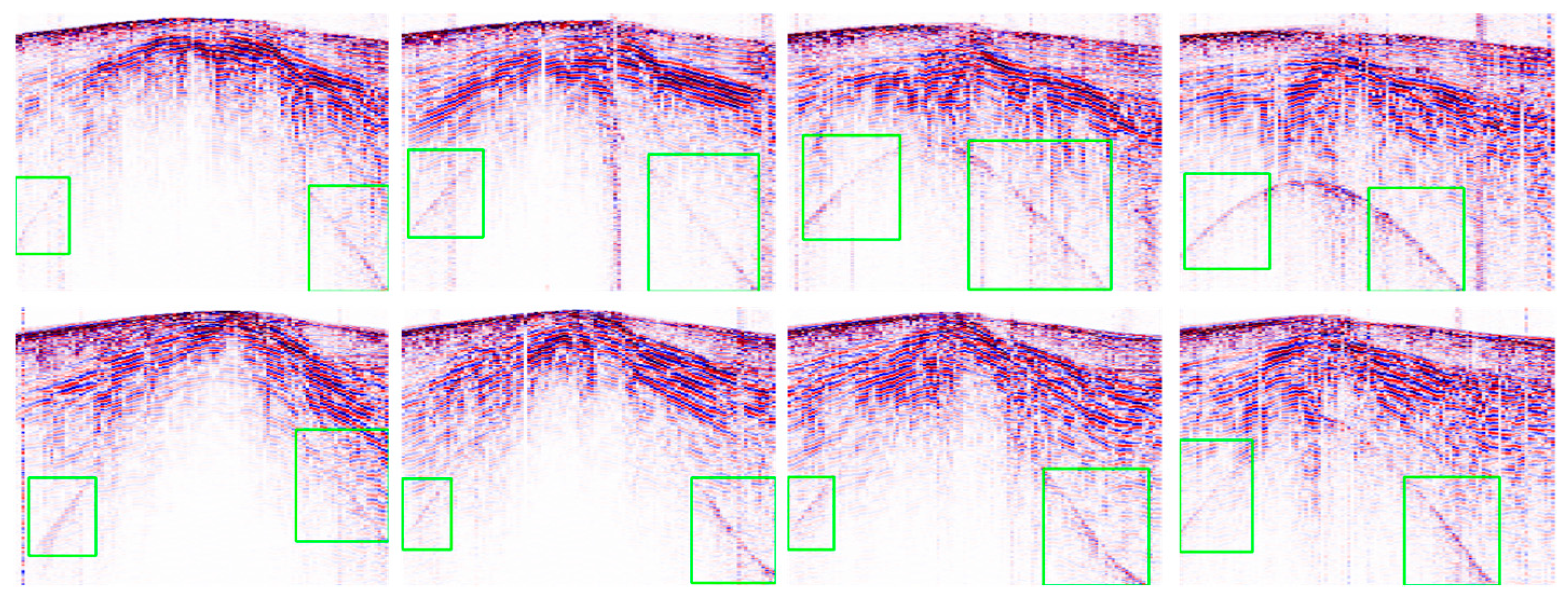
6. Field Data Validation
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, X. Adaptive detection and suppression method for sub-frequency division of acoustic waves and strong energy interference. Oil Geophys. Explor. 1999, 34, 373–380. [Google Scholar]
- Mondol, N.H. Seismic exploration. In Petroleum Geoscience: From Sedimentary Environments to Rock Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2015; pp. 427–454. [Google Scholar]
- Karastathis, V.; Louis, I.F. The airwave in hammer reflection seismic data. Bol. Geofis. Teor. Appl 1997, 39, 13–23. [Google Scholar]
- Meunier, J. Seismic Acquisition from Yesterday to Tomorrow; Society of Exploration Geophysicists: Tulsa, OK, USA, 2011. [Google Scholar]
- Talagapu, K.K. 2D and 3D Land Seismic Data Acquisition and Seismic Data Processing; Department of Geophysics, College of Science and Technology, Andhra University: Visakhapatnam, India, 2005. [Google Scholar]
- Wang, Y.; Zhang, G.; Chen, T.; Liu, Y.; Shen, B.; Liang, J.; Hu, G. Data and model dual-driven seismic deconvolution via error-constrained joint sparse representation. Geophysics 2023, 88, 1–112. [Google Scholar] [CrossRef]
- Cui, X. Seismic acquisition quality monitoring under complex geological conditions. Oil Geophys. Explor. 2003, 1, 11–16. [Google Scholar]
- Luo, W. Research and Application of Seismic Data Acquisition Quality Control Technology. Ph.D. Thesis, Southwest Petroleum University, Chengdu, China, 2016. [Google Scholar]
- Tian, C.; Cheng, Y. Research and application of field seismic data acquisition quality monitoring technology. Complex Oil Gas Reserv. 2011, 4, 25–27. [Google Scholar]
- Zhao, Z.; Ding, J. On-site quality monitoring technology for seismic data acquisition. Inn. Mong. Petrochem. 2009, 35, 98–99. [Google Scholar]
- Mousavi, S.M.; Beroza, G.C. Deep-learning seismology. Science 2022, 377, eabm4470. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, Q.; Lan, Z.; Chen, K.; Zhou, J.; Gao, P.; Zhang, W. Identifying microseismic events using a dual-channel CNN with wavelet packets decomposition coefficients. Comput. Geosci. 2022, 166, 105164. [Google Scholar] [CrossRef]
- Gan, L.; Wu, Q.; Huang, Q.; Tang, R. Quality classification and inversion of receiver functions using convolutional neural network. Geophys. J. Int. 2023, 232, 1833–1848. [Google Scholar] [CrossRef]
- Zhang, X.; Mao, L.; Yang, Y.; Zhou, Z. Study on the noise reduction method for semiaerial transient electromagnetic data based on LSTM. Comput. Tech. Geophys. Geochem. Explor. 2024, 46, 423–433. [Google Scholar]
- Li, Q.; Wang, X.; Zhang, Y.; Wen, X.; Chen, Y.; Wang, C.; Liao, W. Fault recognition method and application based on 3D U-Net++convolution neural network. Comput. Tech. Geophys. Geochem. Explor. 2024, 46, 284–291. [Google Scholar]
- Feng, Q.; Li, Y. Denoising deep learning network based on singular spectrum analysis—DAS seismic data denoising with multichannel SVDDCNN. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]
- Li, W.; Liu, H.; Wang, J. A Deep learning method for denoising based on a fast and flexible convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5902813. [Google Scholar] [CrossRef]
- Tibi, R.; Young, C.J.; Porritt, R.W. Comparative Study of the Performance of Seismic Waveform Denoising Methods Using Local and Near-Regional Data. Bull. Seism. Soc. Am. 2023, 113, 548–561. [Google Scholar] [CrossRef]
- Li, S.; Liu, B.; Ren, Y.; Chen, Y.; Yang, S.; Wang, Y.; Jiang, P. Deep-learning inversion of seismic data. arXiv 2019, arXiv:1901.07733. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, Q.; Yusifov, A.; Shi, Y. Applications of supervised deep learning for seismic interpretation and inversion. Lead. Edge 2019, 38, 526–533. [Google Scholar] [CrossRef]
- Gao, Y.; Li, H.; Li, G.; Wei, P.; Zhang, H. Deep learning for high-resolution multichannel seismic impedance inversion. Geophysics 2024, 89, WA323–WA335. [Google Scholar] [CrossRef]
- Tang, R.; Li, F.; Shen, F.; Gan, L.; Shi, Y. Fast forecasting of water-filled bodies position using transient electromagnetic method based on deep learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4502013. [Google Scholar] [CrossRef]
- Tang, R.; Gan, L.; Li, F.; Shen, F. A Fast Three-dimensional Imaging Scheme of Airborne Time Domain Electromagnetic Data using Deep Learning. TechRxiv 2024. [Google Scholar] [CrossRef]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object detection with deep learning: A review. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef]
- Shao, F.; Chen, L.; Shao, J.; Ji, W.; Xiao, S.; Ye, L.; Zhuang, Y.; Xiao, J. Deep learning for weakly-supervised object detection and localization: A survey. Neurocomputing 2022, 496, 192–207. [Google Scholar] [CrossRef]
- Kellenberger, B.; Marcos, D.; Tuia, D. Detecting mammals in UAV images: Best practices to address a substantially imbalanced dataset with deep learning. Remote Sens. Environ. 2018, 216, 139–153. [Google Scholar] [CrossRef]
- Kellenberger, B.; Volpi, M.; Tuia, D. Fast animal detection in UAV images using convolutional neural networks. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2017, Fort Worth, TX, USA, 23–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 866–869. [Google Scholar]
- Audebert, N.; Boulch, A.; Le Saux, B.; Lefèvre, S. Distance transform regression for spatially-aware deep semantic segmentation. Comput. Vis. Image Underst. 2019, 189, 102809. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Bochkovskiy, A. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Jocher. YOLOv5 by Ultralytics. 2020. Available online: https://github.com/ultralytics/yolov5 (accessed on 1 December 2024).
- Wang, S.; Pan, H.; Weifeng, G.; Bian, C.; Zhang, X.; Dong, B. YOLO-DCANet: Seismic velocity spectrum picking method based on deformable convolution and attention mechanism. In Proceedings of the Fifth International Conference on Geology, Mapping, and Remote Sensing (ICGMRS 2024), Wuhan, China, 12–14 April 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13223, pp. 559–564. [Google Scholar]
- Pang, D.; Liu, G.; He, J.; Li, W.; Fu, R. Automatic remote sensing identification of co-seismic landslides using deep learning methods. Forests 2022, 13, 1213. [Google Scholar] [CrossRef]
- Zhu, X.; Shragge, J. Toward real-time microseismic event detection using the YOLOv3 algorithm. Earth arXiv 2022. preprint. [Google Scholar]
- Wang, D.; Zhang, Y.; Zhang, R.; Nie, G.; Wang, W. Detection and assessment of post-earthquake functional building ceiling damage based on improved YOLOv8. J. Build. Eng. 2024, 98, 111315. [Google Scholar] [CrossRef]
- Lee, D.; Choi, S.; Lee, J.; Chung, W. Efficient seismic numerical modeling technique using the yolov2-based expanding domain method. J. Seism. Explor. 2022, 31, 425–449. [Google Scholar]
- Li, J.; Li, K.; Tang, S. Automatic arrival-time picking of P- and S-waves of microseismic events based on object detection and CNN. Soil Dyn. Earthq. Eng. 2023, 164, 107560. [Google Scholar] [CrossRef]
- Park, S.; Kim, J.; Jeon, K.; Kim, J.; Park, S. Improvement of gpr-based rebar diameter estimation using yolo-v3. Remote Sens. 2021, 13, 2011. [Google Scholar] [CrossRef]
- Ilmak, D.; Iban, M.C.; Şeker, D.Z. A Geospatial Dataframe of Collapsed Buildings in Antakya City after the 2023 Kahramanmaraş Earthquakes Using Object Detection Based on Yolo and VHR Satellite Images. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 3915–3919. [Google Scholar]
- Li, J.; Meng, J.B.; Li, P. Detecting the Bull’s-Eye Effect in Seismic Inversion Low-Frequency Models Using the Optimized YOLOv7 Model. Appl. Geophys. 2024, 1–11. [Google Scholar] [CrossRef]
- Kustu, T.; Taskin, A. Deep learning and stereo vision based detection of post-earthquake fire geolocation for smart cities within the scope of disaster management: İstanbul case. Int. J. Disaster Risk Reduct. 2023, 96, 103906. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Z.; Wu, J.; Tian, Y.; Tang, H.; Guo, X. Real-time vehicle detection based on improved YOLO v5. Sustainability 2022, 14, 12274. [Google Scholar] [CrossRef]
- Khanam, R.; Hussain, M. What is YOLOv5: A deep look into the internal features of the popular object detector. arXiv 2024, arXiv:2407.20892. [Google Scholar]
- Chen, F.; Zhang, L.; Kang, S.; Chen, L.; Dong, H.; Li, D.; Wu, X. Soft-NMS-enabled YOLOv5 with SIOU for small water surface floater detection in UAV-captured images. Sustainability 2023, 15, 10751. [Google Scholar] [CrossRef]
- Miao, F.; Yao, L.; Zhao, X. Adaptive margin aware complement-cross entropy loss for improving class imbalance in multi-view sleep staging based on eeg signals. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2927–2938. [Google Scholar] [CrossRef]
- Ding, J.; Cao, H.; Ding, X.; An, C. High accuracy real-time insulator string defect detection method based on improved YOLOv5. Front. Energy Res. 2022, 10, 928164. [Google Scholar] [CrossRef]
- Liu, W.; Quijano, K.; Crawford, M.M. YOLOv5-Tassel: Detecting tassels in RGB UAV imagery with improved YOLOv5 based on transfer learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8085–8094. [Google Scholar] [CrossRef]
- Sharma, A.; Pathak, J.; Prakash, M.; Singh, J.N. Object detection using OpenCV and python. In Proceedings of the 2021 3rd international Conference on Advances in Computing, Communication Control and Networking (ICAC3N), Greater Noida, India, 17–18 December 2021; IEEE: New York, NY, USA, 2021; pp. 501–505. [Google Scholar]
- Hegde, J.; Rokseth, B. Applications of machine learning methods for engineering risk assessment—A review. Saf. Sci. 2020, 122, 104492. [Google Scholar] [CrossRef]
- Shi, Y.; Liao, J.; Gan, L.; Tang, R. Lithofacies Prediction from Well Log Data Based on Deep Learning: A Case Study from Southern Sichuan, China. Appl. Sci. 2024, 14, 8195. [Google Scholar] [CrossRef]
- Gan, L.; Tang, R.; Li, F.; Shen, F. A Deep learning estimation for probing Depth of Transient Electromagnetic Observation. Appl. Sci. 2024, 14, 7123. [Google Scholar] [CrossRef]







| Application Description | Reference |
|---|---|
| Seismic velocity spectrum picking | Wang et al., 2024 [37] |
| Real-time co-seismic landslide detection | Pang et al., 2022 [35] |
| Detection of co-seismic collapsed buildings | Wang et al., 2024 [37] Ilmak and Iban, 2024 [41] |
| Microseismic event detection | Zhu and Shragge, 2022 [36] |
| Local velocity anomalies detection from Seismic inversion models | Li and Meng, 2024 [42] |
| Seismic numerical modeling | Lee et al., 2022 [38] |
| Arrival-time picking of P- and S-waves of microseismic events | Li et al., 2023 [39] |
| Post-earthquake fire detection | Kustu and Taskin, 2023 [43] |
| Seismic noise detection (this work) |
| Category | Precision | Recall | F1-Score | Support | TPR | FPR | Dice Index | Jaccard Index |
|---|---|---|---|---|---|---|---|---|
| 0 (No airwave) | 1.0 | 0.98 | 0.99 | 410 | 0.9565 | 0.0220 | 0.8889 | 0.8 |
| 1 (airwave) | 0.83 | 0.96 | 0.89 | 46 |
| Category | Precision | Recall | F1-Score | Support | TPR | FPR | Dice Index | Jaccard Index |
|---|---|---|---|---|---|---|---|---|
| 0 (No airwave) | 0.94 | 1.0 | 0.97 | 31 | 1.0 | 0.06 | 0.954 | 0.913 |
| 1 (airwave) | 1.0 | 0.91 | 0.95 | 23 |
| Train Time (h) | Precision | Recall | mAP@0.5 | mAP50:95 | Inference (ms) | Parameter (MB) | FLOPs@640 (B) | |
|---|---|---|---|---|---|---|---|---|
| yolov5l | 0.88 | 0.997 | 1 | 0.995 | 0.98 | 10.1 | 46.5 | 109.1 |
| yolov5m | 0.554 | 0.97 | 1 | 0.995 | 0.945 | 8.2 | 21.2 | 49 |
| yolov5s | 0.318 | 0.987 | 0.951 | 0.992 | 0.847 | 6.4 | 7.2 | 16.5 |
| yolov5n | 0.24 | 0.975 | 0.94 | 0.992 | 0.772 | 6.3 | 1.9 | 4.5 |
| P | R | mAP50 | mAP50:95 | |
|---|---|---|---|---|
| Twilight | 0.97 | 1 | 0.995 | 0.945 |
| Cividis | 0.825 | 0.85 | 0.826 | 0.805 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Gan, L.; Zhang, Z.; Huang, X.; Shen, F.; Chen, G.; Tang, R. Airwave Noise Identification from Seismic Data Using YOLOv5. Appl. Sci. 2024, 14, 11636. https://doi.org/10.3390/app142411636
Liang Z, Gan L, Zhang Z, Huang X, Shen F, Chen G, Tang R. Airwave Noise Identification from Seismic Data Using YOLOv5. Applied Sciences. 2024; 14(24):11636. https://doi.org/10.3390/app142411636
Chicago/Turabian StyleLiang, Zhenghong, Lu Gan, Zhifeng Zhang, Xiuju Huang, Fengli Shen, Guo Chen, and Rongjiang Tang. 2024. "Airwave Noise Identification from Seismic Data Using YOLOv5" Applied Sciences 14, no. 24: 11636. https://doi.org/10.3390/app142411636
APA StyleLiang, Z., Gan, L., Zhang, Z., Huang, X., Shen, F., Chen, G., & Tang, R. (2024). Airwave Noise Identification from Seismic Data Using YOLOv5. Applied Sciences, 14(24), 11636. https://doi.org/10.3390/app142411636






