Stability Analysis of the Landfill Slope with an Engineered Berm Under Composite Failure Mode

Abstract

In order to increase the capacity of landfills while ensuring a certain degree of stability of such structures, an engineered berm is typically constructed at the front slope of the landfill. For this type of landfill slopes, this paper primarily focuses on the construction and verification of stability assessment models for such structures. Initially, the calculation models of the safety factor were established, considering over and under berm failure modes separately. Subsequently, through error analysis, it was determined that it is feasible to evaluate the stability of this type of landfills by substituting the true safety factor with the average safety factor obtained from the calculation model. The analysis for parameters and slip surfaces was then conducted to investigate the impact of parameters associated with the engineered berm on the landfill slope stability. Finally, a visual comparison and brief discussion were conducted on the average safety factors under translational and composite failure modes. Thus, the critical failure modes under specific working conditions can be reasonably ascertained, which holds significant practical implications for enhancing the reliability of stability assessment of such landfill slopes.

1. Introduction

The engineered berm is frequently built at the front slope of landfills, which can not only increase the storage capacity of the landfill but also improve the stability of the landfill slope [1,2,3]. Theoretically, it can be said that maintaining the stable operation of this type of landfill inevitably requires reliable design of berms. The specific design of a berm needs to consider which failure mode this type of landfill slopes may resist. From a practical perspective, the failure of landfill slopes is mainly dominated by translational failure along the liner system [4]. Considering the existence of the berm, however, the failure of landfill slopes can be divided into two types, namely over-berm and under-berm failure modes [5,6]. Furthermore, the limit equilibrium method is commonly used to establish a stability assessment model for landfill slopes based on specific failure modes [7,8,9], and it is also used to analyze the structural stability in tunnels and deep excavations [10]. Meanwhile, due to the existence of the berm, the evaluation model is strongly correlated with the geometric shape of this structure. From the perspective of the cross-sectional shape of berms, they can be thus divided into two categories, namely triangular and trapezoidal berms [11].

Regardless of the geometric shape of the berm constructed in the landfill, the three-wedge method is often used to analyze the stability of such landfill slopes. This method was developed from the two-wedge method proposed by Qian et al. [12,13] and further extended to consider the effects of leachate level and seismic load on the slope stability [14,15]. Feng et al. [16,17,18] divided the sliding body with a triangular berm into three parts, i.e., active, passive and block wedges, and then proposed the three-wedge method based on the principle of limit equilibrium when that type of landfill slopes occurred the under-berm failure. Considering the effect of earthquakes on structural stability, Feng and Gao [19] used the pseudo-static method to introduce horizontal seismic loads to construct an assessment model for seismic stability of landfill slopes, and further Sun and Ruan [11] extended the above-mentioned model by increasing the effect of vertical seismic loads. For the failure mode of the over berm, Gao et al. [20] used the three-wedge method to build up a stability analysis model for this type of landfill slopes. When conducting seismic design of this structure in earthquake prone areas, Chen et al. [21] extended the above analysis model based on the Newmark method to carry out engineering design considering permanent seismic displacement.

When designing the landfill slope with an engineering berm, considering only the over-berm or under-berm failure mode may lead to unreliable design results. Therefore, it is necessary to analyze the stability of the landfill slope simultaneously under both failure modes. For the landfill slope with a trapezoidal berm, Qian and Koerner [6], respectively, established safety factor calculation models to resist the two types of failure modes mentioned above and conducted slope stability analysis using the three-wedge method. Subsequently, Choudhury and Savoikar [22] developed these calculation models by introducing seismic loads using the pseudo-static method, and furthermore, considering the dynamic characteristics of seismic loads, Ruan et al. [23,24] investigated the pseudo-dynamic stability of this type of landfill slopes. Apart from seismic loads, blasting vibration loads may also affect the stability of landfill slopes for dynamic loads due to the rapid development of transportation infrastructure construction. Considering the above practical situation, Chen et al. [25] studied the influence of this type of loads on the stability of the landfill slope with a trapezoidal berm. Currently, reinforced soil retaining walls are used as berms, and the cross-sectional shape of the structure is generally rectangular. Under these conditions, the stability analysis of landfill slopes usually only considers the under-berm failure mode. Considering the effect of leachate pressure, Mahapatra et al. [26] carried out reliability design for this type of berms.

The above studies are all based on the scenario where the instability of the landfill is a translational failure mode. Although this failure mode is commonly seen in the on-site investigation results of instability in large landfills [4], there is another failure mode, the composite failure mode, that may either lead to translational failure or occur directly, which is often overlooked [27]. In this failure mode, the critical slip surface consists of two parts, one is a log-spiral slip surface in the waste mass and the other is a translational slip surface along the liner system. This may be due to the different creep characteristics of the waste mass and liners, just as accurately simulating the creep process of rocks may require two contact models [28]. For this failure mode, Thiel [29] and Fowmes et al. [30] mentioned it in their research, but did not provide an analytical model. Ruan et al. [31] introduced the log-spiral mechanism into the internal failure of landfills, and then constructed a safety factor calculation model to evaluate the static stability of the landfill cell against the composite failure mode based on the limit equilibrium principle. Additionally, Ruan et al. [32] expanded the stability evaluation model by considering the effect of seismic loads.

Based on the above analysis and engineering practice requirements, it can be seen that when evaluating the stability of the landfill slope with an engineering berm, in addition to considering the stability performance of the structure against translational failure modes, it is also necessary to analyze the safety redundancy of the structure against composite failure modes. In the paper, first, the implicit function equations of the safety factor were derived under the failure modes of over berm and under berm, respectively. Second, through error analysis, the feasibility of using the average safety factor instead of the true safety factor to evaluate the stability of the landfill slope was verified. Then the influence of the geometric parameters of the engineered berm and the shear strength index at the interface of liners over berm and under berm on the stability of the landfill slope was analyzed. Finally, a comparative analysis was conducted on the stability of the landfill slope, including different failure modes such as composite and translational failure modes.

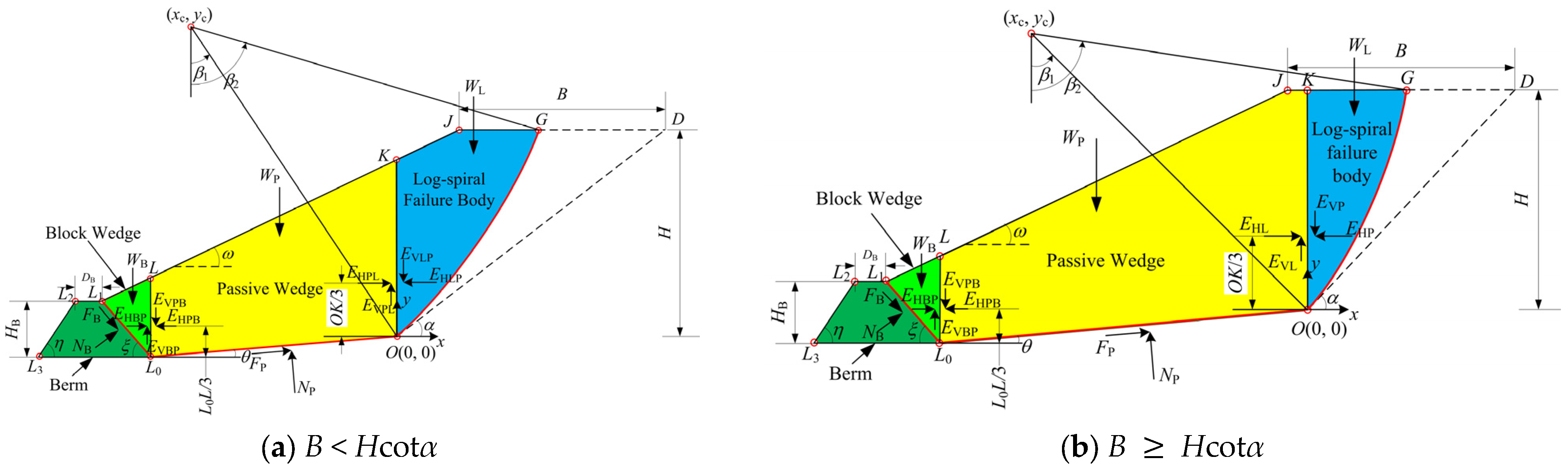
2. Computational Model

2.1. Basic Assumptions

When analyzing static stability of the landfill slope with an engineered berm against the composite failure mode, the failure body in the limit equilibrium state can be divided into three parts: the block wedge (region L₀LL₁, as in Figure 1; or region L₀LL₁L₂L₃, as in Figure 2), the passive wedge (region OKLL₀, as in Figure 1a and Figure 2a; or region OKJLL₀, as in Figure 1b and Figure 2b), and the log-spiral failure body (region OGJK, as in Figure 1a and Figure 2a; or region OGK, as in Figure 1b and Figure 2b). The limit equilibrium analysis of the block wedge, log-spiral failure body, and passive wedge is carried out sequentially, and equilibrium equations are established separately to obtain the calculation formulas for normal force from passive wedge acting on block wedge (i.e., E_HPB) and normal force from passive wedge acting on log-spiral failure body (i.e., E_HPL), as well as the expression for the relationship between normal forces from block wedge and log-spiral failure body acting on passive wedge (i.e., E_HBP and E_HLP). Based on the relationship between E_HPB = E_HBP and E_HPL = E_HLP, the implicit function equation for evaluating the safety factor of the landfill with an engineered berm against the composite failure mode is constructed.

Considering the geometric parameters of the landfill slope studied, the limit equilibrium analysis for sliding bodies can be divided into two situations, namely (a): B < Hcotα (as in Figure 1a and Figure 2a) and (b): B $\ge$ Hcotα (as in Figure 1b and Figure 2b). In Figure 1 and Figure 2, O(0, 0) is the origin of Cartesian coordinates; (x_c, y_c) is the pole of polar coordinates in Cartesian coordinates; W_B, W_L and W_P are the weights of block wedge, log-spiral failure body, and passive wedge, respectively; N_P and F_P are the normal and frictional forces, respectively, acting on the bottom of passive wedge; N_B and F_B are the normal and frictional forces, respectively, acting on the bottom of block wedge; E_HLP and E_VLP are the normal and frictional forces, respectively, acting on the passive wedge from log-spiral failure body; E_HPL and E_VPL are the normal and frictional forces, respectively, acting on the log-spiral failure body from passive wedge; E_HPB and E_VPB are the normal and frictional forces, respectively, acting on the block wedge from passive wedge; E_HBP and E_VBP are the normal and frictional forces, respectively, acting on the passive wedge from block wedge; H is the height of back slope; H_B is the height of engineered berm; B is the top width of waste mass; D_B is the top width of the engineered berm; ω is the angle of the front slope measured from the horizontal; α is the angle of the back slope measured from the horizontal; θ is the angle of the bottom of the passive wedge measured from the horizontal; ξ is the angle of the back slope of the engineered berm measured from the horizontal; η is the angle of the front slope of the engineered berm measured from the horizontal; β₁ and β₂ are the angles of point O and point G in the polar coordinates, respectively.

To successfully build up an analytical model for analyzing static stability of the landfill with an engineered berm against composite failure mode, it is necessary to make some reasonable assumptions. The specific assumptions are as follows: (1) the waste mass belongs to homogeneous Coulomb material, and its failure and the failure at the liner interface meet the Mohr–Coulomb strength criterion; (2) the potential slip surface runs along a log-spiral inside the landfill and enters the bottom lining system of the landfill after passing through the toe of the back slope (i.e., point O); (3) the potential slip surface appears within the range of JD at the top of the landfill; (4) the line of action of E_HPL or E_HLP is at one-third of the height (i.e., OK) from the bottom of the interface between passive wedge and log-spiral failure body; (5) the line of action of E_HBP or E_HPB is at one-third of the height (i.e., L₀L) from the bottom of the interface between block wedge and passive wedge; (6) the safety factor on the potential slip surface is equal everywhere.

2.2. Equations of Equilibrium When Over-Berm Failure Occurs

The frictional forces acting on the bottom of block and passive wedges, respectively, in Figure 1 and Figure 2 are as follows:

$$F_{\mathrm{B}}=C_{\mathrm{B}}/FS+N_{\mathrm{B}}\tan {\delta }_{\mathrm{B}}/FS$$

(1)

$$F_{\mathrm{P}}=C_{\mathrm{P}}/FS+N_{\mathrm{P}}\tan {\delta }_{\mathrm{P}}/FS$$

(2)

where FS is the safety factor on potential slip surface; δ_P is the interface friction angle of liner components beneath passive wedge; C_P is the apparent cohesive force between liner components beneath passive wedge, i.e., c_{P ×} OL₀, c_P is the apparent cohesion between liner components beneath passive wedge; δ_B is the interface friction angle of liner components beneath block wedge; when over-berm failure occurs in Figure 1, C_B is the apparent cohesive force between liner components beneath the block wedge, i.e., c_B × L₀L₁; when under-berm failure occurs in Figure 2, C_B is equal to c_B × L₀L₃; c_B is the apparent cohesion between liner components beneath the block wedge.

The frictional forces acting on the side of the block wedge and the log-spiral failure body, respectively, next to the passive wedge, E_VPB and E_VPL, and the side of the passive wedge next to the log-spiral failure body and the block wedge, respectively, E_VLP and E_VBP, in Figure 1 and Figure 2 are as follows:

$$E_{\mathrm{V}\mathrm{P}\mathrm{B}}={C_{\mathrm{P}\mathrm{B}}/FS}_{\mathrm{V}}+E_{\mathrm{H}\mathrm{P}\mathrm{B}}\tan {\varphi }_{\mathrm{S}\mathrm{W}}/F{S}_{\mathrm{V}}$$

(3)

$$E_{\mathrm{V}\mathrm{P}\mathrm{L}}={C_{\mathrm{P}\mathrm{L}}/FS}_{\mathrm{V}}+E_{\mathrm{H}\mathrm{P}\mathrm{L}}\tan {\varphi }_{\mathrm{S}\mathrm{W}}/F{S}_{\mathrm{V}}$$

(4)

$$E_{\mathrm{V}\mathrm{L}\mathrm{P}}={C_{\mathrm{P}\mathrm{L}}/FS}_{\mathrm{V}}+E_{\mathrm{H}\mathrm{L}\mathrm{P}}\tan {\varphi }_{\mathrm{S}\mathrm{W}}/F{S}_{\mathrm{V}}$$

(5)

$$E_{\mathrm{V}\mathrm{B}\mathrm{P}}={C_{\mathrm{P}\mathrm{B}}/FS}_{\mathrm{V}}+E_{\mathrm{H}\mathrm{B}\mathrm{P}}\tan {\varphi }_{\mathrm{S}\mathrm{W}}/F{S}_{\mathrm{V}}$$

(6)

where FS_V is the safety factor at the interface between two adjacent wedges; ϕ_SW is the internal friction angle of waste mass; C_PB is the apparent cohesive force at the interface between passive and block wedges, i.e., C_PB = c_SW × LL₀, and c_SW is the apparent cohesion of waste mass; C_PL is the apparent cohesive force at the interface between passive wedge and log-spiral failure body, i.e., C_PL = c_SW × OK.

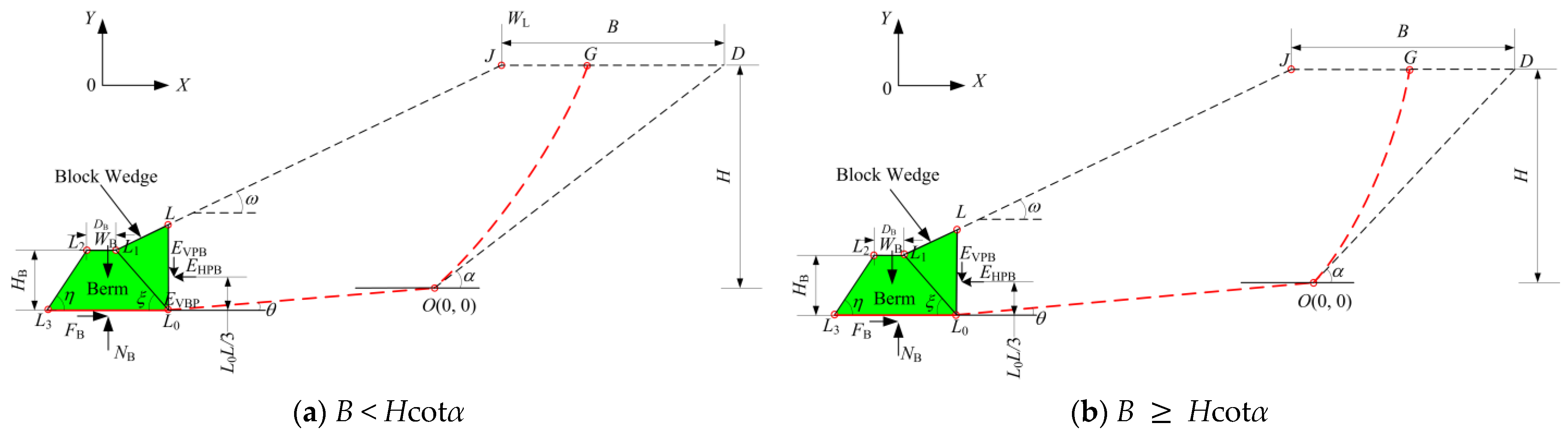
2.2.1. Equations of Equilibrium About Block Wedge

In accordance with the equilibrium condition of the vertical force acting on the block wedge, i.e., ${\displaystyle \sum F_{\mathrm{Y}}}=0$, as shown in Figure 3, it can be determined that

$$N_{\mathrm{B}}\cos \xi =W_{\mathrm{B}}+F_{\mathrm{B}}\sin \xi +E_{\mathrm{VPB}}$$

(7)

Substituting Equations (1) and (3) into Equation (7) offers

$$N_{\mathrm{B}}\left(\cos \xi -\sin \xi \tan {\delta }_{\mathrm{B}}/FS\right)-C_{\mathrm{B}}\sin \xi /FS=W_{\mathrm{B}}+C_{\mathrm{P}\mathrm{B}}/F{S}_{\mathrm{V}}+E_{\mathrm{HPB}}\tan {\varphi }_{\mathrm{SW}}/F{S}_{\mathrm{V}}$$

(8)

According to the equilibrium condition of the horizontal force acting on the block wedge, i.e., ${\displaystyle \sum F_{\mathrm{X}}}=0$, as shown in Figure 3, the equilibrium equation is as follows:

$$N_{\mathrm{B}}\sin \xi +F_{\mathrm{B}}\cos \xi =E_{\mathrm{HPB}}$$

(9)

Substituting Equation (1) into Equation (9) and rearranging for N_B yields

$$N_{\mathrm{B}}={\displaystyle \frac{E_{\mathrm{HPB}}-C_{\mathrm{B}}\cos \xi /FS}{\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/FS}}$$

(10)

Substituting Equation (10) into Equation (8) and rearranging for E_HPB produces

$$E_{\mathrm{HPB}}={\displaystyle \frac{\left(W_{\mathrm{B}} + C_{\mathrm{P}\mathrm{B}}/F{S}_{\mathrm{V}}\right)\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/FS\right)+C_{\mathrm{B}}/FS}{\left(\cos \xi -\sin \xi \tan {\delta }_{\mathrm{B}}/FS\right)-\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/FS\right)\tan {\varphi }_{\mathrm{SW}}/F{S}_{\mathrm{V}}}}$$

(11)

Based on the geometrical characteristics of the engineering berm, the following formulas for C_B, C_PB and W_B can be derived:

$$C_{\mathrm{B}}=c_{\mathrm{B}}{H}_{\mathrm{B}}/\sin \xi$$

(12)

$$C_{\mathrm{PB}}=c_{\mathrm{SW}}{H}_{\mathrm{B}}\left(1+\cos \xi \tan \omega \right)$$

(13)

$$W_{\mathrm{B}}=0.5{\gamma }_{\mathrm{SW}}{H}_{\mathrm{B}}^2\left(1+\cot \xi \tan \omega \right)\cot \xi$$

(14)

2.2.2. Equations of Equilibrium About Log-Spiral Failure Body

We perform limit equilibrium analysis on the log-spiral failure body under the over-berm failure mode and establish a moment equilibrium equation. The schematic diagrams of limit equilibrium analysis for log-spiral failure body are shown in Figure 4. Moreover, the mathematical equation of the log-spiral slip surface in polar coordinates and the definition of related parameters can be found in the paper of Ruan et al. [31]. The moment equilibrium equation about the log-spiral failure body for the poles (x_c, y_c) can therefore be written as follows:

$$M_{W_{\mathrm{L}}}=M_{E_{\mathrm{HPL}}}+M_{E_{\mathrm{VPL}}}+M_{C_{\mathrm{L}}}$$

(15)

where $M_{W_{\mathrm{L}}}$ is the moment stemmed from weight of the log-spiral failure body, $W_{\mathrm{L}}$; $M_{E_{\mathrm{HPL}}}$ is the moment generated by normal force from the passive wedge acting on the log-spiral failure body, $E_{\mathrm{HPL}}$; $M_{E_{\mathrm{VPL}}}$ is the moment produced by frictional force acting on the side of the log-spiral failure body next to the passive wedge, $E_{\mathrm{VPL}}$; $M_{C_{\mathrm{L}}}$ is the moment resulted from apparent cohesive force acting on the log-spiral slip surface, $C_{\mathrm{L}}$.

In Equation (15), $M_{W_{\mathrm{L}}}$ represents the driving moment responsible for the occurrence of failure, while $M_{E_{\mathrm{HPL}}}$, $M_{E_{\mathrm{VPL}}}$, and $M_{C_{\mathrm{L}}}$ denote the resisting moments counteracting the trend of instability. $M_{W_{\mathrm{L}}}$ can be calculated by modifying the result of Leshchinsky and San [33] and combining the two different scenarios in Figure 4 to obtain the calculation formula of $M_{W_{\mathrm{L}}}$, which can be written as Equations (18) and (20), respectively. $M_{E_{\mathrm{VPL}}}$ and $M_{E_{\mathrm{HPL}}}$ can be derived directly from the geometric relationships in Figure 4, namely Equations (16), (19), and (21). $M_{C_{\mathrm{L}}}$ can be obtained by reorganizing the derivation result of Ruan et al. [34], as shown in Equation (17). Here are the specific forms of these equations:

$$M_{E_{\mathrm{VPL}}}=E_{\mathrm{VPL}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)$$

(16)

$$M_{C_{\mathrm{L}}}={\displaystyle \frac{c_{\mathrm{SW}}}{FS}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }$$

(17)

There are two calculation formulas for $M_{W_{\mathrm{L}}}$ and $M_{E_{\mathrm{HPL}}}$, which are shown as follows:

(1) when B < Hcotα

$$\begin{array}{l}{M}_{W_{\mathrm{L}}}={\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)\left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta }\\ -0.5{\gamma }_{\mathrm{SW}}{\left(H\cot \alpha -B\right)}^2\tan \omega \left[A{e}^{-\psi {\beta }_1}\sin {\beta }_1+\left(H\cot \alpha -B\right)/3\right]\end{array}$$

(18)

$$M_{E_{\mathrm{HPL}}}=E_{\mathrm{HPL}}\lfloor A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\left(H-H\cot \alpha \tan \omega +B\tan \omega \right)/3\rfloor$$

(19)

(2) when B $\ge$ Hcotα

$$M_{W_{\mathrm{L}}}={\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)\left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta }$$

(20)

$$M_{E_{\mathrm{HPL}}}=E_{\mathrm{HPL}}\lfloor A{e}^{-\psi {\beta }_1}\cos {\beta }_1-H/3\rfloor$$

(21)

Substituting Equation (4) into Equation (16) and rearranging it, we can obtain

$$M_{E_{\mathrm{VPL}}}=C_{\mathrm{PL}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)/F{S}_{\mathrm{V}}+E_{\mathrm{HPL}}\tan {\varphi }_{\mathrm{SW}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)/F{S}_{\mathrm{V}}$$

(22)

When B < Hcotα, substituting Equations (17)–(19) and (22) into Equation (15) and rearranging it, the calculation formula for E_HPL can be attained as follows:

$$\begin{array}{l}{E}_{\mathrm{HPL}}=\left\{{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)\left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta }-0.5{\gamma }_{\mathrm{SW}}{\left(H\cot \alpha -B\right)}^2\tan \omega \right.\\ \left.\times \left[A{e}^{-\psi {\beta }_1}\sin {\beta }_1+\left(H\cot \alpha -B\right)/3\right]-{\displaystyle \frac{c_{\mathrm{SW}}}{FS}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }-{\displaystyle \frac{C_{\mathrm{PL}}}{F{S}_{\mathrm{V}}}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right\}/\left[A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\left(H-H\cot \alpha \tan \omega \right.\right.\\ \left.\left.+B\tan \omega \right)/3+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\tan {\varphi }_{\mathrm{SW}}/F{S}_{\mathrm{V}}\right]\end{array}$$

(23)

When B $\ge$ Hcotα, substituting Equations (17) and (20)–(22) into Equation (15) and rearranging it, the calculation formula for E_HPL can be obtained as follows:

$$\begin{array}{l}{E}_{\mathrm{HPL}}=\left\{{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)\left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -\frac{c_{\mathrm{SW}}}{FS}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }}\right.\\ \left.-{\displaystyle \frac{C_{\mathrm{PL}}}{F{S}_{\mathrm{V}}}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right\}/\left(A{e}^{-\psi {\beta }_1}\cos {\beta }_1-H/3+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\tan {\varphi }_{\mathrm{SW}}/F{S}_{\mathrm{V}}\right)\end{array}$$

(24)

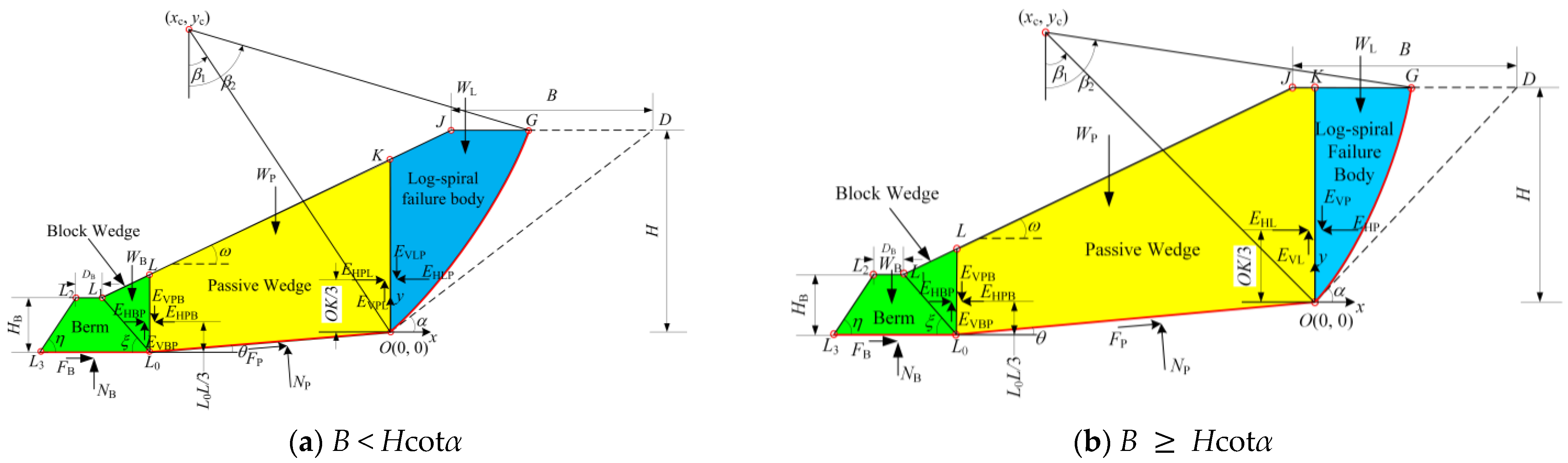
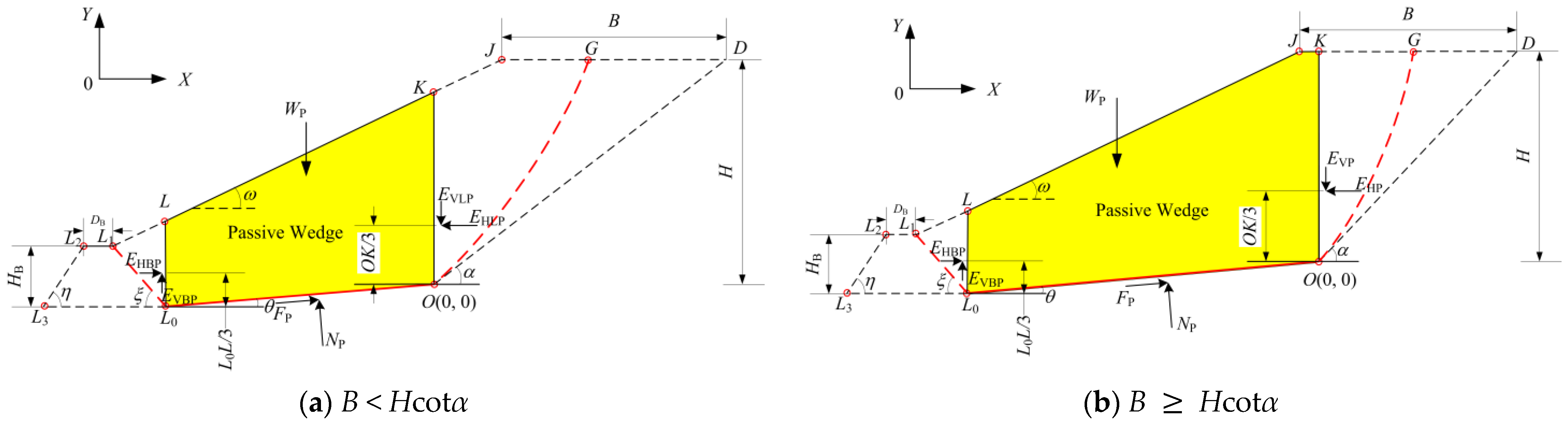
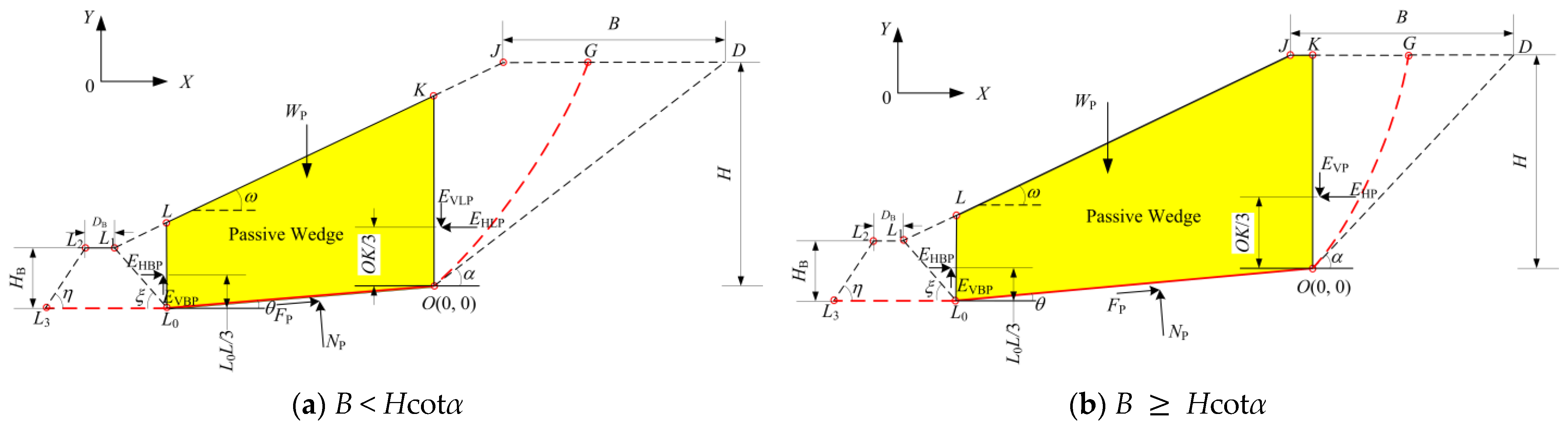
2.2.3. Equations of Equilibrium About Passive Wedge

In accordance with the equilibrium condition of the vertical force acting on the passive wedge, i.e., ${\displaystyle \sum F_{\mathrm{Y}}}=0$, as shown in Figure 5, we can obtain

$$W_{\mathrm{P}}+E_{\mathrm{VLP}}=N_{\mathrm{P}}\cos \theta +F_{\mathrm{P}}\sin \theta +E_{\mathrm{VBP}}$$

(25)

Substituting Equation (2) into Equation (25) yields

$$N_{\mathrm{P}}\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/FS\right)=W_{\mathrm{P}}+\left(E_{\mathrm{HLP}}-E_{\mathrm{HBP}}\right)\tan {\varphi }_{\mathrm{SW}}/F{S}_{\mathrm{V}}+\left(C_{\mathrm{P}\mathrm{L}}-C_{\mathrm{P}\mathrm{B}}\right)/F{S}_{\mathrm{V}}-C_{\mathrm{P}}\sin \theta /FS$$

(26)

In line with the equilibrium condition of the horizontal force acting on the passive, i.e., ${\displaystyle \sum F_{\mathrm{X}}}=0$, as shown in Figure 5, the equilibrium equation is as follows:

$$E_{\mathrm{HBP}}+F_{\mathrm{P}}\cos \theta =E_{\mathrm{HLP}}+N_{\mathrm{P}}\sin \theta$$

(27)

Substituting Equation (2) into Equation (27) and rearranging it, we can derive

$$N_{\mathrm{P}}={\displaystyle \frac{E_{\mathrm{HBP}}-E_{\mathrm{HLP}}+C_{\mathrm{P}}\cos \theta /FS}{\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/FS}}$$

(28)

Substituting Equation (28) into Equation (26) produces

$$\begin{array}{l}\left(E_{\mathrm{HLP}}-E_{\mathrm{HBP}}\right)\left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/FS\right)+\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/FS\right)\tan {\varphi }_{\mathrm{SW}}/F{S}_{\mathrm{V}}\right]\\ =\left[W_{\mathrm{P}}+\left(C_{\mathrm{P}\mathrm{L}}-C_{\mathrm{P}\mathrm{B}}\right)/F{S}_{\mathrm{V}}\right]\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/FS\right)-C_{\mathrm{P}}/FS\end{array}$$

(29)

where the calculation formulas for C_P, C_PL, and W_P can be derived based on the geometric parameters of the landfill. The specific formula is as follows:

$$C_{\mathrm{P}}=c_{\mathrm{P}}\left[H-\left(H\cot \alpha -B\right)\tan \omega -H_{\mathrm{B}}\left(1+\cot \xi \tan \omega \right)\right]/\left[\left(\tan \omega -\tan \theta \right)\cos \theta \right]$$

(30)

However, C_PL and W_P have two types of calculation formulas due to the geometric characteristics of the landfill, which can be written as

(1) when B < Hcotα

$$C_{\mathrm{PL}}=c_{\mathrm{SW}}\left[H-\left(H\cot \alpha -B\right)\tan \omega \right]$$

(31)

$$W_{\mathrm{P}}=0.5{\gamma }_{\mathrm{SW}}\left\{{\left[H-\left(H\cot \alpha -B\right)\tan \omega \right]}^2-{\left[H_{\mathrm{B}}\left(1+\cot \xi \tan \omega \right)\right]}^2\right\}/\left(\tan \omega -\tan \theta \right)$$

(32)

(2) when B $\ge$ Hcotα

$$C_{\mathrm{PL}}=c_{\mathrm{SW}}H$$

(33)

$$W_{\mathrm{P}}=0.5{\gamma }_{\mathrm{SW}}\left\{{\left[H-\left(H\cot \alpha -B\right)\tan \omega \right]}^2-{\left[H_{\mathrm{B}}\left(1+\cot \xi \tan \omega \right)\right]}^2\right\}/\left(\tan \omega -\tan \theta \right)-0.5{\gamma }_{\mathrm{SW}}{\left(B-H\cot \alpha \right)}^2\tan \omega$$

(34)

2.3. Equations of Equilibrium When Under-Berm Failure Occurs

Similar to the derivation process in Section 2.2.1, based on the equilibrium condition of the vertical force acting on the block wedge, i.e., ${\displaystyle \sum F_{\mathrm{Y}}}=0$, as shown in Figure 6, we can obtain

$$N_{\mathrm{B}}=W_B+E_{\mathrm{VPB}}$$

(35)

According to the equilibrium condition of the horizontal force acting on the block wedge, i.e., ${\displaystyle \sum F_{\mathrm{X}}}=0$, as shown in Figure 6, the equilibrium equation is as follows:

$$F_{\mathrm{B}}=E_{\mathrm{HPB}}$$

(36)

Substituting Equation (1) into Equation (36) and rearranging it, we can obtain

$$N_{\mathrm{B}}={\displaystyle \frac{E_{\mathrm{HPB}}-C_{\mathrm{B}}/FS}{\tan {\delta }_{\mathrm{B}}/FS}}$$

(37)

Substituting Equation (37) into Equation (35) and rearranging it, it can be determined that

$$E_{\mathrm{HPB}}={\displaystyle \frac{\left(W_{\mathrm{B}}+C_{\mathrm{P}\mathrm{B}}/F{S}_{\mathrm{V}}\right)\tan {\delta }_{\mathrm{B}}/FS+C_{\mathrm{B}}/FS}{1-\tan {\delta }_{\mathrm{B}}\tan {\varphi }_{\mathrm{SW}}/\left(F{S}_{\mathrm{V}}FS\right)}}$$

(38)

In terms of the geometric characteristics of the engineered berm, it can be concluded that the calculation formula for C_PB is the same as Equation (13). The calculation formulas for C_B and W_B are written as follows:

$$C_{\mathrm{B}}=c_{\mathrm{B}}\left[D_{\mathrm{B}}+H_{\mathrm{B}}\left(\cot \eta +\cot \xi \right)\right]$$

(39)

$$W_{\mathrm{B}}=0.5{\gamma }_{\mathrm{SW}}{H}_{\mathrm{B}}^2\left(1+\cot \xi \tan \omega \right)\cot \xi +0.5{\gamma }_{\mathrm{B}}{H}_{\mathrm{B}}\left[2D_{\mathrm{B}}+H_{\mathrm{B}}\left(\cot \eta +\cot \xi \right)\right]$$

(40)

Because the equilibrium conditions for the log-spiral failure body and passive wedge shown in Figure 7 and Figure 8 are identical to those in Figure 4 and Figure 5, the equations regarding E_HPL and its relationship with E_HBP are derived; however, these are exactly the same as Equations (23), (24), and (29).

2.4. Implicit Function Equations of the Safety Factor

The safety factor at the interface between two wedges, FS_V, must not be less than one so as to meet the shear strength criteria for the waste soil, and it should not be less than the safety factor for entire structure of the landfill slope [35]. Therefore, the maximum and minimum safety factors can be determined by the following assumptions: (1) the implicit function equation of the maximum safety factor, FS_max, can be derived when assuming FS_V = FS_max; however, if the calculated result of FS_max is less than one, it is necessary to assume FS_V = 1 and recalculate FS_max; (2) the implicit function equation about the minimum safety factor, FS_min, can be obtained when assuming FS_V = ∞.

2.4.1. Implicit Function Equations When Over-Berm Failure Occurs

(1) when B < Hcotα

By assuming FS_V = ∞, substituting Equations (11) and (23) into Equation (29) and rearranging it, an implicit function equation of FS_min can be obtained as follows:

$$\begin{array}{l}\left\{\left[W_{\mathrm{B}}\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\min }\right)+C_{\mathrm{B}}/F{S}_{\min }\right]/\left(\cos \xi -\sin \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\min }\right)-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\right.\\ \times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -0.5{\gamma }_{\mathrm{SW}}{\left(H\cot \alpha -B\right)}^2\tan \omega \left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1+\left(H\cot \alpha -B\right)/3\right)\\ \left.\left.-{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\min }}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }\right]/\left[A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\left(H-H\cot \alpha \tan \omega \right.\right.\left.\left.+B\tan \omega \right)/3\right]\right\}\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\min }\right)-W_{\mathrm{P}}\left(\sin \theta \right.\\ \left.-\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\min }\right)+C_{\mathrm{P}}/F{S}_{\min }=0\end{array}$$

(41)

By assuming FS_V = FS, substituting Equations (11) and (23) into Equation (29) and rearranging it, an implicit function equation of FS_max can be obtained as follows:

$$\begin{array}{l}\left\{\left[\left(W_{\mathrm{B}}+C_{\mathrm{PB}}/F{S}_{\max }\right)\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)+C_{\mathrm{B}}/F{S}_{\max }\right]/\left[\left(\cos \xi -\sin \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)-\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)\right.\right.\\ \left.\times \tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right]-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -0.5{\gamma }_{\mathrm{SW}}{\left(H\cot \alpha -B\right)}^2\\ \times \tan \omega \left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1+\left(H\cot \alpha -B\right)/3\right)\left.-{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\max }}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta -}{\displaystyle \frac{C_{\mathrm{PL}}}{F{S}_{\max }}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right]/\left[A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\left(H-H\cot \alpha \tan \omega \right.\right.\\ \left.+B\tan \omega \right)/3+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\left.\left.\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right]\right\}\left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right]\\ -\left[W_{\mathrm{P}}+\left(C_{\mathrm{PL}}-C_{\mathrm{PB}}\right)/F{S}_{\max }\right]\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+C_{\mathrm{P}}/F{S}_{\max }=0\end{array}$$

(42)

If FS_max calculated by solving Equation (42) is less than one, the implicit function equation for FS_max needs to be redefined. Assuming FS_V = 1 and rearranging Equation (42), the implicit function equation about FS_max can be rewritten as follows:

$$\begin{array}{l}\left\{\left[\left(W_{\mathrm{B}}+C_{\mathrm{PB}}\right)\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)+C_{\mathrm{B}}/F{S}_{\max }\right]/\left[\left(\cos \xi -\sin \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)-\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)\right.\right.\\ \left.\times \tan {\varphi }_{\mathrm{SW}}\right]-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -0.5{\gamma }_{\mathrm{SW}}{\left(H\cot \alpha -B\right)}^2\\ \times \tan \omega \left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1+\left(H\cot \alpha -B\right)/3\right)\left.-{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\max }}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta -}{C}_{\mathrm{PL}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right]/\left[A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\left(H-H\cot \alpha \right.\right.\\ \left.\times \tan \omega +B\tan \omega \right)/3+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\left.\left.\tan {\varphi }_{\mathrm{SW}}\right]\right\}\left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\tan {\varphi }_{\mathrm{SW}}\right]\\ -\left[W_{\mathrm{P}}+\left(C_{\mathrm{PL}}-C_{\mathrm{PB}}\right)/F{S}_{\max }\right]\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+C_{\mathrm{P}}/F{S}_{\max }=0\end{array}$$

(43)

(2) when B $\ge$ Hcotα

By assuming FS_V = ∞ and substituting Equations (11) and (24) into Equation (29), an implicit function equation of FS_min can be obtained as follows:

$$\begin{array}{l}\left\{\left[W_{\mathrm{B}}\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\min }\right)+C_{\mathrm{B}}/F{S}_{\min }\right]/\left(\cos \xi -\sin \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\min }\right)-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\right.\\ \times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta \left.\left.-{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\min }}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }\right]/\left(A{e}^{-\psi {\beta }_1}\cos {\beta }_1-H/3\right)\right\}\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\min }\right)\\ -W_{\mathrm{P}}\left(\sin \theta \right.\left.-\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\min }\right)+C_{\mathrm{P}}/F{S}_{\min }=0\end{array}$$

(44)

By assuming FS_V = FS and substituting Equations (11) and (24) into Equation (29) and rearranging it, an implicit function equation of FS_max can be obtained as follows:

$$\begin{array}{l}\left\{\left[\left(W_{\mathrm{B}}+C_{\mathrm{PB}}/F{S}_{\max }\right)\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)+C_{\mathrm{B}}/F{S}_{\max }\right]/\left[\left(\cos \xi -\sin \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)-\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)\right.\right.\\ \left.\times \tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right]-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\max }}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }\\ -\left.{\displaystyle \frac{C_{\mathrm{PL}}}{F{S}_{\max }}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right]/\left.\left(A{e}^{-\psi {\beta }_1}\cos {\beta }_1-H/3+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right)\right\}\left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+\left(\sin \theta -\cos \theta \right.\right.\\ \left.\left.\times \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right]-\left[W_{\mathrm{P}}+\left(C_{\mathrm{PL}}-C_{\mathrm{PB}}\right)/F{S}_{\max }\right]\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+C_{\mathrm{P}}/F{S}_{\max }=0\end{array}$$

(45)

If FS_max calculated by solving Equation (45) is less than one, the implicit function equation for FS_max needs to be rebuilt. Assuming FS_V = 1 and rearranging Equation (45), the implicit function equation for FS_max can be improved as follows:

$$\begin{array}{l}\left\{\left[\left(W_{\mathrm{B}}+C_{\mathrm{PB}}\right)\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)+C_{\mathrm{B}}/F{S}_{\max }\right]/\left[\left(\cos \xi -\sin \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)-\left(\sin \xi +\cos \xi \tan {\delta }_{\mathrm{B}}/F{S}_{\max }\right)\right.\right.\\ \left.\times \tan {\varphi }_{\mathrm{SW}}\right]-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\max }}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }\\ \left.-C_{\mathrm{PL}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right]/\left[A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\right.H/3+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\left.\left.\tan {\varphi }_{\mathrm{SW}}\right]\right\}\left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\right.+\left(\sin \theta -\cos \theta \right.\\ \left.\times \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\left.\tan {\varphi }_{\mathrm{SW}}\right]-\left[W_{\mathrm{P}}+\left(C_{\mathrm{PL}}-C_{\mathrm{PB}}\right)/F{S}_{\max }\right]\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+C_{\mathrm{P}}/F{S}_{\max }=0\end{array}$$

(46)

2.4.2. Implicit Function Equations When Under-Berm Failure Occurs

(1) when B < Hcotα

By assuming FS_V = ∞ and substituting Equations (38) and (23) into Equation (29), an implicit function equation of FS_min can be determined as follows:

$$\begin{array}{l}\left\{\left(W_{\mathrm{B}}\tan {\delta }_{\mathrm{B}}/F{S}_{\min }+C_{\mathrm{B}}/F{S}_{\min }\right)-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\right.\left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta \\ -0.5{\gamma }_{\mathrm{SW}}{\left(H\cot \alpha -B\right)}^2\tan \omega \left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1+\left(H\cot \alpha -B\right)/3\right)\left.-{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\min }}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }\right]/\left[A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\left(H-H\right.\right.\\ \left.\left.\times \cot \alpha \tan \omega \left.+B\tan \omega \right)/3\right]\right\}\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\min }\right)-W_{\mathrm{P}}\left(\sin \theta \right.\left.-\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\min }\right)+C_{\mathrm{P}}/F{S}_{\min }=0\end{array}$$

(47)

By assuming FS_V = FS and substituting Equations (38) and (23) into Equation (29) and rearranging it, an implicit function equation of FS_max can be obtained as follows:

$$\begin{array}{l}\left\{\left[\left(W_{\mathrm{B}}+C_{\mathrm{PB}}/F{S}_{\max }\right)\tan {\delta }_{\mathrm{B}}/F{S}_{\max }+C_{\mathrm{B}}/F{S}_{\max }\right]/\left(1-\tan {\delta }_{\mathrm{B}}\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }^2\right)\right.-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\\ \times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -0.5{\gamma }_{\mathrm{SW}}{\left(H\cot \alpha -B\right)}^2\tan \omega \left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1+\left(H\cot \alpha -B\right)/3\right)-{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\max }}}\\ \left.\times {\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta -}{\displaystyle \frac{C_{\mathrm{PL}}}{F{S}_{\max }}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right]/\left[A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\left(H-H\cot \alpha \tan \omega \right.\right.\left.+B\tan \omega \right)/3+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\left.\left.\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right]\right\}\\ \times \left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right]-\left[W_{\mathrm{P}}+\left(C_{\mathrm{PL}}-C_{\mathrm{PB}}\right)/F{S}_{\max }\right]\\ \times \left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+C_{\mathrm{P}}/F{S}_{\max }=0\end{array}$$

(48)

If FS_max fixed on by solving Equation (48) is less than one, the implicit function equation for FS_max needs to be redefined. Assuming FS_V = 1 and rearranging Equation (48), the implicit function equation about FS_max can be obtained as follows:

$$\begin{array}{l}\left\{\left[\left(W_{\mathrm{B}}+C_{\mathrm{PB}}/F{S}_{\max }\right)\tan {\delta }_{\mathrm{B}}/F{S}_{\max }+C_{\mathrm{B}}/F{S}_{\max }\right]/\left(1-\tan {\delta }_{\mathrm{B}}\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }^2\right)\right.-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\\ \times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -0.5{\gamma }_{\mathrm{SW}}{\left(H\cot \alpha -B\right)}^2\tan \omega \left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1+\left(H\cot \alpha -B\right)/3\right)-{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\max }}}\\ \left.\times {\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta -}{C}_{\mathrm{PL}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right]/\left[A{e}^{-\psi {\beta }_1}\cos {\beta }_1-\left(H-H\cot \alpha \tan \omega \right.\right.\left.+B\tan \omega \right)/3+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\left.\left.\tan {\varphi }_{\mathrm{SW}}\right]\right\}\\ \times \left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\tan {\varphi }_{\mathrm{SW}}\right]-\left[W_{\mathrm{P}}+\left(C_{\mathrm{PL}}-C_{\mathrm{PB}}\right)\right]\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\\ +C_{\mathrm{P}}/F{S}_{\max }=0\end{array}$$

(49)

(2) when B $\ge$ Hcotα

By assuming FS_V = ∞ and substituting Equations (38) and (24) into Equation (29), an implicit function equation of FS_min can be obtained as follows:

$$\begin{array}{l}\left\{\left(W_{\mathrm{B}}\tan {\delta }_{\mathrm{B}}/F{S}_{\min }+C_{\mathrm{B}}/F{S}_{\min }\right)-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\right.\left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta \\ \left.\left.-{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\min }}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta }\right]/\left(A{e}^{-\psi {\beta }_1}\cos {\beta }_1-H/3\right)\right\}\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\min }\right)-W_{\mathrm{P}}\left(\sin \theta \right.\left.-\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\min }\right)\\ +C_{\mathrm{P}}/F{S}_{\min }=0\end{array}$$

(50)

By assuming FS_V = FS and substituting Equations (38) and (24) into Equation (29) and rearranging it, an implicit function equation of FS_max can be determined as follows:

$$\begin{array}{l}\left\{\left[\left(W_{\mathrm{B}}+C_{\mathrm{PB}}/F{S}_{\max }\right)\tan {\delta }_{\mathrm{B}}/F{S}_{\max }+C_{\mathrm{B}}/F{S}_{\max }\right]/\left(1-\tan {\delta }_{\mathrm{B}}\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }^2\right)\right.-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\\ \times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\max }}}\left.{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta -}{\displaystyle \frac{C_{\mathrm{PL}}}{F{S}_{\max }}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right]/\left(A{e}^{-\psi {\beta }_1}\cos {\beta }_1-H/3\right.\\ \left.\left.+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right)\right\}\left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right]\\ -\left[W_{\mathrm{P}}+\left(C_{\mathrm{PL}}-C_{\mathrm{PB}}\right)/F{S}_{\max }\right]\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+C_{\mathrm{P}}/F{S}_{\max }=0\end{array}$$

(51)

If FS_max obtained from solving Equation (51) is less than one, the implicit function equation for FS_max needs to be recalculated. Assuming FS_V = 1 and rearranging Equation (51), the implicit function equation about FS_max can be obtained as follows:

$$\begin{array}{l}\left\{\left[\left(W_{\mathrm{B}}+C_{\mathrm{PB}}\right)\tan {\delta }_{\mathrm{B}}/F{S}_{\max }+C_{\mathrm{B}}/F{S}_{\max }\right]/\left(1-\tan {\delta }_{\mathrm{B}}\tan {\varphi }_{\mathrm{SW}}/F{S}_{\max }\right)\right.-\left[{\gamma }_{\mathrm{SW}}{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}\left(A{e}^{-\psi \beta }\cos \beta -A{e}^{-\psi {\beta }_2}\cos {\beta }_2\right)}\right.\\ \times \left(A{e}^{-\psi \beta }\sin \beta \right)\left(A{e}^{-\psi \beta }\right)\left(\cos \beta -\psi \sin \beta \right)d\beta -{\displaystyle \frac{c_{\mathrm{SW}}}{F{S}_{\max }}}\left.{\displaystyle {\int }_{{\beta }_1}^{{\beta }_2}{\left(A{e}^{-\psi \beta }\right)}^{2}d\beta -}{C}_{\mathrm{PL}}\left(A{e}^{-\psi {\beta }_1}\sin {\beta }_1\right)\right]/\left(A{e}^{-\psi {\beta }_1}\cos {\beta }_1-H/3\right.\\ \left.\left.+A{e}^{-\psi {\beta }_1}\sin {\beta }_1\tan {\varphi }_{\mathrm{SW}}\right)\right\}\left[\left(\cos \theta +\sin \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)\tan {\varphi }_{\mathrm{SW}}\right]\\ -\left[W_{\mathrm{P}}+\left(C_{\mathrm{PL}}-C_{\mathrm{PB}}\right)\right]\left(\sin \theta -\cos \theta \tan {\delta }_{\mathrm{P}}/F{S}_{\max }\right)+C_{\mathrm{P}}/F{S}_{\max }=0\end{array}$$

(52)

2.5. Calculation of the Safety Factor

To ensure the minimum and maximum values of the safety factor calculated by the constructed model under the composite failure mode of the landfill slope with an engineered berm are reasonable, certain judgment conditions should be defined in programming to eliminate unreasonable values. Readers can refer to the paper by Ruan et al. [31].

A calculation program can be developed using MATLAB software (https://www.mathworks.com/products/matlab.html, accessed on 3 October 2024) to determine the FS_max and FS_min for two types of berm failure modes. The calculation flowchart can be designed with reference to the flowchart presented in the paper of Ruan et al. [31].

3. Results

3.1. Error Analysis

The average safety factor, FS_ave, is defined as (FS_max + FS_min)/2. Qian et al. [12] proved that the upper limit of the relative error between the true safety factor, FS_true, and FS_ave is less than the relative error, Δ, between FS_ave and FS_min, that is, Δ = (FS_ave − FS_min)/FS_min. And it is explained that when the relative error between FS_true and FS_ave is not greater than 5%, FS_ave can be used as a substitute for FS_true to assess the degree of stability of landfill slopes.

For the sake of a thorough analysis of the range variation of Δ regarding the engineered berm, the characteristic parameters related to that berm are investigated. The basic parameters are as follows: (1) Geometric parameters: H = 30 m, B = 40 m, H_B = 7.5 m, D_B = 3 m, ω = 14° (i.e., 4[H]:1[V]), α = 18.4° (i.e., 3[H]:1[V]), θ = 1.1° (i.e., the slope is 2%), ξ = 26.6° (i.e., 2[H]:1[V]), η = 63.4° (i.e., 0.5[H]:1[V]); (2) Mechanical parameters of waste mass and berm: γ_SW = 10.20 kN/m³, ϕ_SW = 30°, c_SW = 3.0 kN/m², γ_B = 18 kN/m³; (3) Shear strength between liner components beneath passive wedge: δ_P = 18°, c_P = 11.5 kN/m²; (4) Shear strength between liner components beneath block wedge: (i) δ_B = 18°, c_B = 11.5 kN/m² under the over-berm failure mode and (ii) δ_B = 32°, c_B = 8 kN/m² under the under-berm failure mode.

3.1.1. Analysis of the Safety Factor When Over-Berm Failure Occurs

From Figure 9a, it can be seen that FS_max, FS_min, and FS_ave all increase with the increase in H_B. When H_B increases from 3 m to 15 m, FS_max increases by 8.56%, FS_ave increases by 6.60%, and FS_min increases by 4.53%. It can be seen that the increase in the above three types of safety factors gradually decreases.%

Figure 9b shows that that Δ increases with the increase in H_B. Specifically, when H_B = 3 m, 6 m, 9 m, 12 m, and 15 m, Δ is 2.86%, 3.14%, 3.58%, 4.16%, and 4.89%, respectively. Thus, the maximum value of Δ is 4.89%.

From Figure 10a, it can be seen that FS_max, FS_min, and FS_ave all slightly decrease and then increase with the increase in ξ.

Figure 10b shows that that Δ increases with the increase in α. And it can be determined that when ξ = 15°, 20°, 25°, 30°, 35°, 40°, 45°, Δ = 3.22%, 3.26%, 3.32%, 3.41%, 3.53%, 3.71%, 3.95%. It can be concluded that the maximum value of Δ is 3.95%.

From Figure 11a, it can be seen that FS_max, FS_min and FS_ave all increase with the increase in δ_B. When δ_B increases from 12° to 30°, FS_max, FS_ave, and FS_min increase by 2.55%, 2.19%, and 1.81%, respectively. The changing trend of the safety factor is the same as the effect of H_B on the safety factor.

Figure 11b shows that Δ increases as δ_B increases. Specifically, when δ_B = 12°, 15°, 18°, 21°, 24°, 27°, and 30°, Δ is 3.25%, 3.29%, 3.35%, 3.40%, 3.47%, 3.55%, and 3.64%, respectively. Thus, the maximum value of Δ is 3.64%.

From Figure 12a, it can be seen that FS_max, FS_min and FS_ave all increase with the increase in c_B. When c_B increases from 0 to 30 kN/m², FS_max, FS_ave, and FS_min increase by 2.36%, 2.28%, and 2.20%, respectively. It can be seen that the increase above three safety factors gradually decreases, but the difference among those not significant.

Figure 12b shows that Δ increases with the increase in c_B. And it can be determined that when c_B = 0, 5 kN/m², 10 kN/m², 15 kN/m², 20 kN/m², 25 kN/m², 30 kN/m², Δ = 3.31%, 3.33%, 3.34%, 3.36%, 3.37%, 3.38%, 3.40%. It can be concluded that the maximum value of Δ is 3.40%.

3.1.2. Analysis of the Safety Factor When Under-Berm Failure Occurs

Figure 13a shows that FS_max, FS_min, and FS_ave all increase as H_B increases. When H_B increases from 3 m to 15 m, FS_max, FS_ave, and FS_min increase by 6.59%, 6.35%, and 6.10%, respectively. The rate of increase in these safety factors gradually diminishes, but the differences in their rates are not significant.

From Figure 13b, it can be seen that Δ increases with the increase in H_B. And it can be determined that when H_B = 3 m, 6 m, 9 m, 12 m, 15 m, Δ = 2.75%, 2.80%, 2.86%, 2.94%, 2.99%. It can be concluded that the maximum value of Δ is 2.99%.

Figure 14a shows that that FS_max, FS_min and FS_ave all decrease with the increase in ξ. When ξ increases from 15° to 45°, FS_max, FS_ave, and FS_min decrease by 3.62%, 3.57%, and 3.53%, respectively. It can be seen that the increase above three safety factors is gradually decreasing, but their decrease rates is similar to the impact of H_B on the safety factor.

From Figure 14b, it can be seen that Δ increases with the increase in ξ. And it can be determined that when ξ = 15°, 20°, 25°, 30°, 35°, 40°, 45°, Δ = 2.867%, 2.837%, 2.831%, 2.826%, 2.822%, 2.818%, 2.815%. It can be concluded that the maximum value of Δ is 2.867%.

Figure 15a shows that FS_max, FS_min, and FS_ave all increase as δ_B increases. When δ_B increases from 15° to 40°, FS_max, FS_ave, and FS_min increase by 5.38%, 5.19%, and 4.98%, respectively. The rate of increase in these safety factors gradually diminishes, but the differences between them are not significant.

From Figure 15b, it can be seen that Δ first slightly decreases and then increases with the increase in δ_B. And it can be determined that when δ_B = 15°, 20°, 25°, 30°, 35°, 40°, Δ = 2.742%, 2.741%, 2.792%, 2.815%, 2.855%, 2.938%. It can be concluded that the maximum value of Δ is 2.938%.

Figure 16a shows that FS_max, FS_min and FS_ave all increase with the increase in c_B. When c_B increases from 0 to 20 kN/m², FS_max, FS_ave, and FS_min increase by 1.45%, 1.47%, and 1.49%, respectively. It can be seen that there is almost no difference in the increase in the above three safety factors.

From Figure 16b, it can be seen that Δ decreases approximately linearly with the increase in c_B. And it can be determined that when c_B = 0, 4 kN/m², 8 kN/m², 12 kN/m², 16 kN/m², 20 kN/m², Δ = 2.839%, 2.834%, 2.829%, 2.824%, 2.819%, 2.814%. It can be concluded that the maximum value of Δ is 2.839%.

Through the analysis of Δ above, it can be found that the maximum value of Δ is 4.89%. In other words, the values of Δ are all within 5%. Therefore, it is feasible to use FS_ave to approximate FS_true to evaluate the degree of stability of the landfill with an engineered berm against composite failure modes.

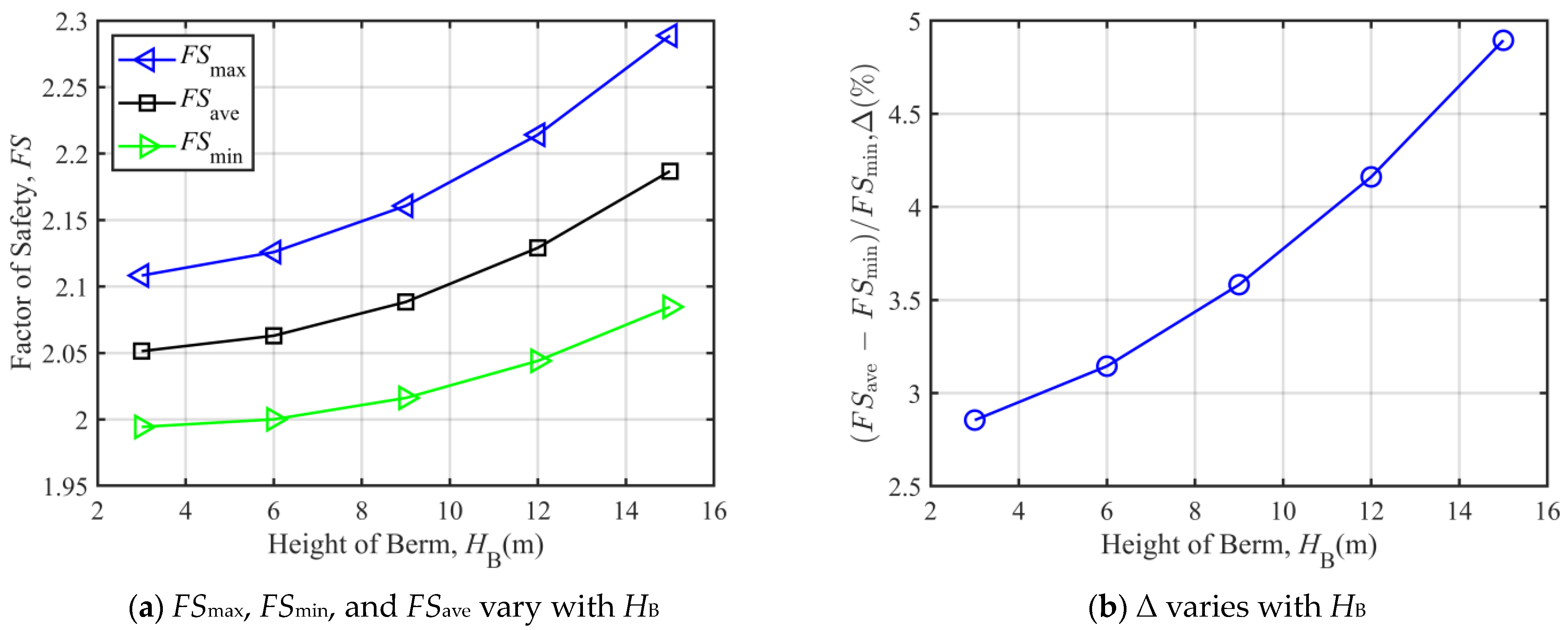
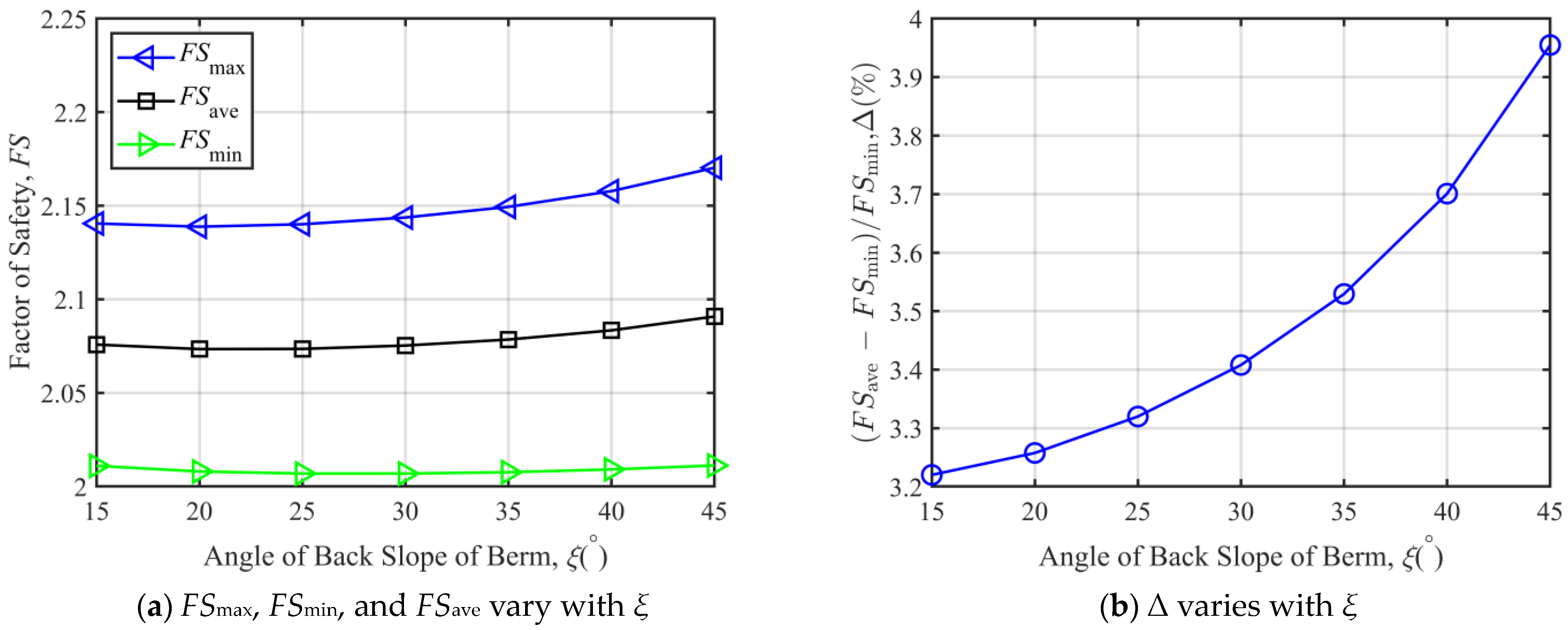
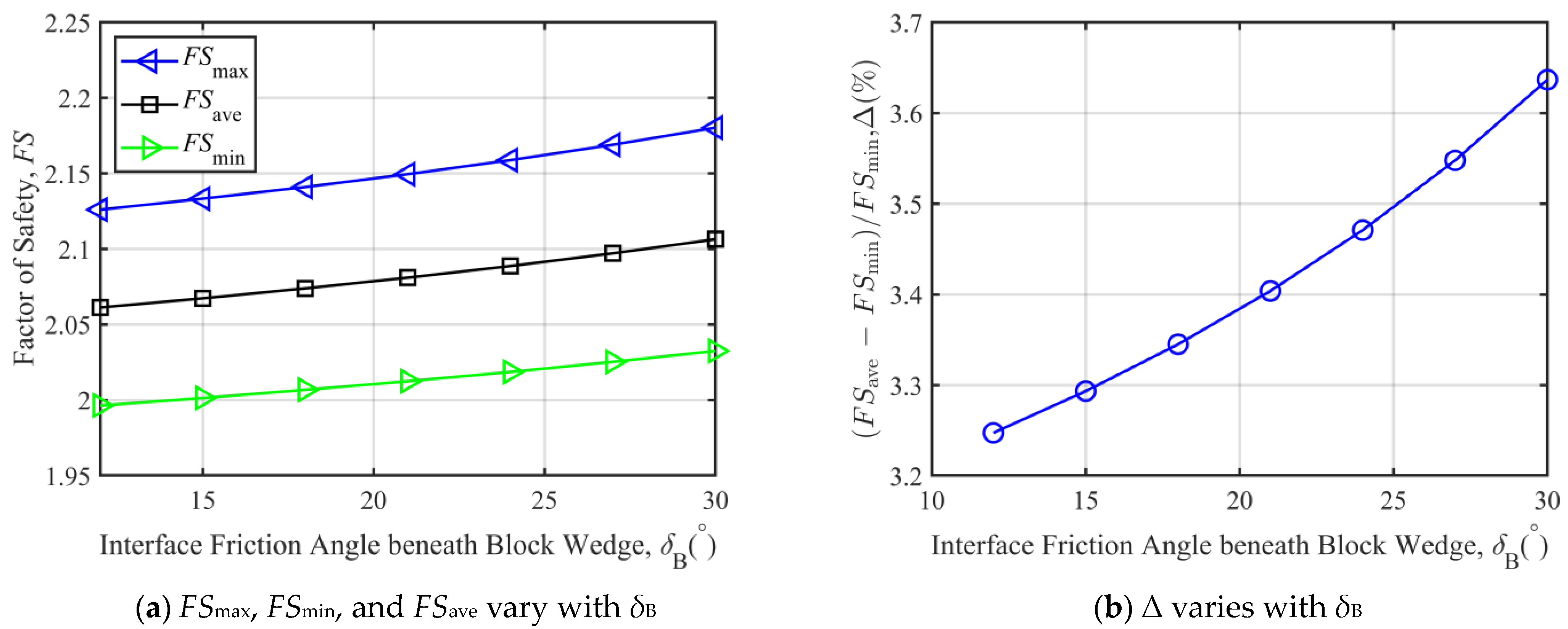
3.2. Parametric Analysis

To analyze the influence of related parameters of the engineered berm on the average safety factor, FS_ave, the parametric analysis was conducted, and the basic parameter values are shown in Section 3.1.

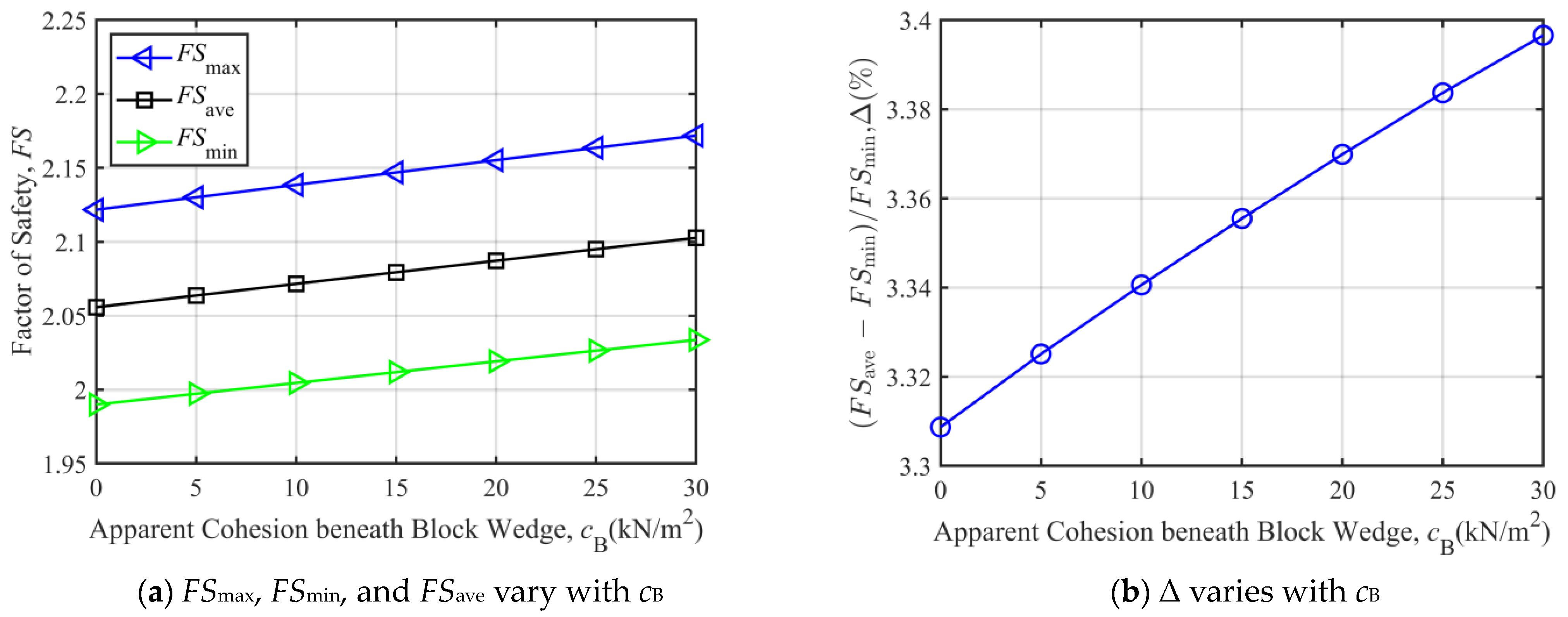
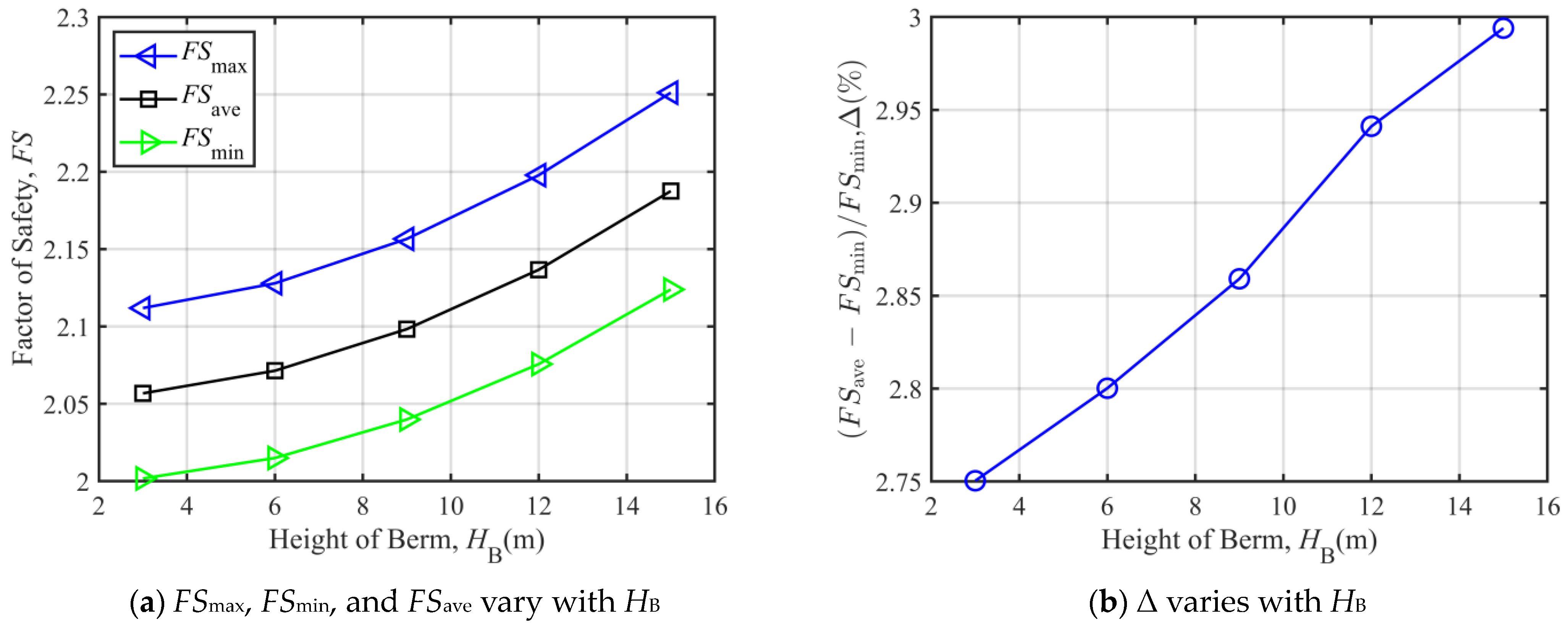
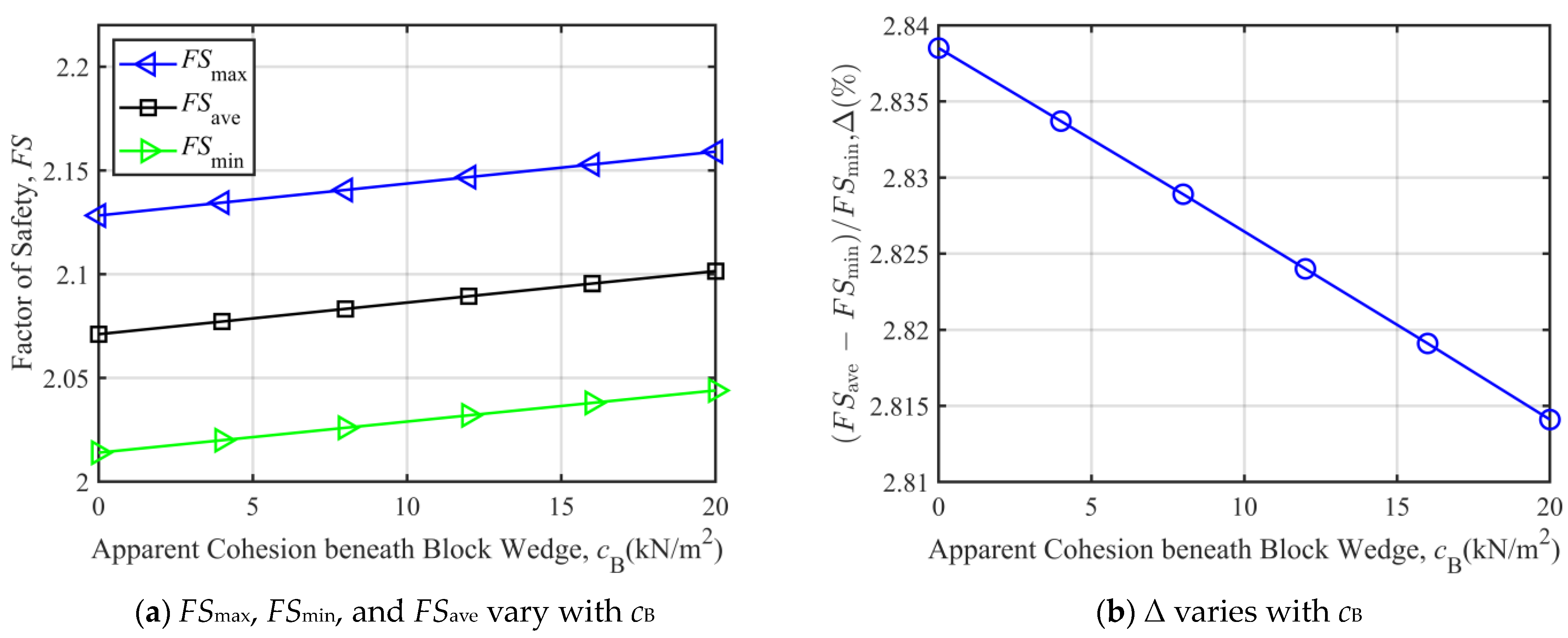
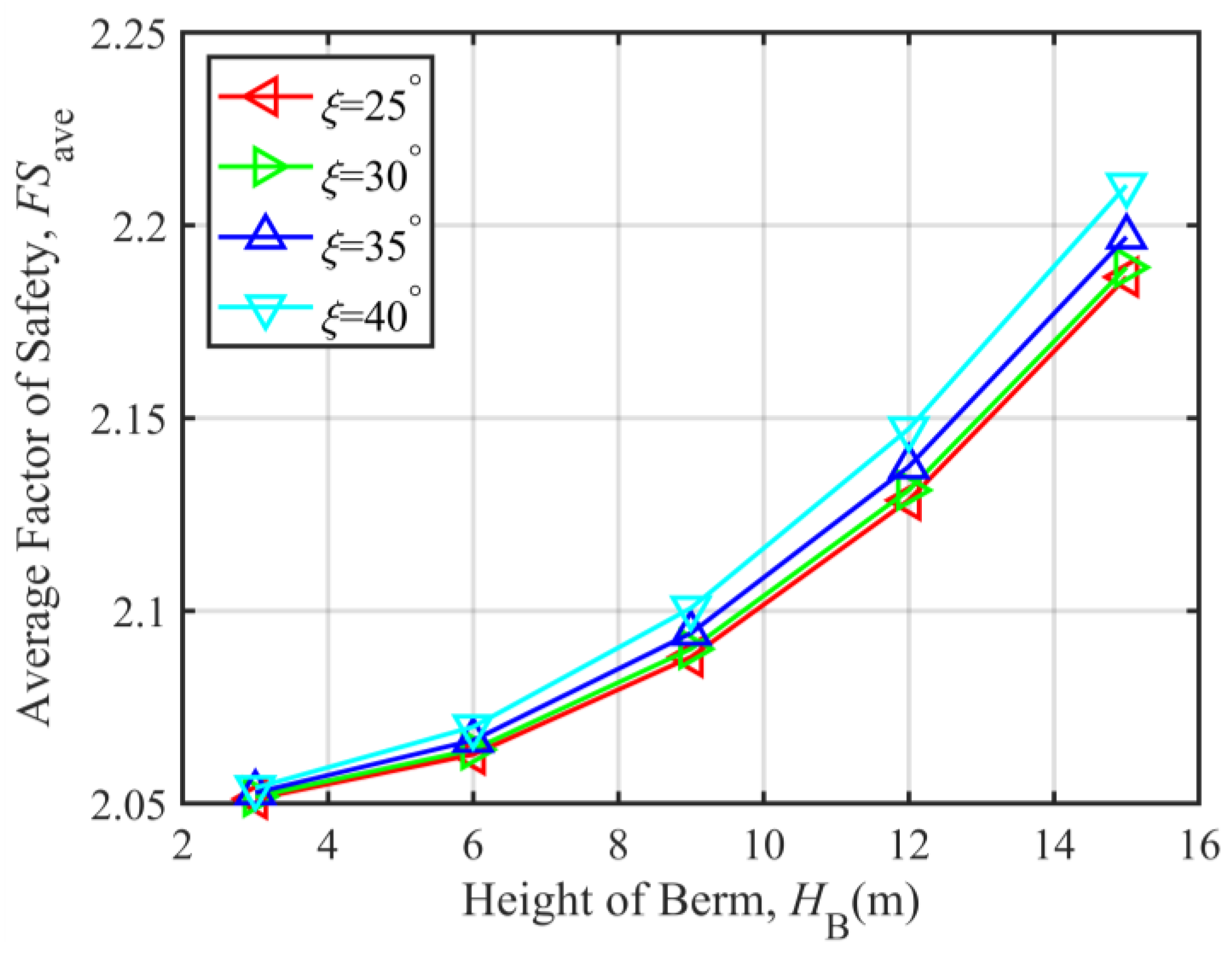
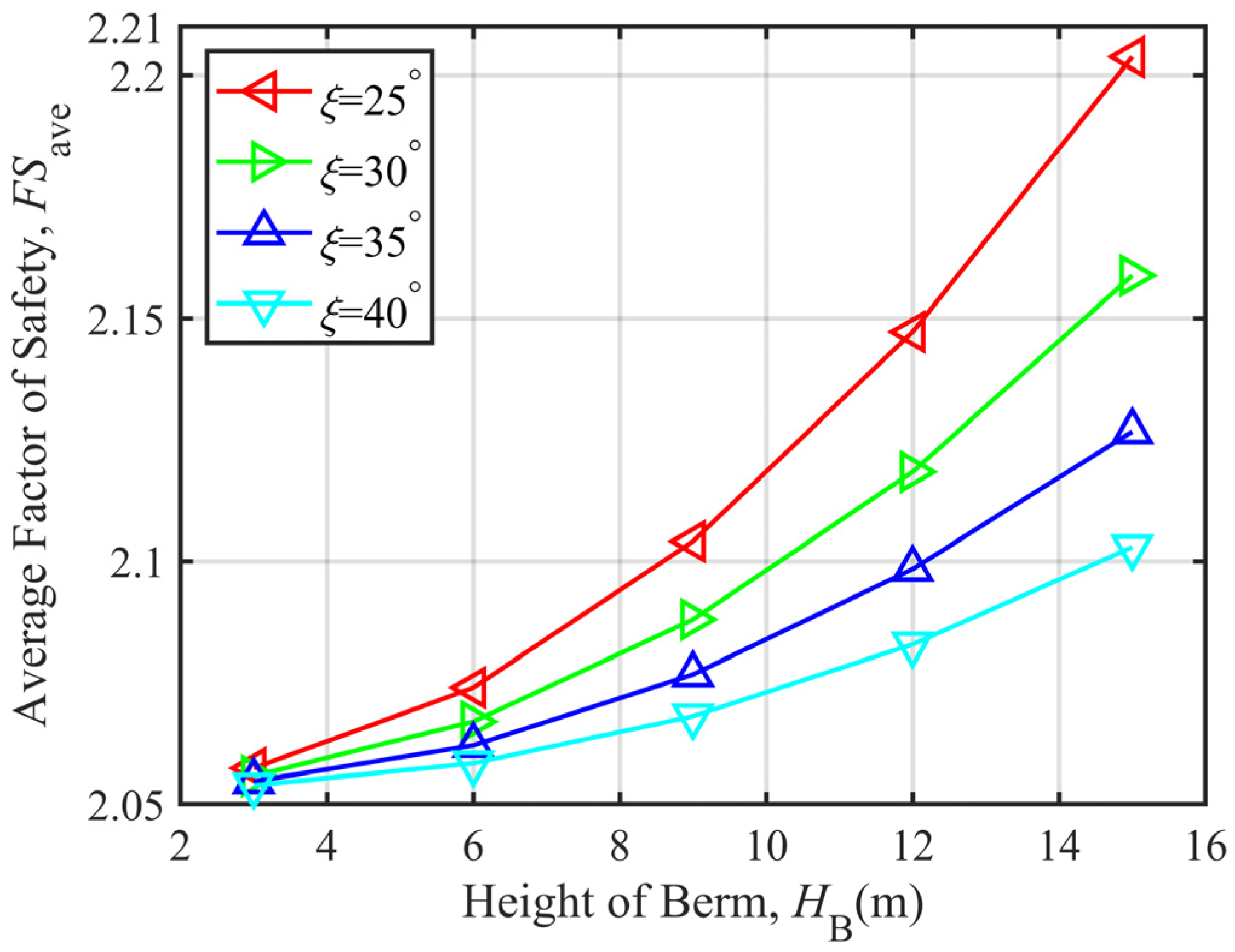
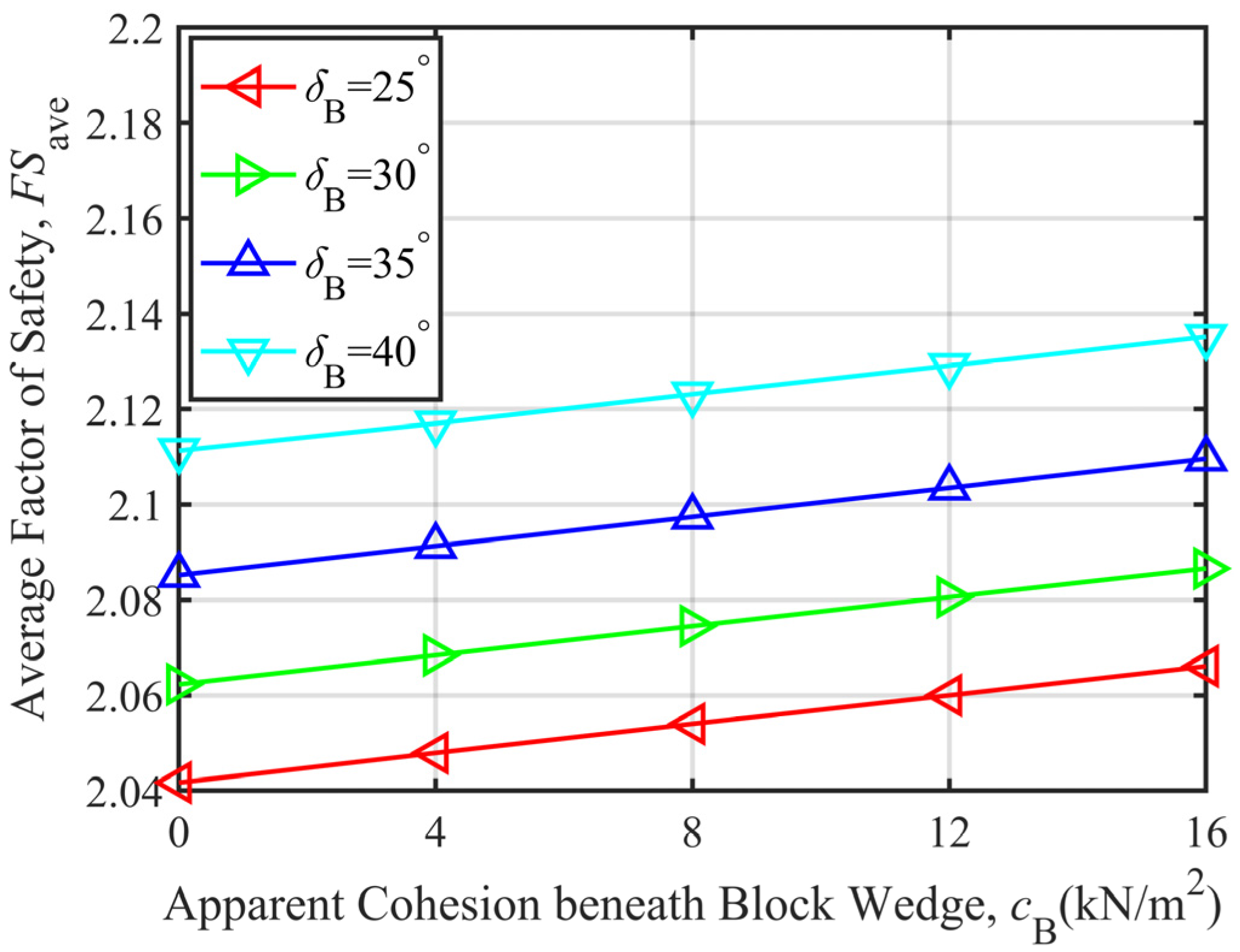
3.2.1. Parametric Analysis When Over-Berm Failure Occurs

It can be seen from Figure 17 that as H_B increases, FS_ave increases, and as ξ increases, FS_ave also increases. When H_B changes from 3 m to 15 m, FS_ave increases by 6.60% when ξ = 25°; when ξ = 30°, FS_ave increases by 6.69%; when ξ = 35°, FS_ave increases by 7.02%; when ξ = 40°, FS_ave increases by 7.61%. Therefore, it can be found that with the increase in ξ, the influence of H_B on FS_ave gradually becomes stronger.

It can be clearly observed in Figure 18 that as c_B increases, FS_ave increases, and as δ_B increases, FS_ave also increases. When c_B varies from 0 to 20 kN/m², FS_ave increases by 1.44% when δ_B = 12°; when δ_B = 15°, FS_ave increases by 1.51%; when δ_B = 18°, FS_ave increases by 1.53%; when δ_B = 21°, FS_ave increases by 1.55%. It can be thus summarized that the influence of c_B on FS_ave slightly increases as δ_B increases.

3.2.2. Parametric Analysis When Under-Berm Failure Occurs

It can be found out from Figure 19 that as H_B increases, FS_ave increases, while as ξ increases, FS_ave decreases accordingly. When H_B varies from 3 m to 15 m, FS_ave increases by 7.12% when ξ = 25°; when ξ = 30°, FS_ave increases by 5.01%; when ξ = 35°, FS_ave increases by 3.50%; when ξ = 40°, FS_ave increases by 2.39%. As a result, it can be concluded that as ξ increases, the effect of H_B on FS_ave gradually weakens.

Figure 20 shows that FS_ave either increases with c_B or increases with δ_B. When c_B changes from 0 to 16 kN/m², FS_ave increases by 1.20% for δ_B = 25°, 1.18% for δ_B = 30°, 1.17% for δ_B = 35°, and 1.13% for δ_B = 40°. Thus, it can be judged that with the increase in δ_B, the influence of c_B on FS_ave slightly weakens.

3.3. Slip Surface Analysis

The analysis of the critical log-spiral slip surface considers two failure modes of the engineered berm, and for the basic parameter values, one needs to refer to Section 3.1.

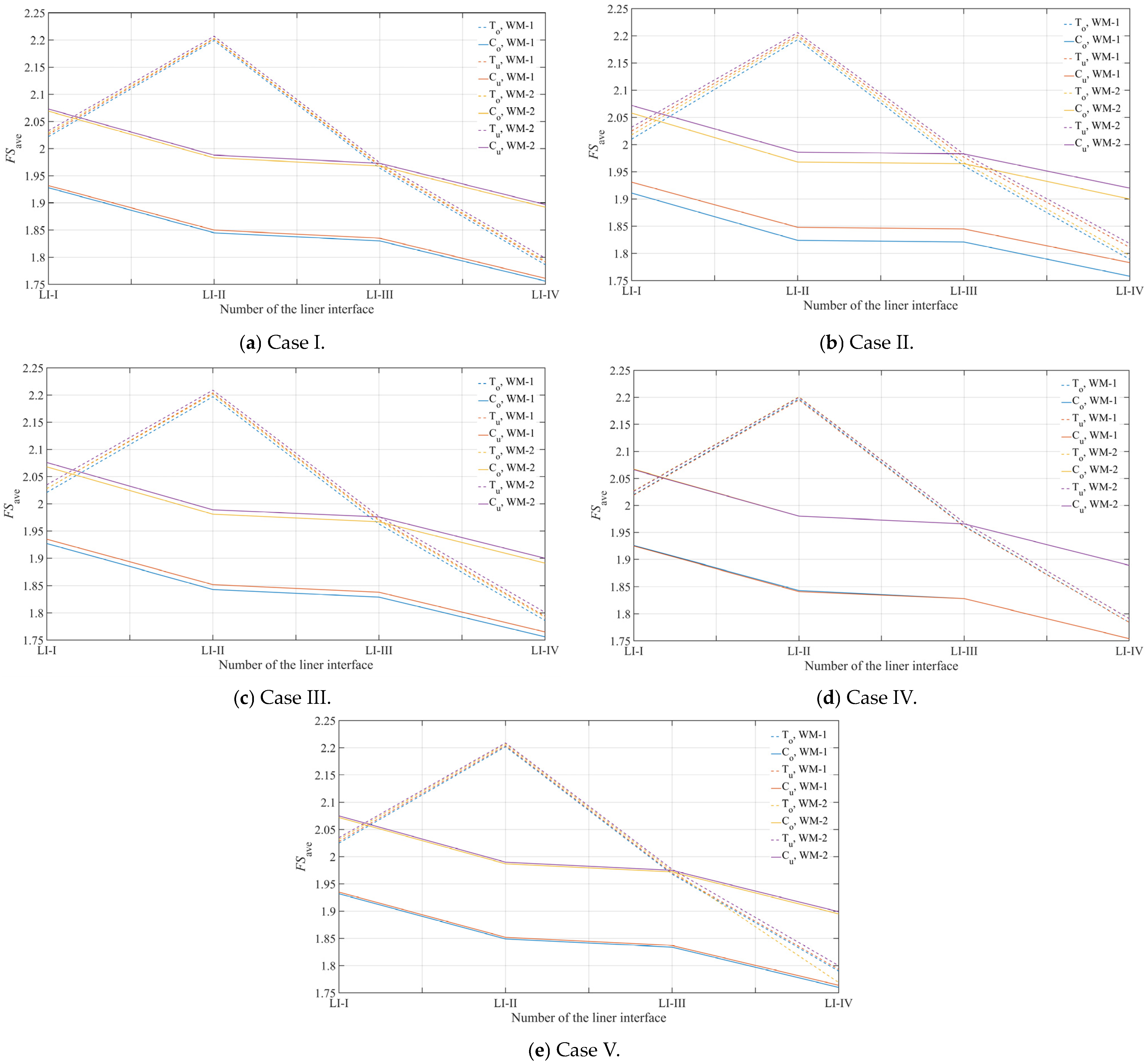
3.3.1. Slip Surface Analysis When Over-Berm Failure Occurs

The influence of δ_B on the critical log-spiral slip surface is as shown in Figure 21a. In this figure, (I) represents the working condition of δ_B = 12° and (II) represents the working condition of δ_B = 30°. In (I), FS_min = 1.996, FS_max = 2.126, and FS_min = 2.033; FS_max = 2.180 in (II). From Figure 21a, it can be clearly seen that as δ_B increases, the critical log-spiral slip surface gradually shifts to the right.

The influence of c_B on the critical slip surface is as shown in Figure 21b. In this figure, (I) represents the working condition of c_B = 0 and (II) represents the working condition of c_B = 30 kN/m². In (I), FS_min = 1.990 and FS_max = 2.122, and in (II), FS_min = 2.034, FS_max = 2.172. It can be easily observed from Figure 21b that as c_B increases, the critical log-spiral slip surface gradually shifts to the right.

From Figure 21a,b, it can be determined that as δ_B or c_B increases, the horizontal spacing between the critical log-spiral slip surfaces generated by FS_min and FS_max, respectively, increases accordingly.

3.3.2. Slip Surface Analysis When Under-Berm Failure Occurs

The influence of δ_B on the critical log-spiral slip surface is as shown in Figure 21c. In this figure, (I) represents the working condition of δ_B = 15° and (II) represents the working condition of δ_B = 40°. In (I), FS_min = 1.965 and FS_max = 2.073, FS_min = 2.063, FS_max = 2.184 in (II). From Figure 21c, it can be seen that as δ_B increases, the critical log-spiral slip surface gradually shifts to the right.

The influence of c_B on the critical log-spiral slip surface is as shown in Figure 21d. In the figure, (I) represents the working condition of c_B = 0; (II) represents the working condition of c_B = 20 kN/m². In (I), FS_min = 2.014 and FS_max = 2.128; in (II), FS_min = 2.044, FS_max = 2.159. From Figure 21d, it can be seen that as c_B increases, the critical log-spiral slip surface gradually shifts to the right.

From Figure 21c,d, the horizontal spacing between the critical log-spiral slip surfaces generated by FS_min and FS_max, respectively, only undergo slight changes.

4. Discussion

In order to investigate the reliability of the method proposed in this paper in analyzing the stability of the landfill with an engineered berm, the average safety factor, FS_ave, against composite failure mode was compared with that against translational failure mode. Referring to Technical code [36], the shear strength values of four types of liner interfaces are shown in

Table 1. Peak and residual shear strength values of four types of liner interfaces at bottom and back slope, respectively.

No	Liner Interface	Peak Shear Strength		Residual Shear Strength
		δP (°)	cP (kN/m2)	δA (°)	cA (kN/m2)
LI-I	GMX1/GT2	30	5	15	2
LI-II	GMX/CCL3	27	10	18	10
LI-III	GMX/GCL	28	3	16	0
LI-IV	GT/GN4	27	0	14	0

. The shear strength of the liner interface can generally reach its peak value at the bottom of the landfill slope, while only residual values can be exerted at its back slope [29]. For the shear strength value of waste mass, any type can be selected according to Technical code [34], i.e., ϕ_SW = 12°, c_SW = 15 kN/m² (WM-1), while the other type can be selected according to the paper by Chen et al. [37], i.e., ϕ_SW = 17°, c_SW = 6 kN/m² (WM-2).

For the comparison of safety factors under the action of the engineered berm, the over-berm and under-berm failure modes were considered separately. Under these two failure modes, parameter value combinations for five working conditions are provided as shown in

Table 2. Geometric and mechanical parameters for the engineered berm when over-berm failure occurs.

	Case I	Case II	Case III	Case IV	Case V
HB (m)	3	10	3	3	3
ξ (°)	26.6	26.6	18.4	26.6	26.6
δB (°)	18	18	18	10	18
cB (kN/m2)	11.5	11.5	11.5	11.5	20

and

Table 3. Geometric and mechanical parameters for the engineered berm when under-berm failure occurs.

	Case I	Case II	Case III	Case IV	Case V
HB (m)	3	10	3	3	3
ξ (°)	26.6	26.6	18.4	26.6	26.6
δB (°)	32	32	32	20	32
cB (kN/m2)	8	8	8	8	12

, respectively. The other unchanged parameter values are as follows: H = 70 m, B = 100 m, α = 18.4°, ω = 14°, θ = 1.1°, D_B = 3 m, η = 63.4°, γ_SW = 10.2 kN/m³, γ_B = 18 kN/m³.

When analyzing the stability of the landfill slope in Figure 22, T indicates translational failure while C indicates composite failure. In addition, considering the type of failure of the engineered berm, Subscript o represents the over-berm failure mode, and Subscript u represents the under-berm failure mode. The bold font in the above tables suggests that the safety factor calculated for resisting the composite failure mode is lower than the value calculated for resisting the translational failure mode, and the italic bold font implies that the safety factors calculated for resisting the two failure modes are no different.

From Figure 22a–e, it can be seen that FS_ave calculated against the composite failure mode is smaller than that against the translational failure mode when using WM-1 for waste mass, regardless of whether the instability to the engineered berm is over-berm failure or under-berm failure. In other words, the critical failure mode of the landfill slope at this time is composite. In Figure 22b, when WM-2 is used for waste mass and under-berm failure mode is considered to occur, it can be observed that FS_ave produced by C_u is almost equal to that produced by T_u under the working condition of LI-III. In other working conditions with WM-2, it can be seen that the critical failure modes of the landfill under conditions of LI-II and LI-III are consistent with the above situation.

For the stability analysis of landfill slopes currently containing composite liner systems, it is necessary to conduct translational failure analysis. However, simultaneously verifying the stability under the composite failure mode can obviously reduce the risk of instability.

5. Conclusions

This paper established a static calculation model for evaluating the stability of a landfill with an engineered berm against composite failure mode. Through relevant assumptions, implicit function equations for the maximum and minimum safety factors under different failure modes of the engineered berm were obtained. The maximum and minimum safety factor values were calculated through MATLAB programming. Through error analysis, it was verified that using the average safety factor instead of the true safety factor to evaluate the static stability of the landfill with an engineered berm against composite failure modes is feasible. Furthermore, the influence of relevant parameters of the engineered berm on the landfill stability and the critical slip surface was analyzed, and the following conclusions were drawn:

(1) When the height of berm remains constant, the ability of the landfill slope to resist over-berm failure can be improved by increasing the value of the angle of the back slope of the berm. In addition, for the over-berm failure mode, a larger value of interface friction angle of liner components beneath the block combined with appropriate apparent cohesion between liner components beneath the block is more conducive to improving the stability of the landfill slope.

(2) Unlike the situation when over-berm failure occurs, a specific height of berm requires a smaller value of the angle of the back slope of the berm to resist under-berm failure. At this point, the combination of the interface friction angle of liner components beneath the block and the apparent cohesion between liner components beneath the block has the opposite effect on the stability of the landfill slope compared to the situation when over-berm failure occurs.

(3) Regardless of over-berm failure or under-berm failure, as the interface friction angle of liner components beneath the block or the apparent cohesion between liner components beneath the block increases, the critical log-spiral slip surface gradually shifts to the right. In addition, the changes in the mechanical parameters of the engineered berm have a significant impact on the horizontal spacing of the critical log-spiral slip surfaces corresponding to the maximum and minimum safety factors in the over-berm failure mode while having little effect on the corresponding horizontal spacing in the under-berm failure mode.

(4) Whether it is over-berm failure or under-berm failure, the geometric and mechanical parameters of the engineered berm have little effect on the transition between translational and composite failure of the landfill slope, while the mechanical parameters of the waste mass have a significant effect.