Bilateral Matching Decision Model and Calculation of High-Speed Railway Train Crew Members

Abstract

To meet the preference demands of the crew members of high-speed railway trains while forming a crew team, and to automate the compilation of adaptable crew member schemes, a bilateral matching decision method for crew members is proposed based on complete preference order information. This method first describes the mutual selection process between the chief stewards and stewards of a high-speed railway train as a one-to-many bilateral matching decision process between the chief stewards and stewards Subsequently, by constructing a virtual train chief stewards, the original one-to-many bilateral matching relationship between the chief stewards and stewards is transformed into a one-to-one bilateral matching relationship between the virtual chief stewards for modeling. Then, a dual-objective integer programming model is established with the minimum sum of preference order values as the objective. Finally, an optimization solver is used to calculate the problem under different scales, and a genetic algorithm is designed for large-scale scenarios. The analysis results of numerical examples show that the model and algorithm of train crew members based on bilateral matching decisions can meet the actual requirements of the crew department and have good application value.

1. Introduction

The research field of high-speed railway crew planning has consistently been a prominent focus within high-speed railway management optimization. Current studies have yielded substantial findings primarily concentrated on optimizing crew routing and formulating crew schedules. Tian Zhiqiang [1] modeled the problem as a set-covering model with minimum cost as the optimization objective, utilizing an improved ant colony algorithm for computation. Zhang Zheming [2] developed a space–time state network integrated with crew regulations, formulated an integer programming model for the network, and designed a Lagrangian algorithm for solving the problem. Hoffmann [3] proposed an arc-flow model aimed at minimizing crew costs, employing column generation techniques to enhance solution efficiency. Fuentes [4] introduced a crew scheduling model based on network flow to reduce labor costs, further implementing a time-based personnel clustering decomposition approach to solve the problem. Hanczar [5] designed a two-stage model and devised separate solution algorithms for large-scale instances, validating the model’s and algorithm’s effectiveness through simulation studies. A review of prior research reveals that the majority of these studies have focused predominantly on reducing labor costs or minimizing working hours, with limited consideration for crew perspectives in the formulation of crew schedules.

In the research of similar topics in aviation systems, several studies based on the perspective of crew members have emerged. Felici [6] established a preference-based integer programming model and designed a heuristic algorithm to solve this problem. Maenhout [7] integrated crew preferences into the objective function of the model, designing a decentralized search algorithm and comparing it with a branch-and-price algorithm based on the constructed integer programming model. Quesnel [8] incorporated crew preferences into this problem, establishing a preference-based mathematical model and employing a column generation algorithm to solve it. Bahareh [9] developed a scheduling model based on crew preferences and qualifications, and used a genetic algorithm to solve this problem, aiming to achieve an optimized crew scheduling scheme.

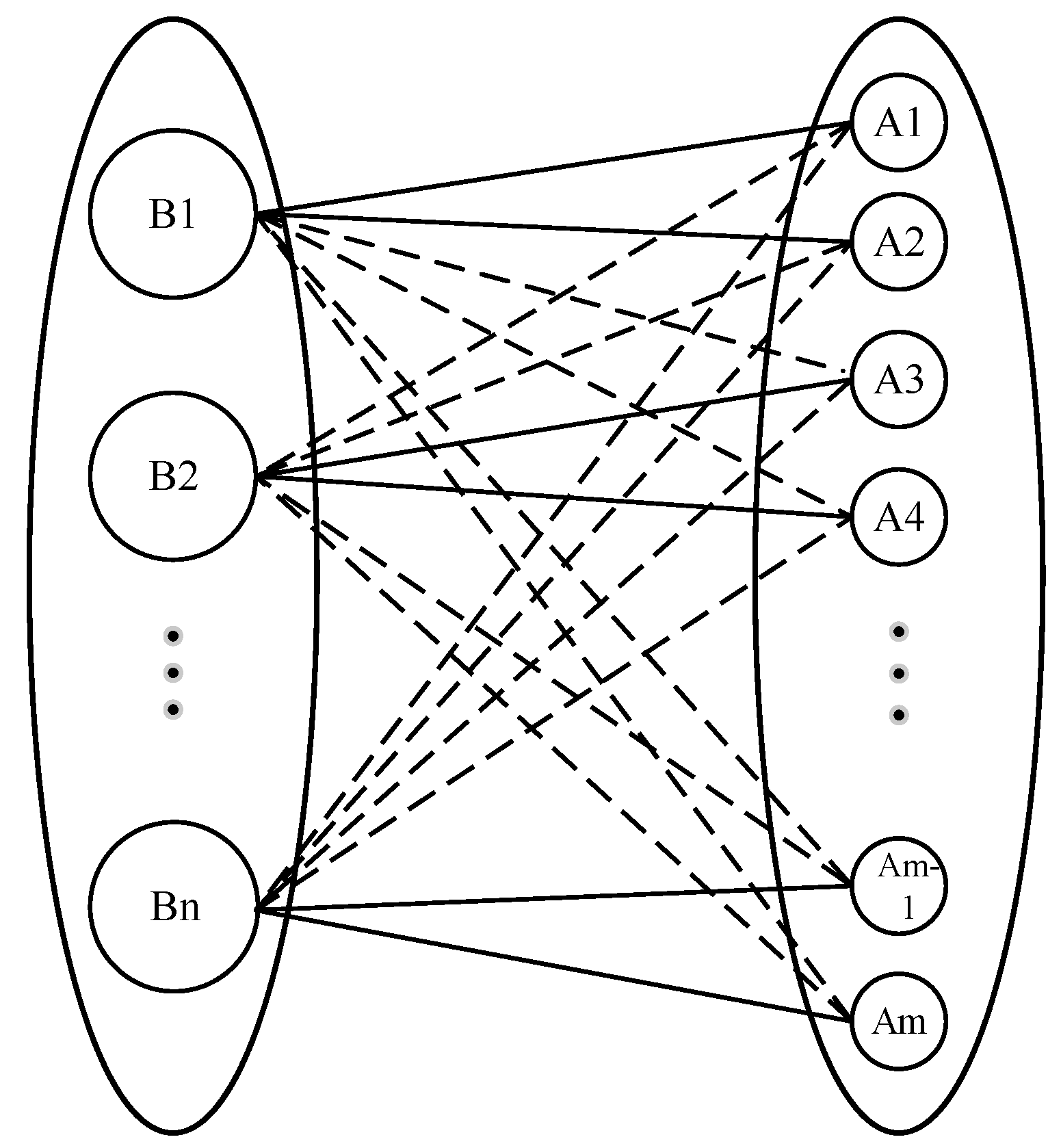
In recent years, the efficiency of team collaboration in high-speed railway crew operations has been declining, coupled with increasing personnel turnover. Thus, exploring crew scheduling methods from the perspective of crew members has become particularly important. In practice, the preparation of high-speed railway crew plans typically involves three main steps: first, the matching of crew members; second, the generation of crew routes; and finally, the matching of crew members to the generated crew routes. Steward matching forms the foundation of crew plan preparation. If crew members with high satisfaction can be identified during the matching process, it can significantly enhance their job satisfaction and team collaboration efficiency, while also improving personnel stability. However, current research in this area remains relatively limited. Against this backdrop, the theory of bilateral matching decisions offers a novel research approach.

Bilateral matching theory addresses the problem of matching discrete resources between two disjoint sets and has become a research hotspot in recent years. It is widely applied in various fields, including male–female marriage matching, person–position matching, and matching between students and mentors. Numerous scholars have conducted in-depth studies on this problem, focusing on aspects such as stability and satisfaction. GALE et al. [10] established the definitions of stable and optimal matchings through the study of student admissions and marriage issues, confirming the existence of stable matchings using the Gale–Shapley algorithm. Yu D [11] designed a bilateral matching model based on intuitionistic fuzzy functions for person–job matching, obtaining optimal results through multi-objective decision-making models. Li Mingyang [12] converted matching preference order information into satisfaction levels to construct an optimization model for the maximum weight matching problem, achieving optimal bilateral matching results. Kong Dezai [13] introduced a preference list simplification rule to reduce the scale of bilateral matching problems and demonstrated that stability constraints within the optimization model can yield one-to-many stable matching solutions. Jia Fuqiang [14] created a bipartite graph focused on travelers and routes, proving from a graph theory perspective that the stable matching of this bipartite graph determines the final path selection, and established two types of multi-objective optimization models considering and disregarding the effects of traffic flow and capacity. Kong Dezai [15] targeted bilateral matching issues with individual and reciprocal preferences, built a stable matching optimization model to maximize overall subject satisfaction, and transformed the multi-objective optimization model into a single-objective model using a weighted sum method based on membership functions to find the optimal stable matching schemes for bilateral subjects. Yang Qin [16] converted the one-to-many bilateral matching issue between rescuers and rescue tasks into a one-to-one perfect matching problem, establishing a bilateral matching decision model that maximizes perceptual congruence and acceptance. Liu Jie [17] transformed the one-to-many bilateral matching problem between instructors and graduate students into a one-to-one issue, developing a preference-based perceived satisfaction function for both teachers and students using prospect theory, and solved it using a genetic algorithm. Xiao Hanqiang [18] under the conditions of bilateral subject satisfaction and intermediary benefits, calculated the prospective values between parties using prospect theory and constructed a dual-objective optimization model aiming to maximize the aggregate prospective values. Yuan Duoning [19] addressed the one-to-many bilateral matching issue between elective surgery patients and surgeons, creating a multi-objective optimization model to achieve a stable matching scheme that meets expectation levels, using a non-dominated sorting genetic algorithm with an elite strategy. Kong Dezai [20] focused on bilateral matching problems where one party provides preference order information and the other has reciprocal preferences, devising a stable matching optimization model that maximizes satisfaction for both sides and determined that the optimal solution corresponds to Pareto efficient matches. Le Qi [21] investigated the bilateral matching problem using triangular intuitionistic fuzzy number information to achieve the highest triangular intuitionistic fuzzy satisfaction for venture capitalists and enterprises, building a multi-objective bilateral matching model and converting it into a single-objective model using linear weighting and centroid methods to obtain the “best” bilateral matching scheme. Li Woyuan [22] transformed interval intuitionistic fuzzy set matrices into score function matrices to build a bilateral matching model based on score functions and matching matrices. Zhang Lili [23] constructed an advantageous attribute scale based on objective evaluations of subjects, introduced a formula for individual comprehensive situations, converted multi-objective optimization into single-objective optimization using a subordination-weighting method, and used the Hungarian method to secure the matching scheme with the highest satisfaction and stability. For the one-to-many two-sided matching problem based on ordinal preference information, Li Mingyang [24] constructs a multi-objective optimization model with the goal of minimizing the sum of ordinal values for each party under stable matching conditions. The multi-objective optimization model is then transformed into a single-objective optimization model to obtain the optimal matching result.

From an application perspective, the aforementioned studies extend the bilateral matching theory to various domains, including marriage, doctor–patient, admissions, and rescue scenarios, encompassing matching subjects such as individual-to-individual, individual-to-job, and individual-to-resource. Theoretically, these studies address the conversion of one-to-many bilateral matching issues into one-to-one scenarios by defining virtual subjects, thereby constructing multi-objective optimization models using linear programming techniques. These models are further simplified into single-objective formulations, or solved using intelligent multi-objective optimization algorithms, effectively resolving bilateral matching problems.

The problem of crew matching in the field of high-speed railway crew planning research involves matching between individuals, where the process can be viewed as a decision-making process with the chief steward and stewards as the primary entities in bilateral matching. By introducing bilateral matching decision theory, theoretical support can be provided for efficient and stable crew matching. Accordingly, this paper applies bilateral matching decision theory to the problem of crew matching in high-speed railway trains. Based on the preference order theory, a one-to-many bilateral matching multi-objective optimization model is developed, considering the satisfaction of both matching entities. Optimization solvers and intelligent optimization algorithms are employed to conduct simulations and calculations for various problem scales under different scenarios. This not only enhances the field of high-speed railway crew planning research with significant application value but also expands the application scope of bilateral matching theory.

2. Problem Description and Modeling

In the current model for high-speed railway crew matching, the standard configuration comprises one chief steward matched with three stewards. Both chief stewards and stewards, serving as the primary subjects in bilateral matching, conduct comprehensive evaluations and assign quantitative scores to each other. This process yields a complete preference order of one party for the overall profile of the other, providing a quantitative measure of satisfaction between the matched subjects [3].

2.1. Symbol Description

For the convenience of model construction, the symbol definition and description are shown in

Table 1. Symbol representation and meaning.

Symbol	Meaning
$M$	Set of stewards, $M=\left\{1,2,\dots ,m\right\}$
$N$	Set of chief stewards, $N=\left\{1,2,\dots ,n\right\}$
$A$	Set of stewards $A=\left\{A_1,A_2,\dots ,A_m\right\}$, where $A_i$ represents the steward number $i$, $i\in M$
$B$	Set of chief stewards $B=\left\{B_1,B_2,\dots ,B_n\right\}$, where $B_j$ represents the steward number $j$, $j\in N$
$c_j$	Total number of stewards matched by chief steward number $j$, ${\displaystyle \sum _{j=1}^n{c}_j}=m$ (total number of stewards matches the total number of places available)
$r_{ij}$	The complete preference order vector of steward $A_i$ prefers chief steward $B_j$ over chief steward, $r_{ij}$ indicates that steward $A_i$ ranks chief steward $B_j$ in position $r_{ij}$.
$s_{ij}$	The complete preference order vector of steward $B_j$ prefers chief steward $A_i$ over chief steward, $s_{ij}$ indicates that steward $B_j$ ranks chief steward $A_i$ in position $s_{ij}$.
$R$	Steward’s complete preference order matrix for chief stewards, $R=\left[r_{ij}\right]$
$S$	Chief steward’s complete preference order matrix for stewards, $S=\left[s_{ij}\right]$
$\mu$	Mapping function $\mu :A\cup B\to A\cup B$, a multi-valued that assigns stewards from set A to chief stewards in set B.
$\tilde{\mu }$	Modified mapping function $\tilde{\mu }:A\cup \tilde{B}\to A\cup \tilde{B}$, a single-valued mapping that assigns stewards from set A to chief stewards in set B.
$\tilde{B}$	Set of Virtual Chief stewards $\tilde{B}=\left\{{\tilde{B}}_1^1,\cdots ,{\tilde{B}}_1^{c_1},{\tilde{B}}_j^q,{\tilde{B}}_n^1,\cdots ,{\tilde{B}}_n^{c_n}\right\}$, where $q\in \left\{1,2,\dots c_j\right\}$
${\tilde{r}}_{ij}^q$	${\tilde{r}}_{ij}^q$ represents the complete preference order vector of steward $A_i$ for the q-th virtual representation of chief steward $B_j$, where $q\in \left\{1,2,\dots c_j\right\}$.
${\tilde{s}}_{ij}^q$	${\tilde{s}}_{ij}^q$ represents the complete preference order vector of steward $B_j$ for the q-th virtual representation of chief steward $A_i$, where $q\in \left\{1,2,\dots c_j\right\}$.
$\tilde{R}$	The complete preference order matrix of stewards for virtual chief stewards, $\tilde{R}=\left[{\tilde{r}}_{ij}^q\right]$
$\tilde{S}$	The complete preference order matrix of virtual chief stewards for stewards, $\tilde{S}=\left[{\tilde{s}}_{ij}^q\right]$

.

2.2. Construction of the Train Crew Matching Model

The one-to-many bilateral matching decision model in the train crew matching problem is illustrated in Figure 1. In this model, $A_1$ to $A_m$ denote the set of stewards, and $B_1$ to $B_n$ denote the set of chief stewards. The thick solid lines represent the final constructed matching pairs, while the dashed lines represent the mutual preference information between the matching subjects. The evaluation of the matching scheme is based on the satisfaction of the bilateral matching results between the chief stewards and stewards.

2.2.1. Establishing the Complete Preference Order Matrix

The complete preference order vector of stewards for chief stewards is $R_i=\left\{r_{i1},r_{i2},\dots ,r_{in}\right\}$, where $i\in M$, $j\in N$, and $r_{ij}$ represents the ranking of chief steward $B_j$ in the preference order of steward $A_i$. Similarly, the complete preference order vector of chief stewards for stewards is $S_j=\left\{s_{1j},s_{2j},\cdots ,s_{mj}\right\}$, where $s_{ij}$ represents the ranking of steward $A_i$ in the preference order of chief steward $B_j$. The complete preference order matrices are denoted by $R=\left[r_{ij}\right]$ and $S=\left[s_{ij}\right]$. A smaller value of $r_{ij}$ or $s_{ij}$ indicates a higher satisfaction level of the matching [1]. All ranking values in this paper follow a strict ordering: if $j\ne k$, then $r_{ij}\ne r_{ik}$; if $i\ne l$, then $s_{ij}\ne s_{lj}$.

2.2.2. Converting One-to-Many Matching Relationship to One-to-One Matching

The multi-valued mapping $\mu :A\cup B\to A\cup B$ represents a one-to-many bilateral matching between stewards and chief stewards, where $A_i=\mu \left(B_j\right)$ and $B_j=\mu \left(A_i\right)$ both indicate that $A_i$ and $B_j$ are matched in $\mu$. In this context, $\mu \left(A_i\right)=A_i$ indicates that $A_i$ is unmatched in $\mu$, and similarly, $\mu \left(B_j\right)=B_j$ indicates that $B_j$ is unmatched in $\mu$. When $c_j=1$, the one-to-many bilateral matching problem simplifies to a one-to-one bilateral matching problem, and $\tilde{\mu }$ represents a one-to-one bilateral matching.

According to actual work conditions, the number of chief stewards matched by each steward is 1 and the number of stewards matched by each chief steward is $c_j$, given ${\displaystyle {\sum }_{j=1}^n{c}_j=m}$. to facilitate analytical modeling [8], the one-to-many bilateral matching problem is transformed into a one-to-one bilateral matching problem.

For chief steward $B_j$, since the number of matched stewards is $c_j$, $B_j$ can be regarded as having $q$ virtual subjects with the same preference order $q\in \left\{1,2,...c_j\right\}$. The set consisting of virtual chief stewards is denoted as $\tilde{B}=\left\{{\tilde{B}}_1^1,\cdots ,{\tilde{B}}_1^{c_1},{\tilde{B}}_j^q,{\tilde{B}}_n^1,\cdots ,{\tilde{B}}_n^{c_n}\right\}$, where $q\in \left\{1,2,\dots c_j\right\}$. The ${\tilde{B}}_j^q$ represents the virtual chief steward at position $q$ corresponding to chief steward ${\tilde{B}}_j$, The conversion process is shown in Figure 2 below. The complete preference value matrix of the set of chief stewards $\tilde{B}$ to the set of stewards is $\tilde{S}={\left(s_{ij}^q\right)}_{m\times m}$, where ${\tilde{s}}_{ij}^q$ represents the complete preference vector of the virtual chief steward at position $q$ corresponding to the chief steward ${\tilde{B}}_j$ for the steward $A_i$. Similarly, the complete preference value matrix of the stewards to the set of chief stewards $\tilde{B}$ is ${\tilde{R}}^{\prime }={\left(r_{ij}^q\right)}_{m\times m}$, where ${\tilde{r}}_{ij}^q$ represents the complete preference vector of steward $A_i$ for the virtual chief steward at position $q$ corresponding to the chief steward ${\tilde{B}}_j$. Thus, the preference matrices $\tilde{S}$ and $\tilde{R}$ are obtained.

$$\tilde{S}={\left({\tilde{s}}_{ij}^q\right)}_{m\times m}=\left(\begin{array}{lllllllll}{\tilde{s}}_{11}^1& \cdots & {\tilde{s}}_{11}^1& \cdots & {\tilde{s}}_{j1}^q& \cdots & {\tilde{s}}_{n1}^1& \cdots & {\tilde{s}}_{n1}^{c_n}\\ ⋮& & ⋮& & ⋮& & ⋮& & ⋮\\ {\tilde{s}}_{1i}^1& \cdots & {\tilde{s}}_{1i}^{c_1}& \cdots & {\tilde{s}}_{ji}^q& \cdots & {\tilde{s}}_{ni}^1& \cdots & {\tilde{s}}_{ni}^{c_n}\\ ⋮& & ⋮& & ⋮& & ⋮& & ⋮\\ {\tilde{s}}_{1m}^1& \cdots & {\tilde{s}}_{1m}^{c_1}& \cdots & {\tilde{s}}_{jm}^q& \cdots & {\tilde{s}}_{nm}^1& \cdots & {\tilde{s}}_{nm}^{c_n}\end{array}\right)\tilde{R}={\left({\tilde{r}}_{ij}^q\right)}_{m\times m}=\left(\begin{array}{lllllllll}{\tilde{r}}_{11}^1& \cdots & {\tilde{r}}_{11}^{c_1}& \cdots & {\tilde{r}}_{1j}^q& \cdots & {\tilde{r}}_{1n}^1& \cdots & {\tilde{r}}_{1n}^{c_m}\\ ⋮& & ⋮& & ⋮& & ⋮& & ⋮\\ {\tilde{r}}_{i1}^1& \cdots & {\tilde{r}}_{i1}^{c_1}& \cdots & {\tilde{r}}_{ij}^q& \cdots & {\tilde{r}}_{in}^1& \cdots & {\tilde{r}}_{in}^{c_m}\\ ⋮& & ⋮& & ⋮& & ⋮& & ⋮\\ {\tilde{r}}_{m1}^1& \cdots & {\tilde{r}}_{m1}^{c_1}& \cdots & {\tilde{r}}_{mj}^q& \cdots & {\tilde{r}}_{mn}^1& \cdots & {\tilde{r}}_{mn}^{c_m}\end{array}\right)$$

In the transformed one-to-one bilateral matching $\tilde{\mu }$, the preference order values of virtual subjects are equivalent to the original problem’s preference order values, that is, ${\tilde{r}}_{ij}^q=r_{ij}$, where $i\in M, j\in N, q\in \left\{1,2,\dots ,c_j\right\}$; ${\tilde{s}}_{ij}^q=s_{ij}$, where $i\in M, j\in N, q\in \left\{1,2,\dots ,c_j\right\}$. The one-to-one matching model for chief stewards and stewards is obtained as Figure 3.

2.2.3. Model Establishment

In summary, a bilateral matching optimization model (M1) considering stability is established with the objective of minimizing the complete preference order value of both the stewards and chief stewards:

$$Min{Z}_1={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\tilde{r}}_{ij}^q}}{x}_{ij}^q$$

(1)

$$Min{Z}_2={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\tilde{s}}_{ij}^q{x}_{ij}^q}}$$

(2)

s.t.

$${\displaystyle \sum _{i=1}^m{x}_{ij}^q}\le 1 j\in N,q\in \{1,2,\dots ,c_j\}$$

(3)

$${\displaystyle \sum _{j=1}^n{x}_{ij}^q}\le 1 i\in M,q\in \{1,2,\dots ,c_j\}$$

(4)

$$x_{ij}^q\in \left\{0,1\right\} i\in M,j\in N,q\in \{1,2,\dots ,c_j\}$$

(5)

In the model M1: Equations (1) and (2) are the objective functions; Equation (3) indicates that each steward can only be matched with one virtual chief steward; Equation (4) indicates that each virtual chief steward can only be matched with one steward; and Equation (5) defines the range of decision variables.

This model is a multi-objective integer optimization model where the objective functions have non-negative characteristics, and the two objective functions share the same dimensions. Therefore, a linear weighting method is used to linearly weight the two objectives, resulting in a single objective function. The model is then converted into a single-objective optimization model (M2) for computation. The expression for mathematical model M2 is:

$$MinZ={\alpha }_1{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\tilde{r}}_{ij}^q}}{x}_{ij}^q+{\alpha }_2{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\tilde{s}}_{ij}^q{x}_{ij}^q}}$$

(6)

s.t.

$${\displaystyle \sum _{i=1}^m{x}_{ij}^q}\le 1 j\in N,q\in \{1,2,\dots ,c_j\}$$

(7)

$${\displaystyle \sum _{j=1}^n{x}_{ij}^q}\le 1 i\in M,q\in \{1,2,\dots ,c_j\}$$

(8)

$$x_{ij}^q\in \left\{0,1\right\} i\in M,j\in N,q\in \{1,2,\dots ,c_j\}$$

(9)

Refer to the above model (6)–(9) as M2, which is a single-objective integer optimization model. Specialized optimization software such as Cplex, Lingo, and Gurobi can be used to obtain the exact solution of this mathematical model. In practical work, it is usually considered that the positions of stewards and chief stewards are equally important in the matching process. Therefore, during the solving process, this equality can be assumed. In this study, the problem was solved using Python programming language on a Windows 10 system with an Intel i7-1165G7 processor, utilizing the Gurobi optimization solver. Assuming a passenger line has 4 chief stewards and 12 stewards, each chief steward $B_j$ evaluates the stewards $A_i$ based on their own preferences, work abilities, and other indicators, resulting in a preference order vector $s_{ij}$, as shown in

Table 2. The complete preference order of the chief stewards to stewards.

	$A_1$	$A_2$	$A_3$	$A_4$	$A_5$	$A_6$	$A_7$	$A_8$	$A_9$	$A_{10}$	$A_{11}$	$A_{12}$
$B_1$	9	5	8	11	2	10	4	3	12	7	1	6
$B_2$	8	1	2	12	9	5	6	11	3	4	10	7
$B_3$	12	6	7	5	1	8	11	10	4	2	9	3
$B_4$	12	6	3	5	9	8	1	2	4	10	7	11

.

Steward $A_i$, based on their own preferences and management abilities, comprehensively evaluates chief steward $B_j$, resulting in a preference order vector $r_{ij}$, as shown in

Table 3. The complete preference order of the stewards to chief stewards.

	$B_1$	$B_2$	$B_3$	$B_4$
$A_1$	4	2	1	3
$A_2$	3	4	1	2
$A_3$	3	1	2	4
$A_4$	4	2	3	1
$A_5$	4	2	3	1
$A_6$	4	1	3	2
$A_7$	2	4	1	3
$A_8$	4	1	3	2
$A_9$	4	3	2	1
$A_{10}$	3	4	1	2
$A_{11}$	3	4	1	2
$A_{12}$	4	2	3	1

.

The one-to-many bilateral matching process between the chief steward and the stewards can be described as follows: First, according to the equations, the problem is transformed into a one-to-one bilateral matching problem. The one-to-many preference orders $r_{ij}$ and $s_{ij}$ are transformed into one-to-one preference orders ${\tilde{r}}_{ij}^q$ and ${\tilde{s}}_{ij}^q$, resulting in the following matrices:

$$\tilde{S}=\left[{\tilde{s}}_{ij}^q\right]=\left[\begin{array}{l}958112104312716\\ 958112104312716\\ 958112104312716\\ 812129561134107\\ 812129561134107\\ 812129561134107\\ 126751811104293\\ 126751811104293\\ 126751811104293\\ 126359812410711\\ 126359812410711\\ 126359812410711\end{array}\right]\tilde{R}=\left[{\tilde{r}}_{ij}^q\right]=\left[\begin{array}{l}444222111333\\ 333444111222\\ 333111222444\\ 444222333111\\ 444222333111\\ 444111333222\\ 222444111333\\ 444111333222\\ 444333222111\\ 333444111222\\ 333444111222\\ 444222333111\end{array}\right]$$

The obtained results are shown in

Table 4. One-to-many matching between stewards and chief stewards.

Matching Scheme Between Stewards and Chief Stewards	Running Time	Objective Function
$\tilde{u}=\left\{\left(B_1,\left\{A_5,A_{12},A_2\right\}\right),\left(B_2,\left\{A_3,A_6,A_8\right\}\right),\left(B_3,\left\{A_4,A_{10},A_{11}\right\}\right),\left(B_4,\left\{A_1,A_7,A_9\right\}\right)\right\}$	0.20944	31.5

.

That is, chief steward $B_1$ is matched with stewards $A_2$, $A_5$, and $A_{12}$; chief steward $B_2$ is matched with stewards $A_3$, $A_6$, and $A_8$; chief steward $B_3$ is matched with stewards $A_4$, $A_{10}$, and $A_{11}$; chief steward $B_4$ is matched with stewards $A_1$, $A_7$, and $A_9$.

Simulations were conducted 10 times for each of the scenarios where the number of chief attendants is 20, 40, 60, and 80. In each simulation, the preference orders of stewards for chief attendants and of chief attendants for stewards were randomly generated by the computer. The average values of the computation results are shown in

Table 5. Simulation time and results under different problem scales.

Solution Strategy	Number of Chief Stewards	The Average Runtime Running Time (s)	The Average Objective Function
Gurobi	20	1.5	270.7
Gurobi	40	15.0	733.0
Gurobi	60	72.4	1366.0
Gurobi	80	335.4	2080.0

.

Based on the analysis of the above data, it can be concluded that the greater the number of chief stewards, the longer the average runtime. As the number of chief stewards increases from 20 to 80, the average runtime increases significantly. The larger the problem size, the higher the difficulty to solve it, and the growth of runtime is nonlinear. When the number of chief stewards increases from 20 to 40, the runtime increases from 1.5 to 15. When the number of chief stewards increases from 40 to 80, the runtime increases from 15 to 335.4, showing exponential growth.

When the number of chief stewards reaches 90, using Gurobi to solve this problem results in a memory overflow. This indicates that while optimization solvers can be used to solve such problems when the computational scale is small, their limitations become apparent with larger computational scales. In existing research, heuristic algorithms are also widely applied in solving bilateral matching problems. For example, genetic algorithms [17,19] have been repeatedly used to solve bilateral matching problems. Therefore, this paper designs a genetic algorithm to solve this problem to meet the needs of solving large-scale instances in practical work.

3. Algorithm Design

The genetic algorithm is a population-based intelligence algorithm founded on random, this paper designs a genetic algorithm to solve the bilateral matching model for crew members. By using real-number encoding, the matching scheme of chief stewards and stewards is represented as chromosomes. Subsequently, a fitness function is constructed, and crossover and mutation operations are applied to alter the matching relationships between the bilateral subjects. The core idea is to find the optimal crew shift matching scheme that satisfies the bilateral subjects’ preferences through iterative processes, while ensuring one-to-one matching between the bilateral subjects.

3.1. Coding

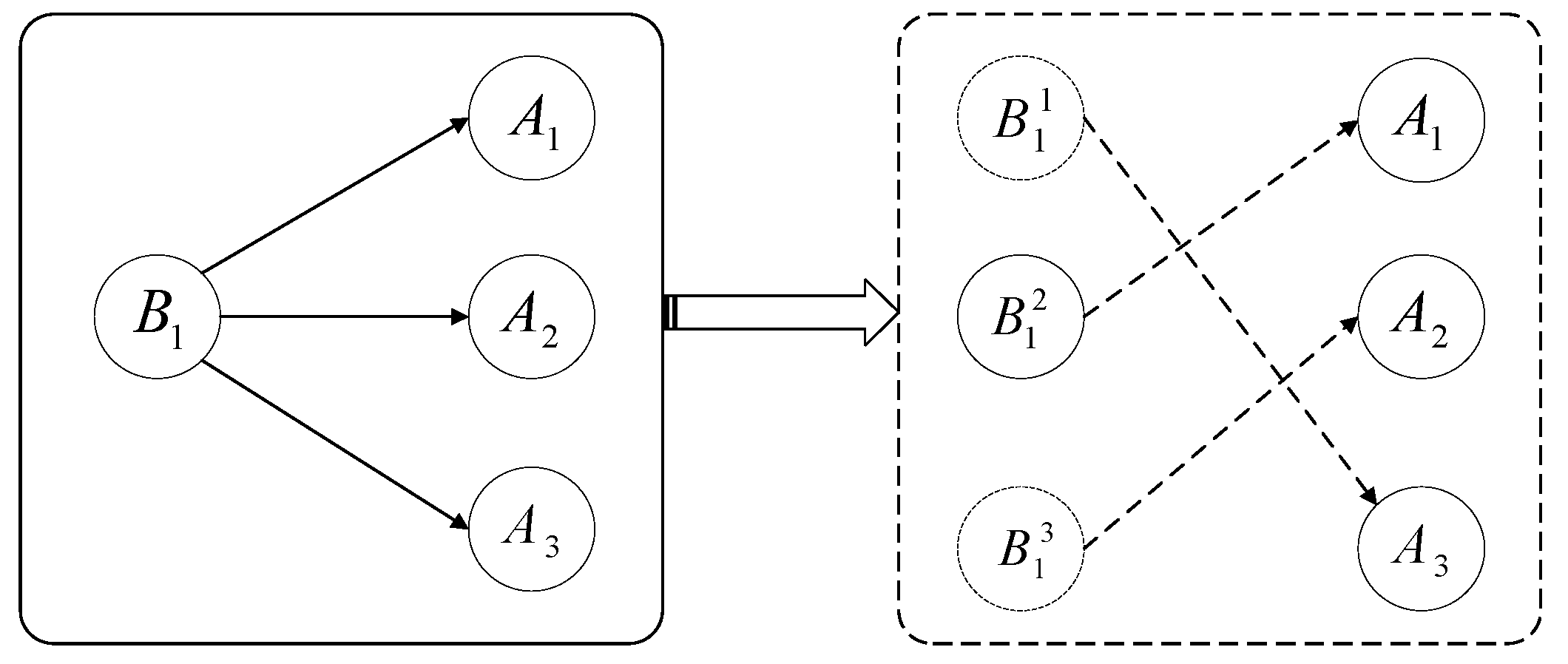
For the characteristics of the problem, this paper adopts a real number coding scheme. The coding method represents the steward $A_i$ by number $i$, which is expressed as a gene position on the chromosome, arranged in increasing order of natural numbers. The virtual chief steward ${\tilde{B}}_j^q$ is expressed as a gene value on the chromosome. The chromosome can be represented as ${\mathrm{y}}_h$, where $y_h\in Y\left(Y=\left[y_1,y_2,y_3,\cdots ,y_h,\cdots ,y_H\right]\right)$. Here, $y_h$ denotes an individual $h$, and $Y$ represents a population with a size of $H$. The coding scheme is shown in Figure 4.

3.2. Initial Population Generation

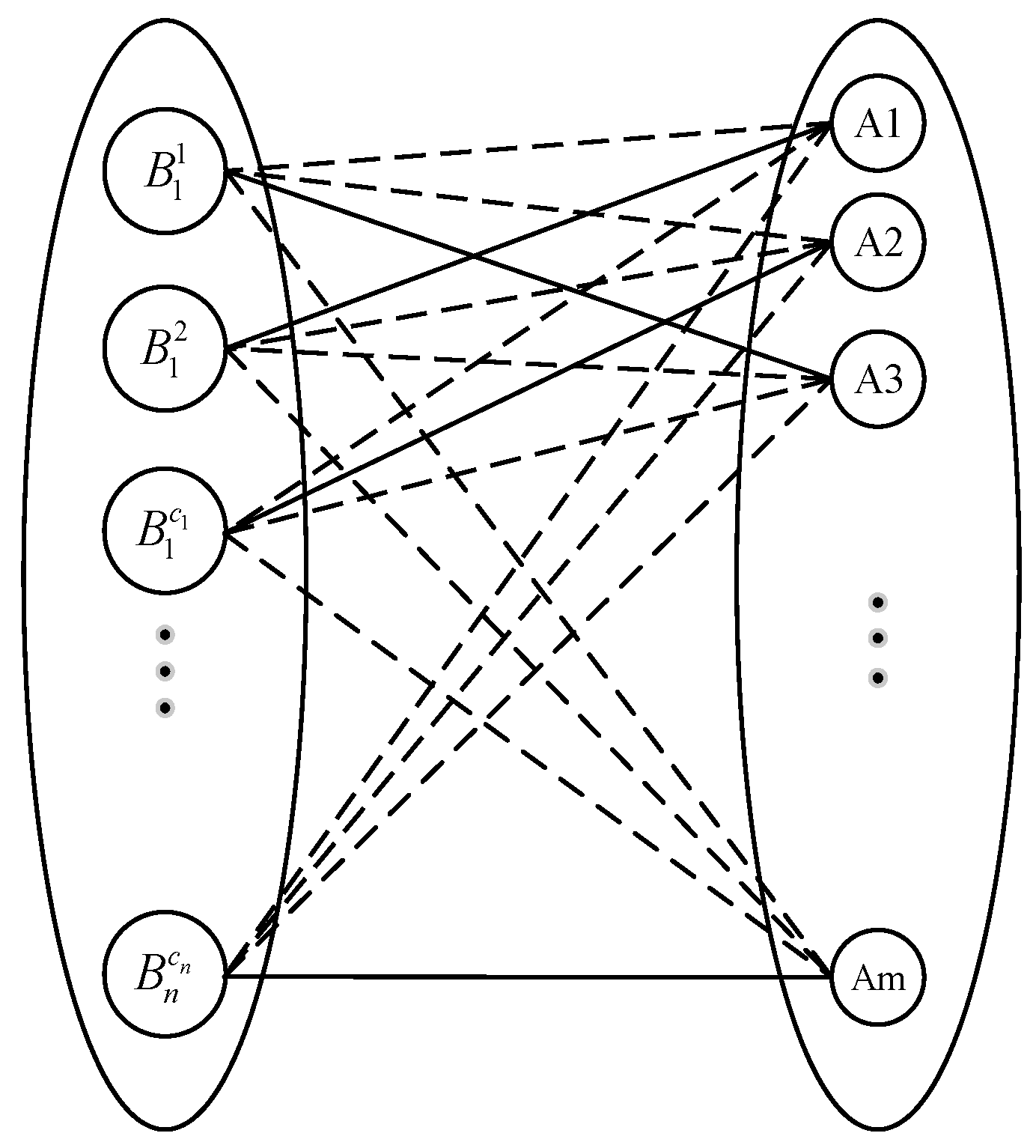
In generating the initial population, a virtual chief steward number is first generated in the first locus according to the principle of the smallest preference order. Then, the virtual chief steward number with the smallest preference order among the remaining virtual chief stewards is selected in the second locus. This process continues sequentially until one-to-one matches are generated for all virtual chief stewards and stewards. By adopting the above coding scheme, the chromosome can always satisfy the one-to-one matching of virtual chief stewards and stewards during genetic manipulation.

3.3. Construction of Fitness Function

The objective function in mathematical model M2 is used as the fitness function in the genetic algorithm can be written as $f\left(y_h,l\right)=Z={\alpha }_1{Z}_1+{\alpha }_2{Z}_2$; $f\left(y_h,l\right)$ represents the fitness function, $l$ denotes any iteration, $L$ is the total number of iterations, and $l\in \left[1,L\right]$.

3.4. Selection and Replication

This paper adopts the roulette selection method, first calculating the total fitness value of the current population ${\displaystyle \sum _{h=1}^{H}f\left(y_h,l\right)}$, and then calculating the selection probability $P_h=f\left(y_h,l\right)/{\displaystyle \sum _{h=1}^{H}f\left(y_h,l\right)}$ for each chromosome, and the cumulative probability AC_yh for each chromosome is calculated as follows: $A{C}_{yh}=A{C}_{yh-1}+P_{yh}$. A random number $random\in \left[0,1\right]$ is generated. If $random\le A{C}_1$, the chromosome $y_1$ is selected. If $random>A{C}_1$, and the random number satisfies $A{C}_{h-1}\le random\le A{C}_h$, the chromosome $y_h$ is selected.

3.5. Crossover and Mutation

To perform crossover at a probability $r_c$ on the genes of the chromosome, this paper adopts a single-point crossover method, randomly selecting the crossover locus to exchange genes with the corresponding locus of another chromosome. The resulting chromosome may not necessarily satisfy the one-to-one matching constraints between virtual chief stewards and stewards. It is corrected according to the following method: first, generate a virtual chief steward number in the first locus, then select one of the remaining virtual chief stewards randomly in the second locus, and so on until one-to-one matches for all virtual chief stewards and stewards are generated.

For mutation, the basic bit mutation operation is used. With a mutation probability $r_m$, a certain gene locus is randomly specified to perform the mutation operation. That is, for the chromosomal genes, a real number between (0, 1) is randomly selected. If the real number is smaller than $r_m$, a natural number is randomly chosen from 1 to m to replace the corresponding gene value. Conversely, if the gene value remains unchanged, to satisfy the one-to-one matching constraint between the virtual chief steward and the steward, the chromosomes are corrected according to the crossover step method, which determines the new individual after mutation.

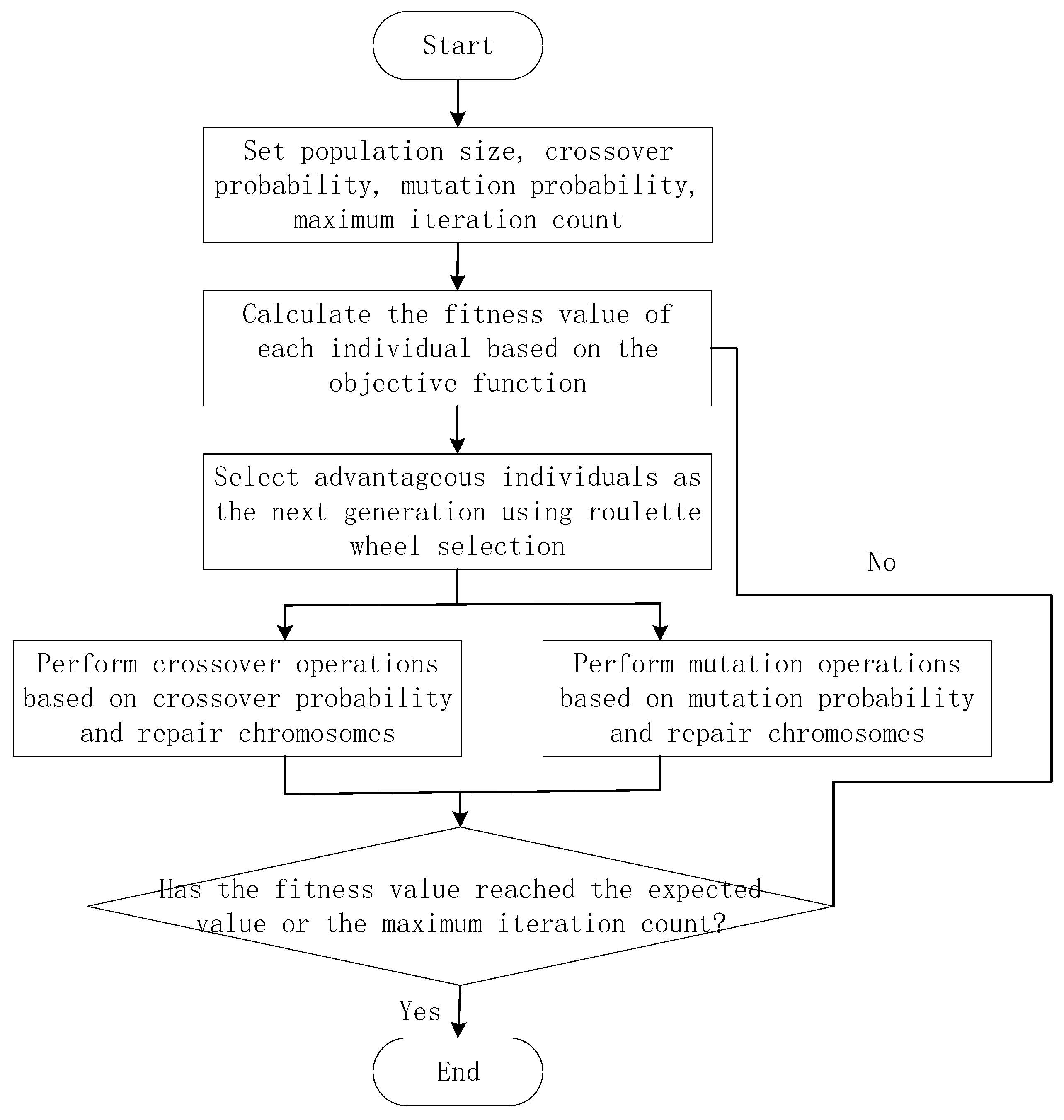
3.6. Algorithm Steps

Step 1: Set $l=0$, and randomly generate $H$ initial individuals as the initial population.

Step 2: Evaluate all current individuals using the fitness function to calculate their fitness values.

Step 3: Determine whether the algorithm termination condition is satisfied. If satisfied, output the result; otherwise, proceed to the next step.

Step 4: Perform the selection operation. To avoid the destruction of excellent individuals during crossover and mutation, a combination of roulette wheel selection and elitism strategy is used for selection.

Step 5: Perform crossover and mutation operations. With crossover probability $r_c$ and mutation probability $r_m$, apply crossover and mutation operations to the selected individuals as described above.

Step 6: Check the loop termination condition. If the number of iterations has not reached the maximum number of loops set, go to Step 2; otherwise, the algorithm ends, and the results are output, terminating the operation.

The genetic algorithm process is shown in Figure 5.

4. Numerical Example

To verify the effectiveness of the genetic algorithm in terms of solution quality and time, the optimal solution obtained by Gurobi and the average satisfactory solution obtained by the designed genetic algorithm (GA) were compared for different scales of crew chief stewards (2, 4, 8, 16, 32, 64). The experimental values presented below are the average of ten trials. The genetic algorithm was implemented using Python, with basic parameter settings as follows: population size of 80, crossover probability of 0.99, mutation probability of 0.01, and a maximum of 200 generations.

From the analysis of the data in

Table 6. Comparison of Problem Computation and Results for Different Scales and Solution Strategies.

Number of Chief Stewards	Solving Strategy	The Average Runtime Running Time (s)	The Average Objective Function	Solving Strategy	The Average Runtime Running Time (s)	The Average Objective Function
2	Gurobi	0.03	10.0	GA	1.8	10.0
4	Gurobi	0.11	30.5	GA	3.0	35.5
8	Gurobi	0.14	67.5	GA	7.8	102.5
16	Gurobi	0.70	178.0	GA	32.0	333.1
32	Gurobi	9.80	566.0	GA	205.0	1188.6
64	Gurobi	95.0	1476.0	GA	389.0	4472.4

, it can be observed that Gurobi consistently has a significantly shorter runtime compared to the Genetic Algorithm (GA) across all numbers of conductors. For instance, when the number of conductors is 64, Gurobi’s average runtime is 95 s, while GA requires 389 s. As the number of conductors increases, the runtime of both algorithms grows exponentially, but the growth rate of GA is notably faster. Gurobi performs excellently in terms of the objective function value, which increases gradually with the number of conductors but remains consistently lower than the corresponding value for GA. For example, when the number of conductors is 64, Gurobi’s objective function value is 1476, whereas GA’s is 4472.4. The objective function value of GA also increases substantially with the number of conductors, and in some cases, it is several times greater than that of Gurobi. The trend changes in computation time and objective function for different scales are shown in Figure 6.

To verify the effectiveness and feasibility of the genetic algorithm in solving large-scale problems, we conducted a simulation with 90 chief stewards and 270 stewards. The chief stewards performed a comprehensive evaluation of the stewards’ work ability and other indicators, providing the complete preference order vector $s_{ij}$. For details, see

Table 7. The complete preference order of the chief stewards to stewards.

	$A_1$	$A_2$	$A_3$	…	$A_{268}$	$A_{269}$	$A_{270}$
$B_1$	198	216	21		72	145	258
$B_2$	206	215	24		254	167	160
$B_3$	47	266	40		94	155	131
…
$B_{89}$	248	105	151		218	242	48
$B_{90}$	236	226	61		219	202	21

.

Steward $B_j$ combines his own preferences and conducts a comprehensive evaluation of chief steward $A_i$ based on indicators such as management ability, and provides the preference order vector $r_{ij}$, as shown in

Table 8. The complete preference order of the stewards to chief stewards.

	$B_1$	$B_2$	$B_3$	…	$B_{88}$	$B_{89}$	$B_{90}$
$A_1$	44	72	33		61	12	43
$A_2$	17	40	31		22	28	16
$A_3$	53	58	67		40	55	50
…
$A_{269}$	55	15	49		82	78	16
$A_{270}$	23	21	3		18	71	19

.

The one-to-many bilateral matching relationship is transformed into a one-to-one bilateral matching relationship, resulting in the preference matrix of the virtual chief stewards to the stewards, and the preference matrix of the stewards to the virtual chief stewards, $r_{ij}^q$, $s_{ij}^q$.

$$\tilde{S}=\left[{\tilde{s}}_{ij}^q\right]=\left[\begin{array}{l}19821621\cdots 72145258\\ 19821621\cdots 72145258\\ 19821621\cdots 72145258\\ 20621524\cdots 254167160\\ 20621524\cdots 254167160\\ 20621524\cdots 254167160\\ 248105151\cdots 21824248\\ 248105151\cdots 21824248\\ 248105151\cdots 21824248\\ 23622661\cdots 21920221\\ 23622661\cdots 21920221\\ 23622661\cdots 21920221\end{array}\right]\tilde{R}=\left[{\tilde{r}}_{ij}^q\right]=\left[\begin{array}{lllllllllllll}44& 44& 44& 72& 72& 72& \cdots & 12& 12& 12& 43& 43& 43\\ 17& 17& 17& 40& 40& 40& \cdots & 28& 28& 28& 16& 16& 16\\ 53& 53& 53& 58& 58& 58& \cdots & 55& 55& 55& 50& 50& 50\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \cdots & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 55& 55& 55& 15& 15& 15& \cdots & 78& 78& 78& 16& 16& 16\\ 23& 23& 23& 21& 21& 21& \cdots & 71& 71& 71& 19& 19& 19\end{array}\right]$$

Based on the above data, the designed genetic algorithm is combined to solve the bilateral matching model of the crew shift. The algorithm is programmed in Python language, and the basic parameters are set as follows: the population size $N$ is 80, the crossover probability $P_c$ is 0.65, the mutation probability $P_m$ is 0.05, and the maximum number of generations gen is 100. The different sizes of the chief stewards, 120 and 150, are calculated, and the solution results are shown in

Table 9. Simulation time and results under different problem scales.

Number of Chief Stewards	Crew Matching Scheme	Running Time(s)	Objective Function
90	$\tilde{u}=\left\{\left(B_1,\left\{A_{66},A_{125},A_{238}\right\}\right),\left(B_2,\left\{A_{248},A_{75},A_{134}\right\}\right)\cdot \cdot \cdot \left(B_{89},\left\{A_{95},A_{154},A_{176}\right\}\right),\left(B_{90},\left\{A_{14},A_{74},A_{254}\right\}\right)\right\}$	387.8	22,111.5
120	$\tilde{u}=\left\{\left(B_1,\left\{A_{66},A_{125},A_{238}\right\}\right),\left(B_2,\left\{A_{248},A_{75},A_{134}\right\}\right)\cdot \cdot \cdot \left(B_{89},\left\{A_{95},A_{154},A_{176}\right\}\right),\left(B_{90},\left\{A_{14},A_{74},A_{254}\right\}\right)\right\}$	664.7	39,868.5
150	$\tilde{u}=\left\{\left(B_1,\left\{A_{66},A_{125},A_{238}\right\}\right),\left(B_2,\left\{A_{248},A_{75},A_{134}\right\}\right)\cdot \cdot \cdot \left(B_{89},\left\{A_{95},A_{154},A_{176}\right\}\right),\left(B_{90},\left\{A_{14},A_{74},A_{254}\right\}\right)\right\}$	1322.2	62,912.0

:

5. Conclusions

The main conclusions obtained in this paper are as follows:

1. Considering the gaps in the research field of high-speed railway crew planning regarding crew matching, this study seeks the optimal matching scheme among crew members based on job matching degree. It provides technical means to solve this problem, verifies the validity of the constructed models and algorithms, optimizes the composition of train crews, and offers decision-making support for high-speed railway crew management and optimization.

2. A multi-objective optimization model of one-to-many bilateral matching is constructed for the high-speed railway crew matching problem, based on the decision theory of bilateral matching and the theory of complete preference order. This expands the application field of bilateral matching theory.

3. When solving the one-to-many bilateral matching model with an optimization solver, the solver fails to obtain a solution within an acceptable time frame as the problem size increases. Therefore, a genetic algorithm (GA) is designed to solve the problem for large-scale scenarios. Analysis of the results shows that Gurobi excels in both solving speed and objective function value, making it suitable for scenarios with high requirements for both time and quality. Although GA is well-suited for solving large and complex problems, its performance in terms of runtime and objective function value is inferior to Gurobi. In scenarios that require higher solution precision, it is advisable to optimize the algorithm to achieve higher-quality solutions.

4. This paper only considers the problem-solving method based on the complete preference order information of the matching subject. To further improve the universality of the model, future work will consider the bilateral matching decision-making methods of the crew under different conditions, such as uncertain information and multi-attribute information, and will fully consider the matching relationship between the manager and the managed.