Classification of Real-World Objects Using Supervised ML-Assisted Polarimetry: Cost/Benefit Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
- (i)
- Only two linear polarizations (horizontal and vertical) are used in both PSG and PSA; four measurements per data point are performed yielding the MMEs , , , and .
- (ii)
- Multiple angles are used for the linear polarizers in both PSG and PSA, so that at least nine measurements per data point are performed resulting in the MMEs listed in (i) plus .
2.2. Statistical Analysis of Input Attributes
3. ML Architectures and Results
3.1. RFs with Different Sets of Input Attributes
- Attributes , , and .The results obtained with these attributes are shown in Figure 3. Considering only MMEs , and , the overall classification accuracy obtained with the optimized ANN is 72.4%. It is easily seen that some classes are poorly identified, which means that the number of attributes is insufficient.
- Attributes , , , , , , and .Considering these eight MMEs as attributes, the overall classification accuracy obtained with the optimized ANN is 88.1% (we do not present the confusion table for brevity). The results are much better than with the minimal set, but the classes “leaves” and “rocks” are still not well distinguished.
- All MMEs as attributes.The results obtained with the complete set of attributes are shown in Figure 3 (right panel). Considering , , , , , , and as attributes, the overall classification accuracy obtained with the optimized ANN is 93.85%. The accuracy obtained is now very good.
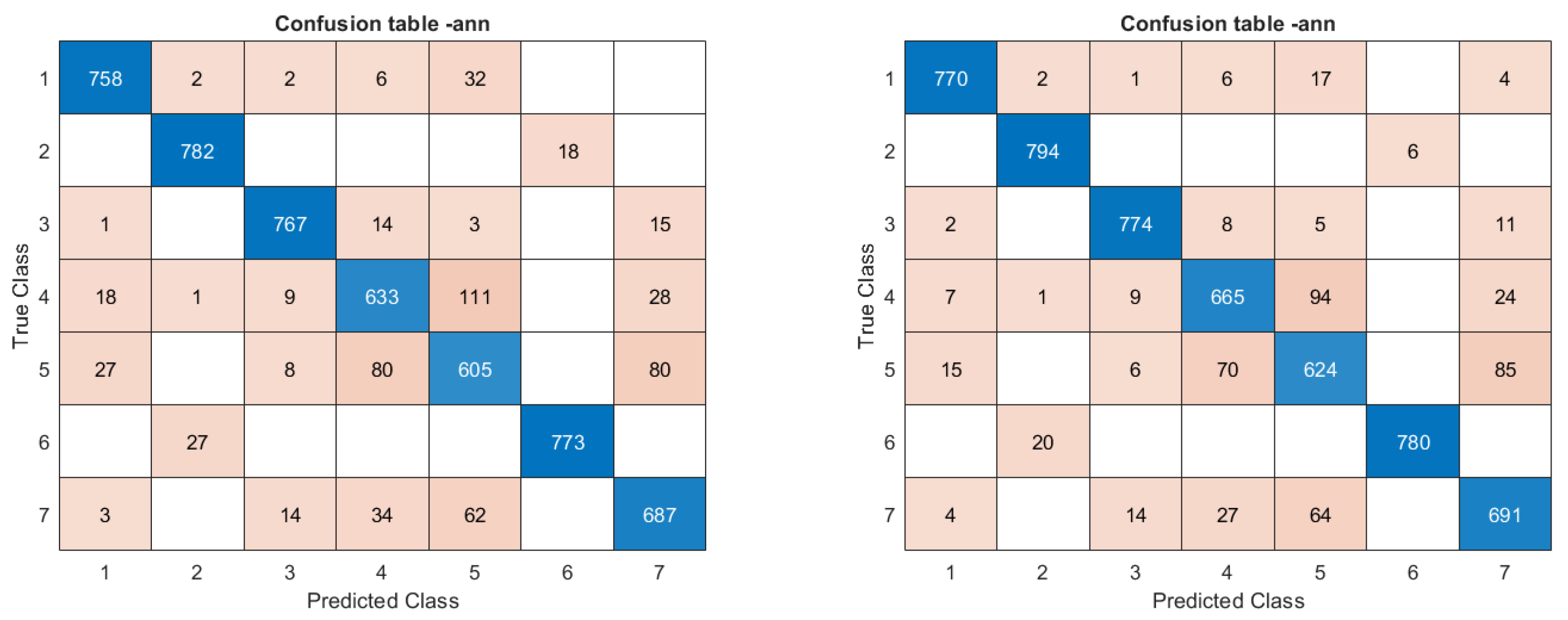
3.2. ANNs with Different Sets of Input Attributes
- Attributes , , and vs. , , and plus AoI.The results obtained with these attributes are shown in Figure 4. Considering only MMEs , , and , the overall classification accuracy obtained with the optimized ANN is 74.14%. It is easily seen that some classes are poorly identified, which means that the number of attributes is not enough. However, the results are better than when using RF. By adding AoI to the list of attributes, the accuracy obtained raises to 77.28 % (see the right panel of Figure 4). Still, the classes “leaves”, “rocks”, and “wood” present rather poor rates of success with these sets of input parameters.
- Attributes , , , , , , vs. , , , , , , plus AoI.By using as attributes just the MMEs , , , , , , and , the accuracy obtained is now 89.3% (Figure 5, right panel). The results are better than when using RF. The results are much better than with the minimal set, but the classes “leaves” and “rocks” are still not well distinguished. By adding the angle of incidence to the list of attributes, the accuracy obtained is now 91% (right panel). Once again, AoI appears to be an important input parameter.
- All MMEs plus AoI as attributes.With the full set of MMEs as attributes, the accuracy increases to 95.9% (see Figure 6), whereas with the angle of incidence added to the list it reaches 96.2%, a relatively small advantage in comparison with the other cases. We may understand it as being due to the fact that the compatibility of the not fully independent MME values already determines AoI implicitly. The numbers obtained here are very similar to those quoted in Ref. [9], also obtained with the full set of MMEs but with a slightly different database and definition of classes.
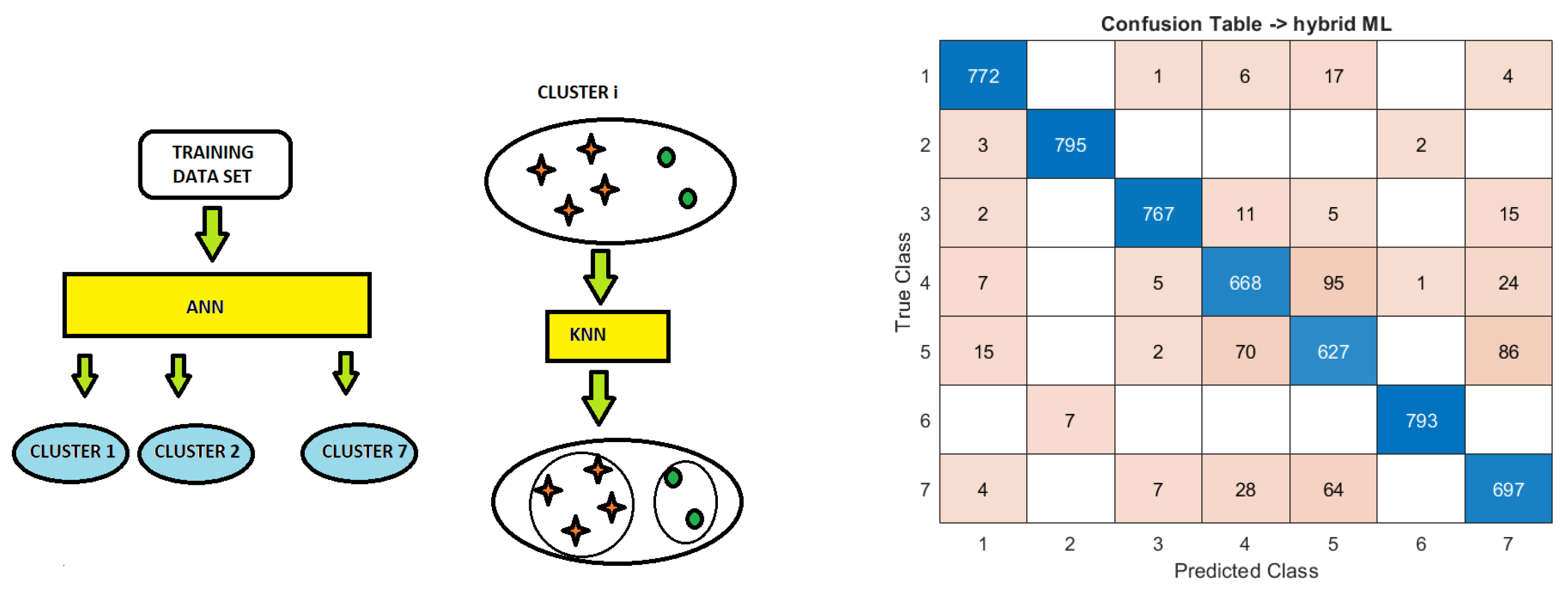
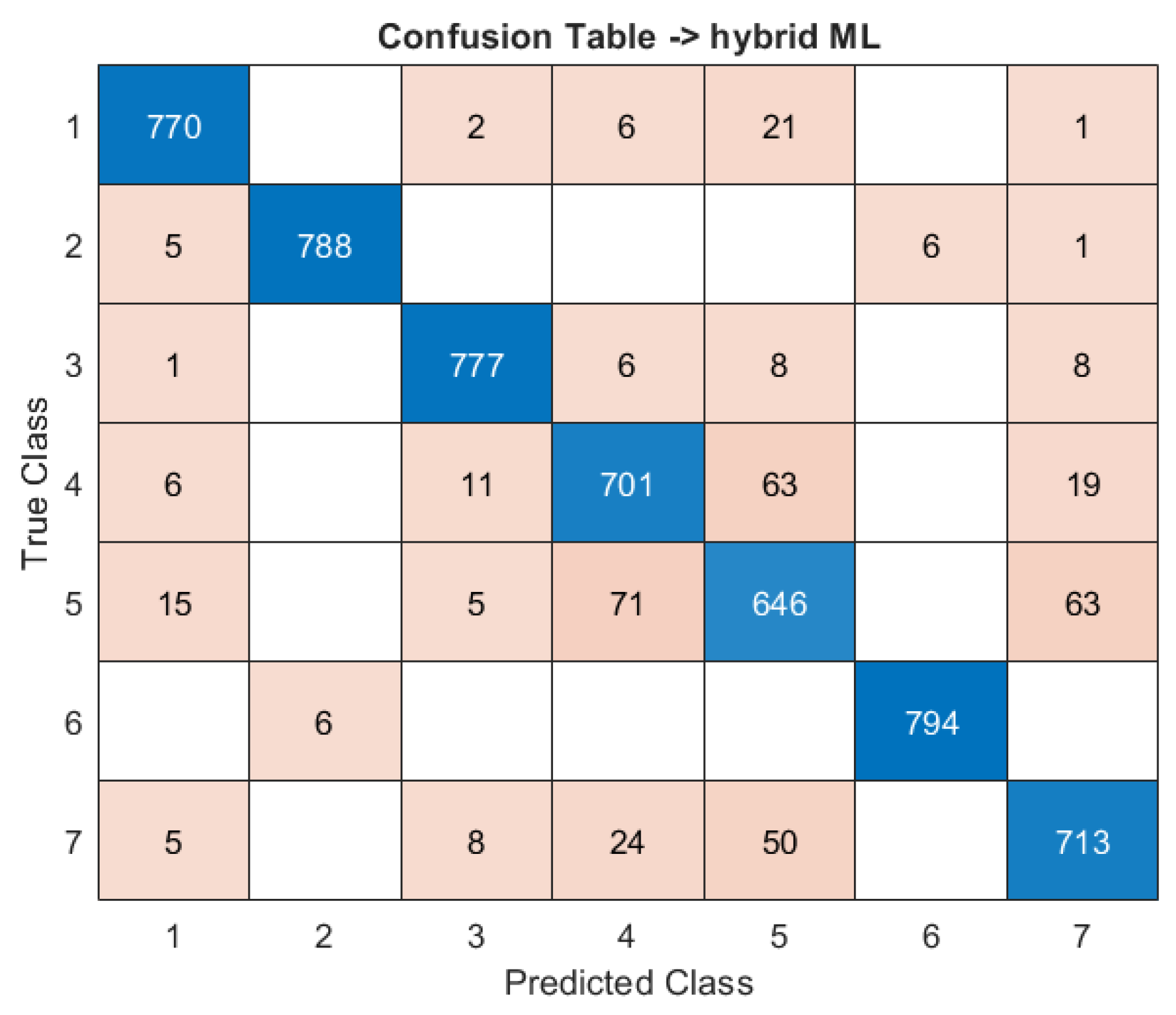
3.3. ANN-KNN Classifier
3.4. Recall Metric of Classifiers’ Performance
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Ouyang, W.; Wang, X.; Fieguth, P.; Chen, J.; Liu, X.; Pietikäinen, M. Deep Learning for Generic Object Detection: A Survey. Int. J. Comput. Vis. 2020, 128, 261–318. [Google Scholar] [CrossRef]
- Kaur, K.; Singh, S. A comprehensive review of object detection with deep learning. Digit. Signal Process. 2023, 132, 103812. [Google Scholar] [CrossRef]
- Galvão, L.; Abbod, M.; Kalganova, T.; Palade, V.; Huda, N. Pedestrian and Vehicle Detection in Autonomous Vehicle Perception Systems—A Review. Sensors 2021, 21, 7267. [Google Scholar] [CrossRef] [PubMed]
- Ghali, R.; Akhloufi, M.A. Deep Learning Approaches for Wildland Fires Remote Sensing: Classification, Detection, and Segmentation. Remote Sens. 2023, 15, 1821. [Google Scholar] [CrossRef]
- Qi, S.; Huang, Z.; Ma, X.; Huang, J.; Zhou, T.; Zhang, S.; Dong, Q.; Bi, J.; Shi, J. Classification of atmospheric aerosols and clouds by use of dual-polarization lidar measurements. Opt. Express 2021, 29, 23461–23476. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar] [CrossRef]
- Brown, J.P.; Roberts, R.G.; Card, D.C.; Saludez, C.L.; Keyser, C.X. Hybrid passive polarimetric imager and lidar combination for material classification. Opt. Eng. 2020, 59, 073106. [Google Scholar] [CrossRef]
- Quéau, Y.; Leporcq, F.; Lechervy, A.; Alfalou, A. Learning to classify materials using Mueller imaging polarimetry. Fourteenth Int. Conf. Qual. Control. Artif. Vis. 2019, 11172, 246–252. [Google Scholar] [CrossRef]
- Estevez, I.; Oliveira, F.; Braga-Fernandes, P.; Oliveira, M.; Rebouta, L.; Vasilevskiy, M. Urban objects classification using Mueller Matrix polarimetry and machine learning. Opt. Express 2022, 30, 28385–28400. [Google Scholar] [CrossRef]
- Goldstein, D. Polarized Light; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar] [CrossRef]
- Shibayama, T.; Yamaguchi, Y.; Yamada, H. Polarimetric Scattering Properties of landslides in Forested Areas and the Dependence on the Local Incident Angle. Remote Sens. 2015, 7, 15424–15442. [Google Scholar] [CrossRef]
- Shaleb-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Ma, P.; Li, C.; Rahaman, M.M.; Yao, Y.; Zhang, J.; Zou, S.; Zhao, X.; Grzegorzek, M. A state-of-the-art survey of object detection techniques in microorganism image analysis: From classical methods to deep learning approaches. Artif. Intell. Rev. 2023, 56, 1627–1698. [Google Scholar] [CrossRef]
- Mokayed, H.; Quan, T.Z.; Alkhaled, L.; Sivakumar, V. Real-Time Human Detection and Counting System Using Deep Learning Computer Vision Techniques. Artif. Intell. Appl. 2023, 1, 221–229. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J. An Important Contribution to Nonparametric Discriminant Analysis and Density Estimation. Int. Stat. Rev. 1951, 57, 233–247. [Google Scholar] [CrossRef]
- Vapnik, V.; Chervonenkis, A. On a class of algorithms of learning pattern recognition. Autom. Remote. Control 1964, 25, 838–845. [Google Scholar]
- Quinlan, J. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Morgan, J.; Sonquist, S. Problems of analysis in survey data and a proposal. J. Am. Stat. Assoc. 1963, 58, 415–434. [Google Scholar] [CrossRef]
- Hunt, E.; Marin, J.; Stone, P. Experiments in Induction; Academic: New York, NY, USA, 1966. [Google Scholar]
- Ho, T. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Design of an Intelligent Automaton. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Karri, S.; De Silva, L.; Lai, C.; Yong, S. Classification and Prediction of Driving Behaviour at a Traffic Intersection Using SVM and KNN. SN Comput. Sci. 2021, 2, 209. [Google Scholar] [CrossRef]
- Li, N.; Chen, H.; Kolmanovsky, I.; Girard, A. An Explicit Decision Tree Approach for Automated Driving. In Proceedings of the ASME 2017 Dynamic Systems and Control Conference, Tysons, VA, USA, 11–13 October 2017. [Google Scholar] [CrossRef]
- Cichosz, P.; Pawelczak, L. Imitation learning of car driving skills with decision trees and random forests. Int. J. Appl. Math. Comput. Sci. 2014, 24, 579–597. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, K.; Prakasha, G.; Teja, H. Self-Driving Car Using Neural Networks and Computer Vision. In Proceedings of the 2022 International Interdisciplinary Humanitarian Conference for Sustainability (IIHC), Bengaluru, India, 18–19 November 2022. [Google Scholar] [CrossRef]
- Bachute, M.; Subhedar, J. Autonomous Driving Architectures: Insights of Machine Learning and Deep Learning Algorithms. Mach. Learn. Appl. 2021, 6, 100164. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, W.; Wang, Z.; Zhang, W.; Zheng, W.; Cao, W.; Nan, J.; Lian, Y.; Burke, A. Autonomous driving system: A comprehensive survey. Expert Syst. Appl. 2024, 242, 122836. [Google Scholar] [CrossRef]
- Meimetis, D.; Daramouskas, I.; Perikos, I.; Hatzilygeroudis, I. Real-time multiple object tracking using deep learning methods. Neural Comput. Appl. 2023, 35, 89–118. [Google Scholar] [CrossRef]
- Usmani, K.; Krishnan, G.; O’Connor, T.; Javidi, B. Deep learning polarimetric three-dimensional integral imaging object recognition in adverse environmental conditions. Opt. Express 2021, 29, 12215–12228. [Google Scholar] [CrossRef] [PubMed]
- Pierangeli, D.; Conti, C. Single-shot polarimetry of vector beams by supervised learning. Nat. Commun. 2023, 14, 1831. [Google Scholar] [CrossRef]
- Makkithaya, K.N.; Melanthota, S.K.; Kistenev, Y.V.; Bykov, A.; Novikova, T.; Meglinski, I.; Mazumder, N. Machine Learning in Tissue Polarimetry. In Optical Polarimetric Modalities for Biomedical Research. Biological and Medical Physics, Biomedical Engineering; Mazumder, N., Kistenev, Y.V., Borisova, E., Prasada, K.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Rodríguez, C.; Estévez, I.; González-Arnay, E.; Campos, J.; Lizana, A. Optimizing the classification of biological tissues using machine learning models based on polarized data. J. Biophoton. 2023, 16, e202200308. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, X.; Zhai, J.; Hu, H. PODB: A learning-based polarimetric object detection benchmark for road scenes in adverse weather conditions. Inf. Fusion 2024, 108, 102385. [Google Scholar] [CrossRef]
- Brown, C. Coefficient of Variation, Applied Multivariate Statistics in Geohydrology and Related Sciences; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 6th ed.; Pergamon Press: Oxford, UK, 1980; pp. 633–664. [Google Scholar]
- MatLab Help Center. MathWorks. 2022. Available online: https://www.mathworks.com/help/stats/treebagger.html (accessed on 15 August 2024).
- Steinbach, M.; Tan, P. kNN: K-Nearest Neighbors. In The Top Ten Algorithms in Data Mining; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]
- Precision and Recall. SciKit-Learn. 2024. Available online: https://scikit-learn.org/1.5/auto_examples/model_selection/plot_precision_recall.html (accessed on 1 November 2024).
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
- Nunes-Pereira, E.J.; Peixoto, H.; Teixeira, J.; Santos, J. Polarization-coded material classification in automotive LIDAR aiming at safer autonomous driving implementations. Appl. Opt. 2020, 59, 2530. Available online: https://opg.optica.org/ao/abstract.cfm?URI=ao-59-8-2530 (accessed on 22 November 2024). [CrossRef] [PubMed]
- Rodrigues, M.; Borges, J.; Lopes, C.; Pereira, R.; Vasilevskiy, M.; Vaz, F. Gas Sensors Based on Localized Surface Plasmon Resonances: Synthesis of Oxide Films with Embedded Metal Nanoparticles, Theory and Simulation, and Sensitivity Enhancement Strategies. Appl. Sci. 2021, 11, 5388. [Google Scholar] [CrossRef]
- Altayeva, A.; Omarov, N.; Tileubay, S.; Zhaksylyk, A.; Bazhikov, K.; Kambarov, D. Convolutional LSTM Network for Real-Time Impulsive Sound Detection and Classification in Urban Environments. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 0141164. [Google Scholar] [CrossRef]
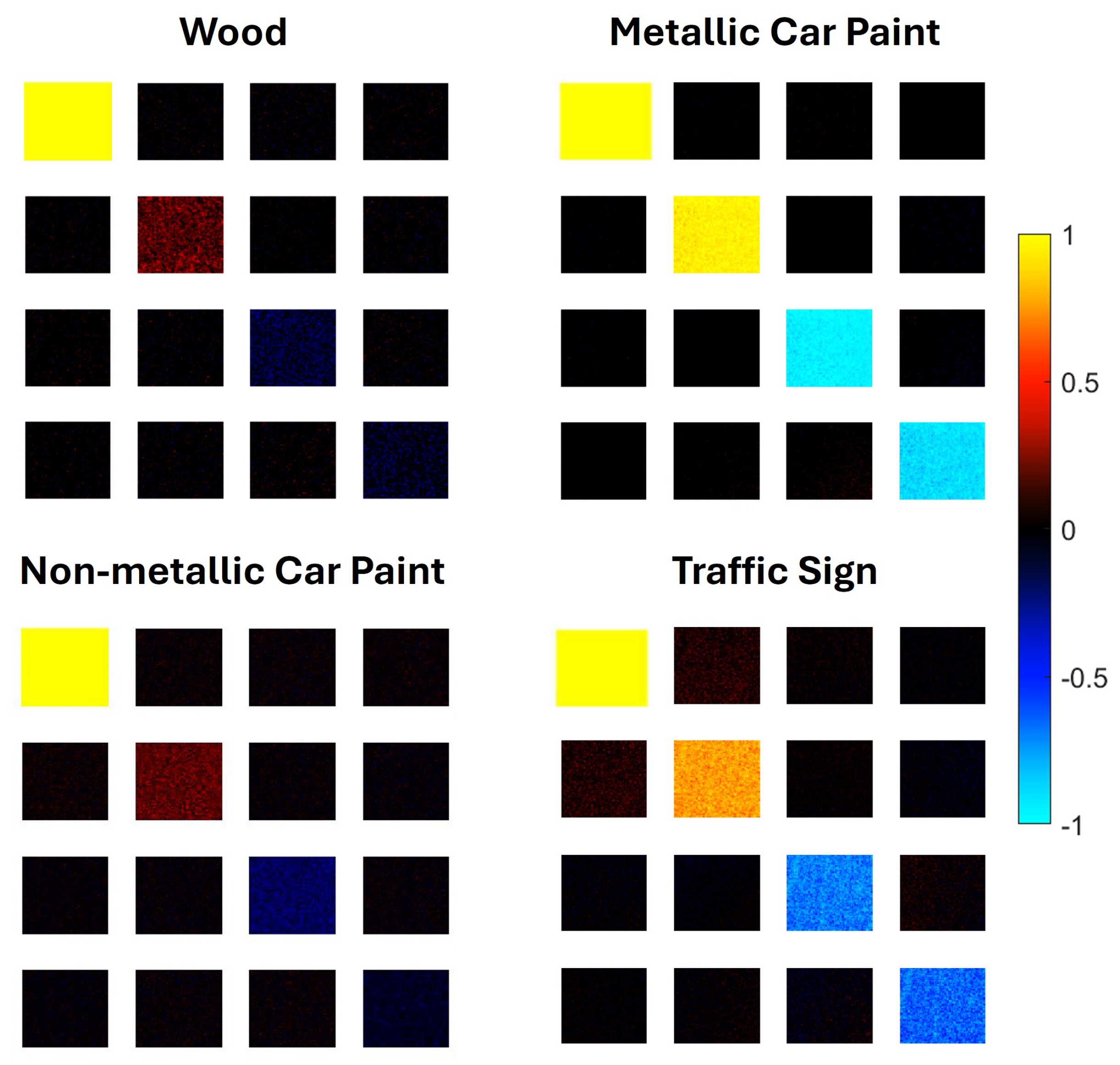




| Number, i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Description | Usual (solid) car paint | Car paint with metal flakes | Clothes (cotton, polyester, viscose, etc.) | Tree leaves | Granite stones used in pavements | Traffic signs (front side) | Tree trunk pieces |
| Short name | carP-C | carP-M | clothes | leaves | rocks | traf. sign | wood |
| Class | carP-C | carP-M | Clothes | Leaves | Rocks | Traf. Sign | Wood |
|---|---|---|---|---|---|---|---|
| Recall | 96.2% | 99.2% | 96.7% | 83.1% | 78% | 97.5% | 86.3% |
| Class | carP-C | carP-M | Clothes | Leaves | Rocks | Traf. Sign | Wood |
|---|---|---|---|---|---|---|---|
| Recall | 96.2% | 98.5% | 97.1% | 87.6% | 80.8% | 99.2% | 89.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, R.M.S.; Oliveira, F.; Romanyshyn, N.; Estevez, I.; Borges, J.; Clain, S.; Vasilevskiy, M.I. Classification of Real-World Objects Using Supervised ML-Assisted Polarimetry: Cost/Benefit Analysis. Appl. Sci. 2024, 14, 11059. https://doi.org/10.3390/app142311059
Pereira RMS, Oliveira F, Romanyshyn N, Estevez I, Borges J, Clain S, Vasilevskiy MI. Classification of Real-World Objects Using Supervised ML-Assisted Polarimetry: Cost/Benefit Analysis. Applied Sciences. 2024; 14(23):11059. https://doi.org/10.3390/app142311059
Chicago/Turabian StylePereira, Rui M. S., Filipe Oliveira, Nazar Romanyshyn, Irene Estevez, Joel Borges, Stephane Clain, and Mikhail I. Vasilevskiy. 2024. "Classification of Real-World Objects Using Supervised ML-Assisted Polarimetry: Cost/Benefit Analysis" Applied Sciences 14, no. 23: 11059. https://doi.org/10.3390/app142311059
APA StylePereira, R. M. S., Oliveira, F., Romanyshyn, N., Estevez, I., Borges, J., Clain, S., & Vasilevskiy, M. I. (2024). Classification of Real-World Objects Using Supervised ML-Assisted Polarimetry: Cost/Benefit Analysis. Applied Sciences, 14(23), 11059. https://doi.org/10.3390/app142311059










