Underwater Acoustic Signal LOFAR Spectrogram Denoising Based on Enhanced Simulation
Abstract
1. Introduction
2. Materials and Methods
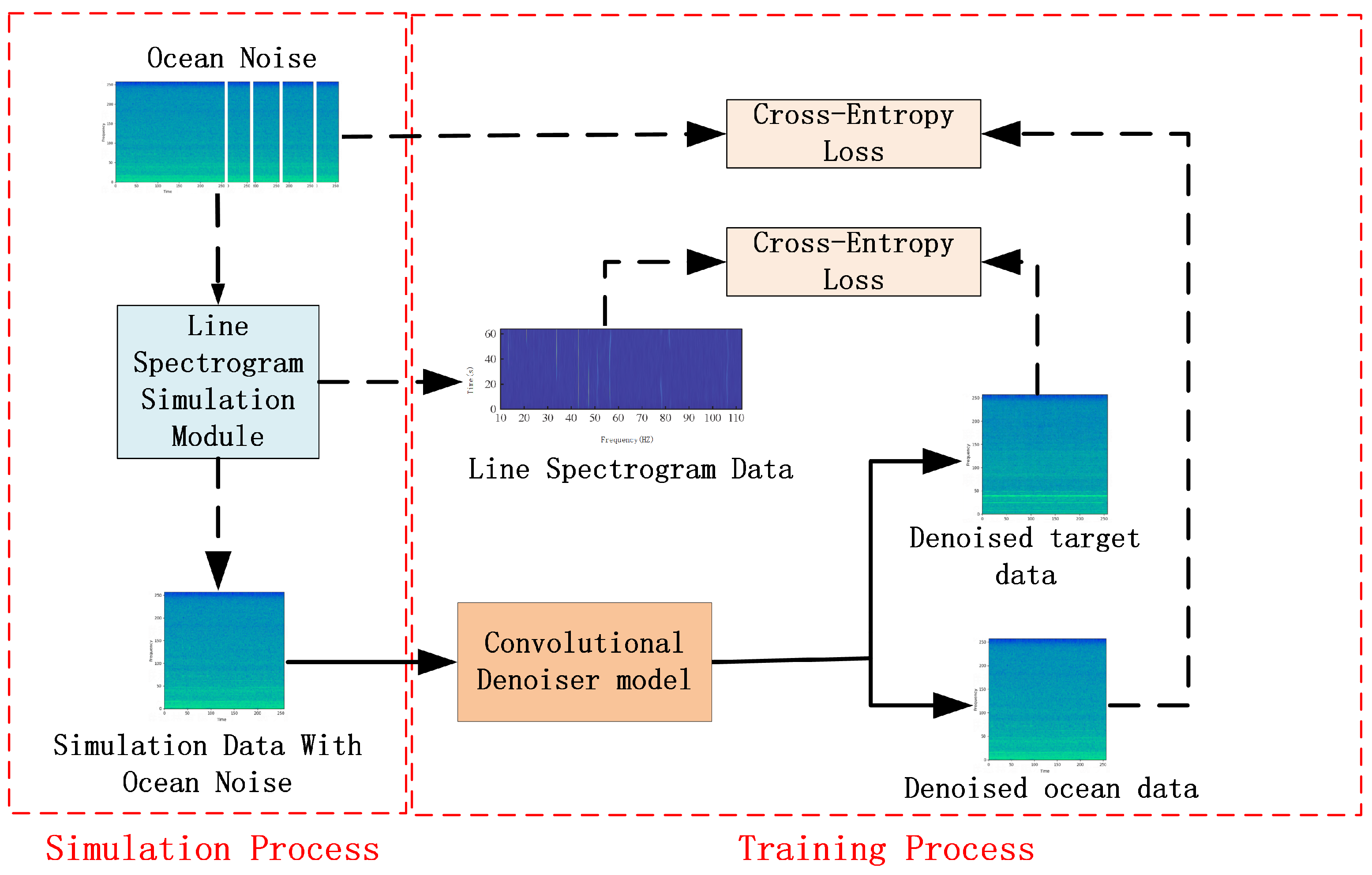
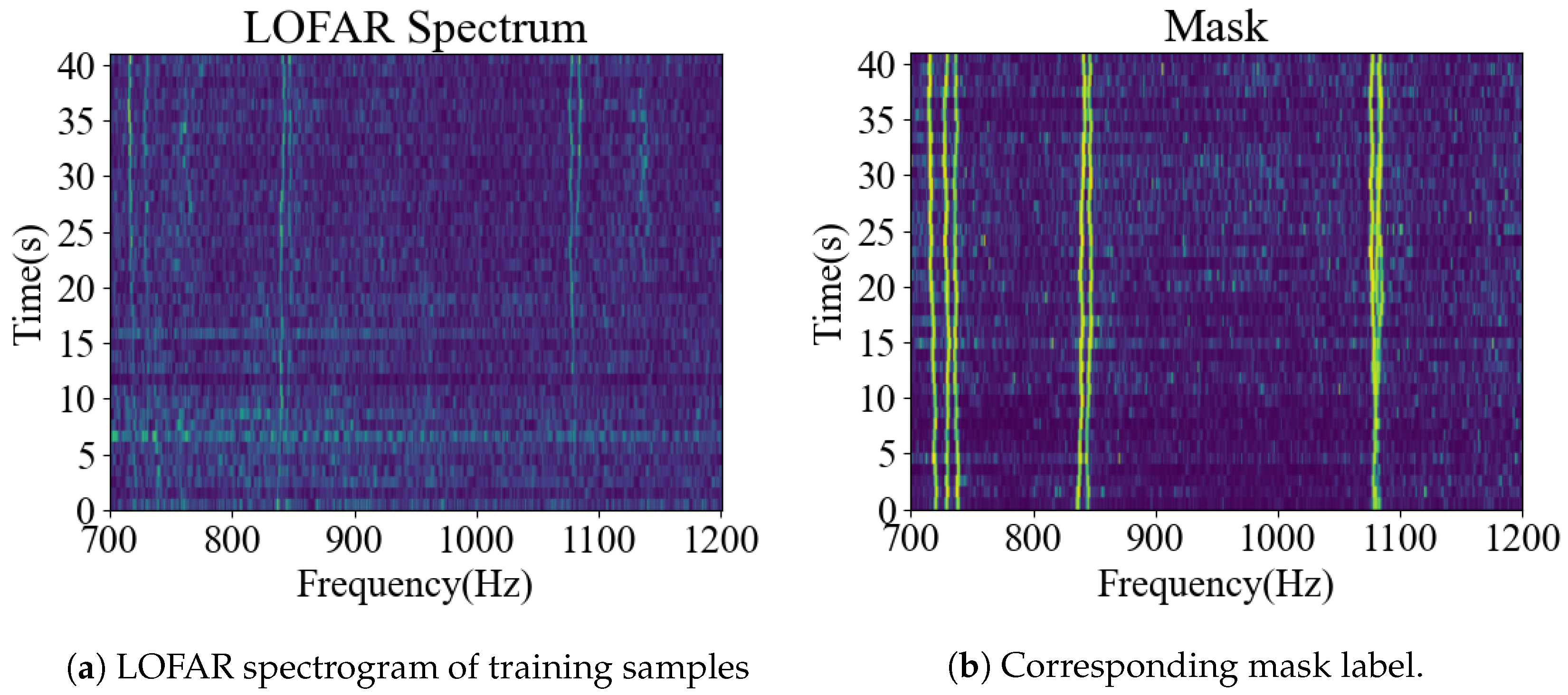
2.1. Training Data Simulation Method
| Algorithm 1 Time-Domain Underwater Acoustic Target Data Simulation Algorithm |
|
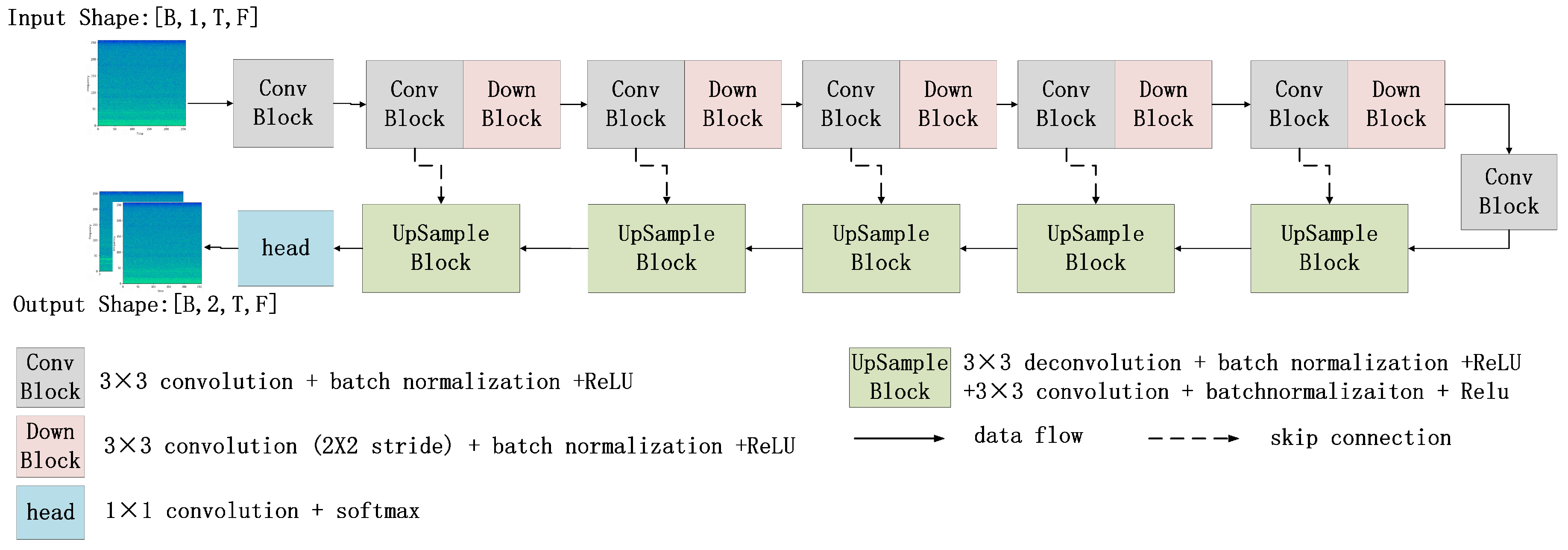
2.2. Convolutional Denoising Model
3. Experiments and Analysis
3.1. Experimental Settings
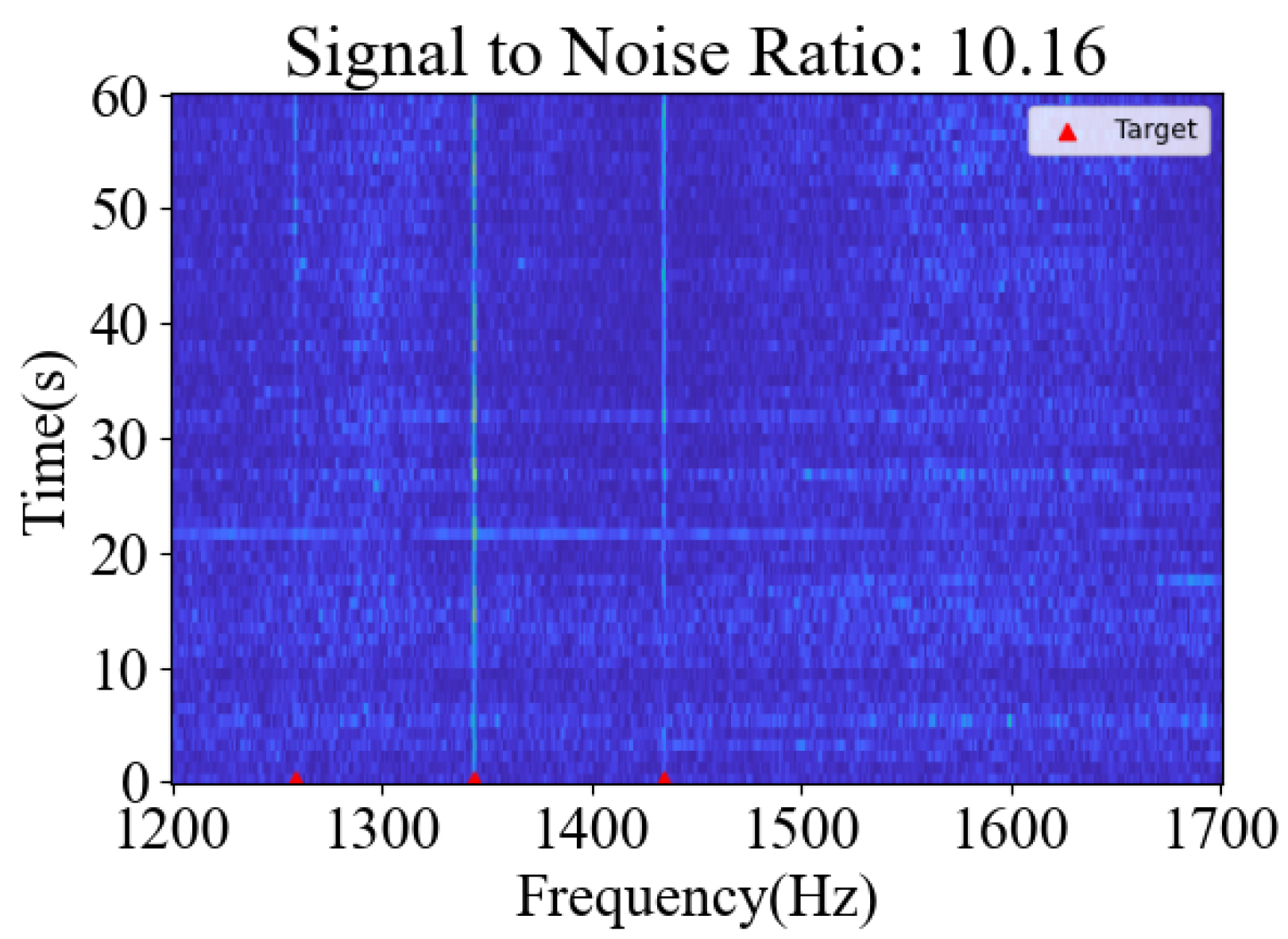
3.2. Datasets
3.3. Measuring Metrics
4. Results
4.1. Comparison with Baselines
4.2. Model Transferability Validation
4.3. Discussion and Analysis
5. Conclusions
5.1. Main Conclusion
5.2. Limitations and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, M.F.; Jayakody, D.N.K.; Chursin, Y.A.; Affes, S.; Sonkin, D. Recent advances and future directions on underwater wireless communications. Arch. Comput. Methods Eng. 2020, 27, 1379–1412. [Google Scholar] [CrossRef]
- Wang, P.; Peng, Y. Research on underwater acoustic target recognition based on LOFAR spectrogram and deep learning method. In Proceedings of the 2020 5th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 19–20 September 2020; pp. 666–670. [Google Scholar] [CrossRef]
- Chen, J.; Han, B.; Ma, X.; Zhang, J. Underwater target recognition based on multi-decision LOFAR spectrogram enhancement: A deep-learning approach. Future Internet 2021, 13, 265. [Google Scholar] [CrossRef]
- Lu, H.; Shang, J.; Chen, Y.; Ma, Q. A LOFAR spectrogram multi-sub-band matching method for passive target recognition. In Proceedings of the 2nd International Conference on Signal Image Processing and Communication (ICSIPC 2022), Qingdao, China, 20–22 May 2022; Volume 12246, pp. 139–150. [Google Scholar] [CrossRef]
- Yao, H.; Gao, T.; Wang, Y.; Wang, H.; Chen, X. Mobile_ViT: Underwater Acoustic Target Recognition Method Based on Local–Global Feature Fusion. J. Mar. Sci. Eng. 2024, 12, 589. [Google Scholar] [CrossRef]
- Yao, Q.; Wang, Y.; Yang, Y. Underwater Acoustic Target Recognition Based on Data Augmentation and Residual CNN. Electronics 2023, 12, 1206. [Google Scholar] [CrossRef]
- Raj, K.M.; Murugan, S.S.; Natarajan, V.; Radha, S. Denoising algorithm using wavelet for underwater signal affected by wind driven ambient noise. In Proceedings of the 2011 International Conference on Recent Trends in Information Technology (ICRTIT), Chennai, India, 3–5 June 2011; pp. 943–946. [Google Scholar] [CrossRef]
- Li, Y.-X.; Wang, L. A novel noise reduction technique for underwater acoustic signals based on complete ensemble empirical mode decomposition with adaptive noise, minimum mean square variance criterion and least mean square adaptive filter. Def. Technol. 2020, 16, 543–554. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, L.; Yan, H.; Bai, Y.; Wang, P. Denoising and baseline drift removal method of MEMS hydrophone signal based on VMD and wavelet threshold processing. IEEE Access 2019, 7, 59913–59922. [Google Scholar] [CrossRef]
- Li, Y.-X.; Jiao, S.-B.; Gao, X. A novel signal feature extraction technology based on empirical wavelet transform and reverse dispersion entropy. Def. Technol. 2021, 17, 1625–1635. [Google Scholar] [CrossRef]
- Ju, D.; Chi, C.; Li, Y.; Zhang, C.; Huang, H. A line spectrum Enhancement Algorithm Based on Unsupervised Deep Learning. Ship Sci. Technol. 2020, 42, 117–120. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, X.; Wu, B. Research on LOFAR spectrogram Enhancement of Passive Sonar Target signal Based on Long Short-Term Memory Networks. Electroacoust. Technol. 2020, 44, 101–103. [Google Scholar] [CrossRef]
- Li, Y.; Ma, X.; Wang, L.; Liu, Y. Denoising and Reconstruction of Pulsed signal in Non-Gaussian Environments Based on Deep Learning. Appl. Acoust. 2021, 40, 142–146. [Google Scholar] [CrossRef]
- Yin, J.; Luo, W.; Li, L.; Han, X.; Guo, L.; Wang, J. Enhancement of Underwater Acoustic Signal Based on Denoising Autoencoder. J. Commun. 2019, 40, 119–126. [Google Scholar] [CrossRef]
- Cao, L.; Peng, Y.; Mu, L.; Sun, Y.; Xu, J. A Water Sound Signal Recognition Method Based on Deep Convolutional Networks and Convolutional Denoising Autoencoders. Cyber Secur. Data Gov. 2023, 42, 35–3845. [Google Scholar] [CrossRef]
- Luo, W. Research on Sonar Signal Feature Enhancement Technology Based on Deep Learning. Master’s Thesis, Harbin Engineering University, Harbin, China, 2020. [Google Scholar] [CrossRef]
- Jiang, Y. Research on Recognition and Separation of Underwater Acoustic signal Based on Generative Adversarial Networks. Master’s Thesis, Harbin Engineering University, Harbin, China, 2021. [Google Scholar] [CrossRef]
- Gu, T.; Zhang, Q.; Li, J. Study on spectrogram Line Enhancement of Underwater Targets Based on Time-Frequency Attention Mechanism Network. J. Electron. Inf. 2024, 46, 92. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention (MICCAI 2015), Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Ma, T.; Yan, S.; Wang, W. An underwater acoustic signal denoising algorithm based on U-Net. In Proceedings of the 2023 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Zhengzhou, China, 14–17 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Song, Y.; Liu, F.; Shen, T. A novel noise reduction technique for underwater acoustic signals based on dual-path recurrent neural network. IET Commun. 2023, 17, 135–144. [Google Scholar] [CrossRef]
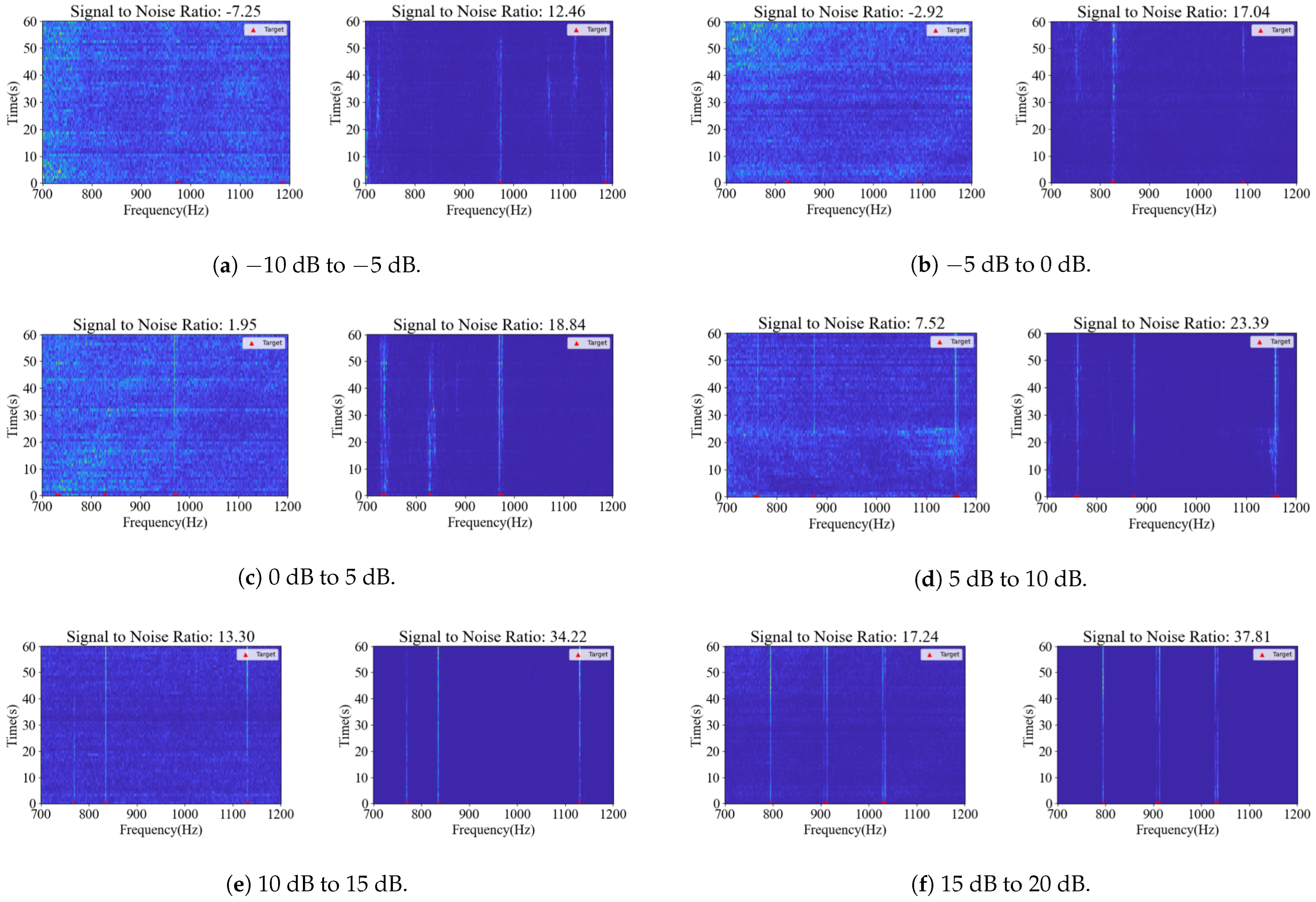
| SNR Range | MSCU-Net [20] | DPRNN [21] | CDM (Ours) | |||
|---|---|---|---|---|---|---|
| G | Recall | G | Recall | G | Recall | |
| −10 dB to −5 db | 0.8834 | 0.1853 | 3.9762 | 0.1676 | 10.7929 | 0.2294 |
| −5 dB to 0 dB | 2.6540 | 0.6563 | 8.7896 | 0.6347 | 18.0306 | 0.6780 |
| 0 dB to 5 dB | 5.2922 | 0.8414 | 10.9292 | 0.8543 | 20.9799 | 0.9061 |
| 5 dB to 10 dB | 9.3417 | 0.8423 | 13.6969 | 0.8825 | 21.0083 | 0.9631 |
| 10 dB to 15 dB | 13.9782 | 0.8547 | 13.9269 | 0.8892 | 21.5888 | 0.9965 |
| 15 dB to 20 dB | 18.1433 | 0.8571 | 16.3986 | 0.8362 | 21.7486 | 0.9965 |
| G | Recall | ||||
|---|---|---|---|---|---|
| 12.80 dB | 30.10 dB | 17.30 | 6 | 6 | 1 |
| SNR range | G | Recall | ||
|---|---|---|---|---|
| −10 dB to −5 dB | 9.55 | 106 | 300 | 0.3533 |
| −5 dB to 0 dB | 14.68 | 244 | 323 | 0.7554 |
| 0 dB to 5 dB | 16.65 | 265 | 280 | 0.9464 |
| 5 dB to 10 dB | 17.71 | 276 | 278 | 0.9928 |
| 10 dB to 15 dB | 19.62 | 293 | 294 | 0.9966 |
| 15 dB to 20 dB | 21.16 | 249 | 249 | 1 |
| G | Recall | ||||
|---|---|---|---|---|---|
| 11.15 dB | 26.33 dB | 15.18 | 189 | 213 | 0.8873 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, T.; Feng, S.; Yang, J.; Yu, K.; Zhou, J.; Chen, D. Underwater Acoustic Signal LOFAR Spectrogram Denoising Based on Enhanced Simulation. Appl. Sci. 2024, 14, 10931. https://doi.org/10.3390/app142310931
He T, Feng S, Yang J, Yu K, Zhou J, Chen D. Underwater Acoustic Signal LOFAR Spectrogram Denoising Based on Enhanced Simulation. Applied Sciences. 2024; 14(23):10931. https://doi.org/10.3390/app142310931
Chicago/Turabian StyleHe, Tianxiang, Sheng Feng, Jie Yang, Kun Yu, Junlin Zhou, and Duanbing Chen. 2024. "Underwater Acoustic Signal LOFAR Spectrogram Denoising Based on Enhanced Simulation" Applied Sciences 14, no. 23: 10931. https://doi.org/10.3390/app142310931
APA StyleHe, T., Feng, S., Yang, J., Yu, K., Zhou, J., & Chen, D. (2024). Underwater Acoustic Signal LOFAR Spectrogram Denoising Based on Enhanced Simulation. Applied Sciences, 14(23), 10931. https://doi.org/10.3390/app142310931






