An Integrated Model for Dam Break Flood Including Reservoir Area, Breach Evolution, and Downstream Flood Propagation
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydrodynamic Model
2.1.1. Governing Equation
2.1.2. Numerical Method
2.2. Breach Evolution Model
2.2.1. Breach Flow Calculation
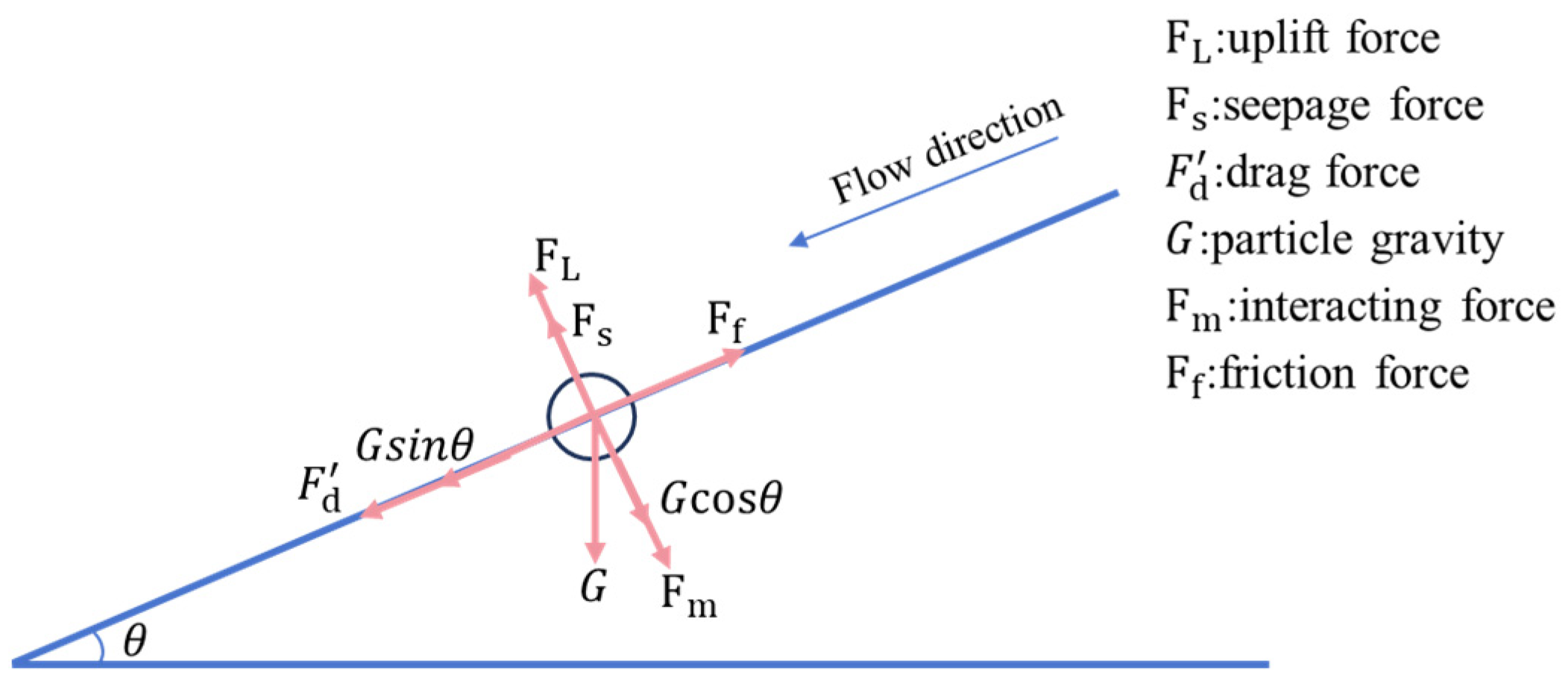
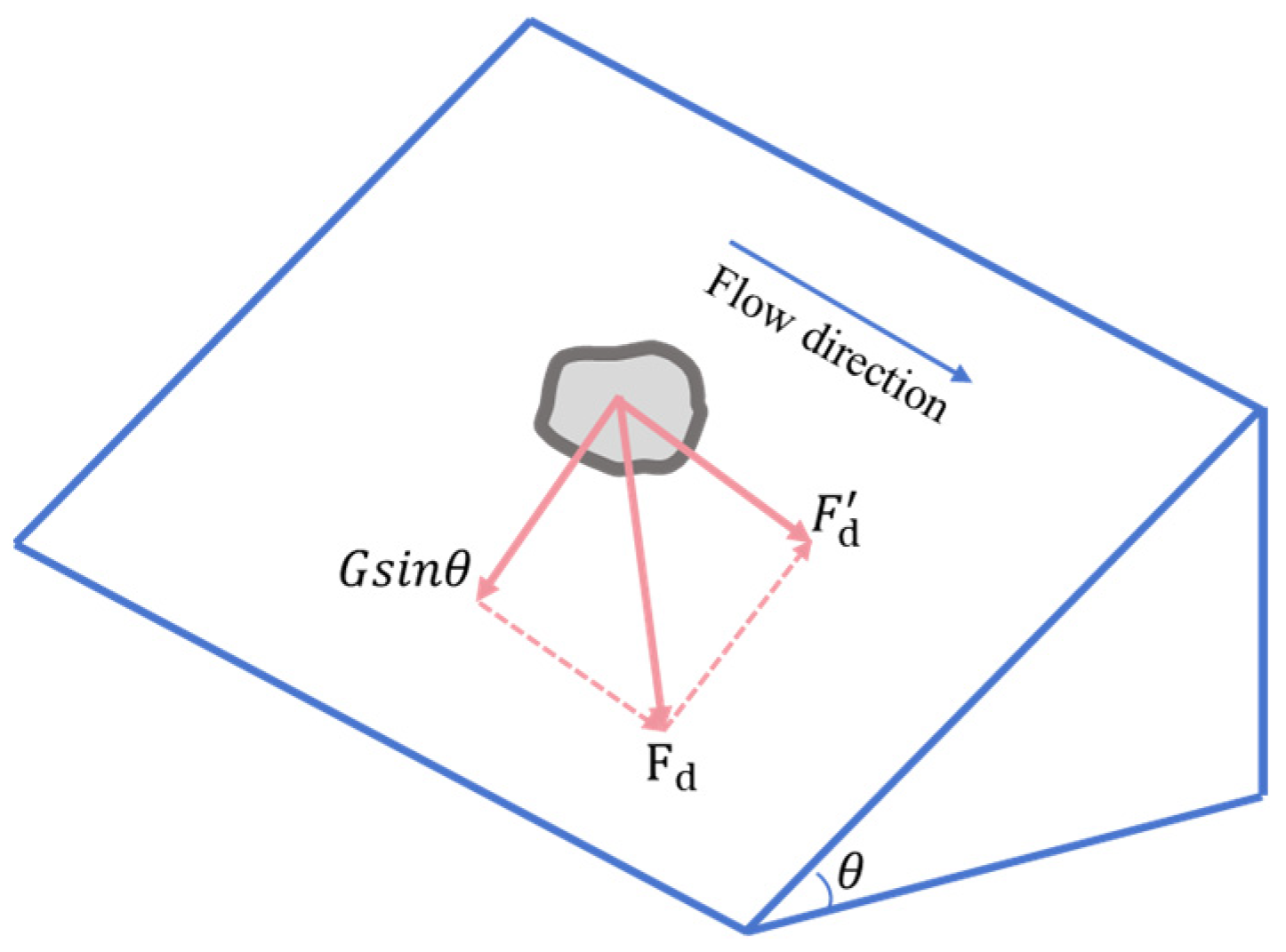
2.2.2. Starting Erosion Condition of the Breach
2.2.3. Breach Vertical Erosion Module
2.2.4. Breach Lateral Evolution Module
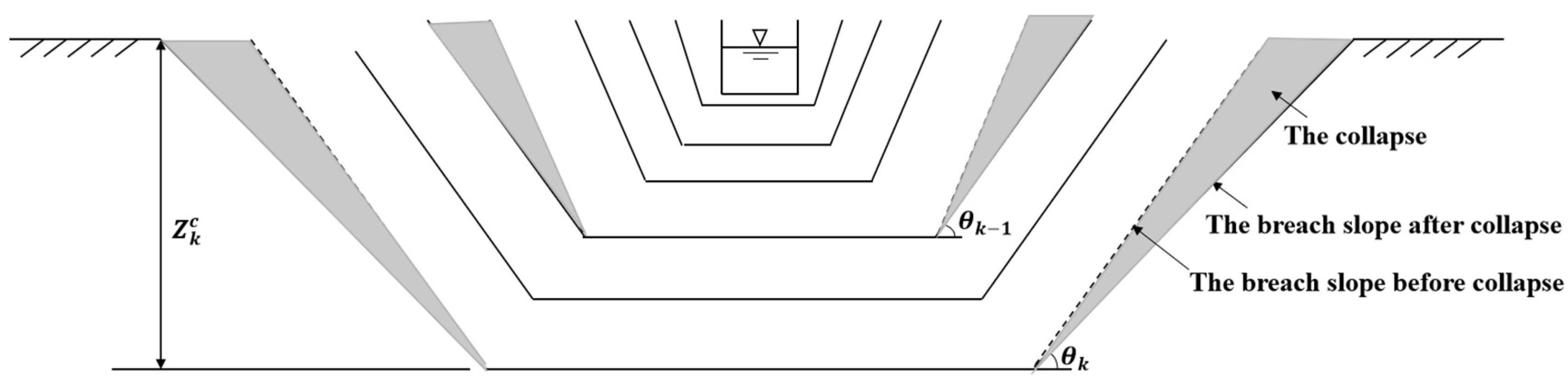
2.2.5. Side Slope Stability Module
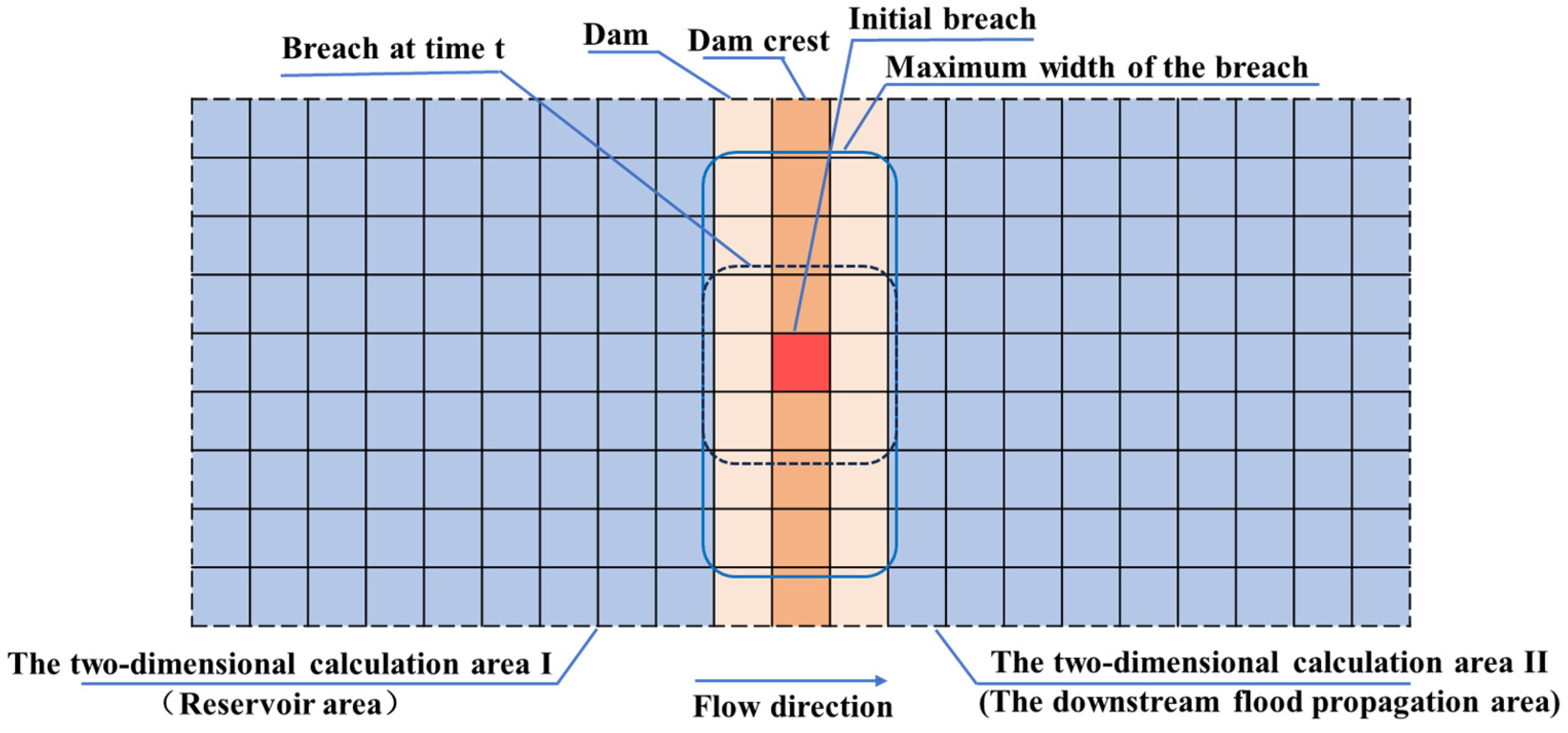
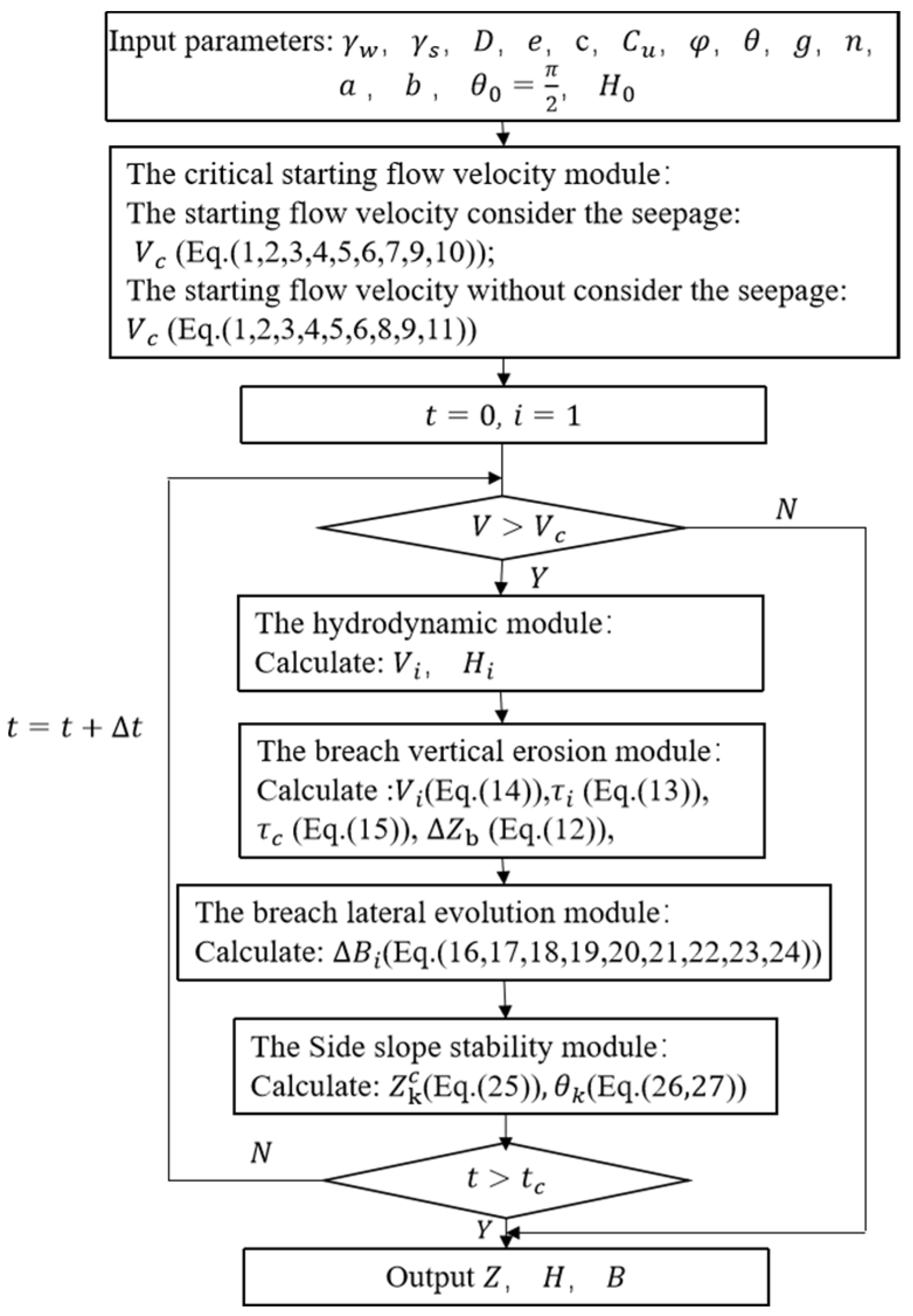
2.3. Integrated Model Construction
2.4. Comparison
2.5. Case Study
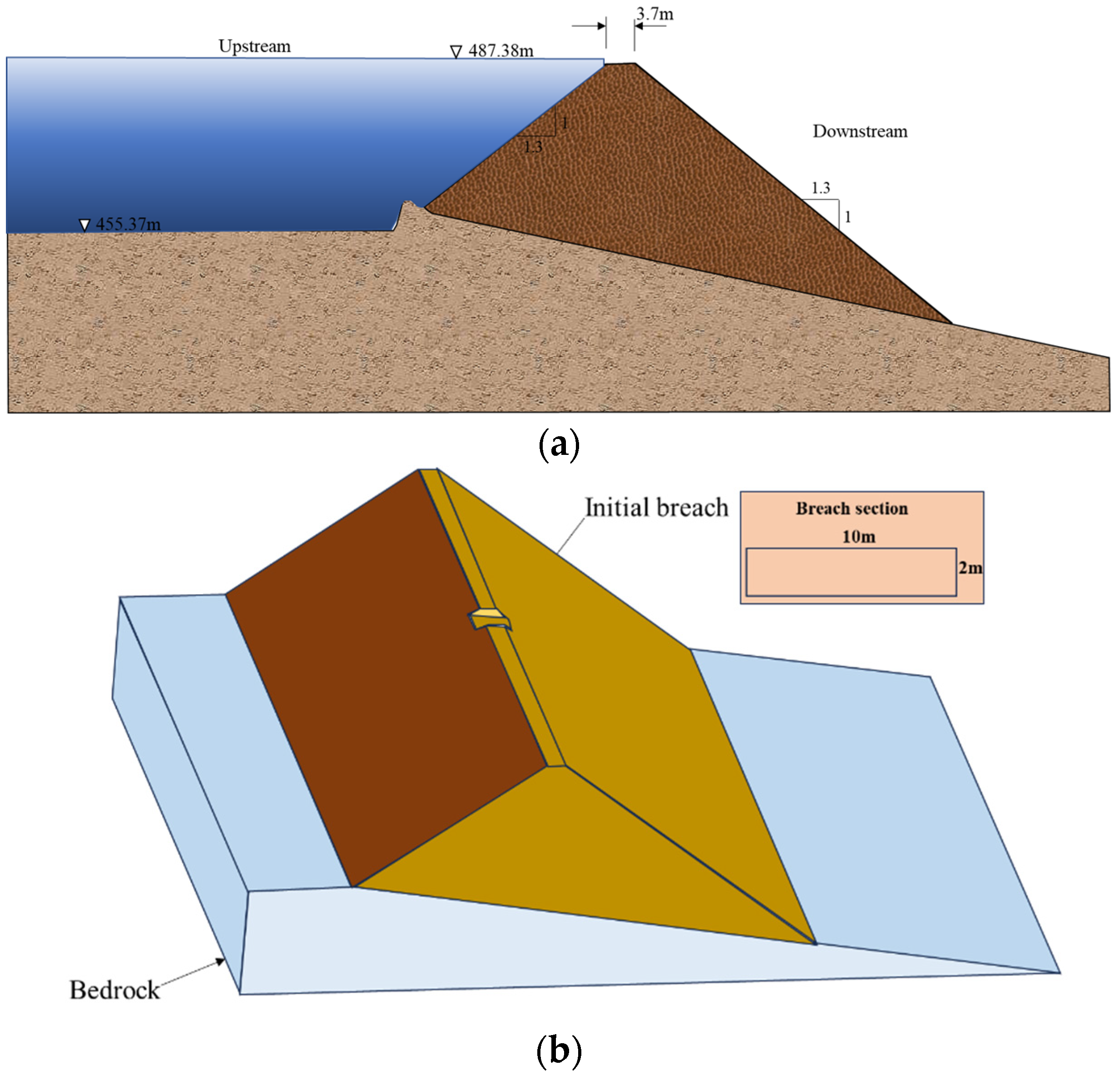
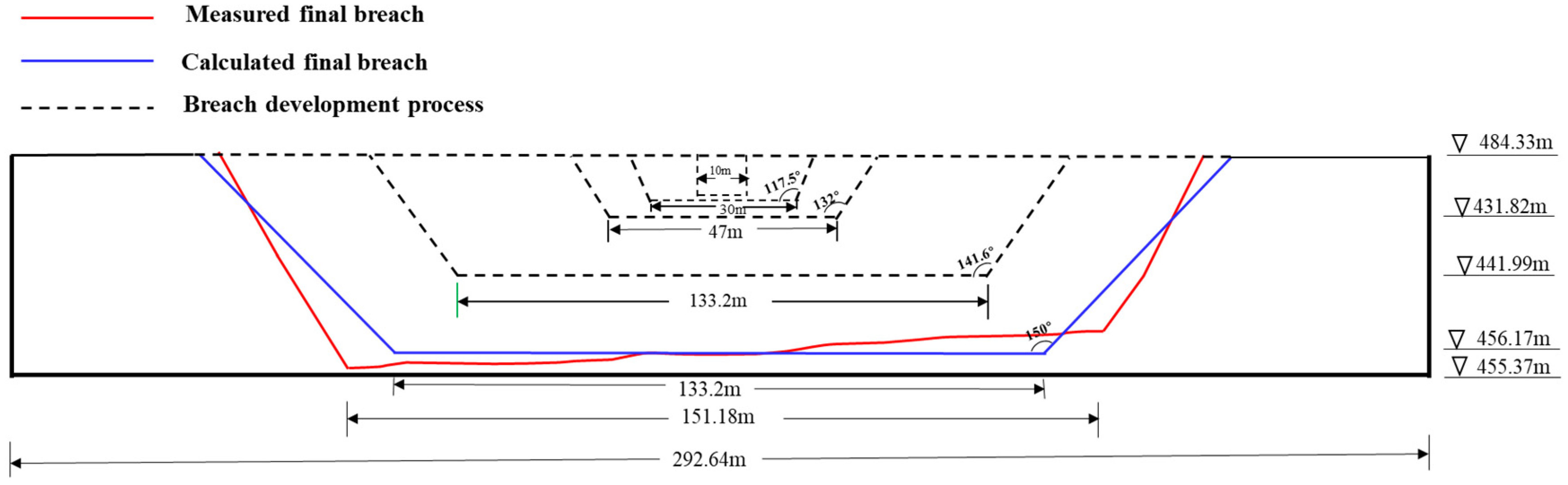
2.5.1. Taum Sauk Dam
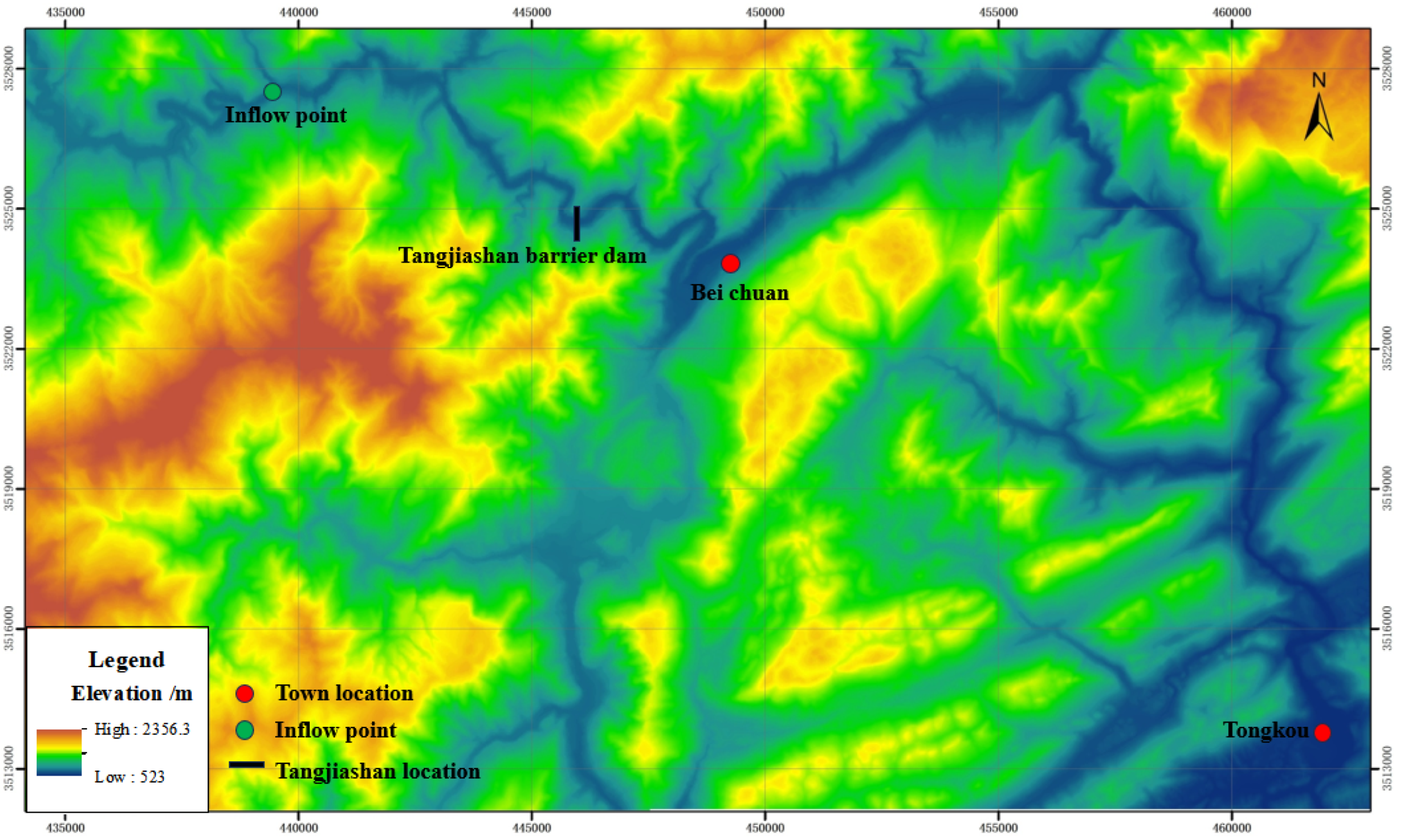
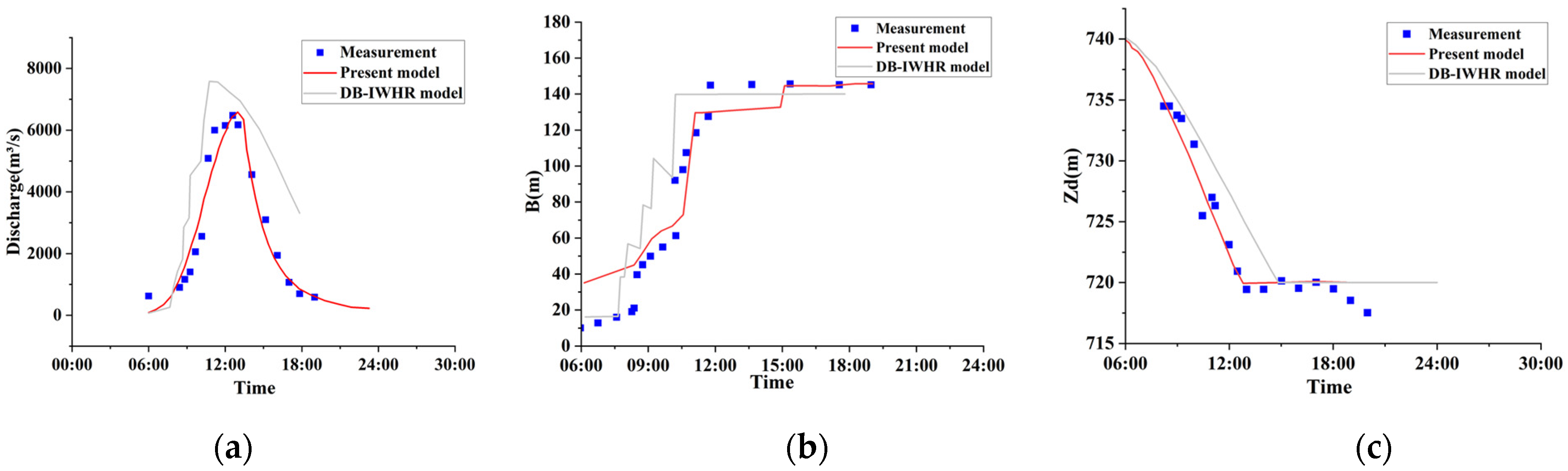
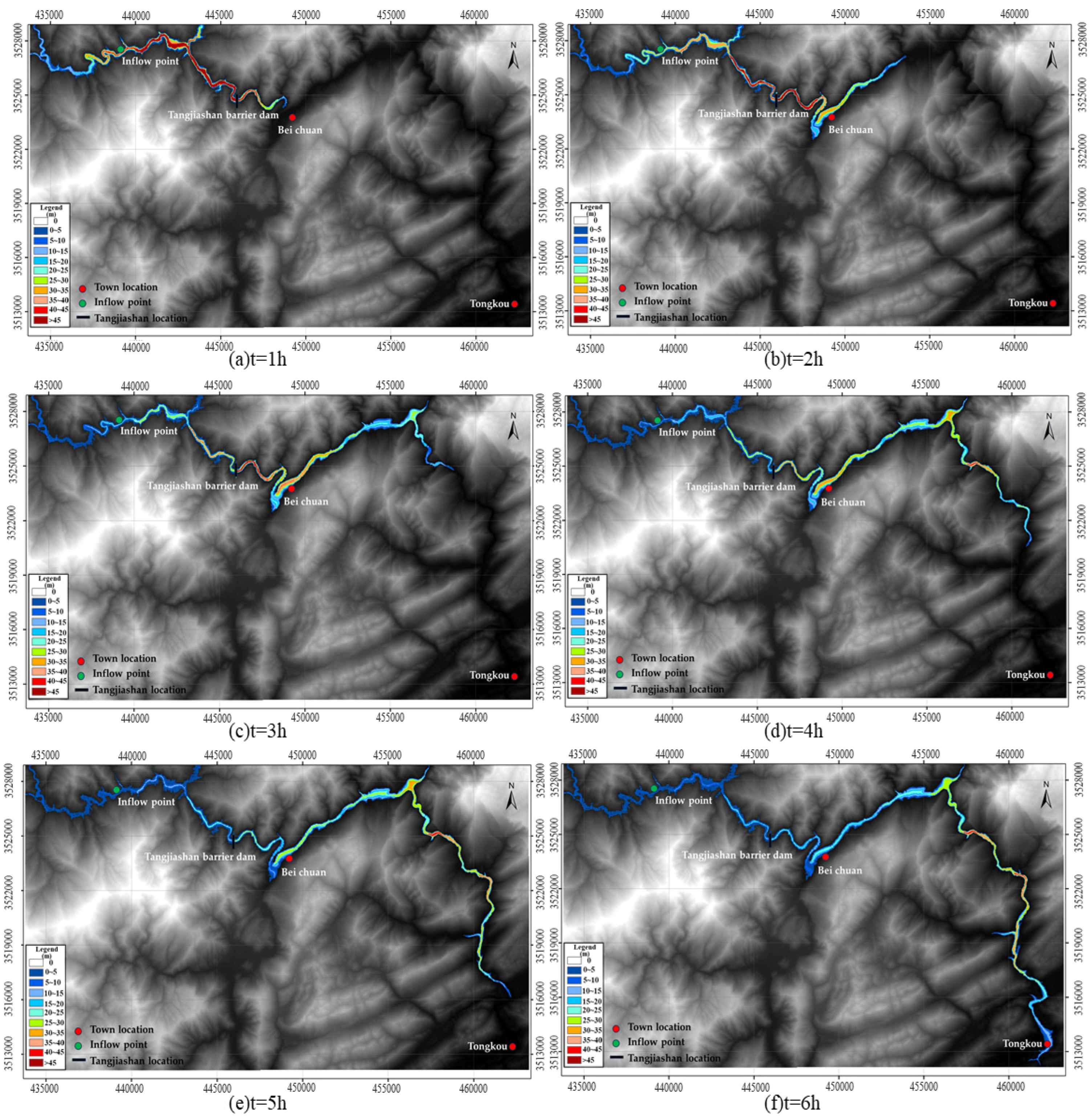
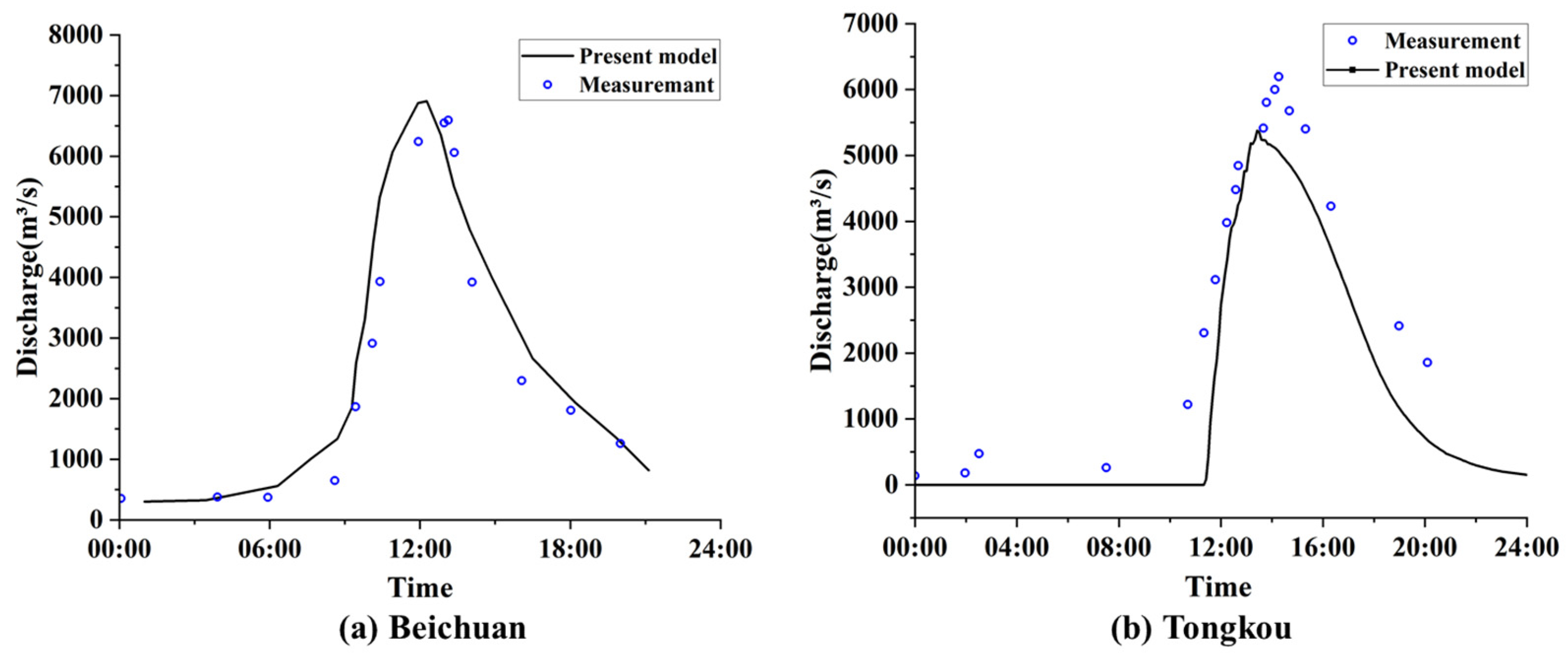
2.5.2. Tangjiashan Landslide Dam
3. Results and Discussion
3.1. Results Analysis
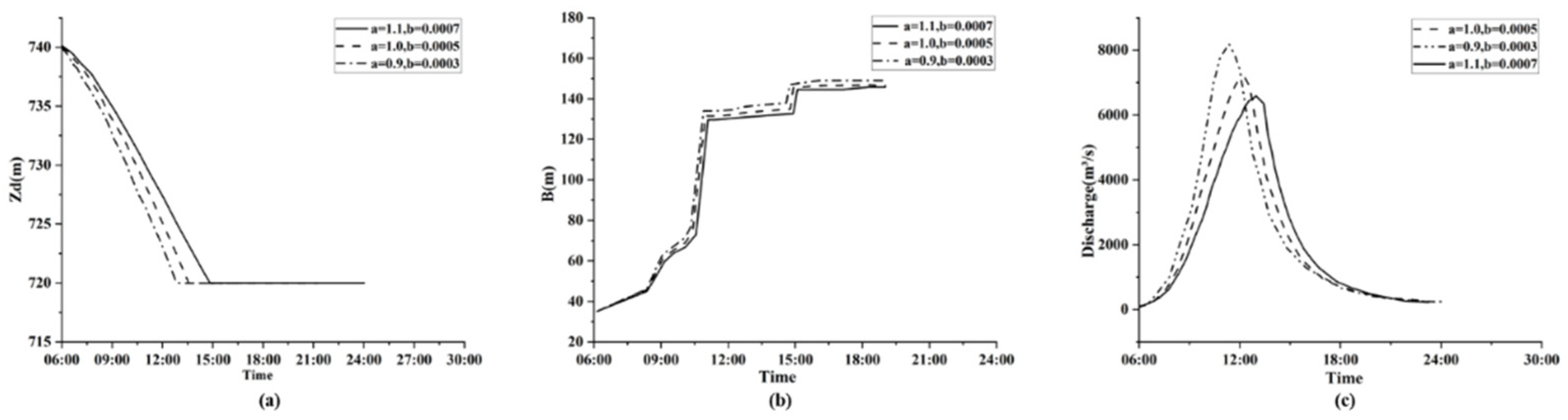
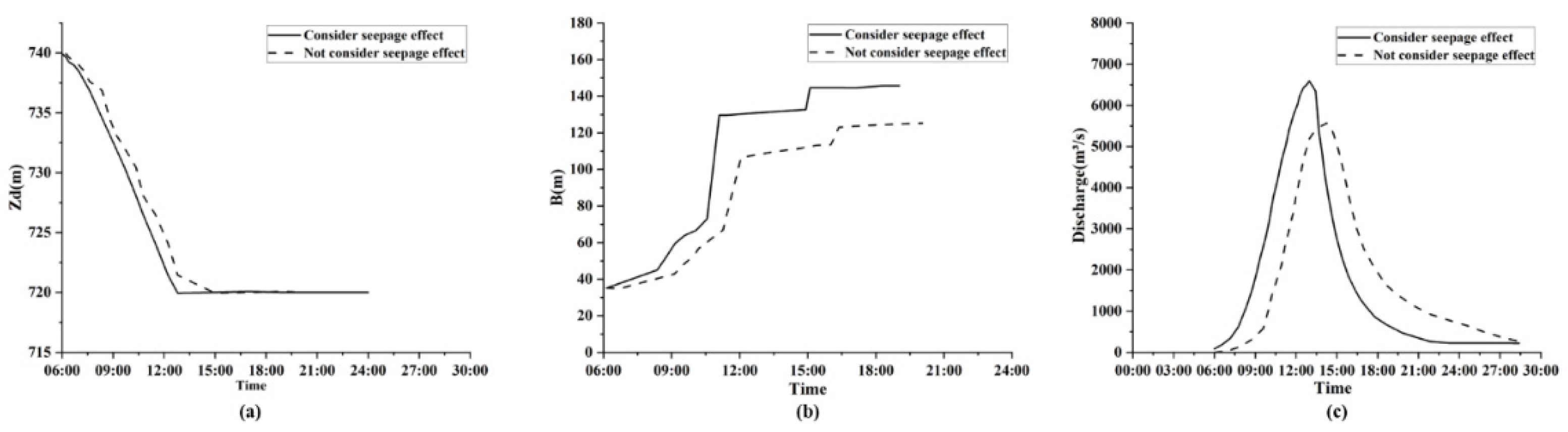
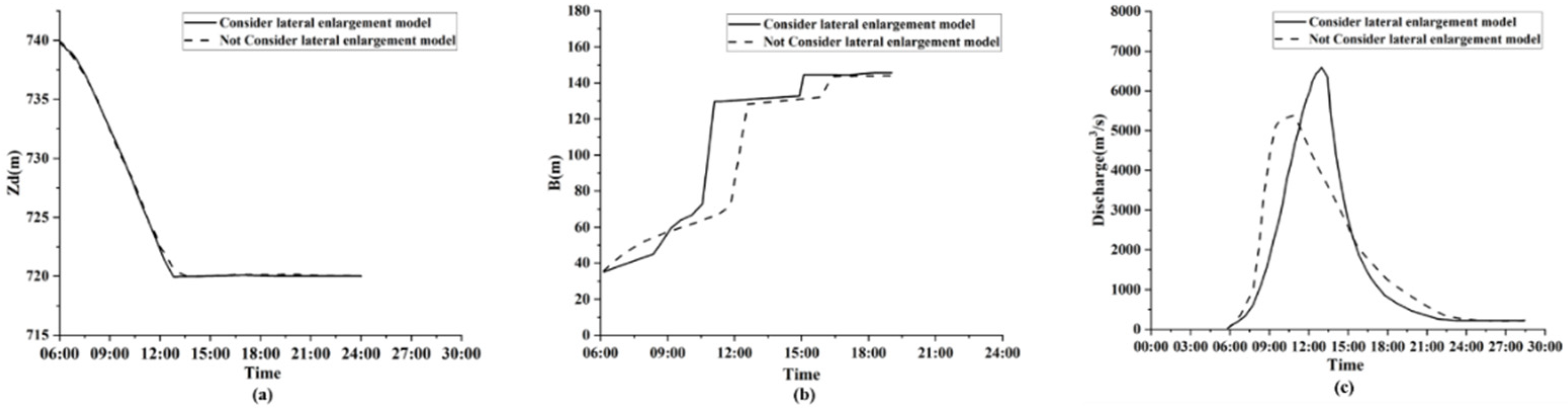
3.2. Sensitivity Analysis
3.2.1. Influence of the Parameter Related to the Erosion Module
3.2.2. Influence of the Infiltration Module
3.2.3. Influence of the Breach Lateral Evolution Module
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Li, Z.; Ge, W.; Wu, S. Risk Evaluation Model of Life Loss Caused by Dam-Break Flood and Its Application. Water 2019, 11, 1359. [Google Scholar] [CrossRef]
- World Meteorological Organization Report. Provisional State of the Global Climate 2023; United Nations Publications: New York, NY, USA, 2023. [Google Scholar]
- Mirauda, D.; Albano, R.; Sole, A.; Adamowski, J. Smoothed Particle Hydrodynamics Modeling with Advanced Boundary Conditions for Two-Dimensional Dam-Break Floods. Water 2020, 12, 1142. [Google Scholar] [CrossRef]
- ICOLD. Lessons from Dam Incidents; ICOLD: Paris, France, 1975. [Google Scholar]
- Zhong, Q.; Wu, W.; Chen, S.; Wang, M. Comparison of simplified physically based dam breach models. Nat. Hazards 2016, 84, 1385–1418. [Google Scholar] [CrossRef]
- Esin, A. Prediction of the cyclic hardening stress—strain curve. J. Strain Anal. Eng. Des. 1980, 15, 235–237. [Google Scholar] [CrossRef]
- Cecilio, C.B.; Tsay, K.D. Discussion of ‘Breaching Characteristics of Dam Failures’ by Thomas C. MacDonald and Jennifer Langridge-Monopolis (May, 1984). J. Hydraul. Eng. 1985, 111, 1123–1125. [Google Scholar] [CrossRef]
- U.S. Bureau of Reclamation (USBR). Downstream Hazards Classification Guidelines; U.S. Bureau of Reclamation: Denver, CO, USA, 1995.
- Vonthun, J.; Gillette, D. Guidance on Breach Parameters; U.S. Bureau of Reclamation: Denver, CO, USA, 1990.
- Froehlich, D.C. Peak Outflow from Breached Embankment Dam. J. Water Resour. Plan. Manag. 1995, 121, 90–97. [Google Scholar] [CrossRef]
- Froehlich, D.C. Predicting Peak Discharge from Gradually Breached Embankment Dam. J. Hydrol. Eng. 2016, 21, 04016041. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.M. Breaching Parameters for Earth and Rockfill Dams. J. Geotech. Geoenvironmental Eng. 2009, 135, 1957–1970. [Google Scholar] [CrossRef]
- Mei, S.; Chen, S.; Zhong, Q. Parametric model for breaching analysis of earth-rock dam. Adv. Eng. Sci. 2018, 50, 7. [Google Scholar]
- Singh, V.P.; Scarlatos, C.A. Breach erosion of earthfill dams and floodrouting: BEED model. Nat. Hazards 1985, 1, 161–180. [Google Scholar] [CrossRef]
- Fread, D.L. BREACH: An Erosion Model for Earthen Dam Failure; Hydrologic Research Laboratory, National Weather Service, NOAA: Silver Spring, MD, USA, 1988.
- Mohamed, A.A.A.; Samuels, P.G.; Morris, M.W.; Ghataora, G.S. Improving the accuracy of prediction of breach formation through embankment dams and flood embankments. In Proceedings of the Conference on Fluvial Hydraulics (River Flow 2002), Louvain-la-Neuve, Belgium, 4–6 September 2002. [Google Scholar]
- Morris, M.; Hassan, M.; Kortenhaus, A.; Geisenhainer, P.; Visser, P.; Zhu, Y. Modelling breach initiation and growth. In Flood Risk Management: Research and Practice: CRC Press: Boca Raton, FL, USA, 2008; pp. 581–591. [CrossRef]
- Temple, D.M.; Hanson, G.J.; Neilsen, M.L. WINDAM—Analysis of Overtopped Earth Embankment Dams. In Proceedings of the 2006 ASAE Annual Meeting, Portland, Oregon, 9–12 July 2006. [Google Scholar]
- Wu, W. Simplified Physically Based Model of Earthen Embankment Breaching. J. Hydraul. Eng. 2013, 139, 837–851. [Google Scholar] [CrossRef]
- Zhong, Q.; Chen, S.; Deng, Z. Breach mechanism and numerical modeling of barrier dam due to overtopping failure. Sci. Sin. Technol. 2018, 48, 959–968. [Google Scholar] [CrossRef]
- Graf, W.H. Hydraulics of Sediment Transport; Water Resources Publications: Littleton, CO, USA, 1971. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, L.; Yu, S.; Chen, S.; Zhou, X.; Sun, P.; Li, X. Back Analysis of the Draining Process of the Tangjiashan Barrier Lake. J. Hydraul. Eng. 2015, 141, 05014011.1–05014011.14. [Google Scholar] [CrossRef]
- Wang, Z.; Bowles, D.S. Three-dimensional non-cohesive earthen dam breach model. Part 1: Theory and methodology. Adv. Water Resour. 2006, 29, 1528–1545. [Google Scholar] [CrossRef]
- Cao, Z.; Yue, Z.; Pender, G. Landslide dam failure and flood hydraulics. Part II: Coupled mathematical modelling. Nat. Hazards 2011, 59, 1021–1045. [Google Scholar] [CrossRef]
- Liu, W.; He, S. Dynamic simulation of a mountain disaster chain: Landslides, barrier lakes, and outburst floods. Nat. Hazards 2018, 90, 757–775. [Google Scholar] [CrossRef]
- Zhang, D.; Li, D.; Chen, Z. Coupled one-and two-dimensional hydrodynamic models for levee-breach flood and its application. J. Hydroelectr. Eng. 2010, 29, 149–154. [Google Scholar]
- Xiong, Y. A Dam Break Analysis Using HEC-RAS. J. Water Resour. Prot. 2011, 3, 370–379. [Google Scholar] [CrossRef]
- DHI Water Environment. A Modelling System for Rivers and Channels User Guide; DHI Water Environment: Cambridge, CA, USA, 2012. [Google Scholar]
- Zhang, D.; Quan, J.; He, X.; Dong, T. Development and application of 1D dam-break flood analysis system based on GIS. J. Hydraul. Eng. 2013, 44, 1475–1481. [Google Scholar]
- Annunziato, A.; Dogan, G.G.; Yalciner, A.C. Modeling Dam Break Events Using Shallow Water Model. Eng 2023, 4, 1851–1870. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z.; Mei, C.; Wang, K.; Zhou, G. Urban flood analysis for different design storm hyetographs in Xiamen Island based on TELEMAC-2D. Chin. Sci. Bull. 2019, 64, 2055–2066. [Google Scholar] [CrossRef]
- Albu, L.-M.; Enea, A.; Iosub, M.; Breabăn, I.-G. Dam Breach Size Comparison for Flood Simulations. A HEC-RAS Based, GIS Approach for Drăcșani Lake, Sitna River, Romania. Water 2020, 12, 1090. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, X. Application of mathematical model for dam-break flood flow. Eng. J. Wuhan Univ. 2011, 44, 178–181. [Google Scholar]
- Ma, L.; Hou, J.; Zhang, D. Study on 2-D numerical simulation coupling with breach evolution in flood propagation. J. Hydraul. Eng. 2019, 50, 15. [Google Scholar]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. In Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería; Elsevier: Amsterdam, The Netherlands, 2014; Volume 30, pp. 1–10. [Google Scholar]
- MITECO. Technical Guide for the Classification of Dams; Ministerio Para la Transición Ecológica y el Reto Demográfico(MITECO): Madrid, Spain, 2021.
- Xu, D.; David, P.; Ji, C.; Xu, B.; Liu, H. Simulation of Flood Propagation in Cities Using Large Scale Parallel Computation of Shallow Water Equations. J. Tianjin Univ. (Sci. Technol.) 2016, 4, 341–348. [Google Scholar]
- Liang, Q.; Xia, X.; Hou, J. Catchment-scale High-resolution Flash Flood Simulation Using the GPU-based Technology. Procedia Eng. 2016, 154, 975–981. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Sharif, B.; Kalyanapu, A.; Ghafoor, S.; Dullo, T.; Gangrade, S.; Kao, S.-C.; Norman, M.; Evans, K. TRITON: A Multi-GPU open source 2D hydrodynamic flood model. Environ. Model. Softw. 2021, 141, 105034. [Google Scholar] [CrossRef]
- Echeverribar, I.; Morales-Hernández, M.; Brufau, P.; García-Navarro, P. 2D numerical simulation of unsteady flows for large scale floods prediction in real time. Adv. Water Resour. 2019, 134, 103444. [Google Scholar] [CrossRef]
- Shao, X.; Wang, X. Introduction to River Mechanics, 2nd ed.; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Han, Q.; He, M. The Threshold Motion of Sediment and Its Starting Speed; Science Press: Beijing, China, 1999. [Google Scholar]
- Martin, C.S. Effect of a Porous Sand Bed on Incipient Sediment Motion. Water Resour. Res. 1970, 6, 1162–1174. [Google Scholar] [CrossRef]
- Lauer, J.W.; Parker, G. Modeling framework for sediment deposition, storage, and evacuation in the floodplain of a meandering river: Application to the Clark Fork River, Montana. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Zhang, Q.; Chen, S.; Jin, S.; Zhong, Q. Back analysis of the breach flood of the “11.03” Baige barrier lake at the Upper Jinsha River. Sci. Sin. Technol. 2020, 50, 763–774. [Google Scholar] [CrossRef]
- Chen, Z.; Ping, Z.; Wang, N.; Yu, S.; Chen, S. An approach to quick and easy evaluation of the dam breach flood. Sci. China Technol. Sci. 2019, 62, 1773–1782. [Google Scholar] [CrossRef]
- Annandale, G.W. Scour Technology-Mechanics and Engineering Practice; Mcgraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Zhong, Q.M.; Chen, S.S.; Mei, S.A.; Cao, W. Numerical simulation of landslide dam breaching due to overtopping. Landslides 2017, 15, 1183–1192. [Google Scholar] [CrossRef]
- Zhong, Q.; Chen, S.; Shan, Y. Numerical modeling of breaching process of Baige dammed lake on Jinsha River. Adv. Eng. Sci. 2020, 52, 29–37. [Google Scholar]
- Cai, Y.; Zhang, X.; Xue, R.; Wang, M.; Deng, Q. Numerical simulation of overtopping breach processes caused by failure of landslide dams. Environ. Fluid Mech. 2022, 22, 839–863. [Google Scholar] [CrossRef]
- Singh, V.P. Dam Breach Modeling Technology; Springer Nature: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Froehlich, D.C. Embankment Dam Breach Parameters Revisited; American Society of Civil Engineers: Reston, VA, USA, 1995. [Google Scholar]
- Fread, D.L. The NWS Dam Break Flood Forecasting Model; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1984.
- Mei, S.; Zhong, Q.; Yang, M.; Chen, S.; Shan, Y.; Zhang, L. Overtopping-Induced breaching process of concrete-faced rockfill dam: A case study of Upper Taum Sauk dam. Eng. Fail. Anal. 2023, 144, 106982. [Google Scholar] [CrossRef]
- Kalyanapu, A.J.; Shankar, S.; Pardyjak, E.R.; Judi, D.R.; Burian, S.J. Assessment of GPU computational enhancement to a 2D flood model. Environ. Model. Softw. 2011, 26, 1009–1016. [Google Scholar] [CrossRef]
- Rydlund, P.H. Peak Discharge, Flood Profile, Flood Inundation, and Debris Movement Accompanying the Failure of the Upper Reservoir at the Taum Sauk Pump Storage Facility near Lesterville, Missouri, U.S, Geological Survey Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2010.
- Zhong, Q.; Chen, S.; Zhao, L.; Ren, Q.; Cao, W. Numerical simulation of overtopping failure process of a barrier dam. Joumal Hohai Univ. (Nat. Sci.) 2012, 40, 7. [Google Scholar]
- Hu, X.; Luo, G.; Wang, J. Seepage stability analysis and dam-breaking mode of Tangjiashan barrier dam. Chin. J. Rock Mech. Eng. 2010, 29, 1409–1417. [Google Scholar]
- Zhong, Q.M.; Chen, S.S.; Deng, Z. Numerical model for homogeneous cohesive dam breaching due to overtopping failure. J. Mt. Sci. 2017, 14, 571–580. [Google Scholar] [CrossRef]

| No. | Models | Breach Flow Calculation | Breach Vertical Erosion | Breach Lateral Evolution | Breach Side Slope Stability |
|---|---|---|---|---|---|
| 1 | DAMBRK [53] | Weir formula | Assumed linear erosion | Linearly related to vertical erosion | No consider breach stability |
| 2 | HR BREACH [16] | Variable weir plus 1D steady nonuniform equation | Various equations, noncohesive and cohesive soils | Linearly related to vertical erosion | Consider breach stability |
| 3 | WinDAM [18] | Weir formula | Headcut advance, bottom and lateral erosion | Linearly related to vertical erosion | No consider breach stability |
| 4 | MIKE DB [28] | Weir formula | Engelund-Hansen bed load formula | Linearly related to vertical erosion | Consider breach stability |
| 5 | DLBreach [19] | Weir formula | Exponential erosion model | Linearly related to vertical erosion | Consider breach stability |
| 6 | DB-IWHR [22] | Weir formula | The hyperbolic erosion model | Linearly related to vertical erosion | Consider breach stability |
| 7 | NHRI-DB [20] | Weir formula | Exponential erosion model | Linearly related to vertical erosion | Consider breach stability |
| 8 | Integration model | Direct calculation by integration model | The hyperbolic erosion model | Newly proposed | Consider breach stability |
| Basic Information | Taum Sauk Dam | Tangjiashan Landslide Dams |
|---|---|---|
| Location | 90°49′6″ E, 37°32′8″ N | 104°25′57″ E, 31°50′40″ N |
| Volume (m3) | 5.366 × 106 | 2.3 × 107 |
| Dam crest elevation (m) | 487.38 | 742.5 |
| Dam bottom elevation (m) | 455.37 | 639.5 |
| Dam height (m) | 32.01 | 103 |
| Dam crest width (m) | 3.7 | 300 |
| Dam breach bottom elevation (m) | 456 | 717.5 |
| Final breach depth (m) | 31.38 | 25 |
| Upstream slope ratio (vertical/horizontal) | 1:1.3 | 1:1.5 |
| Downstream slope ratio (vertical/horizontal) | 1:1.3 | 1:1.5 |
| Initial breach width (m) | 10 | 8 |
| Initial breach depth (m) | 2 | 13 |
| Average particle size (m) | 0.01 | 0.03 |
| 0.46 | 0.4 | |
| Average density of dam material (kg/m3) | 2.65 × 103 | 2.6 × 103 |
| Internal friction angle (°) | 38 | 45 |
| Cohesive force (kPa) | 20 | 60 |
| Erosion parameter | a = 1.0, b = 0.0005 | a = 1.1, b = 0.0007 |
| Parameter | Measured Data | Distributed Simulation Results | Relative Error | Integration Model Results | Relative Error | DLBreach | Relative Error |
|---|---|---|---|---|---|---|---|
(m3/s) | 8180 | 9362.7 | 21.11% | 8300 | 7.37% | 8398.7 | 2.67% |
| (m) | 199.95 | —— | —— | 210.7 | 5.38% | 130.00 | 25.96% |
| (m) | 28.16 | —— | —— | 28.16 | 0.00% | 28.4 | 0.85% |
| (s) | 480 | 360 | −25.00% | 502 | 4.58% | 780 | 62.5% |
| (min) | 25 | —— | —— | 32 | 28.00% | 40 | 60.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wang, Z.; Zhang, D.; Xiang, L. An Integrated Model for Dam Break Flood Including Reservoir Area, Breach Evolution, and Downstream Flood Propagation. Appl. Sci. 2024, 14, 10921. https://doi.org/10.3390/app142310921
Liu H, Wang Z, Zhang D, Xiang L. An Integrated Model for Dam Break Flood Including Reservoir Area, Breach Evolution, and Downstream Flood Propagation. Applied Sciences. 2024; 14(23):10921. https://doi.org/10.3390/app142310921
Chicago/Turabian StyleLiu, Huiwen, Zhongxiang Wang, Dawei Zhang, and Liyun Xiang. 2024. "An Integrated Model for Dam Break Flood Including Reservoir Area, Breach Evolution, and Downstream Flood Propagation" Applied Sciences 14, no. 23: 10921. https://doi.org/10.3390/app142310921
APA StyleLiu, H., Wang, Z., Zhang, D., & Xiang, L. (2024). An Integrated Model for Dam Break Flood Including Reservoir Area, Breach Evolution, and Downstream Flood Propagation. Applied Sciences, 14(23), 10921. https://doi.org/10.3390/app142310921







