Establishing Lightweight and Robust Prediction Models for Solar Power Forecasting Using Numerical–Categorical Radial Basis Function Deep Neural Networks
Abstract
1. Introduction
- This is the first study to incorporate the concepts of ensemble models and lightweight deep learning models into robust predictions of solar power generation.
- We customized an NC-RBF-DNN based on the distribution characteristics of the input factor data of solar power forecasting to establish lightweight models using the train–dismantle deep learning model method.
- We designed a heap-based factor combination search algorithm to find multiple combinations of suitable factors based on the factor importance ranking obtained by the NC-RBF-DNN; after the factor combinations are input to the lightweight models, they produce near-optimal prediction results.
2. Related Works
2.1. Related Works: Solar Power Forecasting
2.2. Related Works: Lightweight Deep Learning Models
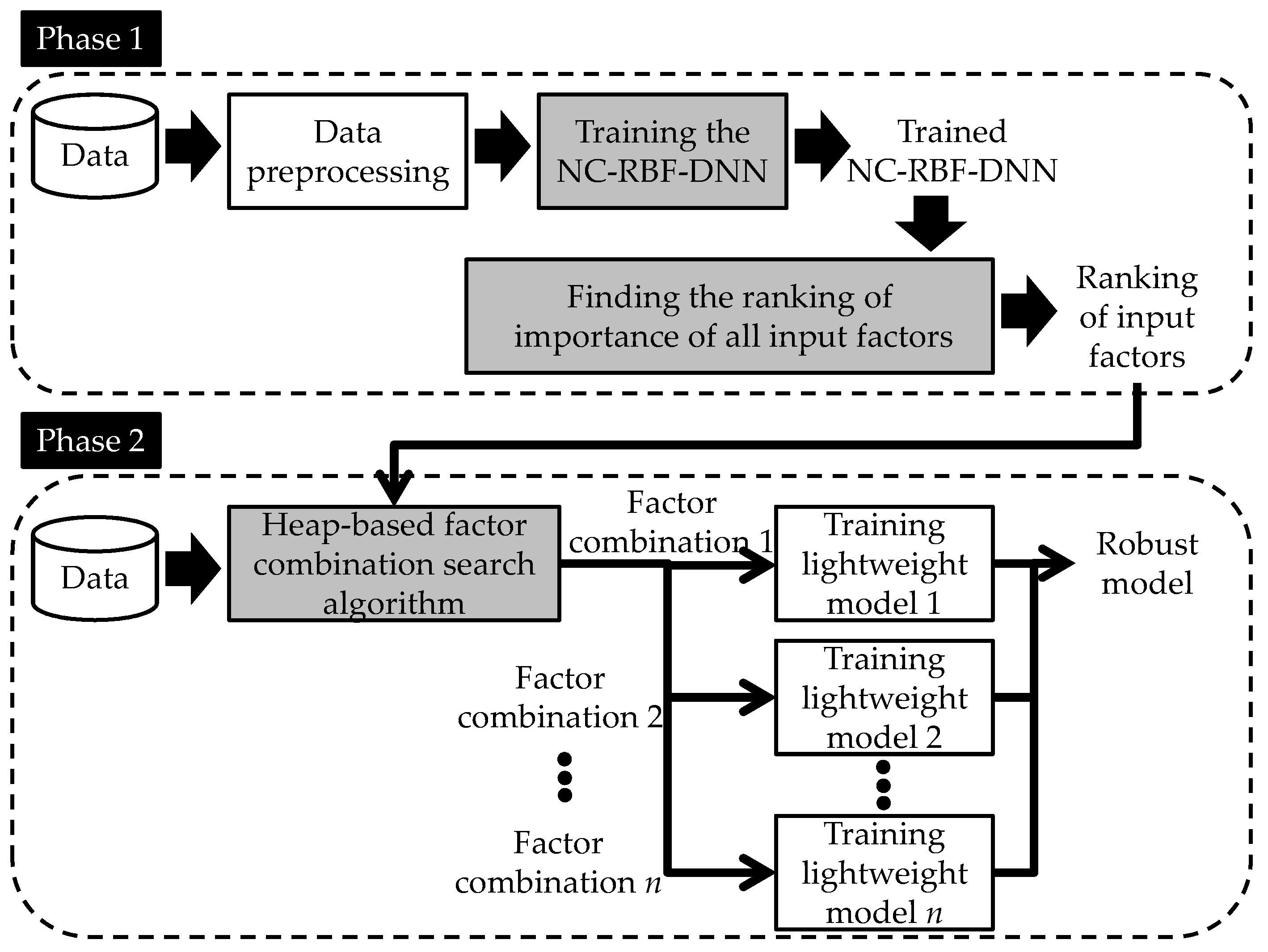
3. Methods
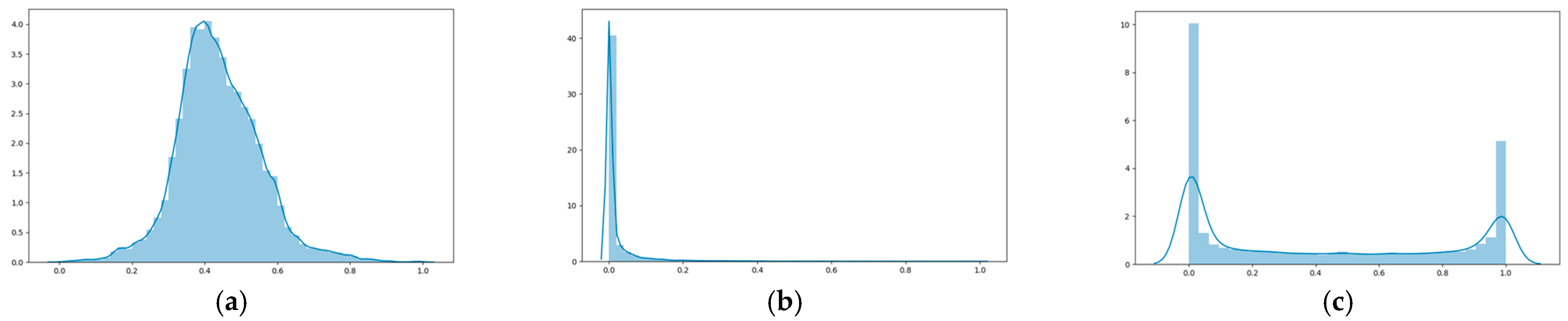
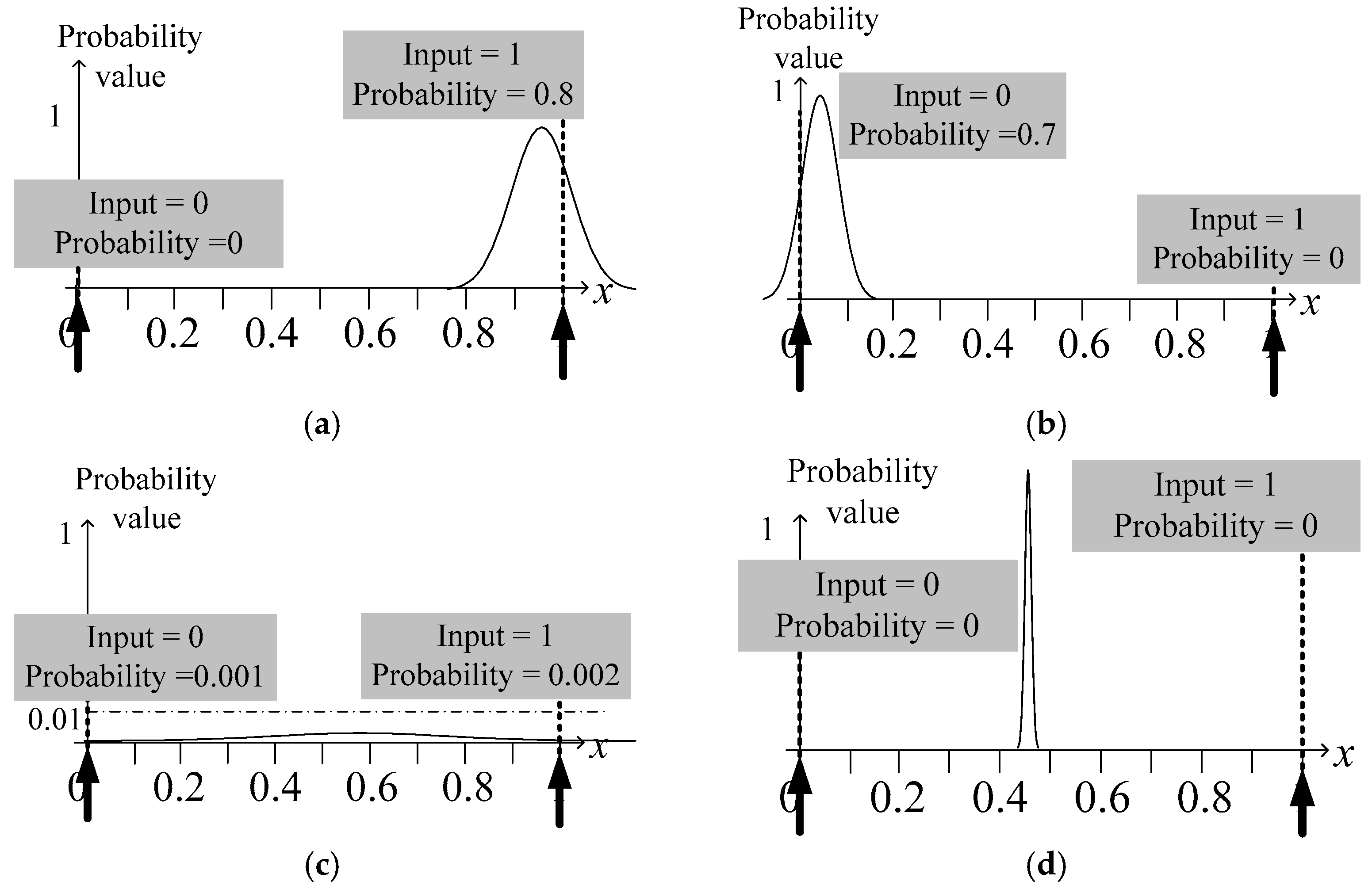
3.1. Preprocessing of Historical Weather Data
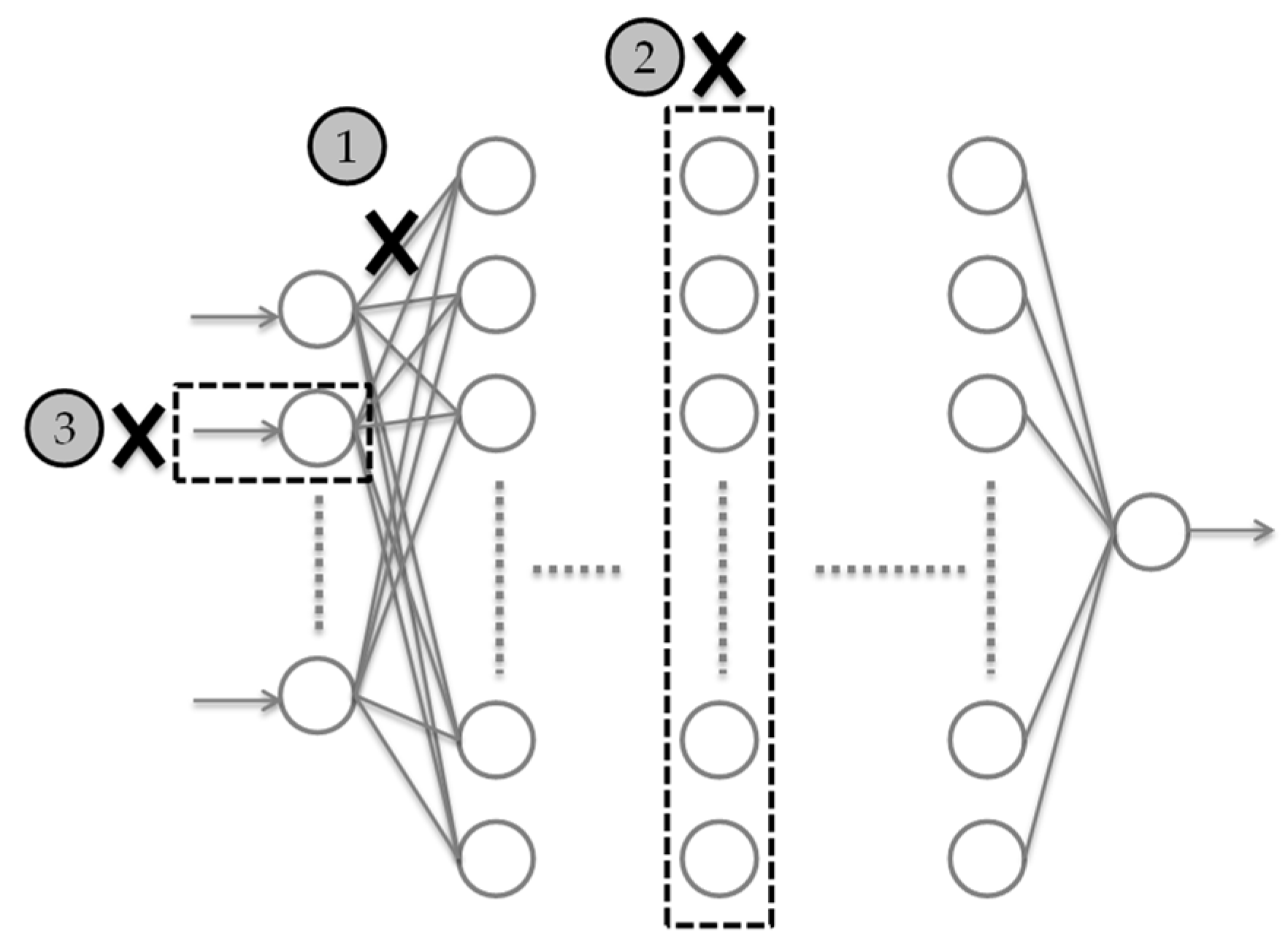
3.2. Training and Dismantling NC-RBF-DNN to Obtain Importance Ranking of Factors
3.2.1. Architecture of NC-RBF-DNN
3.2.2. Factor Ranking Algorithm
3.3. Factor Combination Search Algorithm
4. Simulations
4.1. Introduction to Dataset and Experiment Parameters
4.2. NC-RBF-DNN Modeling Accuracy
4.3. Reasonableness of Factor Importance Ranking Obtained by NC-RBF-DNN
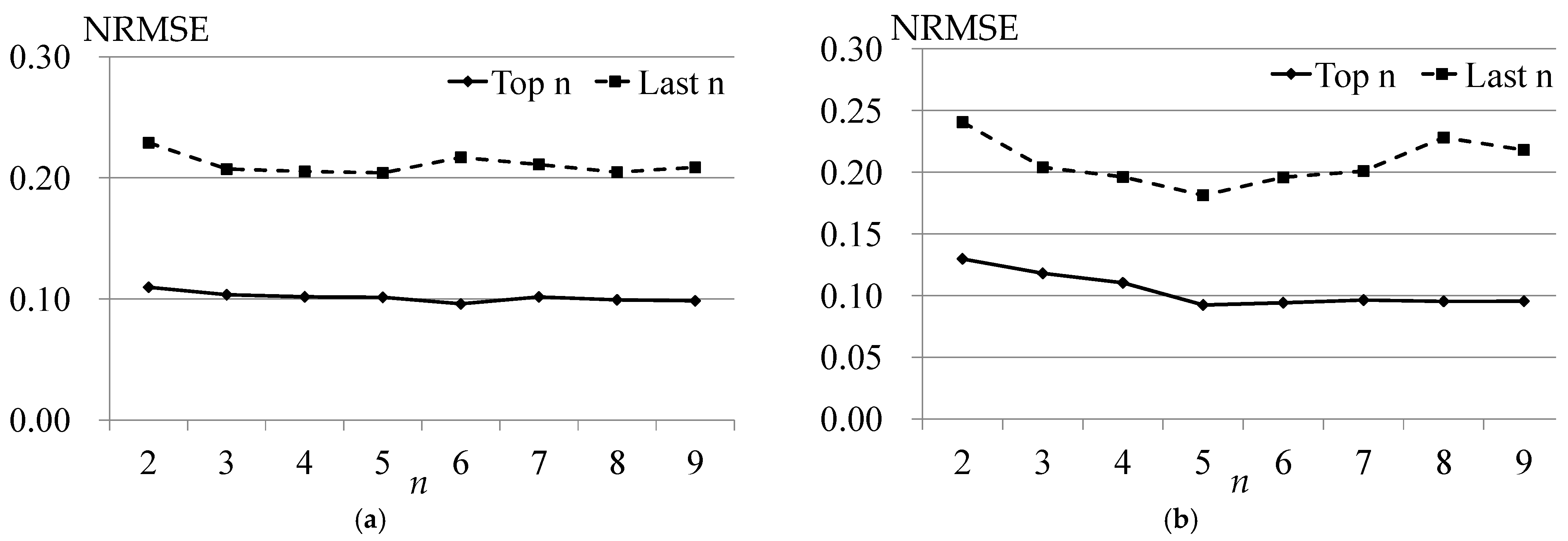
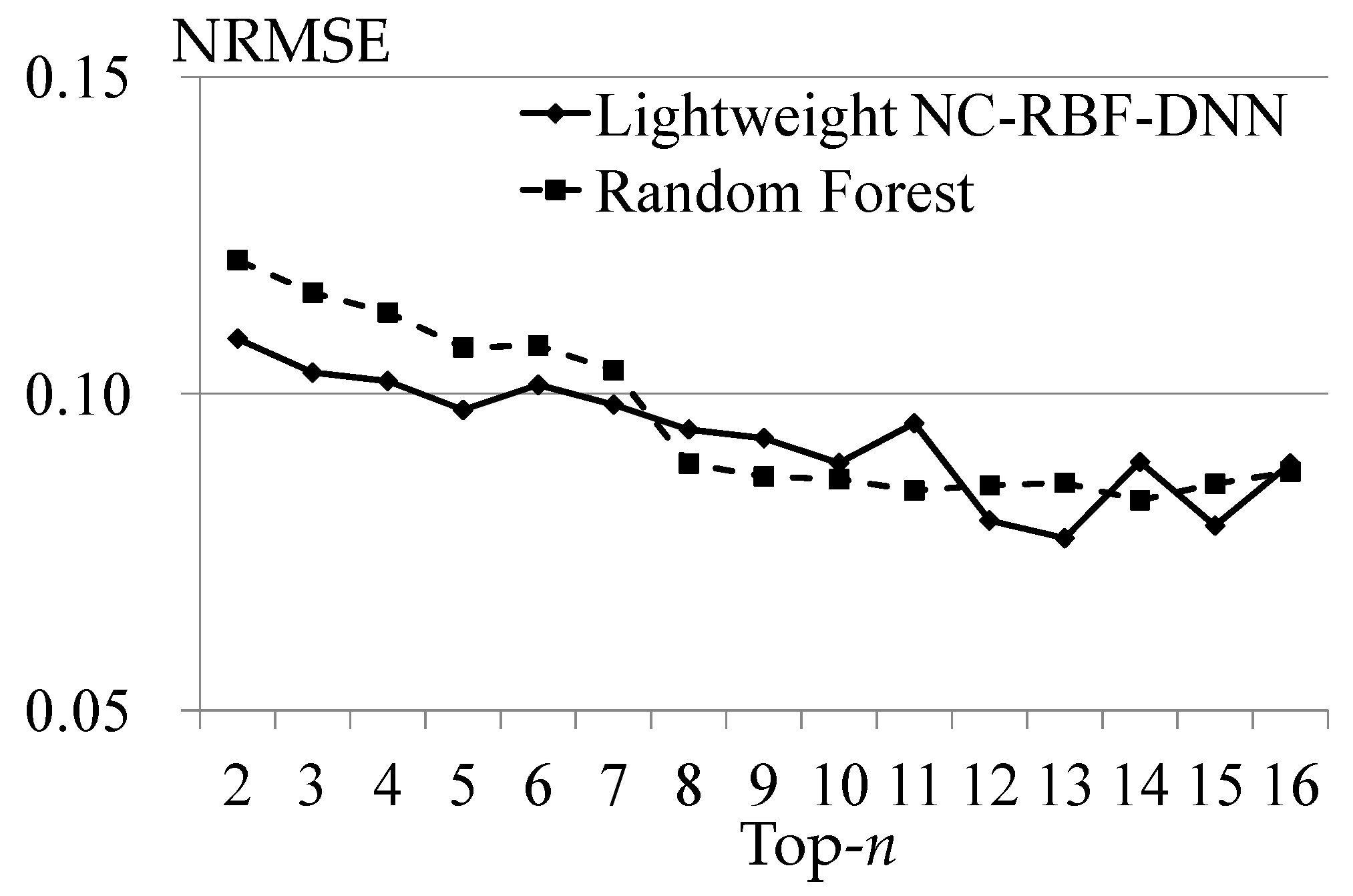
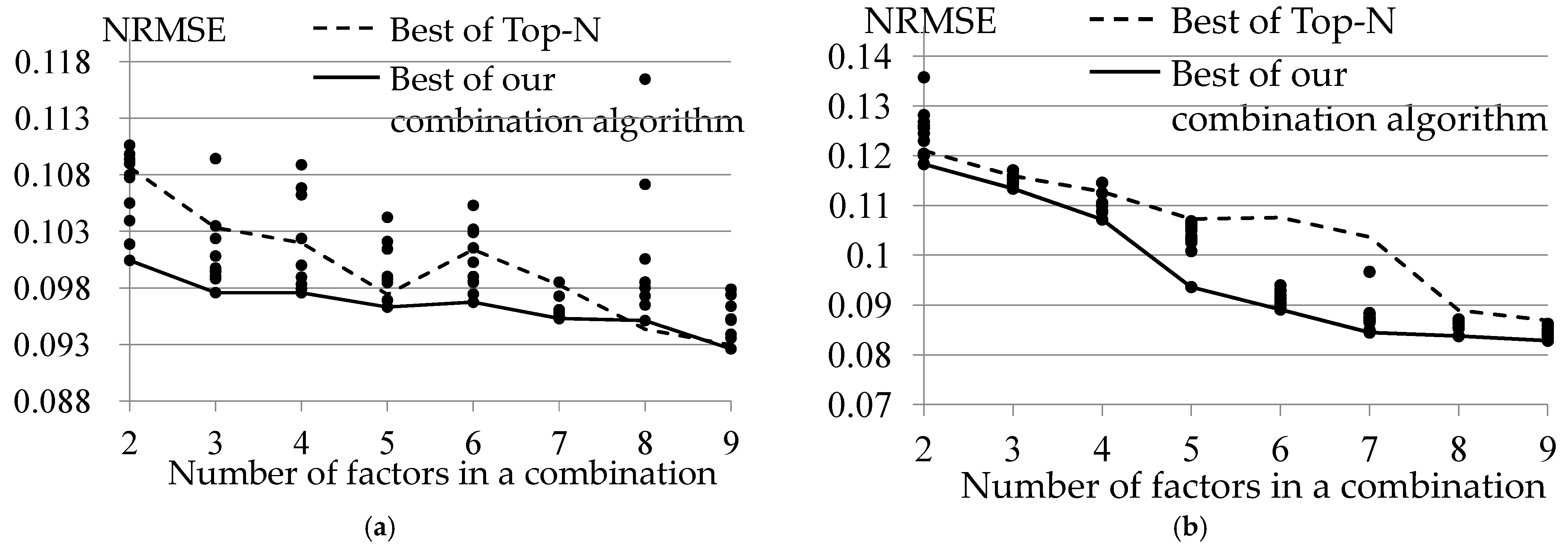
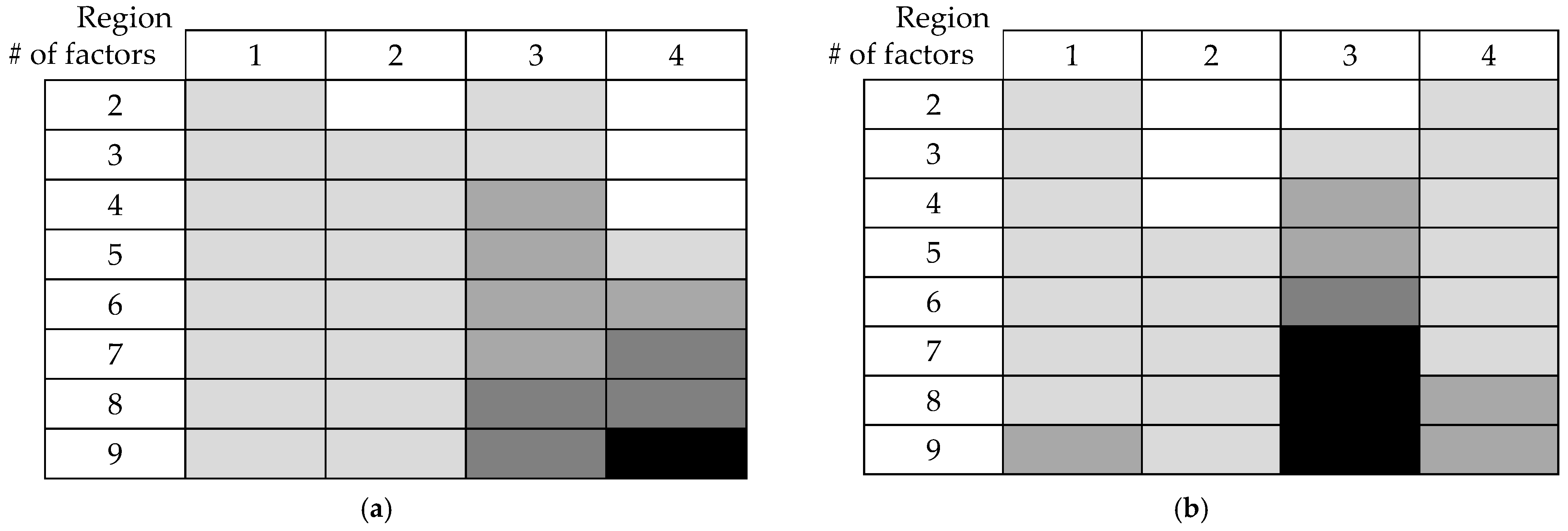
4.4. Verification of Validity of Factor Combination Search Algorithm
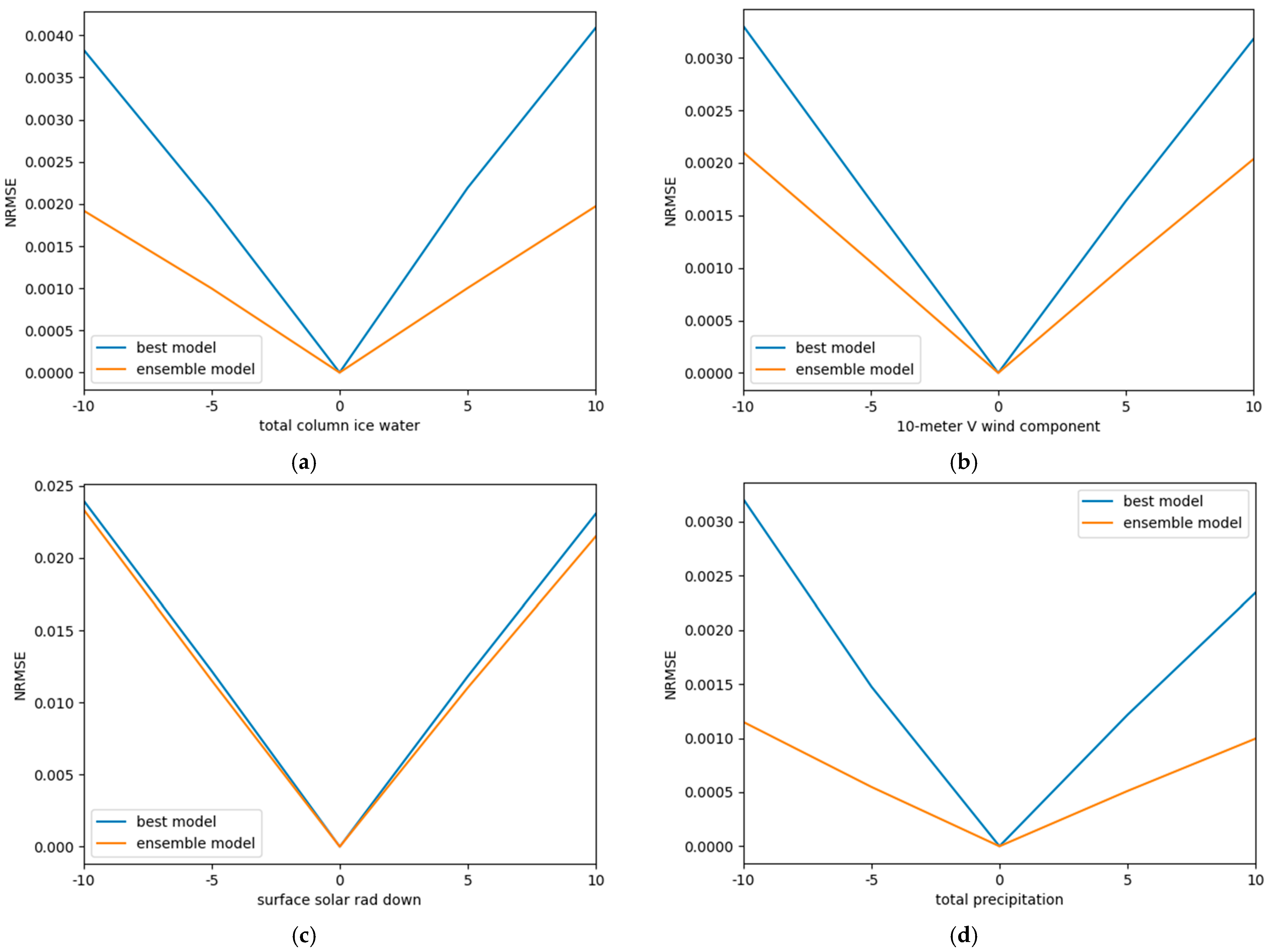
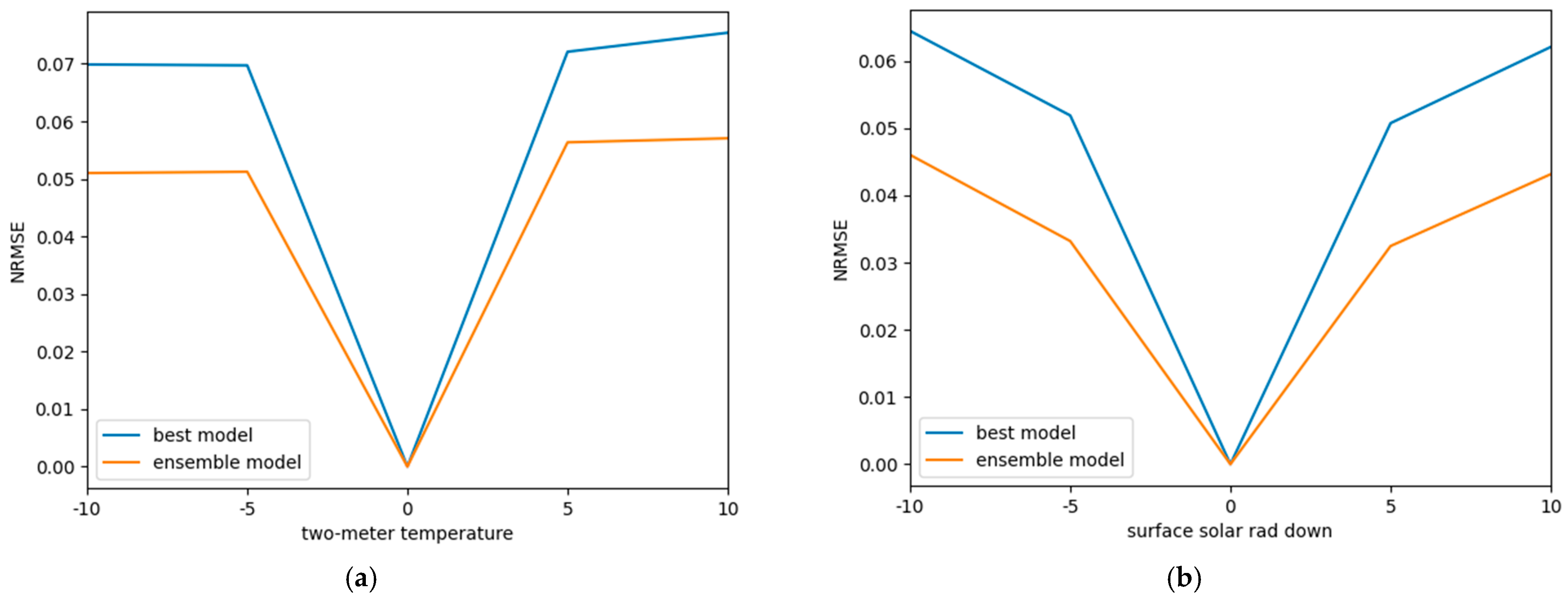
4.5. Performance of Proposed Model with Inputs Containing Errors
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lotfi, M.; Javadi, M.; Osório, G.J.; Monteiro, C.; Catalão, J.P.S. A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation. Energies 2020, 13, 216. [Google Scholar] [CrossRef]
- Bracale, A.; Carpinelli, G.; De Falco, P. A Probabilistic Competitive Ensemble Method for Short-Term Photovoltaic Power Forecasting. IEEE Trans. Sustain. Energy 2017, 8, 551–560. [Google Scholar] [CrossRef]
- Salinas, L.M.; Jirón, L.A.C.; Rodríguez, E.G. A simple physical model to estimate global solar radiation in the central zone of Chile. In Proceedings of the 24th International Cartographic Conference, Santiago, Chile, 15–21 November 2009; pp. 1–9. [Google Scholar]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced Methods for Photovoltaic Output Power Forecasting: A Review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Boilley, A.; Thomas, C.; Marchand, M.; Wey, E.; Blanc, P. The Solar Forecast Similarity Method: A New Method to Compute Solar Radiation Forecasts for the Next Day. Energy Procedia 2016, 91, 1018–1023. [Google Scholar] [CrossRef]
- Dambreville, R.; Blanc, P.; Chanussot, J.; Boldo, D. Very short term forecasting of the Global Horizontal Irradiance using a spatio-temporal autoregressive model. Renew. Energy 2014, 72, 291–300. [Google Scholar] [CrossRef]
- Karteris, M.; Slini, T.; Papadopoulos, A.M. Urban solar energy potential in Greece: A statistical calculation model of suitable built roof areas for photovoltaics. Energy Build. 2013, 62, 459–468. [Google Scholar] [CrossRef]
- Rahul; Gupta, A.; Bansal, A.; Roy, K. Solar Energy Prediction using Decision Tree Regressor. In Proceedings of the 5th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 6–8 May 2021; pp. 489–495. [Google Scholar]
- Kassim, N.M.; Santhiran, S.; Alkahtani, A.A.; Islam, M.A.; Tiong, S.K.; Mohd Yusof, M.Y.; Amin, N. An Adaptive Decision Tree Regression Modeling for the Output Power of Large-Scale Solar (LSS) Farm Forecasting. Sustainability 2023, 15, 13521. [Google Scholar] [CrossRef]
- Khalyasmaa, A.; Eronshenko, S.A.; Chakraverthy, T.P.; Gasi, V.G.; Bollu, S.K.Y.; Caire, R.; Atluri, S.K.R.; Karrolla, S. Prediction of Solar Power Generation Based on Random Forest Regressor Model. In Proceedings of the International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), Novosibirsk, Russia, 21–27 October 2019; pp. 780–785. [Google Scholar]
- Liu, J.; Cao, M.Y.; Bai, D.; Zhang, R. Solar radiation prediction based on random forest of feature-extraction. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Taoyuan, Taiwan, 2–6 November 2018; p. 658012006. [Google Scholar]
- Reddy, K.S.; Ranjan, M. Solar resource estimation using artificial neural networks and comparison with other correlation models. Energy Convers. Manag. 2003, 44, 2519–2530. [Google Scholar] [CrossRef]
- Zarzalejo, L.F.; Ramirez, L.; Polo, J. Artificial intelligence techniques applied to hourly global irradiance estimation from satellite-derived cloud index. Energy 2005, 30, 1685–1697. [Google Scholar] [CrossRef]
- Alam, S.; Kaushik, S.C.; Garg, S.N. Computation of beam solar radiation at normal incidence using artificial neural network. Renew. Energy 2006, 31, 1483–1491. [Google Scholar] [CrossRef]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 2858–2865. [Google Scholar]
- Zhou, H.; Liu, Q.; Yan, K.; Du, Y. Deep Learning Enhanced Solar Energy Forecasting with AI-Driven IoT. Hindawi Wirel. Commun. Mob. Comput. 2021, 1, 9249387. [Google Scholar] [CrossRef]
- Jamil, I.; Hong, L.; Iqbal, S.; Aurangzaib, M.; Jamil, R.; Hotb, H.; Alkuhayli, A.; AboRas, K.M. Predictive evaluation of solar energy variables for a large-scale solar power plant based on triple deep learning forecast models. Alex. Eng. J. 2023, 76, 51–73. [Google Scholar] [CrossRef]
- Raj, V.; Dotse, S.-Q.; Sathyajith, M.; Petra, M.I.; Yassin, H. Ensemble Machine Learning for Predicting the Power Output from Different Solar Photovoltaic Systems. Energies 2023, 16, 671. [Google Scholar] [CrossRef]
- Makasis, N.; Narsilio, G.; Bidarmaghz, A. A robust prediction model approach to energy geo-structure design. Comput. Geotech. 2018, 104, 140–151. [Google Scholar] [CrossRef]
- Uddin, M.D.; Nash, S.; Diganta, M.T.M.; Rahman, A.; Olbert, A.I. Robust machine learning algorithms for predicting coastal water quality index. J. Environ. Manag. 2022, 321, 115923. [Google Scholar] [CrossRef]
- Malagutti, N.; Dehghani, A.; Kennedy, R.A. Robust control design for automatic regulation of blood pressure. IET Control Theory Appl. 2013, 7, 387–396. [Google Scholar] [CrossRef]
- Köhler, J.; Soloperto, R.; Müller, M.A.; Allgöwer, F. A Computationally Efficient Robust Model Predictive Control Framework for Uncertain Nonlinear Systems. IEEE Trans. Autom. Control 2020, 66, 794–801. [Google Scholar] [CrossRef]
- Pin, G.; Raimondo, D.M.; Magni, L.; Parisini, T. Robust Model Predictive Control of Nonlinear Systems with Bounded and State-Dependent Uncertainties. IEEE Trans. Autom. Control 2009, 54, 1681–1687. [Google Scholar] [CrossRef]
- Filho, C.M.; Terra, M.H.; Wolf, D.F. Safe Optimization of Highway Traffic With Robust Model Predictive Control-Based Cooperative Adaptive Cruise Control. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3193–3203. [Google Scholar] [CrossRef]
- Terramanti, T.; Luspay, T.; Kulcsár, B.; Péni, T.; Varga, I. Robust Control for Urban Road Traffic Networks. IEEE Trans. Intell. Transp. Syst. 2014, 15, 385–398. [Google Scholar] [CrossRef]
- Liu, H.; Claudel, C.G.; Machemehi, R.; Perrine, K.A. A Robust Traffic Control Model Considering Uncertainties in Turning Ratios. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6539–6555. [Google Scholar] [CrossRef]
- Zhang, C.; Hua, L.; Ji, C.L.; Nazir, M.S.; Peng, T. An evolutionary robust solar radiation prediction model based on WT-CEEDAN and IASO-optimized outlier robust extreme learning machine. Appl. Energy 2022, 322, 119518. [Google Scholar] [CrossRef]
- Sharma, V.; Yang, D.; Walsh, W.; Reindl, T. Short term solar irradiance forecasting using a mixed wavelet neural network. Renew. Energy 2016, 90, 481–492. [Google Scholar] [CrossRef]
- Peng, S.; Chen, R.; Yu, B.; Xiang, M.; Lin, X.; Liu, E. Daily natural gas load forecasting based on the combination of long short term memory, local mean decomposition, and wavelet threshold denoising algorithm. J. Nat. Gas Sci. Eng. 2021, 95, 104175. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, M. Outlier-robust extreme learning machine for regression problems. Neurocomputing 2015, 151, 1519–1527. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Scholtthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Thorey, J.; Chaussin, C.; Mallet, V. Ensemble Forecast of Photovoltaic Power with Online CRPS Learning. Int. J. Forecast. 2018, 34, 762–773. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Lu, S.; Hamann, H.F.; Hodge, B.M.; Lehman, B. A Solar Time Based Analog Ensemble Method for Regional Solar Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 268–279. [Google Scholar] [CrossRef]
- Pan, C.; Tan, J. Day-Ahead Hourly Forecasting of Solar Generation Based on Cluster Analysis and Ensemble Model. IEEE Access 2019, 7, 112921–112930. [Google Scholar] [CrossRef]
- Hassibi, B.; Stork, D.G. Second order derivatives for network pruning: Optimal brain surgeon. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 29 November–2 December 1993; pp. 164–171. [Google Scholar]
- Scardapane, S.; Comminiello, D.; Hussain, A.; Uncini, A. Group sparse regularization for deep neural networks. Neurocomputing 2017, 241, 81–89. [Google Scholar] [CrossRef]
- Wen, W.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Learning structured sparsity in deep neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2074–2082. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Cananda, 7–12 December 2015; pp. 1135–1143. [Google Scholar]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning filters for efficient convnets. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Luo, J.; Wu, J.; Lin, W. ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 25 December 2017; pp. 5068–5076. [Google Scholar]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning convolutional neural networks for resource efficient transfer learning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Panchal, G.; Ganatra, A.; Kosta, Y.P.; Panchal, D. Behaviour Analysis of Multilayer Perceptrons with Multiple Hidden Neurons and Hidden Layers. Int. J. Comput. Theory Eng. 2011, 3, 1793–8201. [Google Scholar]
- Sun, C.; Ma, M.; Zhou, Z.; Tian, S.; Yan, R.; Chen, X. Deep transfer learning based on sparse auto-encoder for remaining useful life prediction on tool in manufacturing. IEEE Trans. Ind. Inform. 2019, 15, 2416–2425. [Google Scholar] [CrossRef]
- Sani, S.; Wiratunga, N.; Massie, S. Learning deep features for kNN-based human activity recognition. In Proceedings of the International Case-Based Reasoning Conference, Trondheim, Norway, 26–28 June 2017. [Google Scholar]
- Mohammed, Y.; Matsumoto, K.; Hoashi, K. Deep feature learning and selection for activity recognition. In Proceedings of the Annual ACM Symposium on Applied Computing, New York, NY, USA, 9 April 2018; pp. 930–939. [Google Scholar]
- Liu, M.; Zhou, M.; Zhang, T.; Xiong, X. Semi-supervised learning quantization algorithm with deep features for motor imagery EEG Recognition in smart healthcare application. Appl. Soft Comput. 2020, 89, 106071. [Google Scholar] [CrossRef]
- Chen, T.C.; Chang, T.Y.; Chow, H.Y.; Li, S.L.; Ou, C.Y. Using Convolutional Neural Networks to Build a Lightweight Flood Height Prediction Model with Grad-Cam for the Selection of Key Grid Cells in Radar Echo Maps. Water 2022, 14, 155. [Google Scholar] [CrossRef]
- Jafarpisheh, N.; Zafereni, E.J.; Teshnehlab, M.; Karimipour, H.; Parizi, R.P.; Srivastava, G. A Deep Neural Network Combined with Radial Basis Function for Abnormality Classification. Mobile Netw. Appl. 2021, 26, 2318–2328. [Google Scholar] [CrossRef]
- Shah, M.H.; Dang, X.Y. Low-complexity deep learning and RBFN architectures for modulation classification of space-time block-code (STBC)-MIMO system. Digit. Signal Process. 2020, 99, 102656. [Google Scholar] [CrossRef]
- Geng, Z.Q.; Shang, D.R.; Han, Y.M.; Zhong, Y.H. Early warning modeling and analysis based on a deep radial basis function neural network integrating an analytic hierarchy process: A case study for food safety. Food Control 2019, 96, 329–342. [Google Scholar] [CrossRef]
- Chen, Y.C.; Li, D.C. Selection of key features for PM2.5 prediction using a wavelet model and RBF-LSTM. Appl Intell. 2021, 51, 2534–2555. [Google Scholar] [CrossRef]
- Chiu, S.M.; Chen, Y.C.; Kuo, C.J.; Hung, L.C.; Hung, M.H.; Chen, C.C. Development of Lightweight RBFDRNN and Automated Framework for CNC Tool-Wear Prediction. IEEE Trans. Instrum. Meas. 2022, 71, 2506711. [Google Scholar] [CrossRef]
- Chen, Y.C.; Liu, S.C.; Chen, B.X.; Loh, C.H.; Ying, J.C. Ensembling-mRBF-LSTM Framework for Prediction of Abnormal Traffic Flows. In Proceedings of the International Conference on Pervasive Artificial Intelligence, Taipei, Taiwan, 3–5 December 2022; pp. 206–213. [Google Scholar]
- Chaibi, Y.; Rhafiki, T.E.; Simón-Allué, R.; Guedea, I.; Luaces, C.; Gajate, O.C.; Kousksou, T.; Zeraouli, Y. Physical models for the design of photovoltaic/thermal collector systems. Solar Energy 2021, 226, 134–146. [Google Scholar] [CrossRef]
- Dolara, A.; Leva, S.; Manzolini, G. Comparison of different physical models for PV power output prediction. Solar Energy 2015, 119, 83–99. [Google Scholar] [CrossRef]
- Mayer, M.J.; Gróf, G. Extensive comparison of physical models for photovoltaic power forecasting. Appl. Energy 2021, 283, 116239. [Google Scholar] [CrossRef]
- Kreider, J.; Kreith, F. Solar Energy Handbook; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of solar energy modeling techniques. Renew. Sustain. Energy Rev. 2012, 16, 2864–2869. [Google Scholar] [CrossRef]
- Sopian, K.; Othman, M.Y.H. Estimates of monthly average daily global solar radiation in Malaysia. Renew. Energy 1992, 2, 319–325. [Google Scholar] [CrossRef]
- Chineke, T.C. Equations for estimating global solar radiation in data sparse regions. Renew. Energy 2008, 33, 827–831. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Mahmoud, M.; Sopian, K. Modeling of Daily Solar Energy on a Horizontal Surface for Five Main Sites in Malaysia. Int. J. Green Energy 2011, 8, 795–819. [Google Scholar] [CrossRef]
- Iheanetu, K.J. Solar Photovoltaic Power Forecasting: A Review. Sustainability 2022, 14, 17005. [Google Scholar] [CrossRef]
- Mansoury, I.; Bourakadi, D.E.; Yahyaouy, A.; Boumhidi, J. A novel decision-making approach based on a decision tree for micro-grid energy management. Indones. J. Electr. Eng. Comput. Sci. 2023, 30, 1150–1158. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S.A.; Shaari, S.; Salhi, H.; Arab, A.H. Methodology for predicting sequences of mean monthly clearness index and daily solar radiation data in remote areas: Application for sizing a stand-alone PV system. Renew. Energy 2008, 33, 1570–1590. [Google Scholar] [CrossRef]
- Rajendran, S.S.P.; Gebremedhin, A. Deep learning-based solar power forecasting model to analyze a multi-energy microgrid energy system. Front. Energy Res. 2024, 12, 1363895. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Merabet, A. Solar Power Forecasting Using Deep Learning Techniques. IEEE Access 2022, 10, 31692–31698. [Google Scholar] [CrossRef]
- Chang, R.; Bai, L.; Hsu, C.-H. Solar power generation prediction based on deep learning. Sustain. Energy Technol. Assess. 2021, 47, 101354. [Google Scholar] [CrossRef]
- Sharadga, H.; Hajimirza, S.; Balog, R.S. Times series forecasting of solar power generation for large-scale photovoltaic plants. Renew. Energy 2020, 150, 797–807. [Google Scholar] [CrossRef]
- Alkandari, M.; Ahmad, I. Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Appl. Comput. Inform. 2020, 231–250. Available online: https://www.emerald.com/insight/content/doi/10.1016/j.aci.2019.11.002/full/html (accessed on 11 November 2024). [CrossRef]
- Plessis, A.A.D.; Stauss, J.M.; Rix, A.J. Short-term solar power forecasting: Investigating the ability of deep learning models to capture low-level utility-scale Photovoltaic system behavior. Appl. Energy 2021, 285, 116395. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Larson, D.P.; Coimbra, C.F.M. A comprehensive dataset for the accelerated development and benchmarking of solar forecasting methods. J. Renew. Sustain. Energy 2019, 11, 036102. [Google Scholar] [CrossRef]
- Sun, Y.C.; Venugopal, V.; Brandt, A.R. Short-term solar power forecast with deep learning: Exploring optimal input and output configuration. Solar Energy 2019, 188, 730–741. [Google Scholar] [CrossRef]
- Paletta, Q.; Arbod, G.; Lasenby, J. Benchmarking of deep learning irradiance forecasting models from sky images—An in-depth analysis. Solar Energy 2021, 224, 855–867. [Google Scholar] [CrossRef]
- Nie, Y.; Paletta, Q.; Scott, A.; Pamares, L.M.; Arbod, G.; Sgouridis, S.; Lasenby, J.; Brandt, A. Sky image-based solar forecasting using deep learning with heterogeneous multi-location data: Dataset fusion versus transfer learning. Appl. Energy 2024, 369, 123467. [Google Scholar] [CrossRef]
- Maciel, J.N.; Ledesma, J.J.G.; Ando Junior, O.H. Hybrid prediction method of solar irradiance applied to short-term photovoltaic energy generation. Renew. Sustain. Energy Rev. 2024, 192, 114185. [Google Scholar] [CrossRef]
- Colak, T.; Qahwaji, R. Automatic Sunspot Classification for Real-Time Forecasting of Solar Activities. In Proceedings of the 3rd International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 14–16 June 2007; pp. 733–738. [Google Scholar]
- Monjoly, S.; Andr’e, M.; Calif, R.; Soubdhan, T. Hourly forecasting of global solar radiation based on multiscale decomposition methods: A hybrid approach. Energy 2017, 119, 288–298. [Google Scholar] [CrossRef]
- Liu, D.; Sun, K. Random forest solar power forecast based on classification optimization. Energy 2019, 187, 115940. [Google Scholar] [CrossRef]
- Subramanian, E.; Karthik, M.M.; Krishna, G.P.; Prasath, D.V.; Kumar, V.S. Solar power prediction using Machine learning. arXiv 2023, arXiv:2303.07875. [Google Scholar]
- Roy, S.; Panda, P.; Srinivasan, G.; Raghunathan, A. Pruning Filters while Training for Efficiently Optimizing Deep Learning Networks. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Wu, D.; Lv, S.; Jiang, M.; Song, H. Using channel pruning-based YOLO v4 deep learning algorithm for the real-time and accurate detection of apple flowers in natural environments. Comput. Electron. Agric. 2020, 178, 105742. [Google Scholar] [CrossRef]
- Chiu, S.-M.; Liou, Y.-S.; Chen, Y.-C.; Lee, Q.; Shang, R.-K.; Chang, T.-Y. Identifying key grid cells for crowd flow predictions based on CNN-based models with the Grad-CAM kit. Appl. Intell. 2022, 53, 13323–13351. [Google Scholar] [CrossRef]
- Soltani, A.; Meinke, H.; Voil, P.D. Assessing linear interpolation to generate daily radiation and temperature data for use in crop simulations. Eur. J. Agron. 2024, 21, 133–148. [Google Scholar] [CrossRef]
- Gore, R.; Gawali, B.; Pachpatte, D. Weather Parameter Analysis Using Interpolation Methods. Artif. Intell. Appl. 2023, 1, 260–272. [Google Scholar] [CrossRef]
- Nagy, G.I.; Barta, G.; Kazi, S.; Borbély, G.; Simon, G. GEFCom2014: Probabilistic solar and wind power forecasting using a generalized additive tree ensemble approach. Int. J. Forecast. 2016, 32, 1087–1093. [Google Scholar] [CrossRef]
- Barta, G.; Nagy, G.B.G.; Kazi, S.; Henk, T. Gefcom 2014—Probabilistic electricity price forecasting. In Intelligent Decision Technologies. In Proceedings of the 7th KES International Conference on Intelligent Decision Technologies, Sorrento, Italy, 17–19 June 2015; pp. 67–76. [Google Scholar]
- Hong, T. Energy Forecasting. Available online: http://blog.drhongtao.com/2017/03/gefcom2014-load-forecasting-data.html (accessed on 11 November 2024).
- Chiu, S.M. The Source Code of RBF-DRNN. Available online: https://github.com/osamchiu/rbf_drnn (accessed on 11 November 2024).




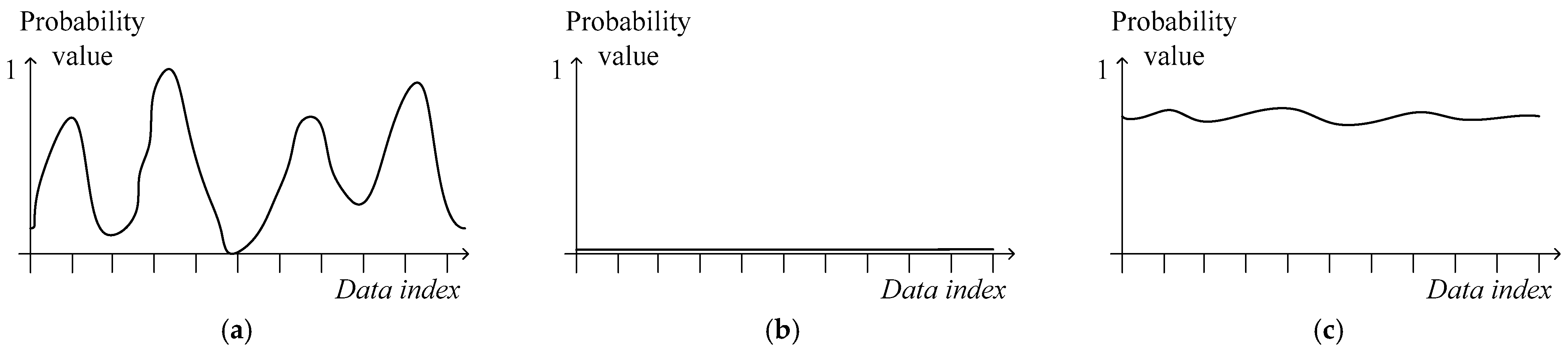

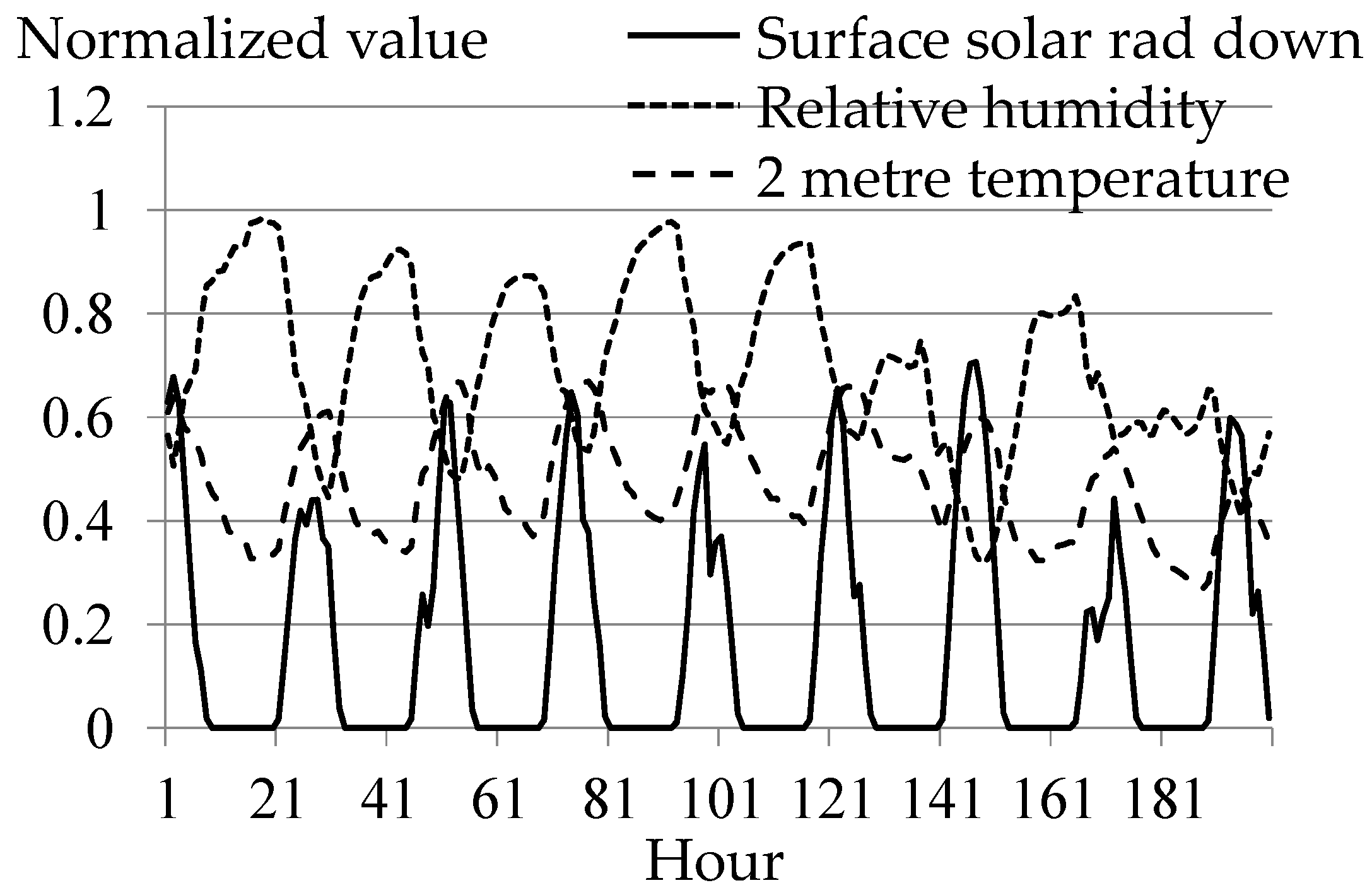

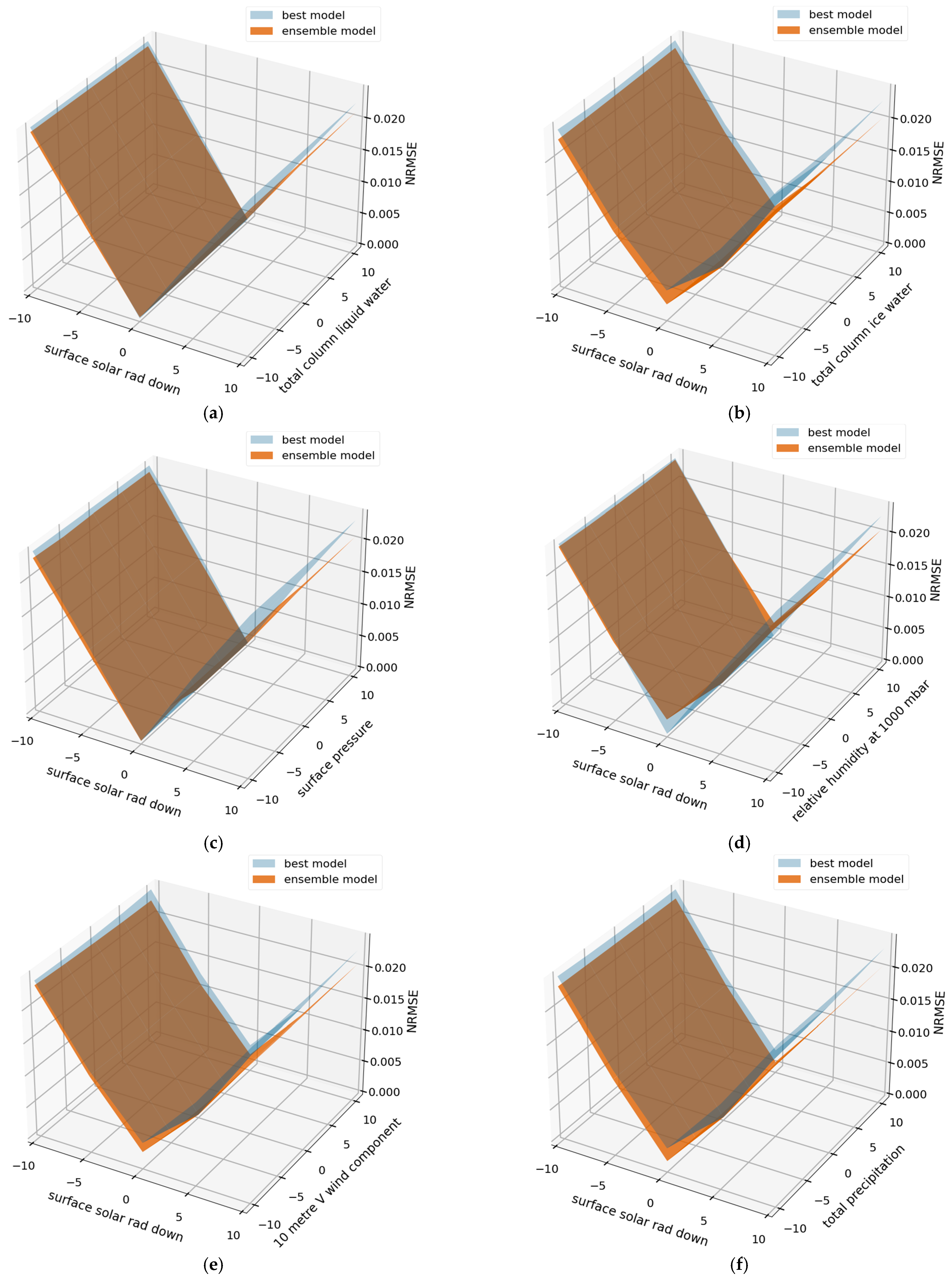
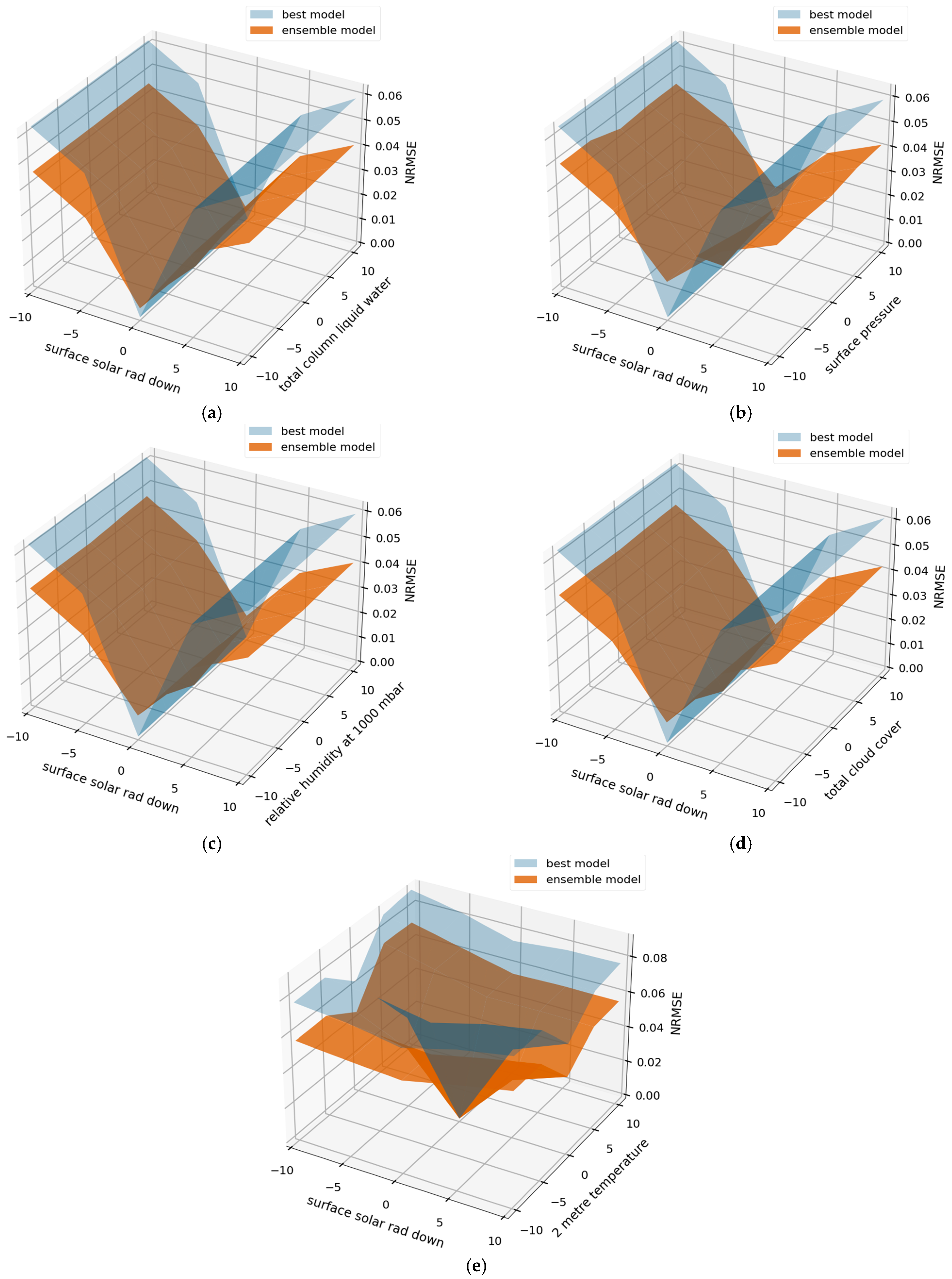
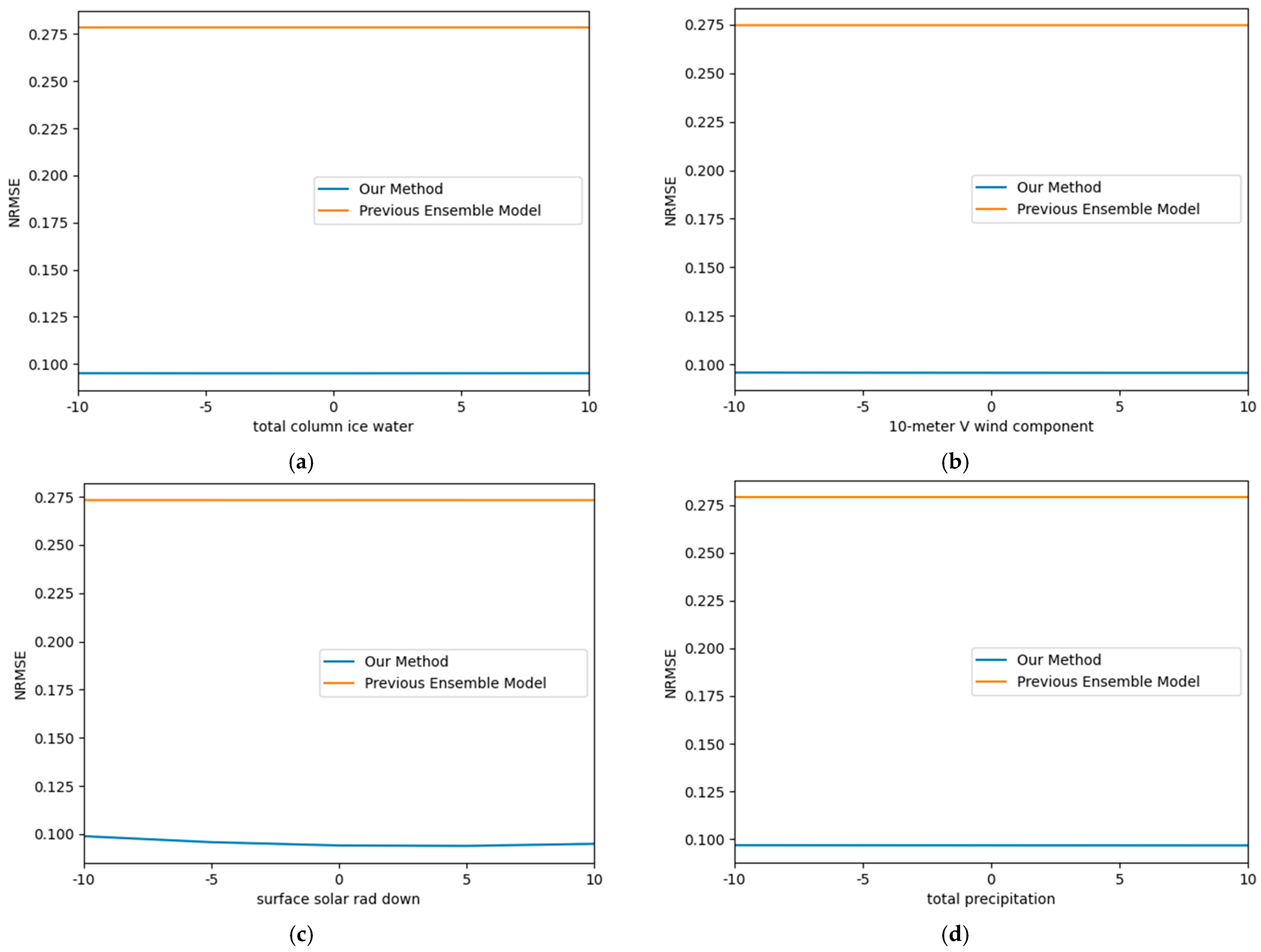
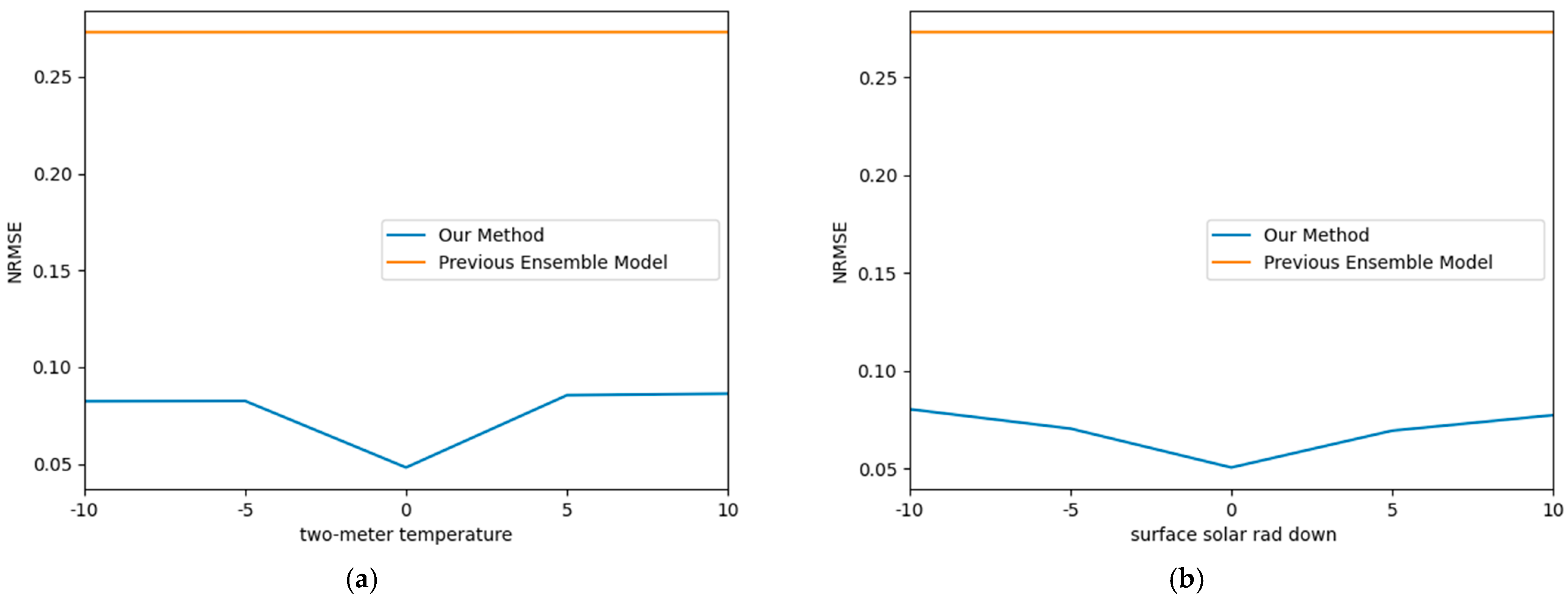
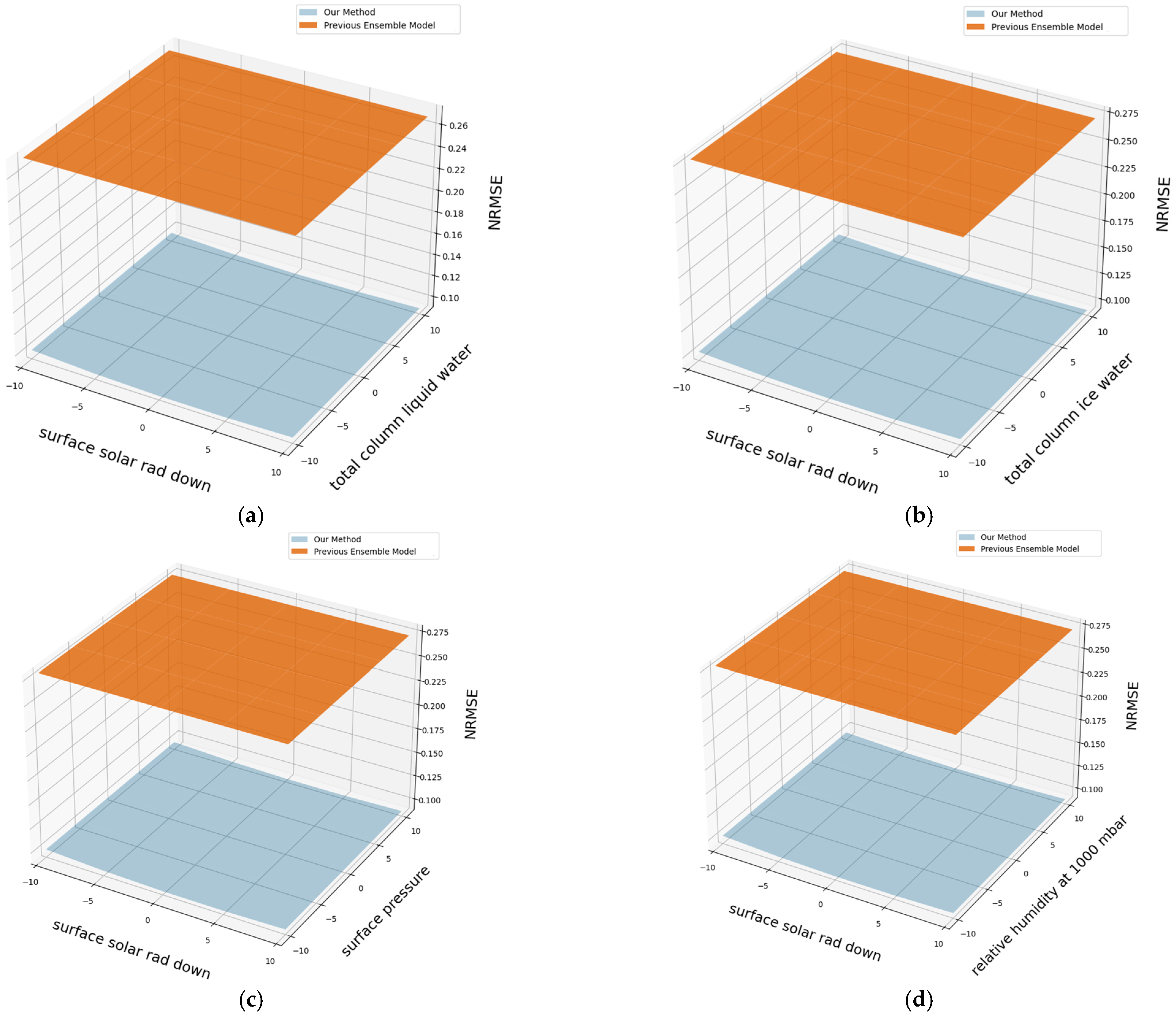
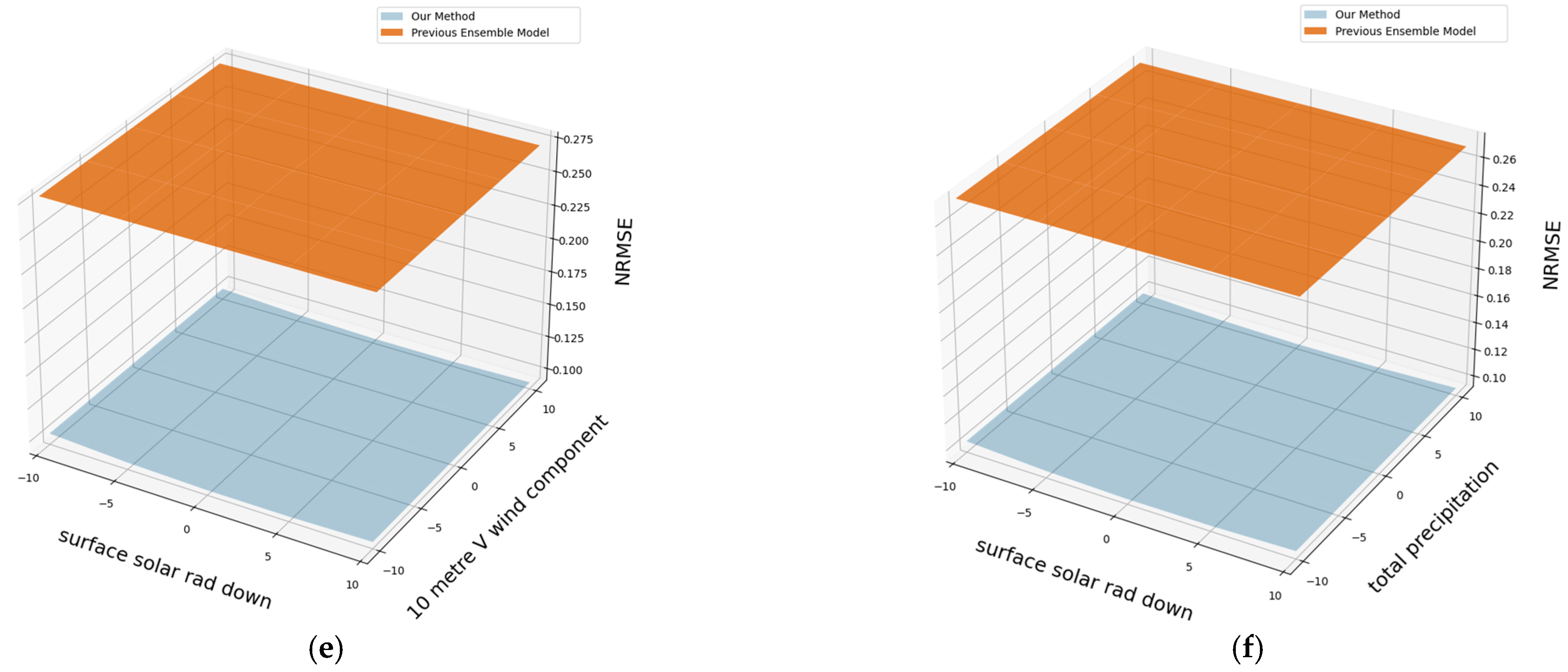
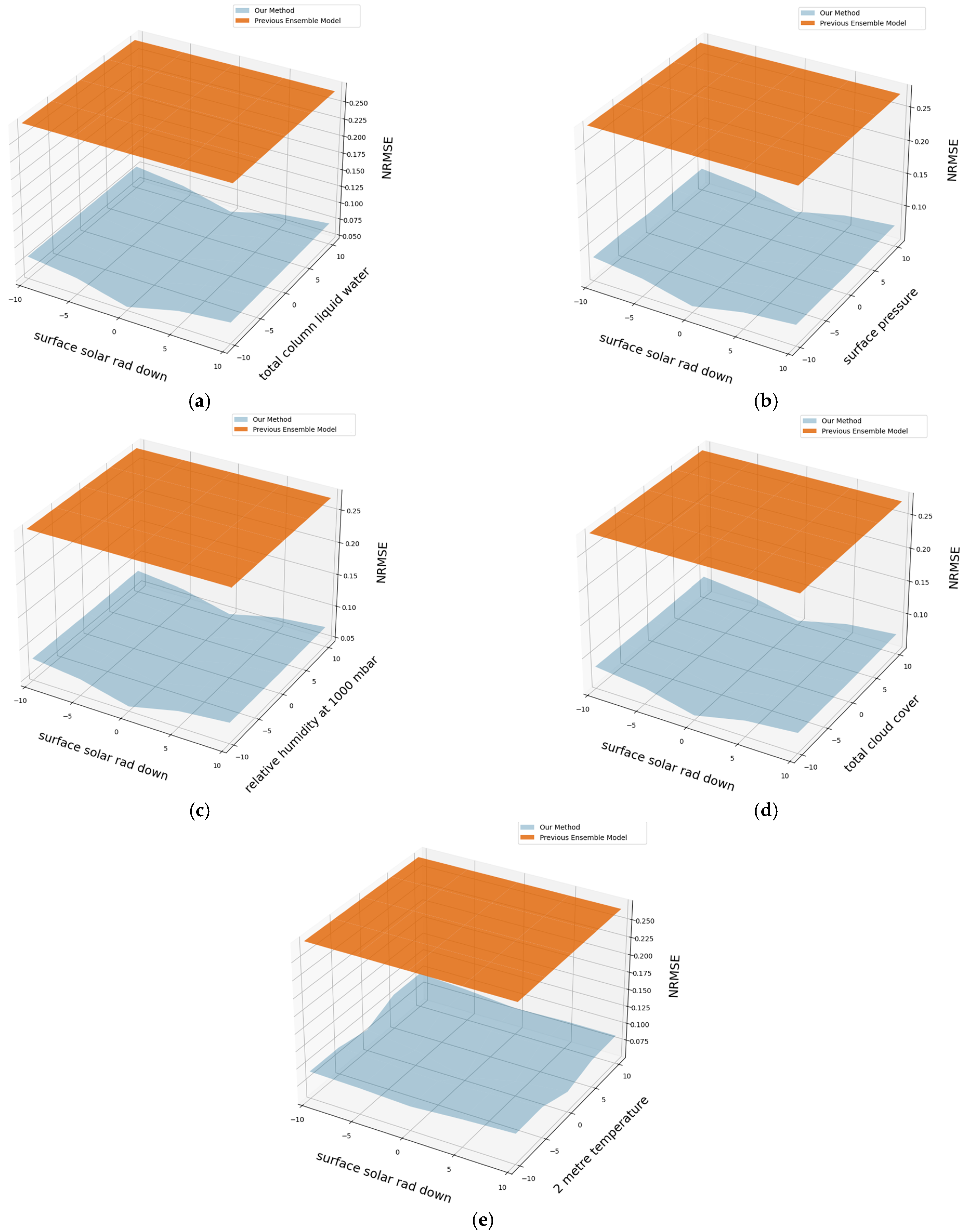
| Type | Name of Factors | Type | Name of Factors |
|---|---|---|---|
| Weather data | Total column liquid water | Weather data | Surface thermal rad down |
| Total column ice water | Top net solar rad | ||
| Surface pressure | Total precipitation | ||
| Relative humidity at 1000 mbar | Power generation | Zone ID | |
| Total cloud cover | Season | ||
| 10 m U wind component | Hour | ||
| 10 m V wind component | Month | ||
| 2 m temperature | Output | Power output | |
| Surface solar rad down |
| Random Forest | DNN | NC-RBF-DNN | |
|---|---|---|---|
| nRMSE | 0.08764 | 0.07935 | 0.07874 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loh, C.-H.; Chen, Y.-C.; Su, C.-T.; Su, H.-Y. Establishing Lightweight and Robust Prediction Models for Solar Power Forecasting Using Numerical–Categorical Radial Basis Function Deep Neural Networks. Appl. Sci. 2024, 14, 10625. https://doi.org/10.3390/app142210625
Loh C-H, Chen Y-C, Su C-T, Su H-Y. Establishing Lightweight and Robust Prediction Models for Solar Power Forecasting Using Numerical–Categorical Radial Basis Function Deep Neural Networks. Applied Sciences. 2024; 14(22):10625. https://doi.org/10.3390/app142210625
Chicago/Turabian StyleLoh, Chee-Hoe, Yi-Chung Chen, Chwen-Tzeng Su, and Heng-Yi Su. 2024. "Establishing Lightweight and Robust Prediction Models for Solar Power Forecasting Using Numerical–Categorical Radial Basis Function Deep Neural Networks" Applied Sciences 14, no. 22: 10625. https://doi.org/10.3390/app142210625
APA StyleLoh, C.-H., Chen, Y.-C., Su, C.-T., & Su, H.-Y. (2024). Establishing Lightweight and Robust Prediction Models for Solar Power Forecasting Using Numerical–Categorical Radial Basis Function Deep Neural Networks. Applied Sciences, 14(22), 10625. https://doi.org/10.3390/app142210625







