Study on the Influence Characteristics of Excavation Face Instability of New Tunnels Orthogonally Crossing Existing Tunnels
Abstract
1. Introduction
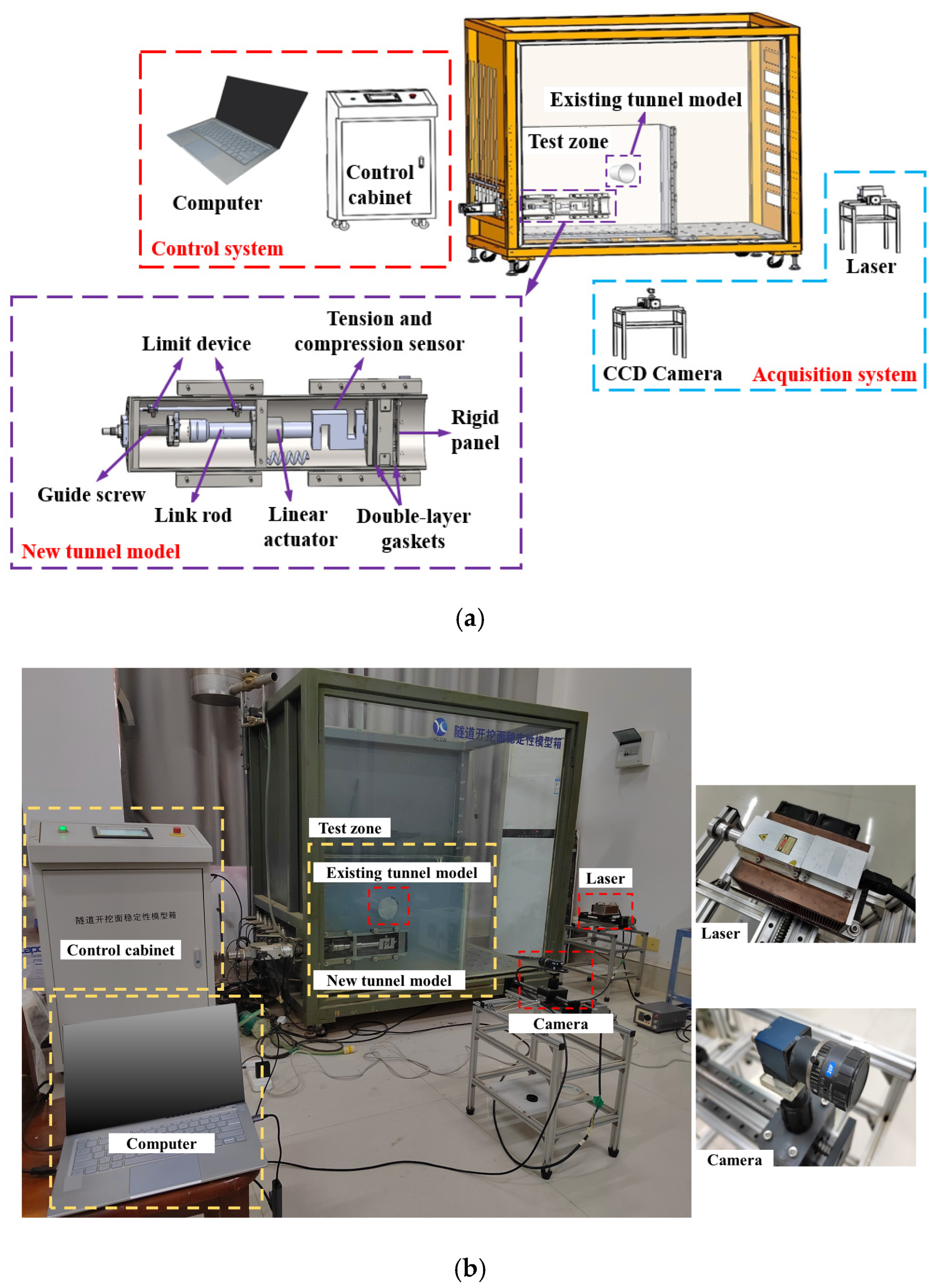
2. Model Test
2.1. Model Test Equipment
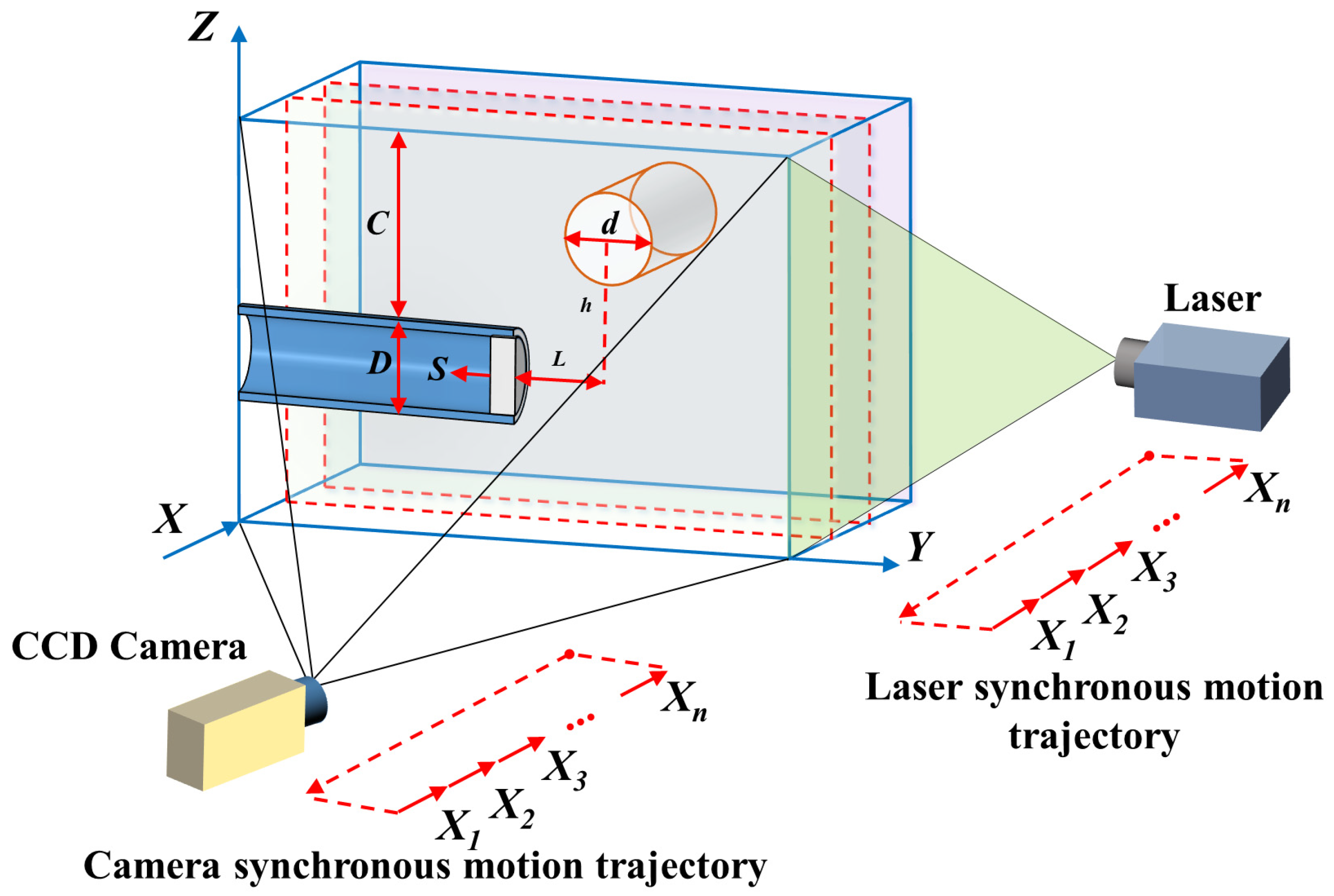
2.2. Test Schemes
2.3. Test Preparation
2.4. Test Procedure
2.5. Test Results
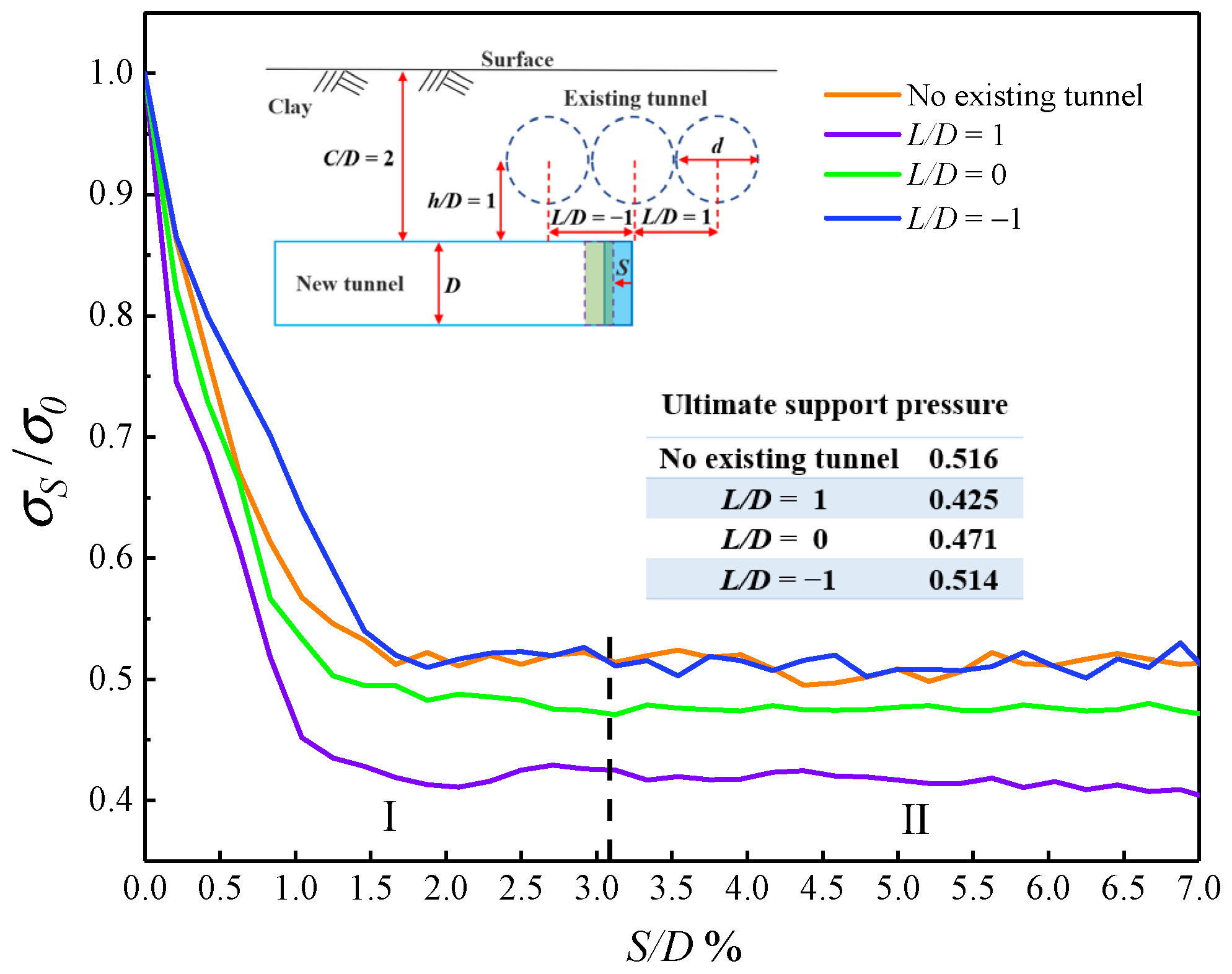
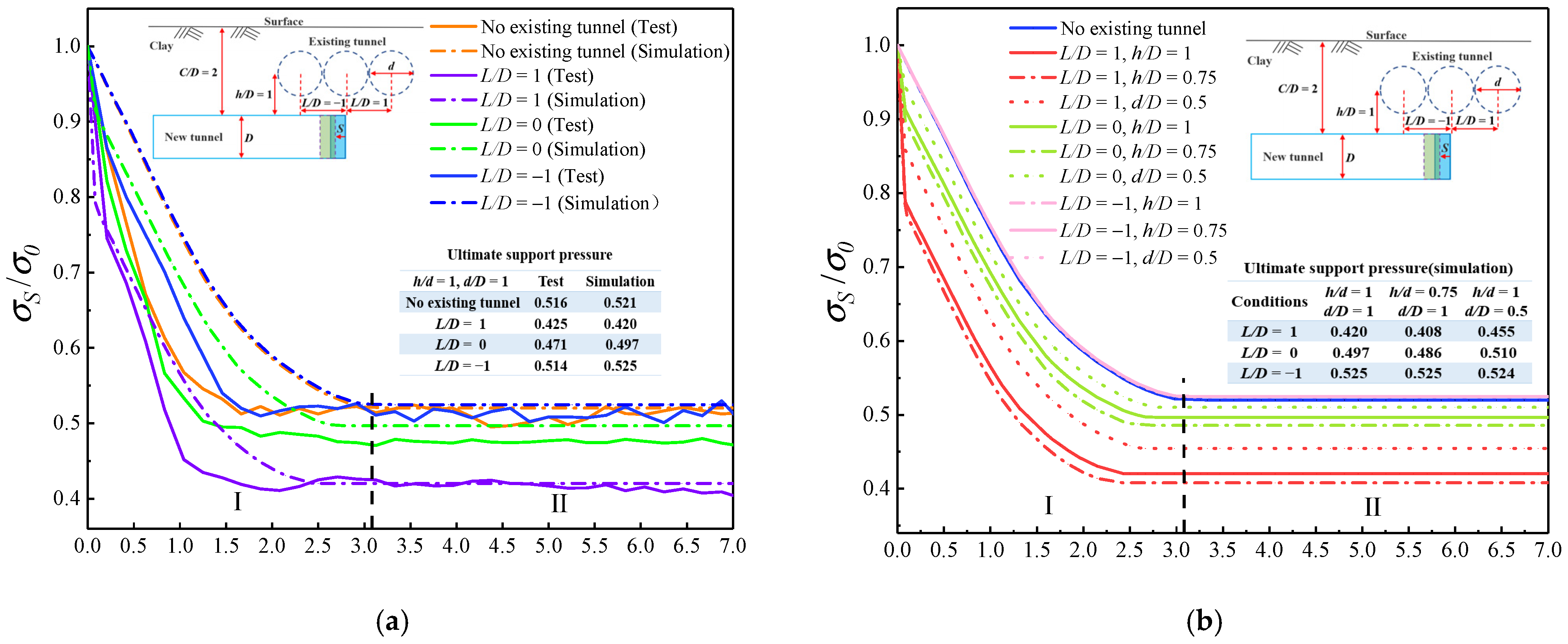
2.5.1. Support Pressure Ratio
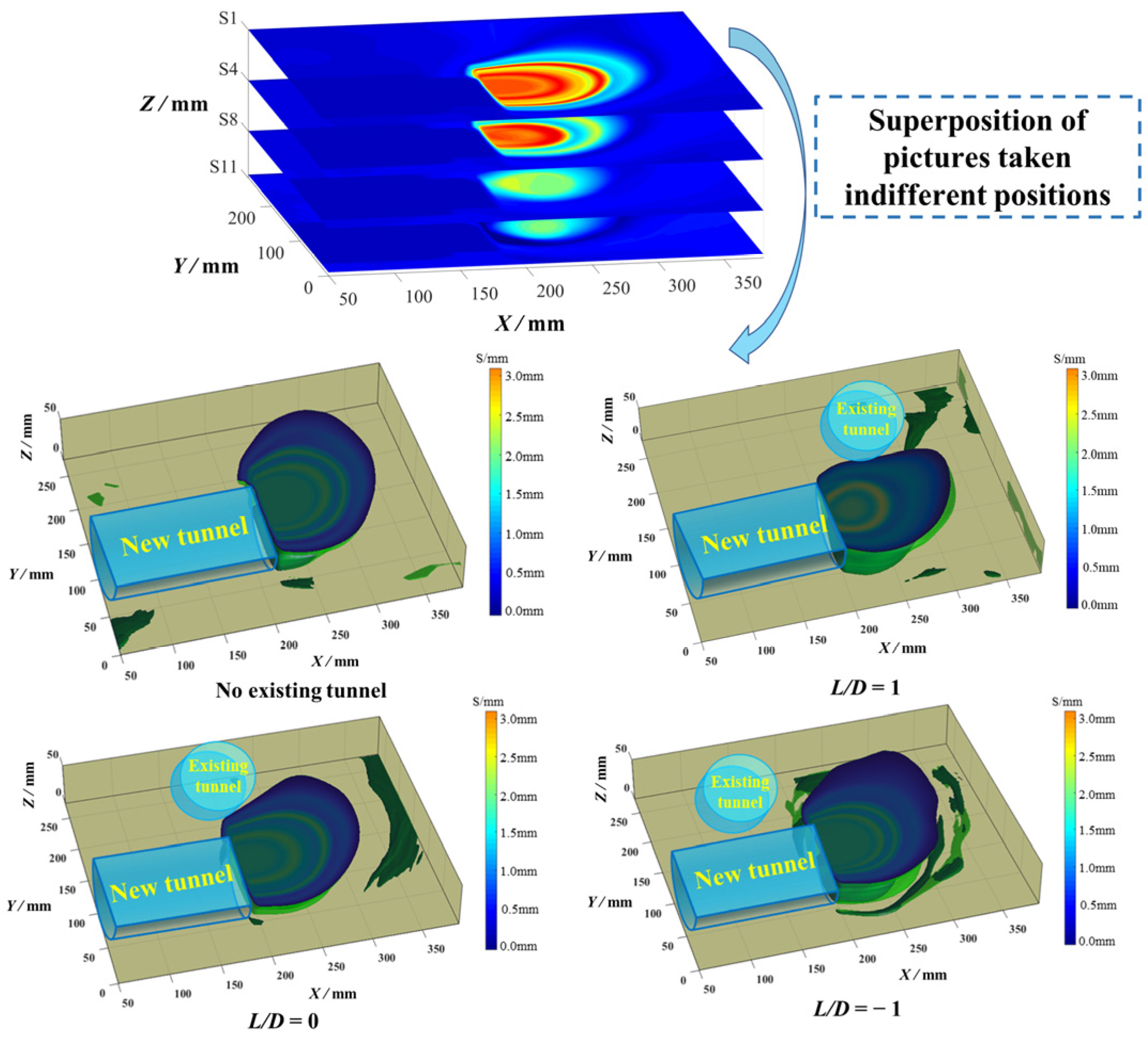
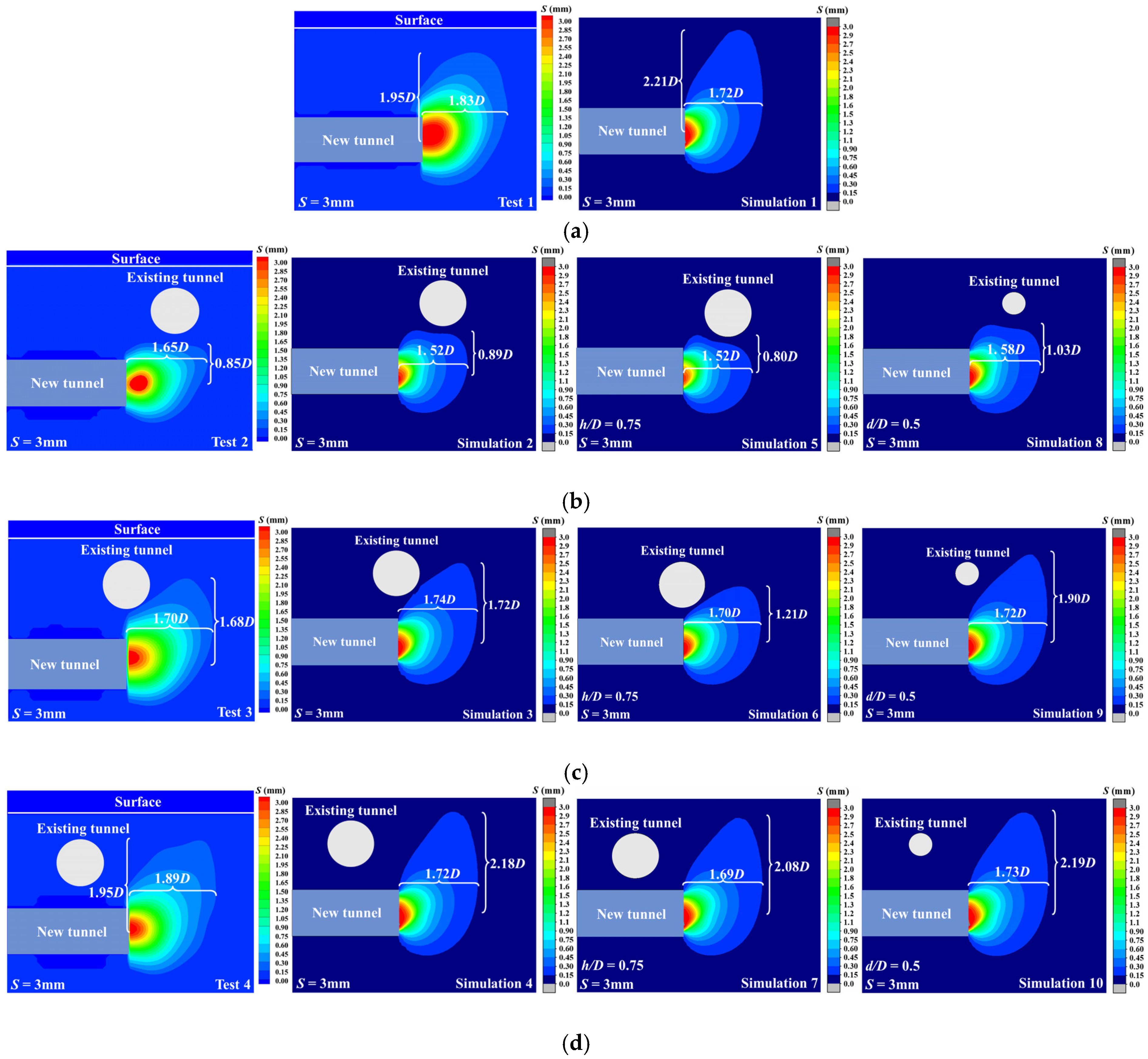
2.5.2. Soil Deformation Patterns
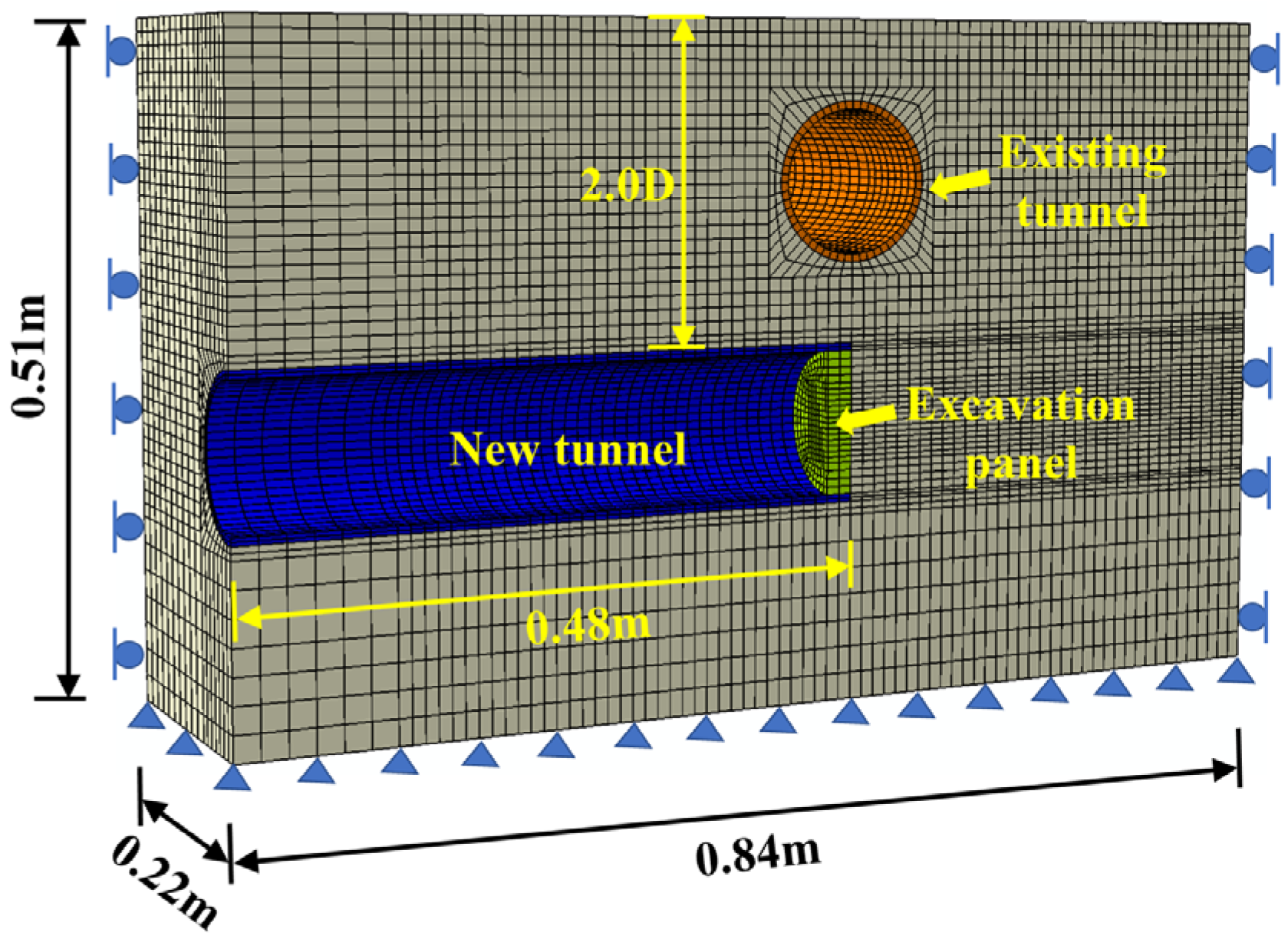
3. Finite Element Simulation
3.1. Finite Element Modeling
3.2. Finite Element Simulation Schemes
3.3. Finite Element Simulation Results
3.3.1. Comparison of Experimental Results with Finite Element Simulation Results
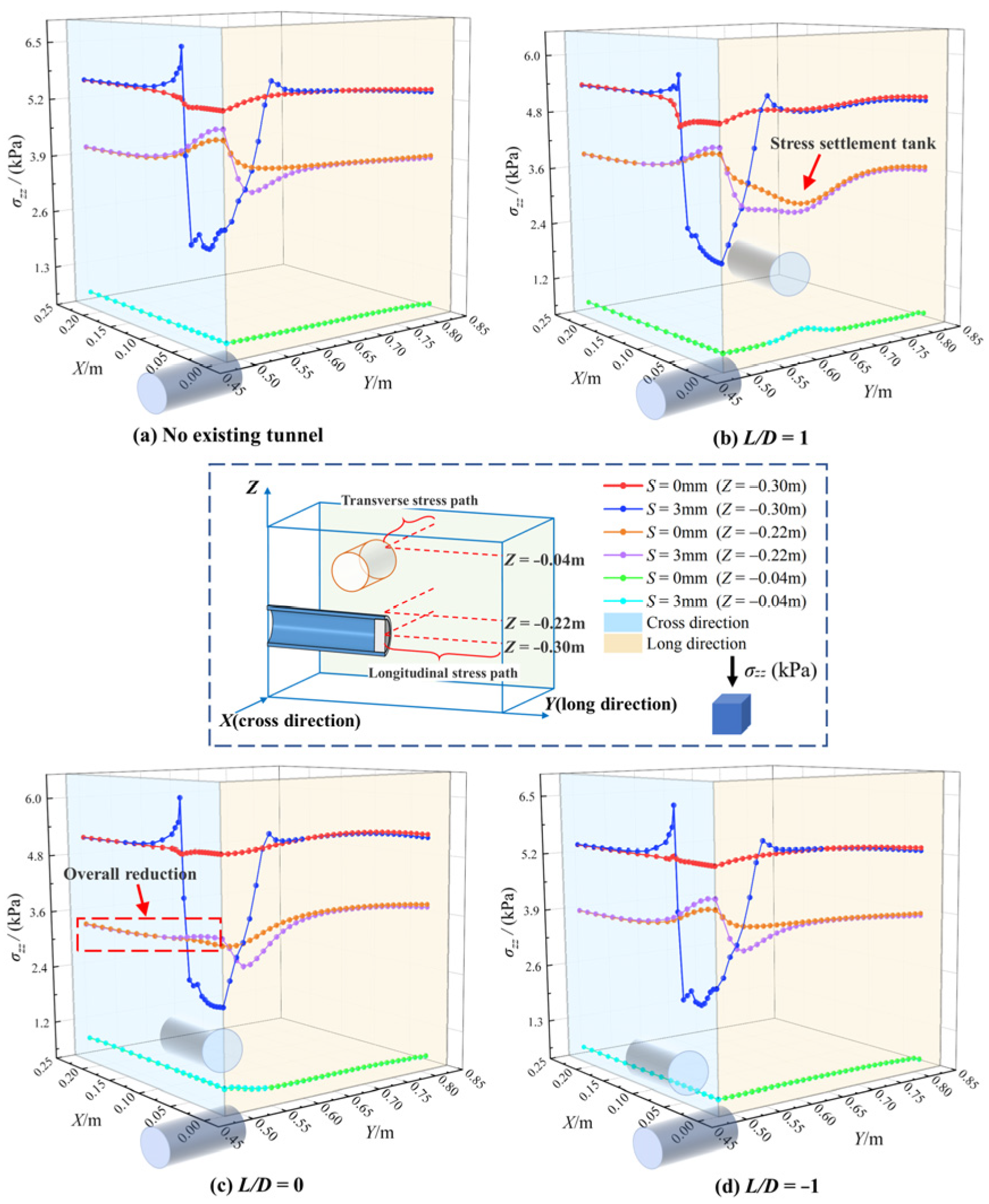
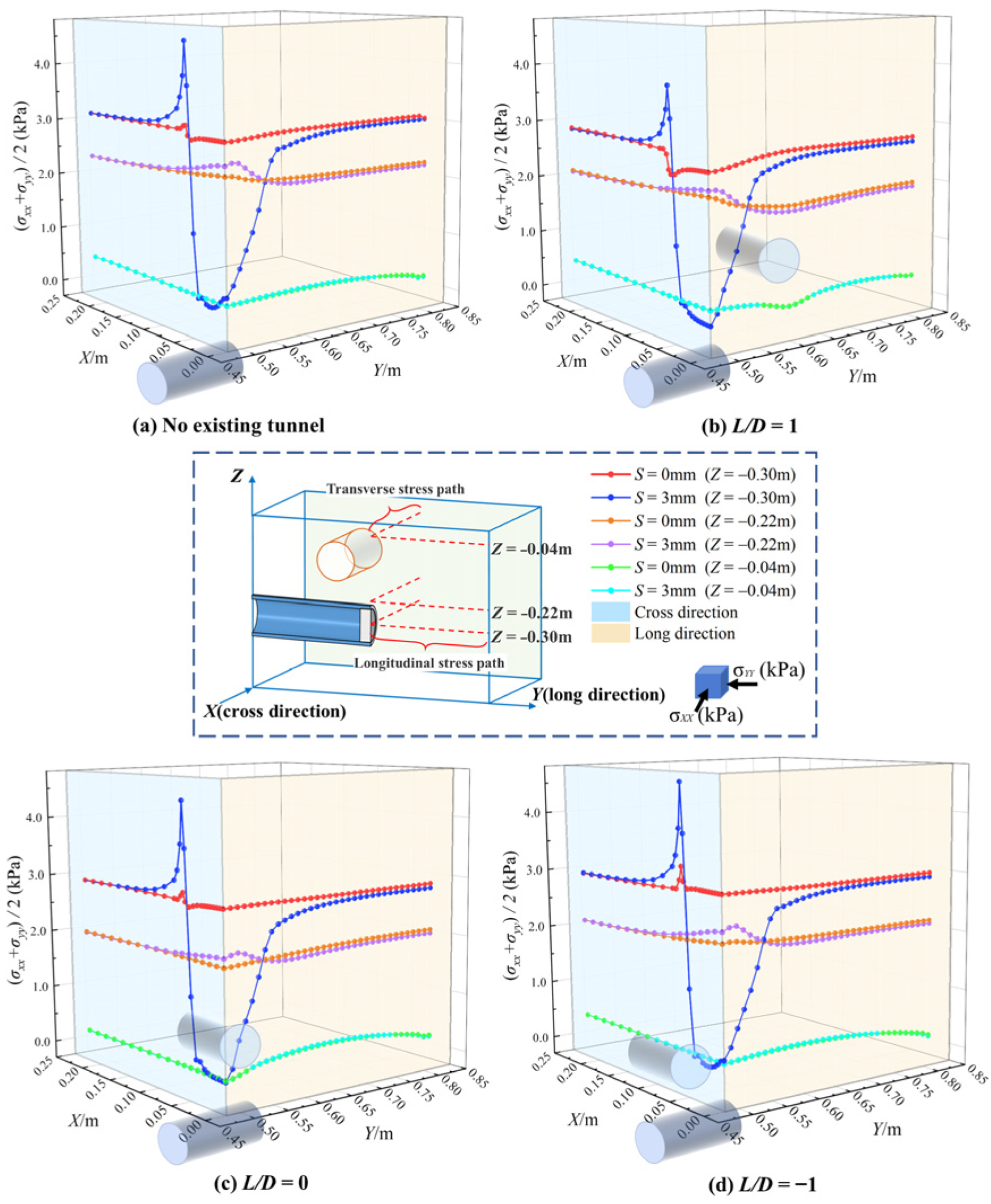
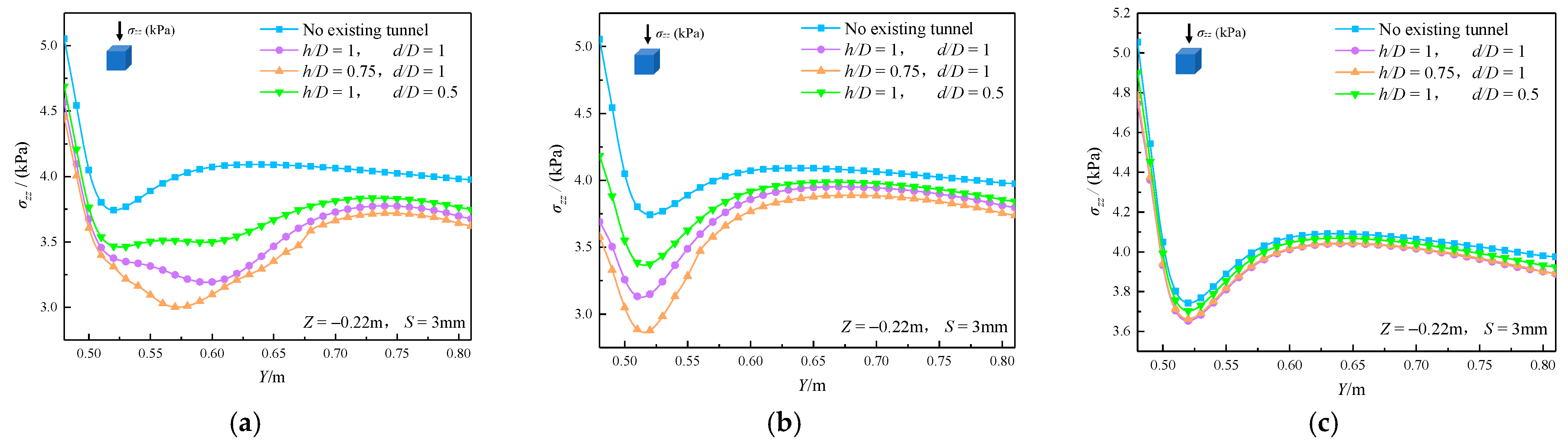
3.3.2. Changes in Soil Stresses
3.3.3. Deformation Trend of Existing Tunnel
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guan, L.; Wang, P.; Ding, H.; Qin, J.; Xu, C.; Feng, G. Analysis of Settlement of an Existing Tunnel Subjected to Undercrossing Tunneling Based on the Modified Vlasov Model. Int. J. Geomech. 2024, 24, 04023300. [Google Scholar] [CrossRef]
- Ou, X.; Liu, Y.; Li, C.; Zhou, X.; Chen, Q.; Zhou, Y.; Zhang, Q. Analysis of the Interaction Effects of Shield Structure Oblique Passing under an Existing Tunnel. Appl. Sci. 2022, 12, 5569. [Google Scholar] [CrossRef]
- Liu, X.; Fang, Q.; Jiang, A. Deformation analysis of existing tunnels with shearing and bending stiffness reduction at movement joints. Tunn. Undergr. Space Technol. 2022, 123, 104408. [Google Scholar] [CrossRef]
- Zhang, D.; Huang, Z.; Li, Z.; Zong, X.; Zhang, D. Analytical solution for the response of an existing tunnel to a new tunnel excavation underneath. Comput. Geotech. 2019, 108, 197–211. [Google Scholar] [CrossRef]
- Fang, Q.; Liu, X.; Zeng, K.; Zhang, X.; Zhou, M.; Du, J. Centrifuge modelling of tunnelling below existing twin tunnels with different types of support. Undergr. Space 2022, 7, 1125–1138. [Google Scholar] [CrossRef]
- Jin, D.; Yuan, D.; Liu, S.; Li, X.; Luo, W. Performance of Existing Subway Tunnels Undercrossed by Four Close-ly Spaced Shield Tunnels. J. Perform. Constr. Facil. 2019, 33, 04018099. [Google Scholar] [CrossRef]
- Jiang, B.; Chen, L.; Yang, J.S.; Wang, S.; Ng, C.W.W. Effects of twin-tunnel excavation on an existing horse-shoe-shaped tunnel considering the influence of a settlement joint. Can. Geotech. J. 2017, 54, 1346–1355. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, L.; Yan, C.; Yan, B.; Wei, P.; Feng, J. Study on Construction Influence of Shield Tunnel of Urban Rail Transit on Large-Section Mining Tunnel. Adv. Civ. Eng. 2020, 2020, 1–20. [Google Scholar] [CrossRef]
- Boonyarak, T.; Ng, C.W.W. Three-dimensional influence zone of new tunnel excavation crossing underneath existing tunnel. JGS Spec. Publ. 2016, 2, 1513–1518. [Google Scholar] [CrossRef]
- Fu, J.; Zhao, N.; Qu, Y.; Yang, J.; Wang, S. Effects of twin tunnel undercrossing excavation on the operational high speed railway tunnel with ballastless track. Tunn. Undergr. Space Technol. 2022, 124, 104470. [Google Scholar] [CrossRef]
- Lai, H.; Zheng, H.; Chen, R.; Kang, Z.; Liu, Y. Settlement behaviors of existing tunnel caused by obliquely un-der-crossing shield tunneling in close proximity with small intersection angle. Tunn. Undergr. Space Technol. 2020, 97, 103258. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Zhou, H.; Sun, C.; Lin, D. Model Test on Approaching the Construction of Multi-Line Over-lapping Shield Tunnels for Up- and Down-Crossing. Processes 2022, 10, 500. [Google Scholar] [CrossRef]
- Yang, J.; Liu, C.; Chen, Q.; Xie, X. Performance of overlapped shield tunneling through an integrated physical model tests, numerical simulations and real-time field monitoring. Undergr. Space 2017, 2, 45–59. [Google Scholar] [CrossRef]
- Lin, Q.; Lu, D.; Lei, C.; Tian, Y.; Kong, F.; Du, X. Mechanical response of existing tunnels for shield un-der-crossing in cobble strata based on the model test. Tunn. Undergr. Space Technol. 2022, 125, 104505. [Google Scholar] [CrossRef]
- Li, P.; Du, S.; Ma, X.; Yin, Z.; Shen, S. Centrifuge investigation into the effect of new shield tunnelling on an existing underlying large-diameter tunnel. Tunn. Undergr. Space Technol. 2014, 42, 59–66. [Google Scholar] [CrossRef]
- Weng, X.; Yu, H.; Niu, H.; Hu, J.; Han, W.; Huang, X. Interactive effects of crossing tunnel construction on ex-isting tunnel: Three-dimensional centrifugal test and numerical analyses. Transp. Geotech. 2022, 35, 100789. [Google Scholar] [CrossRef]
- Iskander, M.G.; Lai, J.; Oswald, C.J.; Mannheimer, R.J. Development of a Transparent Material to Model the Geotechnical Properties of Soils. Geotech. Test. J. 1994, 17, 425–433. [Google Scholar] [CrossRef]
- Iskander, M.G.; Liu, J.; Sadek, S. Transparent Amorphous Silica to Model Clay. J. Geotech. Geoenviron. Eng. 2002, 128, 262–273. [Google Scholar] [CrossRef]
- Ezzein, F.M.; Bathurst, R.J. A Transparent Sand for Geotechnical Laboratory Modeling. Geotech. Test. J. 2011, 34, 590–601. [Google Scholar] [CrossRef]
- Guzman, I.L.; Iskander, M. Geotechnical Properties of Sucrose-Saturated Fused Quartz for Use in Physical Modeling. Geotech. Test. J. 2013, 36, 448–454. [Google Scholar] [CrossRef]
- Ni, Q.; Hird, C.C.; Guymer, I. Physical modelling of pile penetration in clay using transparent soil and particle image velocimetry. Géotechnique 2010, 60, 121–132. [Google Scholar] [CrossRef]
- Qi, C.; Zheng, J.; Zuo, D.; Chen, G. Measurement on soil deformation caused by expanded-base pile in trans-parent soil using particle image velocimetry (PIV). J. Mt. Sci. 2017, 14, 1655–1665. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Zhao, Z.; Ni, H.; Su, Z.; Li, Z. Experimental study of displacement field of layered soils sur-rounding laterally loaded pile based on transparent soil. J. Soils Sediments 2021, 21, 3072–3083. [Google Scholar] [CrossRef]
- Le, X.; Cui, X.; Zhang, M.; Xu, Z.; Dou, L. Behavior Investigation of Necking Pile with Caps Assisted with Transparent Soil Technology. Sustainability 2022, 14, 8681. [Google Scholar] [CrossRef]
- Wang, Z.; Li, C.; Ding, X. Application of transparent soil model tests to study the soil-rock interfacial sliding mechanism. J. Mt. Sci. 2019, 16, 935–943. [Google Scholar] [CrossRef]
- Ma, S.; Duan, Z.; Huang, Z.; Liu, Y.; Shao, Y. Study on the stability of shield tunnel face in clay and clay-gravel stratum through large-scale physical model tests with transparent soil. Tunn. Undergr. Space Technol. 2022, 119, 104199. [Google Scholar] [CrossRef]
- Duan, Z.; Yang, J.; Ma, S.; Huang, Z. Study on instability mechanism of tunnel face in clay-gravel strata under confined water conditions based on DEM-CFD coupling method. Comput. Geotech. 2023, 164, 105769. [Google Scholar] [CrossRef]
- Ma, S.; Wei, R.; Shao, Y.; Huan, Z.; Duan, Z. 3D visual model tests on stability of tunnel excavation surface based on transparent soil. Chin. J. Geotech. Eng. 2021, 43, 1798–1806. [Google Scholar]
- Kirsch, A. Experimental investigation of the face stability of shallow tunnels in sand. Acta Geotech. 2010, 5, 43–62. [Google Scholar] [CrossRef]
- Lü, X.; Zhou, Y.; Huang, M.; Zeng, S. Experimental study of the face stability of shield tunnel in sands under seepage condition. Tunn. Undergr. Space Technol. 2018, 74, 195–205. [Google Scholar] [CrossRef]
- Wallace, J.F.; Rutherford, C.J. Geotechnical Properties of LAPONITE RD®. Geotech. Test. J. 2015, 38, 20140211. [Google Scholar] [CrossRef]
- Chini, C.M.; Wallace, J.F.; Rutherford, C.J.; Peschel, J.M. Shearing Failure Visualization via Particle Tracking in Soft Clay Using a Transparent Soil. Geotech. Test. J. 2015, 38, 20140210. [Google Scholar] [CrossRef]
- Ye, T. Experimental Observation and Theoretical Analysis on the Bubbles’Shape Within Transparent Soft Soil; Zhejiang University: Zhejiang, China, 2018. [Google Scholar]
- Liu, Y.; Lei, H.; Ma, C.; Guan, B. Three-dimensional stability analysis of shied tunnel face adjacent to existing tun-nels. Chin. J. Geotech. Eng. 2023, 45, 1374–1383. [Google Scholar]
- Lei, H.; Liu, Y.; Hu, Y.; Jia, R.; Zhang, Y. Active Stability of the Shield Tunneling Face Crossing an Adjacent Existing Tunnel: Transparent Clay Model Test and DEM Simulation. Can. Geotech. J. 2023, 60, 864–884. [Google Scholar] [CrossRef]





| Schemes | Stratum | New Tunnel Depth (C/D) | Tunnel-to-Diameter Ratio (d/D) | Relative Vertical Distance (h/D) | Relative Horizontal Distance (L/D) |
|---|---|---|---|---|---|
| 1 | Clay | 2 | 1 | No existing tunnel | |
| 2 | Clay | 2 | 1 | 1 | 1 |
| 3 | Clay | 2 | 1 | 1 | 0 |
| 4 | Clay | 2 | 1 | 1 | −1 |
| Parameter | Value |
|---|---|
| Reported shipped water content, % | <10% |
| Refractive index | 1.5 |
| Specific gravity | 2.53 |
| Liquid limit, LL | 1150 |
| Plasticity index, PI | 910 |
| Surface area, nm2 | 1100 |
| Single crystal dimension, nm | 25 × 0.92 |
| Parameter | Value |
|---|---|
| Permeability coefficient, cm/s | 0.405~1.14 × 10−7 |
| Coefficient of consolidation, cm2/s | 3.555~13.520 × 10−6 |
| Porosity ratio | 12.244~22.417 |
| Cohesion, kPa | 0.555 |
| Angle of internal friction, ° | 11.034° |
| Material | γ (kN/m3) | E/MPa | v | c/kPa | φ/° |
|---|---|---|---|---|---|
| Clay | 19.8 | 0.063 | 0.3 | 0.555 | 11.034 |
| Excavation panel | 78.5 | 206,000 | 0.3 | — | — |
| Tunnel lining | 25 | 34,500 | 0.2 | — | — |
| Conditions | Stratum | Depth of Tunnel C/D | Existing Tunnel Diameter d/D | Vertical Spacing of Two Tunnels h/D | Horizontal Spacing of Double Tunnels L/D |
|---|---|---|---|---|---|
| 1 | Clay | 2 | 1 | No existing tunnel | |
| 2 | Clay | 2 | 1 | 1 | 1 |
| 3 | Clay | 2 | 1 | 1 | 0 |
| 4 | Clay | 2 | 1 | 1 | −1 |
| 5 | Clay | 2 | 1 | 0.75 | 1 |
| 6 | Clay | 2 | 1 | 0.75 | 0 |
| 7 | Clay | 2 | 1 | 0.75 | −1 |
| 8 | Clay | 2 | 0.5 | 1 | 1 |
| 9 | Clay | 2 | 0.5 | 1 | 0 |
| 10 | Clay | 2 | 0.5 | 1 | −1 |
| Working Condition | 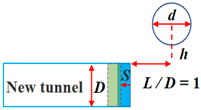 | 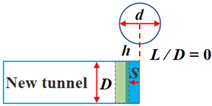 | 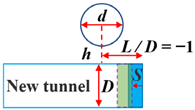 |
| Schemes 2~4 h/D = 1 d/D = 1 S = 3 mm |  | 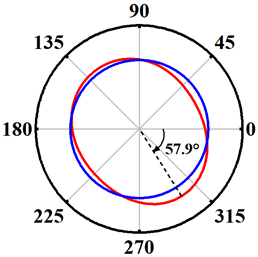 | 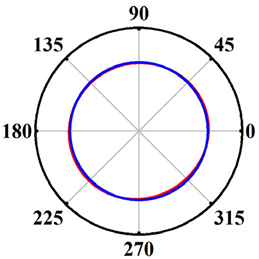 |
| Schemes 5~7 h/D = 0.75 d/D = 1 S = 3 mm | 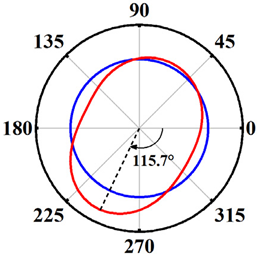 | 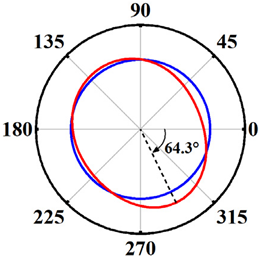 | 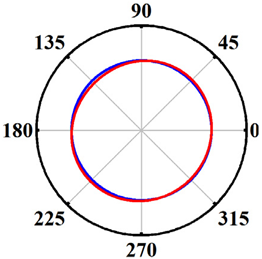 |
| Schemes 8~10 h/D = 1 d/D = 0.5 S = 3 mm | 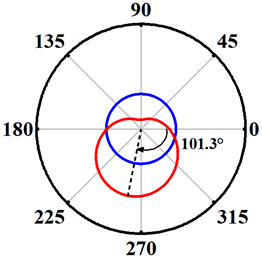 | 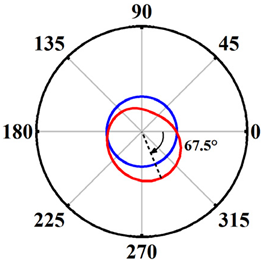 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, S.; Zhou, Z.; Duan, Z.; Huang, Z.; He, B.; An, P.; Li, J. Study on the Influence Characteristics of Excavation Face Instability of New Tunnels Orthogonally Crossing Existing Tunnels. Appl. Sci. 2024, 14, 10521. https://doi.org/10.3390/app142210521
Ma S, Zhou Z, Duan Z, Huang Z, He B, An P, Li J. Study on the Influence Characteristics of Excavation Face Instability of New Tunnels Orthogonally Crossing Existing Tunnels. Applied Sciences. 2024; 14(22):10521. https://doi.org/10.3390/app142210521
Chicago/Turabian StyleMa, Shaokun, Zhang Zhou, Zhibo Duan, Zhen Huang, Benfu He, Pengtao An, and Jinmei Li. 2024. "Study on the Influence Characteristics of Excavation Face Instability of New Tunnels Orthogonally Crossing Existing Tunnels" Applied Sciences 14, no. 22: 10521. https://doi.org/10.3390/app142210521
APA StyleMa, S., Zhou, Z., Duan, Z., Huang, Z., He, B., An, P., & Li, J. (2024). Study on the Influence Characteristics of Excavation Face Instability of New Tunnels Orthogonally Crossing Existing Tunnels. Applied Sciences, 14(22), 10521. https://doi.org/10.3390/app142210521






