Abstract
Carbon fiber-reinforced plastic (CFRP) composites are prone to damage during both manufacturing and operational phases, making the classification and identification of defects critical for maintaining structural integrity. This paper presents a novel dual-modal feature classification approach for the eddy current detection of CFRP defects, utilizing a Parallel Real–Imaginary/Swin Transformer (PRI-SWT) model. Built using the Transformer architecture, the PRI-SWT model effectively integrates the real and imaginary components of sinusoidal voltage signals, demonstrating a significant performance improvement over traditional classification methods such as Support Vector Machine (SVM) and Vision Transformer (ViT). The proposed model achieved a classification accuracy exceeding 95%, highlighting its superior capability in terms of addressing the complexities of defect detection. Furthermore, the influence of key factors—including the real–imaginary fusion layer, the number of layers, the window shift size, and the model’s scale—on the classification performance of the PRI-SWT model was systematically evaluated.
1. Introduction
Carbon fiber-reinforced plastic (CFRP) composites are widely utilized in various fields due to their exceptional mechanical properties and chemical resistance [1,2]. Their structural components have gained increasing acceptance for use in aerospace [3,4,5], marine applications, wind energy [6], and sports equipment [7]. A high proportion of composite materials being used in an aircraft often indicates the advanced nature of their manufacturing processes. For instance, the Airbus A380, a milestone in aviation, employed a significant amount of carbon fiber composite materials in its fuselage, wing surfaces, vertical tail, and doors. This application of composites led to a total weight reduction of 10% to 40% and a reduction in design costs by 15% to 30%. Consequently, the A380 was recognized not only as the most spacious civil aircraft ever built but also as the most advanced, efficient, and cost-effective, setting a benchmark for 21st-century aviation [8].
Despite these advantages, CFRP composites were found to be prone to various degrees of damage and defect formation during both manufacturing and service, which posed serious threats to safety [9,10]. To address the critical issue of CFRP defect detection, numerous nondestructive testing (NDT) methods were developed. Common NDT techniques used for detecting CFRP defects included ultrasonic testing [11], infrared thermography, eddy current thermography, X-ray inspection, computed tomography (CT), and eddy current NDT [12]. Among these methods, eddy current nondestructive testing (ENDT) garnered significant attention due to its advantages, such as the absence of a need for coupling agents and the simplicity of the equipment. ENDT proved capable of detecting various forms of damage in CFRPs, including cracks, impact damage [13], delamination, and in-plane fiber ripples [14,15,16]. The accurate identification and classification of these defects were crucial for ensuring product safety, reliability, and economic efficiency.
Research on CFRP defect classification algorithms has attracted considerable scholarly interest. For example, Li et al. [17] proposed a defect classification method using Support Vector Machines (SVMs) based on the energy characteristics of CFRP ultrasonic inspection results, demonstrating its effectiveness through experimental validation. Anish et al. [18] conducted the ultrasonic detection of three types of CFRP defects—impact damage, foreign body inclusions, and porosity—and employed an artificial neural network (ANN) to classify these defects based on time domain ultrasonic echo signals, achieving a high classification accuracy that met project requirements. Similarly, Sebastian et al. [19] introduced various intelligent classification methods into the CFRP automated fiber layup process, enhancing detection and production efficiency. The authors noted that increasing the depth of the network could improve the applicability of visual classification methods.
Recent advances in hardware, particularly the iterative development of GPUs, have driven the rapid evolution of deep neural network algorithms, which require substantial computational power. Deep convolutional neural networks (DCNNs), Inception (GoogLeNet), Vision Transformer (ViT), and Swin Transformer models display outstanding performance in machine learning tasks such as natural language processing, image classification, object detection, and image segmentation [20,21]. The use of deep network models in image classification tasks is becoming increasingly prevalent. For instance, Liu et al. [22] utilized a dense convolutional neural network (DCNN) to classify infrared thermography detection results, identifying debonding, delamination, and cracks in CFRPs. Their experiments showed that DenseNet-121 outperformed other CNN architectures, such as AlexNet, VGG-16, and ResNet-50, achieving a classification accuracy of 98.48%, thus highlighting the potential of deep neural networks for use in CFRP defect classification. Lu et al. [23] employed a Swin Transformer-based U-Net structure for crack detection and classification tasks, demonstrating a superior performance compared to other algorithms when used on a customized dataset.
Additionally, the Transformer model has exhibited outstanding performance in terms of identifying and classifying defects in various contexts, including rail surfaces [24], insulators in transmission lines [25], and metal surfaces [26]. Alif et al. [27] compared the classification performance of CNNs and ViT, concluding that ViT methods hold great promise in terms of predictive maintenance and the safety of railroads. ViT image classification methods have also been successfully applied in medical disease detection [28], chemical pipeline inspections [29], crop disease detection [30], product manufacturing damage detection [31], and industrial printed circuit board (PCB) classification [32].
To the best of the authors’ knowledge, existing CFRP eddy current NDT defect classification methods predominantly rely on manual analysis and basic machine learning techniques. These approaches suffer from limitations such as subjectivity, high labor costs, and low resolution. Advanced computer vision algorithms, including Vision Transformers (ViTs) and Swin Transformer models, present promising solutions to these challenges. Compared to traditional image classification methods like Support Vector Machines (SVMs) and convolutional neural networks (CNNs), the ViT model offers superior accuracy and generalization for CFRP defect classification. This is attributed to its enhanced global sensing capabilities.
However, purely vision-based methods typically extract features from single images, focusing on aspects such as the magnitude and phase components of the CFRP eddy current system’s output voltage signals, as shown in Figure 1.
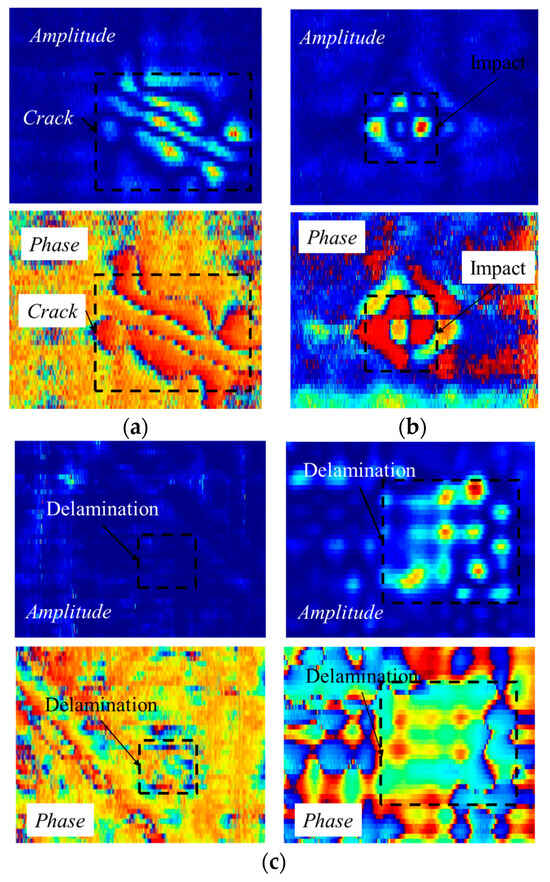
Figure 1.
The figure presents the eddy current testing (ECT) results for the detection of cracks, delamination, and low-velocity impact damage in carbon fiber-reinforced polymer (CFRP) materials. Results were obtained utilizing a nine-array ECT probe. The sinusoidal voltage signal generated by the output coil of the probe is processed through a lock-in amplifier, yielding two output signals. The subsequent data processing of these signals results in amplitude and phase images of the scanning process. (a) Crack defect; (b) impact defect; (c) delamination defect.
These methods often overlook the interdependence between the complex signal components. In CFRP defect eddy current testing, the output sinusoidal voltage signal from the detection coil is passed through a lock-in amplifier to the data acquisition card, where it is assessed. The data are then processed to generate magnitude and phase detection results of the complex voltage signal. These signals are distinct yet deeply interrelated; they both reflect the same defect type but contain different semantic information with different meanings. Extracting their complementary information is a pressing challenge that needs to be addressed in the field of CFRP defect detection.
Additionally, the dual-modal fusion strategy is widely employed in fields such as medicine, scientific research, and industrial applications. For instance, in healthcare, dual-modal fusion is utilized to combine imaging data, such as MRI or CT scans, with electronic health records (EHRs). This integration enhances diagnostic accuracy by correlating visual anomalies with patient history and clinical data, which facilitates more informed decision-making. Similarly, in robotics and human–computer interactions, dual-modal fusion combines visual and auditory information to improve object recognition and navigation. Robots can analyze camera feeds to identify objects while processing audio cues, enabling them to interact more effectively with their environment and with humans.
In the realm of sentiment analysis, dual-modal approaches that integrate text and audio have demonstrated improved accuracy in terms of understanding emotions. By considering both the content of spoken language and the vocal tone, these systems capture nuances in sentiment that single-modal analyses might miss. Additionally, dual-modal fusion plays a critical role in security and surveillance, where video data are often combined with biometric information, such as facial recognition, to enhance identification accuracy and improve real-time threat detection.
Therefore, this paper proposes a dual-modal fusion Parallel Real–Imaginary/Swin Transformer (PRI-SWT) network for use detecting CFRP defects from complex signal images using eddy current testing. The proposed model employs two parallel Swin Transformers (SWTs) to independently compute self-attention and generate feature maps for the real and imaginary components of the signal. A fusion layer—either a convolutional layer or a linear projection layer—is incorporated into the model to capture the relationships between the real and imaginary parts of the complex signal. By dividing the input image into several shiftable windows and calculating key metrics such as self-attention scores and relative positional encodings within each window, the PRI-SWT model significantly enhances both computational efficiency and classification accuracy. The model outperforms traditional algorithms, such as Support Vector Machine (SVM) and Vision Transformer (ViT), in CFRP defect classification, underscoring the substantial research effort invested in improving detection accuracy.
This study quantitatively evaluates the effects of different factors—including the type of fusion layer, the number of layers, and the window shift size—on the performance of the PRI-SWT model using multiple classification metrics. Notably, the real and imaginary components typically represent different types of modal information; thus, effectively fusing both modalities enables the model to more accurately distinguish CFRP defect features, resulting in a substantial improvement in detection performance. The results reveal that a single-layer linear fusion provides optimal performance, with all evaluation metrics achieving their highest values.
The structure of the paper is as follows: Section 2 outlines the concept and classifications of multi-modal fusion. Section 3 introduces the Support Vector Machine (SVM) model, the Vision Transformer (ViT) model, and the Parallel Real–Imaginary/Swin Transformer (PRI-SWT) model for classifying CFRP defect detection images. Section 4 evaluates the performance of these models in terms of classifying CFRP defects and analyzes the impact of various factors on the classification performance of the PRI-SWT model.
2. Introduction and Definition of Multi-Modal Fusion
Given the limitations of using single-modal approaches to handle complex data, multi-modal learning has emerged as a powerful alternative. Multi-modal learning refers to a machine learning paradigm in which data from multiple distinct modalities (e.g., images, signals, text) are utilized to improve a model’s performance by integrating complementary information from diverse sources. This approach is particularly effective in applications where different types of data provide unique but related insights, thereby enhancing our overall understanding of the task.
Figure 2 provides a general overview of the multi-modal learning process, illustrating how data from different modalities are integrated to improve a model’s performance. In multi-modal learning, three key but distinct concepts are often highlighted: multi-modal representation, cross-modal alignment, and multi-modal fusion. Each concept addresses a different aspect of how information from multiple sources can be processed, offering independent strategies for improving a model’s performance based on the specific nature of the data and the task at hand.
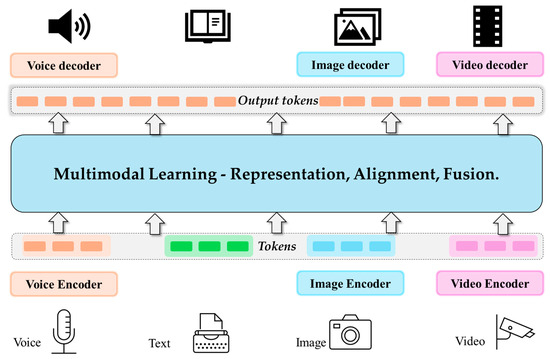
Figure 2.
The figure illustrates the basic framework of multi-modal learning, where data from various modalities, such as images, text, and speech, are encoded into tokens and input into the multi-modal learning model. The output tokens are then converted back into their respective natural data types.
2.1. Multi-Modal Representation
Multi-modal representation focuses on encoding data from different modalities into a unified form that can be jointly processed by a machine learning model. The challenge arises from the inherent differences between these modalities. For instance, images, signals, and textual data each possess distinct structures, distributions, and features. The goal of multi-modal representation is to capture the significant characteristics of each modality while ensuring that their combined representation is both coherent and meaningful in the context of the specific task.
In the eddy current testing (ECT) of CFRP composites, the real and imaginary components of the voltage signal represent different aspects of a material’s response to the electromagnetic field. The real component is typically more sensitive to surface defects, such as cracks, while the imaginary component is better suited for detecting deeper issues, such as delamination or low-velocity impact damage. A proper multi-modal representation should encode both components into a unified format that preserves their individual strengths while allowing the model to exploit the complementary nature of these signals.
2.2. Cross-Modal Alignment
Cross-modal alignment, in contrast, focuses on synchronizing or aligning data from different modalities to ensure that their relationships can be fully understood and utilized by the model. Unlike multi-modal representation, which emphasizes how data are encoded, cross-modal alignment ensures that different modalities are interpreted in a consistent and comparable manner. This is particularly crucial when modalities do not naturally correspond to each other in terms of time, space, or semantics. Figure 3 presents the general workflow of cross-modal alignment.
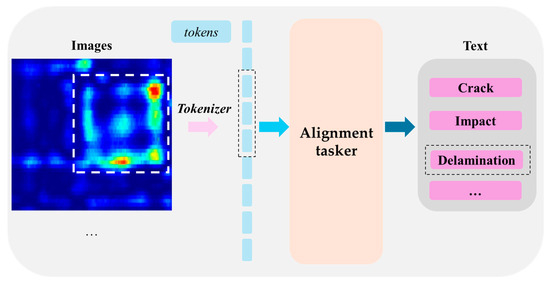
Figure 3.
One specific type of cross-modal alignment is explicit expanded modal alignment. The figure shows a schematic diagram illustrating the correspondence between the image modality and the text data modality.
In the context of eddy current testing, cross-modal alignment ensures that the real and imaginary components of the signal are interpreted in a way that emphasizes their shared relevance to defect detection. For instance, surface cracks may appear differently in the real component compared to the imaginary component, yet both are indicators of the same physical defect. Cross-modal alignment guarantees that these differences are correctly interpreted by the model, enabling it to use information from both modalities for accurate defect identification and characterization.
2.3. Multi-Modal Fusion
2.3.1. Definition and Concepts of Multi-Modal Fusion
Multi-modal fusion refers to the process of integrating information from different modalities to enhance a model’s ability to make accurate predictions or inferences. The key challenge in multi-modal fusion is determining when and how data from various modalities should be combined to maximize the advantages of their complementary information. This fusion process can occur at different stages within the learning pipeline, and each fusion strategy has its own strengths and trade-offs.
- Data-level fusion
In data-level fusion, raw data from multiple modalities are combined at the input stage, before feature extraction or model processing. This approach directly integrates the original data, which can help to preserve all the information derived from each modality. However, it may also lead to issues such as information redundancy, noise amplification, and difficulties in managing modalities with different formats or scales. For example, in the eddy current testing (ECT) of CFRP composites, the fusion of raw real and imaginary voltage signals could result in overlapping information or an imbalance in their contributions to defect detection. Additionally, raw data fusion might fail to fully leverage the complementary strengths of each modality’s unique features.
- Feature-level fusion
Feature-level fusion occurs after independent feature extraction has been conducted for each modality, where the high-level representations of the data are combined. This approach is particularly effective in multi-modal learning, as it allows the model to focus on the most relevant and informative aspects of each modality. By merging the extracted features, the model can take advantage of the complementary strengths of each modality while minimizing the influence of irrelevant or noisy data. In the context of ECT for CFRP composites, feature-level fusion enables the real component’s sensitivity to surface defects, such as cracks, to complement the imaginary component’s strength in identifying deeper issues, such as delamination or low-velocity impact damage. This method not only captures the distinctive characteristics of each signal but also provides a more comprehensive understanding of the material’s structural integrity.
- Decision-level fusion
In decision-level fusion, each modality is processed independently to generate separate predictions, which are then combined to make a final decision. This can be achieved through techniques such as majority voting, weighted averaging, or other ensemble methods. While decision-level fusion preserves the independence of each modality’s prediction process, it often misses the opportunity to exploit deeper interdependences between the modalities. For instance, in CFRP defect detection, relying solely on separate predictions from the real and imaginary signals may overlook potential interactions between these modalities that could enhance the model’s overall accuracy and sensitivity. Figure 4 provides an illustration of the different types of multi-modal fusion.
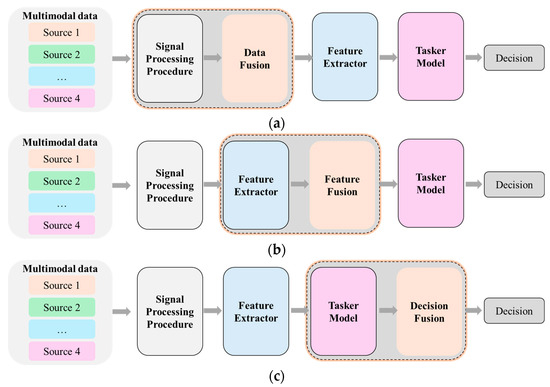
Figure 4.
Different types of multi-modal fusion. (a) Data-level fusion; (b) feature-level fusion; (c) decision-level fusion.
2.3.2. Feature-Level Fusion: Advantages and Applications
Building on the previous discussion of multi-modal fusion strategies, this section elaborates on the specific advantages and applications of feature-level fusion. Feature-level fusion is particularly beneficial in scenarios where each modality provides complementary insights into the same underlying phenomenon. By extracting and combining high-level features from each modality, this approach maximizes data utility while minimizing the influence of noise and irrelevant information.
- Capturing complementary information.
Each modality emphasizes different aspects of the data, making feature extraction essential for identifying and leveraging their complementary characteristics. This leads to a more comprehensive understanding of the underlying phenomenon.
- Enhancing model robustness.
Fusing features from different modalities increases the model’s robustness, reducing its sensitivity to deficiencies in any single modality. This ensures that the model remains effective, even under suboptimal conditions.
- Flexibility and scalability.
Feature-level fusion provides flexibility by allowing independent feature extraction for each modality. This modular approach facilitates the use of different architectures, optimized for each modality, and supports the integration of additional modalities or more advanced feature extraction techniques as needed, enhancing the model’s scalability.
2.3.3. Relevance to the PRI-SWT Model
In this study, feature-level fusion is applied to integrate the real and imaginary components of voltage signals obtained from the eddy current testing (ECT) of carbon fiber-reinforced polymer (CFRP) composites. The real and imaginary components contain complementary information, with the real component being more sensitive to surface features and the imaginary component being better suited for detecting subsurface defects.
By employing feature-level fusion, the proposed model independently extracts high-level features from both signal components and combines them to form a comprehensive representation of the material. Single-modal approaches often miss critical information that can be captured by other modalities. For example, relying solely on visual data may lead to researchers overlooking key defect details that could be better identified through accompanying textual or audio data analysis. This limitation can result in incomplete analysis and limit the accuracy of decision-making. Dual-modal fusion mitigates these limitations by integrating diverse information sources, allowing for a more comprehensive understanding of the subject matter. This fusion not only enhances the robustness of defect detection but also enriches the context by providing multiple perspectives on the same phenomenon. This approach enhances the model’s ability to detect and characterize various types of defects, particularly those that manifest differently in the real and imaginary signal spaces. By leveraging the strengths of each modality, the model improves detection accuracy and robustness, even in the presence of noise or incomplete data. Moreover, the modular architecture of feature-level fusion allows for future extensions, enabling the integration of additional modalities or more advanced feature extraction techniques, making it highly adaptable to evolving nondestructive testing requirements.
3. PRI-SWT Dual-Modal Fusion Model for CFRP Defect Detection
In this study, eddy current testing (ECT) was performed on CFRP defects, including cracks, delamination, and low-velocity impact damage, using a high-precision nine-grid eddy current probe system. The resulting ECT images were augmented using data augmentation techniques, generating training and testing sets for the dual-modal fusion PRI-SWT model. After obtaining these images, machine learning and deep neural network methods were applied to classify the defects. The core aim of this study is the development of the Dual-Modal Parallel Real–Imaginary/Swin Transformer (PRI-SWT) model, which integrates both the real and imaginary components of the eddy current signals. Dual-modal fusion is the process of integrating and leveraging information from two distinct modalities—such as text and images, audio and video, and different types of sensor data—to enhance the understanding and performance of a system. This approach capitalizes on the complementary strengths of each modality, enabling more comprehensive data representations and improved outcomes in tasks such as classification, recognition, and prediction. This dual-modal fusion approach is pivotal as it allows the model to leverage the complementary information from both signal components, enhancing detection accuracy and robustness in classifying CFRP defects.
The integration of real and imaginary data is crucial for capturing the complex characteristics of defects. Traditional methods, which often rely on single-modality inputs, may miss critical information, potentially leading to misclassification. By incorporating dual modalities, the PRI-SWT model offers a more comprehensive understanding of defect features, presenting improved generalization across various defect types and conditions. The following sections present the CFRP defect detection and classification algorithm used in this study, highlighting its innovative aspects and the critical role the PRI-SWT model will play in advancing detection capabilities.
3.1. Conventional Methods
3.1.1. Support Vector Machines
Support Vector Machines (SVM) are powerful tools used for linear classification, and they are especially effective in scenarios where the separation of classes is crucial. In this context, we assume that labeled sample data , where represents the set of samples. Here, is the coefficient vector corresponding to the hyperplane. The hyperplane that can separate the linear sample set is expressed as follows:
This leads to an equivalent optimization problem, which can be formulated as follows:
To enhance the model’s robustness and avoid overfitting, a penalty term is introduced. This allows for the development of a more flexible model that can better generalize to unseen data, leading to the following expression:
In this context, is defined as , where is the penalty term, and is the size of the data sample set.
In cases where a dataset is linearly inseparable, it becomes necessary to project the data into a higher-dimensional space using a kernel function. This transformation enables the originally inseparable dataset to become separable in this higher-dimensional space.
Once the data are embedded in this new space, the hyperplane defined by (3) can effectively separate the transformed data, as depicted in Figure 5.
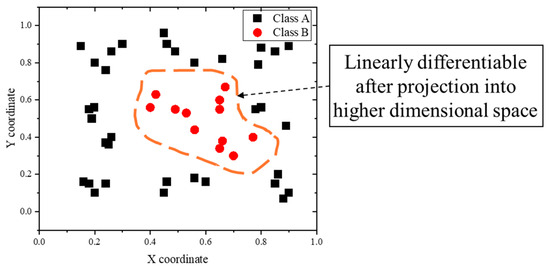
Figure 5.
SVM processing of linearly non-separable datasets, with the high-dimensional hyperplane projected as a curve in the original space.
3.1.2. Vision Transformer Model
In recent years, advancements in deep learning have led to significant improvements in computer vision tasks, particularly through the development of innovative architectures. One such architecture is the Vision Transformer (ViT), which leverages a self-attention mechanism to effectively analyze visual data. This mechanism enables the model to focus on the correlations between input vector tokens, allowing it to capture global interdependencies in the data. This is an advantage over the limited receptive field of convolutional neural networks (CNNs). The typical structure of a Vision Transformer model is illustrated in Figure 6. The input images in the model are obtained through the eddy current testing of CFRP specimens with cracks, delamination, and impact damage. This is conducted using the constructed CFRP eddy current nondestructive testing system. The specific experimental setup and CFRP test specimens with defects are shown in Figure 6.
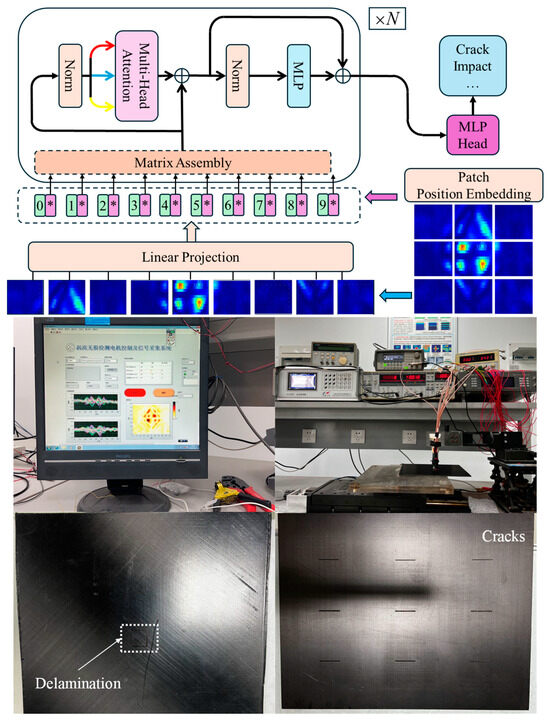
Figure 6.
The basic framework of Vi-T, obtaining the final classification result through steps such as linear projection and multi-head attention computation. The figure also illustrates the CFRP eddy current nondestructive testing (NDT) system, which primarily consists of key components such as a function signal generator, an eddy current probe, a lock-in amplifier, a low-voltage DC power supply, a motion controller, a data acquisition card, and an industrial control computer. Additionally, the figure shows several CFRP test specimens with defects, including CFRP samples with delamination and crack defects. The upper-left figure shows the Chinese software interface of the CFRP eddy current testing system.
In the Vision Transformer (ViT) model, a “patch embedding” linear mapping layer segments input image data into a sequence of “patches.” A classification token is then added, and these token vectors are passed into the encoder module. The vectors are processed through multiple encoder layers before reaching the classification layer, which outputs the predicted defect categories. The self-attention process, which highlights the relationships between tokens, is illustrated in Figure 7.
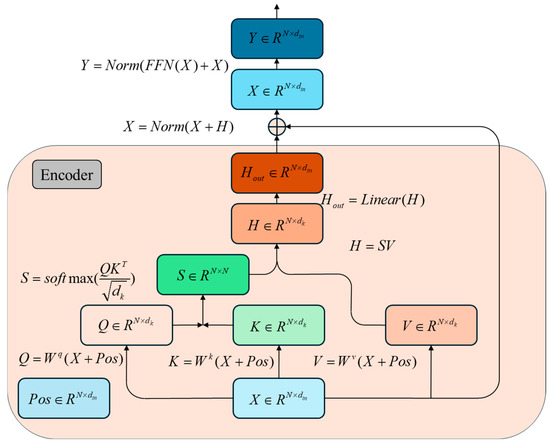
Figure 7.
The figure illustrates the mathematical computation process used for self-attention. Here, represents the input image tensor, which is derived by segmenting the input image into individual patches and then concatenating these patches along the feature channel dimension. The “width” and “height” dimensions of the three-dimensional feature tensor are then flattened into a one-dimensional format, resulting in a feature matrix with dimensions After adding a positional encoding matrix of the same dimensions, the query (, key (), and value () matrices are computed. Using the query and key matrices, the self-attention score matrix is obtained. Finally, this self-attention score matrix is multiplied by the value matrix to produce the resulting feature map, which maintains the same dimensions. During the computation process, the dimensional information of the , and matrices differs slightly from that of the input feature tensor, typically represented as . This can also be set to , depending on the specific application context. The dimensions of the linear mapping matrices and are all . The attention score matrix has dimensions of . Therefore, when this matrix is multiplied with the value matrix (which has dimensions ), the resulting output feature map maintains the dimensions of . If we set , the output feature map’s dimensions will match those of the input feature map.
In this process, denotes query vectors, indicates key vectors, represents value vectors, refers to the self-attention score matrix, signifies the linear mapping layer, refers to the normalization layer, and indicates the feed-forward network layer. Typically, a multi-head self-attention mechanism is employed, where the and matrices undergo parallel computation across multiple heads, followed by matrix combination:
where denotes the weight matrix of the linear projection, is the input, and are the corresponding weight matrices. Here, represents the dimension size of the input vector. In multi-head attention, the linear mapping matrix is partitioned into submatrices with dimensions , where the number of heads is denoted as and each head has a dimension . The resulting single-head matrices and each have dimensions of . When these are concatenated, the output feature map retains the dimensions of . After passing through a final linear mapping layer with dimensions of , the output feature map has the same dimensions as the input feature map. This multi-head self-attention mechanism enables the model to capture more detailed information from the token vectors, thereby enhancing the expressiveness and generalization of the Vision Transformer model.
3.2. Parallel Real–Imaginary/Swin Transformer Multi-Modal Fusion Model
In CFRP eddy current detection, the data consist of two images representing the amplitude and phase information of the sinusoidal signal. To effectively extract defective features, it is crucial to merge these two intrinsically linked images. However, the high resolution and large volume of images pose significant challenges, as the self-attention mechanism in traditional Vision Transformer (ViT) models requires substantial memory and processing power, making it less efficient for such tasks.
To address these issues, the innovative PRI-SWT model was designed, as illustrated in Figure 8. This model introduces an innovative approach by first concatenating the magnitude phase (or real–imaginary) images along the channel dimension, enabling parallel processing within the PRI-SWT framework. The complex input tensor, which combines the real and imaginary components of the CFRP detection signal, is processed through the first split layer and decoupled into two separate signals. These signals are then directed into two parallel SWT feature extractors—one above the other—to extract feature maps that are rich in low-level semantic information. Subsequently, various fusion layers, such as linear mapping layers or convolutional layers, are utilized to perform feature fusion and the concatenation of the two feature maps, which have different characteristics. This process enables complementary information exchange. The resulting fused feature map is then remapped and decoupled into two distinct feature maps, allowing for further high-level semantic information fusion. The complex input tensor, which integrates both the real and imaginary components of the CFRP detection signal, is processed through the first split layer, effectively decoupling it into two signals. These signals are subsequently routed into two parallel SWT feature extractors—one positioned above the other—to extract feature maps rich in low-level semantic information. Following this, different types of fusion layers, such as linear mapping layers or convolutional layers, are employed to perform feature fusion between the two distinct feature maps. This process facilitates complementary information exchange. The resulting fused feature map is then mapped and decoupled again into two separate feature maps, allowing for the continuation of high-level semantic information fusion. The PRI-SWT model not only addresses the computational challenges posed by high-resolution image data but also maximizes the utilization of complementary information from the amplitude and phase signals, thereby improving the accuracy and robustness of CFRP defect detection. Its ability to efficiently process large-scale data while preserving critical defect features demonstrates its superiority in tackling complex defect detection tasks.
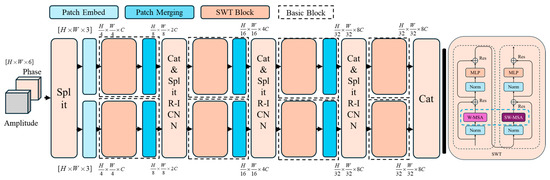
Figure 8.
The left side of the figure presents a schematic representation of the PRI-SWT model, detailing all its structures and operational processes. This includes key modules such as the separation layer, the patch embedding layer, the patch merging layer, the Swin Transformer module, and the fusion layer. The figure also provides information on the dimensions of the feature map tensors corresponding to the outputs of different modules. As the depth of the layers increases, the resolution of the feature maps gradually decreases, while the number of feature channels steadily increases. On the right side, the figure illustrates the internal details of the Swin Transformer module, which primarily comprises the window multi-head self-attention calculation module, the shifted window multi-head attention calculation module, the normalization layer, and the linear mapping MLP layer.
To enhance the exchange of information between different windows, the windows are artificially shifted, allowing for new self-attention feature maps to be calculated within these shifted windows, as depicted in Figure 9. This method not only optimizes the attention mechanism but also ensures that crucial defect features are effectively captured. Finally, the relevant features are extracted through real–imaginary (R-I) convolutional layer fusion, producing classification results after several stages of processing.
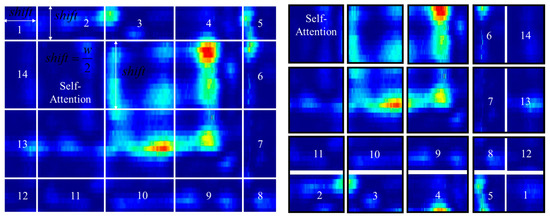
Figure 9.
The working mechanism of the Sliding Window Transformer. The image is segmented into numbered windows based on varying offset values and window sizes. These windows are then shifted and padded horizontally and vertically, forming structured regions for self-attention computation.
The design of the dual-modal fusion approach used in the PRI-SWT model is both innovative and essential in addressing the limitations of existing methods. It significantly improves classification performance, as will be demonstrated in subsequent validation experiments, where the PRI-SWT model is shown to outperform traditional classifiers such as SVM and ViT.
4. Results Analysis
4.1. Evaluation Indicators
To rigorously validate the effectiveness of the proposed PRI-SWT model and to clearly demonstrate its advantages over traditional methods such as SVM and ViT, a thorough performance evaluation is required. Establishing a set of comprehensive evaluation metrics is critical for ensuring a robust comparison. These indicators will not only quantify classification accuracy but also provide valuable insights into each model’s specific strengths and limitations. The following key metrics have been identified to assess model performance:
Confusion matrix: This matrix provides a detailed analysis of the model’s classification performance across multiple categories. It reveals the level of confusion between categories and highlights the probability of misclassification, offering valuable insights into areas where the model may struggle.
Top-1 accuracy and top-2 accuracy: These metrics evaluate accuracy by determining whether the correct classification result appears within the first- or second-ranked categories in the probability list produced by each classification node. These metrics are crucial for understanding the model’s ability to deliver correct classifications.
We used the following macro indicators:
Precision: defined as the ratio of the diagonal element in the confusion matrix to the sum of the elements in the corresponding row, precision indicates how many of the selected instances are relevant.
Recall: calculated as the sum of the elements in the corresponding column, recall measures the model’s ability to identify all relevant instances.
Macro-P:
Macro-R:
where and are the precision and recall values for each category, respectively, and is the number of categories.
Macro-F1:
This metric provides the harmonic mean value of precision and recall, offering a single score that captures both aspects of performance. It balances the trade-off between precision and recall, making it a valuable measure of overall classification effectiveness.
Kappa coefficient: This metric assesses the consistency of classification outcomes. Higher Kappa values typically indicate greater accuracy and reliability regarding the model’s predictions. The Kappa coefficient is calculated as follows:
where represents the observed agreement, and represents the expected agreement by chance.
4.2. Model Configuration
To effectively address the triple classification problem of CFRP defects, experiments were conducted using the PRI-SWT, ViT, and SVM models within a carefully structured experimental setup. The implementation was performed using Python 3.9 and Torch 2.0, with computations accelerated by an NVIDIA GeForce RTX 3080 graphics card to ensure optimal performance. To maintain consistency across the dataset, all images in the sample set were uniformly resized to 224 × 224 pixels. The specific parameters used for model configuration are detailed in Table 1 below.

Table 1.
Experiment parameters.
4.3. Model Comparisons
Following the model’s configuration, the consistent and fair comparison of classification performance was ensured by maintaining uniform dataset segmentation and parameters across the PRI-SWT, SVM, and ViT models. Both SVM and ViT were trained using either magnitude or phase images. The confusion matrices are shown in Figure 10, where 1 corresponds to crack defects, 2 to delamination, and 3 to impact damage. The detailed performance metrics for each model are presented in Table 2.
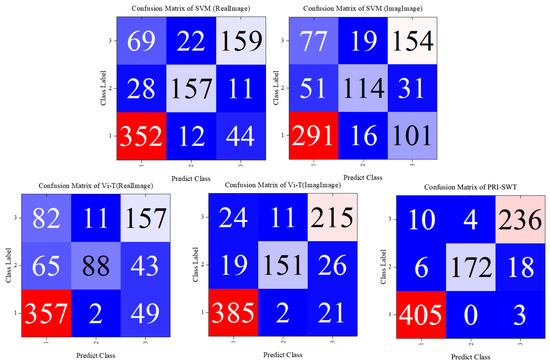
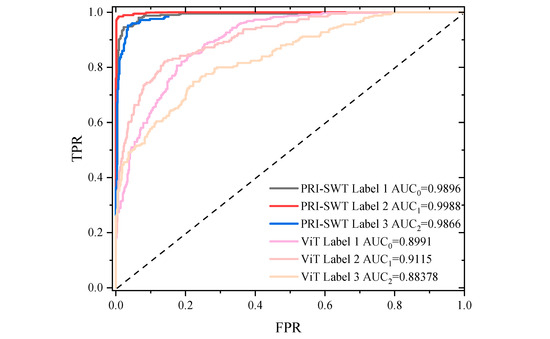
Figure 10.
The figure provides detailed confusion matrices for several classification models. It also includes the ROC curves for the typical ViT and PRI-SWT models, with the AUC values for the classification of the three CFRP defect types clearly indicated in the ROC curve images. In the figures, labels 0, 1, and 2 correspond to crack, delamination, and impact damage defects, respectively. The results demonstrate the relative superiority of the PRI-SWT model.

Table 2.
Comparison of evaluation indicators.
Building on the previous performance comparison, the PRI-SWT model demonstrates significant improvements over traditional methods. The ViT model, when using phase images, achieved macro-P, macro-R, macro-F1, and Kappa scores of 88.1%, 85.8%, 86.9%, and 80.9%. In comparison, the PRI-SWT model improved these metrics by 7.1%, 8%, 7.6%, and 11.5%, respectively, due to its ability to fuse magnitude and phase information from CFRP eddy current detection. This fusion ensures the comprehensive extraction of defect characteristics and reduces the risk of missing key information when relying on a single image.
CFRP defects vary widely in terms of size, with cracks ranging from small to medium scales, and impact damage covering larger areas, as shown in Figure 11.
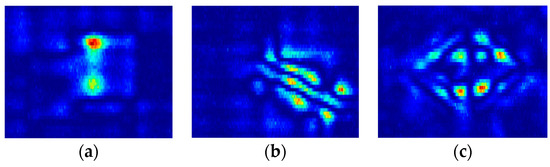
Figure 11.
Eddy current testing results for three types of CFRP defect: (a) crack of small size; (b) crack of medium size; (c) low-velocity impact of large size. The three types of CFRP defects vary in shape and scale.
CNN models, while generally more sensitive to smaller features, tend to struggle with larger defects. In contrast, the PRI-SWT model, utilizing Transformer capabilities, captures both small- and large-scale features, resulting in significantly improved classification performance.
The validation set accuracy versus epoch training curves for both the ViT and PRI-SWT models are illustrated in Figure 12. The PRI-SWT model not only demonstrates superior convergence during training, achieving up to 97% accuracy on the validation set, but also outperforms the ViT model in terms of both speed and stability. As shown in Figure 12, the training curves indicate that PRI-SWT converges more rapidly and maintains higher accuracy throughout the process. This enhanced performance is attributed to its innovative architecture, which effectively merges magnitude and phase information for the more comprehensive extraction of defect characteristics. The PRI-SWT model stabilizes around epoch 20, showcasing its robustness in handling the complexities of CFRP defect classification.
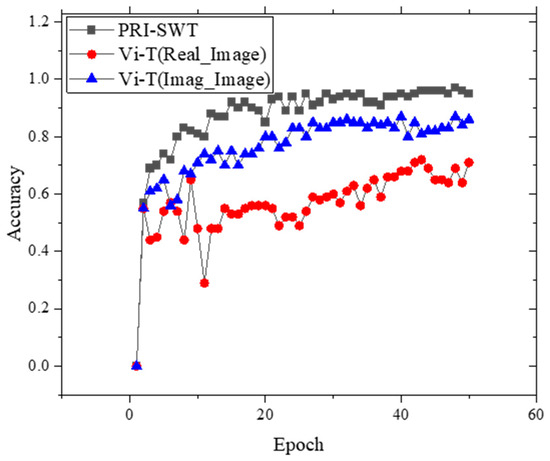
Figure 12.
Accuracy curves of Vi-T and PRI-SWT models for the first 50 training epochs.
4.4. Ablation Experiment
Building on the strong performance of the PRI-SWT model, ablation experiments were conducted to further investigate which design choices most significantly contribute to its classification accuracy. These experiments are crucial for optimizing model architecture and understanding the impact of various components. The focus was on evaluating different fusion network architectures—comparing convolutional versus linear mapping layers to integrate real and imaginary information—as well as assessing the influence of moving window size, network depth, and embedding vector dimensionality within the PRI-SWT model.
4.4.1. R-I Fusion Layer
The selection of real–imaginary fusion layers is critical for optimizing classification performance within the PRI-SWT model. This study compared two fusion approaches—2D convolutional layers and linear projection layers—while also analyzing the effect of varying the number of layers. Figure 13 presents the confusion matrices, where categories 1, 2, and 3 represent cracking, delamination, and low-velocity impact damage, respectively.
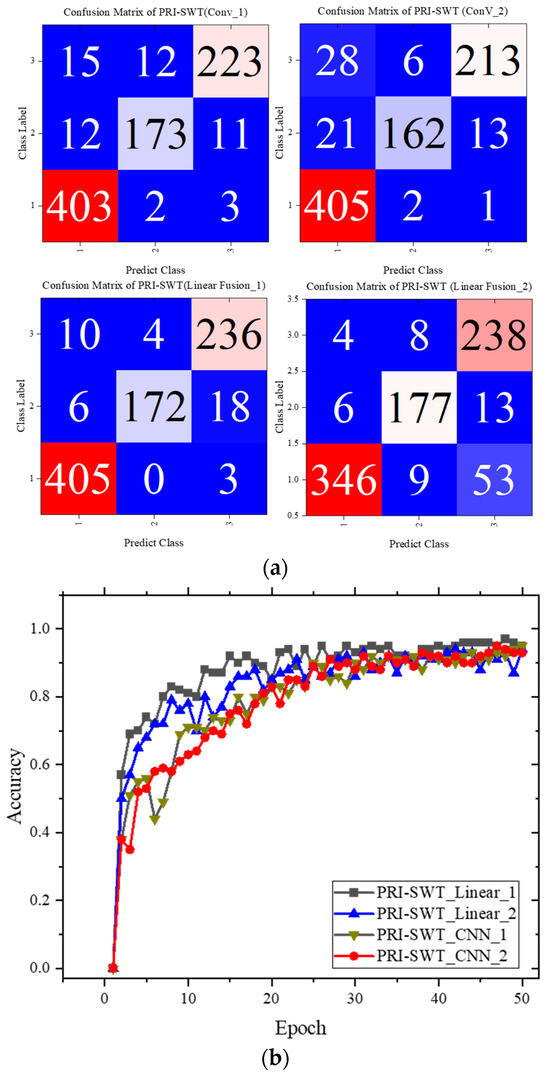
Figure 13.
Model’s accuracy curves and confusion matrix when using different fusion layers. (a) Confusion matrix; (b) training curves. The performance of the linear fusion layer surpasses that of the CNN fusion layer. However, increasing the number of fusion layers tends to decrease the model’s overall performance.
In the early stages of training, the linear projection fusion layer showed a clear advantage, with a steeper increase in accuracy compared to other methods. As training progressed, the accuracy across all models stabilized at around 95%, with the PRI-SWT model achieving the highest accuracy of 97% using a single linear mapping layer. The detailed multi-classification metrics for each model are summarized in Table 3.

Table 3.
Effects of the fusion layer.
Notably, the data indicate that increasing the number of fusion layers did not enhance performance, which was likely due to overfitting. The PRI-SWT model, utilizing a single linear mapping layer, demonstrated superior metrics, with a macro-F1 score 1.7% higher and a Kappa coefficient 2.6% higher than the corresponding scores of a model with a single convolutional fusion layer. These results highlight the effectiveness of the linear projection approach in capturing relevant features while maintaining model robustness, establishing the PRI-SWT model as a superior choice for CFRP defect classification. The superior performance of the linear mapping layer over the convolutional layer in the PRI-SWT model can be attributed to several key factors. First, the linear layer enables a simpler, more direct transformation of the real and imaginary components, preserving crucial cross-modal relationships. Second, it reduces the risk of overfitting because it has fewer parameters, as evidenced by the drop in performance with additional convolutional layers. Finally, the linear projection efficiently merges magnitude and phase information, resulting in faster convergence and improved feature extraction, leading to higher classification accuracy.
4.4.2. Shift Window
The PRI-SWT model employs a different approach compared to the Vision Transformer (ViT) model, which calculates attention scores across patches spanning the entire image. Instead, PRI-SWT uses a shifted window technique, computing attention scores within each window, significantly reducing computational costs. This method enhances information exchange and improves the model’s global perception. This section explores two key aspects: the effects of varying window shift values on classification performance and the impact of the window size itself.
The effects of varying the window shift size on model performance are summarized in Table 4, with accuracy curves for three scenarios involving the linear projection fusion layer depicted in Figure 14.

Table 4.
Effects of shifted values.
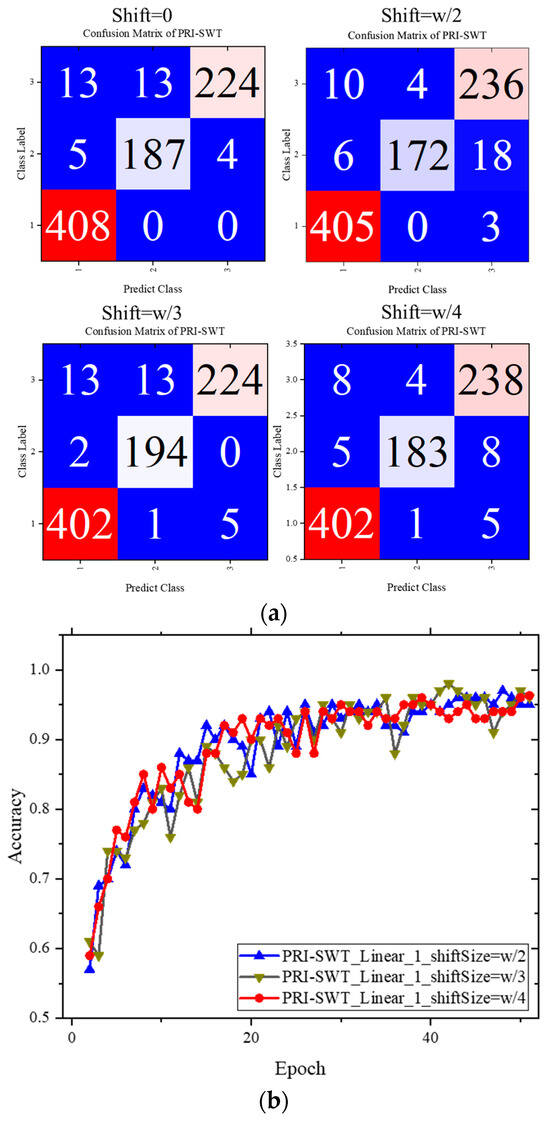
Figure 14.
Model accuracy curves and confusion matrix obtained using different shifted values. (a) Confusion matrix; (b) accuracy curves. A smaller window size results in slightly higher final classification performance compared to the other cases.
As shown in Table 4, refers to the window size. It was found that reducing the window shift size led to significant improvements in classification performance. This enhancement was likely due to the model’s ability to capture more localized information regarding CFRP defects, thereby aiding in the accurate identification of cracks, delamination, and impact damage. Figure 14 further supports this observation, showing that accuracy trends remained consistent across all cases. Smaller window shifts consistently yielded continued accuracy improvements throughout the training process, ultimately culminating in the optimal model configuration.
In addition to the window shift size, the actual window size itself significantly influences the performance of the PRI-SWT model. Smaller windows enhance computational efficiency and improve the perception of local information, but they may limit the model’s ability to capture global features. Therefore, it is essential to adjust window sizes carefully to optimize classification performance for different tasks.
The results regarding varying window sizes are presented in Figure 15. PRI-SWT classification metrics are shown in Table 5. Notably, increasing the window size reduced the macro-P to 94% and lowered the Kappa coefficient by 1.8%. The model with a larger window size encountered difficulties in differentiating between crack and impact damage, likely because it struggled to focus on localized CFRP defect regions, allowing nondefective information to interfere with classification decisions. Nevertheless, larger windows did facilitate a smoother convergence process for accuracy.
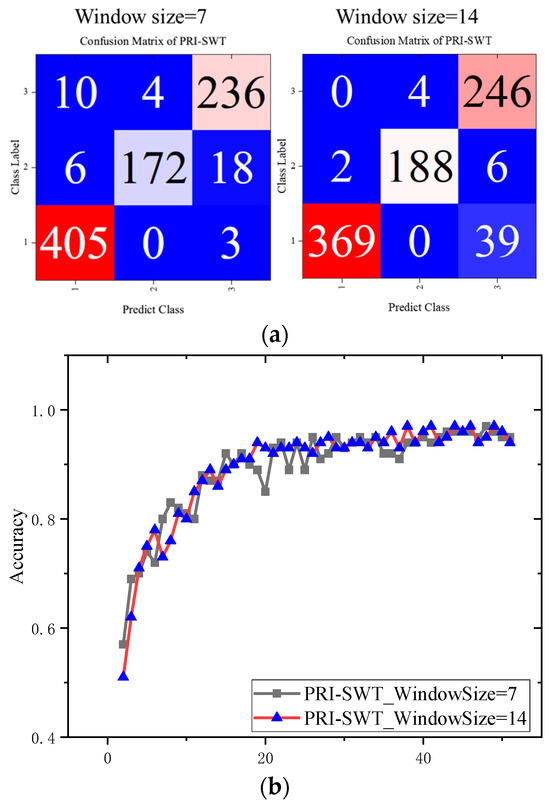
Figure 15.
Model accuracy curves and confusion matrix using different window sizes. (a) Confusion matrix; (b) training curves.

Table 5.
Effects of window sizes.
4.4.3. Depth of PRI-SWT
Understanding the impact of network depth is crucial for optimizing the PRI-SWT model’s performance, as it directly influences the model’s ability to capture complex features while maintaining computational efficiency. An analysis was conducted to assess the impact of network depth on classification performance. While deeper architectures can capture complex semantic details more effectively, they also introduce challenges such as increased computational requirements, a higher risk of overfitting, and more difficult training.
The original model’s architecture comprised four basic blocks with depths of . By doubling the depth of the first two blocks, we created configurations of and [4,4,4,6]. The corresponding confusion matrices and multi-classification metrics for these configurations are shown in Figure 16 and Table 6.
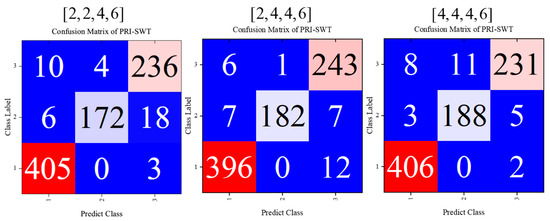
Figure 16.
Model’s confusion matrix using different depths of PRI-SWT. Increasing the network depth can enhance the performance of the PRI-SWT model; however, it also leads to higher computational costs, requiring a balance between the two.

Table 6.
Evaluation indicators of models of different depths.
Transitioning from the configuration of to resulted in notable improvements, with macro-P reaching 0.963, macro-R reaching 0.957, and macro-F1 reaching 0.960. This enhancement underscores the model’s ability to extract intricate patterns and details from the data.
However, further increasing the network depth to demonstrated diminishing returns as performance gains were negligible. This suggests that the model may have reached a performance plateau, indicating a limit to the benefits of adding additional layers. Furthermore, while deeper networks can initially improve accuracy, they also introduce a higher risk of overfitting. As depth increases, the model’s propensity to memorize training data may hinder its ability to generalize effectively to unseen data.
Additionally, the trade-off between computational efficiency and model depth becomes evident. Deeper architectures require more computational resources, leading to increased training and inference times. As a result, the marginal performance improvements gained from additional depth may not justify the added complexity and resource demands. Thus, the careful consideration of network depth is essential for optimizing classification performance in the PRI-SWT model.
5. Conclusions
The PRI-SWT model was developed to address the challenges of multi-defect classification in CFRP materials using complex voltage signals. In the experiment, eddy current testing was performed on CFRP specimens with cracks, delamination, and impact damage using a nine-element probe. Amplitude and phase images, reflecting the characteristics of these defects, were collected. Through a series of data acquisition and processing steps, a total of 2612 crack defect images, 1750 impact damage images, and 1372 delamination defect images were generated, providing comprehensive data on the electromagnetic response characteristics of various defect types.
To ensure the diversity of the model’s training data, the dataset was carefully split into training and validation sets. Specifically, for crack defect images, there were 1828 training images and 784 validation images; for impact damage, there were 1225 training images and 525 validation images; and for delamination defects, there were 960 training images and 412 validation images. The dataset was divided along a 7:3 ratio, allowing the model to be trained on a large dataset while its performance on unseen data was evaluated using the validation set. This approach enhances the model’s generalization ability and mitigates issues such as overfitting and underfitting. The results demonstrate that the macro-F1 score improved by 29.4%, reaching 0.945, while the Kappa coefficient improved by 46.8%, achieving 0.924, compared to the SVM and Vision Transformer (ViT) algorithms.
Ablation experiments confirmed that the linear projection fusion layer outperforms the 2D convolutional fusion layer, with a macro-F1 score of 0.945 versus one of 0.928 for the convolutional layer, highlighting its superior effectiveness in information integration.
Additionally, reducing window displacement improved classification performance, achieving a macro-P score of 0.963, while increasing the window size led to a macro-F1 score of 0.961. Deepening the network further enhanced the model’s performance, as reflected in a Kappa coefficient of 0.946. Smaller window shifts allowed for improved capture of localized defect features, whereas larger windows provided valuable contextual information.
These advancements demonstrate the significant potential of the PRI-SWT model regarding accurate CFRP defect classification, promoting more reliable nondestructive testing in engineering applications.
Although the PRI-SWT model has made significant improvements in recognition and classification performance for CFRP defect eddy current testing, it is important to note the increased training and inference time costs associated with the complexity of the network. The introduction of strategies, such as dual parallel information flow and fusion reasoning layers, further contributes to the increased time overhead. For the ViT model, the typical inference time is 11.2 s, while the Swin Transformer model offers some improvement, reducing the inference time to 10.56 s. However, the PRI-SWT model requires approximately 30.59 s. When classification accuracy is prioritized over the time cost, PRI-SWT is an excellent choice. However, this comes with challenges in terms of industrial real-time detection applications due to its increased computational demands.
In future research, the scalability of the PRI-SWT model will be tested on more complex defect types, such as delamination defects and fiber wrinkles. Additionally, to further enhance the model’s classification performance, future directions will include integrating a wider range of CFRP defect detection results, such as ultrasonic testing and pulse eddy current thermography imaging, thereby leveraging the benefits of multi-modal fusion technology. Furthermore, a pressing issue remains the high computational cost. Future efforts will focus on strategies such as using caching techniques and optimizing the model’s architecture to mitigate this challenge.
Author Contributions
Conceptualization, R.W.; Writing—original draft, R.W.; Supervision, C.T., H.J. and J.Q.; Funding acquisition, J.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further in-quiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ozkan, D.; Gok, M.S.; Karaoglanli, A.C. Carbon fiber reinforced polymer (CFRP) composite materials, their characteristic properties, industrial application areas and their machinability. In Engineering Design Applications III: Structures, Materials and Processes; Springer: Berlin/Heidelberg, Germany, 2020; pp. 235–253. [Google Scholar]
- Vijayan, D.S.; Sivasuriyan, A.; Devarajan, P.; Stefańska, A.; Wodzyński, Ł.; Koda, E. Carbon fibre-reinforced polymer (CFRP) composites in civil engineering application—A comprehensive review. Buildings 2023, 13, 1509. [Google Scholar] [CrossRef]
- Pawlak, A.M.; Górny, T.; Dopierała, Ł.; Paczos, P. The use of CFRP for structural reinforcement—Literature review. Metals 2022, 12, 1470. [Google Scholar] [CrossRef]
- Xu, J.; Chen, M.; Davim, J.P.; El Mansori, M. A review on the machinability of aerospace-grade CFRP/titanium stacks. Adv. Mater. Lett. 2021, 12, 011591. [Google Scholar] [CrossRef]
- Asyraf, M.; Ilyas, R.; Sapuan, S.; Harussani, M.; Hariz, H.; Aiman, J.; Baitaba, D.M.; Sanjay, M.; Ishak, M.; Norkhairunnisa, M. Advanced composite in aerospace applications: Opportunities, challenges, and future perspective. In Advanced Composites in Aerospace Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 471–498. [Google Scholar]
- Teng, H.; Li, S.; Cao, Z.; Li, S.; Li, C.; Ko, T.J. Carbon fiber composites for large-scale wind turbine blades: Applicability study and comprehensive evaluation in China. J. Mar. Sci. Eng. 2023, 11, 624. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, present and future prospective of global carbon fibre composite developments and applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar] [CrossRef]
- Mrazova, M. Advanced composite materials of the future in aerospace industry. Incas Bull. 2013, 5, 139. [Google Scholar]
- Mayuet Ares, P.F.; Girot Mata, F.; Batista Ponce, M.; Salguero Gómez, J. Defect analysis and detection of cutting regions in CFRP machining using AWJM. Materials 2019, 12, 4055. [Google Scholar] [CrossRef]
- Berger, D.; Brabandt, D.; Bakir, C.; Hornung, T.; Lanza, G.; Summa, J.; Schwarz, M.; Herrmann, H.-G.; Pohl, M.; Stommel, M. Effects of defects in series production of hybrid CFRP lightweight components–detection and evaluation of quality critical characteristics. Measurement 2017, 95, 389–394. [Google Scholar] [CrossRef]
- Wang, B.; He, P.; Kang, Y.; Jia, J.; Liu, X.; Li, N. Ultrasonic Testing of Carbon Fiber-Reinforced Polymer Composites. J. Sens. 2022, 2022, 5462237. [Google Scholar] [CrossRef]
- Schumacher, D.; Meyendorf, N.; Hakim, I.; Ewert, U. Defect recognition in CFRP components using various NDT methods within a smart manufacturing process. AIP Conf. Proc. 2018, 1949, 020024. [Google Scholar]
- Hasebe, S.; Higuchi, R.; Yokozeki, T.; Takeda, S.-I. Internal low-velocity impact damage prediction in CFRP laminates using surface profiles and machine learning. Compos. Part B Eng. 2022, 237, 109844. [Google Scholar] [CrossRef]
- Farnand, K.; Zobeiry, N.; Poursartip, A.; Fernlund, G. Micro-level mechanisms of fiber waviness and wrinkling during hot drape forming of unidirectional prepreg composites. Compos. Part A Appl. Sci. Manuf. 2017, 103, 168–177. [Google Scholar] [CrossRef]
- Han, S.; Li, Q.; Cui, Z.; Xiao, P.; Miao, Y.; Chen, L.; Li, Y. Non-destructive testing and structural health monitoring technologies for carbon fiber reinforced polymers: A review. Nondestruct. Test. Eval. 2024, 39, 725–761. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Yin, W.; Chen, H.; Zhou, G.; Ma, H.; Tan, D. Parameters impact analysis of CFRP defect detection system based on line laser scanning thermography. Nondestruct. Test. Eval. 2024, 39, 1169–1194. [Google Scholar] [CrossRef]
- Li, X.B.; Hu, H.W.; Li, L.; Tong, L.J. Defect Inspection and Classification of CFRP with Complex Surface by Ultrasonic. Adv. Mater. Res. 2011, 213, 297–301. [Google Scholar] [CrossRef]
- Poudel, A.; Chu, T.P. Pattern Recognition Algorithms for Automated Defect Classification of Ultrasonic Signals. In Proceedings of the ASNT 24th Research Symposium 2015, Anaheim, CA, USA, 16–19 March 2015; pp. 84–92. [Google Scholar]
- Meister, S.; Wermes, M.; Stüve, J.; Groves, R.M. Investigations on Explainable Artificial Intelligence methods for the deep learning classification of fibre layup defect in the automated composite manufacturing. Compos. Part B Eng. 2021, 224, 109160. [Google Scholar] [CrossRef]
- Kumar, S.; Choudhary, S.; Jain, A.; Singh, K.; Ahmadian, A.; Bajuri, M.Y. Brain tumor classification using deep neural network and transfer learning. Brain Topogr. 2023, 36, 305–318. [Google Scholar] [CrossRef]
- Khetarpal, P.; Nagpal, N.; Al-Numay, M.S.; Siano, P.; Arya, Y.; Kassarwani, N. Power quality disturbances detection and classification based on deep convolution auto-encoder networks. IEEE Access 2023, 11, 46026–46038. [Google Scholar] [CrossRef]
- Liu, G.; Gao, W.; Liu, W.; Chen, Y.; Wang, T.; Xie, Y.; Bai, W.; Li, Z. Automatic Defect Classification for Infrared Thermography in CFRP based on Deep Learning Dense Convolutional Neural Network. J. Nondestruct. Eval. 2024, 43, 73. [Google Scholar] [CrossRef]
- Lu, W.; Qian, M.; Xia, Y.; Lu, Y.; Shen, J.; Fu, Q.; Lu, Y.C.P. Crack detection based on the U-Net framework combined with Swin Transformer. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; p. 106241. [Google Scholar]
- Si, C.; Luo, H.; Han, Y.; Ma, Z. Rail-STrans: A Rail Surface Defect Segmentation Method Based on Improved Swin Transformer. Appl. Sci. 2024, 14, 3629. [Google Scholar] [CrossRef]
- Xi, Y.; Zhou, K.; Meng, L.-W.; Chen, B.; Chen, H.-M.; Zhang, J.-Y. Transmission line insulator defect detection based on swin transformer and context. Mach. Intell. Res. 2023, 20, 729–740. [Google Scholar] [CrossRef]
- Tang, D.; Zhao, Y. Inception meets Swin Transformer: A Novel Approach for Metal Defect Recognition. Acad. J. Sci. Technol. 2024, 9, 176–185. [Google Scholar] [CrossRef]
- Alif, M.A.R.; Hussain, M.; Tucker, G.; Iwnicki, S. BoltVision: A Comparative Analysis of CNN, CCT, and ViT in Achieving High Accuracy for Missing Bolt Classification in Train Components. Machines 2024, 12, 93. [Google Scholar] [CrossRef]
- Wang, H.; Ji, Y.; Song, K.; Sun, M.; Lv, P.; Zhang, T. ViT-P: Classification of genitourinary syndrome of menopause from OCT images based on vision transformer models. IEEE Trans. Instrum. Meas. 2021, 70, 1–14. [Google Scholar] [CrossRef]
- Chen, P.; Li, R.; Fu, K.; Zhong, Z.; Xie, J.; Wang, J.; Zhu, J. A cascaded deep learning approach for detecting pipeline defects via pretrained YOLOv5 and ViT models based on MFL data. Mech. Syst. Signal Process. 2024, 206, 110919. [Google Scholar] [CrossRef]
- Su, W.; Yang, Y.; Zhou, C.; Zhuang, Z.; Liu, Y. Multiple Defect Classification Method for Green Plum Surfaces Based on Vision Transformer. Forests 2023, 14, 1323. [Google Scholar] [CrossRef]
- Smith, A.D.; Du, S.; Kurien, A. Vision transformers for anomaly detection and localisation in leather surface defect classification based on low-resolution images and a small dataset. Appl. Sci. 2023, 13, 8716. [Google Scholar] [CrossRef]
- An, K.; Zhang, Y. LPViT: A transformer based model for PCB image classification and defect detection. IEEE Access 2022, 10, 42542–42553. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).