FastSLAM-MO-PSO: A Robust Method for Simultaneous Localization and Mapping in Mobile Robots Navigating Unknown Environments

Abstract

In the realm of mobile robotics, the capability to navigate and map uncharted territories is paramount, and Simultaneous Localization and Mapping (SLAM) stands as a cornerstone technology enabling this capability. While traditional SLAM methods like Extended Kalman Filter (EKF) and FastSLAM have made strides, they often struggle with the complexities of non-linear dynamics and non-Gaussian noise, particularly in dynamic settings. Moreover, these methods can be computationally intensive, limiting their applicability in real-world scenarios. This paper introduces an innovative enhancement to the FastSLAM framework by integrating Multi-Objective Particle Swarm Optimization (MO-PSO), aiming to bolster the robustness and accuracy of SLAM in mobile robots. We outline the theoretical underpinnings of FastSLAM and underscore its significance in robotic autonomy for mapping and exploration. Our approach innovates by crafting a specialized fitness function within the MO-PSO paradigm, which is instrumental in optimizing the particle distribution and addressing the challenges inherent in traditional particle filtering methods. This strategic fusion of MO-PSO with FastSLAM not only circumvents the pitfalls of particle degeneration, but also enhances the overall robustness and precision of the SLAM process across a spectrum of operational environments. Our empirical evaluation involves testing the proposed method on three distinct simulation benchmarks, comparing its performance against four other algorithms. The results indicate that our MO-PSO-enhanced FastSLAM method outperforms the traditional particle filtering approach by significantly reducing particle degeneration and ensuring more reliable and precise SLAM performance in challenging environments. This research demonstrates that the integration of MO-PSO with FastSLAM is a promising direction for improving SLAM in mobile robots, providing a robust solution for accurate mapping and localization even in complex and unknown settings.

1. Introduction

Simultaneous Localization and Mapping (SLAM) [1] stands as a cornerstone technology in the fields of autonomous navigation and robotics, providing machines with the ability to explore and map new territories without prior knowledge of the environment. This technology is not only crucial for the autonomous operation of robots, but also forms the basis for higher-level functionalities such as environmental perception, strategic decision-making, and autonomous pathfinding. By integrating sensor data from sources like LiDAR, optical cameras, and inertial sensors, SLAM facilitates the concurrent creation of environmental maps and the precise positioning of the robot in real-time. This dual capability is vital for robots to function autonomously, especially in environments that are subject to constant change [2]. As the frontier of technology advances, SLAM has become a fundamental element of smart systems, driving innovation and progress in the automation sector [3]. The ongoing research and refinement of SLAM techniques are of significant importance for the advancement of intelligent systems and their applications in the future. The effective implementation of SLAM in unknown and dynamically changing environments, however, presents substantial technical hurdles that the field must address to ensure the reliability and efficiency of robotic systems.

FastSLAM [4] is a prominent approach to the SLAM challenge, renowned for its efficiency in navigating the complexities of non-linear systems and handling noise that does not conform to the traditional Gaussian model. This algorithm employs a synergistic approach by integrating the robustness of particle filtering with the precision of the Extended Kalman Filter (EKF) [5]. While Gaussian noise is predictable and follows a standard bell-shaped distribution, real-world scenarios often present noise patterns that are non-Gaussian, complicating the task for SLAM algorithms. FastSLAM addresses this by segmenting the SLAM process into two principal tasks: the robot’s pose estimation, which is managed by particle filtering to accommodate non-linear dynamics, and the landmark estimation, which is processed by the EKF to handle each landmark individually. This bifurcation significantly alleviates computational burden and supports the algorithm’s scalability in expansive environments. Despite these strengths, FastSLAM faces notable difficulties when operating in settings with extensive environments or under conditions with substantial noise interference [6]. The phenomenon of particle degeneration can occur, where the diversity among particles is compromised, potentially impeding comprehensive exploration of the state space. In the course of multiple iterations, the algorithm may encounter a situation where only a few particles with substantial weights come to dominate the posterior distribution, overshadowing the majority. Such a scenario impairs the algorithm’s capacity to accurately capture the true posterior probability and leads to a suboptimal use of computational resources.

Building upon the challenges faced by FastSLAM in maintaining robustness amidst particle degeneration, particularly in complex and dynamic settings, the introduction of Multi-Objective Particle Swarm Optimization (MO-PSO) [7] presents a novel perspective. MO-PSO is an evolutionary computation technique inspired by the social behavior of bird flocking and fish schooling, which is adept at handling multi-objective optimization problems. Unlike traditional Particle Swarm Optimization (PSO) [8], which focuses on a single objective, MO-PSO is designed to optimize multiple conflicting objectives simultaneously, providing a more comprehensive solution landscape. The algorithm guides a swarm of particles through the search space, allowing them to adapt their positions and velocities based on both personal and collective experiences, thereby converging towards a set of optimal solutions rather than a single point. This approach is particularly advantageous for addressing the multifaceted degradation issues inherent in FastSLAM, as it can simultaneously enhance the diversity and representativeness of the particle population, ensuring a more accurate and resilient SLAM performance.

The motivation behind integrating MO-PSO with FastSLAM stems from the need to address the limitations of traditional single-objective optimization methods in the context of SLAM. By leveraging the multi-objective capabilities of MO-PSO, this research aims to propose a new method that not only mitigates particle degeneration, but also enhances the overall accuracy and robustness of the SLAM process. Our primary contributions include the development of a novel optimization strategy that harnesses the strengths of MO-PSO to optimize the distribution and diversity of particles within the FastSLAM framework. The proposed integration of FastSLAM with MO-PSO is underpinned by a carefully designed methodology that focuses on enhancing particle filtering through a multi-objective optimization approach. The design of our method involves the development of a bespoke fitness function that not only evaluates the particles’ contribution to the current estimation, but also promotes diversity to counteract degeneration. To validate the effectiveness of our proposed method, we have meticulously designed a series of experiments. These experiments are conducted across various simulated environments, providing a controlled setting to assess performance. We have selected a set of state-of-the-art SLAM algorithms for comparative analysis, ensuring a thorough evaluation of our method against existing solutions. The performance metrics for these experiments include accuracy of pose estimation, map quality, computational efficiency, and robustness in the presence of dynamic changes, providing a comprehensive assessment of our MO-PSO-enhanced FastSLAM approach.

The structure of this paper is as follows: The first section sets the stage by introducing the background and motivation behind SLAM technology. The second section offers a concise review of the fundamental principles of SLAM and PSO algorithms, with an emphasis on the multi-objective optimization context. The third section details the design and implementation of the proposed FastSLAM-MO-PSO algorithm. The fourth section presents the experimental results and performance evaluation. Finally, the last section summarizes the findings and suggests directions for future research.

2. Preliminaries

In this section, we begin with an exposition on the fundamentals of Multi-Objective Optimization (MOO), establishing a foundation for understanding the complex trade-offs inherent in optimizing multiple goals simultaneously. We then proceed to delve into the principles of PSO, elucidating its potential as a robust optimization tool.

2.1. Multi-Objective Optimization Fundamentals

MOO [9] is fundamentally concerned with finding a set of solutions where no single solution is superior to another in all objectives. This concept is mathematically formalized through the notion of Pareto dominance. A solution x is said to dominate another solution y if x is at least as good as y in all objectives and strictly better in at least one objective. Mathematically, this can be expressed as

$$\mathit{x}\prec \mathit{y} \mathrm{if} f_i(\mathit{x})\le f_i(\mathit{y}) \forall i \in N \mathrm{and} f_j(\mathit{x})<f_j(\mathit{y}) \exists j \in N$$

(1)

where f_i(·) and f_j(·) represent the i-th and the j-th objective functions, and N represents the total number of objective functions. A Pareto optimal solution is defined as one that is not outperformed by any other solution within the search space. The set of all such Pareto optimal solutions constitutes what is known as the Pareto front.

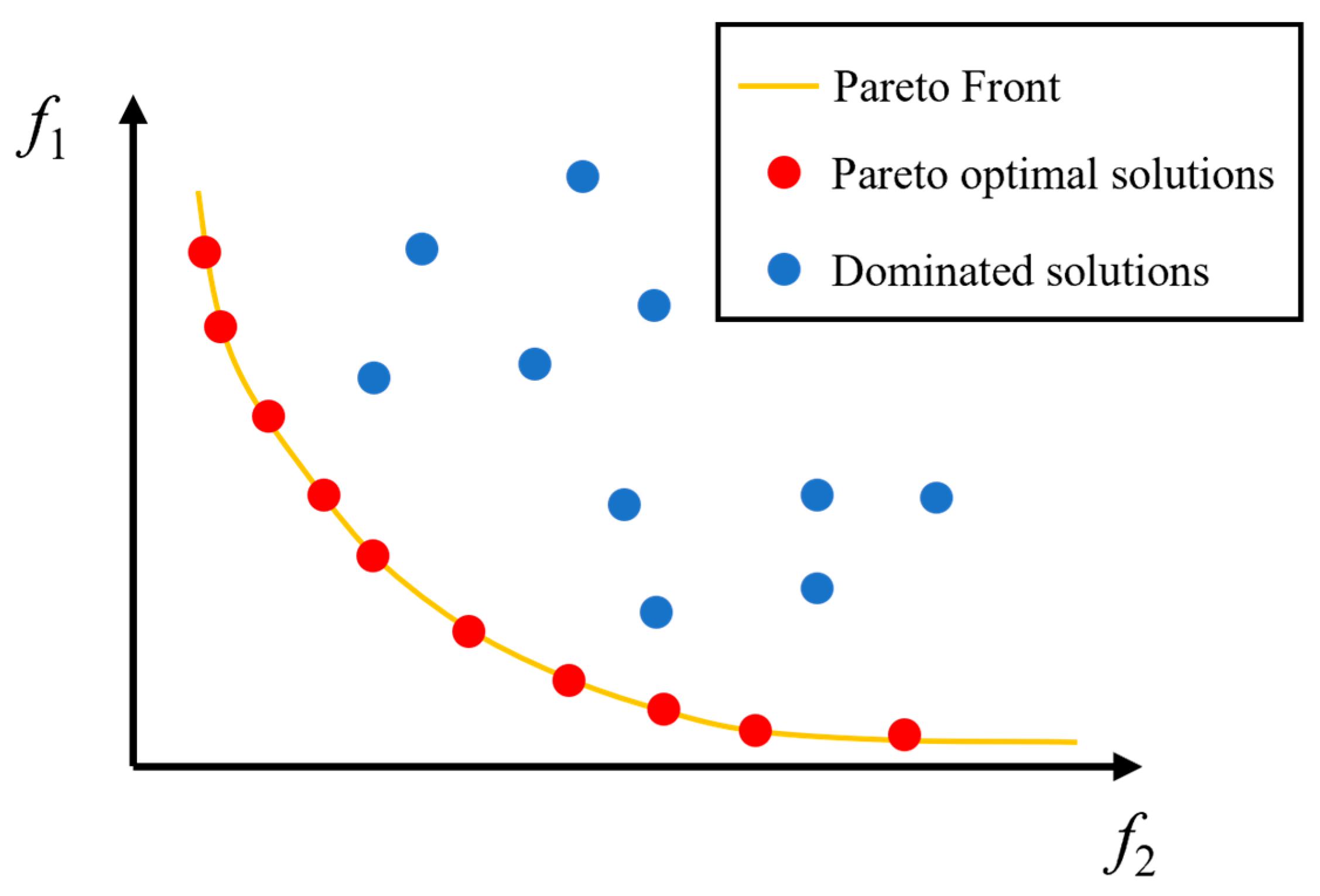
Representing solutions in a multi-objective space typically involves a vector of objective values, where each dimension corresponds to an objective. For instance, a solution x in a bi-objective problem can be represented as x = (x₁, x₂, …, x_n; f₁(x), f₂(x)), where x₁, x₂, …, x_n are the decision variables and f₁(x), f₂(x) are the objective functions evaluated at x. As depicted in Figure 1, circular markers represent the projected positions of solution x in the coordinate system under objectives f₁ and f₂. Assuming both f₁ and f₂ are minimization problems, it can be observed that the red points form a Pareto front, as illustrated by the orange line, where points on the Pareto front are non-dominating with respect to each other.

The challenge in multi-objective optimization is to converge to a set of solutions that closely approximate the true Pareto front while maintaining a diverse spread across the front. This balance between convergence and diversity is crucial for providing decision-makers with a comprehensive view of the trade-offs inherent in the problem. The performance of a multi-objective optimization algorithm is often evaluated based on its ability to generate a well-distributed set of solutions that accurately represent the Pareto front.

In summary, MOO is about navigating the intricate landscape of trade-offs inherent in problems with multiple objectives. It aims to identify a set of solutions, known as the Pareto front, that offer the best possible compromises among these objectives. This process is not merely about finding any solution; it is about uncovering a diverse array of solutions that collectively represent the full spectrum of possible trade-offs. This is particularly beneficial in complex and dynamic environments where traditional SLAM methods may struggle due to their limited ability to balance multiple performance criteria.

2.2. PSO

PSO is an optimization technique modeled after the collective behavior exhibited by social organisms, such as bird flocking and fish schooling, which was proposed in 1995 by Kennedy and Eberhart. This method leverages the collective intelligence of a population of entities, termed particles, to search for optimal solutions in a problem domain. In the PSO paradigm, particles traverse the search space, adjusting their trajectories based on their own best-known positions and the best-known position of the swarm. This collaborative search mechanism enables the identification of optimal solutions by capitalizing on both individual and collective experiences [10,11].

Each particle within the swarm maintains an archive of its best-encountered solution, denoted as p_best, and the swarm collectively maintains the best solution found thus far, referred to as g_best. The velocity and position updates for each particle are steered by the following equations:

$$v_i^{t+1}=w·v_i^t+c_1·r_1·(p_{\mathrm{best},i}-x_i^t)+c_2·r_2·(g_{\mathrm{best}}-x_i^t)$$

(2)

$$x_i^{t+1}=x_i^t+v_i^{t+1}$$

(3)

Here, $v_i^t$ and $x_i^t$ represent the velocity and position of particle i at iteration t, respectively. The terms c₁ and c₂ are positive constants that determine the influence of the personal best and global best positions on the velocity update. r₁ and r₂ are random numbers uniformly distributed between 0 and 1, which introduce stochastic elements to the search process. The inertia weight w controls the impact of the previous velocity on the current velocity, thereby balancing exploration and exploitation in the search space.

The elegance of PSO lies in its simplicity and adaptability, as it does not rely on the gradient of the objective function, making it a robust choice for non-linear and non-convex optimization scenarios [12]. Its capacity for swift convergence in expansive, multi-dimensional search spaces is particularly valuable for complex optimization tasks. In the context of SLAM, where the goal is often to find a single, globally optimal solution for the robot’s pose and landmark positions, PSO’s propensity for local convergence is less of a drawback. Instead, its ability to efficiently navigate the solution space and mitigate particle degradation makes PSO an advantageous choice for enhancing the performance of SLAM algorithms like FastSLAM.

Moreover, the diversity of solutions provided by MOO can offer additional flexibility. For instance, different solutions on the Pareto front can be selected based on specific mission requirements or changing environmental conditions, allowing for greater adaptability and robustness in real-world SLAM applications. This flexibility is crucial for SLAM systems that must operate in diverse and unpredictable environments, where the ability to adapt to new conditions quickly is essential. Therefore, the integration of PSO with multi-objective optimization is particularly beneficial for SLAM, as it combines the efficient search capabilities of PSO with the comprehensive solution set provided by MOO. This synergy enables SLAM systems to not only find optimal solutions, but also to maintain a diverse set of good solutions that can be adapted to various scenarios.

2.3. FastSLAM

FastSLAM is a probabilistic approach that addresses the SLAM challenge by synergizing the strengths of Particle Filtering (PF) and the EKF. This method is particularly adept at handling SLAM in environments where the robot must navigate and map without prior knowledge, offering a robust solution to the problem of data association and state estimation.

The essence of FastSLAM lies in its ability to decompose the complex SLAM problem into two parallel and conditional tasks: estimating the robot’s pose and predicting the positions of landmarks within the environment. This decomposition is grounded in the principle that the prediction of landmark positions can be considered independently for each particle representing the robot’s pose, thus significantly reducing the computational burden.

In the FastSLAM framework, a set of particles is utilized to represent the distribution of the robot’s pose, with each particle carrying an estimate of the trajectory and associated landmarks. The algorithm proceeds by iteratively predicting the robot’s pose at each time step using a motion model, which encapsulates the control inputs and accounts for system noise. This prediction is expressed as:

$$x_k=f(x_{k-1},u_k)+{\omega }_k$$

(4)

where x_k is the estimated pose, f(·) denotes the motion model function, u_k represents the control inputs, and w_k is the process noise.

Subsequently, the EKF is applied within the context of each particle to refine the estimates of landmark positions. This refinement is crucial for updating the map as the robot navigates through the environment. The EKF updates are based on the observation model, which correlates the robot’s pose with the observed landmarks. A critical aspect of FastSLAM is the resampling step, which is triggered to maintain diversity within the particle set and to prevent the degeneration of particles that could lead to suboptimal solutions. This step ensures that particles with higher weights, indicating a better fit to the observed data, are favored, thereby enhancing the overall robustness of the algorithm.

Despite its computational efficiency and the ability to handle large environments with numerous landmarks, FastSLAM can encounter challenges in dynamic settings where noise characteristics are not static. The algorithm’s performance is contingent upon accurate noise statistics, which may vary over time. This variability can lead to inefficiencies and inaccuracies in the estimation process.

The incorporation of multi-objective optimization strategies into the FastSLAM framework presents a compelling opportunity to further enhance its capabilities. MO-PSO’s ability to handle multiple conflicting objectives simultaneously could potentially optimize various aspects of the SLAM process, such as balancing the trade-off between estimation accuracy and computational load. In this paper, by integrating MO-PSO, the FastSLAM algorithm could benefit from improved adaptability to changing environmental conditions and enhanced robustness in the presence of dynamic noise characteristics, setting the stage for more sophisticated and resilient SLAM solutions in future work.

3. Related Works of Enhancements to SLAM

In this section, we introduce the essentials of FastSLAM, highlighting its role in the domain of robotics and autonomous navigation. This section culminates with a discussion on the various enhancement strategies for SLAM, including the integration with evolutionary algorithms and general improvement approaches for FastSLAM.

3.1. Evolutionary Algorithm-Based Improvements to SLAM

Evolutionary algorithms represent a class of computational models inspired by biological evolution, which are particularly adept at handling complex optimization problems. In the context of FastSLAM, these algorithms offer a promising avenue for improvement by leveraging their robust search capabilities to enhance the exploration and exploitation of the solution space. This section delves into the integration of evolutionary algorithms with FastSLAM, highlighting how such an integration leads to significant enhancements in the algorithm’s performance. We will review the key contributions of incorporating evolutionary strategies into FastSLAM, setting the stage for a discussion of our proposed improvements in subsequent literature references.

Vahdat et al. [13] proposed two sample-based evolutionary methods for global localization of mobile robots: differential evolution (DE) and PSO. These methods were designed to address the limitations of traditional probabilistic approaches, such as the Kalman filter, by accommodating non-linear and non-Gaussian noise distributions. The DE and PSO algorithms demonstrated superior performance over the standard Monte Carlo localization algorithm in terms of convergence rate, accuracy, and computational cost. The experimental results indicated that these evolutionary methods required fewer individuals or particles for convergence, highlighting their potential for efficient global localization in mobile robotics applications. Moreno et al. [14] introduced an evolutionary localization algorithm known as the Evolutive Localization Filter (ELF). This algorithm is founded on evolutionary computation principles and addresses the global localization challenge by stochastically searching for the optimal robot pose estimate within the state space. The ELF leverages observation and motion errors, derived from probabilistic perception and motion models, to evolve a population of pose solutions. The algorithm was successfully integrated into a mobile robot equipped with a laser range finder, demonstrating effectiveness, robustness, and computational efficiency in experimental evaluations. Zhang et al. [15] presented a hybrid localization approach that integrates the particle filter with PSO. This method, termed the Particle Swarm Optimization Filter (POF), focuses on accurate and robust localization in environments with a priori known maps. The POF algorithm excels in symmetrical environments, a common challenge for traditional localization techniques. The experimental results showcased that the proposed method achieved robust and precise positioning outcomes in indoor settings, utilizing fewer particles compared to benchmark algorithms, thereby reducing computational costs and enhancing navigation efficiency. Luis Moreno et al. [16] developed a novel global localization filter that amalgamates DE with the Markov Chain Monte Carlo (MCMC) approach. This filter, termed the Differential Evolution Markov Chain Filter, represents the robot’s pose as a set of potential location estimates weighted by a fitness function. The integration of evolutionary optimization with the statistical robustness of MCMC resulted in a significant reduction in population requirements compared to previous versions. The filter was tested in both simulated and real-world maps, yielding promising results in terms of localization accuracy and computational efficiency.

Despite the numerous evolutionary approaches integrated to address SLAM challenges, the shortcomings of traditional single-objective optimization methods have become increasingly evident. These single-objective algorithms, which tend to concentrate on optimizing only one aspect of the SLAM process, often fall short in tackling the intricate and multifaceted issues associated with particle degeneration. In response, the integration of multi-objective optimization algorithms presents a promising avenue. These algorithms are designed to handle multiple objectives simultaneously, allowing for a more holistic optimization of the SLAM process. By considering various aspects of the algorithm’s performance, multi-objective optimization algorithms can enhance the distribution and diversity of particles, thereby mitigating the degradation issue and improving the overall robustness and accuracy of the SLAM solution in complex and dynamic environments.

3.2. Other Improvements to FastSLAM

This section primarily introduces improvements to FastSLAM, beginning with FastSLAM 2.0. Montemerlo et al. [17] presented an enhanced algorithm for SLAM, titled FastSLAM 2.0. This algorithm employs a sophisticated particle filtering technique, which considers recent sensor measurements in its proposal distribution. This modification leads to a more efficient utilization of particles, particularly in scenarios characterized by high motion noise relative to sensor noise. The researchers demonstrated the convergence of their algorithm for linear SLAM problems and reported a marked enhancement in accuracy over the original FastSLAM through real-world experiments. Lv et al. [18] introduced an improved FastSLAM algorithm that amalgamates revised genetic resampling with the square root unscented particle filter (SR-UPF). This innovative approach tackles the traditional shortcomings, such as particle depletion and the linear approximation of non-linear functions. The integration of genetic resampling and SR-UPF enriches particle diversity and bolsters estimation precision. The algorithm’s performance was validated through simulations and experiments, which revealed superior estimation accuracy and reliability compared to the conventional FastSLAM. Pei et al. [19] advanced the FastSLAM system by implementing a distributed structure, resulting in a more robust system for autonomous robot navigation. Their system employs a distributed unscented particle filter and a linear observation model, effectively addressing the computational challenges and potential faults triggered by changing feature points. The algorithm’s convergence was mathematically proven in the mean square sense, and simulations confirmed the algorithm’s ability to reduce computational complexity while sustaining high estimation accuracy and system fault tolerance. These findings underscore the distributed potential for enhancing robotic navigation in complex environments.

Lei et al. [20] proposed a novel framework termed IFastSLAM, which enhances the performance of the conventional FastSLAM algorithm by integrating PSO. They introduced an adaptive genetic algorithm for resampling to increase particle diversity and employed fractional differential theory and chaotic optimization to refine the PSO approach. This innovation accelerated the algorithm’s iteration and prevented premature convergence, leading to superior performance in simulations and field experiments. Yasuda et al. [21] presented a strategy to augment the precision of self-positioning in FastSLAM by considering multiple candidate particles. This approach stored several candidates and utilized them to determine the next step’s self-position estimate. By maintaining multiple particles, the proposed method achieved more robust self-position estimation and mapping compared to the traditional FastSLAM. The performance was evaluated through numerical simulations, demonstrating improved accuracy with an increase in candidate particles. Karacam et al. [22] developed an improved adaptive FastSLAM algorithm known as AFastSLAM, which incorporates a time-varying noise estimator. This algorithm utilized maximum likelihood estimation, expectation maximization criterion, and a one-step smoothing algorithm in importance sampling to enhance the FastSLAM method. The AFastSLAM algorithm was shown to provide significantly more accurate and consistent estimates for both robot and landmark positions across various simulations with different initial process and measurement noise values.

The advancements in FastSLAM have been marked by significant strides, with researchers introducing various innovative approaches to enhance its performance. From the introduction of FastSLAM 2.0, which employs sophisticated particle filtering techniques, to the integration of genetic algorithms and fractional differential theory, each improvement aims to address specific challenges such as particle depletion and the linear approximation of non-linear functions. These enhancements have collectively contributed to more efficient particle utilization, improved estimation accuracy, and enhanced system robustness in the face of dynamic environments and high motion noise.

Building on these foundational improvements, our proposed FastSLAM-MO-PSO algorithm introduces a multi-objective optimization approach to further optimize the SLAM process. By harnessing the strengths of MO-PSO, our algorithm aims to achieve a more balanced and comprehensive optimization of the SLAM process. With the FastSLAM-MO-PSO, we aim to leverage the collective benefits of these advancements, offering a robust solution that stands to meet the demands of modern autonomous navigation challenges.

4. FastSLAM-MO-PSO

The FastSLAM-MO-PSO algorithm is designed to address the intricate interplay between direct measurement accuracy and environmental constraints in the domain of SLAM. Recognizing that traditional SLAM methods often struggle to balance the precision of direct measurements with the broader implications of environmental factors, this algorithm introduces a multi-objective optimization framework to concurrently optimize these aspects.

The core motivation behind this design is the acknowledgment that in SLAM, the accuracy of a robot’s pose estimation is not solely dependent on the measurement data, but is also significantly influenced by the environmental context. For instance, the presence of unexpected obstacles or the variability in sensor range can drastically affect the mapping outcome. By integrating MO-PSO with FastSLAM, the algorithm aims to achieve a more holistic optimization that considers both the fidelity of direct measurements and the adaptability to environmental constraints.

The FastSLAM-MO-PSO algorithm implements this dual focus through a sophisticated measurement probability model, where two distinct objectives are defined:

Direct Measurement Objective: This objective encapsulates the probability of accurate range measurements considering local measurement noise, the likelihood of detecting unexpected objects, and the scenario of not hitting any object or measurement failures. It is designed to maximize the probability of obtaining accurate and reliable direct measurements.

The Direct Measurement Objective focuses on the accuracy and reliability of measurements obtained from the sensor. In our implementation, this objective is mathematically formalized by incorporating the measured values z and the true values z_star. The calculation begins with the probability of measuring the correct range, denoted as prob_hit, which is computed using a normal distribution to account for local measurement noise:

$$prob\_hit={\displaystyle \frac{1}{\sqrt{2\mathrm{\pi }{\mathrm{\sigma }}_{\mathrm{hit}}^2}}}\exp \left(-{\displaystyle \frac{{(\mathrm{z}-{\mathrm{z}}_{\mathrm{star}})}^2}{2{\mathrm{\sigma }}_{\mathrm{hit}}^2}}\right)$$

(5)

where σ_hit = 20 represents the standard deviation of the measurement noise, indicating how much the measured values can deviate from the true value due to inaccuracies inherent in the sensor. Next, we calculate the probability of hitting unexpected objects, represented by prob_short. This probability is modeled using an exponential decay function:

$$prob\_short={\mathrm{\lambda }}_{\mathrm{short}}\times \exp \left(-{\mathrm{\lambda }}_{\mathrm{short}}\times \mathrm{z}\right)$$

(6)

In the above context, λ_short = 0.15 is the rate parameter of the exponential distribution, which determines how quickly the probability of hitting unexpected objects decreases with increasing distance.

The overall Direct Measurement Objective is expressed as:

$$obj1=p_{hit}\times prob\_hit+p_{short}\times prob\_short$$

(7)

where p_hit = 0.8 reflects the prior probability of obtaining accurate measurements, suggesting a strong reliability of the sensor. The value p_short = 0.05 indicates the prior probability of this event.

Environmental Constraint Objective: This objective accounts for the probability of random measurements within the sensor’s range and the constraints imposed by the maximum sensor range. It ensures that the mapping process is aware of and adapts to the environmental boundaries. We consider the probability of not hitting anything or experiencing measurement failures, denoted as prob_max:

$$prob\_max=\left\{\begin{array}{ll}1\hfill & if z=radar\_range\hfill \\ 0\hfill & otherwise\hfill \end{array}\right.$$

(8)

Finally, we incorporate the probability of random measurements, which we assume to be uniformly distributed within the radar’s range:

$$prob\_rand={\displaystyle \frac{1}{radar\_range}}$$

(9)

For the Environmental Constraint Objective, we aim to ensure that the SLAM algorithm is aware of its operational boundaries. This objective is formulated by combining the probabilities associated with boundary conditions and random measurements. The mathematical formalization is as follows:

$$obj2=p_{max}\times prob\_max+p_{rand}\times prob\_rand$$

(10)

where the parameter p_max = 0.1 reflects the prior probability of this occurrence, indicating that there is a 10% chance the sensor will detect a measurement at its maximum range. The parameter p_rand = 0.05 denotes the prior probability of receiving a random measurement.

The MO-PSO is designed to optimize two critical objectives in tandem, thereby enhancing the capability of particles to navigate the solution space more effectively. The velocity and position adjustments for these particles are steered by two key factors: the best solutions identified by individual particles, referred to as p_best, and the best solution discovered collectively by the swarm, termed g_best. This dual-steering mechanism ensures a balanced approach between venturing into unexplored territories and capitalizing on already promising areas.

Following the presentation of the MO-PSO flowchart in Figure 2, the algorithm’s detailed procedure unfolds as follows: Initially, the population P is generated based on the problem model, with dimensions of N × D, where N denotes the number of particles and D represents the dimensions of the decision space. In 2D mapping scenario, D is allocated to 3, corresponding to the x and y coordinates and the orientation angle θ. Subsequently, the primary Pareto front solution set is extracted from P and stored in an archive, acting as a reservoir for candidate solutions.

The iterative optimization loop then commences, signified by Gen, which denotes the number of generations. The loop initiates with g set to 0 and persists until it reaches the predetermined Gen, at which juncture the loop is terminated. Within each generation, an offspring population O is generated based on PSO operations. Given the multi-objective context, the g_best for each particle must serve the role of guidance within the objective space. The offspring population O is subsequently evaluated and amalgamated with the original population P. From this consolidated population, the primary Pareto front is selected and incorporated into the archive, ensuring that all solutions within the archive are mutually non-dominating. To uphold the original population size of N, density-based selection is applied to eliminate excess solutions, thereby ensuring the population remains at N.

Ultimately, the solutions within the archive are utilized to initialize the particles prior to particle filtering, with the objective of achieving preemptive optimization. Should the number of solutions in the archive fall short for particle filtering, the solutions within the archive are replicated and subjected to Gaussian perturbation to expand the solution set. This strategic introduction of MO-PSO not only enriches the diversity of the solution space, but also enhances the algorithm’s responsiveness to the intricacies of the mapping environment.

5. Experiments

In this section, we present a rigorous experimental framework designed to thoroughly assess the efficacy of our proposed FastSLAM-MO-PSO algorithm. The experimental setup is structured around four principal components to provide a comprehensive evaluation. Firstly, we have established a novel benchmark for evaluating FastSLAM and its variants, which encompasses three distinct environments—small, medium, and large—along with various environmental elements that are typically encountered in practical scenarios. This benchmark is crafted to challenge the algorithms with real-world complexities, thereby providing an accurate assessment of their performance under genuine conditions. Secondly, we conduct a comparative analysis involving the original FastSLAM, its single-objective variant FastSLAM-PSO, the differential evolution-based FastSLAM-DE [23], and the multi-objective variants FastSLAM-NSGA, FastSLAM-MODE, and our proposed FastSLAM-MO-PSO. This comparison underscores the performance benefits and the necessity of adopting a multi-objective approach in the context of FastSLAM-MO-PSO. Additionally, we conducted a time analysis across all algorithms to evaluate their efficiency. This analysis focuses on the inherent performance of the various algorithms, revealing their strengths in practical applications. This comprehensive evaluation is crucial for understanding not only how the algorithms perform in theory, but also how they can be effectively applied in practice. Lastly, we visually present the experimental results across different parameter settings. These visual representations serve as a graphical benchmark to intuitively demonstrate the effectiveness of our proposed algorithm. They allow for a direct comparison of performance across various experimental setups, effectively highlighting the performance disparities under different configurations. It is noteworthy that all the figures and visualizations presented throughout this manuscript have been generated using the Python language, ensuring reproducibility and facilitating further research in this domain.

For the experimental configuration, several parameters were carefully adjusted to optimize the performance of the FastSLAM-MO-PSO algorithm. The social constant c₂, which directs particles towards the swarm’s best position, and the cognitive constant c₁, responsible for steering particles towards their personal best positions, were both calibrated to 1.5. These values are pivotal for effectively balancing exploration and exploitation within the search space. The inertia weight, denoted as w, was set to 0.5 to maintain equilibrium between the global search for new solutions and the exploitation of already identified promising areas. To ensure a smooth start to the optimization process, the initial velocities of the particles, v_i, were set to zero, preventing any erratic behavior at the beginning of the iterations. Lastly, to maintain the integrity of the map and prevent particles from venturing outside the defined boundaries, the algorithm enforces constraints on the particle distribution.

5.1. Benchmark Introduction

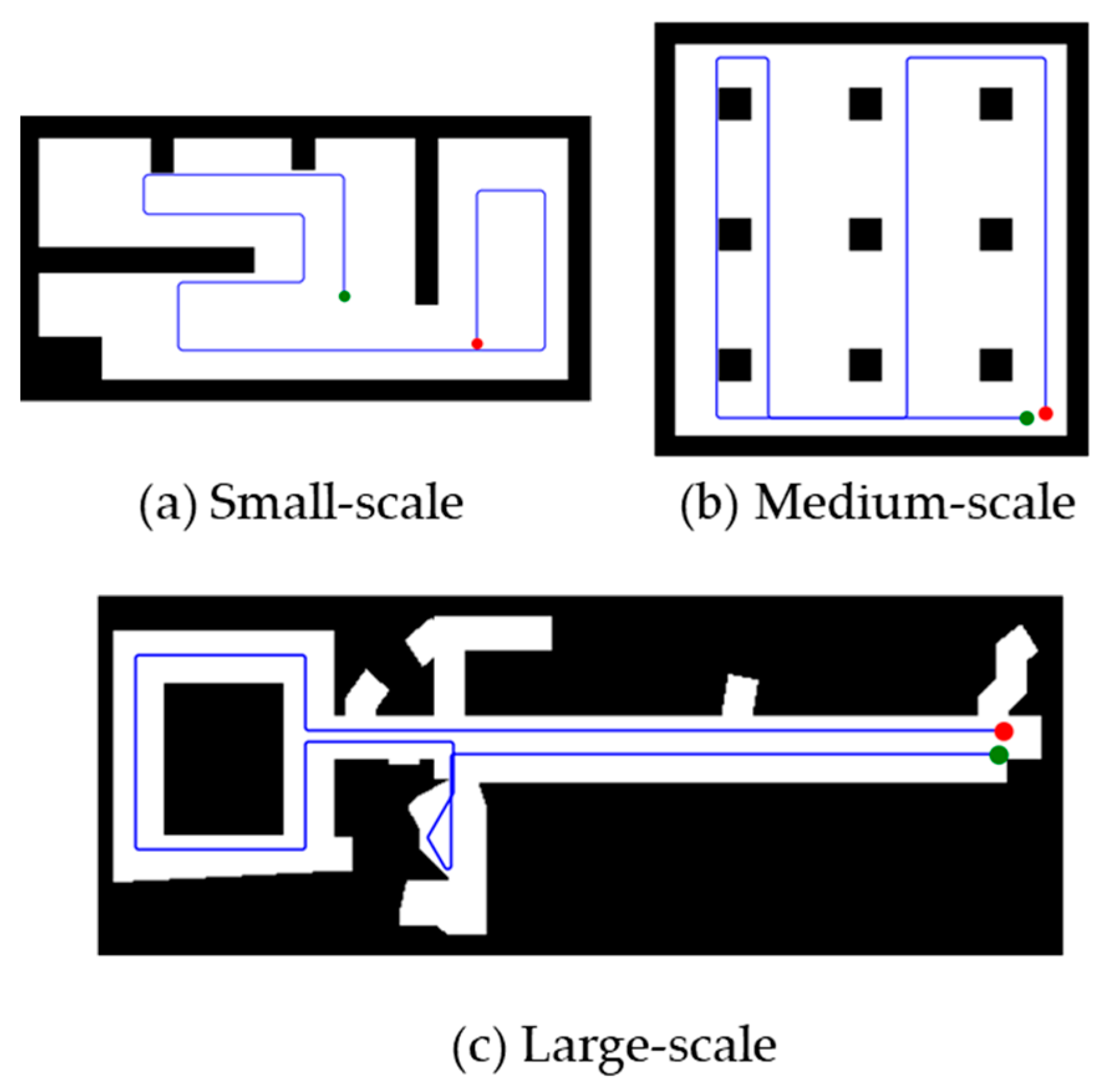
We have crafted a benchmark, as illustrated in Figure 3. Figure 3a depicts a modest environment characterized by well-defined obstacles and landmarks, which serves as a foundational testbed for evaluating the algorithm’s core competencies within a confined and predictable space. Figure 3b introduces a medium-scale scenario, incorporating a mix of open areas and densely packed obstacles, emulating a real-world environment replete with diverse topographical attributes. This scenario is designed to stress-test the SLAM algorithms, assessing their flexibility and adaptability in the face of varied and intricate spatial configurations. Advancing to a more complex setting, Figure 3c portrays a vast corridor, thereby increasing the intricacy for SLAM algorithms. The extensive corridor design is purposed to scrutinize the algorithm’s adeptness at managing large-scale spatial data and sustaining precise particle distribution across expansive areas. Collectively, these scenarios offer an extensive experimental framework for evaluating the performance of FastSLAM-MO-PSO. Within this simulation, all distances are represented in a single unit for consistency, which facilitates the comparison of different scenarios and the assessment of the algorithm’s performance without the need for real-world unit conversion. This unit is arbitrary and used solely for the purposes of this study, allowing for a standardized evaluation of the SLAM algorithm across various simulated environments. They enable a detailed evaluation of the algorithm’s map accuracy, trajectory estimation proficiency, and overall SLAM effectiveness across a spectrum of environmental scales and complexities.

Our experiments are conducted within simulated environments, which provide a controlled and reproducible testing ground. This approach offers several advantages, including the ability to systematically vary environmental parameters such as obstacle density, sensor noise levels, and initial position and orientation variations. Obstacle density, defined by the number and distribution of obstacles within the simulated environment, can significantly affect the navigation path and mapping accuracy. Sensor noise levels, which represent the degree of noise introduced into the sensor data, simulate different sensor qualities and environmental conditions, thereby influencing the algorithm’s performance. Initial position and orientation variations, determining the starting points and orientations of the robot, can impact the initial localization and subsequent mapping process. The simulated setting allows for a thorough exploration of the algorithm’s capabilities and limitations in a safe and controlled manner, ensuring that our findings are robust and applicable to a broad range of potential real-world applications. This methodology is not only efficient, but also aligns with best practices in algorithm development and validation, ensuring that our proposed FastSLAM-MO-PSO algorithm is rigorously tested and ready for practical deployment. Additionally, by concentrating on obstacle density, we have designed a relevant analysis in environments characterized by varying degrees of clutter.

5.2. Comparison Between FastSLAM and FastSLAM-PSO

5.2.1. Small-Scale Scenario

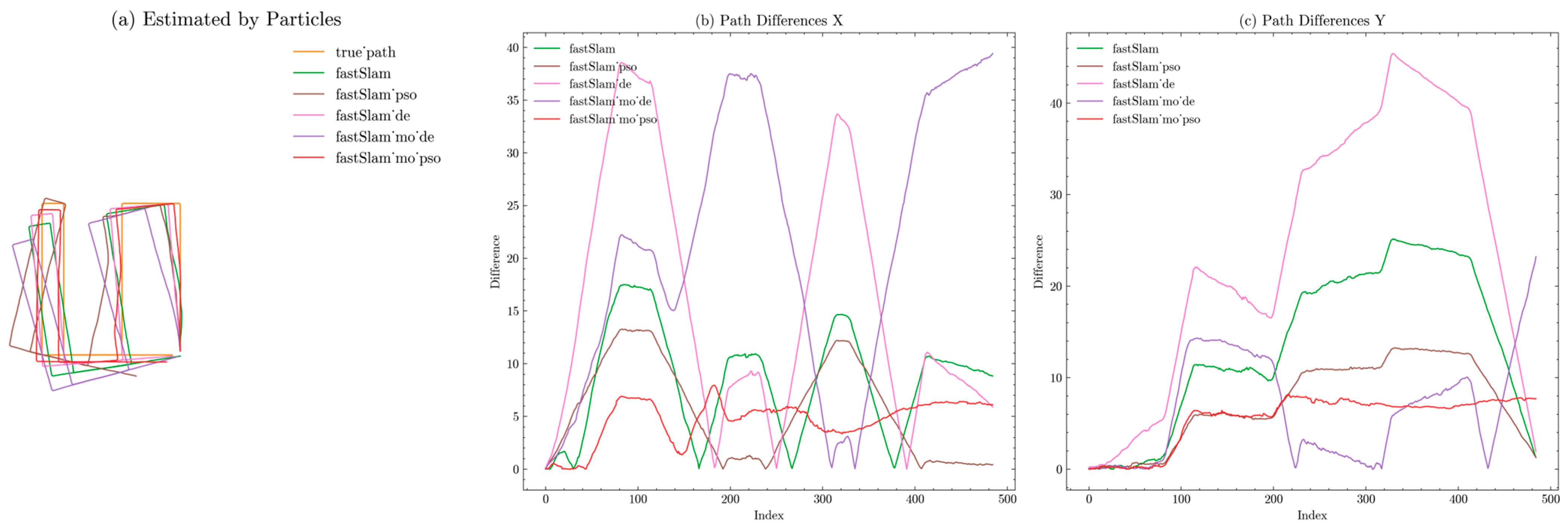
As shown in Figure 4, the true trajectory is depicted in orange, with FastSLAM in green, FastSLAM-PSO in brown, FastSLAM-DE in pink, FastSLAM-MO-DE in purple, and our proposed FastSLAM-MO-PSO in red. Figure 4a presents a comparative analysis of the estimated particle paths, revealing that the red path, representing FastSLAM-MO-PSO, exhibits the least overall deviation from the actual orange path. The figures depict the deviation of the estimated paths from the true path. A lower deviation indicates a closer alignment with the true path, signifying better performance. The y-axis in Figure 4, Figure 5 and Figure 6 represents this deviation, measured in the consistent arbitrary units used throughout our simulation. The performance of the SLAM algorithms is thus inversely related to the deviation shown; the smaller the deviation, the more accurate and robust the SLAM solution. This suggests a superior alignment with the true trajectory, underscoring the enhanced accuracy afforded by the integration of multi-objective optimization with PSO.

Figure 4b delves into the discrepancies between the algorithmic solutions and the true path along the x-axis. Here, FastSLAM-MO-PSO demonstrates consistent performance, closely followed by FastSLAM-PSO. While FastSLAM-MO-PSO experiences an increase in deviation mid-way, it recovers with improved accuracy in the later stages, potentially due to the inherent high-performance capabilities. Collectively, the algorithms augmented with evolutionary strategies, particularly FastSLAM-MO-PSO, significantly outperform the conventional FastSLAM, indicating the substantial benefits of incorporating evolutionary components. The initial segment of FastSLAM-MO-DE appears promising; however, it suffers from significant drift in the later stages. This could be attributed to the inherent search capabilities of DE, which may not be as adept as PSO in navigating complex environments. Overall, the PSO-based algorithms consistently demonstrate stronger performance than their DE counterparts.

This distinction is further accentuated in Figure 4c, where DE-integrated algorithms underperform in comparison to the original FastSLAM. This is likely due to the vertical distribution of the map scenario, creating a narrow, elongated structure along the Y-axis that challenges precise localization. Algorithms based on PSO, however, exhibit commendable performance, with FastSLAM-MO-PSO leading the pack. The superior performance of FastSLAM-MO-PSO can be attributed to the multi-objective optimization approach, which allows for a more nuanced exploration of the solution space. By simultaneously optimizing for multiple objectives, such as mapping accuracy and trajectory fidelity, the algorithm can better adapt to the intricacies of the environment. The PSO component significantly bolsters the algorithm’s performance by adeptly navigating through the intricate landscape, optimizing the distribution of particles, and swiftly adapting to local environmental variations. Its well-known balance of exploration and exploitation likely plays a crucial role in enhancing the precision with which sensor data-derived estimates are refined.

5.2.2. Medium-Scale Scenario

In the analysis of the medium-scale map experiment, we observed distinct trends among the various SLAM algorithms, highlighting the strengths of multi-objective optimization approaches, particularly FastSLAM-MO-PSO. The results are shown in Figure 5.

Considering the x-axis, all algorithms exhibited noticeable deviations during the initial 0–150 time steps, indicating the common challenges faced in accurately navigating the environment’s initial layout. Between 250 and 400 time steps, a trend of increasing deviation was observed across all algorithms except for the two multi-objective algorithms, FastSLAM-MO-DE and FastSLAM-MO-PSO. This suggests that non-multi-objective algorithms struggled to maintain accuracy over time, likely due to the accumulation of estimation errors and the complexity of dynamically updating the map and trajectory consistent with actual movements. This trend underscores the advantage of multi-objective algorithms in sustaining performance. Overall, FastSLAM-MO-PSO demonstrated consistent performance in map building, without significant fluctuations, while other algorithms showed considerable variation. This highlights the stability and robustness of the FastSLAM-MO-PSO algorithm. Concurrently, the medium-scale map experiment also revealed the superiority of PSO-based algorithms, with FastSLAM-MO-PSO leading in performance among all contenders.

On the y-axis, the performance trends were similar across all algorithms, indicating that they encountered comparable difficulties in the medium-scale map environment. FastSLAM-MO-PSO maintained a stable performance, whereas others exhibited significant instability with large fluctuations. This consistency in the latter part of the experiment can be attributed to the algorithm’s ability to leverage accumulated information effectively. However, the performance of FastSLAM-MO-DE deteriorated significantly in the later stages, deviating substantially from the endpoint. This substantial error is likely due to the inherent limitations of the DE algorithm in fine-tuning the trajectory accurately, especially in complex environments. In summary, the medium-scale map experiment reaffirms the resilience and reliability of the FastSLAM-MO-PSO algorithm. Its stable performance and ability to adapt to the evolving map with minimal deviation highlight the effectiveness of integrating multi-objective optimization with PSO. While all algorithms faced similar challenges, the multi-objective algorithms, especially FastSLAM-MO-PSO, showcased their superiority by maintaining a higher level of accuracy and stability throughout the experiment.

5.2.3. Large-Scale Scenario

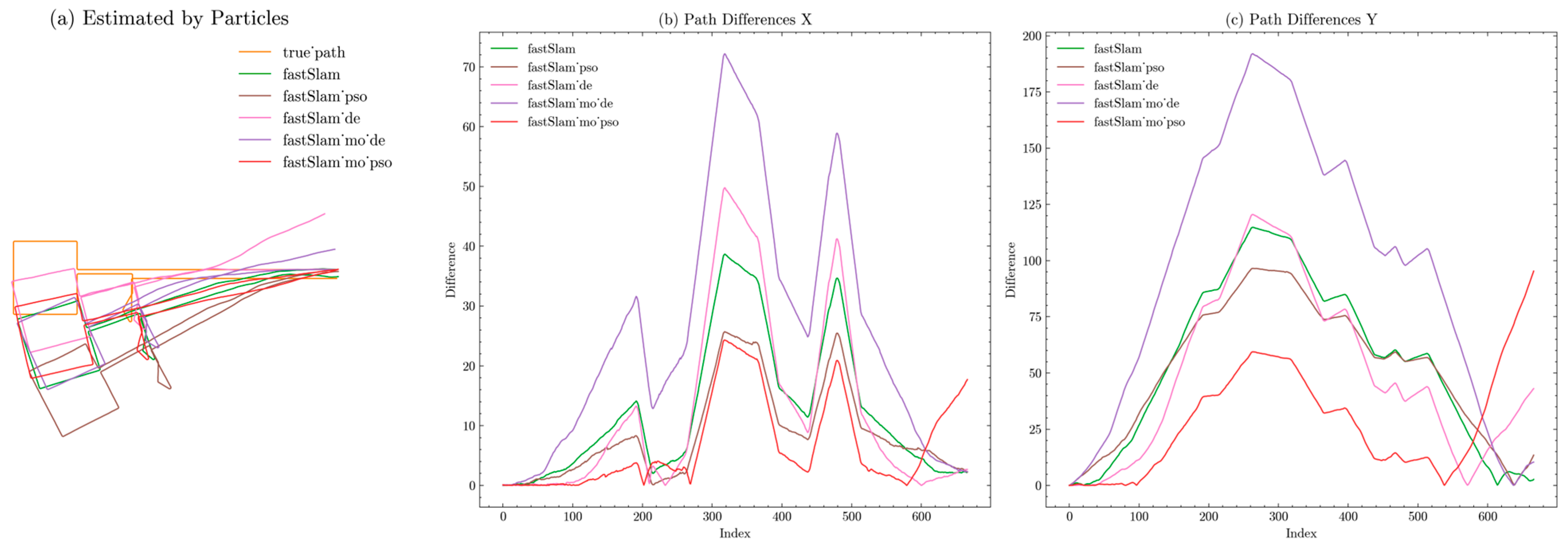
Figure 6 illustrates the outcomes of the algorithms in addressing the SLAM problem within a large-scale scenario. In the large-scale map experiment, the performance trends of all algorithms on both the x and y axes were consistent, indicating that the map design posed equivalent challenges to each algorithm. This uniformity in trend across algorithms suggests that the map effectively captured the complexities and nuances that are typically encountered in real-world environments, thereby validating the efficacy of the map design as a comprehensive testbed for SLAM algorithms.

The overall performance exhibited a bifurcated pattern. Algorithms that incorporated DE, such as FastSLAM-DE, tended to perform worse than the base FastSLAM algorithm. This could be attributed to the DE’s search mechanism, which may not have been adept at handling the intricate dynamics of large-scale maps, leading to suboptimal adjustments in the trajectory and map estimation. Conversely, algorithms that integrated PSO, particularly FastSLAM-PSO and FastSLAM-MO-PSO, demonstrated superior performance over the base FastSLAM. This enhancement underscores the effectiveness of PSO in optimizing particle distribution and enhancing the responsiveness of the SLAM process to environmental changes.

FastSLAM-MO-PSO maintained a relatively low deviation and led in performance for the majority of the experiment. However, a noticeable increase in error was observed towards the end. This late-stage deviation could be due to the increased complexity and variability in the map’s latter sections, which may have overwhelmed the algorithm’s capacity to maintain the same level of precision as in the earlier stages. The accumulation of small errors over a large and intricate map could also contribute to the final deviation, highlighting the need for further refinement in handling large-scale spatial data.

This experiment not only substantiated the effectiveness of the FastSLAM-MO-PSO algorithm, but also showcased the merits of the benchmark design. The large-scale map, with its inherent challenges, provided a robust platform for evaluating the algorithms’ capabilities in a manner that reflects real-world conditions. The ability of the benchmark to challenge the algorithms and reveal their strengths and weaknesses is a testament to its design, offering valuable insights into the performance characteristics of each SLAM variant. This comprehensive analysis serves as a foundation for further algorithmic improvements and provides a clear direction for future research in the field of SLAM.

5.3. Time Analysis

The experimental data presented in

Table 1. The time analysis results.

	FastSLAM	FastSLAM-DE	FastSLAM-PSO	FastSLAM-MO-DE	FastSLAM-MO-PSO
Scene_1	4101.973994 (s)	7867.448255 (s)	7140.355758 (s)	7311.061464 (s)	6462.207688 (s)
Scene_2	7334.884456 (s)	16,145.49226 (s)	15,157.19925 (s)	13,401.55571 (s)	11,099.08987 (s)
Scene_3	6159.537662 (s)	12,651.76538 (s)	11,456.88336 (s)	8440.059285 (s)	70,362.45773 (s)

elucidates the comparative mapping times of various SLAM algorithms across three diverse scenarios. While FastSLAM records the swiftest mapping times, algorithms that integrate optimization techniques, such as PSO, exhibit markedly better performance in accuracy and robustness, albeit with modest increases in runtime. Both FastSLAM-PSO and FastSLAM-MO-PSO show longer mapping times compared to FastSLAM, but demonstrate significantly enhanced performance. This trade-off signifies the algorithms’ capacity for a more exhaustive exploration of the solution space, culminating in improved mapping results. Notably, FastSLAM-MO-PSO, which embraces a multi-objective optimization strategy, surpasses FastSLAM-PSO, indicating that a multi-objective framework excels at balancing the competing requirements of mapping precision and computational expedience.

Moreover, the results indicate that PSO-based algorithms, namely FastSLAM-PSO and FastSLAM-MO-PSO, exhibit shorter runtimes compared to their DE counterparts, FastSLAM-DE and FastSLAM-MO-DE. This suggests that PSO is more adept at steering the optimization process within the SLAM framework. The dynamic velocity and position update mechanisms of PSO likely contribute to its efficiency, as they empower particles to adapt more fluidly to the evolving landscape of the solution space. Conversely, DE’s mutation and crossover operations may introduce unwarranted complexity, leading to extended runtimes, particularly in more intricate scenarios.

In conclusion, the experimental analysis across varying scenarios consistently illustrates that the integration of multi-objective optimization, notably PSO, into the SLAM process yields superior mapping performance compared to conventional and single-objective approaches. The enhanced accuracy and robustness of FastSLAM-MO-PSO, despite its slightly longer runtime, highlight the advantages of adopting a multi-objective optimization strategy for SLAM algorithms. This strategy not only elevates the quality of mapping outcomes, but also lays a more dependable foundation for autonomous navigation in complex environments.

5.4. Analysis of Mapping Results

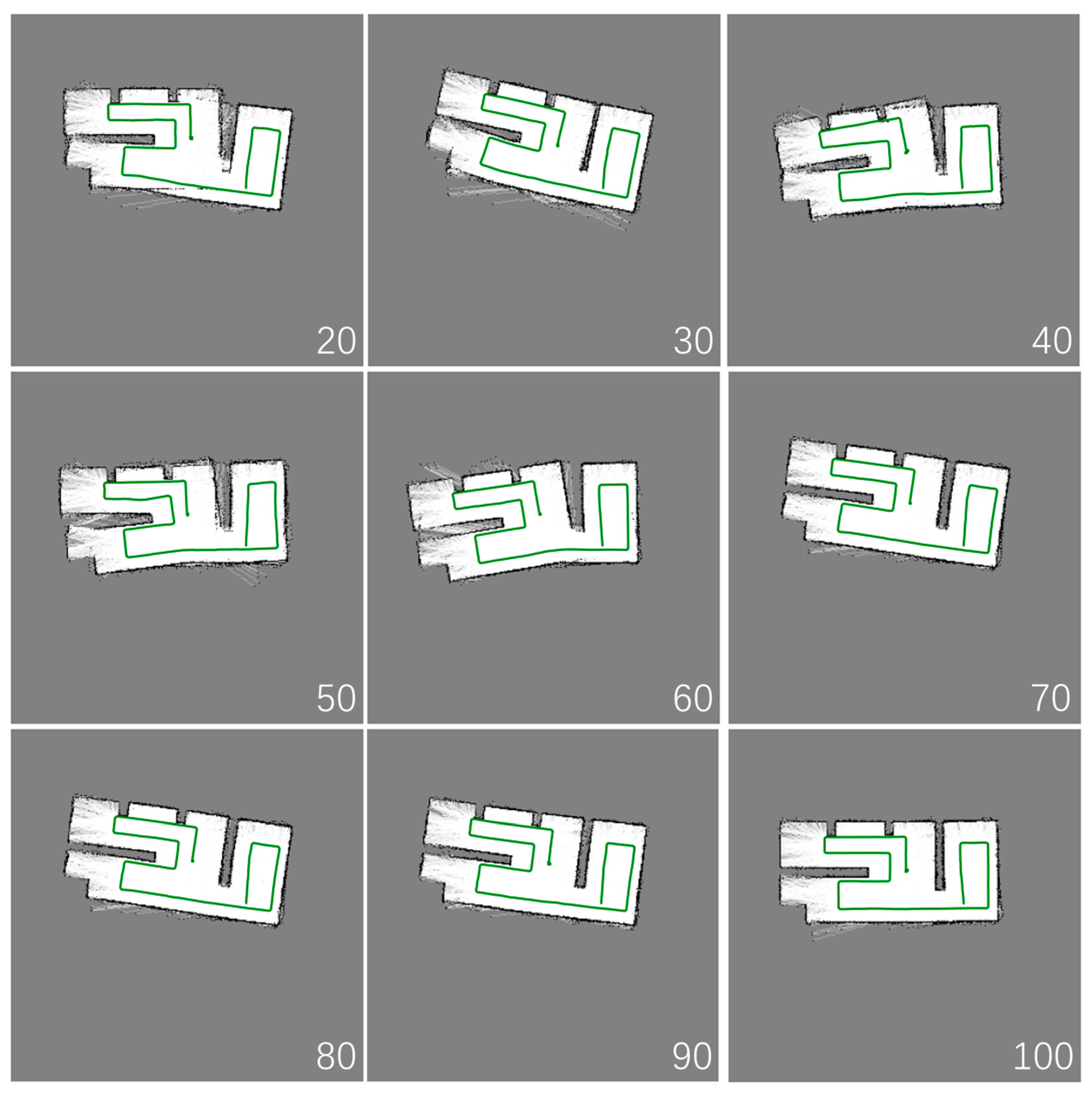
As illustrated in Figure 7, our experiments in Scenario 1 systematically varied the particle count N from 20 to 100, commencing from N = 20 due to the poor mapping observed at N = 10. The results indicate a positive correlation between particle count and the quality of mapping and localization, underscoring the effectiveness of our algorithm and its dependence on an adequate number of particles for precise environmental representation.

The performance of the SLAM algorithm notably improves beyond a particle count of 70, suggesting this threshold as a critical point for the algorithm to efficiently model the environment. Particularly at N = 100, the algorithm yields mapping results that are not only accurate, but also stable in terms of overall direction, indicating a high level of performance. The maps generated are ready for direct application with minimal further optimization, signifying the algorithm’s readiness for practical use. While the outcomes at N = 80 and N = 90 are satisfactory, minor deficits in detail suggest room for fine-tuning to achieve perfection. The performance enhancement with an increased number of particles can be attributed to the algorithm’s ability to better approximate the posterior distribution of the robot’s pose and landmarks. A higher particle count facilitates a more detailed exploration of the state space, reducing uncertainty in the mapping process and leading to more precise localization.

However, the slight decrease in detail at N = 80 and N = 90 suggests that while a higher particle count improves overall performance, it also increases the computational load, potentially affecting the algorithm’s ability to refine details. This observation indicates an optimal range for the particle count, beyond which the law of diminishing returns may apply. In conclusion, the experiments conducted in Scenario 1 provide compelling evidence of the FastSLAM-MO-PSO algorithm’s sensitivity to the number of particles and its impact on mapping quality. The results validate the algorithm’s effectiveness within an optimal particle count range and highlight the need for a balanced approach to ensure both accuracy and computational efficiency.

In summary, the comprehensive experimental evaluation across varying scales and complexities has conclusively demonstrated the superior performance of the FastSLAM-MO-PSO algorithm in comparison to the conventional FastSLAM and its DE counterpart. The FastSLAM-MO-PSO algorithm, with its integration of Particle Swarm Optimization, has exhibited a heightened level of accuracy and robustness in mapping and trajectory tracking. This enhancement is attributed to the ability to effectively manage the optimization of particles, thereby mitigating the degradation typically associated with traditional SLAM approaches. The global search capabilities of PSO have been instrumental in refining the particle distribution, leading to a more reliable and precise estimation of the robot pose and the surrounding environmental landmarks. The experimental outcomes consistently show that FastSLAM-MO-PSO maintains its superiority in terms of mapping quality and localization accuracy, highlighting the benefits of integrating multi-objective optimization strategies into SLAM algorithms.

5.5. Analysis of the Impact of Environmental Factor Obstacle Density

In this section, we analyze the impact of obstacle density on the algorithm’s performance. It is important to note that obstacle density is independent of scenario size. Within our benchmark, the small-scale scenario presents the simplest scenario, while the medium-scale scenario poses the greatest challenge in terms of obstacle density, with the large-scale scenario falling somewhere in between.

In the simplest scenario with low obstacle density, all algorithms, including FastSLAM, FastSLAM-PSO, FastSLAM-DE, and FastSLAM-MO-PSO, performed relatively well. However, as indicated in Section 5.2.1, FastSLAM-MO-PSO showed a slight edge in terms of mapping accuracy and trajectory tracking, which can be attributed to its ability to optimize particle distribution effectively in less complex environments. The medium obstacle density scenario, as in Section 5.2.3, posed a more significant challenge. Here, the performance gap between the algorithms became more pronounced. While FastSLAM struggled with increased noise and potential particle degeneration, FastSLAM-PSO and FastSLAM-DE showed improvements, but were still outperformed by FastSLAM-MO-PSO. The integration of MO-PSO allowed for better adaptation to the environment’s complexities, as evidenced by the superior accuracy and robustness of FastSLAM-MO-PSO. In the high obstacle density scenario, as in Section 5.2.2, the differences in performance were most striking. FastSLAM-MO-PSO continued to demonstrate its superiority, maintaining a lower deviation from the true trajectory compared to the other algorithms. The challenges faced by FastSLAM and FastSLAM-DE in this scenario were more pronounced, with increased deviations and inaccuracies in mapping and localization. FastSLAM-MO-PSO’s multi-objective optimization approach allowed it to navigate the dense environment more effectively, showcasing its adaptability and robustness.

The comparative analysis of the algorithms across the three scenarios clearly indicates that FastSLAM-MO-PSO is the most robust and accurate SLAM solution under varying environmental conditions. As the obstacle density increases, the performance of traditional SLAM algorithms like FastSLAM declines, while FastSLAM-MO-PSO maintains its performance, demonstrating the benefits of multi-objective optimization in complex environments.

6. Conclusions

In this research, we introduced an innovative enhancement to the FastSLAM algorithm by integrating MO-PSO, creating the FastSLAM-MO-PSO framework. This integration addresses the critical challenges of particle degradation and the need for robustness in complex and dynamic SLAM scenarios. Our approach harnesses the multi-objective optimization capabilities of MO-PSO to balance the competing demands of mapping accuracy and computational efficiency, leading to a more holistic optimization of the SLAM process. The FastSLAM-MO-PSO algorithm employs a specialized fitness function that guides particles towards areas of higher posterior probability, thereby mitigating particle degradation and enhancing the overall robustness and accuracy of the SLAM solution. Through a series of comprehensive experiments, we demonstrated the effectiveness of our proposed method. The results consistently showed that FastSLAM-MO-PSO outperformed traditional particle filtering approaches, especially in terms of localization accuracy and resistance to particle degeneration.

The strength of FastSLAM-MO-PSO is its resilience in environments with high noise levels and large-scale spaces, where traditional SLAM algorithms often falter. Our algorithm effectively utilizes the global search capabilities of MO-PSO to optimize particle distribution, resulting in improved estimation accuracy and robustness. This advancement places FastSLAM-MO-PSO at the cutting edge of SLAM technology, offering a viable solution for real-world applications that demand high precision and reliability. The insights from this study underscore the potential of swarm intelligence techniques in enhancing SLAM algorithms. Our successful approach indicates that by refining particle distribution through multi-objective optimization, we can achieve superior SLAM performance even in challenging conditions characterized by high noise levels and expansive spaces. Future work will explore adaptive mechanisms that dynamically adjust particle counts and other MO-PSO parameters in real-time, based on environmental conditions and algorithmic states, further enhancing the adaptability and efficiency of SLAM in diverse operational scenarios.