A Method to Improve Underwater Positioning Reference Based on Topological Distribution Constraints of Multi-INSs

Abstract

This study investigates a data fusion method for underwater multi-inertial navigation based on topological distribution constraints, aimed at improving the positional accuracy of navigation systems on ships, and generating an underwater position reference. First, the state equation of single-axis rotational inertial navigation system (SRINS) is introduced to compensate for the equivalent gyroscope zero bias caused by gravity and magnetic field. Second, a flexible lever error equation based on the influence of flexural deformation angles between SRINSs is proposed. Third, by using the position difference between SRINSs as a measurement, the state and measurement equations of a centralized Kalman filter are analyzed. We conducted two sets of car experiments to verify the proposed data fusion method and a data acquisition system was used to synchronously collect measurement data from three SRINSs. Experimental results show that the proposed method can effectively improve overall positioning accuracy, with the root mean square (RMS) of longitude error reduced by approximately 8.4360%, latitude error RMS reduced by approximately 6.9174%, and overall positioning error RMS reduced by approximately 9.9492%. In certain conditions where other positioning methods are unavailable, such as underwater navigation, the proposed RINSs data fusion method can provide a highly reliable position reference.

1. Introduction

Rotational modulation technology can counteract constant errors in inertial navigation systems (INSs), and thus improve navigation accuracy [1,2]. In situations where absolute positioning methods are unavailable, like underwater, this technology can be used to generate a position reference. Single-axis rotating inertial navigation systems (SRINS) rotate around the azimuth axis of the inertial measurement unit (IMU) during the rotational modulation, effectively reducing the impact of gyroscope drift and accelerometer bias in the roll and pitch axes on positioning results [2]. Dual-axis RINSs and tri-axis RINSs rotate around multiple axes during their rotational modulations, theoretically compensating for all gyroscope drifts and accelerometer biases which affect the INS results [1,2]. However, dual-axis RINSs and tri-axis RINSs are large, costly, and less reliable. Therefore, it is necessary to study how to use an SRINS, which is simple in structure, resistant to shock and vibration, and low in cost, to achieve a high-accuracy underwater position reference.

From the perspective of improving the navigation accuracy of the SRINS itself, researchers have conducted extensive explorations [3,4,5]. Wang Z et al. focused on the impact of the temperature field on the performance of the IMU in SRINSs and proposed a multivariate regression method with a temperature gradient and a BP neural network method considering the coupling items of temperature variables, improving the navigation accuracy of SRINSs by up to 47.41% [3]. Li K et al. used horizontal accelerometer outputs, horizontal attitude errors, and heading angles as measurements for the Kalman filter to design an online self-calibration scheme, estimating non-repeatable errors at system startup and improving the positional accuracy of SRINSs by about 50% [4]. Therefore, the research on improving the accuracy of the SRINS itself is already quite sufficient. To further improve positioning accuracy, other measurement devices must be introduced to constrain the inertial navigation calculations.

To ensure the safety and reliability of navigation, a ship’s center is equipped with a high-precision central INS and multiple lower-precision backup INSs [6]. Additionally, weapon systems are equipped with low-precision INSs on their platforms to ensure targeting accuracy. Therefore, multi-INS data fusion technology is commonly used in transfer alignment. To ensure the alignment accuracy, it is necessary to maintain the temporal and spatial consistency between the primary and secondary INSs [7,8,9]. Kuznetsov I. M. estimated the time synchronization errors during the transfer alignment process, finding that for primary and secondary INSs with time delays of 500 ms and 750 ms, the time estimation errors could reach 20 ms and 60 ms, respectively [7]. Yang J. modeled the dynamic flexible lever arms during the transfer alignment process, establishing a measurement model that matches relative attitude angles and flexible lever arms, thereby reducing the misalignment angle errors of the secondary INSs [8]. However, transfer alignment technology is only used during the alignment process. After alignment, the secondary INSs navigate independently without information exchange with the primary INS. Additionally, transfer alignment mainly focuses on improving the alignment accuracy of the secondary INSs, with little research on enhancing the accuracy of the primary INS [9,10].

To fully utilize the measurement information from multiple INSs on ships and improve the overall positioning accuracy of redundant INSs, many scholars have studied data fusion methods [11,12,13,14,15,16]. Wu Q. used two dual-axis RINSs with different rotation paths to estimate the gyroscope and accelerometer biases [11,12,13]. Ming Hua estimated the installation deviation angles between two INSs, achieving a misalignment estimation error of only $1^{″}$ [15]. Wang M. performed self-calibration of two INSs every four minutes, estimating and compensating for installation errors and misalignment angle errors [16]. These methods can estimate the errors of redundant INSs and compensate for them during navigation calculations individually, thereby improving navigation accuracy.

To obtain comprehensive position information, Qiu T. designed a multi-INS data fusion method based on confidence analysis, which improved navigation accuracy and system reliability [17]. Liang W. developed a velocity error prediction model that predicts and compensates for the velocity errors caused by inertial sensor errors, in order to enhance the overall positioning accuracy [18,19,20]. The aforementioned studies assume that the lever arms between multiple RINSs are constant. However, Li X. found that the ship deformation affects the navigation accuracy of multi-INS data fusion [21]. As a result, it is necessary to analyze the function of flexible lever arms to improve overall fusion accuracy. Additionally, Cai Q. and his colleagues discovered that rotational modulation technology cannot modulate the equivalent gyroscope geographic zero bias caused by the Earth’s gravity and magnetic fields [22,23]. Therefore, this error must be considered when establishing the error equations for RINSs.

This study focuses on three sets of SRINSs and proposes a Kalman data fusion filtering equation for multiple INSs under the constraint of topologically distributed flexible arms. The major contributions of this study are as follows. (1) Considering the equivalent gyro geographic zero bias that cannot be modulated by the SRINS, the state equation and state transition matrix are improved and optimized. (2) A model is established between the flexible lever arms and dynamic deformation angles of RINSs installed at different positions, laying a theoretical foundation for the derivation of the measurement equation. (3) A data acquisition device is used to send One Pulse Per Second (1PPS) synchronization signals to multiple RINSs and simultaneously collect measurement data from these RINSs, ensuring the time consistency of the measurement data. The novelty of the proposed method lies in using the flexible lever arms between three SRINSs as a constraint condition and the position difference between these RINSs as a measurement, and thereby improving the overall positioning accuracy of the RINSs.

The remainder of this paper is organized as follows. Section 2 defines the coordinate systems and proposes the state equation of the SRINS, including the equivalent gyro geographic zero bias. The relationship between the flexible lever arms and the flexural deformation angle is derived in Section 3. Section 4 establishes a 63-dimensional Kalman filtering equation by using the 45-dimensional state quantities of the three SRINSs, as well as the lever arms, flexural deformation angles, and flexural deformation angle rates between RINSs. Section 5 verifies the Kalman filtering equation established in Section 4 through car trials, and analyzes the lever arm estimation results and positioning errors in the data fusion process. Finally, the conclusion based on this work is given in Section 6.

2. Single-Axis Rotating Inertial Navigation Systems

2.1. Definition of an SRINS Coordinate System

Before introducing the error equations of the SRINS, it is necessary to define the relevant coordinate systems. The coordinate systems used in this paper mainly include the navigation coordinate system (n-frame, the body coordinate system (b-frame), the platform coordinate system (p-frame), and the IMU measurement coordinate system (t-frame). The n-frame is represented by $o_n{x}_n{y}_n{z}_n$, with $o_n{x}_n$ pointing to the geographic east, $o_n{y}_n$ pointing to the geographic north, and $o_n{z}_n$ pointing upward, perpendicular to the local rotating ellipsoid surface. The b-frame is represented by $o_b{x}_b{y}_b{z}_b$, with $o_b{x}_b$ pointing to the right along the transverse axis of the body, $o_b{y}_b$ pointing forward along the longitudinal axis of the body, and $o_b{z}_b$ pointing upward, perpendicular to the body. The attitude matrix of the b-frame relative to the n-frame is represented by $C_b^n$.

Since the IMU of the INS is fixed to the platform of the rotation mechanism, the t-frame can be considered to coincide with the p-frame. Generally, an SRINS uses the z axis as its rotation axis. Assuming that at the initial moment, the b-frame coincides with the p-frame, when rotating counterclockwise around the z axis at an angular velocity $\omega$ (as shown in Figure 1), the attitude matrix between the b-frame and the p-frame can be expressed as:

$${\mathit{C}}_b^p=\left[\begin{array}{ccc}cos\omega t& sin\omega t& 0\\ -sin\omega t& cos\omega t& 0\\ 0& 0& 1\end{array}\right]$$

(1)

Figure 1. Rotation Diagram.

The rotation path of the SRINS used in this paper is shown in Figure 2. The IMU rotates back and forth at an angular velocity of $6^{\circ }$/s. During one modulation cycle, the rotation mechanism controls the IMU to rotate clockwise for one full turn, and then immediately rotate counterclockwise for one full turn. There is no time interval between the two modulation cycles.

Figure 2. Schematic Diagram of SRINS Rotating Paths.

During the rotational modulation, the constant drift of the gyroscope and the zero bias of the accelerometer in the b-frame for an SRINS can be expressed as follows:

$${\mathsf{\epsilon }}^b={\mathit{C}}_p^b\left(t\right){\mathsf{\epsilon }}^p=\left[\begin{array}{ccc}cos\omega t& -sin\omega t& 0\\ sin\omega t& cos\omega t& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\hfill {\epsilon }_x^p\hfill \\ \hfill {\epsilon }_y^p\hfill \\ \hfill {\epsilon }_z^p\hfill \end{array}\right]=\left[\begin{array}{c}{\epsilon }_x^{p}cos\omega t-{\epsilon }_y^{p}sin\omega t\\ {\epsilon }_x^{p}sin\omega t+{\epsilon }_y^{p}cos\omega t\\ {\epsilon }_z^p\end{array}\right]$$

(2)

$${\nabla }^b={\mathit{C}}_p^b\left(t\right){\nabla }^p=\left[\begin{array}{ccc}cos\omega t& -sin\omega t& 0\\ sin\omega t& cos\omega t& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\nabla }_x^p\\ {\nabla }_y^p\\ {\nabla }_z^p\end{array}\right]=\left[\begin{array}{c}{\nabla }_x^{p}cos\omega t-{\nabla }_y^{p}sin\omega t\\ {\nabla }_x^{p}sin\omega t+{\nabla }_y^{p}cos\omega t\\ {\nabla }_z^p\end{array}\right]$$

(3)

From the equations above, it can be seen that the constant drift of the gyroscope and the zero bias of the accelerometer perpendicular to the axis are modulated into sinusoidal signals. Therefore, using the modulation method shown in Figure 2, the equivalent constant drift of the gyroscope and the equivalent zero bias of the accelerometer in the b-frame within one modulation cycle can be expressed as follows:

$$\begin{array}{c}{\displaystyle \frac{1}{T}}{\int }_0^T{\epsilon }^{b}dt={\displaystyle \frac{1}{T}}({\int }_0^{T/2}{\epsilon }^{b}dt+{\int }_{T/2}^T{\epsilon }^{b}dt)\hfill \\ ={\displaystyle \frac{1}{T}}\left({\int }_0^{T/2}\left[\begin{array}{c}{\epsilon }_x^{p}cos\omega t-{\epsilon }_y^{p}sin\omega t\\ {\epsilon }_x^{p}sin\omega t+{\epsilon }_y^{p}cos\omega t\\ {\epsilon }_z^p\end{array}\right]dt+{\int }_{T/2}^T\left[\begin{array}{c}{\epsilon }_x^{p}cos\omega t+{\epsilon }_y^{p}sin\omega t\\ -{\epsilon }_x^{p}sin\omega t+{\epsilon }_y^{p}cos\omega t\\ {\epsilon }_z^p\end{array}\right]dt\right)\hfill \\ =\left[\begin{array}{c}0\\ 0\\ {\epsilon }_z^p\end{array}\right]\hfill \end{array}$$

(4)

$$\begin{array}{c}{\displaystyle \frac{1}{T}}{\int }_0^T{\nabla }^{b}dt={\displaystyle \frac{1}{T}}({\int }_0^{T/2}{\nabla }^{b}dt+{\int }_{T/2}^T{\nabla }^{b}dt)\hfill \\ ={\displaystyle \frac{1}{T}}\left({\int }_0^{T/2}\left[\begin{array}{c}{\nabla }_x^{p}cos\omega t-{\nabla }_y^{p}sin\omega t\\ {\nabla }_x^{p}sin\omega t+{\nabla }_y^{p}cos\omega t\\ {\nabla }_z^p\end{array}\right]dt+{\int }_{T/2}^T\left[\begin{array}{c}{\nabla }_x^{p}cos\omega t+{\nabla }_y^{p}sin\omega t\\ -{\nabla }_x^{p}sin\omega t+{\nabla }_y^{p}cos\omega t\\ {\nabla }_z^p\end{array}\right]dt\right)\hfill \\ =\left[\begin{array}{c}0\\ 0\\ {\nabla }_z^p\end{array}\right]\hfill \end{array}$$

(5)

Therefore, by using periodic rotational modulation technology, the zero bias in the roll and pitch axes of the SRINS in the b-frame can be modulated to zero, thereby reducing navigation errors. However, the heading axis bias cannot be effectively modulated, so for the SRINS, the biases of the gyroscope and accelerometer on the z-axis still exist and need to be considered when establishing the state equations of the SRINS.

2.2. Error Model of the SRINS

In the p-frame, the actual angular velocity and specific force sensed by the IMU are represented by ${\mathsf{\omega }}_{ip}^p$ and ${\mathit{f}}_{ip}^p$, respectively, and they satisfy the following conditions:

$$\left\{\begin{array}{c}{\mathsf{\omega }}_{ip}^p={\mathit{C}}_b^p{\mathsf{\omega }}_{ib}^b+{\mathsf{\omega }}_{bp}^p\\ {\mathit{f}}_{ip}^p={\mathit{C}}_b^p{\mathit{f}}_{ib}^b+{\mathit{f}}_{bp}^p\end{array}\right.$$

(6)

In the p-frame, the platform only has an angular velocity in the z-direction relative to the b-frame, and there are no linear accelerations, so:

$${\mathsf{\omega }}_{bp}^p={\left[\begin{array}{ccc}0& 0& \omega \end{array}\right]}^T$$

$${\mathit{f}}_{bp}^p=\mathbf{0}$$

If the measurement errors are represented by $\delta {\mathsf{\omega }}_{ip}^p$ and $\delta {\mathit{f}}_{ip}^p$, then the angular velocity and specific force measured by the IMU can be expressed as:

$$\left\{\begin{array}{c}{\tilde{\mathsf{\omega }}}_{ip}^p={\mathsf{\omega }}_{ip}^p+\delta {\mathsf{\omega }}_{ip}^p\\ {\tilde{\mathit{f}}}_{ip}^p={\mathit{f}}_{ip}^p+\delta {\mathit{f}}_{ip}^p\end{array}\right.$$

(7)

If the control error of the indexing mechanism is ignored, then:

$$\delta {\mathsf{\omega }}_{ip}^p={\mathit{C}}_b^p\delta {\mathsf{\omega }}_{ib}^b+\delta {\mathsf{\omega }}_{bp}^p={\mathit{C}}_b^p\delta {\mathsf{\omega }}_{ib}^b$$

$$\delta {\mathit{f}}_{ip}^p={\mathit{C}}_b^p\delta {\mathit{f}}_{ib}^b+\delta {\mathit{f}}_{bp}^p={\mathit{C}}_b^p\delta {\mathit{f}}_{ib}^b$$

According to the error equations of the strapdown inertial navigation system (SINS) provided in  [24], the error equation of the SRINS can be expressed as:

$$\begin{array}{c}\dot{\varphi }=-{\mathsf{\omega }}_{in}^n\times \varphi +\delta {\mathsf{\omega }}_{in}^n-{\mathit{C}}_b^n{\mathit{C}}_p^b\delta {\mathsf{\omega }}_{ip}^p\hfill \\ \delta \dot{\mathit{v}}={\mathit{f}}^n\times \varphi -(2\delta {\mathsf{\omega }}_{ie}^n+\delta {\mathsf{\omega }}_{en}^n)\times {\mathit{v}}^n-(2{\mathsf{\omega }}_{ie}^n+{\mathsf{\omega }}_{en}^n)\times \delta {\mathit{v}}^n+{\mathit{C}}_b^n{\mathit{C}}_p^b\delta {\mathit{f}}_{ip}^p+\delta {\mathit{g}}^n\hfill \\ \delta \dot{L}={\displaystyle \frac{1}{R_M+h}}\delta v_N-{\displaystyle \frac{v_N}{{(R_M+h)}^2}}\delta h\hfill \\ \delta \dot{\lambda }={\displaystyle \frac{secL}{R_N+h}}\delta v_E+{\displaystyle \frac{v_{E}secLtanL}{R_N+h}}\delta L-{\displaystyle \frac{v_{E}secL}{{(R_N+h)}^2}}\delta h\hfill \\ \delta \dot{h}=\delta v_U\hfill \end{array}$$

(8)

In the equation above, $\varphi$ represents the misalignment angle error from the n-frame to the computational coordinate system (n’-frame), so the actual direction cosine matrix is:

$${\mathit{C}}_b^n={\mathit{C}}_{n^{\prime }}^n{\mathit{C}}_b^{n^{\prime }}=(\mathit{I}+\varphi \times ){\mathit{C}}_b^{n^{\prime }}$$

${\mathit{v}}^n$ represents the velocity in the n-frame; $\delta {\mathit{v}}^n$ represents the velocity error, and $\delta {\mathit{v}}^n=\left[\begin{array}{ccc}\delta v_E& \delta v_N& \delta v_U\end{array}\right]$; L, $\lambda$, h represent the latitude, longitude, and altitude in the n-frame, respectively; $\delta L$, $\delta \lambda$, $\delta h$ represent the latitude, longitude, and altitude errors, respectively; $R_M$ and $R_N$ represent the meridian radius of curvature and the prime vertical radius of curvature; and ${\mathsf{\omega }}_{ie}^n$ and ${\mathit{g}}^n$ represent the Earth’s rotation angular velocity and the Earth’s gravitational acceleration.

2.3. State Equations of the SRINS

It is known that the single-axis rotation modulation technique can modulate the constant drift of the gyroscope and the accelerometer bias to zero in the roll and pitch axes in the b-frame. However, as indicated in references  [22,23], the gyroscope is affected by the gravitational field and the geomagnetic field, resulting in an equivalent bias in the geographic frame (g-frame, which is consistent with n-frame). This unmodulatable equivalent bias in the g-frame can cause significant errors in navigation results. Therefore, in this paper, zero biases ${\epsilon }_x^b$, ${\epsilon }_y^b$ modulated by rotating machine are replaced by the equivalent biases ${\epsilon }_x^n$, ${\epsilon }_y^n$ in the geographic frame. Due to the accelerometer’s sensitivity to the gravitational field and the geomagnetic field, its zero bias is still represented by ${\nabla }_x^b$ and ${\nabla }_y^b$.

The state equation for the SRINS can be written as:

$${\dot{\mathit{X}}}_{SRINS}={\mathit{F}}_{SRINS}{\mathit{X}}_{SRINS}+\mathit{Gu}$$

(9)

where ${\mathit{F}}_{SRINS}$ is the state transition matrix of the SRINS, $\mathit{u}$ is the state noise matrix, and $\mathit{G}$ is the state noise transition matrix.

The elements in the state vector are:

$${\mathit{X}}_{SRINS}={\left[\begin{array}{cccc}\varphi & \delta {\mathit{v}}^n& \delta {\mathit{p}}^n& \begin{array}{cc}\left[\begin{array}{ccc}\hfill {\epsilon }_x^n\hfill & {\epsilon }_y^n& {\epsilon }_z^b\end{array}\right]& {\nabla }^b\end{array}\end{array}\right]}^T$$

(10)

For the SRINS, ${\epsilon }_x^b$ and ${\epsilon }_y^b$ can be modulated. ${\nabla }^b$ represents the accelerometer bias. Therefore, ${\mathit{F}}_{SRINS}$ can be expressed as:

$${\mathit{F}}_{SRINS}=\left[\begin{array}{ccccc}{\mathit{F}}_{11}& {\mathit{F}}_{12}& {\mathit{F}}_{13}& {\mathit{F}}_{14}& {\mathit{O}}_{3\times 3}\\ {\mathit{F}}_{21}& {\mathit{F}}_{22}& {\mathit{F}}_{23}& {\mathit{O}}_{3\times 3}& {\mathit{F}}_{25}\\ {\mathit{O}}_{3\times 3}& {\mathit{F}}_{32}& {\mathit{F}}_{33}& {\mathit{O}}_{3\times 3}& {\mathit{O}}_{3\times 3}\\ & & {\mathit{O}}_{6\times 15}& & \end{array}\right]$$

(11)

where:

$${\mathit{F}}_{11}=-({\mathsf{\omega }}_{in}^n\times )$$

$${\mathit{F}}_{12}=\left[\begin{array}{ccc}0& -{\displaystyle \frac{1}{R_M+h}}& 0\\ {\displaystyle \frac{1}{R_N+h}}& 0& 0\\ {\displaystyle \frac{tanL}{R_N+h}}& 0& 0\end{array}\right]$$

$${\mathit{F}}_{13}=\left[\begin{array}{ccc}0& 0& {\displaystyle \frac{v_N}{{(R_M+h)}^2}}\\ -{\omega }_{ie}sinL& 0& -{\displaystyle \frac{v_E}{{(R_N+h)}^2}}\\ {\omega }_{ie}cosL+{\displaystyle \frac{v_E{sec}^{2}L}{R_N+h}}& 0& -{\displaystyle \frac{v_{E}tanL}{{(R_N+h)}^2}}\end{array}\right]$$

$${\mathit{F}}_{14}\approx \left[\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& -{\mathit{C}}_b^n(3,3)\end{array}\right]$$

$${\mathit{F}}_{21}=({\mathit{f}}^n\times )$$

$${\mathit{F}}_{22}=({\mathit{v}}^n\times )\left[\begin{array}{ccc}0& -{\displaystyle \frac{1}{R_M+h}}& 0\\ {\displaystyle \frac{1}{R_N+h}}& 0& 0\\ {\displaystyle \frac{tanL}{R_N+h}}& 0& 0\end{array}\right]-\left[(2{\mathsf{\omega }}_{ie}^n+{\mathsf{\omega }}_{en}^n)\times \right]$$

$$\left\{\begin{array}{c}\beta =0.00530240\\ {\beta }_1=0.00000582\\ {\beta }_2=3.08\times {10}^{-6}{s}^{-2}\\ {\beta }_3=8.08\times {10}^{-9}{s}^{-2}\end{array}\right.$$

$$\begin{array}{c}{\mathbf{F}}_{23}=({\mathbf{v}}^n\times )\left[\begin{array}{ccc}0& 0& {\displaystyle \frac{v_N}{{(R_M+h)}^2}}\\ -2{\omega }_{ie}sinL& 0& -{\displaystyle \frac{v_E}{{(R_N+h)}^2}}\\ 2{\omega }_{ie}cosL+{\displaystyle \frac{v_E{sec}^{2}L}{R_N+h}}& 0& -{\displaystyle \frac{v_{E}tanL}{{(R_N+h)}^2}}\end{array}\right]\hfill \\ +\left[\begin{array}{ccc}0& 0& 0\\ -2{\beta }_{3}hcos2L& 0& -{\beta }_{3}sin2L\\ -g_e(\beta -4{\beta }_{1}cos2L)sin2L& 0& {\beta }_2\end{array}\right]\hfill \end{array}$$

$${\mathit{F}}_{25}={\mathit{C}}_b^n$$

$${\mathit{F}}_{32}=\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h}}& 0\\ {\displaystyle \frac{secL}{R_N+h}}& 0& 0\\ 0& 0& 1\end{array}\right]$$

$${\mathit{F}}_{33}=\left[\begin{array}{ccc}0& 0& -{\displaystyle \frac{v_N}{{(R_M+h)}^2}}\\ {\displaystyle \frac{v_{E}secLtanL}{R_N+h}}& 0& -{\displaystyle \frac{v_{E}secL}{{(R_N+h)}^2}}\\ 0& 0& 0\end{array}\right]$$

3. The Model of Flexible Arm

3.1. Deformation Angle Modeling

Underwater vehicles can experience deformation due to impacts from water currents and their own loads. This deformation can cause changes in the lever arms between SRINSs installed at different positions, leading to changes in the positional relationship between the two SRINSs [21]. The flexural deformation can be represented as the sum of static and dynamic deformation angles. The static deformation angle does not change over time, while the dynamic deformation angle can be described using a second-order Markov process [25]:

$$\begin{array}{c}{\ddot{\theta }}_i+2{\beta }_i{\dot{\theta }}_i+{\beta }_i^2{\theta }_i={w^{\prime }}_i,i=x,y,z\hfill \\ {\beta }_i=2.146/{\tau }_i,i=x,y,z\hfill \end{array}$$

(12)

where ${\tau }_i$ represents the correlation time of the deformation angles along three axes, which is determined based on the operating environment and motion conditions of different carriers; ${\sigma }_i^2$ is the estimated variance of ${\theta }_i$, and $w_i^{\prime }$ is a random white noise with variance satisfying:

$$Q_i^{\prime }=4{\beta }_i^3{\sigma }_i^2(i=x,y,z)$$

Let $\theta \left(t\right)$ be the flexural deformation angle and $\mu \left(t\right)$ be the rate of change of the flexural deformation angle, satisfying $\mu \left(t\right)=\dot{\theta }\left(t\right)$ at time t, then we have:

$$\left\{\begin{array}{c}\hfill {\dot{\theta }}_x\left(t\right)={\mu }_x\left(t\right)\hfill \\ \hfill {\dot{\theta }}_y\left(t\right)={\mu }_y\left(t\right)\hfill \\ \hfill {\dot{\theta }}_z\left(t\right)={\mu }_z\left(t\right)\hfill \end{array}\right.$$

(13)

Then, the differential equation for the dynamic deformation angle can be written as:

$$\left\{\begin{array}{c}\hfill {\dot{\mu }}_x\left(t\right)=-{\beta }_x^2{\theta }_x\left(t\right)-2{\beta }_x{\omega }_x\left(t\right)+{w^{\prime }}_x\left(t\right)\hfill \\ \hfill {\dot{\mu }}_y\left(t\right)=-{\beta }_y^2{\theta }_y\left(t\right)-2{\beta }_y{\omega }_y\left(t\right)+{w^{\prime }}_y\left(t\right)\hfill \\ \hfill {\dot{\mu }}_z\left(t\right)=-{\beta }_z^2{\theta }_z\left(t\right)-2{\beta }_z{\omega }_z\left(t\right)+{w^{\prime }}_z\left(t\right)\hfill \end{array}\right.$$

(14)

3.2. Relationship Between Lever Arms and Deformation Angles

In the coordinate system of $SRIN{S}_1$, it is observed that $SRIN{S}_2$ rotates ${\theta }_x^{p_1}$ around the x-axis. In the coordinate system of $SRIN{S}_2$, it is sensed that its own p-frame rotates ${\theta }_x^{p_2}$ around the x-axis, as shown in Figure 3. In Figure 3, $o_1$ represents the center of $SRIN{S}_1$; $o_2^{\prime }$ represents the original center of $SRIN{S}_2$; $o_2$ represents the new center of $SRIN{S}_2$ after undergoing flexural deformation; and A is the center of the circular arc $o_1{o}_2$ corresponding to the flexural curve, and the y-axes of both $SRIN{S}_1$ and $SRIN{S}_2$ are tangent to this arc segment. Therefore, the relationship between ${\theta }_x^{p_1}$ and ${\theta }_x^{p_2}$ exists:

$${\theta }_x^{p_2}=2{\theta }_x^{p_1}$$

(15)

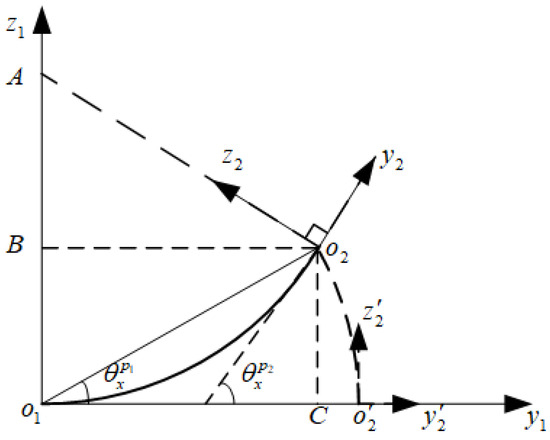
Figure 3. Schematic Diagram of Flexural Deformation Caused by ${\theta }_x^{p_1}$.

Let the lever arms between two SRINSs be ${\mathit{r}}_0^{p_1}=\left[\begin{array}{ccc}{r}_{x0}^{p_1}& r_{y0}^{p_1}& r_{z0}^{p_1}\end{array}\right]$, then:

$$o_{1}C=B{o}_2=A{o}_{2}sin{\theta }_x^{p_2}={\displaystyle \frac{r_{y0}^{p_1}}{{\theta }_x^{p_2}}}sin{\theta }_x^{p_2}$$

(16)

$$AB=A{o}_{2}cos{\theta }_x^{p_2}={\displaystyle \frac{r_{y0}^{p_1}}{{\theta }_x^{p_2}}}cos{\theta }_x^{p_2}$$

(17)

Then, the projection of the lever arm component $r_{y0}^{p_1}$ in the y, z direction under the influence of the flexural angle ${\theta }_x^{p_1}$ can be estimated as:

$$\left\{\begin{array}{c}\Delta r_y^{p_1}\left({\theta }_x^{p_1},r_{y0}^{p_1}\right)=o_{1}C-o_1{o^{\prime }}_2=-\left(1-{\displaystyle \frac{sin{\theta }_x^{p_2}}{{\theta }_x^{p_2}}}\right)r_{y0}^{p_1}\hfill \\ \Delta r_z^{p_1}\left({\theta }_x^{p_1},r_{y0}^{p_1}\right)=A{o}_1-AB={\displaystyle \frac{1-cos{\theta }_x^{p_2}}{{\theta }_x^{p_2}}}{r}_{y0}^{p_1}\hfill \end{array}\right.$$

(18)

In the same way, the projection of the lever arm component $r_{z0}^{p_1}$ in the y, z direction under the influence of the flexural angle ${\theta }_x^{p_1}$ can be estimated as:

$$\left\{\begin{array}{cc}\hfill \Delta r_y^{p_1}\left({\theta }_x^{p_1},r_{z0}^{p_1}\right)\hfill & =-{\displaystyle \frac{1-cos{\theta }_x^{p_2}}{{\theta }_x^{p_2}}}{r}_{z0}^{p_1}\hfill \\ \hfill \Delta r_z^{p_1}\left({\theta }_x^{p_1},r_{z0}^{p_1}\right)\hfill & =\left({\displaystyle \frac{sin{\theta }_x^{p_2}}{{\theta }_x^{p_2}}}-1\right)r_{z0}^{p_1}\hfill \end{array}\right.$$

(19)

Then, under the influence of the flexural angle ${\theta }_x^{p_1}$, the change in the lever arms in the y, z direction is:

$$\left\{\begin{array}{c}\hfill \Delta r_y^{p_1}\left({\theta }_x^{p_1}\right)=\left({\displaystyle \frac{sin{\theta }_x^{p_2}}{{\theta }_x^{p_2}}}-1\right)r_{y0}^{p_1}-\left({\displaystyle \frac{1-cos{\theta }_x^{p_2}}{{\theta }_x^{p_2}}}\right)r_{z0}^{p_1}\hfill \\ \hfill \Delta r_z^{p_1}\left({\theta }_x^{p_1}\right)=\left({\displaystyle \frac{1-cos{\theta }_x^{p_2}}{{\theta }_x^{p_2}}}\right)r_{y0}^{p_1}+\left({\displaystyle \frac{sin{\theta }_x^{p_2}}{{\theta }_x^{p_2}}}-1\right)r_{z0}^{p_1}\hfill \end{array}\right.$$

(20)

Under the influence of the flexural angle ${\theta }_y^{p_1}$, the change in the lever arms in the x, z direction is:

$$\left\{\begin{array}{cc}\hfill \Delta r_x^{p_1}\left({\theta }_y^{p_1}\right)\hfill & =\left({\displaystyle \frac{sin{\theta }_y^{p_2}}{{\theta }_y^{p_2}}}-1\right)r_{x0}^{p_1}+\left({\displaystyle \frac{1-cos{\theta }_y^{p_2}}{{\theta }_y^{p_2}}}\right)r_{z0}^{p_1}\hfill \\ \hfill \Delta r_z^{p_1}\left({\theta }_y^{p_1}\right)\hfill & =-\left({\displaystyle \frac{1-cos{\theta }_y^{p_2}}{{\theta }_y^{p_2}}}\right)r_{x0}^{p_1}+\left({\displaystyle \frac{sin{\theta }_y^{p_2}}{{\theta }_y^{p_2}}}-1\right)r_{z0}^{p_1}\hfill \end{array}\right.$$

(21)

Under the influence of the flexural angle ${\theta }_z^{p_1}$, the change in the lever arms in the x, y direction is:

$$\left\{\begin{array}{c}\hfill \Delta r_x^{p_1}\left({\theta }_z^{p_1}\right)=\left({\displaystyle \frac{sin{\theta }_z^{p_2}}{{\theta }_z^{p_2}}}-1\right)r_{x0}^{p_1}-\left({\displaystyle \frac{1-cos{\theta }_z^{p_2}}{{\theta }_z^{p_2}}}\right)r_{y0}^{p_1}\hfill \\ \hfill \Delta r_y^{p_1}\left({\theta }_z^{p_1}\right)=\left({\displaystyle \frac{1-cos{\theta }_z^{p_2}}{{\theta }_z^{p_2}}}\right)r_{x0}^{p_1}+\left({\displaystyle \frac{sin{\theta }_z^{p_2}}{{\theta }_z^{p_2}}}-1\right)r_{y0}^{p_1}\hfill \end{array}\right.$$

(22)

Combine equations above, expand the trigonometric functions, and neglect higher-order small quantities. Then:

$$\left\{\begin{array}{c}\Delta r_x^{p_1}=\Delta r_x^{p_1}\left({\theta }_y^{p_1}\right)+\Delta r_x^{p_1}\left({\theta }_z^{p_1}\right)\approx {\displaystyle \frac{{\theta }_y^{p_2}}{2}}{r}_{z0}-{\displaystyle \frac{{\theta }_z^{p_2}}{2}}{r}_{y0}={\theta }_y^{p_1}{r}_{z0}-{\theta }_z^{p_1}{r}_{y0}\hfill \\ \Delta r_y^{p_1}=\Delta r_y^{p_1}\left({\theta }_x^{p_1}\right)+\Delta r_y^{p_1}\left({\theta }_z^{p_1}\right)\approx -{\displaystyle \frac{{\theta }_x^{p_2}}{2}}{r}_{z0}+{\displaystyle \frac{{\theta }_z^{p_2}}{2}}{r}_{x0}=-{\theta }_x^{p_1}{r}_{z0}+{\theta }_z^{p_1}{r}_{x0}\hfill \\ \Delta r_z^{p_1}=\Delta r_z^{p_1}\left({\theta }_x^{p_1}\right)+\Delta r_z^{p_1}\left({\theta }_y^{p_1}\right)\approx {\displaystyle \frac{{\theta }_x^{p_2}}{2}}{r}_{y0}-{\displaystyle \frac{{\theta }_y^{p_2}}{2}}{r}_{x0}={\theta }_x^{p_1}{r}_{y0}-{\theta }_y^{p_1}{r}_{x0}\hfill \end{array}\right.$$

(23)

Therefore, the change in the length of the lever arms caused by the flexural deformation angle can be expressed as:

$$\delta {\mathit{r}}^{p_1}={\mathit{L}}_0{\mathsf{\theta }}^{p_1}$$

(24)

where:

$${\mathit{L}}_0=\left[\begin{array}{ccc}0& r_{z0}^{p_1}& -r_{y0}^{p_1}\\ -r_{z0}^{p_1}& 0& r_{x0}^{p_1}\\ r_{y0}^{p_1}& -r_{x0}^{p_1}& 0\end{array}\right]=-({\mathit{r}}_0^{p_1}\times )$$

Differentiating the equation above, we obtain:

$$\delta {\dot{\mathit{r}}}^{p_1}={\mathit{L}}_0{\dot{\mathsf{\theta }}}^{p_1}$$

(25)

4. Establishing the Data Fusion Kalman Filter Equations

4.1. State Equation

By combining the flexural deformation angle models, the flexible lever arm model, and the error equations of the SRINS, we can establish the state matrices for three sets of SRINS data fusion as follows:

$$\mathit{X}=\left[\begin{array}{cccc}\begin{array}{cccc}{\mathit{X}}_{SRIN{S}_1}& \delta {{\mathit{r}}_2}^{p_1}& {{\mathsf{\theta }}_2}^{p_1}& {{\mathsf{\mu }}_2}^{p_1}\end{array}& {\mathit{X}}_{SRIN{S}_2}& \delta {{\mathit{r}}_3}^{p_1}& \begin{array}{ccc}{{\mathsf{\theta }}_3}^{p_1}& {{\mathsf{\mu }}_3}^{p_1}& {\mathit{X}}_{SRIN{S}_3}\end{array}\end{array}\right]$$

(26)

In the equations, ${\mathit{X}}_{SRIN{S}_1}$ represents the 15-dimensional state matrix of $SRIN{S}_1$, ${\mathit{X}}_{SRIN{S}_2}$ represents the 15-dimensional state matrix of $SRIN{S}_2$, and ${\mathit{X}}_{SRIN{S}_3}$ represents the 15-dimensional state matrix of $SRIN{S}_3$. $\delta {{\mathit{r}}_2}^{p_1}$ represents the lever arm errors between $SRIN{S}_1$ and $SRIN{S}_2$, and $\delta {{\mathit{r}}_3}^{p_1}$ represents the lever arm errors between $SRIN{S}_1$ and $SRIN{S}_3$. ${{\mathsf{\theta }}_2}^{p_1}$ represents the deformation angles between $SRIN{S}_1$ and $SRIN{S}_2$, and ${{\mathsf{\theta }}_3}^{p_1}$ represents the deformation angles between $SRIN{S}_1$ and $SRIN{S}_3$. ${{\mathsf{\mu }}_2}^{p_1}$ represents the deformation angle rates between $SRIN{S}_1$ and $SRIN{S}_2$, and ${{\mathsf{\mu }}_3}^{p_1}$ represents the deformation angle rates between $SRIN{S}_1$ and $SRIN{S}_3$. Therefore, a 63-dimensional state transition matrix can be established as follows:

$$\mathit{F}=\left[\begin{array}{c}\begin{array}{cc}{\mathit{F}}_{RIN{S}_1}& {\mathit{O}}_{15\times 48}\end{array}\\ \begin{array}{ccc}{\mathit{O}}_{9\times 15}& {\mathit{F}}_{r\theta 2}& {\mathit{O}}_{9\times 39}\end{array}\\ \begin{array}{ccc}{\mathit{O}}_{15\times 24}& {\mathit{F}}_{RIN{S}_2}& {\mathit{O}}_{15\times 24}\end{array}\\ \begin{array}{c}\begin{array}{ccc}{\mathit{O}}_{9\times 39}& {\mathit{F}}_{r\theta 3}& {\mathit{O}}_{9\times 15}\end{array}\\ \begin{array}{cc}{\mathit{O}}_{15\times 48}& {\mathit{F}}_{RIN{S}_3}\end{array}\end{array}\end{array}\right]$$

(27)

In the formula, ${\mathit{O}}_{i\times j}$ represents an $i\times j$ zero matrix, ${\mathit{F}}_{SRIN{S}_1}$ represents the state transition matrix of $SRIN{S}_1$, ${\mathit{F}}_{SRIN{S}_2}$ represents the state transition matrix of $SRIN{S}_2$, and ${\mathit{F}}_{SRIN{S}_3}$ represents the state transition matrix of $SRIN{S}_3$. ${\mathit{F}}_{r\theta 2}$ and ${\mathit{F}}_{r\theta 3}$ represent the state transition matrices of the lever arms and flexural deformation angles between $SRIN{S}_1$ and $SRIN{S}_2$, and $SRIN{S}_1$ and $SRIN{S}_3$, respectively. Additionally:

$${\mathit{F}}_{r\theta i}=\left[\begin{array}{ccc}{\mathit{O}}_{3\times 3}& {\mathit{O}}_{3\times 3}& -({\mathit{r}}_i^{p_1}\times )\\ {\mathit{O}}_{3\times 3}& {\mathit{I}}_{3\times 3}& {\mathit{O}}_{3\times 3}\\ {\mathit{O}}_{3\times 3}& {\mathit{F}}_{r\theta i32}& {\mathit{F}}_{r\theta i33}\end{array}\right]$$

$${\mathit{F}}_{r\theta i32}=\left[\begin{array}{ccc}-{\beta }_{ix}^2& 0& 0\\ 0& -{\beta }_{iy}^2& 0\\ 0& 0& -{\beta }_{iz}^2\end{array}\right]$$

$${\mathit{F}}_{r\theta i33}=\left[\begin{array}{ccc}-2{\beta }_{ix}& 0& 0\\ 0& -2{\beta }_{iy}& 0\\ 0& 0& -2{\beta }_{iz}\end{array}\right]$$

$$i=2,3$$

4.2. Measurement Equation

In the n-frame of $SRIN{S}_1$, the positional relationship between the two sets of SRINSs can be expressed as follows:

$$\left[\begin{array}{c}\hfill L_{p_i}^n\hfill \\ \hfill {\lambda }_{p_i}^n\hfill \\ \hfill h_{p_i}^n\hfill \end{array}\right]=\left[\begin{array}{c}\hfill L_{p_1}^n\hfill \\ \hfill {\lambda }_{p_1}^n\hfill \\ \hfill h_{p_1}^n\hfill \end{array}\right]+\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{p_1}^n}}& 0\\ {\displaystyle \frac{sec{L}_{p_1}^n}{R_N+h_{p_1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]{\mathit{C}}_{p_1}^n·{\mathit{r}}_i^{p_1}$$

(28)

In the formula, ${\mathit{p}}_{p_1}^n={\left[\begin{array}{ccc}{L}_{p_1}^n& {\lambda }_{p_1}^n& h_{p_1}^n\end{array}\right]}^T$ and ${\mathit{p}}_{p_i}^n={\left[\begin{array}{ccc}{L}_{p_i}^n& {\lambda }_{p_i}^n& h_{p_i}^n\end{array}\right]}^T$ represent the positions of the two sets of SRINSs in the navigation coordinate system of $SRIN{S}_1$, respectively. ${\mathit{r}}_i^{p_1}=\left[\begin{array}{ccc}{r}_{xi}^{p_1}& r_{yi}^{p_1}& r_{zi}^{p_1}\end{array}\right]$ represents the lever arm between these two sets of SRINSs in the p-frame of $SRIN{S}_1$.

Therefore, the measurement matrix can be established as:

$$\mathit{Z}=\left[\begin{array}{c}{\mathit{Z}}_2\\ {\mathit{Z}}_3\end{array}\right]$$

(29)

$${\mathit{Z}}_i={\mathit{p}}_{p_1}^n+\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{p_1}^n}}& 0\\ {\displaystyle \frac{sec{L}_{p_1}^n}{R_N+h_{p_1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]{\mathit{C}}_{p_1}^n·{\mathit{r}}_i^{p_1}-{\mathit{p}}_{p_i}^n$$

(30)

Due to the presence of measurement and calculation errors, the actual measurement equation can be obtained by adding error terms to equation above:

$${\mathit{Z}}_i={\tilde{\mathit{p}}}_{p_1}^n+\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+{\tilde{h}}_{p_1}^n}}& 0\\ {\displaystyle \frac{sec{\tilde{L}}_{p_1}^n}{R_N+{\tilde{h}}_{p_1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]{\tilde{\mathit{C}}}_{p_1}^n·{\tilde{\mathit{r}}}_i^{p_1}-{\tilde{\mathit{p}}}_{p_i}^n$$

(31)

In this formula above, $i=2,3$ and:

$$\begin{array}{c}{\tilde{\mathbf{p}}}_{p_1}^n={\mathbf{p}}_{p_1}^n+\delta {\mathbf{p}}_{p_1}^n\hfill \\ {\tilde{\mathbf{p}}}_{p_i}^n={\mathbf{p}}_{p_i}^n+\delta {\mathbf{p}}_{p_i}^n\hfill \\ {\tilde{\mathbf{r}}}_i^{p_1}={\mathbf{r}}_i^{p_1}+\delta {\mathbf{r}}_i^{p_1}\hfill \\ {\tilde{\mathbf{C}}}_{p_1}^n=(\mathbf{I}+\varphi \times ){\mathbf{C}}_{p_1}^{n^{\prime }}\hfill \\ \delta {\mathbf{p}}_{p_1}^n={\left[\begin{array}{ccc}\delta L_{p_1}^n& \delta {\lambda }_{p_1}^n& \delta h_{p_1}^n\end{array}\right]}^T\hfill \\ \delta {\mathbf{p}}_{p_i}^n={\left[\begin{array}{ccc}\delta L_{p_i}^n& \delta {\lambda }_{p_i}^n& \delta h_{p_i}^n\end{array}\right]}^T\hfill \\ \delta {\mathbf{r}}_i^{p_1}={\left[\begin{array}{ccc}\delta r_{xi}^{p_1}& \delta r_{yi}^{p_1}& \delta r_{zi}^{p_1}\end{array}\right]}^T\hfill \\ {\tilde{h}}_{p_1}^n=h_{p_1}^n+\delta h_{p_1}^n\hfill \\ {\tilde{L}}_{p_1}^n=L_{p_1}^n+\delta L_{p_1}^n\hfill \end{array}$$

${\tilde{\mathit{p}}}_{p_1}^n$ denotes the position calculated by $SRIN{S}_1$, $\delta {\mathit{p}}_{p_1}^n$ denotes the position error of $SRIN{S}_1$, ${\tilde{\mathit{p}}}_{p_i}^n$ denotes the position calculated by $SRIN{S}_i$, $\delta {\mathit{p}}_{p_i}^n$ denotes the position error of $SRIN{S}_i$, ${\tilde{\mathit{r}}}_i^{p_1}$ denotes the estimated arm length between $SRIN{S}_1$ and $SRIN{S}_i$, $\delta {\mathit{r}}_i^{p_1}$ denotes the error in the arm length between $SRIN{S}_1$ and $SRIN{S}_i$, ${\mathit{C}}_{p_1}^{n^{\prime }}$ denotes the attitude matrix from the p-frame to the n-frame calculated by $SRIN{S}_1$, and $\varphi$ denotes the misalignment angle error of $SRIN{S}_1$. By neglecting second-order small quantities, the measurement equation can be expressed as:

$$\begin{array}{c}{\mathit{Z}}_i\approx \delta {\mathit{p}}_{p_1}^n-\delta {\mathit{p}}_{p_i}^n+\left[\begin{array}{ccc}0& -{\displaystyle \frac{\delta h_{p_1}^n}{{(R_M+h_{p_1}^n)}^2}}& 0\\ -{\displaystyle \frac{\delta h_{p_1}^{n}sec{L}_{p_1}^n}{{(R_N+h_{p_1}^n)}^2}}+{\displaystyle \frac{{sec}^2{L}_{p_1}^{n}sin{L}_{p_1}^n\delta L_{p_1}^n}{(R_N+h_{p_1}^n)}}& 0& 0\\ 0& 0& 0\end{array}\right]{\mathit{C}}_{p_1}^{n^{\prime }}·{\mathit{r}}_i^{p_1}\\ +\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{p_1}^n}}& 0\\ {\displaystyle \frac{sec{L}_{p_1}^n}{R_N+h_{p_1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]{\mathit{C}}_{p_1}^{n^{\prime }}·\delta {\mathit{r}}_i^{p_1}-({\mathit{C}}_{p_1}^{n^{\prime }}·{\mathit{r}}_i^{p_1}\times )\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{p_1}^n}}& 0\\ {\displaystyle \frac{sec{L}_{p_1}^n}{R_N+h_{p_1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]\varphi \end{array}$$

(32)

Therefore, the measurement matrix can be established as:

$$\mathit{H}=\left[\begin{array}{ccc}\begin{array}{c}{\mathit{H}}_{SRIN{S}_{12}}\\ {\mathit{H}}_{SRIN{S}_{13}}\end{array}& \begin{array}{c}{\mathit{H}}_r\\ {\mathit{O}}_{3\times 24}\end{array}& \begin{array}{cc}\begin{array}{c}{\mathit{O}}_{3\times 6}\\ {\mathit{H}}_r\end{array}& \begin{array}{c}\begin{array}{cc}{\mathit{H}}_{SRIN{S}_2}& {\mathit{O}}_{3\times 24}\end{array}\\ \begin{array}{cc}{\mathit{O}}_{3\times 6}& {\mathit{H}}_{SRIN{S}_3}\end{array}\end{array}\end{array}\end{array}\right]$$

(33)

In the formula above, there is:

$${\mathit{H}}_{SRIN{S}_{1i}}=\left[\begin{array}{cccc}{\mathit{H}}_{\varphi i}& {\mathit{O}}_{3\times 3}& {\mathit{H}}_{pi}& {\mathit{O}}_{3\times 6}\end{array}\right](i=2,3)$$

$${\mathit{H}}_r=\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{p_1}^n}}& 0\\ {\displaystyle \frac{1}{\left(R_N+h_{p_1}^n\right)cos{L}_{p_1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]{\mathit{C}}_{p_1}^{n^{\prime }}$$

$${\mathit{H}}_{SRIN{S}_2}=\left[\begin{array}{ccc}{\mathit{O}}_{3\times 6}& -{\mathit{I}}_{3\times 3}& {\mathit{O}}_{3\times 6}\end{array}\right]$$

$${\mathit{H}}_{SRIN{S}_3}=\left[\begin{array}{ccc}{\mathit{O}}_{3\times 6}& -{\mathit{I}}_{3\times 3}& {\mathit{O}}_{3\times 6}\end{array}\right]$$

$${\mathit{H}}_{pi}=\left[\begin{array}{ccc}1& 0& -{\displaystyle \frac{{({\mathit{C}}_{p_1}^{n^{\prime }}·{\mathit{r}}_i^{p_1})}_y}{{(R_M+h_{p_1}^n)}^2}}\\ {\displaystyle \frac{{sec}^2{L}_{p_1}^{n}sin{L}_{p_1}^n{({\mathit{C}}_{p_1}^{n^{\prime }}·{\mathit{r}}_i^{p_1})}_x}{(R_N+h_{p_1}^n)}}& 1& -{\displaystyle \frac{{({\mathit{C}}_{p_1}^{n^{\prime }}·{\mathit{r}}_i^{p_1})}_{x}sec{L}_{p_1}^n}{{(R_N+h_{p_1}^n)}^2}}\\ 0& 0& 1\end{array}\right]$$

$${\mathit{H}}_{\varphi i}=-({\mathit{C}}_{p_1}^{n^{\prime }}·{\mathit{r}}_i^{p_1}\times )\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{p_1}^n}}& 0\\ {\displaystyle \frac{1}{\left(R_N+h_{p_1}^n\right)cos{L}_{p_1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]$$

where ${({\mathit{C}}_{p_1}^n·{\mathit{r}}_i^{p_1})}_x$ represents the component of ${\mathit{C}}_{p_1}^n·{\mathit{r}}_i^{p_1}$ in the x-axis direction; ${({\mathit{C}}_{p_1}^n·{\mathit{r}}_i^{p_1})}_y$ represents the component of ${\mathit{C}}_{p_1}^n·{\mathit{r}}_i^{p_1}$ in the y-axis direction.

4.3. Calculation Process

The computational flowchart of the centralized Kalman filtering (CKF) method based on topological distribution constraints proposed in this paper is shown in Figure 4. Three sets of SRINSs are installed at different positions on the carrier. While receiving the 1PPS synchronization pulse signal, they send out their own measured raw gyro data and accelerometer data. In the acquisition system, firstly, three SRINSs’ positions are calculated by their measurement information at the reception time. This position information is then substituted into the centralized Kalman filter equations. During the Kalman filtering process, the measurements are the position differences between $SRIN{S}_2$ and $SRIN{S}_1$, and between $SRIN{S}_3$ and $SRIN{S}_1$. After filtering, the estimated state information is used to compensate the calculated position information in each SRINS. In the acquisition system, the stored lever arms and the position information of each SRINS calculated by itself are compensated. After compensation, the variance in the estimated error is used to perform weighted averaging on the position information to obtain the final comprehensive position information.

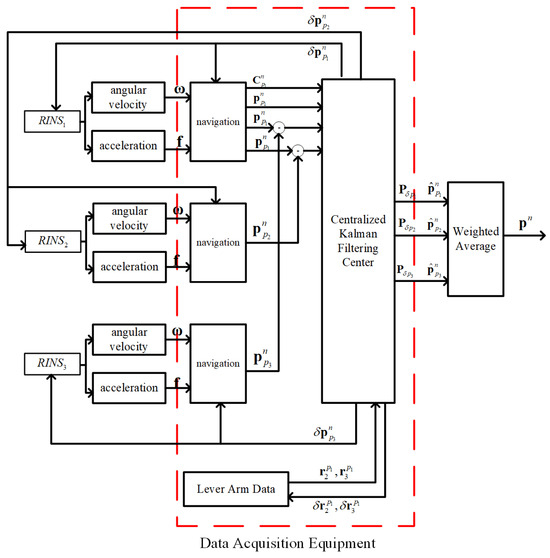
Figure 4. Data Fusion Process of Three Sets of SRINSs.

During navigation, the pseudocode Algorithm 1 for the data fusion calculation of the three sets of SRINSs is as follows:

Algorithm 1: Three SRINSs Data Fusion algorithm.

Input: Gyroscope and accelerometer increments measured by the three sets of SRINSs $wv{m}_1$, $wv{m}_2$, $wv{m}_3$. Output: Comprehensive position ${\mathit{p}}^n$ result after data fusion. For different SRINS i, the inertial navigation calculation process is as follows: 1: ${\mathit{C}}_{pk,i}^n={\mathit{C}}_{pk-1,i}^n(\mathit{I}+T_s{\mathsf{\omega }}_{np,i}^p\times )$ 2: ${\mathit{a}}_{k,i}^n={\mathit{C}}_{pk-1,i}^n{\mathit{f}}_{k,i}^p-(2{\mathsf{\omega }}_{iek-1}^n+{\mathsf{\omega }}_{enk-1}^n)\times {\mathit{v}}_{k-1,i}^n+{\mathit{g}}^n$ 3: ${\mathit{v}}_{k,i}^n={\mathit{v}}_{k-1,i}^n+T_s{\mathit{a}}_{k,i}^n$ 4: $\begin{array}{c}{\mathit{p}}_{k,i}^n=\left[\begin{array}{c}{L}_{k,i}^n\\ {\lambda }_{k,i}^n\\ h_{k,i}^n\end{array}\right]\hfill \\ =\left[\begin{array}{c}{L}_{k-1,i}^n\\ {\lambda }_{k-1,i}^n\\ h_{k-1,i}^n\end{array}\right]+T_s\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{k-1,i}^n}}& 0\\ {\displaystyle \frac{\sec L_{k-1,i}^n}{R_N+h_{k-1,i}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{v}_{Ek-1,i}^n\\ v_{Nk-1,i}^n\\ v_{Uk-1,i}^n\end{array}\right]\hfill \end{array}$ After the three sets of SRINSs have completed their calculations, they enter the Kalman filter process, where the state variables are: $\mathit{X}=\left[\begin{array}{cccc}\begin{array}{cccc}{\mathit{X}}_{RIN{S}_1}& \delta {{\mathit{r}}_2}^{p_1}& {{\mathsf{\theta }}_2}^{p_1}& {{\mathsf{\mu }}_2}^{p_1}\end{array}& {\mathit{X}}_{RIN{S}_2}& \delta {{\mathit{r}}_3}^{p_1}& \begin{array}{ccc}{{\mathsf{\theta }}_3}^{p_1}& {{\mathsf{\mu }}_3}^{p_1}& {\mathit{X}}_{RIN{S}_3}\end{array}\end{array}\right]$, ${\mathit{X}}_{RIN{S}_i}={\left[\begin{array}{cccc}{\varphi }_i& \delta {\mathit{v}}_i^n& \delta {\mathit{p}}_i^n& \begin{array}{cc}\left[\begin{array}{ccc}\hfill {\epsilon }_{x,i}^n\hfill & {\epsilon }_{y,i}^n& {\epsilon }_{z,i}^b\end{array}\right]& {\nabla }_i^b\end{array}\end{array}\right]}^T$ 5: ${\mathbf{Z}}_{k,2}={\mathbf{p}}_1^n+\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{k,1}^n}}& 0\\ {\displaystyle \frac{sec{L}_{k,1}^n}{R_N+h_{k,1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]{\mathbf{C}}_{pk,1}^n·{\mathbf{r}}_{k,2}^{p_1}-{\mathbf{p}}_2^n$ 6: ${\mathbf{Z}}_{k,3}={\mathbf{p}}_1^n+\left[\begin{array}{ccc}0& {\displaystyle \frac{1}{R_M+h_{k,1}^n}}& 0\\ {\displaystyle \frac{sec{L}_{k,1}^n}{R_N+h_{k,1}^n}}& 0& 0\\ 0& 0& 1\end{array}\right]{\mathbf{C}}_{pk,1}^n·{\mathbf{r}}_{k,3}^{p_1}-{\mathbf{p}}_3^n$ 7: ${\mathit{Z}}_k=\left[\begin{array}{c}{\mathit{Z}}_{k,2}\\ {\mathit{Z}}_{k,3}\end{array}\right]$ 8: ${\widehat{\mathit{X}}}_{k/k-1}={\mathit{F}}_{k/k-1}{\widehat{\mathit{X}}}_{k-1}$ 9: ${\mathit{P}}_{k/k-1}={\mathit{F}}_{k/k-1}{\mathit{P}}_{k-1}{\mathit{F}}_{k/k-1}^T+{\mathsf{\Gamma }}_{k-1}{\mathit{Q}}_{k-1}{\mathsf{\Gamma }}_{k-1}^{\mathrm{T}}$ 10: ${\mathit{K}}_k={\mathit{P}}_{k/k-1}{\mathit{H}}_k^{\mathrm{T}}{({\mathit{H}}_k{\mathit{P}}_{k/k-1}{\mathit{H}}_k^{\mathrm{T}}+{\mathit{R}}_k)}^{-1}$ 11: ${\mathit{P}}_k=(\mathit{I}-{\mathit{K}}_k{\mathit{H}}_k){\mathit{P}}_{k/k-1}$ 12: ${\widehat{\mathit{X}}}_k={\widehat{\mathit{X}}}_{k/k-1}+{\mathit{K}}_k({\mathit{Z}}_k-{\mathit{H}}_k{\widehat{\mathit{X}}}_{k/k-1})$ Prediction, Compensation, and Position Output Process: 13: ${\mathit{r}}_{k,2}^{p_1}={\mathit{r}}_{k,2}^{p_1}+\delta {{\mathit{r}}_2}^{p_1},{\mathit{r}}_{k,3}^{p_1}={\mathit{r}}_{k,3}^{p_1}+\delta {{\mathit{r}}_3}^{p_1}$ 14: ${\mathit{p}}_{k,i}^n={\mathit{p}}_{k,i}^n+\delta {\mathit{p}}_i^n,{\mathit{v}}_{k,i}^n={\mathit{v}}_{k,i}^n+\delta {\mathit{v}}_i^n$ 15: ${\mathit{p}}^n={\displaystyle \sum _{i=1}^3}{\displaystyle \frac{{\mathit{P}}_{k,po{s}_i}}{{\mathit{P}}_{k,po{s}_1}+{\mathit{P}}_{k,po{s}_2}+{\mathit{P}}_{k,po{s}_3}}}{\mathit{p}}_{k,i}^n$, where ${\mathit{P}}_{k,po{s}_i}$ represents the position error estimation variance of SRINSi.

In the above algorithm, each RINS has been aligned and does not interfere with others during the alignment process. With synchronized timing, each RINS independently completes its own navigation calculation, and then the calculated results are input into the centralized Kalman filter for filtering calculations. After filtering, the positions, velocities, and arm lengths between each RINS are compensated, and the positions of the RINSs are weighted and averaged to obtain a comprehensive position. When establishing the state and measurement equations, linearization has been performed, so no additional linearization process is involved in the Kalman filter calculations.

5. Experimental Analysis

5.1. Simulation Experiment

We have built a simulation test platform that can generate trajectory routes for underwater submersibles, and generate measurement simulation data for three sets of SRINSs based on the trajectory routes. The parameters of the three sets of SRINSs used in the simulation process are all the same IMU parameters. The deformation angles between the multiple SRINSs during the simulation process have the same correlation time and standard deviation. Other simulation condition parameters are shown in Table 1. The generated trajectory is shown in Figure 5.

Table 1. Simulation Parameters.

Parameter Error Items	Element	Parameter Settings
Gyroscope	Constant Drift	${0.001}^{\circ }$/h
	Random Walk Coefficient	${0.001}^{\circ }/\sqrt{\mathrm{h}}$
	Scale Factor Error	10 ppm
Accelerometer	Constant Bias	$10\mathsf{\mu }\mathrm{g}$
	Random Walk Coefficient	$2\mathsf{\mu }\mathrm{g}/\sqrt{\mathrm{hz}}$
	Scale Factor Error	10 ppm
Initial Attitude Setting	Pitch Angle	$0^{\circ }$
	Roll Angle	$0^{\circ }$
	Heading Angle	$0^{\circ }$
Initial Velocity Setting	Eastward Velocity	0 m/s
	Northward Velocity	0 m/s
	Upward Velocity	0 m/s
Lever between SRINS1 and SRINS2	X-direction	0.255 m
	Y-direction	0.375 m
	Z-direction	0 m
Lever between SRINS1 and SRINS3	X-direction	0.409 m
	Y-direction	0.030 m
	Z-direction	0.800 m
Deformation Angle	Correlation Time	100 s
	Standard Deviation	${0.5}^{\prime }$
Initial Position Setting	Latitude	${24.618804}^{\circ }$
	Longitude	${118.039928}^{\circ }$
	Altitude	0 m
Other Settings	Simulation Duration	8 h
	Simulation Step Size	20 ms

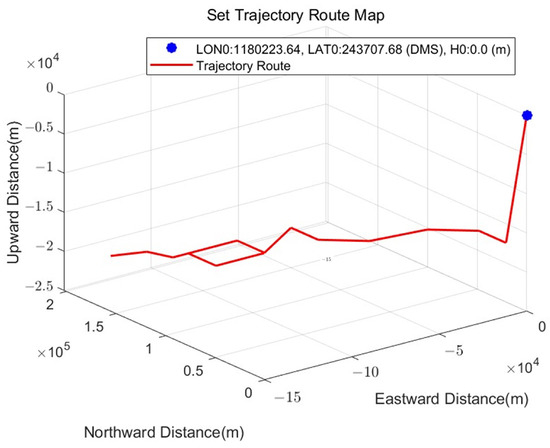
Figure 5. Motion Trajectory.

After generating the raw measurement data from the three sets of SRINSs, the centralized Kalman filter data fusion method proposed in this paper can effectively estimate the arm lengths between multiple SRINSs. This constrains the positions between SRINSs and thus obtains a comprehensive position. Based on the carrier trajectory and the preset parameters, the arm length estimation error and position error under the simulation conditions can be calculated as shown in the Figure 6 and Figure 7.

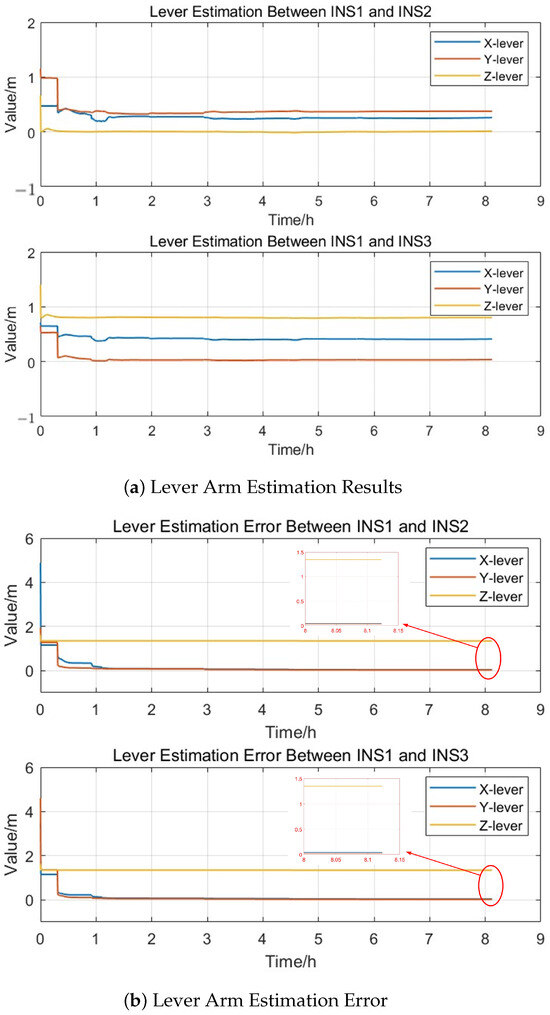
Figure 6. Arm Length Estimation Results Under Simulation Conditions.

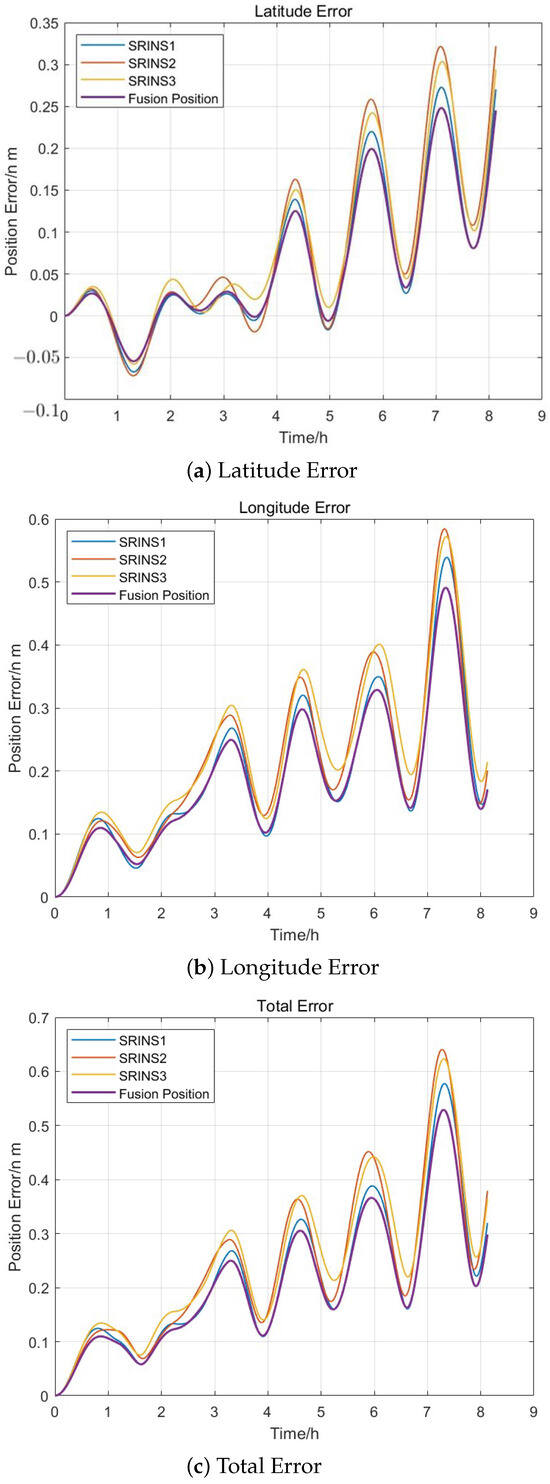
Figure 7. Position Errors Under Simulation Conditions.

The estimation results of the lever arm are shown in Table 2. It can be seen that the arm length estimation error is small, and the estimation result is quite accurate. From Figure 6b, it can be seen that the estimation of the lever arm errors in the x and y directions is convergent. The lever arm between $SRIN{S}_1$ and $SRIN{S}_2$, and between $SRIN{S}_1$ and $SRIN{S}_3$ can be estimated, thereby compensating for the lever arm errors during the data fusion process. Due to the divergence in the vertical direction of the INS, the observability of the arm length in the z direction is weak, resulting in poorer estimation results. However, for positional information such as longitude and latitude, the arm lengths in the x and y directions alone are sufficient to constrain the positions of multiple SRINSs.

Table 2. Lever Arm Estimation Results.

Item		Simulation Experiment	Estimation Error
SRINS1 and SRINS2	x-axis	0.2596 m	0.0046 m
	y-axis	0.3749 m	−0.0001 m
	z-axis	0.0117 m	0.0117 m
SRINS1 and SRINS3	x-axis	0.3990 m	−0.0100 m
	y-axis	0.0192 m	0.0108 m
	z-axis	0.7925 m	0.0075 m

External auxiliary equipment, such as depth sensors, can be used to measure altitude and constrain the altitude channel of inertial navigation calculations, thereby improving the observability of the z-axis lever arm. However, this is not the focus of the current study.

Based on the position provided by simulation trajectory, the position errors of three SRINSs during pure inertial navigation independently are compared with the position errors after applying the multi-inertial navigation data fusion method proposed in this paper, as shown in Figure 7. The RMS value of the position error can be calculated using the following formula, and the calculated values are shown in Table 3:

$$X_{RMS}=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^N}{X}_i^2}{N}}}$$

(34)

Table 3. Comparison of Fusion Accuracy.

Item		Positioning Error (RMS)
		Longitude Error	Latitude Error	Total Error
Simulation Experiment	SRINS1	0.1058 n m	0.2283 n m	0.2516 n m
	SRINS2	0.1272 n m	0.2514 n m	0.2817 n m
	SRINS3	0.1196 n m	0.2609 n m	0.2870 n m
	Data Fusion Result	0.09740 n m	0.2145 n m	0.2356 n m
	Accuracy Increase	7.9785%	6.0212%	6.3645%

In the formula above, $X_{RMS}$ represents the RMS calculation result of the position error, $X_i$ represents the position error, and N represents the total data volume.

The units of the RMS calculation results of the position error in in Table 3 are all nautical miles (n m), and this length unit satisfies 1 n m = 1852 m. In addition, the accuracy improvement results are calculated using the following formula:

$$\eta ={\displaystyle \frac{\left|Er{r}_{Data\_Fusion}-min\{Er{r}_{SRINS1},Er{r}_{SRINS2},Er{r}_{SRINS3}\}\right|}{min\{Er{r}_{SRINS1},Er{r}_{SRINS2},Er{r}_{SRINS3}\}}}$$

(35)

where $Er{r}_{Data\_Fusion}$ represents the RMS of the position error after data fusion, while $Er{r}_{SRINS1}$, $Er{r}_{SRINS2}$, and $Er{r}_{SRINS3}$, respectively, represent the RMS of the position error during pure inertial navigation for $SRIN{S}_1$, $SRIN{S}_2$, and $SRIN{S}_3$. $min\{Er{r}_{SRINS1},$ $Er{r}_{SRINS2},Er{r}_{SRINS3}\}$ represents the minimum value among $Er{r}_{SRINS1}$, $Er{r}_{SRINS2}$, and $Er{r}_{SRINS3}$.

From Table 3, it can be seen that the longitude error decreases by approximately 7.9785%, the latitude error decreases by approximately 6.0212%, and the overall positioning accuracy improves by approximately 6.3645%. Therefore, the method proposed in this paper can effectively estimate the arm lengths between multiple SRINSs, thereby constraining the positions of multiple SRINSs and improving the overall positioning accuracy.

5.2. Data Acquisition Equipment

To ensure the accuracy of time synchronization during the experiment, we have set up a data acquisition system, which consists of a time synchronization module and a data acquisition module as is shown in Figure 8. During the experiment, this system continuously sends 1PPS synchronization signals via the serial port and simultaneously receives raw measurement data from the SRINSs. This data is then timestamped with millisecond precision, aiming at the preprocess of time alignment in subsequent data analysis.

Figure 8. Structure Diagram of Data Acquisition Equipment.

5.3. Sports Vehicles Test Analysis

In the car test discussed in this paper, the three SRINSs used employ laser gyroscopes and quartz flexible accelerometers. The parameters of the gyroscopes and accelerometers, as measured through laboratory static testing, are shown in Table 4 below:

Table 4. Parameters of Laser Gyroscopes and Quartz Flexible Accelerometers.

Item		SRINS1	SRINS2	SRINS3
Laser gyroscope bias stability (100-s smoothing)	x-axis gyroscope	${0.0090}^{\circ }$/h	${0.0084}^{\circ }$/h	${0.0089}^{\circ }$/h
	y-axis gyroscope	${0.0087}^{\circ }$/h	${0.0086}^{\circ }$/h	${0.0083}^{\circ }$/h
	z-axis gyroscope	${0.0081}^{\circ }$/h	${0.0088}^{\circ }$/h	${0.0074}^{\circ }$/h
Quartz flexible accelerometer bias stability (100-s smoothing)	x-axis accelerometer	$6.4591\mathsf{\mu }$g	$8.3776\mathsf{\mu }$g	$6.2241\mathsf{\mu }$g
	y-axis accelerometer	$9.3006\mathsf{\mu }$g	$7.2004\mathsf{\mu }$g	$6.2537\mathsf{\mu }$g
	z-axis accelerometer	$7.3542\mathsf{\mu }$g	$6.4484\mathsf{\mu }$g	$6.4292\mathsf{\mu }$g

Three SRINSs were placed on an experiment vehicle. The installations of some instrumentation are shown in Figure 9 and Figure 10. To better evaluate the navigation results after data filtering and fusion, we integrated a satellite navigation system. The position data measured by this equipment will not be used in the filtering and fusion calculation process. This position information is only used as a high-precision reference for calculating positioning errors. During the experiment, the data acquisition system continuously sent 1PPS synchronization pulses to three RINSs and simultaneously collected raw gyroscope and accelerometer data from these systems, as well as positioning information from the Global Navigation Satellite System (GNSS). This ensured time consistency of the data during the vehicle tests. Two sets of vehicle tests were conducted, each lasting over 2 h. The routes of the two vehicle tests are shown in Figure 11 and Figure 12. Using the GNSS positioning information as the reference, the lever arm estimation results and positioning errors for these two tests are shown in Figure 13, Figure 14, Figure 15 and Figure 16, respectively.

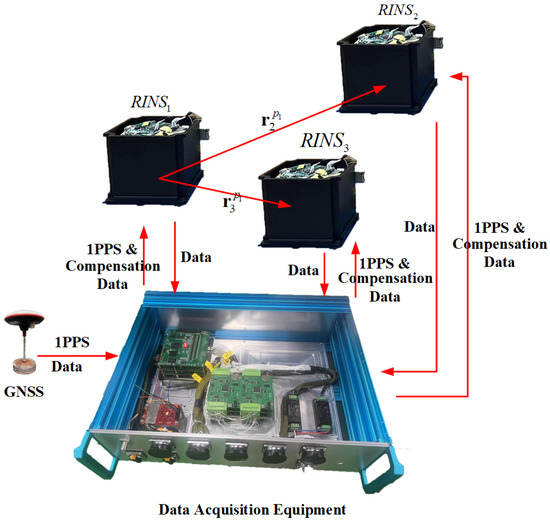
Figure 9. Schematic Diagram of the Equipment Installation Structure.

Figure 10. Installation Diagram of Sports Vehicles Test Equipment.

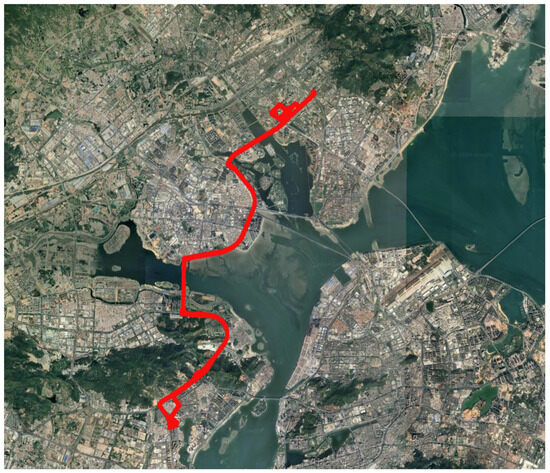
Figure 11. Route Map for the First Trial (location: Xiamen City, Fujian Province, China; starting point latitude: 24.6120529175°; starting point longitude: 118.0733718872°; running time: approximately 2 h and 13 min).

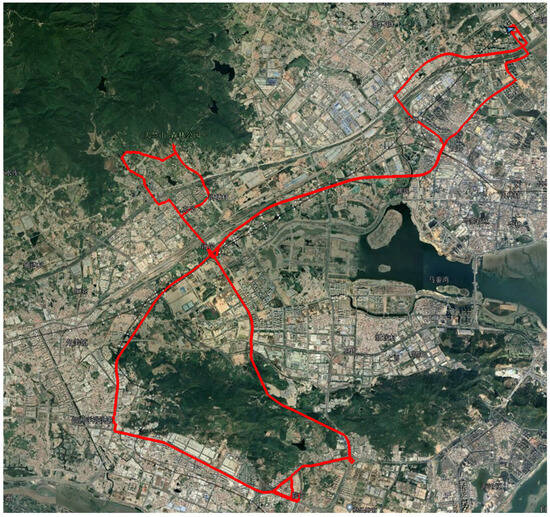
Figure 12. Route Map for the Second Trial (Location: Xiamen City, Fujian Province, China; Starting Point Latitude: 24.6120529175°; Starting Point Longitude: 118.0733718872°; Running Time: approximately 3 h and 45 min).

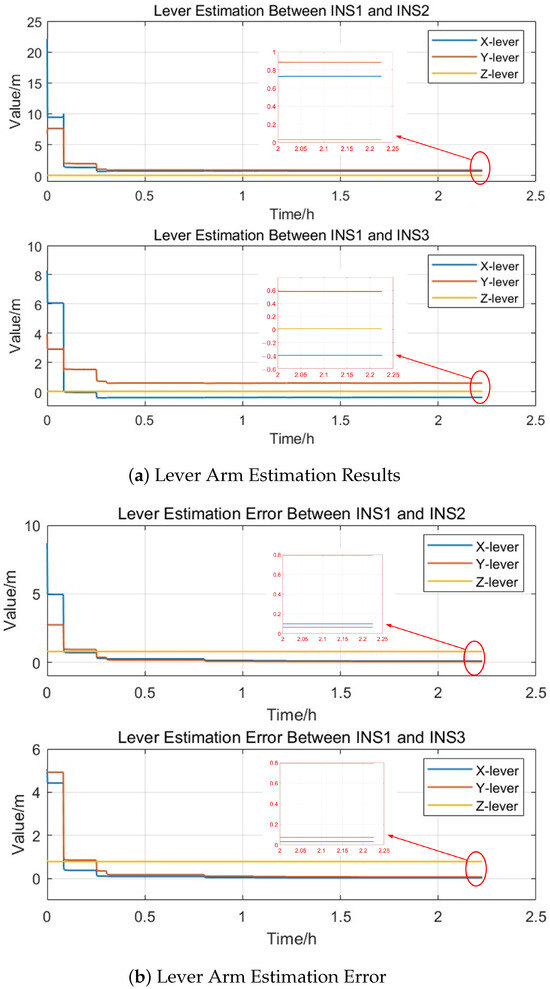
Figure 13. First Experiment Lever Arm Estimation Results.

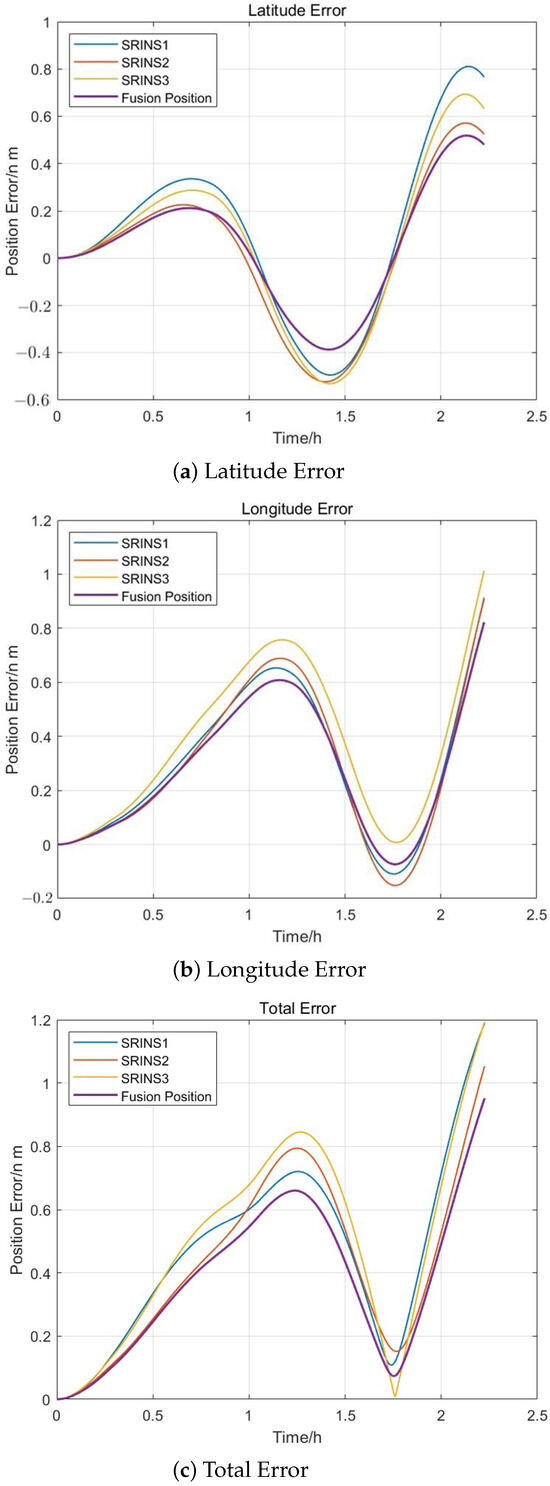
Figure 14. First Experiment Positioning Error.

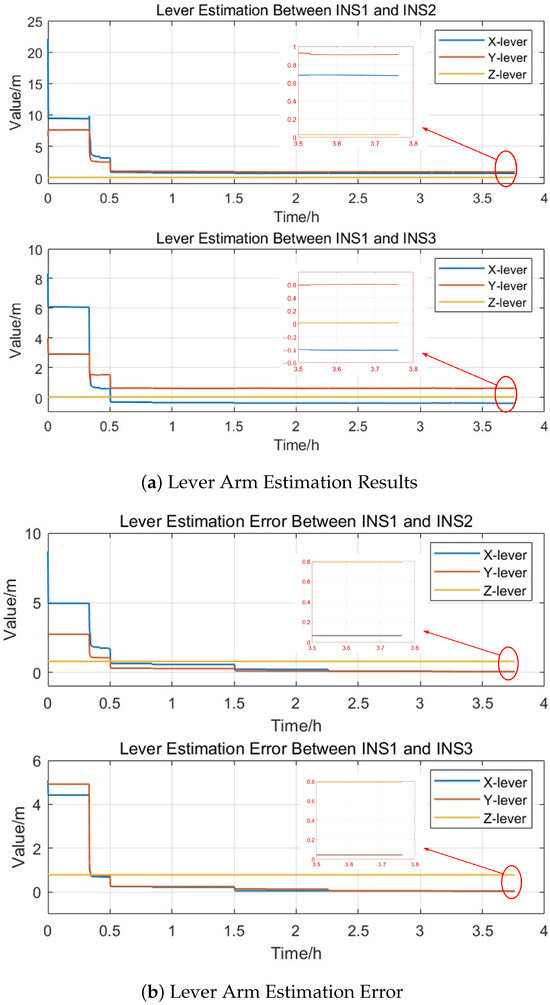
Figure 15. Second Experiment Lever Arm Estimation Results.

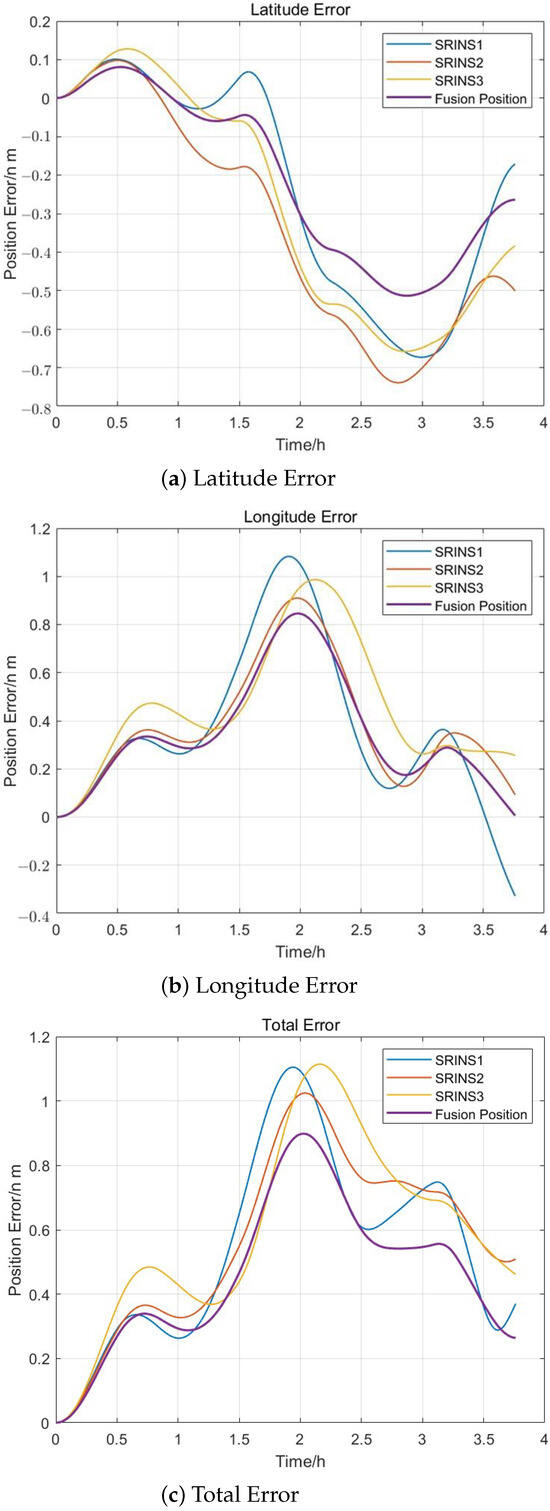
Figure 16. Second Experiment Positioning Error.

Table 5 shows the arm length estimation results of the two car tests. Due to the lack of precise distance measuring equipment, the actual distance between the SRINSs could not be measured, so the estimation error of the arm length cannot be accurately calculated. However, according to Table 5, the arm length estimation results of the two car tests differ by only a few centimeters, indicating high estimation accuracy. Based on the arm lengths obtained during the filtering process, the positions of multiple SRINSs can be constrained, thereby achieving a high-precision comprehensive position.

Table 5. Lever Arm Estimation Results.

Item		The First Experiment	The Second Experiment
SRINS1 and SRINS2	x-axis	0.7305 m	0.6800 m
	y-axis	0.8838 m	0.9146 m
	z-axis	0.0314 m	0.0302 m
SRINS1 and SRINS3	x-axis	−0.3975 m	−0.4069 m
	y-axis	0.5823 m	0.6060 m
	z-axis	0.0127 m	0.0164 m

Based on the position provided by GNSS, the position errors of three SRINSs during pure inertial navigation independently are compared with the position errors after applying the multi-inertial navigation data fusion method proposed in this paper, as shown in Figure 14 and Figure 16. Table 6 shows the RMS values of the position error.

Table 6. Comparison of Fusion Accuracy.

Item		Positioning Error (RMS)
		Longitude Error	Latitude Error	Total Error
The First Trial	SRINS1	0.2989 n m	0.2799 n m	0.4095 n m
	SRINS2	0.3212 n m	0.2228 n m	0.3909 n m
	SRINS3	0.3747 n m	0.2497 n m	0.4503 n m
	Data Fusion Result	0.2801 n m	0.2084 n m	0.3491 n m
	Accuracy Increase	6.3180%	6.4684%	10.6943%
The Second Trial	SRINS1	0.4854 n m	0.4904 n m	0.6900 n m
	SRINS2	0.4852 n m	0.5935 n m	0.7666 n m
	SRINS3	0.4630 n m	0.3933 n m	0.6075 n m
	Data Fusion Result	0.4141 n m	0.3643 n m	0.5516 n m
	Accuracy Increase	10.5539%	7.3664%	9.2041%
Average Accuracy Increase		8.4360%	6.9174%	9.9492%

From Table 6, it can be seen that the longitude error is reduced by approximately 8.4360%; the latitude error is reduced by approximately 6.9174%; and the overall positioning accuracy is improved by approximately 9.9492%. Therefore, the multi-INS data fusion method proposed in this paper can form a position reference, and the accuracy of this position reference is superior to the accuracy when the three sets of SRINSs perform navigation calculations independently.

6. Conclusions

This paper focuses on three sets of SRINSs and proposes a CKF method for multiple INSs based on topological distribution constraints. Considering the influence of the Earth’s magnetic field and gravitational field, this paper optimizes the INS state equations and state transition matrix to establish a more accurate model. Based on a dynamic model of arm length variation under flexural deformation, the positional distance relationships between multiple SRINSs are used as measurement quantities to estimate the arm lengths. Simulation experiments indicate that the estimation results are good, with an error within 0.012 m. Additionally, this paper employs a data acquisition device to send 1PPS signals, and simultaneously collects measurement data. Since the precision of the timestamp is 1ms, the time difference between multiple SRINSs will be a constant value and less than 1ms.

The car test shows that our multi-INSs data fusion method can effectively improve the comprehensive positioning accuracy of SRINSs. Compared to before fusion, the overall positioning error RMS is reduced by about 9.9492 %. Under conditions without absolute positioning information, our data fusion method can be used with multiple low-cost, small-sized SRINSs to provide high-precision positional reference information for underwater unmanned submersibles, ensuring the reliability of navigation position.