A Dynamic Edge Server Placement Scheme Using the Improved Snake Optimization Algorithm
Abstract
1. Introduction
- •
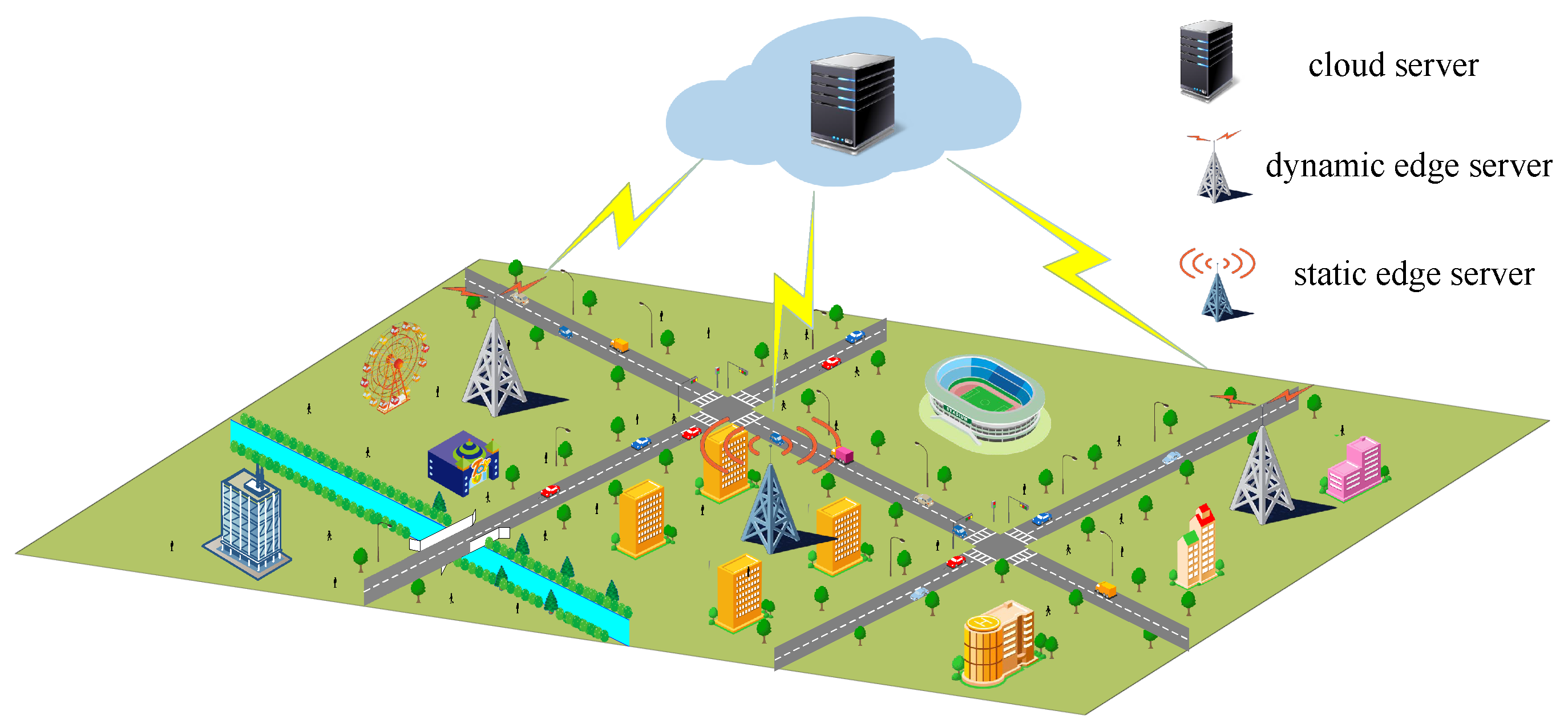
- The edge servers are classified as static or dynamic. Static servers are deployed in densely populated areas, whereas dynamic servers move over time in response to dynamic changes in user locations; the number of dynamic servers can be increased or decreased.
- •
- The snake optimization (SO) algorithm [6] is improved to determine the optimal server placement and to implement operations such as increasing, decreasing, and moving the servers via a dynamic edge-server placement algorithm. The minimum placement-cost algorithm is used to calculate the minimum edge-server movement distance.
2. Related Work
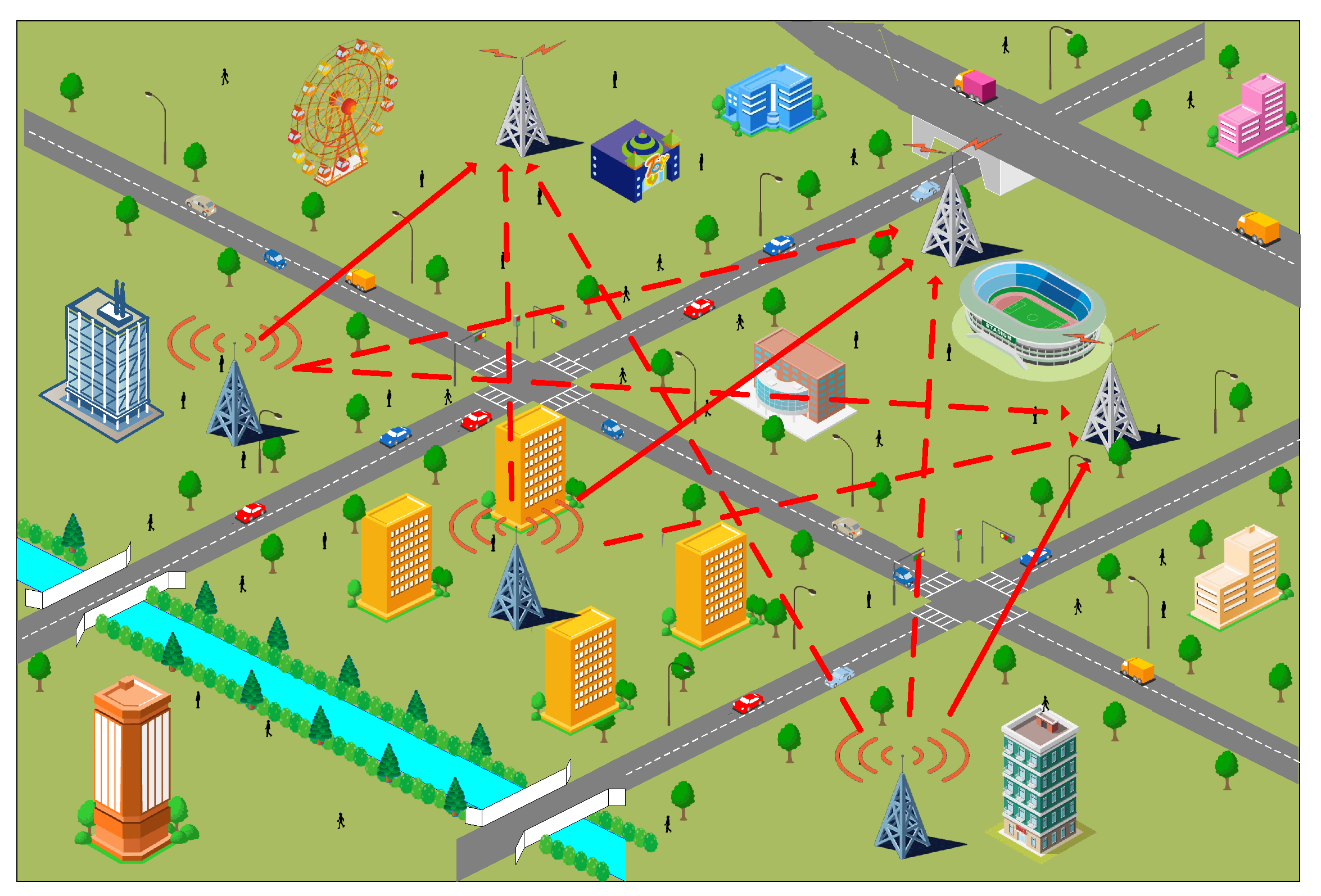
3. System Modeling and Problem Description
3.1. Network Model
3.2. Coverage Model
3.3. Delay Model
3.4. Cost Model
3.5. Problem Description
4. Dynamic Edge-Server Placement
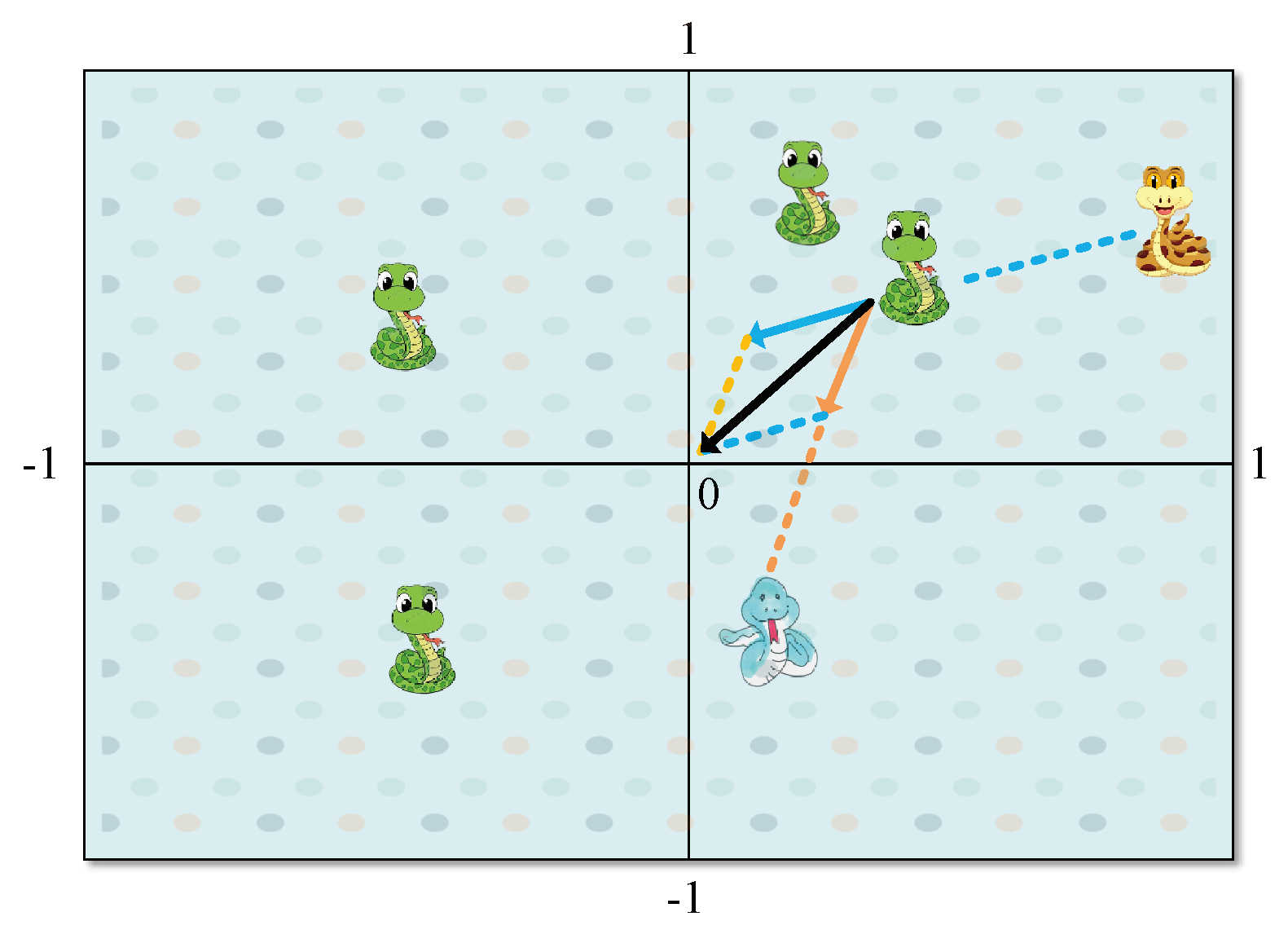
4.1. Snake Optimization Algorithm
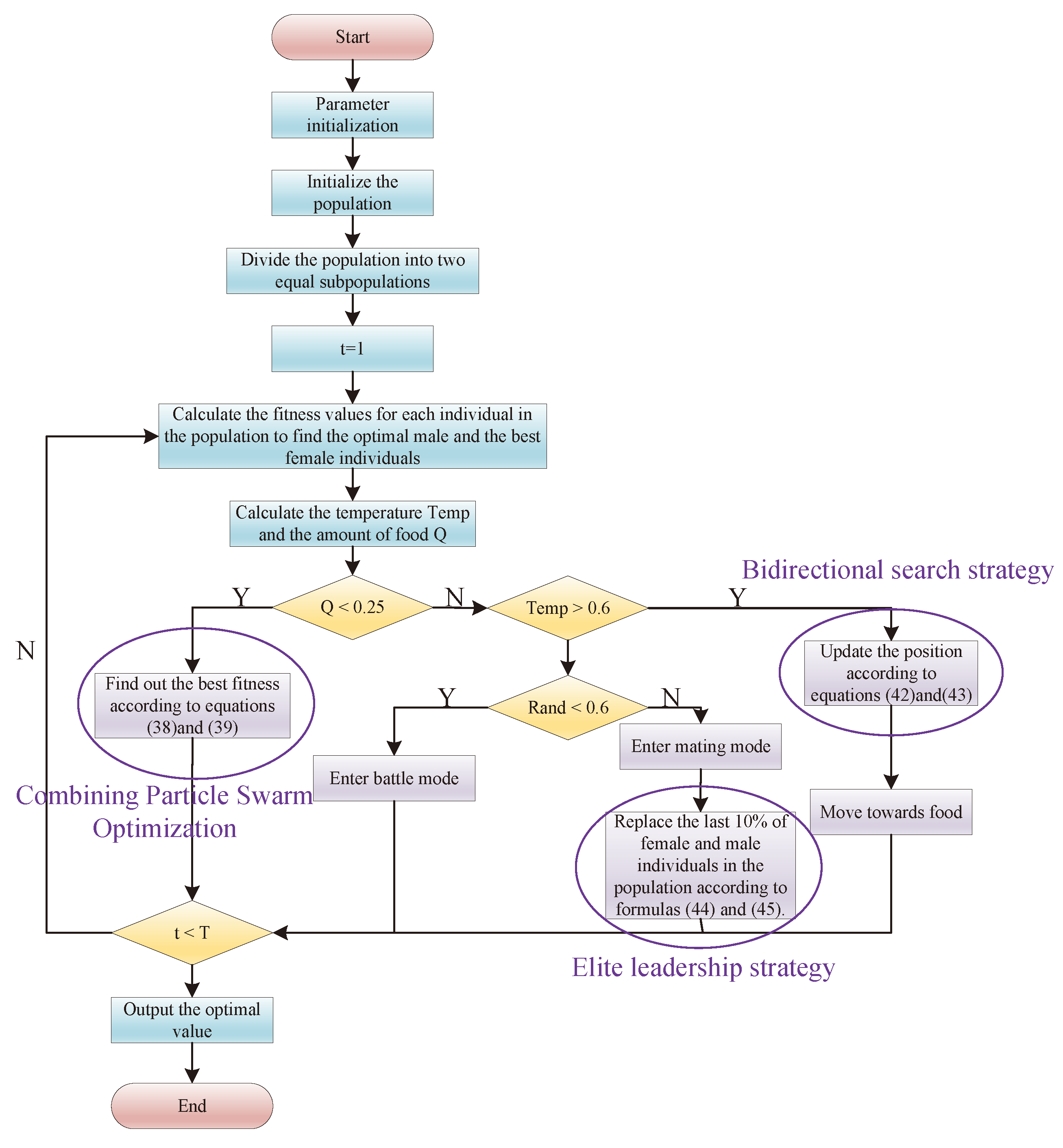
4.2. ISO Algorithm
4.2.1. Combination with PSO
4.2.2. Bidirectional Search Strategy
4.2.3. Elite Leadership Strategy
| Algorithm 1 Improved Snake Optimization Algorithm |
| Inputs: Maximum number of iterations, population size, etc. |
| Output: Optimal value |
| 1: Initialize the edge server location |
| 2: while do |
| 3: Calculate temp, Q, Xworst_m, Xworst_f, pBestm, gBestm, pBestf, gBestf |
| 4: if then |
| 5: Find food, update position according to Equations (38) and (39) |
| 6: else |
| 7: if then |
| 8: Move towards food and update position according to Equations (42) and (43) |
| 9: else |
| 10: if then |
| 11: Enter combat mode and update position according to Equations (28) and (29) |
| 12: else |
| 13: Enter mating mode and update position according to Equations (32) and (33) |
| 14: Select whether to hatch or not; if hatching, update the position according to Equations (44) and (45) |
| 15: end if |
| 16: end if |
| 17: end if |
| 18: end while |
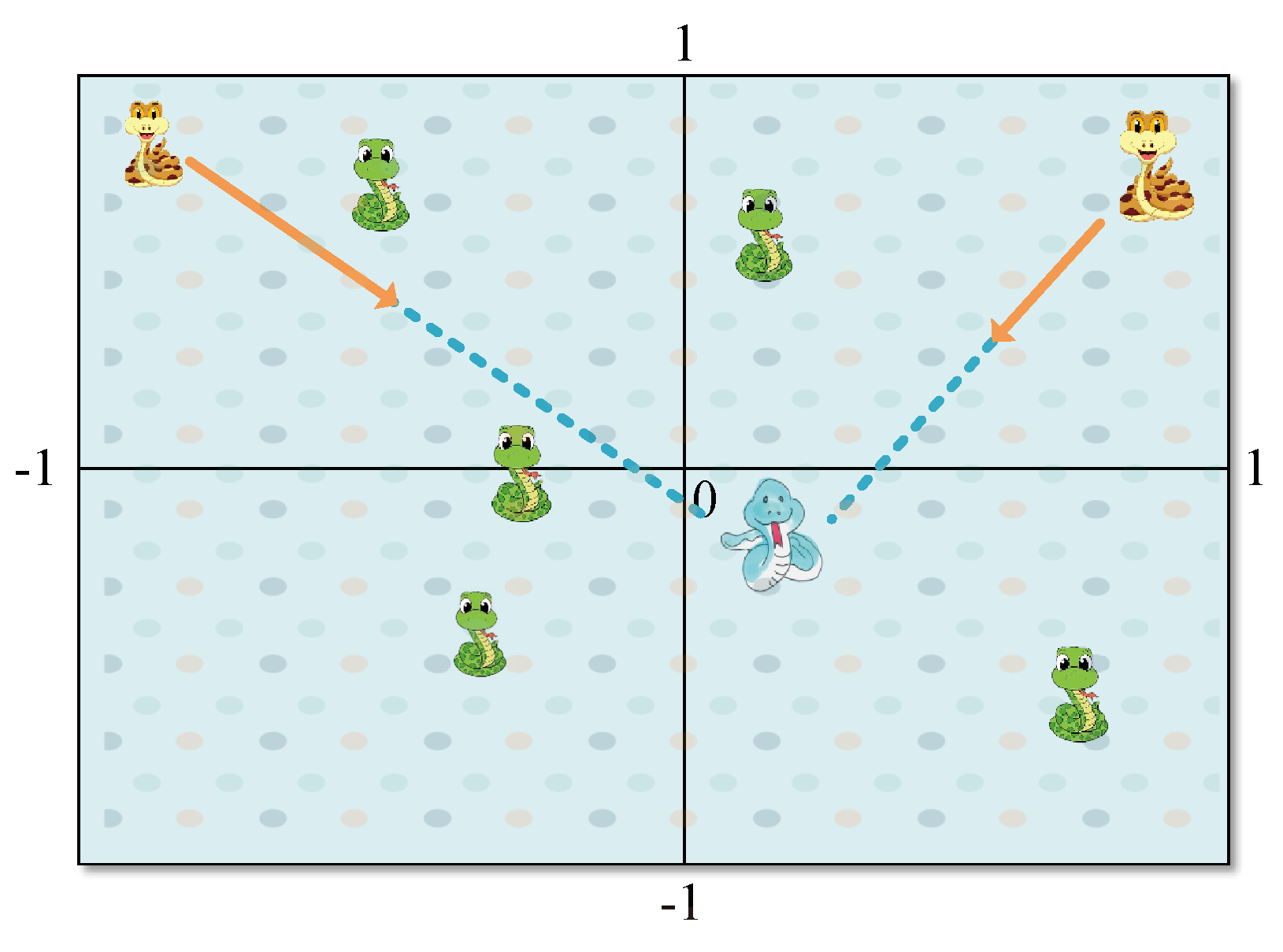
4.3. Dynamic Edge-Server Placement Algorithm
| Algorithm 2 Dynamic Edge-Server Placement Algorithm |
| Input: Location of user distribution at different moments |
| Output: Number and location of dynamic edge servers |
| 1: Find the optimal location for static server placement using the ISO algorithm |
| 2: for to t do |
| 3: Optimize the dynamic-server placement using the ISO algorithm |
| 4: if then |
| 5: do nothing |
| 6: else |
| 7: if then |
| 8: Increase the number of dynamic servers |
| 9: Compute the position and delay using the ISO algorithm |
| 10: else |
| 11: Reduce the number of dynamic servers |
| 12: Calculate the position and delay using the ISO algorithm |
| 13: end if |
| 14: end if |
| 15: end for |
4.4. Minimum Movement Distance Based on Linear Programming Problem
| Algorithm 3 Minimum Placement-Cost Algorithm Based on Interior Point Methods |
| Inputs: Original and new position matrices |
| Output: Minimum cost |
| 1: while do |
| 2: Calculate the gradient and Hessian matrix |
| 3: if then |
| 4: break |
| 5: end if |
| 6: while is not valid do |
| 7: |
| 8: end while |
| 9: |
| 10: end while |
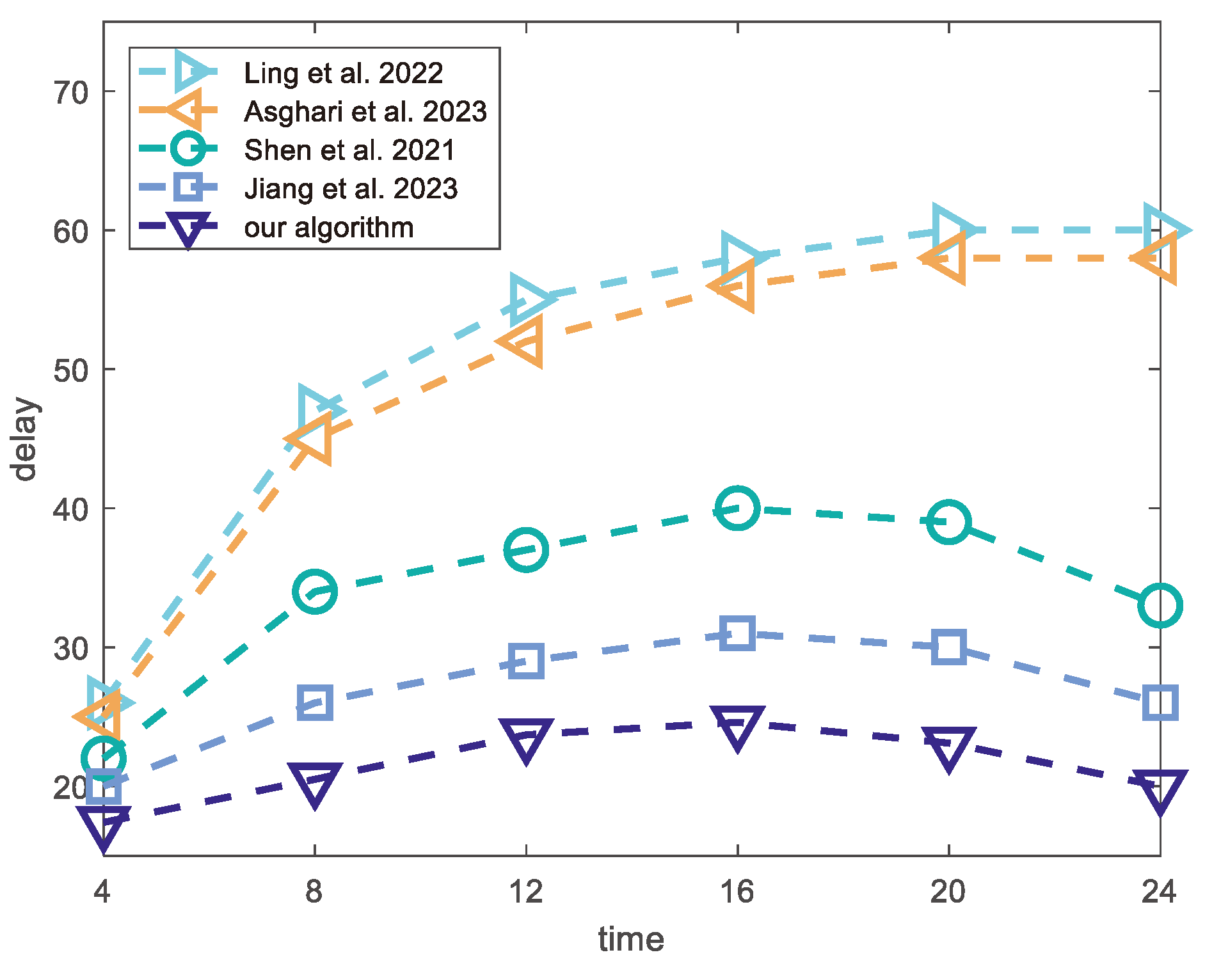
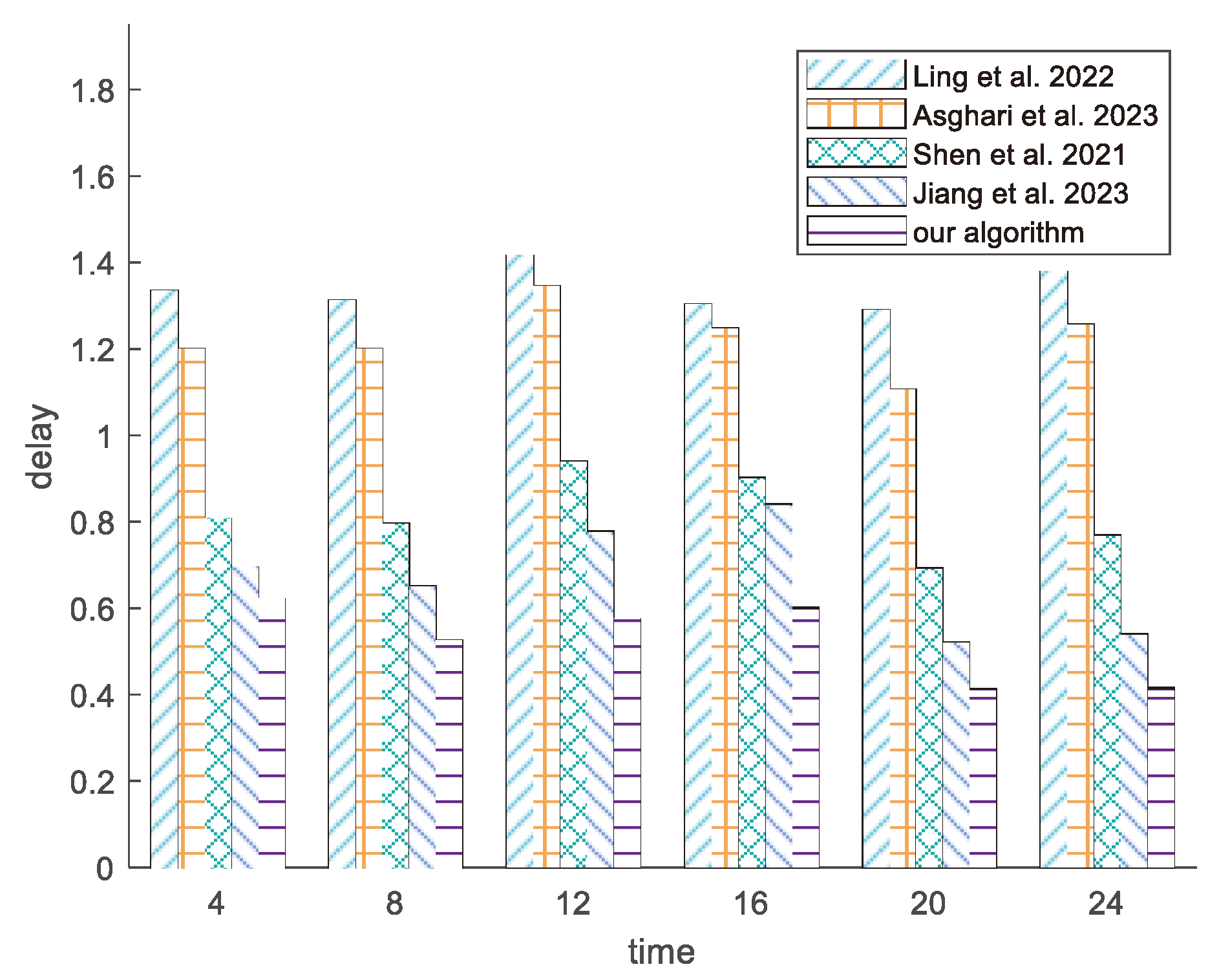
5. Experiment Results and Analysis
5.1. Dataset Processing
5.2. Parameterization
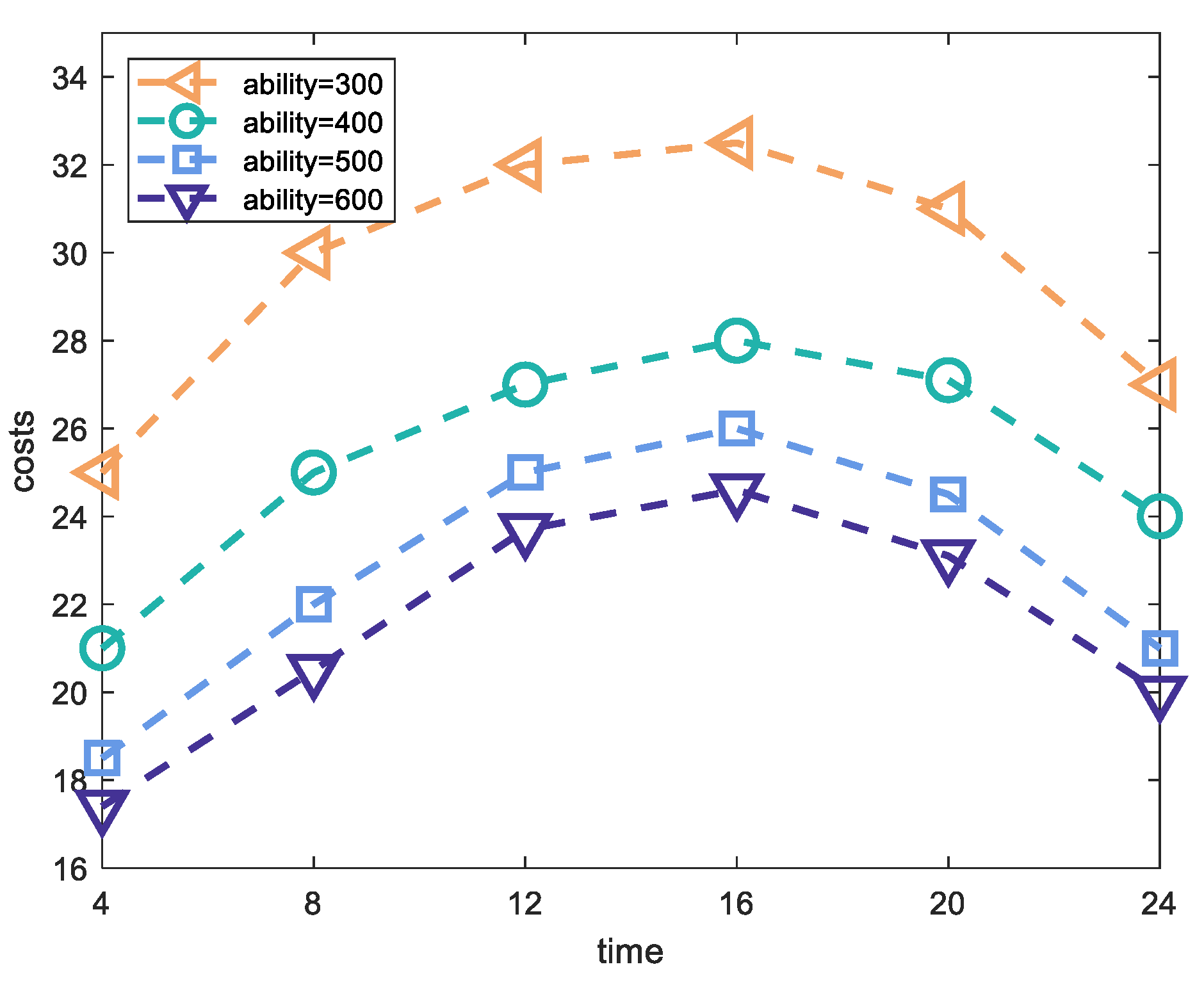
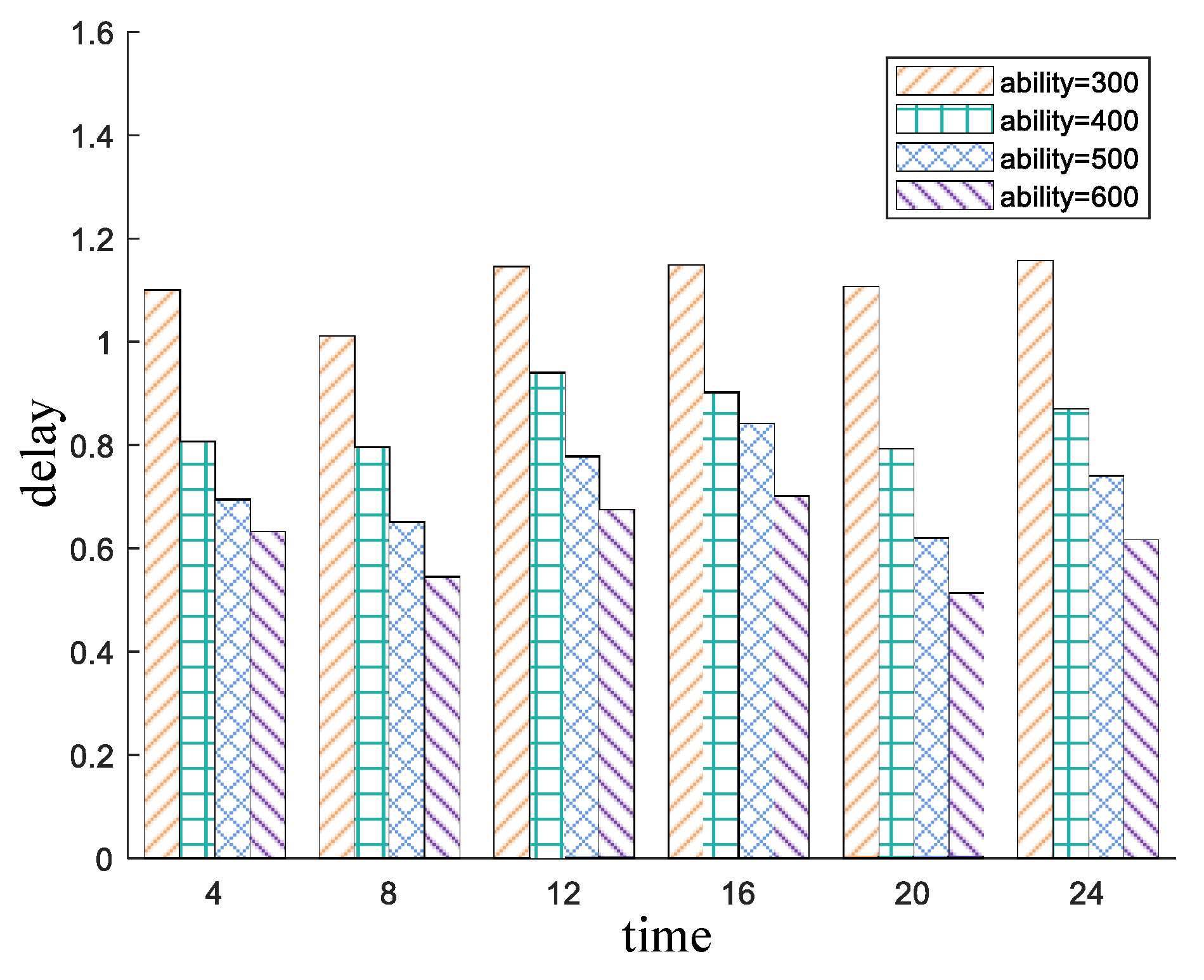
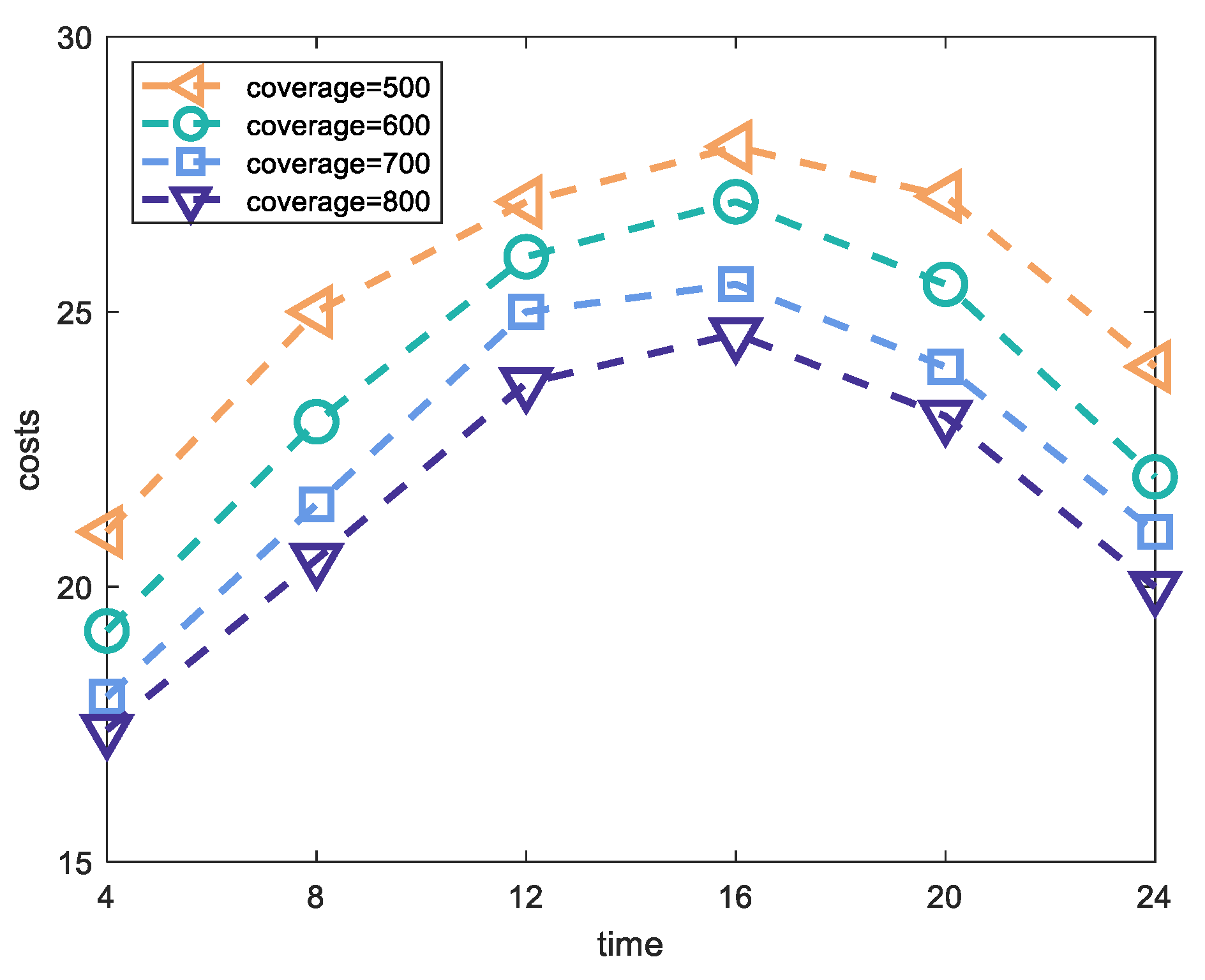
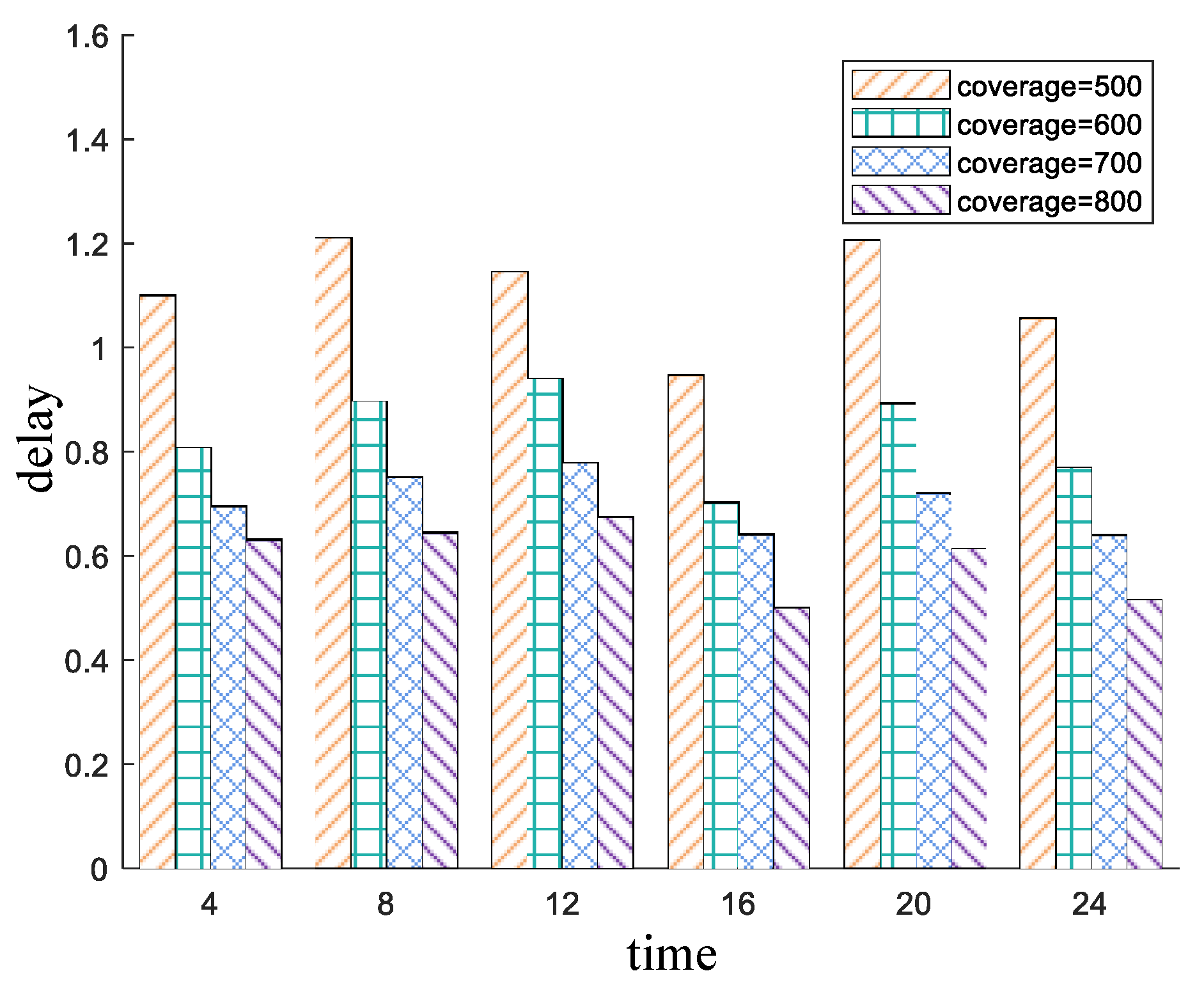
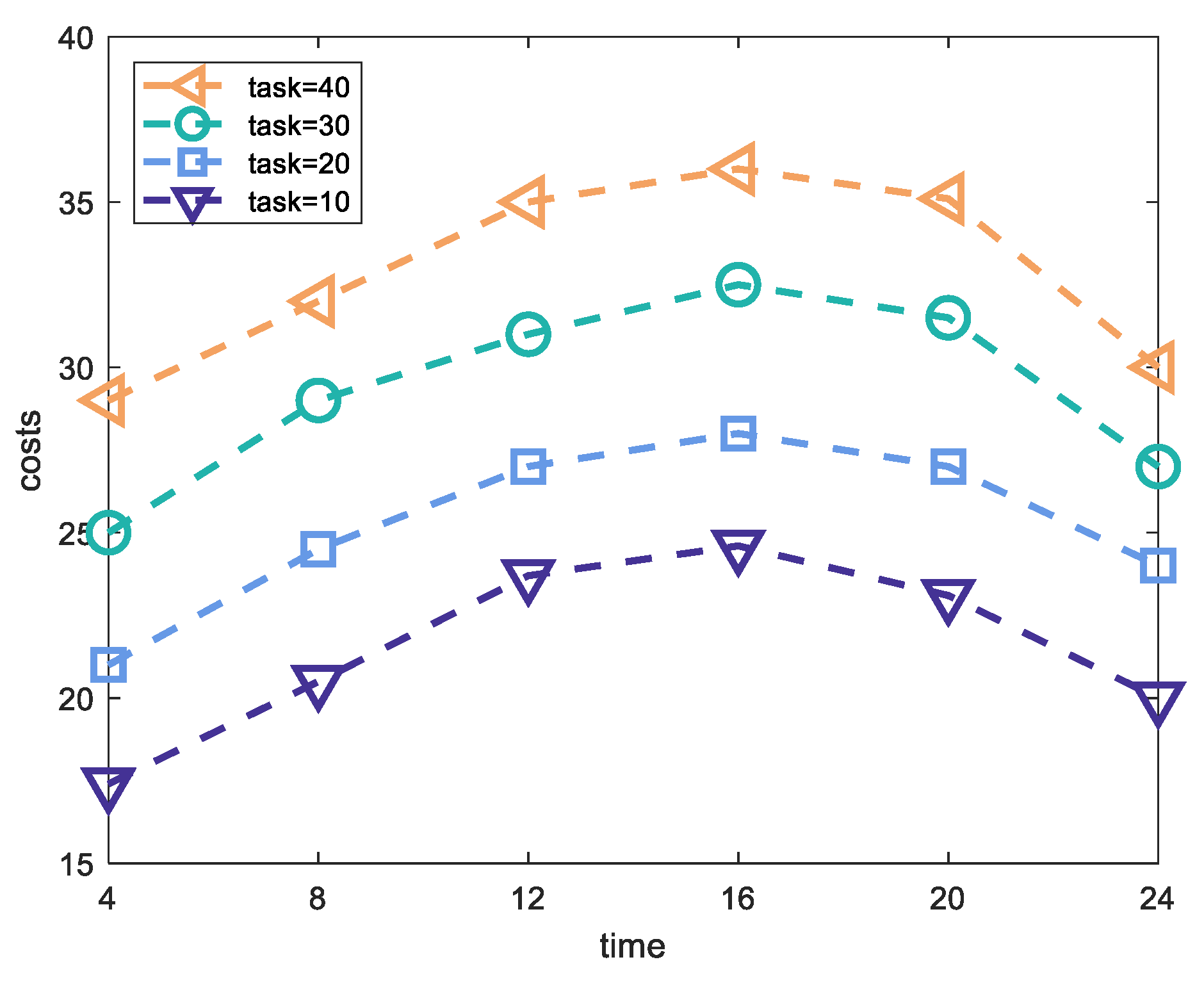
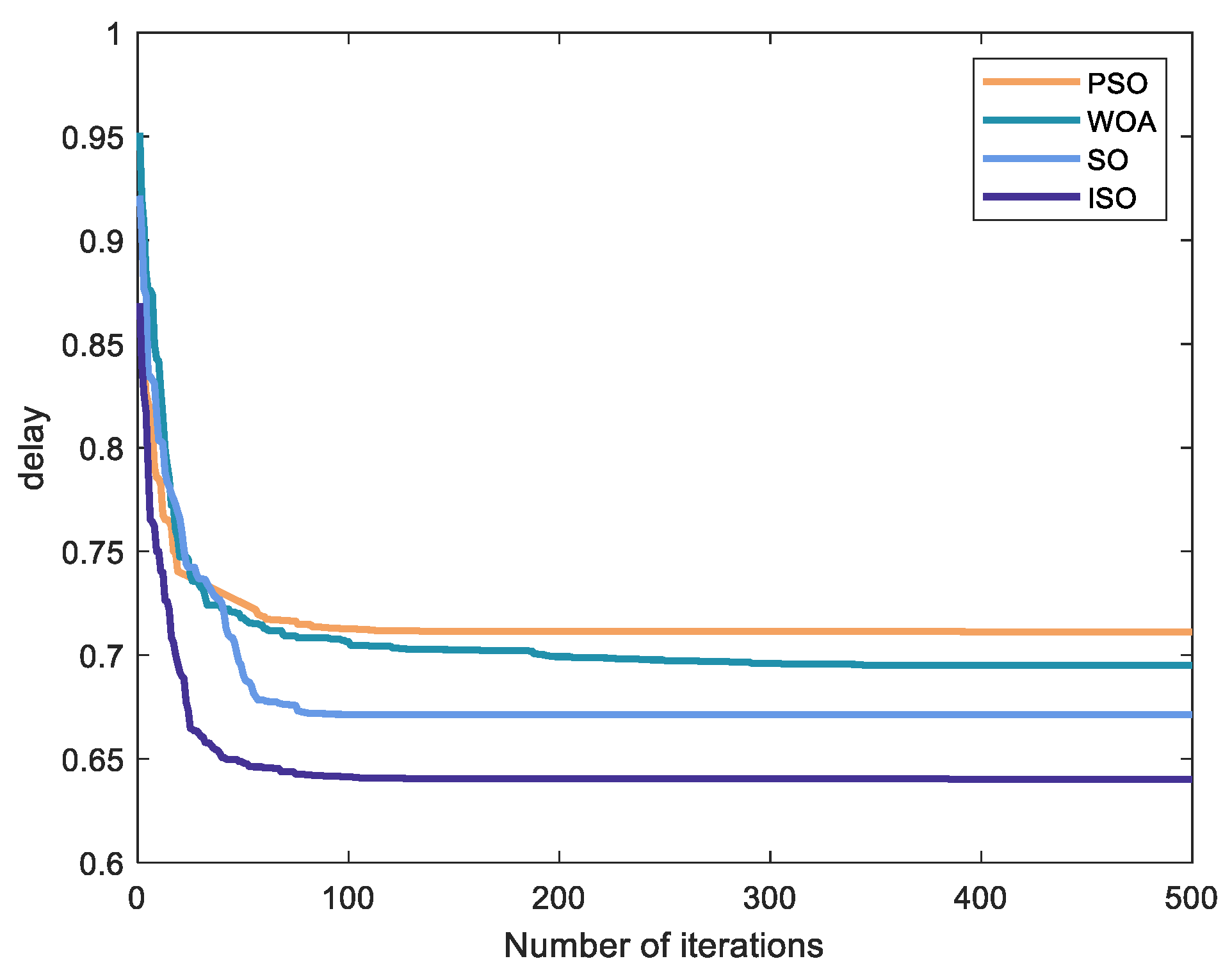
5.3. Experiment Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, K.; Li, L.; Cui, Y.; Wei, T.; Hu, S. Exploring placement of heterogeneous edge servers for response time minimization in mobile edge-cloud computing. IEEE Trans. Ind. Inform. 2020, 17, 494–503. [Google Scholar] [CrossRef]
- Singh, R.; Sukapuram, R.; Chakraborty, S. A survey of mobility-aware Multi-access Edge Computing: Challenges, use cases and future directions. Ad Hoc Netw. 2023, 140, 103044. [Google Scholar] [CrossRef]
- Hou, P.; Li, B.; Wang, Z.; Ding, H. Joint hierarchical placement and configuration of edge servers in C-V2X. Ad Hoc Netw. 2022, 131, 102842. [Google Scholar] [CrossRef]
- Chang, L.; Deng, X.; Pan, J.; Zhang, Y. Edge server placement for vehicular Ad Hoc networks in metropolitans. IEEE Internet Things J. 2021, 9, 1575–1590. [Google Scholar] [CrossRef]
- Xu, X.; Shen, B.; Yin, X.; Khosravi, M.R.; Wu, H.; Qi, L.; Wan, S. Edge server quantification and placement for offloading social media services in industrial cognitive IoV. IEEE Trans. Ind. Inform. 2020, 17, 2910–2918. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Li, B.; Hou, P.; Wang, K.; Peng, Z.; Jin, S.; Niu, L. Deployment of edge servers in 5G cellular networks. Trans. Emerg. Telecommun. Technol. 2022, 33, e3937. [Google Scholar] [CrossRef]
- Li, B.; Hou, P.; Wu, H.; Hou, F. Optimal edge server deployment and allocation strategy in 5G ultra-dense networking environments. Pervasive Mob. Comput. 2021, 72, 101312. [Google Scholar] [CrossRef]
- Feng, C.; Yang, Q.; Quek, T.Q.S.; Wu, W.; Guo, K. Spatially-Temporally Collaborative Service Placement and Task Scheduling in MEC Networks. IEEE Trans. Veh. Technol. 2023, 72, 16650–16666. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Y.; Zheng, Z.; Yu, P.; Shen, J.; Guo, M. Preference-aware edge server placement in the internet of things. IEEE Internet Things J. 2021, 9, 1289–1299. [Google Scholar] [CrossRef]
- Cui, G.; He, Q.; Chen, F.; Jin, H.; Yang, Y. Trading off between user coverage and network robustness for edge server placement. IEEE Trans. Cloud Comput. 2020, 10, 2178–2189. [Google Scholar] [CrossRef]
- Ning, Z.; Yang, Y.; Wang, X.; Guo, L.; Gao, X.; Guo, S.; Wang, G. Dynamic computation offloading and server deployment for UAV-enabled multi-access edge computing. IEEE Trans. Mob. Comput. 2021, 22, 2628–2644. [Google Scholar] [CrossRef]
- Kasi, S.K.; Kasi, M.K.; Ali, K.; Raza, M.; Afzal, H.; Lasebae, A.; Naeem, B.; Islam, S.u.; Rodrigues, J.J.P.C. Heuristic edge server placement in industrial internet of things and cellular networks. IEEE Internet Things J. 2020, 8, 10308–10317. [Google Scholar] [CrossRef]
- He, Z.; Li, K.; Li, K. Cost-efficient server configuration and placement for mobile edge computing. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 2198–2212. [Google Scholar] [CrossRef]
- Lu, J.; Jiang, J.; Balasubramanian, V.; Khosravi, M.R.; Xu, X. Deep reinforcement learning-based multi-objective edge server placement in Internet of Vehicles. Comput. Commun. 2022, 187, 172–180. [Google Scholar] [CrossRef]
- Ling, C.; Feng, Z.; Xu, L.; Huang, Q.; Zhou, Y.; Zhang, W.; Yadav, R. An edge server placement algorithm based on graph convolution network. IEEE Trans. Veh. Technol. 2022, 72, 5224–5239. [Google Scholar] [CrossRef]
- Asghari, A.; Azgomi, H.; Darvishmofarahi, Z. Multi-Objective edge server placement using the whale optimization algorithm and Game theory. Soft Comput. 2023, 27, 16143–16157. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Jin, X.; Huang, Y.; Lu, C. An optimal edge server placement approach for cost reduction and load balancing in intelligent manufacturing. J. Supercomput. 2022, 78, 4032–4056. [Google Scholar] [CrossRef]
- Shen, B.; Xu, X.; Qi, L.; Zhang, X.; Srivastava, G. Dynamic server placement in edge computing toward internet of vehicles. Comput. Commun. 2021, 178, 114–123. [Google Scholar] [CrossRef]
- Jiang, X.; Hou, P.; Zhu, H.; Li, B.; Wang, Z.; Ding, H. Dynamic and intelligent edge server placement based on deep reinforcement learning in mobile edge computing. Ad Hoc Netw. 2023, 145, 103172. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, A.; Ma, X.; Wang, S. Profit-aware edge server placement. IEEE Internet Things J. 2021, 9, 55–67. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, S.; Zhou, A.; Xu, J.; Yuan, J.; Hsu, C. User allocation-aware edge cloud placement in mobile edge computing. Softw. Pract. Exp. 2020, 50, 489–502. [Google Scholar] [CrossRef]
- Wang, S.; Guo, Y.; Zhang, N.; Yang, P.; Zhou, A.; Shen, X. Delay-aware Microservice Coordination in Mobile Edge Computing: A Reinforcement Learning Approach. IEEE Trans. Mob. Comput. 2021, 20, 939–953. [Google Scholar] [CrossRef]


| Parameter | Retrieved Value |
|---|---|
| Channel bandwidth w | 10 MHz |
| User transmission power P | W |
| Path loss factor | 10 |
| Channel gain between user and edge server | 0.1 |
| Noise power | 1.6 × 10−11 |
| Channel gain between user and cloud server | 0.98 |
| Distance from user to cloud server l | 1 × 106 m |
| The number of initial static servers N | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wu, X.; Yuan, P. A Dynamic Edge Server Placement Scheme Using the Improved Snake Optimization Algorithm. Appl. Sci. 2024, 14, 10130. https://doi.org/10.3390/app142210130
Liu J, Wu X, Yuan P. A Dynamic Edge Server Placement Scheme Using the Improved Snake Optimization Algorithm. Applied Sciences. 2024; 14(22):10130. https://doi.org/10.3390/app142210130
Chicago/Turabian StyleLiu, Jinjin, Xiaofeng Wu, and Peiyan Yuan. 2024. "A Dynamic Edge Server Placement Scheme Using the Improved Snake Optimization Algorithm" Applied Sciences 14, no. 22: 10130. https://doi.org/10.3390/app142210130
APA StyleLiu, J., Wu, X., & Yuan, P. (2024). A Dynamic Edge Server Placement Scheme Using the Improved Snake Optimization Algorithm. Applied Sciences, 14(22), 10130. https://doi.org/10.3390/app142210130