Fixed-Time Control with an Improved Sparrow Search Algorithm for Robotic Arm Performance Optimization
Abstract
1. Introduction
- (1)
- The proposed fixed-time control strategy achieves rapid convergence and enhanced vibration suppression for a n-degree-of-freedom robotic arm. This strategy addresses input saturation, output constraints, and system uncertainties to broaden the arm’s application. A novel adaptive law using logarithmic barrier Lyapunov functions (BLFs) was developed within this framework to manage parameter uncertainties and ensure that outputs stay within set limits.
- (2)
- The improved sparrow search algorithm enhances the traditional method by more effectively searching the solution space and identifying optimal control parameters, thus improving the robotic arm’s motion control performance. This algorithm serves as an optimization mechanism in this paper, boosting the effectiveness of the fixed-time control method in order to optimize the arm’s performance.
2. Theoretical Background and Problem Statement
2.1. Input Saturation Nonlinearity
2.2. Barrier Lyapunov Function
2.3. Radial Basis Function Neural Network
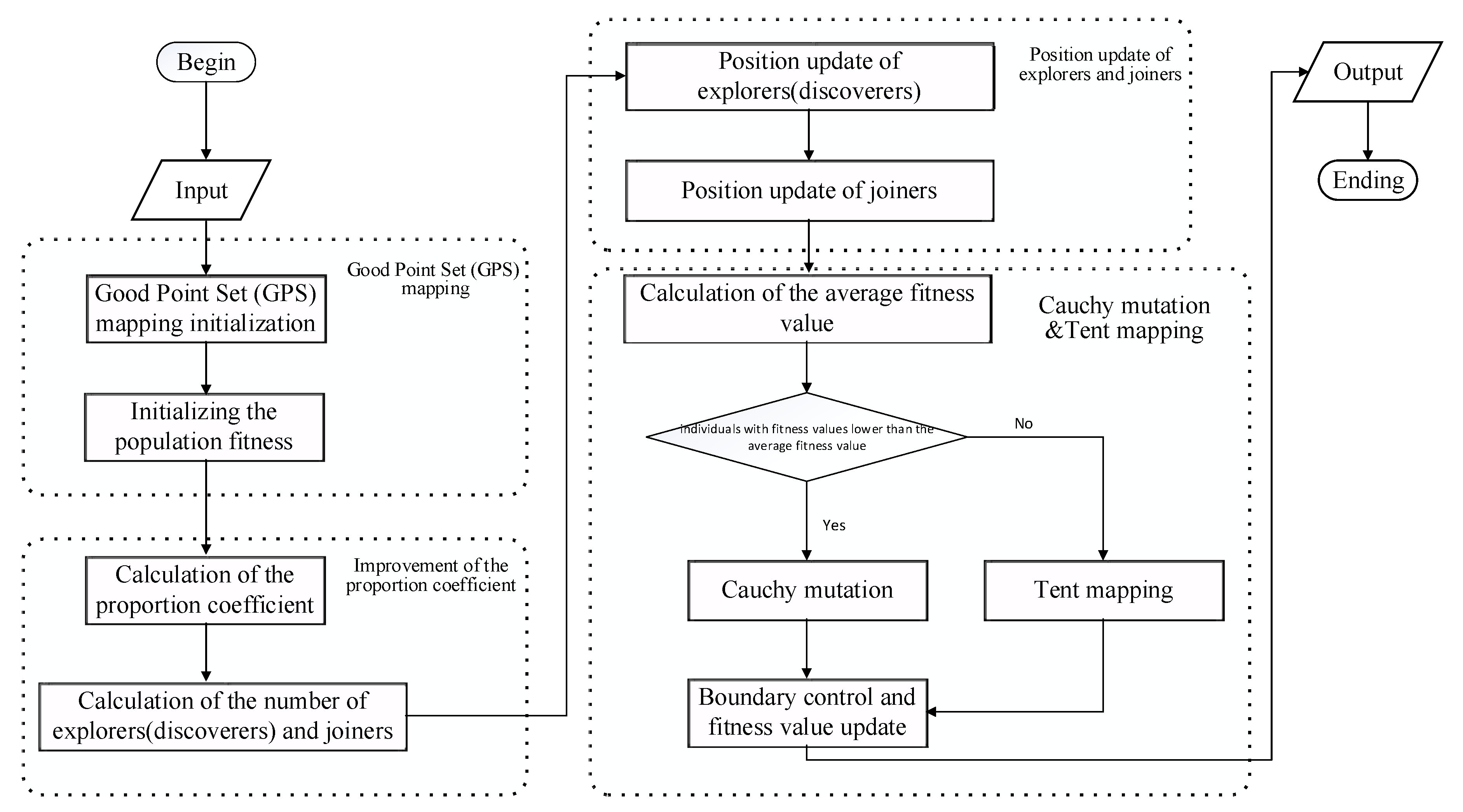
2.4. Improved Sparrow Search Algorithm (ISSA)
- (1)
- The good point set (GPS) is a strategy for generating initial solution sets characterized by high uniformity and low correlation. It is suitable for use in global optimization problems. This strategy involves selecting the smallest prime number greater than , coupled with the use of the cosine function, to create a point set. The specific formula for generating points is as follows:
- (2)
- By dynamically adjusting the proportion of discoverers and joiners, this improvement aims to balance exploration and exploitation capabilities. The proportional coefficient changes dynamically with the number of iterations, allowing for more explorers to investigate the solution space early in the search and increasing the number of joiners later on in order to refine potential solution areas already identified [27].
- (3)
- This enhancement uses an exponential decay factor to adjust the position updates of explorers in order to optimize their efficiency when searching the solution space [25].
- (4)
- This improvement increases population diversity by combining a tent map and Cauchy mutation, thereby enhancing the algorithm’s ability to avoid local optima and explore new areas [29,30,31]. Cauchy mutation is used when an individual’s fitness value is less than the average fitness value of the population. Tent mapping is used when an individual’s fitness value is greater than or equal to the average fitness value of the population.
2.5. Preliminaries
3. Fixed-Time Control Design and Lyapunov Function Proof Process
3.1. Fixed-Time Control Design
3.2. Lyapunov Function Proof
4. Simulation
4.1. Simulation on ISSA Performance
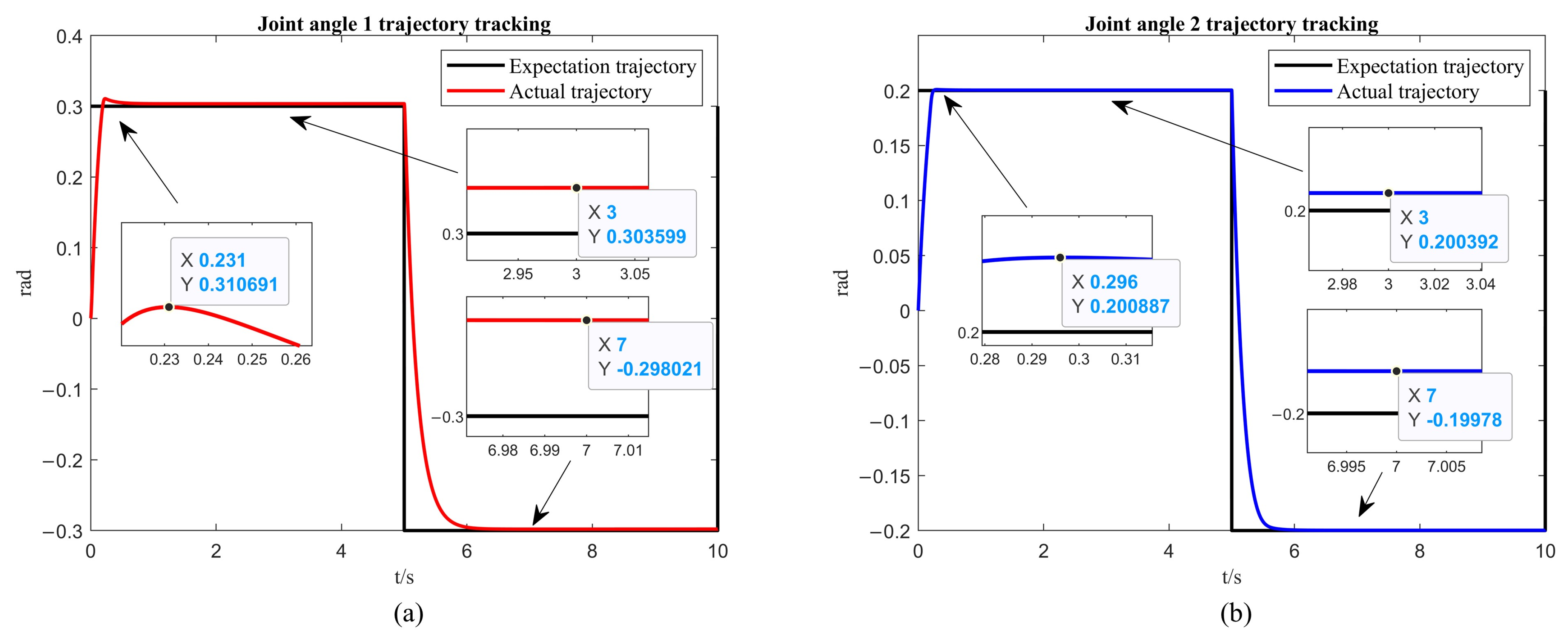
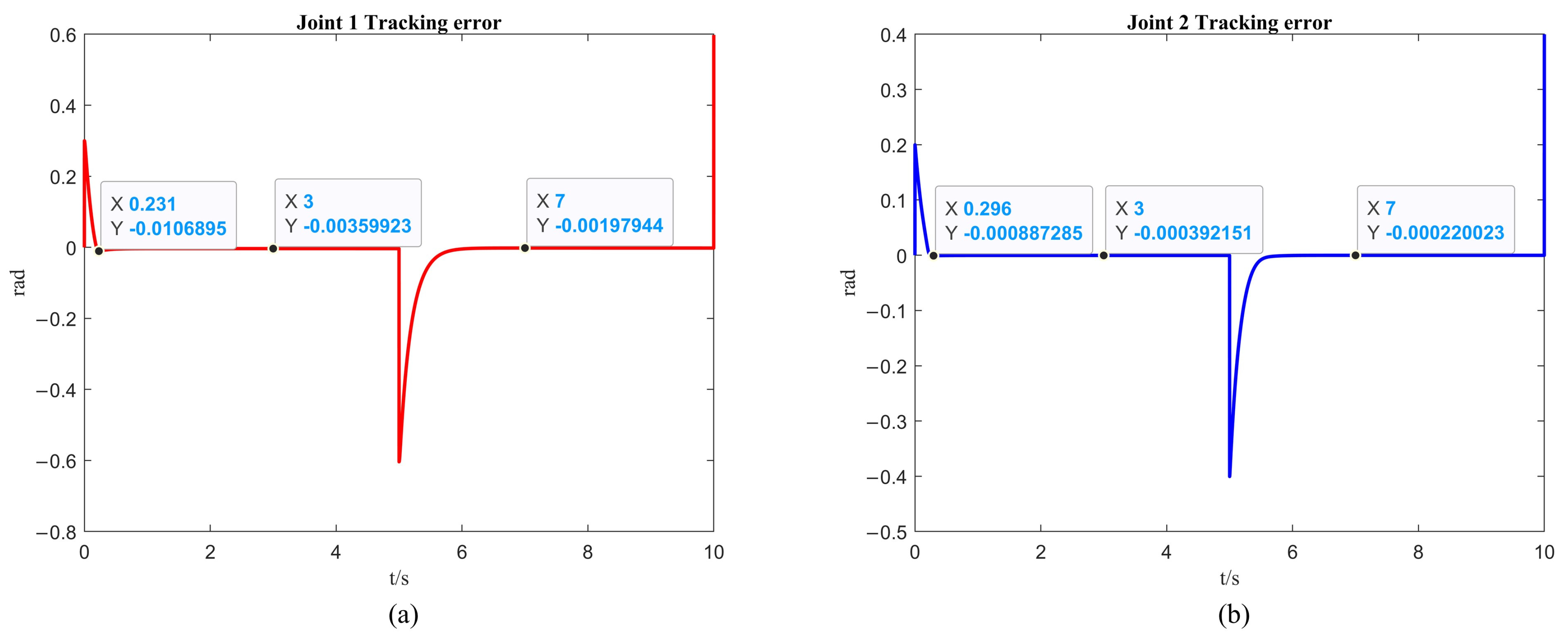
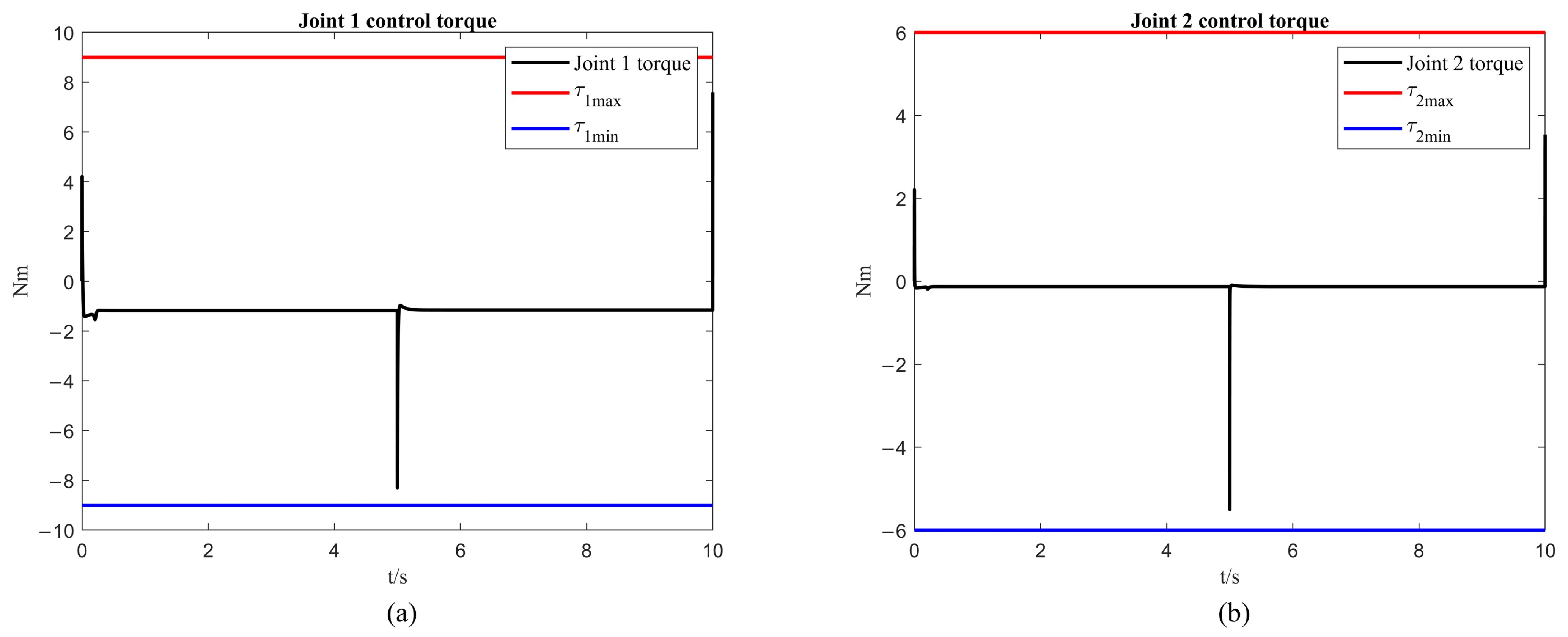
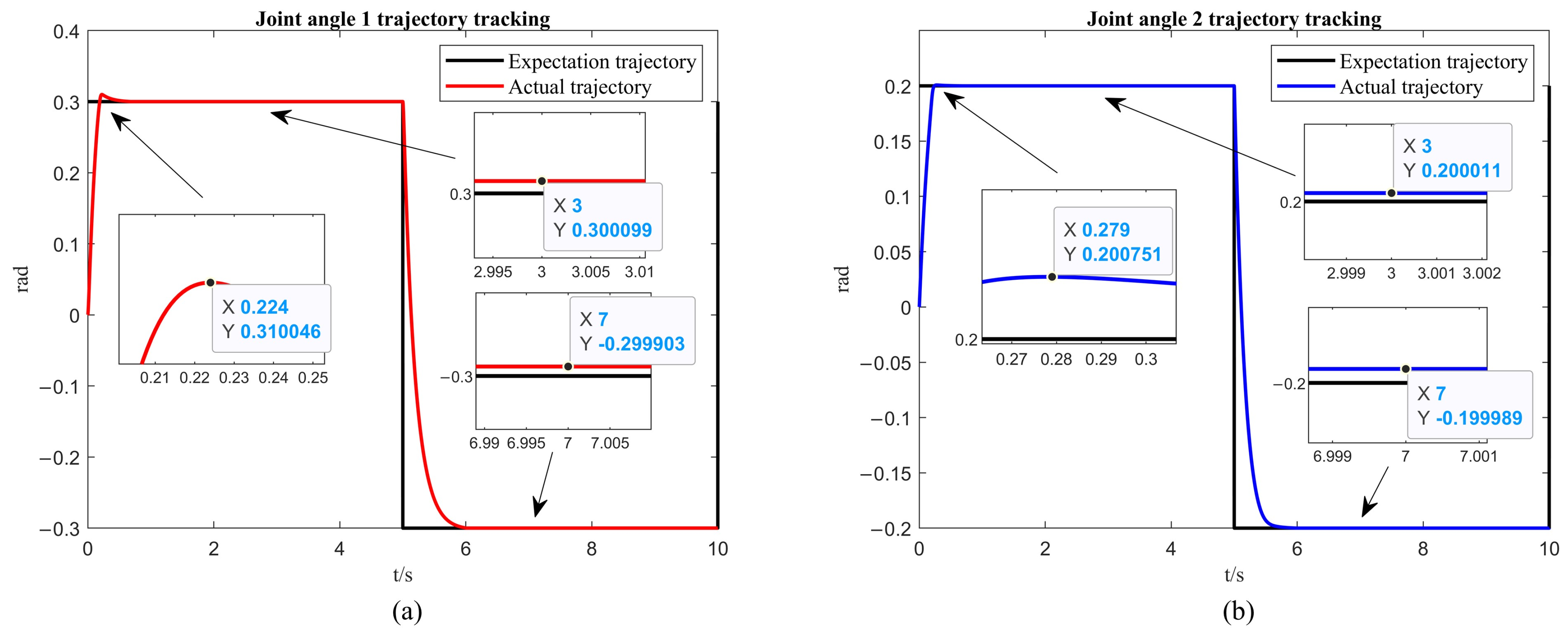
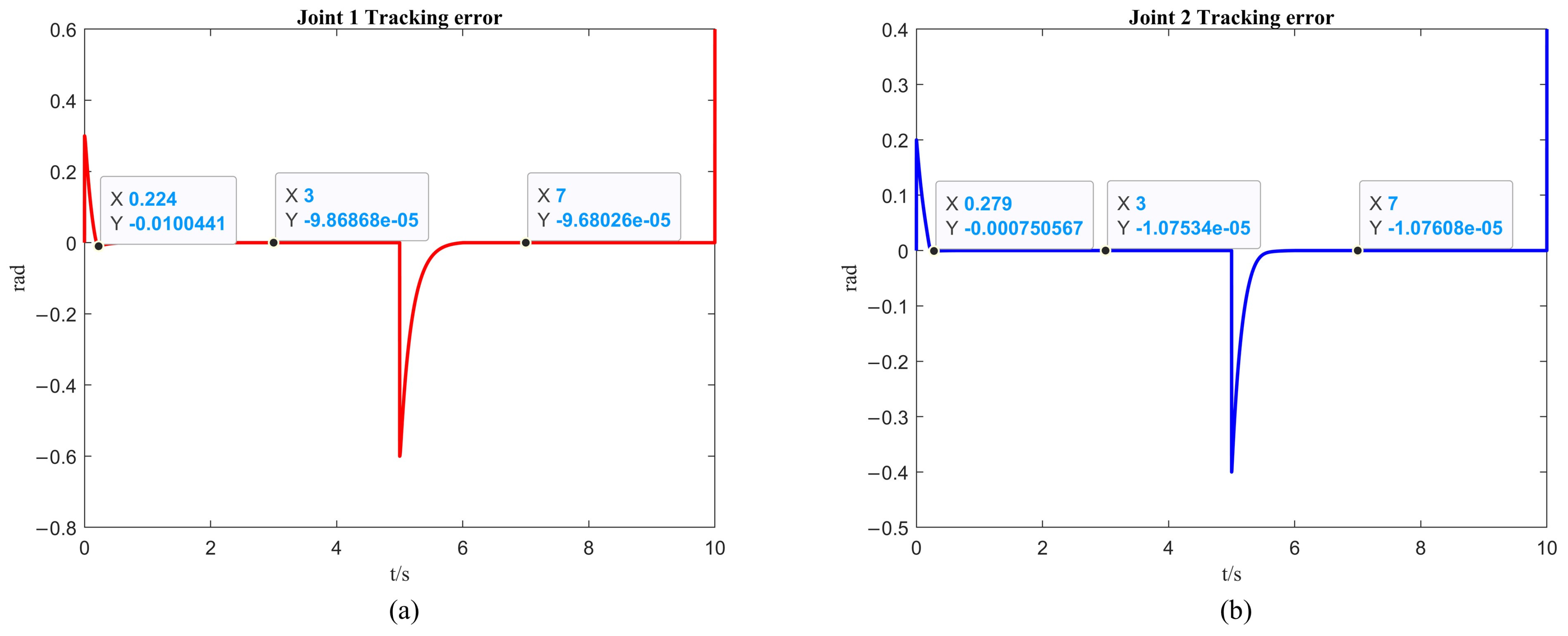
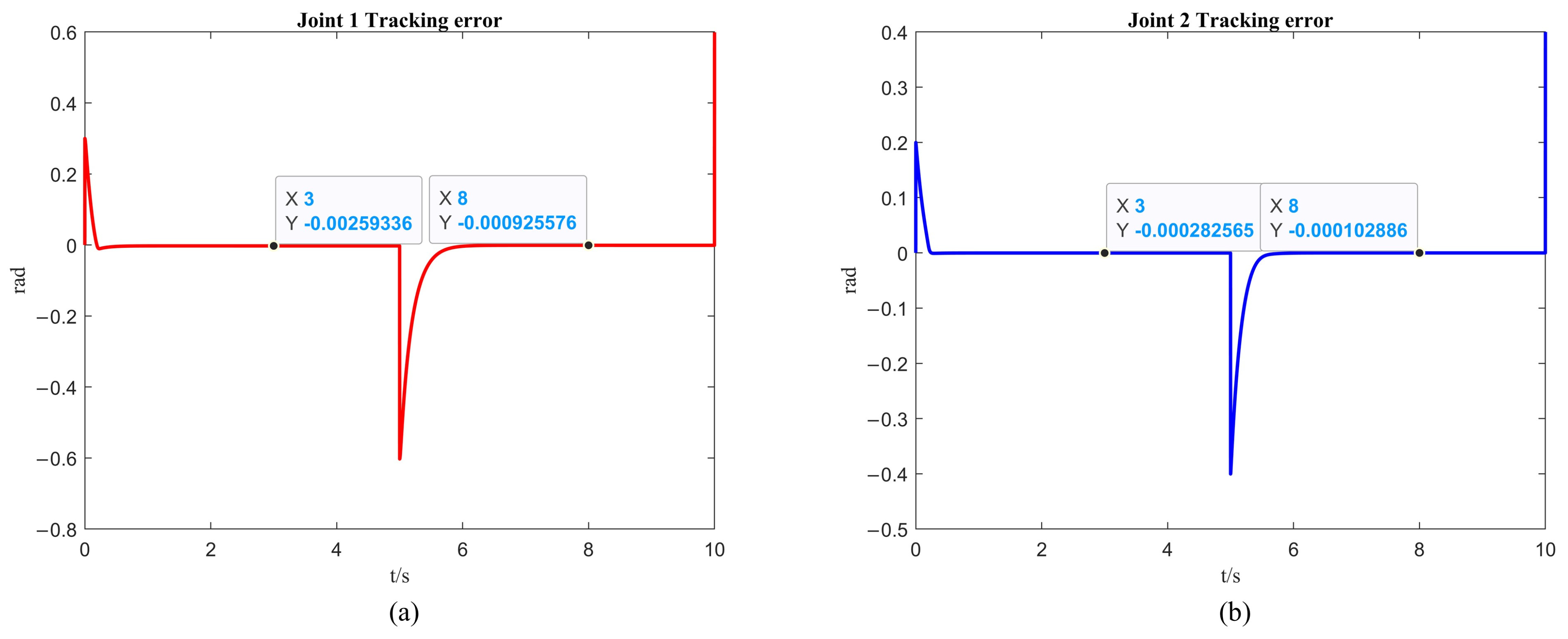
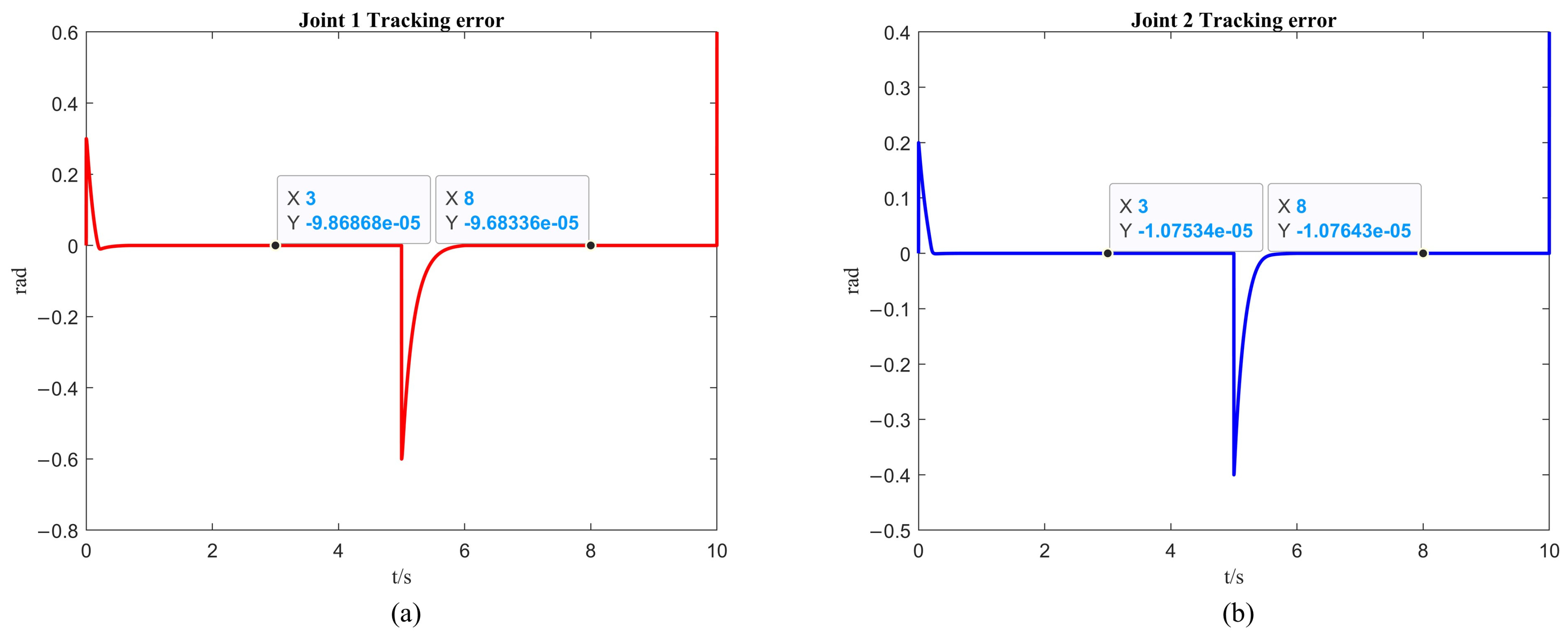
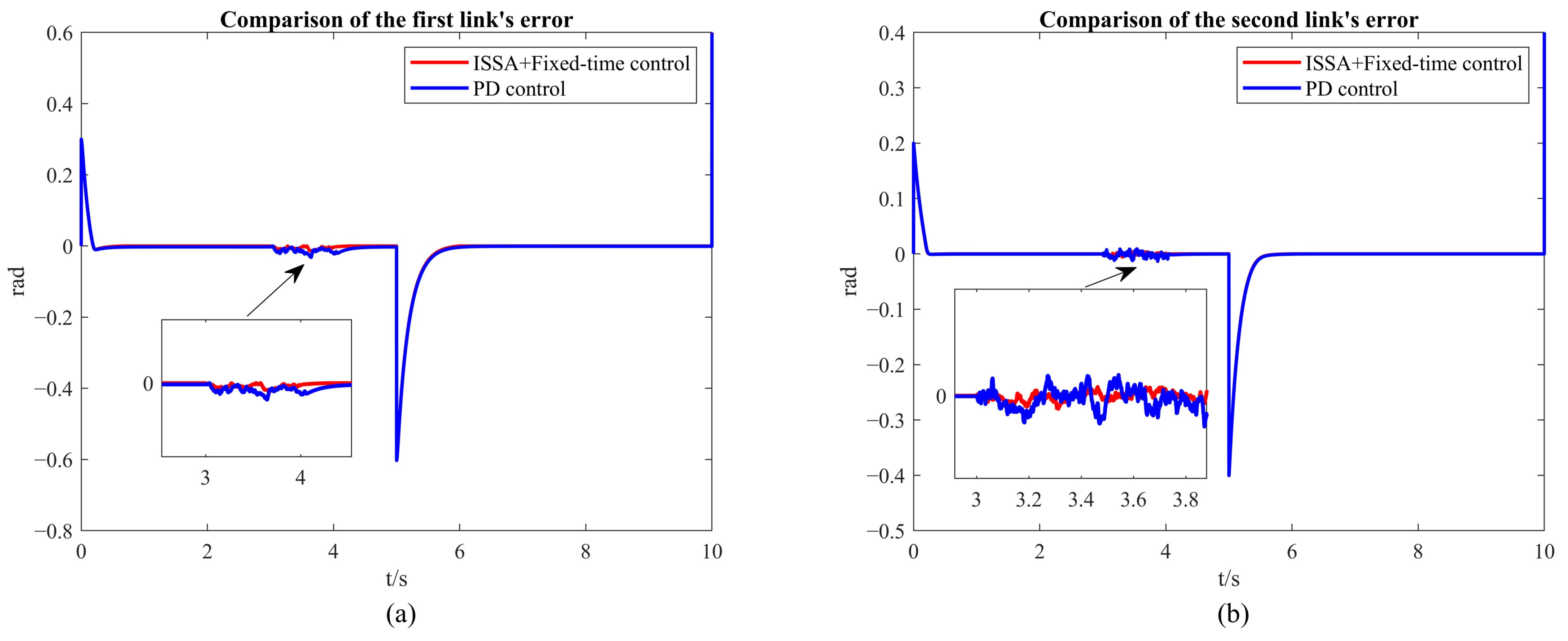
4.2. Two-DOF Robotic Arm Simulation
4.3. Summary
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Li, R.; Qiao, H.; Knoll, A. A Survey of Methods and Strategies for High-Precision Robotic Grasping and Assembly Tasks—Some New Trends. IEEE/ASME Trans. Mechatron. 2019, 24, 2718–2732. [Google Scholar] [CrossRef]
- Hesse, S.; Werner, C.; Pohl, M.; Mehrholz, J.; Puzich, U.; Krebs, H.I. Mechanical Arm Trainer for the Treatment of the Severely Affected Arm After a Stroke. Am. J. Phys. Med. Rehabil. 2008, 87, 779–788. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.L.; Wang, Y.C.; Wang, Y.B.; Xu, K. A review of structures, verification, and calibration technologies of space robotic systems for on-orbit servicing. Sci. China Technol. Sci. 2021, 64, 462–480. [Google Scholar] [CrossRef]
- Hu, J.S.; Chang, N.Y.C.; Yang, J.J.; Wang, J.J.; Lossio, R.G.; Chien, M.C.; Chang, Y.J.; Kai, C.Y.; Su, S.H. FPGA-based embedded visual servoing platform for quick response visual servoing. In Proceedings of the 2011 8th Asian Control Conference (ASCC), Kaohsiung, Taiwan, 15–18 May 2011; pp. 263–268. [Google Scholar]
- Lacquaniti, F.; Licata, F.; Soechting, J.F. The mechanical behavior of the human forearm in response to transient perturbations. Biol. Cybern. 1982, 44, 35–46. [Google Scholar] [CrossRef]
- Zhou, F.; Tian, X.; Tian, L. Reliability Analysis of Quick Coupler Attached to Rescue Manipulator Arm. In Proceedings of the 2019 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Zhangjiajie, China, 6–9 August 2019; pp. 703–708. [Google Scholar]
- Dai, Y.; Li, S.; Chen, X.; Nie, X.; Rui, X.; Zhang, Q. Three-dimensional truss path planning of cellular robots based on improved sparrow algorithm. Robotica 2024, 42, 347–366. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S.; Tay, E.H. Barrier Lyapunov Functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, B.; Liu, D.; Alippi, C. Data-based fault tolerant control for affine nonlinear systems through particle swarm optimized neural networks. IEEE/CAA J. Autom. Sin. 2020, 7, 954–964. [Google Scholar] [CrossRef]
- Lee, H.-W. The Study of Mechanical Arm and Intelligent Robot. IEEE Access 2020, 8, 119624–119634. [Google Scholar] [CrossRef]
- Qiu, Z.-C.; Li, C.; Zhang, X.-M. Experimental study on active vibration control for a kind of two-link flexible manipulator. Mech. Syst. Signal Process. 2019, 118, 623–644. [Google Scholar] [CrossRef]
- Sun, C.; Gao, H.; He, W.; Yu, Y. Fuzzy Neural Network Control of a Flexible Robotic Manipulator Using Assumed Mode Method. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5214–5227. [Google Scholar] [CrossRef]
- Jiao, R.; Chou, W.; Ding, R.; Dong, M. Adaptive robust control of quadrotor with a 2-degree-of-freedom robotic arm. Adv. Mech. Eng. 2018, 10, 1687814018778639. [Google Scholar] [CrossRef]
- Zuo, Z.; Tian, B.; Defoort, M.; Ding, Z. Fixed-time consensus tracking for multiagent systems with high-order integrator dynamics. IEEE Trans. Autom. Control 2017, 63, 563–570. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Krstic, M. Time-varying feedback for stabilization in prescribed finite time. Int. J. Robust Nonlinear Control 2019, 29, 618–633. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y.; Hill, D.J.; Krstic, M. Prescribed-time consensus and containment control of networked multiagent systems. IEEE Trans. Cybern. 2018, 49, 1138–1147. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Song, Y. Leader-following control of high-order multi-agent systems under directed graphs: Pre-specified finite time approach. Automatica 2018, 87, 113–120. [Google Scholar] [CrossRef]
- Orquera, M.; Campocasso, S.; Millet, D. Topological Optimization of a Mechanical System with Adaptive Convergence Criterion. In Advances on Mechanics, Design Engineering and Manufacturing III, Proceedings of the International Joint Conference on Mechanics, Design Engineering & Advanced Manufacturing, JCM 2020, Aix en Provence, France, 2–4 June 2020; Roucoules, L., Paredes, M., Eynard, B., Morer Camo, P., Rizzi, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Moubarak, P.; Ben-Tzvi, P. A globally converging algorithm for adaptive manipulation and trajectory following for mobile robots with serial redundant arms. Robotica 2013, 31, 1299–1311. [Google Scholar] [CrossRef]
- Jin, X. Adaptive fixed-time control for mimo nonlinear systems with asymmetric output constraints using universal barrier functions. IEEE Trans. Autom. Control 2018, 64, 3046–3053. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Hua, C.; Guan, X. Fixed-time backstepping control design for high-order strict-feedback non-linear systems via terminal sliding mode. IET Control Theory Appl. 2017, 11, 1184–1193. [Google Scholar] [CrossRef]
- Meng, D.; Zuo, Z. Signed-average consensus for networks of agents: A nonlinear fixed-time convergence protocol. Nonlinear Dyn. 2016, 85, 155–165. [Google Scholar] [CrossRef]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Zuo, Z. Non-singular fixed-time terminal sliding mode control of non-linear systems. IET Control Theory Appl. 2015, 9, 545–552. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in Sparrow Search Algorithm: A Comprehensive Survey. Arch. Comput. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Ni, Z.; Jin, F.; Li, J.; Li, F. Research on clustering method of improved glowworm algorithm based on good-point set. Math. Probl. Eng. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Kadiyala, K.; Murthy, K. Estimation of regression equation with cauchy disturbances. Can. J. Stat. 1977, 5, 111–120. [Google Scholar] [CrossRef]
- Song, W.; Liu, S.; Wang, X.; Wu, W. An improved sparrow search algorithm. In Proceedings of the 2020 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), Exeter, UK, 7–19 December 2020. [Google Scholar]
- Chen, X.; Huang, X.; Zhu, D.; Qiu, Y. Research on chaotic flying sparrow search algorithm. J. Phys. Conf. Ser. 2021, 1848, 012044. [Google Scholar] [CrossRef]
- Huang, G.-B.; Siew, C.-K. Extreme learning machine: RBF network case. In Proceedings of the ICARCV 2004 8th Control, Automation, Robotics and Vision Conference, Kunming, China, 6–9 December 2004; Volume 2. [Google Scholar]
- Khalfallah, S.; Ghenaiet, A. Radial basis function-based shape optimization of centrifugal impeller using sequential sampling. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 648–665. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Sun, W.; Gu, J.; Yao, B. RBF-Neural-Network-based adaptive robust control for nonlinear bilateral teleoperation manipulators with uncertainty and time delay. IEEE/ASME Trans. Mechatron. 2019, 25, 906–918. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, L.; Yu, H.; Lin, C.; Dong, W. Fuzzy finite-time command filtered control of nonlinear systems with input saturation. IEEE Trans. Cybern. 2017, 48, 2378–2387. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Chen, C.L.P. Adaptive neural control of uncertain MIMO nonlinear systems with state and input constraints. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1318–1330. [Google Scholar] [CrossRef] [PubMed]
- Kong, L.; He, W.; Dong, Y.; Cheng, L.; Yang, C.; Li, Z. Asymmetric bounded neural control for an uncertain robot by state feedback and output feedback. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1735–1746. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Attitude stabilization of rigid spacecraft with finite-time convergence. Int. J. Robust Nonlinear Control 2011, 21, 686–702. [Google Scholar] [CrossRef]
- Wang, H.-Q.; Chen, B.; Lin, C. Adaptive neural tracking control for a class of stochastic nonlinear systems. Int. J. Robust Nonlinear Control 2014, 24, 1262–1280. [Google Scholar] [CrossRef]
- Gao, H.; He, W.; Zhou, C.; Sun, C. Neural network control of a two-link flexible robotic manipulator using assumed mode method. IEEE Trans. Ind. Inform. 2018, 15, 755–765. [Google Scholar] [CrossRef]
- Keighobadi, J.; Mehran, H.-P.; Javad, F. Adaptive neural dynamic surface control of mechanical systems using integral terminal sliding mode. Neurocomputing 2020, 379, 141–151. [Google Scholar] [CrossRef]

| Function Number | Test Functions | Domain | Theoretical Value |
|---|---|---|---|
| F1 | [−100, 100] | 0 | |
| F2 | [−10, 10] | 0 | |
| F3 | [−10, 10] | 0 | |
| F4 | [−100, 100] | 0 | |
| F5 | [−5, 10] | 0 | |
| F6 | [−32, 32] | 0 | |
| F7 | [−50, 50] | 0 | |
| F8 | [−5, 5] | 0.000309 |
| Test Functions | Algorithm | Best Value | Worst Value | Average Value |
|---|---|---|---|---|
| F1 | SSA | 0.0000 × 100 | 4.0130 × 10−267 | 4.0130 × 10−268 |
| ISSA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| PSO | 6.3177 × 10−1 | 2.5751 × 100 | 1.6997 × 100 | |
| Chimp | 7.2228 × 10−10 | 5.0203 × 10−7 | 8.2238 × 10−8 | |
| GWO | 4.4064 × 10−32 | 2.8157 × 10−30 | 6.5511 × 10−31 | |
| WOA | 1.4104 × 10−89 | 6.9762 × 10−79 | 6.9780 × 10−80 | |
| F2 | SSA | 0.0000 × 100 | 1.0519 × 10−103 | 1.0519 × 10−104 |
| ISSA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| PSO | 2.4067 × 100 | 4.9044 × 100 | 3.8305 × 100 | |
| Chimp | 2.9009 × 10−7 | 1.9247 × 10−5 | 5.7236 × 10−6 | |
| GWO | 1.5962 × 10−19 | 2.7536 × 10−18 | 1.3757 × 10−18 | |
| WOA | 2.3018 × 10−59 | 6.1251 × 10−53 | 6.9522 × 10−54 | |
| F3 | SSA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 |
| ISSA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| PSO | 0.0000 × 100 | 1.3654 × 10−10 | 1.4841 × 10−11 | |
| Chimp | 3.2463 × 10−10 | −1.1122 × 10−7 | 2.3298 × 10−8 | |
| GWO | 8.4082 × 10−10 | 1.9413 × 10−7 | 3.1146 × 10−8 | |
| WOA | 0.0000 × 100 | 1.2829 × 10−12 | 1.4072 × 10−13 | |
| F4 | SSA | 0.0000 × 100 | 4.2410 × 10−252 | 4.2410 × 10−253 |
| ISSA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| PSO | 1.4490 × 100 | 2.0563 × 100 | 1.6774 × 100 | |
| Chimp | 2.2011 × 10−2 | 6.0196 × 10−1 | 2.0611 × 10−1 | |
| GWO | 1.7687 × 10−8 | 2.1929 × 10−7 | 5.8221 × 10−8 | |
| WOA | 9.8640 × 10−2 | 8.5463 × 101 | 4.5762 × 101 | |
| F5 | SSA | 0.0000 × 100 | 3.0119 × 10−124 | 3.0119 × 10−125 |
| ISSA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | |
| PSO | 6.2717 × 101 | 1.7519 × 102 | 1.2573 × 102 | |
| Chimp | 1.7803 × 100 | 2.2152 × 101 | 9.1301 × 100 | |
| GWO | 1.4177 × 10−11 | 4.5254 × 10−9 | 1.0949 × 10−9 | |
| WOA | 5.0206 × 102 | 2.9749 × 102 | 4.3256 × 102 | |
| F6 | SSA | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 |
| ISSA | 8.8818 × 10−16 | 8.8818 × 10−16 | 8.8818 × 10−16 | |
| PSO | 1.0527 × 100 | 3.0465 × 100 | 2.2359 × 100 | |
| Chimp | 1.9961 × 101 | 1.9964 × 101 | 1.9963 × 101 | |
| GWO | 5.0626 × 10−14 | 7.5495 × 10−14 | 6.1995 × 10−14 | |
| WOA | 8.8818 × 10−16 | 7.9936 × 10−15 | 4.0856 × 10−15 | |
| F7 | SSA | 1.4742 × 10−6 | 1.4673 × 10−2 | 5.0658 × 10−3 |
| ISSA | 5.7401 × 10−5 | 2.4232 × 10−2 | 3.3781 × 10−3 | |
| PSO | 2.1128 × 10−1 | 9.0880 × 10−1 | 4.6949 × 10−1 | |
| Chimp | 2.6782 × 100 | 2.9905 × 100 | 2.8295 × 100 | |
| GWO | 3.0732 × 10−1 | 7.2904 × 10−1 | 5.0930 × 10−1 | |
| WOA | 1.2416 × 10−1 | 9.4357 × 10−1 | 3.1349 × 10−1 | |
| F8 | SSA | 3.1419 × 10−4 | 1.2254 × 10−3 | 5.2091 × 10−4 |
| ISSA | 3.0750 × 10−4 | 3.6394 × 10−4 | 3.1646 × 10−4 | |
| PSO | 7.9768 × 10−4 | 9.9879 × 10−4 | 9.1620 × 10−4 | |
| Chimp | 1.2354 × 10−3 | 1.3394 × 10−3 | 1.2804 × 10−3 | |
| GWO | 3.0755 × 10−4 | 2.0363 × 10−2 | 4.4465 × 10−3 | |
| WOA | 3.1812 × 10−4 | 6.9223 × 10−4 | 4.9395 × 10−4 |
| Parameters | Meaning | Value | Unit |
|---|---|---|---|
| Mass of link 1 | 3.64 | kg | |
| Mass of link 2 | 0.42 | kg | |
| Length of link 1 | 0.301 | m | |
| Length of link 2 | 0.094 | m | |
| Inertia of link 1 | ; | ||
| Inertia of link 2 | |||
| Time (s) | Error of First Link with Fixed-Time Control (rad) | Error of Second Link with Fixed-Time Control (rad) | Error of First Link with Fixed-Time Control + ISSA (rad) | Error of Second Link with Fixed-Time Control + ISSA (rad) |
|---|---|---|---|---|
| 3 | ||||
| 7 |
| Time (s) | Error of First Link with Fixed-Time Control (rad) | Error of Second Link with Fixed-Time Control (rad) | Error of First Link with Fixed-Time Control + ISSA (rad) | Error of Second Link with Fixed-Time Control + ISSA (rad) |
|---|---|---|---|---|
| From 0 to 5 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Choi, H.-S.; Jung, D.; Cho, H.; Anh, P.H.N.; Vu, M.T. Fixed-Time Control with an Improved Sparrow Search Algorithm for Robotic Arm Performance Optimization. Appl. Sci. 2024, 14, 10096. https://doi.org/10.3390/app142210096
Zhang R, Choi H-S, Jung D, Cho H, Anh PHN, Vu MT. Fixed-Time Control with an Improved Sparrow Search Algorithm for Robotic Arm Performance Optimization. Applied Sciences. 2024; 14(22):10096. https://doi.org/10.3390/app142210096
Chicago/Turabian StyleZhang, Ruochen, Hyeung-Sik Choi, Dongwook Jung, Hyunjoon Cho, Phan Huy Nam Anh, and Mai The Vu. 2024. "Fixed-Time Control with an Improved Sparrow Search Algorithm for Robotic Arm Performance Optimization" Applied Sciences 14, no. 22: 10096. https://doi.org/10.3390/app142210096
APA StyleZhang, R., Choi, H.-S., Jung, D., Cho, H., Anh, P. H. N., & Vu, M. T. (2024). Fixed-Time Control with an Improved Sparrow Search Algorithm for Robotic Arm Performance Optimization. Applied Sciences, 14(22), 10096. https://doi.org/10.3390/app142210096








