Abstract
This work introduces a novel computational approach based on Principal Component Analysis (PCA) for dimensionality reduction of the solution space in optimisation problems with known linear interdependencies among solution variables. By creating synthetic datasets with deliberately engineered properties and applying PCA, the solution space’s remapping significantly reduces its dimensionality, leading to faster computation and more robust convergence in optimisation processes. We demonstrate this method by integrating it with a Genetic Algorithm (GA) for solving the optimal director distribution in liquid crystal (LC) devices, specifically addressing 2D and complex 3D spatial light modulator (SLM) structures such as twisted nematic liquid crystals (TN-LC) and parallel-aligned liquid crystal on silicon (PA-LCoS), respectively. The phase profiles obtained from the director vector distributions for horizontal and vertical high-frequency binary phase gratings closely match the theoretical values derived from minimising the traditional elastic Frank–Oseen functional via Euler–Lagrange equations. Beyond this specific application, our method offers a general framework for reducing computational complexity in optimisation problems by directly reducing the dimensionality of the solution space. This approach is applicable across various optimisation scenarios with well-known linear interdependencies among solution variables, enabling significant reductions in computational costs and improvements in robustness and convergence.
1. Introduction
SLMs are extensively employed for wavefront manipulation, owing to their ability to efficiently shape the intensity, polarization, or phase of light with high spatial resolution. These devices serve numerous purposes in photonics and communications, mainly as programmable diffractive optical elements, ranging from dynamic beam-shaping holography to three-dimensional imaging [1,2,3,4,5,6].
In practical situations, the most common non-ideal behaviour observed in these LC-based devices is the smoothing effect of the director distribution at the borders between adjacent pixels, a phenomenon known as pixel crosstalk. This phenomenon results from the interaction of neighbouring pixels, producing notable deviations from the intended output, especially in patterns with high variations or contrast [7,8,9]. Pixel crosstalk generally arises not only from the natural smoothing of the electric field within the liquid crystal layer, as compared to the electrode voltages, but also from the elastic interactions among dielectric LC molecules, which impede abrupt changes in orientation, thus impacting the electric field. Thus, SLM models with smaller pixels or thicker LC layers experience increased pixel crosstalk, affecting applications that demand high spatial frequency content in phase patterns [9,10,11,12].
To address this problem, minimisation of the precise Frank–Oseen free energy is typically required, most commonly through their derived Euler–Lagrange equations such as in [7,8,13]. This theoretical model has proven to reproduce the measured response of the SLM accurately. While efforts have been made to solve it through alternative machine learning techniques for simple and canonical structures based on 1D or 2D models [14,15], little success has been achieved when handling a higher number of variables or an entire 3D space. Genetic algorithms are evolutionary computation techniques inspired by natural selection and genetics principles, commonly used to generate high-quality solutions to optimisation and search problems in different science disciplines [16,17,18,19,20]. These machine learning algorithms prove especially suitable when other traditional methods fail, such as dealing with complexity issues or non-differentiable objective functions.
Although previous efforts have applied evolutionary machine learning methodologies to minimise the Frank–Oseen free energy, these methods have yet to be adapted for a larger number of variables or voxels representing three-dimensional space [14]. Applying these methods directly to complex 3D structures, in general, is challenging because it requires significantly increased computational power to ensure the process is competitive compared to traditional formalisms. This research paper aims to resolve the nematic cell vector directors within the liquid crystal by directly minimising the Frank–Oseen free energy through a GA framework for the highest possible spatial resolution.
To overcome the challenge of solving the problem for a significantly greater number of variables, we propose a lower-dimensional remapping of the solution space using (PCA). Dimensionality reduction techniques, such as PCA or t-distributed Stochastic Neighbor Embedding (t-SNE) [21], are widely applied across diverse scientific and industrial fields [22,23,24,25,26,27]. Their primary purpose is to enhance visualisation and understanding, particularly when managing high-dimensional datasets. These techniques are most commonly employed to project such high-dimensional data into two dimensions, facilitating efficient plotting and aiding in cluster detection for classification purposes. This allows for gaining insights by representing complex information in an accessible and visually interpretable manner [28,29,30].
However, as stated above, our approach uses these methods specifically for the lower-dimensional remapping of our solution space, leveraging the assumption that it is smooth, or in other words, it features significant spatial autocorrelation. To the best of our knowledge, this technique has not been previously applied, at least within the context of LC research.
The GA routine developed is specifically tailored to operate within the remapped lower-dimensional solution space, aiming to enhance the convergence and efficiency of the optimisation process. The subsequent sections of this paper explore the dimensionality reduction process, detail the routine developed, and present optimisation results across various SLM configurations in three-dimensional space, ultimately demonstrating its effectiveness and applicability.
2. Theory
2.1. Physical Model of the SLM
As mentioned in previous sections, the accurate description of the nematic cell vector distribution of a liquid crystal in the presence of an electric potential involves the minimisation of the so-called Frank–Oseen free energy, which captures the elastic, electric, and surface contributions and is given by the following expression [8,9]:
where
and is the unit director field, , , are the splay, twist, and bend constants, and is the electric field. is the dielectric tensor, which can be expressed as:
where and are the relative permeability for liquid crystals aligned parallel and perpendicular to the electric field direction [8]. The interaction with the external electric field is obtained considering its relationship with the electrostatic potential and the application of Gauss’s Law () (2). Gauss’s Law solution for the electric potential of each 3D space unit, considering the influence of the dielectric tensor in each point, involves derivatives of the dielectric tensor and the electric potential. For computational efficiency, we approximate these derivatives using neighbouring differences. The interested reader can find the explicit closed expressions for this part of the algorithm in [31].
The minimisation of (2) can be done through its derived Euler–Lagrange equations using central finite differences and updating and iteratively until convergence. This procedure is fully defined in the literature, and interested readers can read more about this in [9] and Section 2.3 in [8]. Here, this method has been implemented, and it is considered a reference for comparing the GA method proposed in this work to overcome the implementation of the demanding formalism derived from the application of the Euler–Lagrange equations.
2.2. Lower-Dimensional Remapping: PCA Analysis
Given our objective to address the distribution of unit vector directors in three-dimensional space and leveraging spherical coordinates with a fixed radial distance of , a set of one and one value for each voxel in space is enough to characterise the whole vector solution space. These values are represented as two independent scalar fields (an example is shown in Figure 1a). The angle represents the tilt angle, and is the twist angle of each LC nematic cell. The expected values for and are expected to exhibit a degree of smoothness, which implies gradual variation concerning neighbouring values. This characteristic is informed by practical observations indicating that liquid crystal nematic cells tend to distribute and orientate in a structured or smooth configuration.
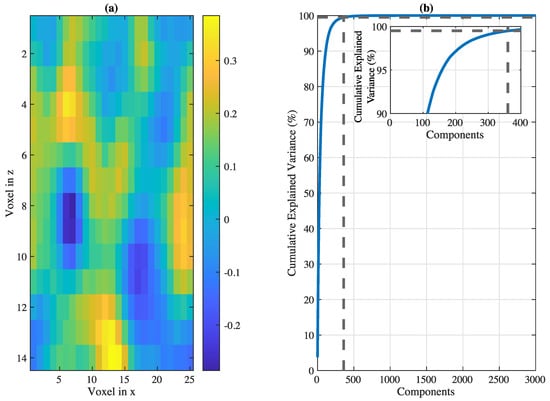
Figure 1.
(a) Section example of a 3D Random Smooth Scalar Field with periodic boundary conditions in the x and y axis. Arbitrary units. Moran’s I = 0.5702. (b) Cumulative Explained Variance of 5184 Principal Components of a 10,000 (20 × 24 × 12 voxels) 3D Random Smooth Scalar Field Samples set. The 99.5% of the variance is represented by dashed lines with the number of principal components required.
The lower-dimensional remapping of the space to be optimised is thus conducted after the assumption that the solution space must be smooth, which leads to a statistical dependence or a positive degree of spatial autocorrelation. One common way of calculating this spatial autocorrelation, the so-called Moran’s I, is given by [32]:
where I is the Moran’s I statistic, n is the number of spatial units, is the value of the variable of interest in unit i, is the mean of the variable of interest, is the spatial weight between units i and j, and W is the sum of spatial weights. Moran’s I ranges from −1 to 1. A positive value indicates positive spatial autocorrelation (similar values cluster together), while a negative value indicates negative spatial autocorrelation (dissimilar values cluster together). Thus, we expected the solution to have a positive Moran’s I.
On the other hand, given a sufficiently large set of random 3D smooth scalar field distributions, we can reconstruct any new smooth scalar field, including our problem’s solution, as a linear combination of a number of those random scalar fields.
The idea here is that since our solution is assumed to be a part of a broader set of ‘all possible smooth scalar fields’, we only need to characterise and seek the solution in a new space of ‘all possible smooth scalar fields’, which since featuring spatial autocorrelation, can be expressed in a way lower number of variables than in the original Cartesian 3D space. To find the minimum number of smooth scalar fields capable of reconstructing any smooth scalar distribution, or in other words, that explains the maximum variance possible, PCA is conveniently used. PCA serves as a method for simplifying and understanding complex datasets by transforming the original data into a new set of maximally uncorrelated coordinates, known as principal components, that highlight the directions in which the data varies the most [33,34,35].
In our case, PCA starts with the original dataset, a matrix where each row corresponds to a different random smooth distribution as shown in Figure 1a, which will either depict the or the distributions and is obtained through repeatedly averaging the elements with respect of its neighbors of initial 3D random uniform scalar distributions. Then, the covariance matrix of the dataset is calculated, representing the relationships between various variables. Following this, the eigenvectors and eigenvalues of the covariance matrix are computed, with each eigenvector representing a principal component and the eigenvalues indicating the variance each component explains. Following this method, principal components are sorted by their eigenvalues’ magnitude. The first x principal components with a cumulative variance close enough to 1 (typically around 0.995) are selected, serving as a new base of variables to express any smooth distribution.
Since the spatial autocorrelation of the set is positive, we can find a sufficient number of principal components significantly lower than the original number of 3D variables, as shown in Figure 1b. Each element represents a smooth scalar field from an optimally selected set that, along with the other principal components, can reconstruct the original space by linear combinations. That set of maximally mutually linearly independent smooth scalar fields will constitute our lower dimensional base, drastically reducing the computational costs of our optimisation problem. Here, we can see that considering between 350 and 400 components, 99.5% of the total variance is fully defined. The choice of using a 99.5% cumulative variance threshold is empirically justified, as capturing a higher percentage of variance would require a significantly larger number of principal components, as shown in Figure 1b, which would undermine the goal of dimensionality reduction. Conversely, selecting fewer components reduces significantly the explained variance which risks capturing the structure of the solution space in an imprecise way, leading to reduced optimization accuracy.
The resolution or the remapping ability to capture more abrupt changes in the field distribution of the vector directors and will depend on the initial dataset properties with which the PCA is conducted. An initial dataset with a stronger smoothness will allow a more substantial dimensional reduction to an even lower dimensional remapping space. However, the system will likely struggle to represent sharper local variations accurately. Furthermore, a larger dataset will facilitate the PCA procedure to better capture and reconstruct the entire 3d space, achieving a higher fidelity and avoiding possible missing features or inhomogeneities. Thus, an appropriate preparation of the procedure parameters is required, analogous to the crucial hyperparameter tuning of any deep learning model.
The method described here can be generalised to include other forms of linear interdependencies beyond spatial autocorrelation, which can similarly be exploited to reduce the dimensionality of an optimisations problem. By constructing a synthetic dataset where these linear relationships are present, PCA can be applied to extract the principal components that capture the majority of the variance within the data and form a reduced set of variables in the same fashion as the described in the present work. This allows the method to be applied to a broader range of scenarios, enabling efficient and robust optimisation.
The novelty of this work lies in its innovative application of PCA specifically through the construction of an artificial dataset with engineered linear interdependencies, while PCA is widely recognised for its effectiveness in reducing dimensionality in naturally occurring datasets, the deliberate creation and use of synthetic datasets exhibiting controlled linear dependencies to enhance complex optimisation systems represents a novel approach. A thorough review of the existing literature reveals that this specific methodology has not been widely documented or applied.
2.3. Genetic Algorithm
As mentioned in the introduction, GAs have been successfully used in LC settings, although not for a higher number of variables. As we handle complex, non-linear, high-dimensional problems, a tool that can explore a large search space, avoid local minima, and optimise without requiring gradient information can be worth the study. The genetic algorithm’s population-based approach allows for a diverse exploration of potential solutions, and since its mechanism and approach significantly differs from the Euler–Lagrange equations-based one it can both add valuable insights and potential improvements on optimisation strategies for liquid crystal systems.
The Genetic Algorithm is an optimisation method for solving minimisation problems. It operates by generating a population of potential solutions named individuals and creating new ones by combining characteristics from two existing ‘parent’ individuals, adding random mutations in the process, and selecting individuals based on testing suitability analogously to genetic inheritance and natural selection work in biology. The algorithm is valued for its simplicity in implementation, lack of need for trial solutions, and generally accurate results. A scheme of the GA deployed is shown in Figure 2a The algorithm begins by generating an initial population of solutions, each of which is evaluated based on a fitness function. The fitness function quantifies how well each solution meets the objective of the optimisation (in our case, minimising the Frank–Oseen free energy). After evaluating the population, the algorithm checks for convergence. This involves determining if the solution meets the pre-defined stopping criteria, if the maximum number of generations has been reached, or if there have been 100 stall iterations without any improvement. If the algorithm has not yet converged, selection occurs, where individuals with better fitness scores are more likely to be chosen as parents. For this purpose, and based on empirical exploration, Stochastic Uniform Selection is used, where individuals are laid out on a line, with each individual assigned a section of the line proportional to its fitness. This method gives individuals with higher fitness a greater chance of being selected but also ensures that even less fit individuals have some chance of being chosen. These parents also undergo crossover—a process where portions of their genetic material are mixed to form offspring solutions. This step encourages exploration of the solution space by creating new combinations of existing individuals’ characteristics. The arithmetic crossover method is selected in our particular setup and based on the empirical exploration of different crossover functions. This method creates offspring by taking a weighted average of the parent’s genes. In our implementation, 20% of the population is taken for crossover. This helps to introduce diversity into the population, allowing the algorithm to explore new areas of the solution space.
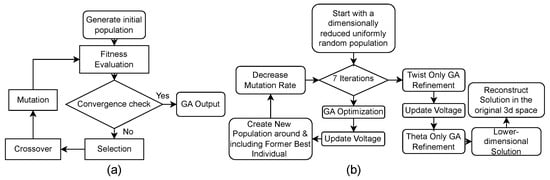
Figure 2.
(a) General Genetic Algorithm Scheme. (b) Specific conducted GA Routine’s Scheme.
Additionally, random mutations are applied to some individuals to introduce a different source of variability, ensuring the algorithm can avoid getting stuck in local minima by exploring regions of the search space that may not be reachable by crossover alone. Here, we use the Gaussian mutation function (mutationgaussian in MATLAB R2024a), which adds random noise drawn from a Gaussian distribution to the selected individuals. The mutation strength is empirically set to a small value (gaussian mutations with standard deviations of 0.003), ensuring mutations are sufficient to explore new solutions yet small enough to ensure convergence. The newly generated individuals then replace the previous population, and the process repeats until the convergence criterion is met.
Since the GA approach consists of a completely different, complementary method from gradient-based Euler–Lagrange alone in the study of LC systems, it might posit an advantage and is worth studying. Furthermore, the GA’s ability to perform a global search without relying on gradient information allows it to explore the solution space more broadly and avoid getting trapped in local minima. This makes it particularly useful for more complex configurations with potential multiple minima or artefacts, where traditional methods might need help or overlook optimal solutions. Therefore, developing a different complementary approach such as GA can become increasingly valuable, especially in more sophisticated scenarios, and enhance our ability to solve and understand liquid crystal configurations.
One of the main challenges in applying genetic algorithms or other optimization techniques to high-dimensional optimization problems is the exponential increase of computational resources with for a higher number of variables, a phenomenon known as the “curse of dimensionality”. The results section demonstrates that this problem is mitigated through our PCA-based lower-dimensional remapping method.
This genetic algorithm finds application in determining LC director configurations that minimise Frank–Oseen free energy. More specifically, the GA method here proposed considers directly Equation (2) instead of the one related to the application of the Euler–Lagrange Equations (see Equations (5) and (6) in [8]). Figure 2b presents its more precise routine schematic. As a start, a uniform random population of the lower-dimensional remapped solution space is created, representing the remapped theta and twist three-dimensional space, which trivially reconstructs the unit nematic director vector distribution using the proper trigonometric transformations. The GA optimisation is then executed with 3500 maximum generations, population sizes of 60 individuals and mutation standard deviations (Gaussian Mutation) of 0.003, and the voltage is updated solving the Gauss’s Law following the procedure defined in [8,31]. The population is reinitialised as a Gaussian distribution around the former best solution. This process is repeated seven times until the convergence criterion is met, with decreasing standard deviations in each new GA optimisation cycle for the population’s re-initialisation. Finally, theta-space-only and twist-space-only optimisation refinements are conducted, following the same logic but with smaller population sizes of 10 individuals, smaller mutation standard deviations (0.0003) and 10,000 maximum generations. The fraction of individuals used for crossover (Crossover Arithmetic function) is set to be 20% during optimisation. The function used to select the fittest individuals is the standard Stochastic Universal Sampling, a variation of the fitness-proportionate selection method, with three best ‘elite’ individuals preserved for the next generation.
The decision to update the voltage only once for each GA optimisation iteration is strategically motivated by computational efficiency and empirical observations. The computational time cost associated with voltage updates for each individual in each algorithm generation is an obvious and relevant consideration, especially in high-resolution optimisation processes. Moreover, practical experience has revealed that infrequent voltage updates significantly reduce the likelihood of the genetic algorithm (GA) getting stuck in local minima, as it prevents the algorithm from oscillating around suboptimal solutions. This approach, along with the PCA-based lower-dimensional remapping, enhances the time costs and robustness of the optimisation process.
3. Results
This study first examines a uniform pixel configuration based on an LC infinite cell. Throughout this work, the pixels are arranged two-dimensionally in the plane, with the z plane representing the direction of light propagation. This configuration enables us to obtain a set of canonical curves related to the director distribution along the thickness of the LC layer. Figure 3 shows solid-line results obtained through the minimisation of the free energy [8,9] via Equation (2), and our scheme based on the genetic algorithm (discrete points in Figure 3). Figure 3a shows the results for an infinite cell in the plane with a small pretilt and a parallel-aligned configuration, with the director lying in the -plane [8,36]. More specifically, the parameters considered are defined in Table 1.1 in [36]. The GA algorithm considers here a mesh of [z,x,y] = [54 × 5 × 5] with a spatial resolution of 0.1 m in the x and y-axis, and 50 nm for the z-axis. This setup implies solving 2700 unknown variables. However, with our PCA-GA method, the unknown variables are decoded by only 314 components. Figure 3a shows the twist angle related to Twisted-Nematic LC structures for different external voltages applied. Again, the results obtained through the genetic algorithm are compared to those obtained by minimising the elastic Frank–Oseen (FO) free energy by the Euler–Lagrange method, showing a good agreement between methods in all cases.
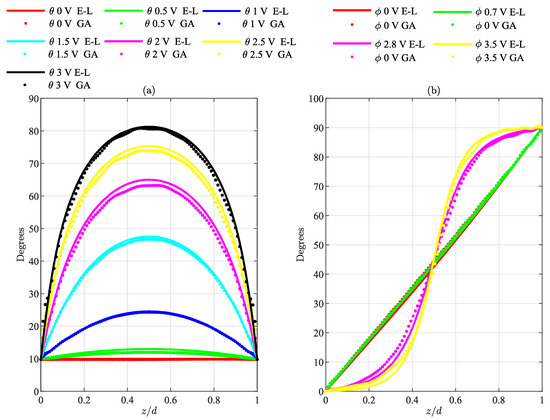
Figure 3.
Numerical comparison of Genetic Algorithm for different LC-based simple systems. (a) Twist angle distribution at various applied voltages for a PA-LCoS. (b) Twist angle distribution at various applied voltages for a TN-LCoS.
The next system analysed is based on a set of binary phase gratings with period 8 m, i.e., each pixel size is 4 m. The fill factor considered in the simulations is close to 90%. The fill factor is the surface ratio between the active pixel size and the total pixel area, which includes the interpixel gap. The parameters considered for the physical parameters of the LC are summarised in Table 1 in [7]. The GA algorithm considers a spatial grid of [z,x,y] = [12 × 13 × 25] for vertical gratings and [z,x,y] = [12 × 25 × 13] for horizontal gratings (with a spatial resolution of 0.32 m for the x and y-axis, and 0.21 m for the z-axis) implying the resolution of 7800 unknown parameters. Here, the PCA-GA scheme solves the problem with only 494 principal components. The number of parameters to be solved by PCA-GA is the same for both types of gratings considered here. Here, the PCA-GA scheme solves the problem with only 494 principal components. The liquid crystal used is the commercially available E7, typically chosen in simulation works [8,13], and the thickness, 3 m, is the range of what present PA-LCoS implement. The binary phase grating generated by the PA-LCoS display with the highest frequency possible is based on two binary phase gratings with a 2-pixel period along the x-axis (horizontal grating with the grating vector defined as ) and y-axis (vertical grating with the grating vector defined as ), respectively. The x-axis is defined parallel to the predominant director orientation, while the y-axis is orthogonal.
Figure 4a,b represents the phase shift profile along the direction of the grating vector for horizontal (x-axis) and vertical (y-axis) binary phase gratings, respectively. Equation (8) in [8] computes the phase shift once the final distribution of is calculated. Figure 4c,e represents the director and voltage distributions for and planes for a two-pixel horizontal grating () with a pixel size of = 4 m. The same planes are represented for a two-pixel vertical grating (, being both unitary vectors) in Figure 4d for plane, and Figure 4f for plane. In this configuration, the LC director has a twist around the z-axis induced by the component of the fringing electric field at the pixel borders. It is worth noting that the director vector is constrained in the at the surfaces; however, for vertical gratings, the director twists angle forces y components of the director angle. This out-of-plane phenomenon has important considerations regarding diffraction efficiency and polarisation [7].
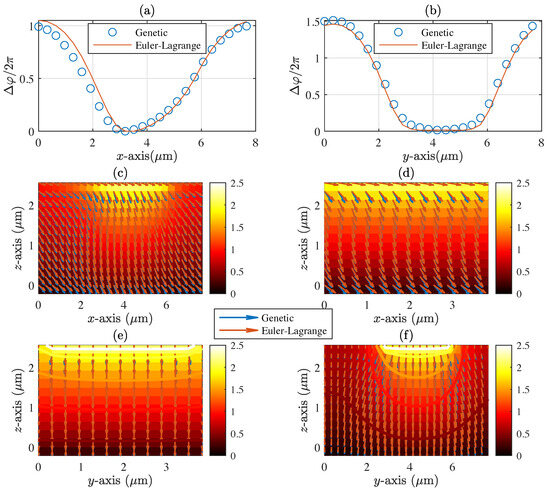
Figure 4.
Numerical calculations for a 2-pixel period binary grating of 4 m. The external voltage applied to the electrode is 2.8 V on the top () and the ground electrode is in the bottom (). (a,b) represent the phase response computed by Equation (12) in [8] for horizontal (grating in x-direction) and vertical (grating in y-direction) gratings, respectively. (c–f) represents the visualisation of the distribution of the voltage (colour map) and the director orientation (blue lines): (c) , y = 2 m and -plane. (d) , x = 2 m and -plane. (e) , x = 2 m and -plane. (f) , x = 2 m and -plane.
The mean absolute errors of our method for the previously presented horizontal grating and the vertical grating, computed as mean absolute differences between and reference (related to the application of the Euler–Lagrange equations for minimising the Frank–Oseen functional in Equation (2)) and and reference for six different pixel voltages are shown in Table 1. It is worth mentioning that the errors for the tilt angle () are larger than those obtained for the twist angle () since, in this device, the director distribution tends to be aligned towards the electric field through the twist angle (as shown in Figure 4c,d). The twist angle, and hence the out-of-plane component, is almost absent in the horizontal grating (Figure 4e). In contrast, a significant out-of-plane distribution arises in vertical gratings (Figure 4f). Considering the tilt and twist angle behaviour for the different cases analysed, it can be stated that the error between the GA and the theoretical distribution of the director in LC is almost negligible, as can be qualitatively corroborated in Figure 4 and quantitatively in Table 1. Hence, the error values shown in Table 1 demonstrate the performance and reliability of our scheme. The higher errors observed in the as observed in Table 1 are likely due to FO free energy function being generally less sensitive to variations in the tilt direction compared to the twist direction, at least for these configurations leading the genetic algorithm to produce large errors when optimizing this variable. This discrepancy thus likely stems from the inherent nature of the FO function and the approximation-based optimization process, which tends to perform better in directions with steeper functional variations.

Table 1.
Mean error between the tilt () and twist () angle between the genetic algorithm (GA) and traditional method for minimising the Frank–Oseen elastic free energy (FO) detailed in [8].
Regarding simulation time and computational performance, both the GA-PCA-based method and the Euler–Lagrange minimisation of the Frank–Oseen functional were fully implemented in MATLAB and executed on a computer with the following specifications: Intel® Core™ i7 13700, 16 GB RAM DDR4-3200 MHz, and 512 GB PCIe NVMe. It is worth noting that the GA algorithm proposed here is currently slower than the Euler–Lagrange method. The GA-PCA-based method is in a seminal stage, whereas the Euler–Lagrange solution takes advantage of MATLAB capabilities in handling matrix operations. Under these conditions, the GA-PCA needs 146.5 s/iteration, achieving good accuracy (see Table 1) after ten iterations. The Euler–Lagrange method takes 34.7 s on average in its running time simulations for the considered convergence criteria (variations in the output smaller than ). Even so, it is worth mentioning that the application of GA without PCA would be unfeasible due to memory and resource constraints. However, the proposed scheme, despite its current limitations, enables simulations that were previously impossible to handle, demonstrating the practical benefits of this research.
4. Conclusions
This work presents a novel computational approach that employs PCA for dimensionality reduction in optimisation problems where solution variables exhibit known interdependencies. By creating synthetic datasets with deliberately engineered properties and applying PCA, we significantly reduce the solution space’s dimensionality, enhancing computational speed and convergence robustness in the optimisation process.
Specifically, this method minimises the Frank–Oseen free energy for the director distribution in LC for SLM-based devices. This dimensionality reduction technique has been successfully applied to this physical problem, achieving good results compared to traditional numerical approaches based on Euler–Lagrange equations. Initally, the method was applied to uniform and two-dimensional TN-LC and PA-LC devices. Subsequently, the PCA-GA method was used for a complete 3D PA-LCoS device configured as a binary phase grating. More specifically, horizontal gratings with the grating vector aligned to the predominant LC direction and vertical gratings with the grating vector perpendicular to the pretilt were analyzed. The results are consistent with those found in the literature and those obtained from the traditional approach, corroborating the proposed scheme. This novel technique facilitates solving such applications without requiring the constrained numerical minimisation of specific, complex-to-implement equations.
While the traditional Euler–Lagrange method may outperform the PCA-GA approach presented regarding running time in our specific cases of study, the genetic algorithm poses unique advantages worth studying. Its ability to perform a broad and global randomised exploration allows it to find potential energy minima that gradient-based methods like the Euler–Lagrange approach might overlook, which can become increasingly important in more complex scenarios.
Furthermore, this PCA-based approach can be adapted to other optimisation problems in different fields where solution variables exhibit known linear interdependencies. By directly reducing the dimensionality of the solution space and ensuring that all possible solutions preserve these pre-assumed interdependencies, our method offers significant potential for advancing optimisation techniques across various disciplines, including materials science, engineering, and computational physics.
In future work, we plan to apply this scheme to various LC-based devices, such as holographic polymer-dispersed liquid crystal (H-PDLC) devices, and focus on improving the method’s performance regarding simulation run time.
Author Contributions
Conceptualization, J.C.-M. and J.F.; methodology, J.C.-M., J.F. and C.N.; software, J.C.-M. and J.J.S.-V.; validation, A.P.B., T.L. and B.N.-R.; investigation, J.C.-M., J.J.S.-V., A.P.B. and B.N.-R.; resources, A.B.; writing—original draft preparation, J.C.-M.; writing—review and editing, C.N., A.B. and J.F.; visualization, J.C.-M. and J.J.S.-V.; supervision, J.F. and C.N.; project administration, A.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the “Generalitat Valenciana” of Spain (projects PROMETEO/2021/006 and CIDEXG/2022/60), “Ministerio de Ciencia, Innovación y Universidades” of Spain (projects PID2021-123124OB-I00 and PID2023-148881OB-I00). A.P.B. thanks the “Ministerio de Ciencia, Innovación y Universidades” for the grant PRE2022-105016, J.J.S.-V. thanks the “Ministerio de Ciencia, Innovación y Universidades” for the grant FPU22/04316, and T.L. thanks the “Universidad de Alicante” of Spain for the grant UAFPU20-23.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GA | Genetic Algorithm |
| PCA | Principal Component Analysis |
| LC | Liquid Crystal |
| LCoS | Liquid Crystal on Silicon |
| SLM | Spatial Light Modulator |
| TN | Twisted Nematic |
| PA | Parallel Aligned |
| FO | Frank–Oseen |
| TN-LC | Twisted nematic Liquid Crystal |
| PALCoS | Parallel Aligned Liquid Crystal on Silicon |
References
- Yu, F.T.S.; Jutamulia, S.; Tanone, A. Applications of liquid crystal spatial light modulators to optical information processing systems. In Liquid Crystals; Khoo, I.C., Ed.; SPIE: Bellingham, WA, USA, 1997. [Google Scholar] [CrossRef]
- Yu, F.T.S.; Jutamulia, S. Spatial light modulators in telecommunication systems. In Spatial Light Modulators: Technology and Applications; Efron, U., Ed.; SPIE: Bellingham, WA, USA, 2001. [Google Scholar] [CrossRef]
- Takaki, Y. Enlargements of Viewing Zone and Screen Size of Holographic Displays Using MEMS SLM Combined with Scanning Systems. Appl. Sci. 2022, 12, 6495. [Google Scholar] [CrossRef]
- Maurer, C.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. What spatial light modulators can do for optical microscopy. Laser Photonics Rev. 2010, 5, 81–101. [Google Scholar] [CrossRef]
- Lazarev, G.; Chen, P.J.; Strauss, J.; Fontaine, N.; Forbes, A. Beyond the display: Phase-only liquid crystal on Silicon devices and their applications in photonics [Invited]. Opt. Express 2019, 27, 16206. [Google Scholar] [CrossRef] [PubMed]
- Brown, G.H. Properties and applications of liquid crystals. J. Electron. Mater. 1973, 2, 403–430. [Google Scholar] [CrossRef]
- Francés, J.; Márquez, A.; Neipp, C.; Puerto, D.; Gallego, S.; Pascual, I.; Beléndez, A. Polarimetric analysis of cross-talk phenomena induced by the pixelation in PA-LCoS devices. Opt. Laser Technol. 2022, 152, 108125. [Google Scholar] [CrossRef]
- Moser, S.; Ritsch-Marte, M.; Thalhammer, G. Model-based compensation of pixel crosstalk in liquid crystal spatial light modulators. Opt. Express 2019, 27, 25046–25063. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, B.; Bos, P.J.; Anderson, J.E.; Pouch, J.J.; Miranda, F.A. Finite-difference time-domain simulation of a liquid-crystal optical phased array. J. Opt. Soc. Am. A 2005, 22, 346. [Google Scholar] [CrossRef]
- Lingel, C.; Haist, T.; Osten, W. Optimizing the diffraction efficiency of SLM-based holography with respect to the fringing field effect. Appl. Opt. 2013, 52, 6877. [Google Scholar] [CrossRef]
- Lu, T.; Pivnenko, M.; Robertson, B.; Chu, D. Pixel-level fringing-effect model to describe the phase profile and diffraction efficiency of a liquid crystal on silicon device. Appl. Opt. 2015, 54, 5903. [Google Scholar] [CrossRef]
- Ronzitti, E.; Guillon, M.; de Sars, V.; Emiliani, V. LCoS nematic SLM characterization and modeling for diffraction efficiency optimization, zero and ghost orders suppression. Opt. Express 2012, 20, 17843. [Google Scholar] [CrossRef]
- Francés, J.; Márquez, A.; Martínez-Guardiola, F.J.; Bleda, S.; Gallego, S.; Neipp, C.; Pascual, I.; Beléndez, A. Simplified physical modeling of parallel-aligned liquid crystal devices at highly non-linear tilt angle profiles. Opt. Express 2018, 26, 12723–12741. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Collings, P.J. The genetic algorithm: Using biology to compute liquid crystal director configurations. Crystals 2020, 10, 1041. [Google Scholar] [CrossRef]
- Lin, W.L.; Yu, T.C.; Lo, Y.L.; Lin, J.F. A Hybrid Approach for Measuring the Parameters of Twisted-Nematic Liquid Crystal Cells Utilizing the Stokes Parameter Method and a Genetic Algorithm. J. Light. Technol. 2009, 27, 4136–4144. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.L.; Zhou, A.; Yuan, D.J.; Xu, Y.S. Optimization of EPB Shield Performance with Adaptive Neuro-Fuzzy Inference System and Genetic Algorithm. Appl. Sci. 2019, 9, 780. [Google Scholar] [CrossRef]
- Qian, L.; Zheng, Y.; Li, L.; Ma, Y.; Zhou, C.; Zhang, D. A New Method of Inland Water Ship Trajectory Prediction Based on Long Short-Term Memory Network Optimized by Genetic Algorithm. Appl. Sci. 2022, 12, 4073. [Google Scholar] [CrossRef]
- Fogue, M.; Sanguesa, J.; Martinez, F.; Marquez-Barja, J. Improving Roadside Unit Deployment in Vehicular Networks by Exploiting Genetic Algorithms. Appl. Sci. 2018, 8, 86. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Kang, H.; Kang, D.Y.; Park, J. Genetic Algorithm Based Deep Learning Neural Network Structure and Hyperparameter Optimization. Appl. Sci. 2021, 11, 744. [Google Scholar] [CrossRef]
- Bai, M.R.; Liu, B. Determination of optimal exciter deployment for panel speakers using the genetic algorithm. J. Sound Vib. 2004, 269, 727–743. [Google Scholar] [CrossRef]
- Li, W.; Cerise, J.E.; Yang, Y.; Han, H. Application of t-SNE to human genetic data. J. Bioinform. Comput. Biol. 2017, 15, 1750017. [Google Scholar] [CrossRef]
- Sánchez-Rico, M.; Alvarado, J.M. Dimensionality reduction techniques as a preliminary step to cluster analysis: A comparison between PCA, t-SNE and UMAP. In Proceedings of the 9th European Congress of Methodology, Valencia, Spain, 21–23 July 2020. [Google Scholar]
- Pareek, J.; Jacob, J. Data compression and visualization using PCA and T-SNE. In Advances in Information Communication Technology and Computing: Proceedings of AICTC 2019; Springer: Singapore, 2021; pp. 327–337. [Google Scholar]
- Li, F.; Li, X.; Wang, F.; Zhang, D.; Xia, Y.; He, F. A Novel P300 Classification Algorithm Based on a Principal Component Analysis-Convolutional Neural Network. Appl. Sci. 2020, 10, 1546. [Google Scholar] [CrossRef]
- Chahboun, S.; Maaroufi, M. Principal Component Analysis and Machine Learning Approaches for Photovoltaic Power Prediction: A Comparative Study. Appl. Sci. 2021, 11, 7943. [Google Scholar] [CrossRef]
- Geng, D.; Zhang, H.; Wu, H. Short-Term Wind Speed Prediction Based on Principal Component Analysis and LSTM. Appl. Sci. 2020, 10, 4416. [Google Scholar] [CrossRef]
- Lee, H.; Choi, S.; Kim, E.; Kim, Y.N.; Lee, J.; Lee, D.U. Effects of Pulsed Electric Field and Thermal Treatments on Microbial Reduction, Volatile Composition, and Sensory Properties of Orange Juice, and Their Characterization by a Principal Component Analysis. Appl. Sci. 2020, 11, 186. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Rastogi, A.K.; Taterh, S.; Kumar, B.S. Dimensionality Reduction Algorithms in Machine Learning: A Theoretical and Experimental Comparison. Eng. Proc. 2023, 59, 82. [Google Scholar] [CrossRef]
- Syarif, I. Dimensionality Reduction Algorithms on High Dimensional Datasets. EMITTER Int. J. Eng. Technol. 2014, 2, 28–38. [Google Scholar] [CrossRef]
- Wang, X. Liquid Crystal Diffractive Optical Elements: Applications and Limitations. Ph.D. Thesis, Kent State University, Kent, OH, USA, 2005. [Google Scholar]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17. [Google Scholar] [CrossRef]
- Kurita, T. Principal component analysis (PCA). In Computer Vision: A Reference Guide; Springer: Cham, Switzerland, 2019; pp. 1–4. [Google Scholar]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Bouwmans, T.; Zahzah, E.H. Robust PCA via Principal Component Pursuit: A review for a comparative evaluation in video surveillance. Comput. Vis. Image Underst. 2014, 122, 22–34. [Google Scholar] [CrossRef]
- Yeh, P.; Gu, C. Optics of Liquid Crystal Displays; Wiley-Interscience: Hoboken, NJ, USA, 2009; p. 792. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).