Path Planning Optimization of the Load Transport Process Using Heuristic Algorithms
Abstract
1. Introduction
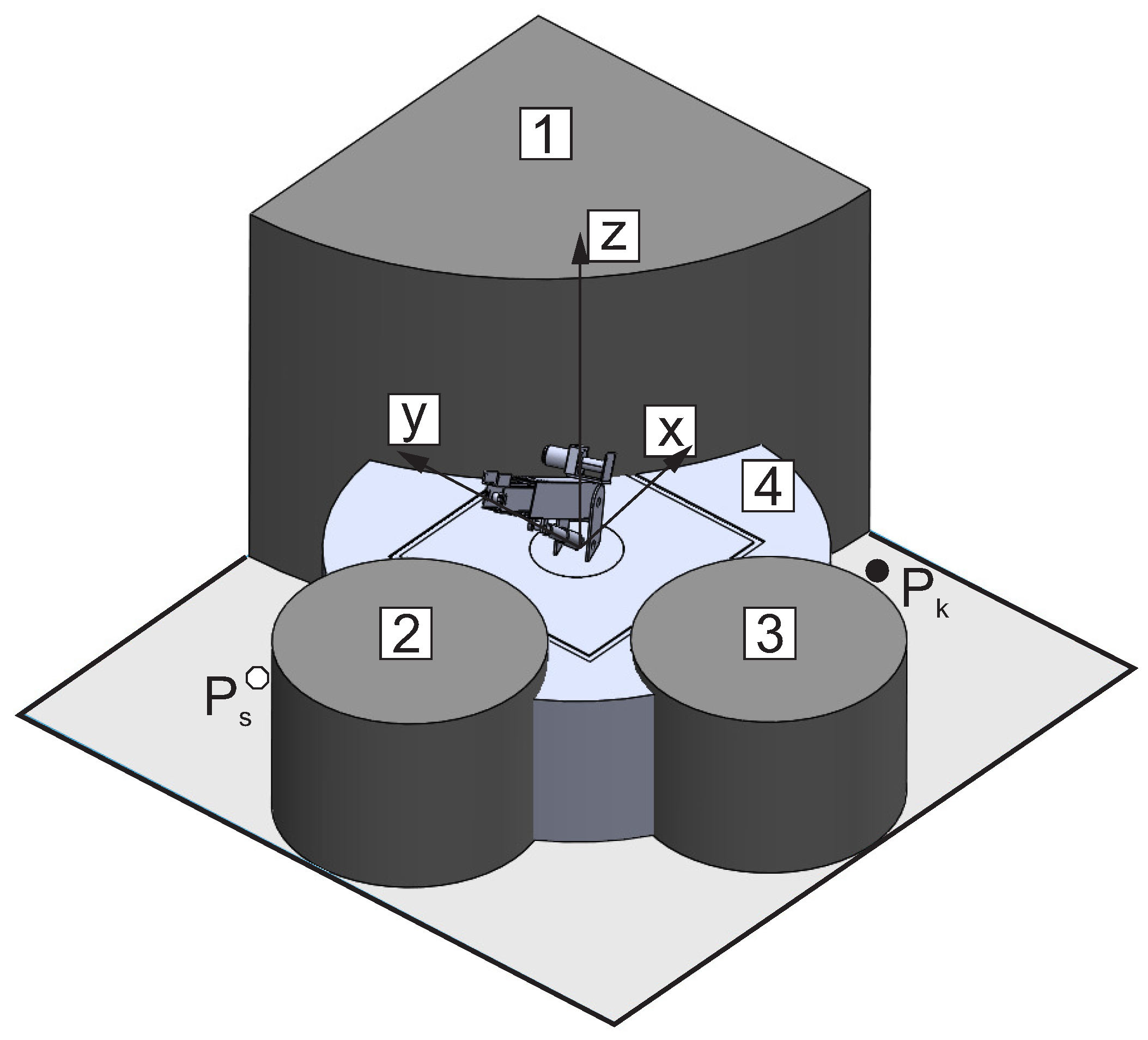
2. Description of the Problem
- Co-ordinates (in mm) of the starting point ,
- Co-ordinates (in mm) for the endpoint ,
- The height of the obstacles: mm, mm, mm, mm,
- The diameter of the obstacles: mm, mm, mm, mm,
- Working area (in mm): .
3. Heuristic Algorithms
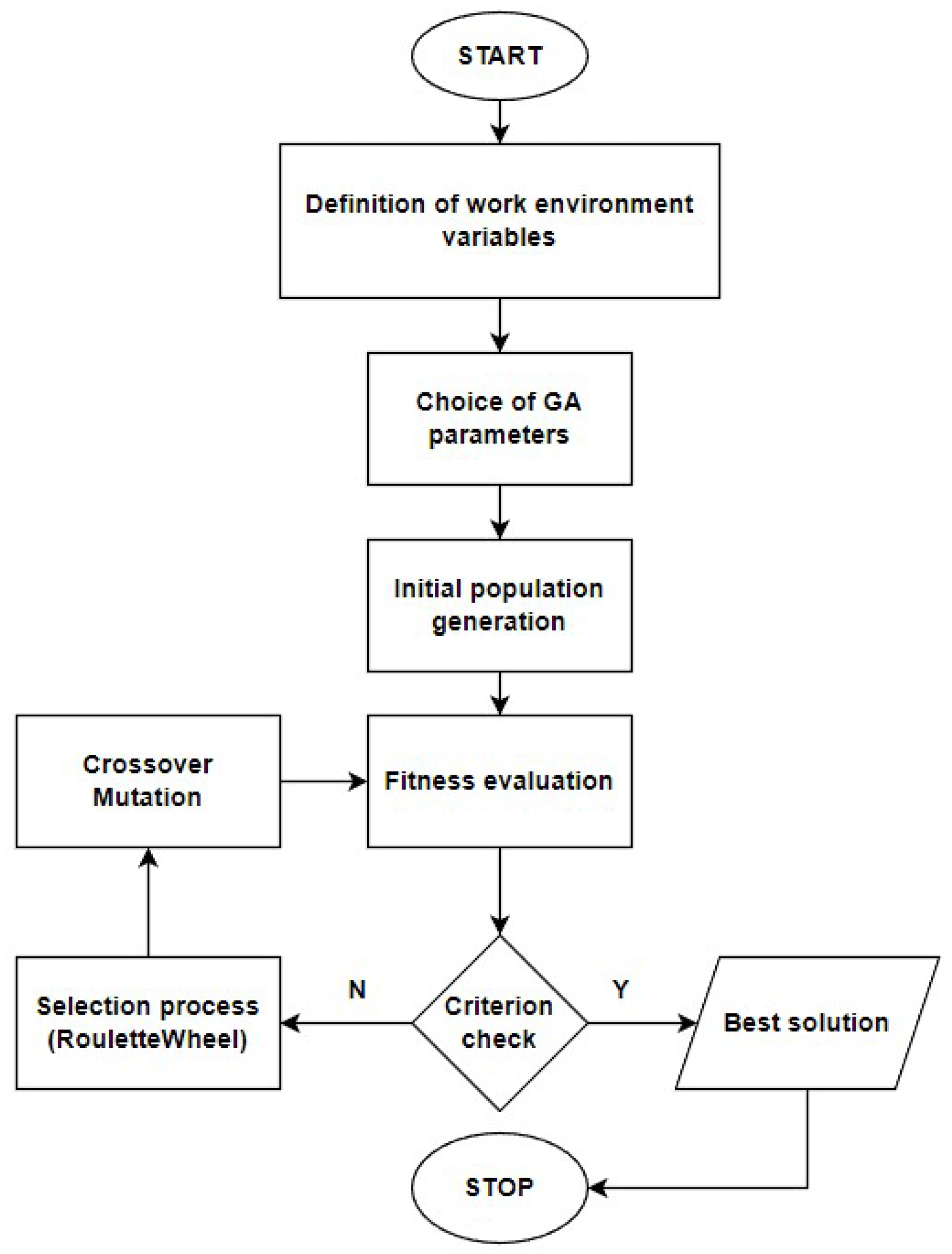
3.1. Genetic Algorithm
- Generate (randomly) a starting population of n-chromosomes, which are the initial solution to the problem,
- Calculate the objective function (adaptation assessment), which allows for determining the quality measure of individuals,
- Terminate the genetic algorithm when the ending criterion of the algorithm is met,
- If the criterion is not met, a new population of individuals is created by applying the selection process and genetic operators, which is again subjected to the stage of the fitness assessment.
3.2. Particle Swarm Optimization
- Specifying the input data,
- Random selection of particle velocities and positions,
- Calculation of the objective function,
- Determination of the best local () and global () position of the particle,
- Speed and location update,
- Recalculation of the objective function,
- Verification and update of location parameters ( and ),
- Assignment of the optimal solution.
- The squeeze factor () prevents a sudden increase in speed and makes it easier to obtain population convergence,
- Learning coefficients () determine the range of motion of the particle during iteration,
- The weighting factor (w) maintains a balance when looking for a local and global solution.
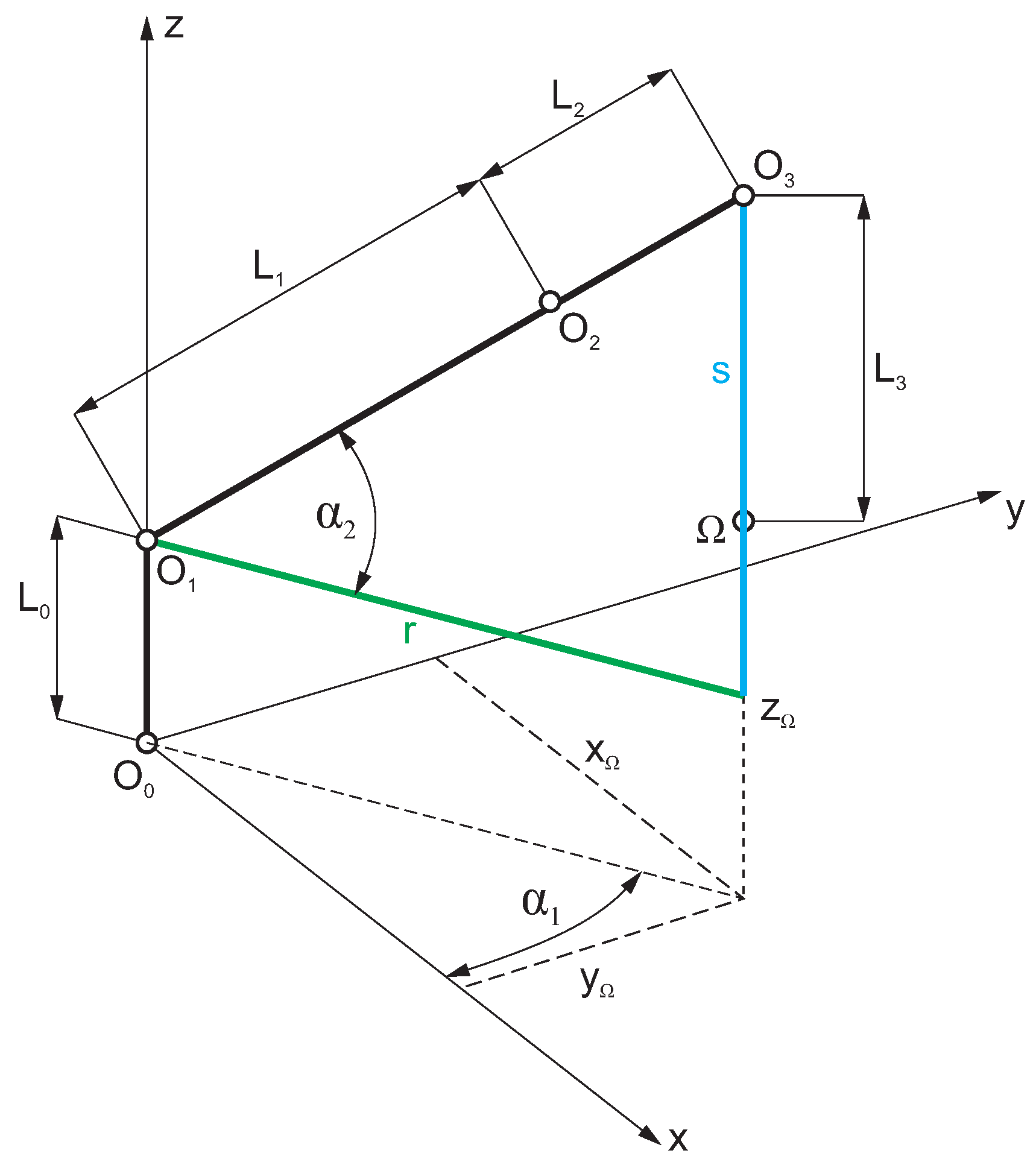
4. Inverse Kinematics Problem
- mm—distance from the ground to the place where the boom cylinder is attached,
- mm—length of the first aluminum profile in which the actuator body is located,
- mm—constant length of the rope, taking into account the height of the carried load (distance from the end of the boom to the lowest point of the carried load).
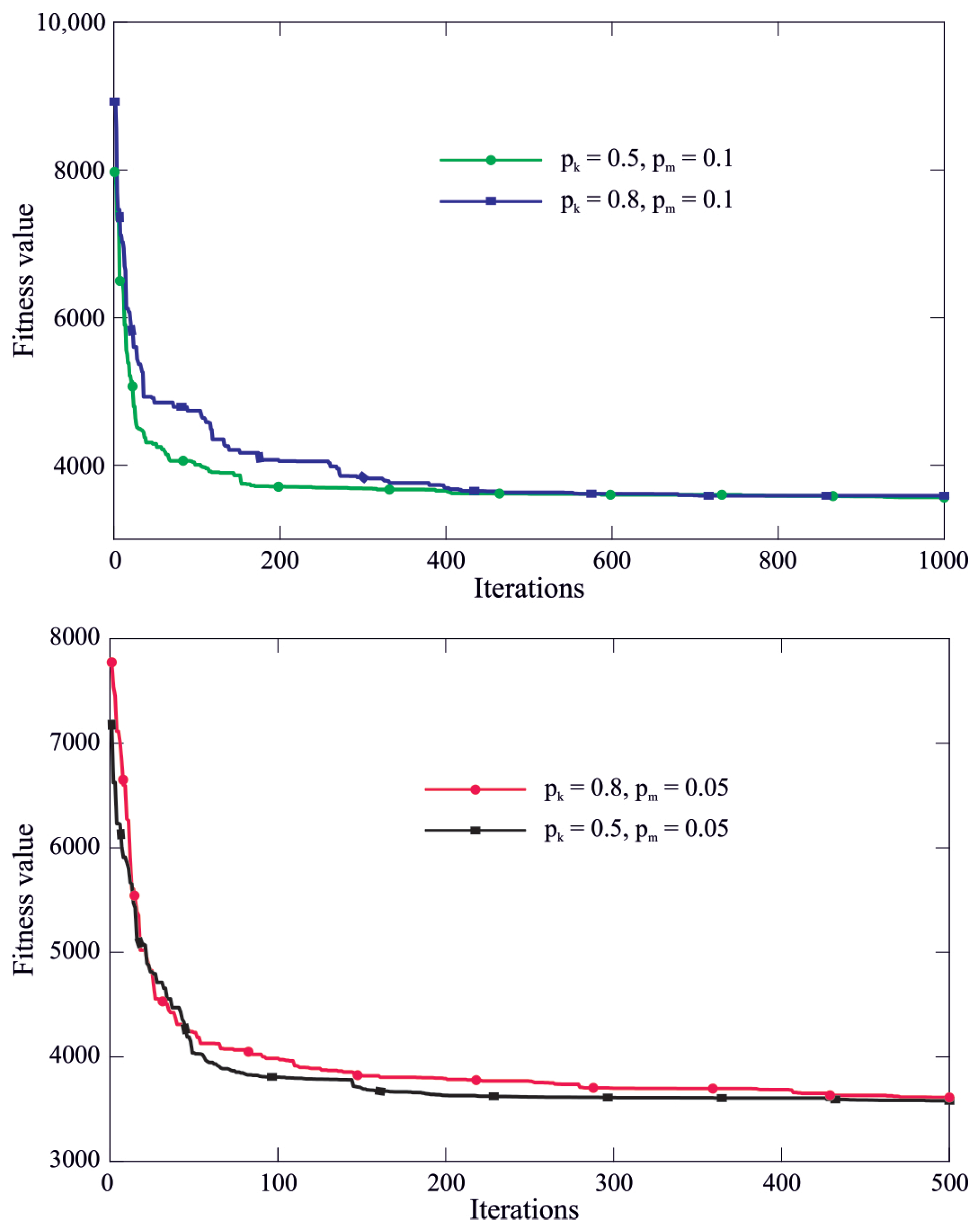
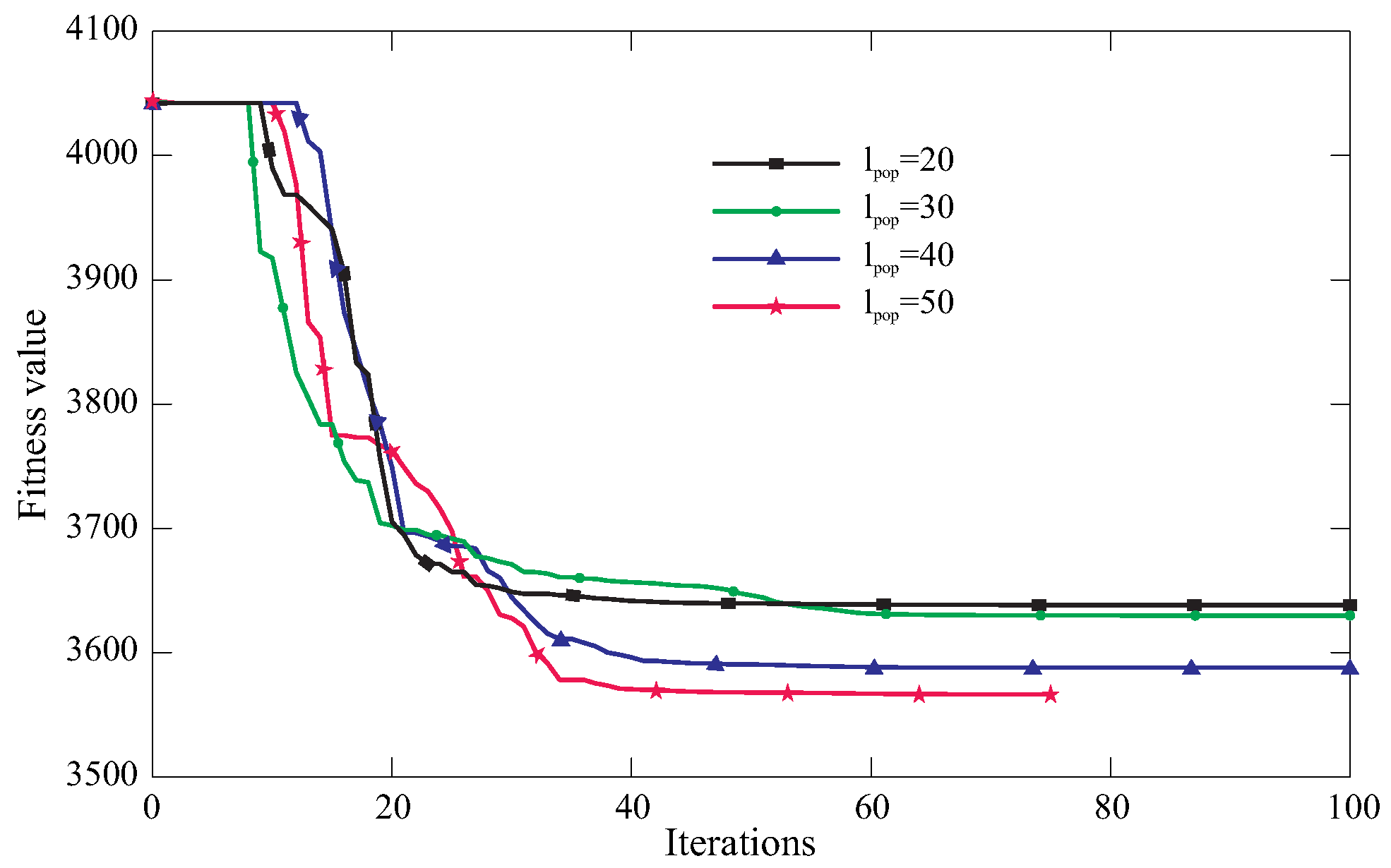
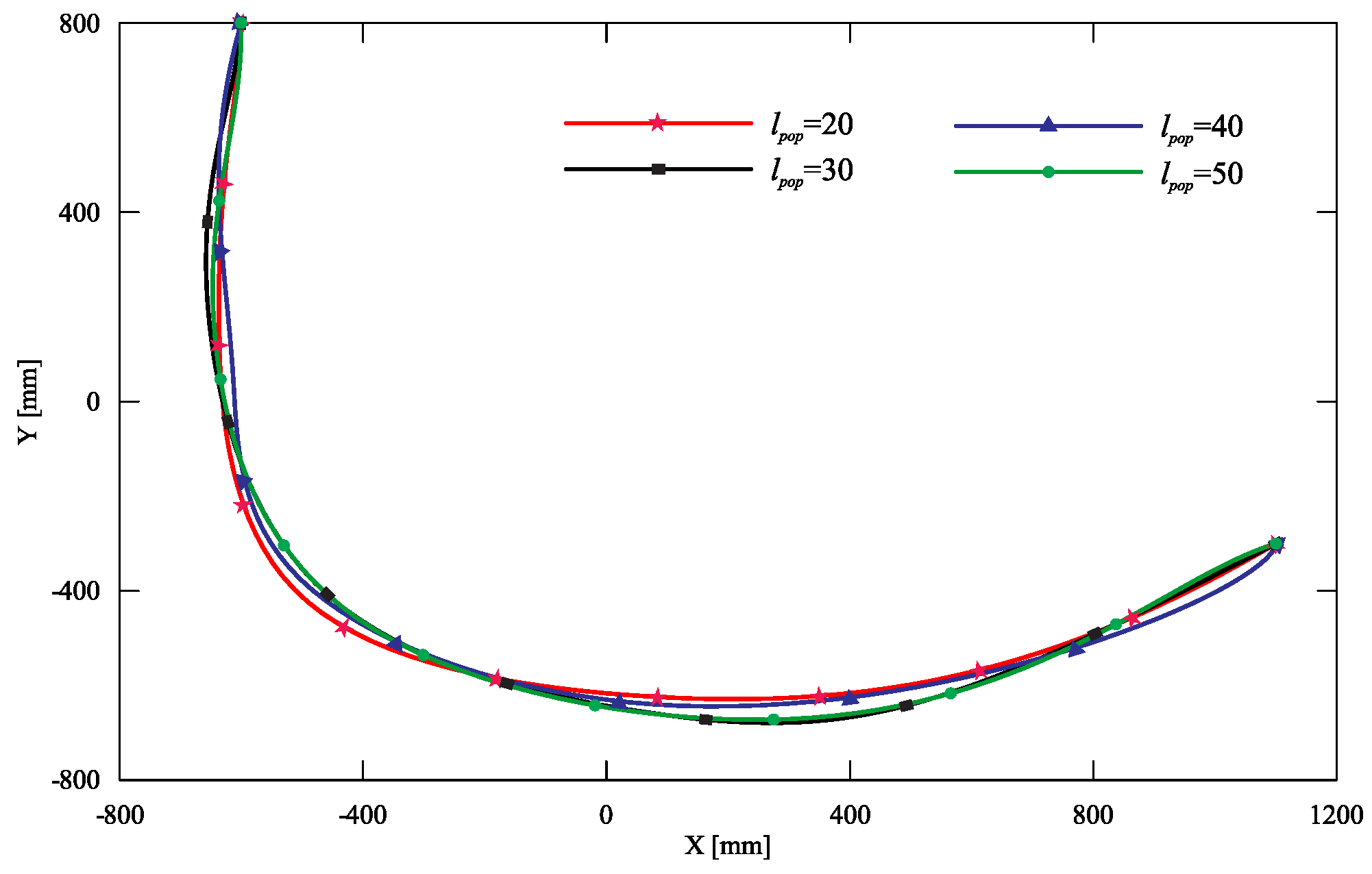
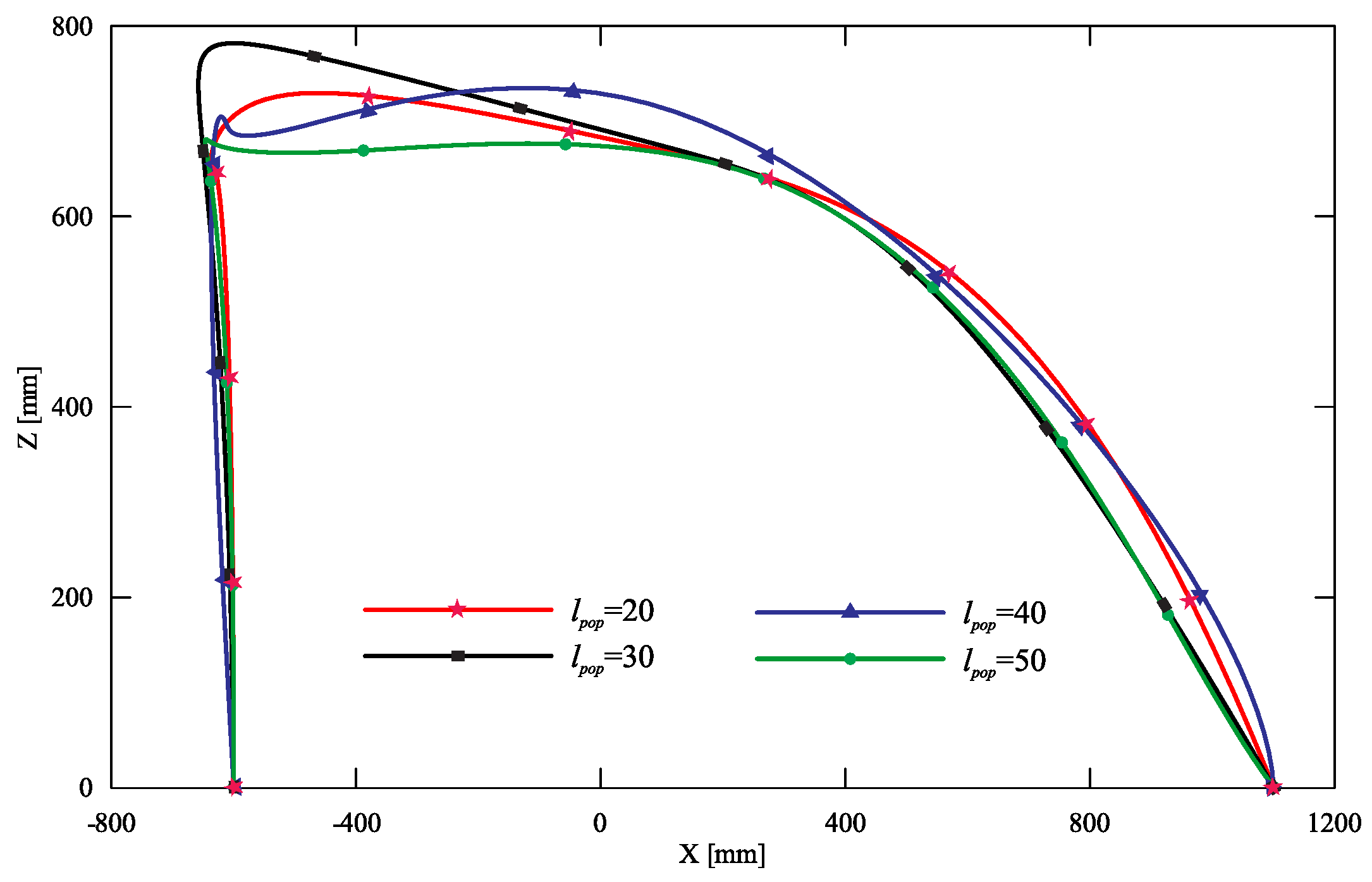
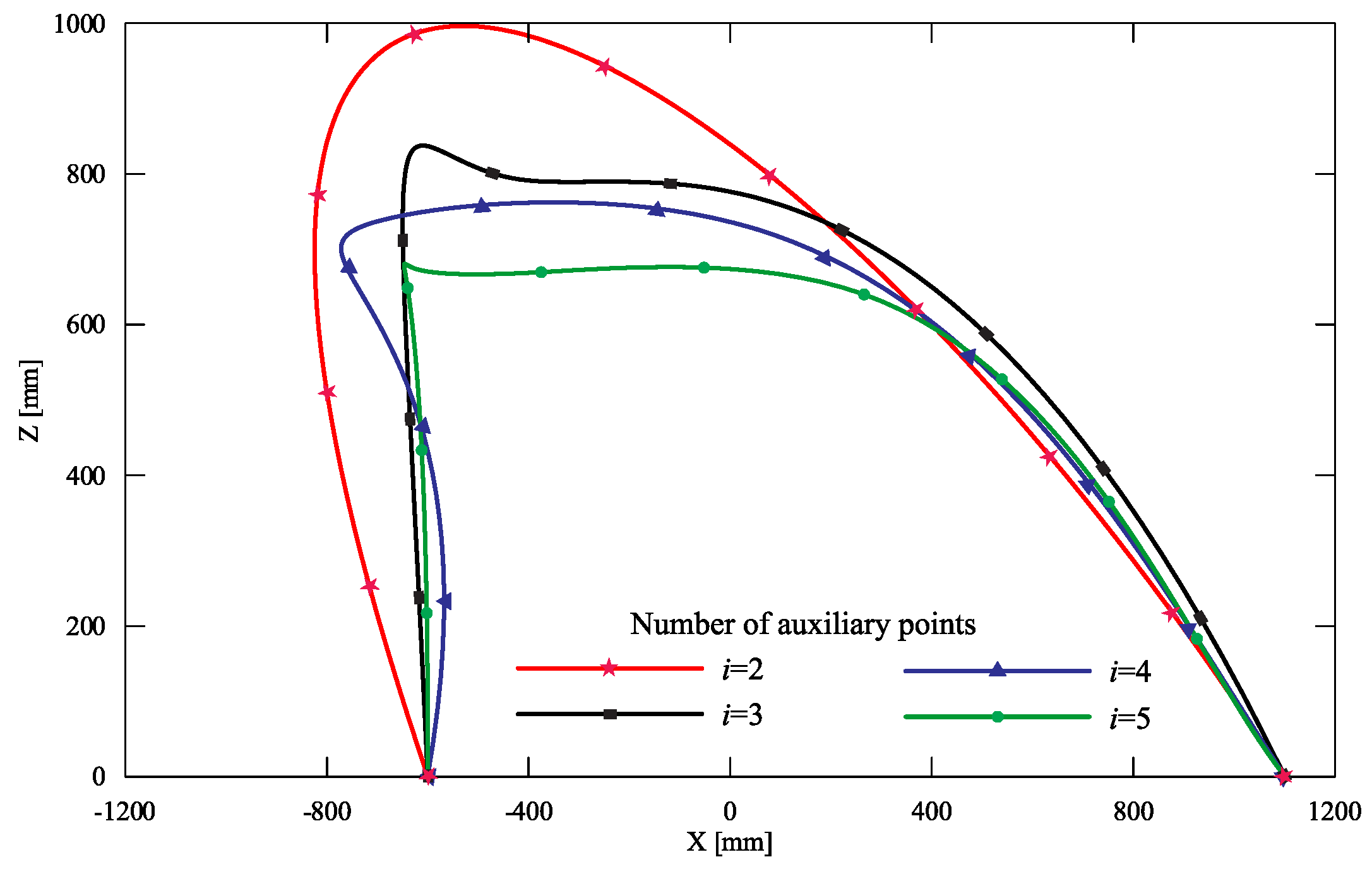
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GA | Genetic algorithm |
| PSO | Particle Swarm Optimization |
| AGV | Automated guided vehicle |
| BIM | Building Information Modeling |
| GWO | Grey Wolf Optimizer |
| PO | Puma Optimizer |
| SA | Simulated annealing |
| CS | Cuckoo search |
References
- Chwastek, S. Optimization of crane mechanisms to reduce vibration. Autom. Constr. 2020, 119, 103335. [Google Scholar] [CrossRef]
- Ermis, K.; Caliskan, M.; Tanriverdi, M. Design optimization of moveable moment stabilization system for access crane platforms. Acta Polytech. 2021, 61, 219–229. [Google Scholar] [CrossRef]
- Peng, B.; Flager, F.L.; Wu, J. A method to optimize mobile crane and crew interactions to minimize construction cost and time. Autom. Constr. 2018, 95, 10–19. [Google Scholar] [CrossRef]
- Yue, L.; Fan, H.; Zhai, C. Joint configuration and scheduling optimization of the dual trolley quay crane and AGV for automated container terminal. J. Phys. Conf. Ser. 2020, 1486, 072080. [Google Scholar] [CrossRef]
- Brzozowski, K.; Maczyński, A. Genetic algorithm in the task of load positioning in the rotation of the crane. Autobusy Tech. Eksploat. Syst. Transp. 2013, 14, 1403–1410. (In Polish) [Google Scholar]
- Hop, D.C.; Hop, N.V.; Anh, T.T.M. Adaptive particle swarm optimization for integrated quay crane and yard truck scheduling problem. Comput. Ind. Eng. 2021, 153, 107075. [Google Scholar] [CrossRef]
- Pan, Z.; Guo, H.; Li, Y. Automated Method for Optimizing Feasible Locations of Mobile Cranes Based on 3D Visualization. Procedia Eng. 2017, 196, 36–44. [Google Scholar] [CrossRef]
- Riga, K.; Jahr, K.; Thielen, C.; Borrmann, A. Mixed integer programming for dynamic tower crane and storage area optimization on construction sites. Autom. Constr. 2020, 120, 103259. [Google Scholar] [CrossRef]
- Farrage, A.; Takahashi, H.; Terauchi, K.; Sasai, S.; Sakurai, H.; Okubo, M.; Uchiyama, N. Modified A* Algorithm for Optimal Motion Trajectory Generation of Rotary Cranes. In Proceedings of the 2023 IEEE International Conference on Mechatronics (ICM), Loughborough, UK, 15–17 March 2023; IEEE: Piscataway, NJ, USA, 2023; Volume 39, pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, Y.; Zhang, P.; Gao, Q.; Han, X. A Hybrid A* Path Planning Algorithm Based on Multi-objective Constraints. In Proceedings of the 2022 Asia Conference on Advanced Robotics, Automation, and Control Engineering (ARACE), Qingdao, China, 26–28 August 2022; IEEE: Piscataway, NJ, USA, 2022; Volume 152, pp. 1–6. [Google Scholar] [CrossRef]
- Hameed, I.A.; Bye, R.T.; Osen, O.L. Grey wolf optimizer (GWO) for automated offshore crane design. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Khodadadi, N.; Barshandeh, S.; Trojovský, P.; Gharehchopogh, F.S.; El-kenawy, E.S.M.; Abualigah, L.; Mirjalili, S. Puma optimizer (PO): A novel metaheuristic optimization algorithm and its application in machine learning. Clust. Comput. 2024, 27, 5235–5283. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, T.; Lee, H. Heuristic algorithm for retrieving containers. Comput. Ind. Eng. 2016, 101, 352–360. [Google Scholar] [CrossRef]
- Cai, P.; Cai, Y.; Chandrasekaran, I.; Zheng, J. Parallel genetic algorithm based automatic path planning for crane lifting in complex environments. Autom. Constr. 2016, 62, 133–147. [Google Scholar] [CrossRef]
- Bertolini, M.; Esposito, G.; Mezzogori, D.; Neroni, M. Optimizing Retrieving Performance of an Automated Warehouse for Unconventional Stock Keeping Units. Procedia Manuf. 2019, 39, 1681–1690. [Google Scholar] [CrossRef]
- Xiang, G.; Xiang, X. 3D trajectory optimization of the slender body freely falling through water using cuckoo search algorithm. Ocean Eng. 2021, 235, 109354. [Google Scholar] [CrossRef]
- Haghighi, H.; Sadati, S.H.; Dehghan, S.M.; Karimi, J. Hybrid Form of Particle Swarm Optimization and Genetic Algorithm For Optimal Path Planning in Coverage Mission by Cooperated Unmanned Aerial Vehicles. J. Aerosp. Technol. Manag. 2020, 12, e4320. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Ratiu, M.; Prichici, M.A. Industrial robot trajectory optimization- a review. MATEC Web Conf. 2017, 126, 02005. [Google Scholar] [CrossRef]
- Shirazi, A.; Ceberio, J.; Lozano, J.A. Spacecraft trajectory optimization: A review of models, objectives, approaches and solutions. Prog. Aerosp. Sci. 2018, 102, 76–98. [Google Scholar] [CrossRef]
- Yan, T.; Lu, F.; Wang, S.; Wang, L.; Bi, H. A hybrid metaheuristic algorithm for the multi-objective location-routing problem in the early post-disaster stage. J. Ind. Manag. Optim. 2023, 19, 4663–4691. [Google Scholar] [CrossRef]
- Lu, F.; Jiang, R.; Bi, H.; Gao, Z. Order Distribution and Routing Optimization for Takeout Delivery under Drone–Rider Joint Delivery Mode. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 774–796. [Google Scholar] [CrossRef]
- Liu, D.; Deng, Z.; Mao, X.; Yang, Y.; Kaisar, E.I. Two-Echelon Vehicle-Routing Problem: Optimization of Autonomous Delivery Vehicle-Assisted E-Grocery Distribution. IEEE Access 2020, 8, 108705–108719. [Google Scholar] [CrossRef]
- Guo, J.; Chen, L.; Tang, B.; Gen, M. Optimal strategies for an uncertain forward and reverse multi-period logistics network using heuristic algorithm: A case study of Shanghai perishable products. Int. J. Internet Manuf. Serv. 2024, 10, 132–164. [Google Scholar] [CrossRef]
- Kwiatoń, P. Modeling and Dynamics Studies, Stability Analysis and Optimization of the Duty Cycle of a Mobile Crane. Ph.D. Thesis, Czestochowa University of Technology, Częstochowa, Poland, 2021. (In Polish). [Google Scholar]
- Skrobek, D. Modeling, Analysis and Optimization of the Duty Cycle of Manipulators with Four Degrees of Freedom. Ph.D. Thesis, Czestochowa University of Technology, Częstochowa, Poland, 2019. (In Polish). [Google Scholar]
- Cekus, D.; Depta, F.; Kubanek, M.; Kuczyński, Ł.; Kwiatoń, P. Event Visualization and Trajectory Tracking of the Load Carried by Rotary Crane. Sensors 2022, 22, 480. [Google Scholar] [CrossRef] [PubMed]
- Jordehi, A.R. A review on constraint handling strategies in particle swarm optimisation. Neural. Comput. Appl. 2015, 26, 1265–1275. [Google Scholar] [CrossRef]
- Gupta, R.; Bhunia, A.; Roy, D. A GA based penalty function technique for solving constrained redundancy allocation problem of series system with interval valued reliability of components. J. Comput. Appl. Math. 2009, 232, 275–284. [Google Scholar] [CrossRef]
- Cekus, D.; Kwiatoń, P.; Šofer, M.; Šofer, P. Application of heuristic methods to the identification of the parameters of discrete-continuous models. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, e140150. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995. [Google Scholar] [CrossRef]
- Cekus, D.; Skrobek, D. The influence of inertia weight on the particle swarm optimization algorithm. J. Appl. Math. Comput. Mech. 2018, 17, 5–11. [Google Scholar] [CrossRef]
- Herlambang, T.; Rahmalia, D.; Yulianto, T. Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) for optimizing PID parameters on Autonomous Underwater Vehicle (AUV) control system. J. Phys. Conf. Ser. 2019, 1211, 012039. [Google Scholar] [CrossRef]
- Taherkhani, M.; Safabakhsh, R. A novel stability-based adaptive inertia weight for particle swarm optimization. Appl. Soft Comput. 2016, 38, 281–295. [Google Scholar] [CrossRef]
- Xu, G. An adaptive parameter tuning of particle swarm optimization algorithm. Appl. Math. Comput. 2013, 219, 4560–4569. [Google Scholar] [CrossRef]
- Liu, Q.; Wei, W.; Yuan, H.; Zhan, Z.H.; Li, Y. Topology selection for particle swarm optimization. Inf. Sci. 2016, 363, 154–173. [Google Scholar] [CrossRef]
- Jordehi, A.R.; Jasni, J. Parameter selection in particle swarm optimisation: A survey. J. Exp. Theor. Artif. Intell. 2013, 25, 527–542. [Google Scholar] [CrossRef]
- Skrobek, D.; Cekus, D. Optimization of the operation of the anthropomorphic manipulator in a three-dimensional working space. Eng. Opt. 2019, 51, 1997–2010. [Google Scholar] [CrossRef]
- Herebin, P.; Pajor, M. Modeling the simple and inverse kinematics of a truck crane with a redundant structure using the MATLAB environment (in Polish). Eng. Model. 2016, 58, 44–50. [Google Scholar]
- D’Souza, A.; Vijayakumar, S.; Schaal, S. Learning inverse kinematics. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No.01CH37180), Maui, HI, USA, 29 October–3 November 2001; IEEE: Piscataway, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Sooda, K.; Nair, T. A Comparative Analysis for Determining the Optimal Path using PSO and GA. Int. J. Comput. Appl. 2011, 32, 8–12. [Google Scholar]
- Khoshahval, F.; Minuchehr, H.; Zolfaghari, A. Performance evaluation of PSO and GA in PWR core loading pattern optimization. Nucl. Eng. Des. 2011, 241, 799–808. [Google Scholar] [CrossRef]
- Alaia, E.B.; Harbaoui, I.; Borne, P.; Bouchriha, H. A Comparative Study of the PSO and GA for the m-MDPDPTW. Int. J. Comput. Commun. Control. 2018, 13, 8. [Google Scholar] [CrossRef]
- Wihartiko, F.D.; Wijayanti, H.; Virgantari, F. Performance comparison of genetic algorithms and particle swarm optimization for model integer programming bus timetabling problem. IOP Conf. Ser. Mater. Sci. Eng. 2018, 332, 012020. [Google Scholar] [CrossRef]




| It | Population Number | ||||||
|---|---|---|---|---|---|---|---|
| 50 | 100 | ||||||
| Number of Waypoints | |||||||
| 8 | 10 | 12 | 8 | 10 | 12 | ||
| 500 | L [mm] | 3618 | 3962 | 3900 | 3651 | 3816 | 4010 |
| T [s] | 70.8 | 76.5 | 84.4 | 151.6 | 157.3 | 164.7 | |
| 1000 | L [mm] | 3613 | 3743 | 3875 | 3564 | 3785 | 3849 |
| T [s] | 143.2 | 156.5 | 185.6 | 307.3 | 297.1 | 312.7 | |
| It | Population Number | ||||||
|---|---|---|---|---|---|---|---|
| 50 | 100 | ||||||
| Number of Waypoints | |||||||
| 8 | 10 | 12 | 8 | 10 | 12 | ||
| 500 | L [mm] | 3754 | 3910 | 3962 | 3619 | 3610 | 3659 |
| T [s] | 73.6 | 80.8 | 86.5 | 147.9 | 164.5 | 180.4 | |
| 1000 | L [mm] | 3660 | 3776 | 3760 | 3630 | 3652 | 3841 |
| T [s] | 143.6 | 159.4 | 177.9 | 292.7 | 320.8 | 359.3 | |
| It | Population Number | ||||||
|---|---|---|---|---|---|---|---|
| 50 | 100 | ||||||
| Number of Waypoints | |||||||
| 8 | 10 | 12 | 8 | 10 | 12 | ||
| 500 | L [mm] | 3617 | 3868 | 3729 | 3803 | 3615 | 3814 |
| T [s] | 86.6 | 81.2 | 87.8 | 150.4 | 169.2 | 183.1 | |
| 1000 | L [mm] | 3598 | 3718 | 3690 | 3682 | 3589 | 3777 |
| T [s] | 161.4 | 179.3 | 176.6 | 299.2 | 330.8 | 361.7 | |
| It | Population Number | ||||||
|---|---|---|---|---|---|---|---|
| 50 | 100 | ||||||
| Number of Waypoints | |||||||
| 8 | 10 | 12 | 8 | 10 | 12 | ||
| 500 | L [mm] | 3676 | 3830 | 3801 | 3579 | 3788 | 3738 |
| T [s] | 73.4 | 79.1 | 83.0 | 142.9 | 154.8 | 167.9 | |
| 1000 | L [mm] | 3742 | 3678 | 3853 | 3678 | 3703 | 3817 |
| T [s] | 153.5 | 153.3 | 167.7 | 281.7 | 317.5 | 343.3 | |
| Population Number | ||||||||
|---|---|---|---|---|---|---|---|---|
| It | Number of Auxiliary Points | |||||||
| i = 2 | i = 3 | i = 4 | i = 5 | |||||
[mm] | [s] | [mm] | [s] | [mm] | [s] | [mm] | [s] | |
| 25 | 3918 | 5.2 | 3847 | 5.3 | 3882 | 5.1 | 3777 | 5.4 |
| 50 | 3921 | 9.5 | 3733 | 9.8 | 3809 | 9.9 | 3677 | 10.2 |
| 75 | 3912 | 14.4 | 3774 | 15.0 | 3810 | 14.5 | 3698 | 15.0 |
| 100 | 3852 | 18.5 | 3704 | 19.5 | 3821 | 19.1 | 3638 | 19.8 |
| Population Number | ||||||||
|---|---|---|---|---|---|---|---|---|
| It | Number of Auxiliary Points | |||||||
| i = 2 | i = 3 | i = 4 | i = 5 | |||||
[mm] | [s] | [mm] | [s] | [mm] | [s] | [mm] | [s] | |
| 25 | 3929 | 6.2 | 3699 | 6.6 | 3897 | 6.4 | 3829 | 6.6 |
| 50 | 3867 | 12.4 | 3678 | 12.2 | 3842 | 12.5 | 3740 | 12.8 |
| 75 | 3899 | 18.5 | 3640 | 18.9 | 3766 | 19.0 | 3659 | 18.7 |
| 100 | 3909 | 24.1 | 3670 | 24.4 | 3701 | 25.1 | 3629 | 24.1 |
| Population Number | ||||||||
|---|---|---|---|---|---|---|---|---|
| It | Number of Auxiliary Points | |||||||
| i = 2 | i = 3 | i = 4 | i = 5 | |||||
[mm] | [s] | [mm] | [s] | [mm] | [s] | [mm] | [s] | |
| 25 | 3932 | 7.8 | 3770 | 7.7 | 3905 | 8.0 | 3751 | 7.7 |
| 50 | 3872 | 14.5 | 3624 | 15.4 | 3739 | 15.2 | 3709 | 15.2 |
| 75 | 3901 | 21.9 | 3705 | 22.3 | 3827 | 22.6 | 3602 | 22.6 |
| 100 | 3869 | 29.2 | 3691 | 28.9 | 3777 | 29.5 | 3587 | 29.2 |
| Population Number | ||||||||
|---|---|---|---|---|---|---|---|---|
| It | Number of Auxiliary Points | |||||||
| i = 2 | i = 3 | i = 4 | i = 5 | |||||
[mm] | [s] | [mm] | [s] | [mm] | [s] | [mm] | [s] | |
| 25 | 3920 | 9.4 | 3660 | 9.2 | 3797 | 9.5 | 3736 | 9.1 |
| 50 | 3937 | 17.2 | 3699 | 17.7 | 3759 | 17.1 | 3630 | 18.2 |
| 75 | 3919 | 25.4 | 3626 | 25.5 | 3751 | 25.3 | 3566 | 26.0 |
| 100 | 3893 | 33.6 | 3683 | 34.0 | 3717 | 34.5 | 3599 | 34.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwiatoń, P.; Cekus, D.; Skrobek, D.; Šofer, M.; Poruba, Z. Path Planning Optimization of the Load Transport Process Using Heuristic Algorithms. Appl. Sci. 2024, 14, 9940. https://doi.org/10.3390/app14219940
Kwiatoń P, Cekus D, Skrobek D, Šofer M, Poruba Z. Path Planning Optimization of the Load Transport Process Using Heuristic Algorithms. Applied Sciences. 2024; 14(21):9940. https://doi.org/10.3390/app14219940
Chicago/Turabian StyleKwiatoń, Paweł, Dawid Cekus, Dorian Skrobek, Michal Šofer, and Zdenek Poruba. 2024. "Path Planning Optimization of the Load Transport Process Using Heuristic Algorithms" Applied Sciences 14, no. 21: 9940. https://doi.org/10.3390/app14219940
APA StyleKwiatoń, P., Cekus, D., Skrobek, D., Šofer, M., & Poruba, Z. (2024). Path Planning Optimization of the Load Transport Process Using Heuristic Algorithms. Applied Sciences, 14(21), 9940. https://doi.org/10.3390/app14219940






