Deep Learning-Based Low-Frequency Passive Acoustic Source Localization
Abstract
1. Introduction
2. Method
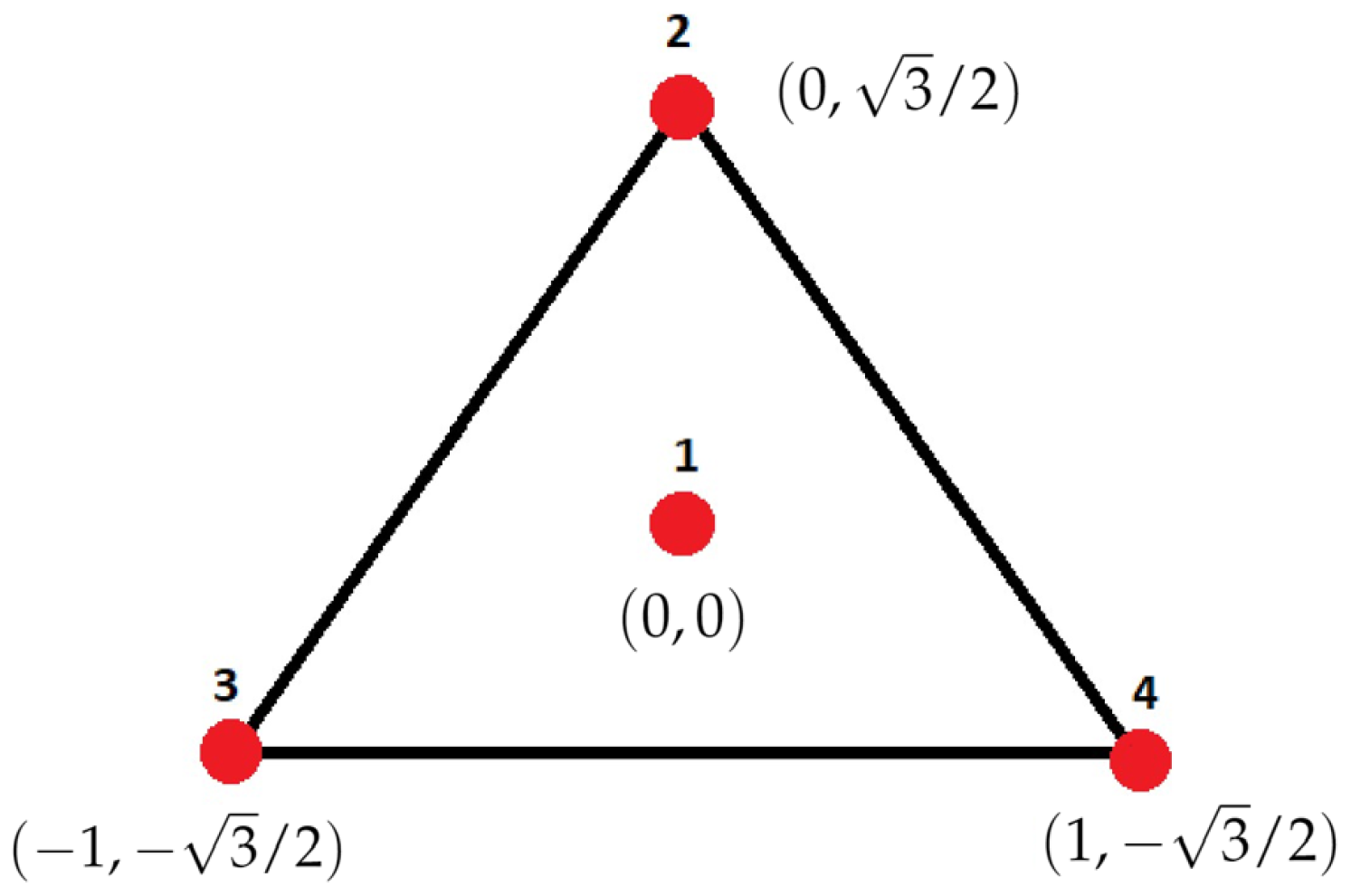
2.1. Microphone Array and Source Simulation
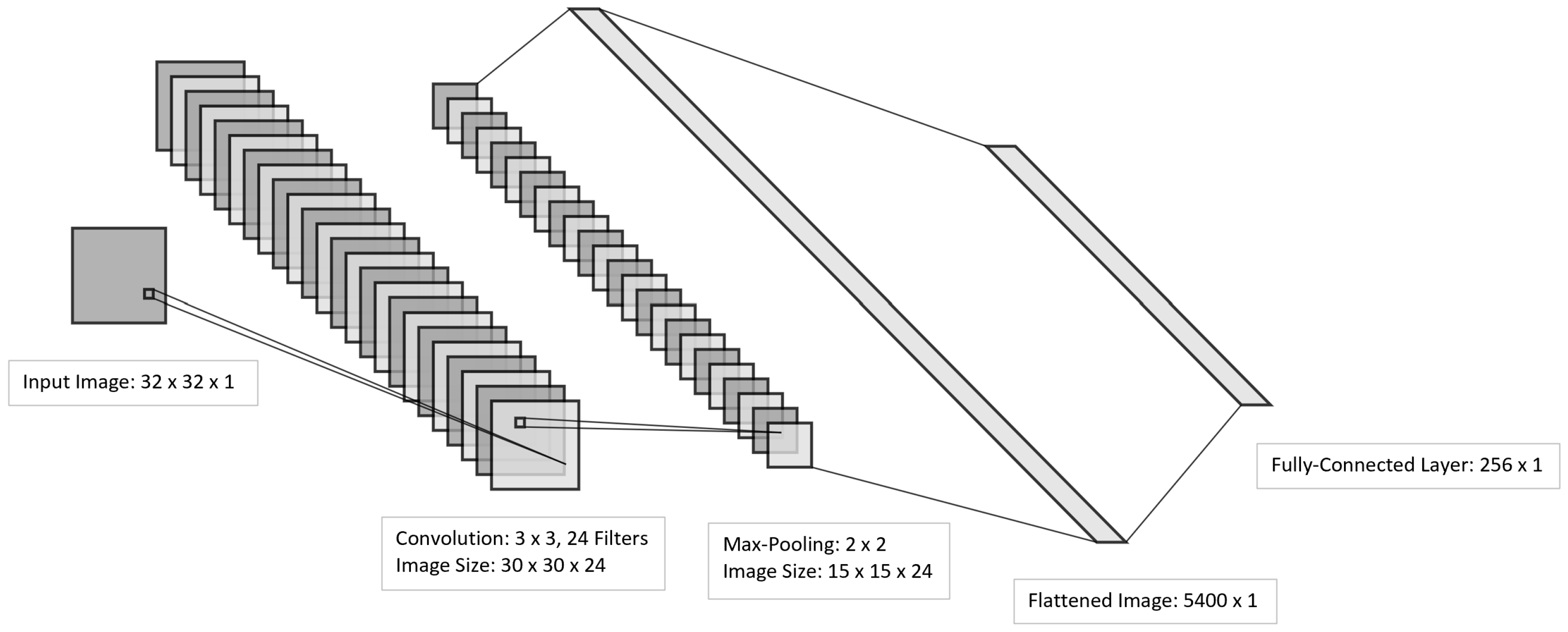
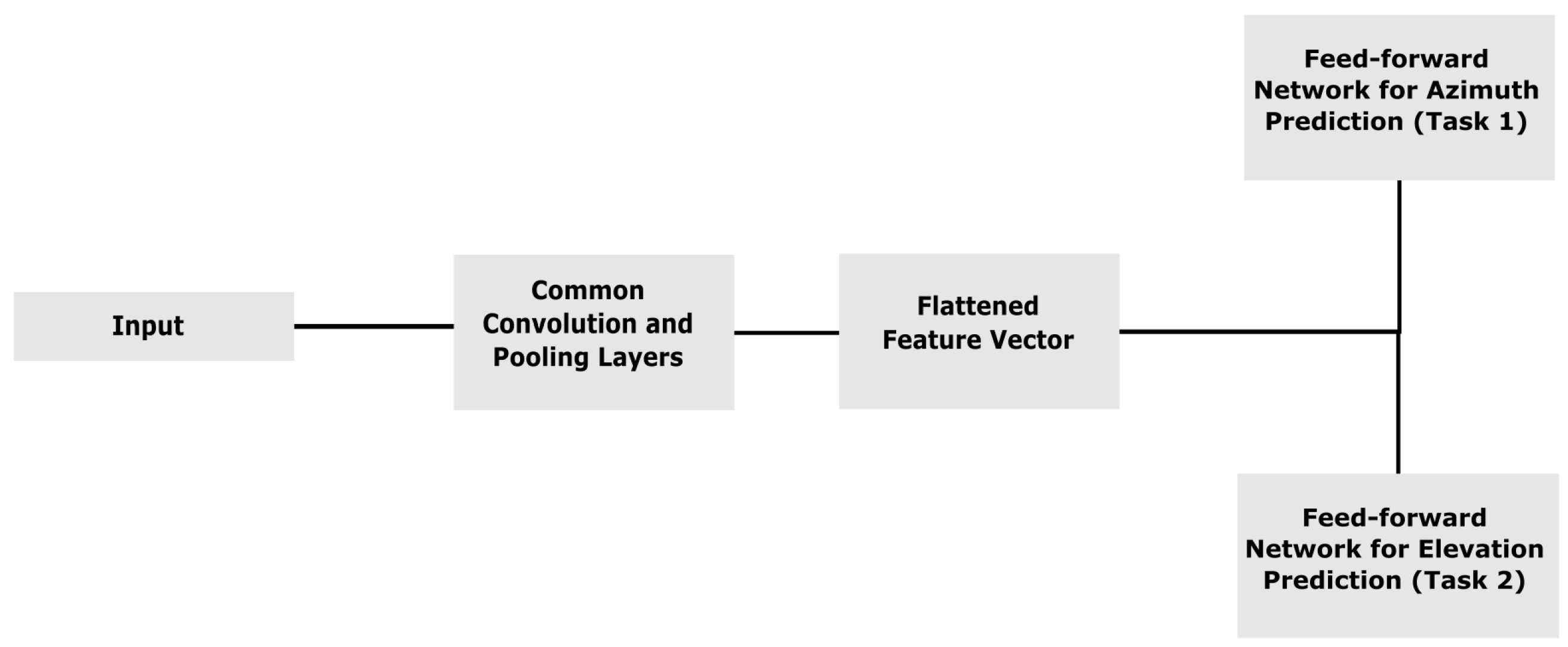
2.2. Convolutional Neural Network
3. Test Case Setups
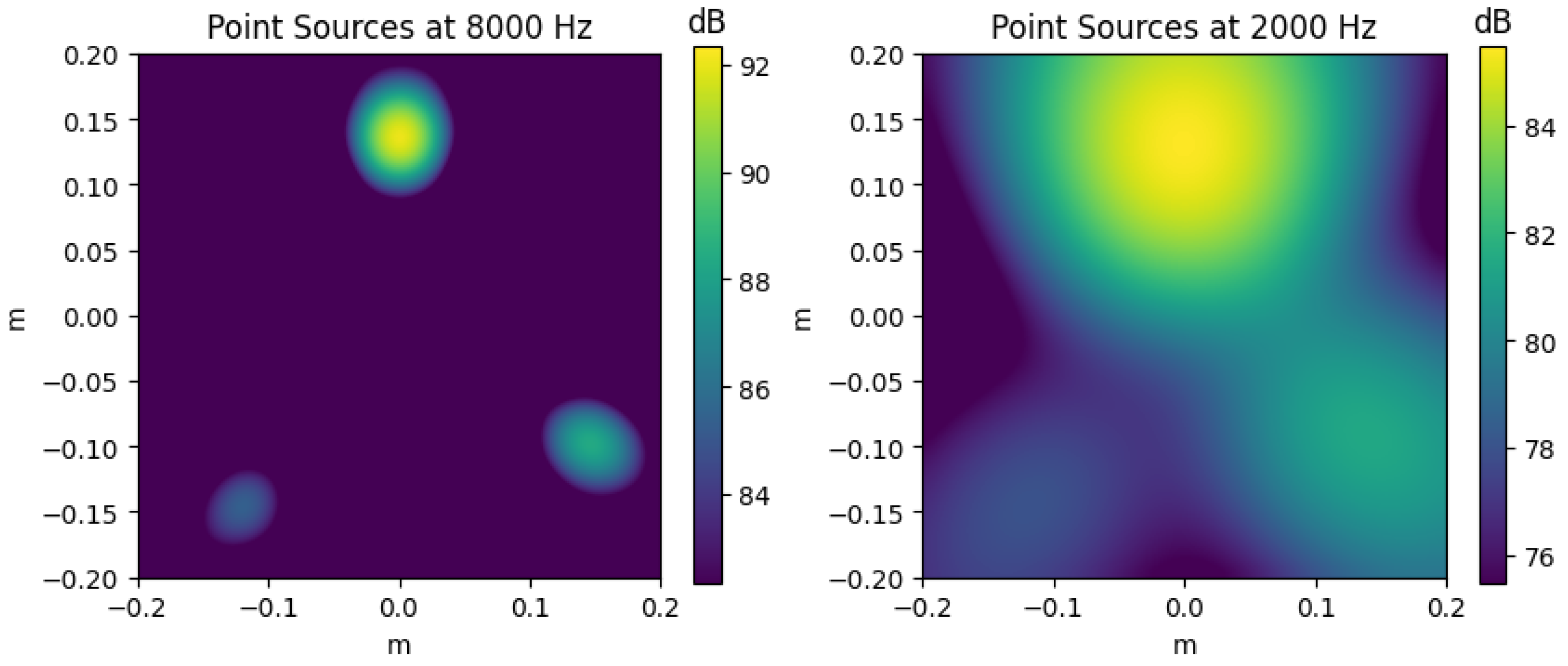
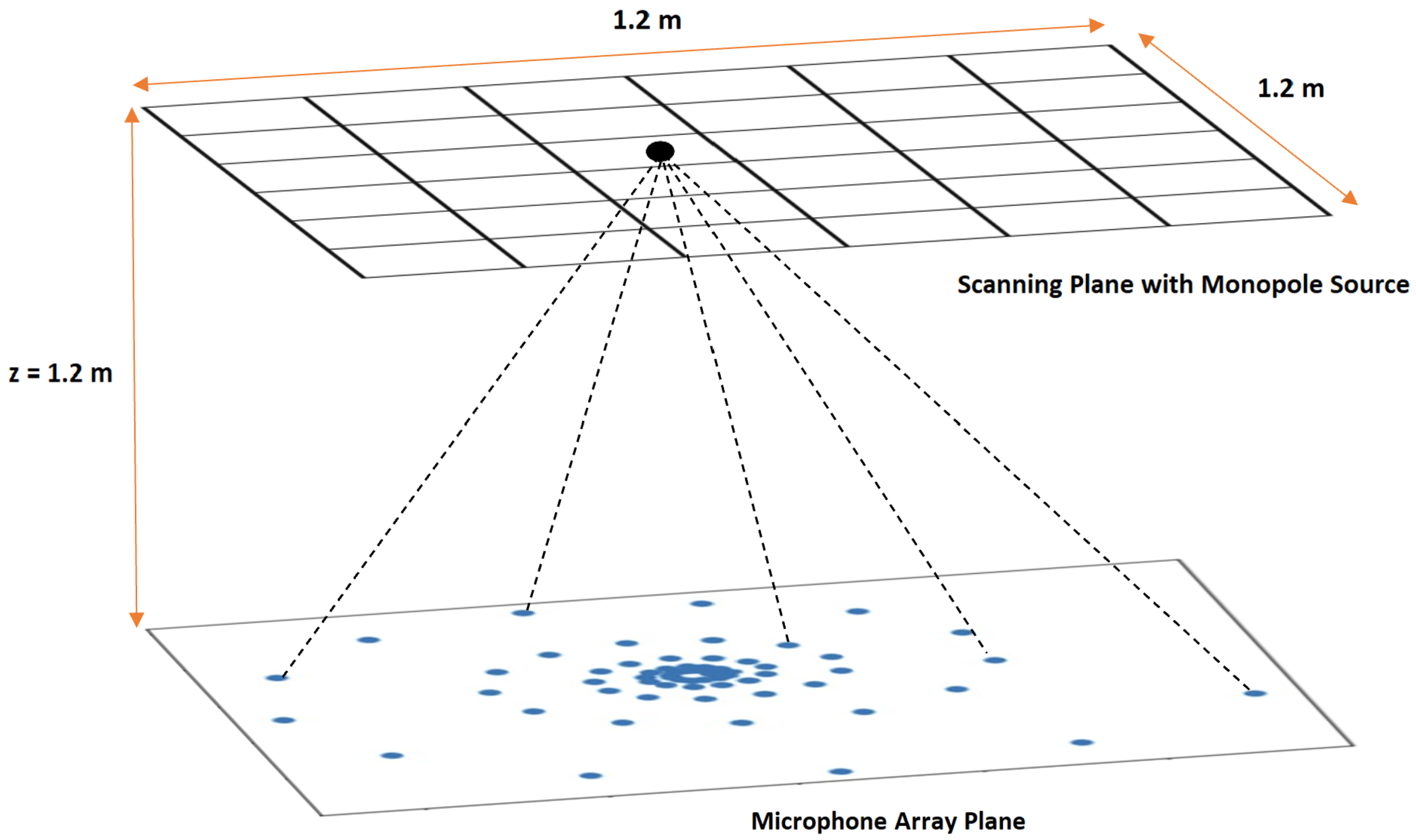
3.1. Case 1: Stationary Source Localization on a Scanning Plane
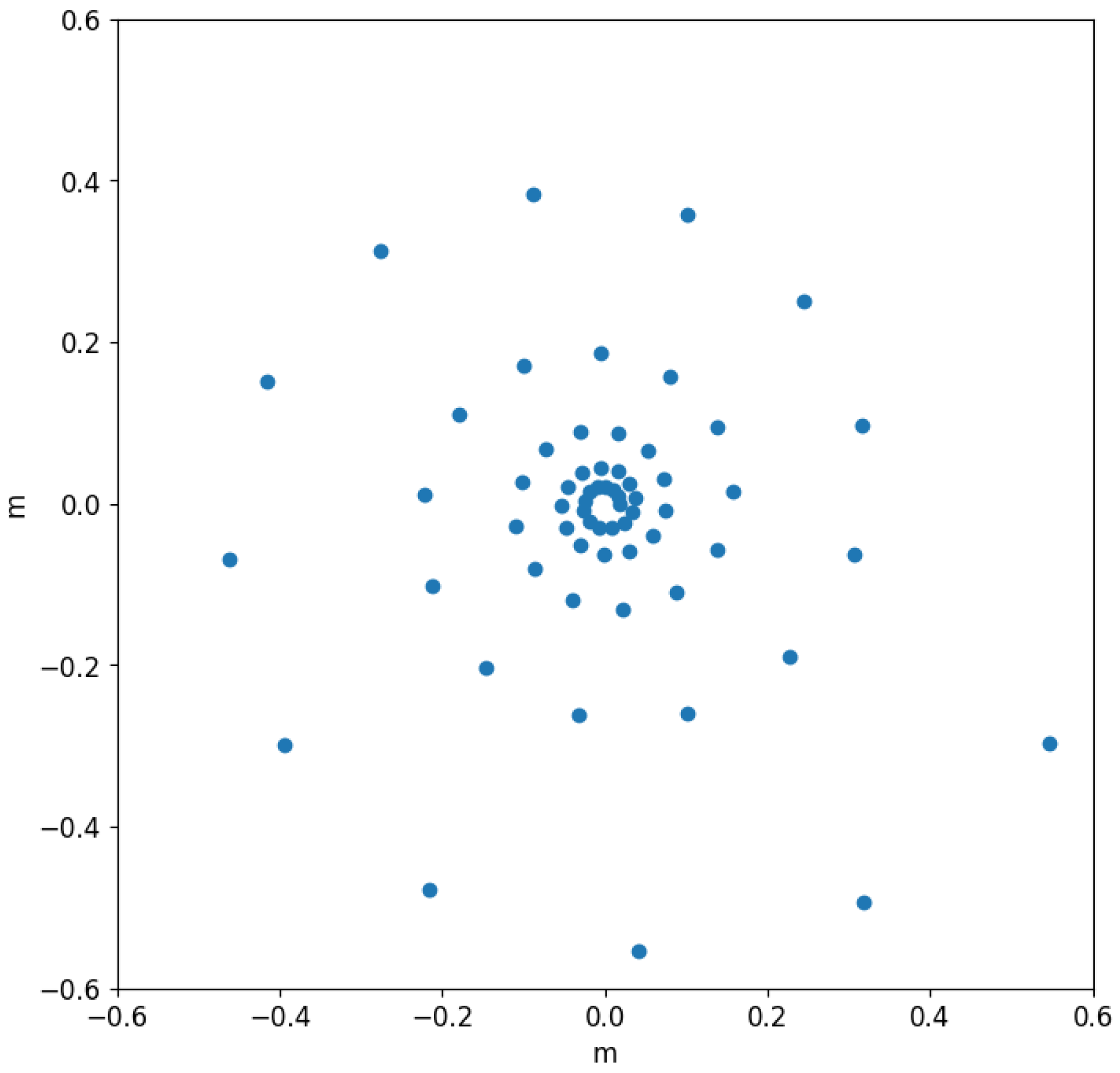
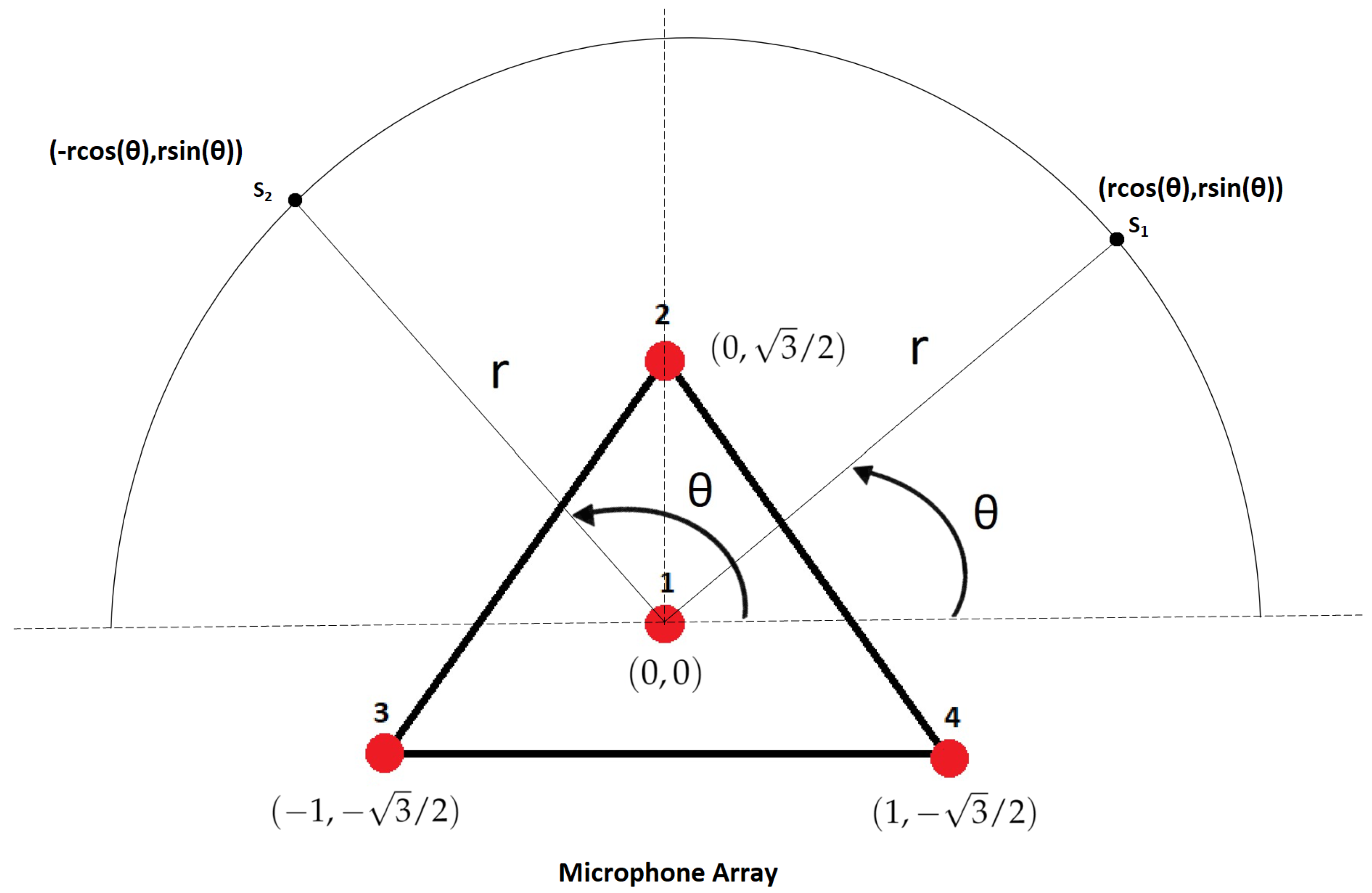
3.2. Case 2: Two-Dimensional ASL on the Horizon
3.2.1. Case 2 (i): Monopole (S1)
3.2.2. Case 2 (ii): Sinusoidal Plane Wave (S2)
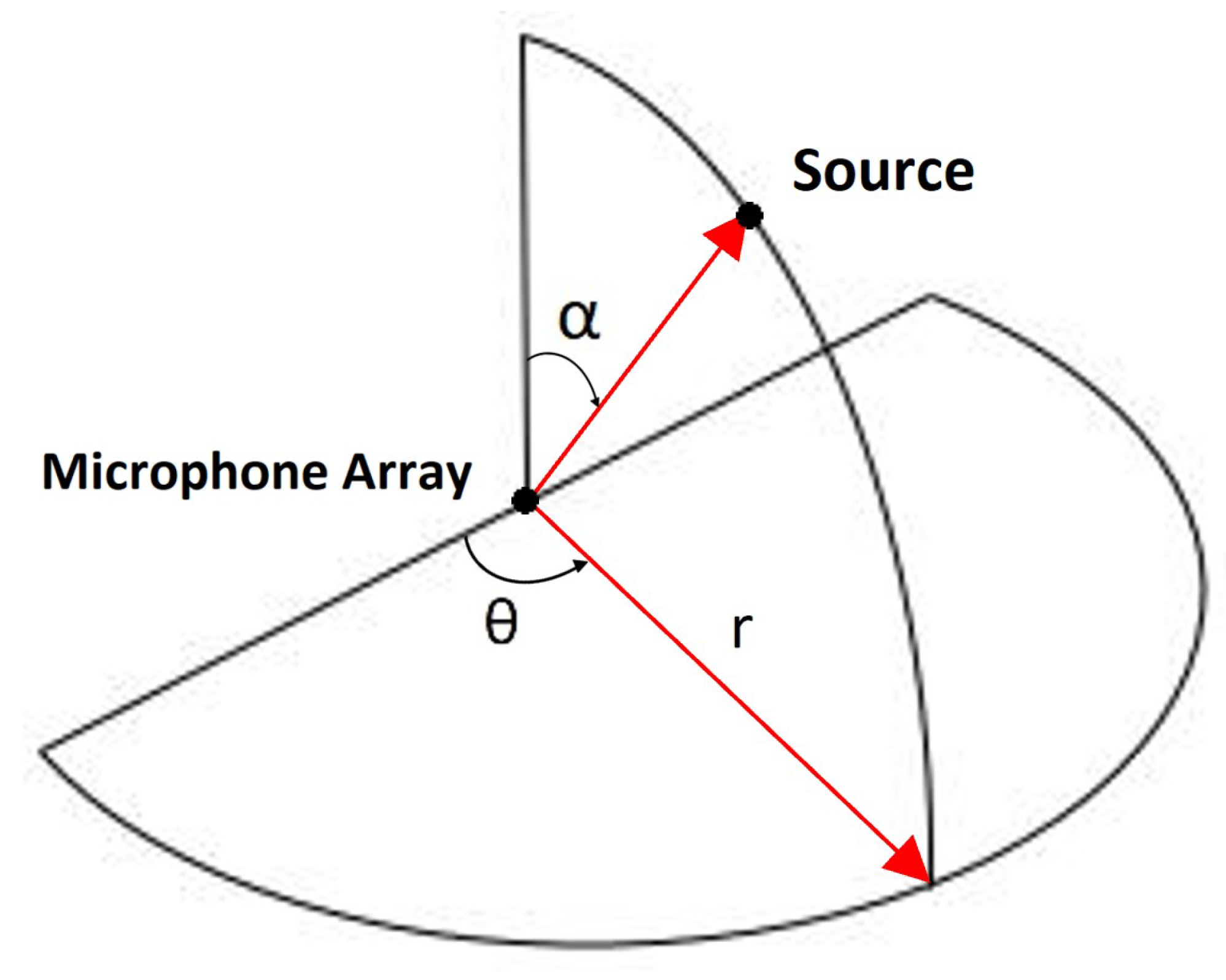
3.3. Case 3: Three-Dimensional ASL
4. Results
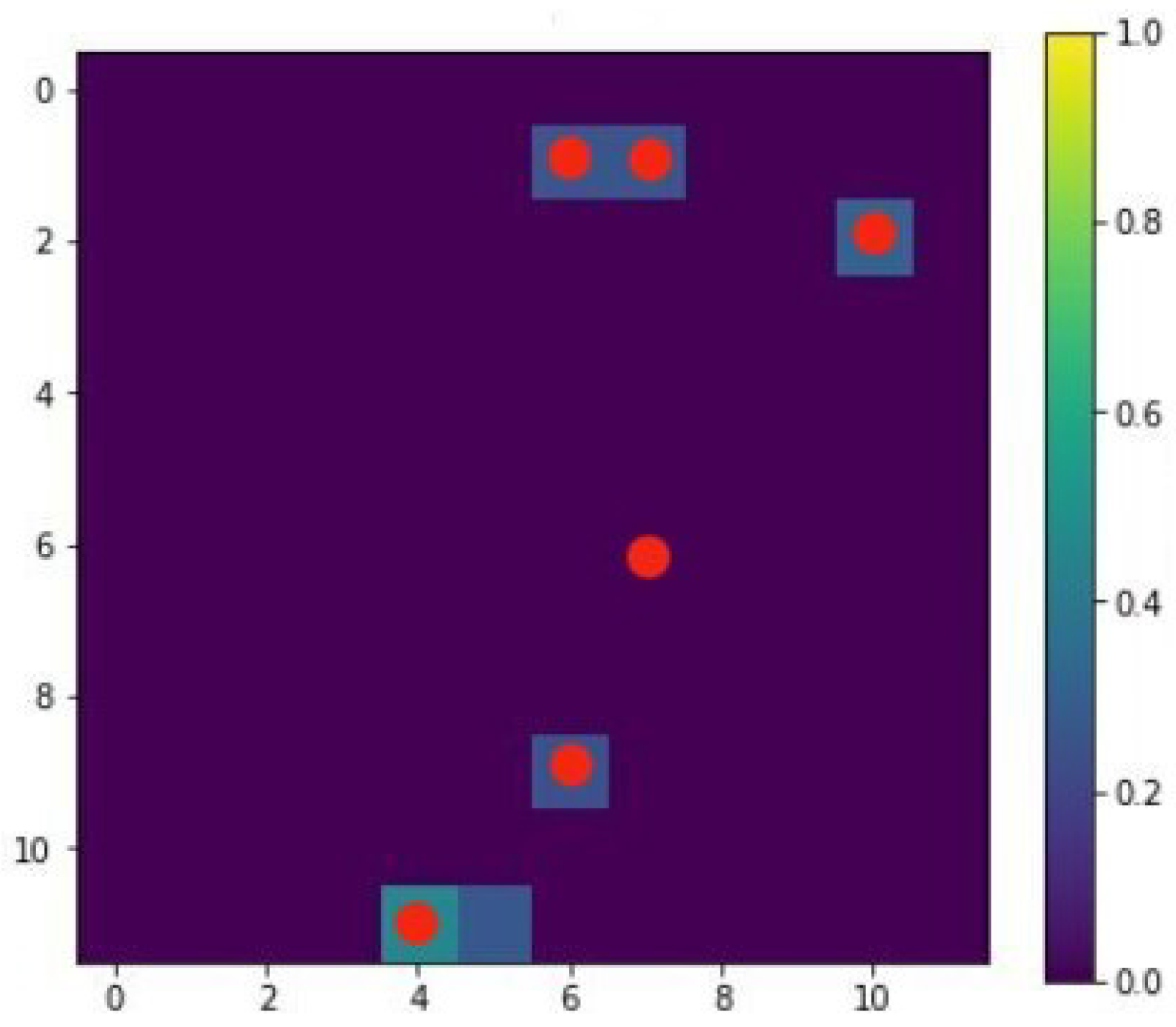
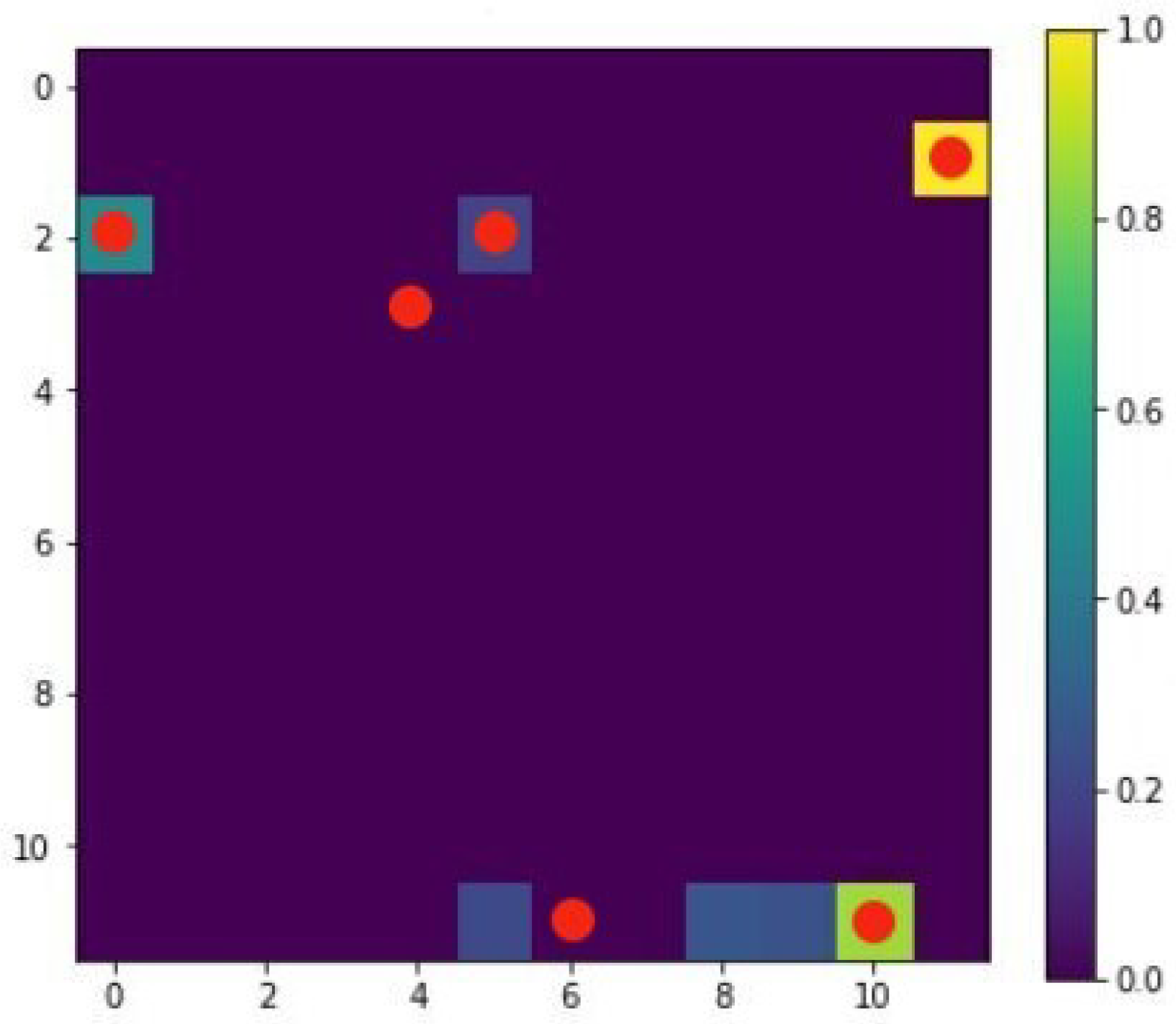
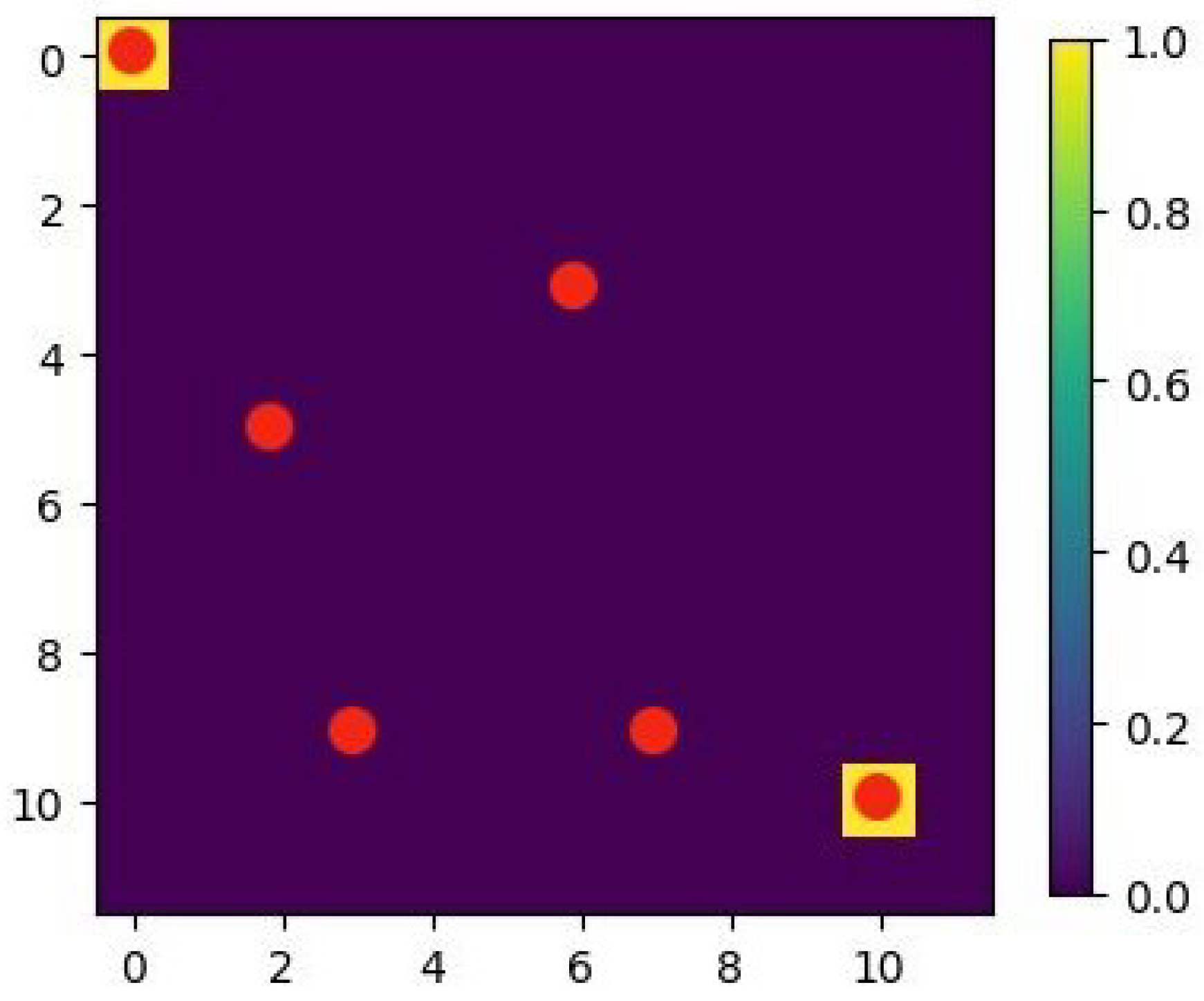
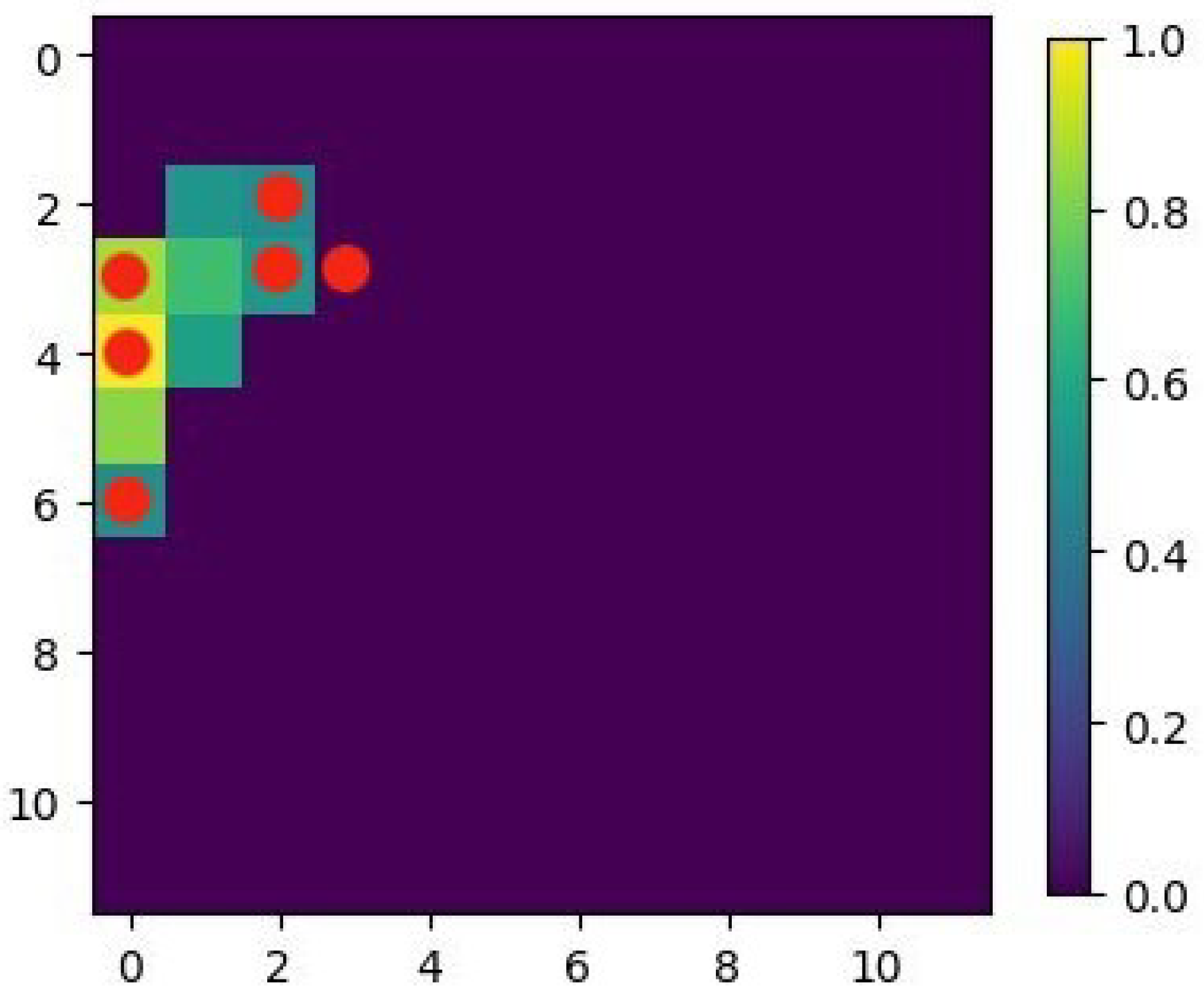
4.1. Case 1
Discussion
4.2. Case 2
4.2.1. Case 2 (i): Monopole (S1)
4.2.2. Case 2 (i): Sinusoidal Plane Wave (S2)
4.2.3. Discussion
4.3. Case 3
4.3.1. Case 3 (i): Monopole (S1)
4.3.2. Case 3 (ii): Sinusoidal Plane Wave (S2)
4.3.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peyvandi, H.; Farrokhrooz, M.; Roufarshbaf, H.; Park, S.J. SONAR systems and underwater signal processing: Classic and modern approaches. In SONAR Systems; IntechOpen: London, UK, 2011; pp. 173–206. [Google Scholar]
- Carter, G. Time delay estimation for passive sonar signal processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 463–470. [Google Scholar] [CrossRef]
- Fernandes, J.d.C.V.; de Moura Junior, N.N.; de Seixas, J.M. Deep learning models for passive sonar signal classification of military data. Remote Sens. 2022, 14, 2648. [Google Scholar] [CrossRef]
- Tosi, P.; Sbarra, P.; De Rubeis, V. Earthquake sound perception. Geophys. Res. Lett. 2012, 39, L24301. [Google Scholar] [CrossRef]
- Hill, D.P.; Fischer, F.G.; Lahr, K.M.; Coakley, J.M. Earthquake sounds generated by body-wave ground motion. Bull. Seismol. Soc. Am. 1976, 66, 1159–1172. [Google Scholar]
- Sylvander, M.; Ponsolles, C.; Benahmed, S.; Fels, J.F. Seismoacoustic recordings of small earthquakes in the Pyrenees: Experimental results. Bull. Seismol. Soc. Am. 2007, 97, 294–304. [Google Scholar] [CrossRef]
- Bocanegra, J.A.; Borelli, D.; Gaggero, T.; Rizzuto, E.; Schenone, C. A novel approach to port noise characterization using an acoustic camera. Sci. Total Environ. 2022, 808, 151903. [Google Scholar] [CrossRef]
- Booth, E.; Humphreys, W. Tracking and characterization of aircraft wakes using acoustic and lidar measurements. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; p. 2964. [Google Scholar]
- Joshi, A.; Rahman, M.M.; Hickey, J.P. Recent Advances in Passive Acoustic Localization Methods via Aircraft and Wake Vortex Aeroacoustics. Fluids 2022, 7, 218. [Google Scholar] [CrossRef]
- Schönhals, S.; Steen, M.; Hecker, P. Towards wake vortex safety and capacity increase: The integrated fusion approach and its demands on prediction models and detection sensors. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 227, 199–208. [Google Scholar] [CrossRef]
- Shams, Q.A.; Zuckerwar, A.J.; Burkett, C.G.; Weistroffer, G.R.; Hugo, D.R. Experimental investigation into infrasonic emissions from atmospheric turbulence. J. Acoust. Soc. Am. 2013, 133, 1269–1280. [Google Scholar] [CrossRef]
- Watson, L.M.; Iezzi, A.M.; Toney, L.; Maher, S.P.; Fee, D.; McKee, K.; Ortiz, H.D.; Matoza, R.S.; Gestrich, J.E.; Bishop, J.W.; et al. Volcano infrasound: Progress and future directions. Bull. Volcanol. 2022, 84, 44. [Google Scholar] [CrossRef]
- Chiariotti, P.; Martarelli, M.; Castellini, P. Acoustic beamforming for noise source localization–Reviews, methodology and applications. Mech. Syst. Signal Process. 2019, 120, 422–448. [Google Scholar] [CrossRef]
- de Santana, L. Fundamentals of Acoustic Beamforming; NATO Educ. Notes EN-AVT; NATO Science and Technology Organization: Brussels, Belgium, 2017; Volume 4. [Google Scholar]
- Gombots, S.; Nowak, J.J.; Kaltenbacher, M. Sound source localization–state of the art and new inverse scheme. Elektrotech. Infor. e & i 2021, 138, 229–243. [Google Scholar]
- Rayleigh, F.R.S. XXXI. Investigations in optics, with special reference to the spectroscope. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1879, 8, 261–274. [Google Scholar] [CrossRef]
- Brooks, T.F.; Humphreys, W.M. A deconvolution approach for the mapping of acoustic sources (DAMAS) determined from phased microphone arrays. J. Sound Vib. 2006, 294, 856–879. [Google Scholar] [CrossRef]
- Xu, P.; Arcondoulis, E.J.; Liu, Y. Acoustic source imaging using densely connected convolutional networks. Mech. Syst. Signal Process. 2021, 151, 107370. [Google Scholar] [CrossRef]
- Sarradj, E.; Herold, G. A Python framework for microphone array data processing. Appl. Acoust. 2017, 116, 50–58. [Google Scholar] [CrossRef]
- Bianco, M.J.; Gerstoft, P.; Traer, J.; Ozanich, E.; Roch, M.A.; Gannot, S.; Deledalle, C.A. Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [CrossRef]
- Grumiaux, P.A.; Kitić, S.; Girin, L.; Guérin, A. A survey of sound source localization with deep learning methods. J. Acoust. Soc. Am. 2022, 152, 107–151. [Google Scholar] [CrossRef]
- Yalta, N.; Nakadai, K.; Ogata, T. Sound source localization using deep learning models. J. Robot. Mechatronics 2017, 29, 37–48. [Google Scholar] [CrossRef]
- Vera-Diaz, J.M.; Pizarro, D.; Macias-Guarasa, J. Towards end-to-end acoustic localization using deep learning: From audio signals to source position coordinates. Sensors 2018, 18, 3418. [Google Scholar] [CrossRef]
- O’Shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Chakrabarty, S.; Habets, E.A. Broadband DOA estimation using convolutional neural networks trained with noise signals. In Proceedings of the 2017 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 15–18 October 2017; pp. 136–140. [Google Scholar]
- Xiao, X.; Zhao, S.; Zhong, X.; Jones, D.L.; Chng, E.S.; Li, H. A learning-based approach to direction of arrival estimation in noisy and reverberant environments. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 2814–2818. [Google Scholar]
- Ma, W.; Liu, X. Phased microphone array for sound source localization with deep learning. Aerosp. Syst. 2019, 2, 71–81. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Niu, H.; Gong, Z.; Ozanich, E.; Gerstoft, P.; Wang, H.; Li, Z. Deep learning for ocean acoustic source localization using one sensor. arXiv 2019, arXiv:1903.12319. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Prime, Z.; Doolan, C. A comparison of popular beamforming arrays. In Proceedings of the Australian Acoustical Society AAS2013 Victor Harbor, Victor Harbor, Australia, 17–20 November 2013; Volume 1, p. 5. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ho, Y.; Wookey, S. The real-world-weight cross-entropy loss function: Modeling the costs of mislabeling. IEEE Access 2019, 8, 4806–4813. [Google Scholar] [CrossRef]
- Varzandeh, R.; Adiloğlu, K.; Doclo, S.; Hohmann, V. Exploiting periodicity features for joint detection and DOA estimation of speech sources using convolutional neural networks. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 566–570. [Google Scholar]
- Amyar, A.; Modzelewski, R.; Li, H.; Ruan, S. Multi-task deep learning based CT imaging analysis for COVID-19 pneumonia: Classification and segmentation. Comput. Biol. Med. 2020, 126, 104037. [Google Scholar] [CrossRef]
- Lakkapragada, A.; Sleiman, E.; Surabhi, S.; Wall, D.P. Mitigating negative transfer in multi-task learning with exponential moving average loss weighting strategies (student abstract). In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 16246–16247. [Google Scholar]



| Cases | Conv. Layers, Dimension | Max-Pool Layers, Dimension | Dense Layers (Nodes), Output Dimension |
|---|---|---|---|
| 1 | 3, (), Filters: 32, 64, 64 | 2, () | 4 (128), Output: 144 |
| 2 (i): S1 | 2, (), Filters: 128, 64 | None | 1 (128), Output: N |
| 2 (ii): S2 | 3, (), Filters: 128, 64, 64 | 2, () | 1 (128), Output: N |
| 3 (i): S1 | 2, (), Filters: 128, 64 | None | (): 1 (128), (): 1 (128), |
| 3 (ii): S2 | 2, (), Filters: 128, 64, 64 | 2, () | (): 1 (128), (): 1 (128), |
| Sources Detected | 300 Hz | 100 Hz |
|---|---|---|
| 6 | 9 | 1 |
| 5 | 70 | 10 |
| 4 | 272 | 39 |
| 3 | 397 | 142 |
| 2 | 210 | 344 |
| 1 | 42 | 348 |
| 0 | 0 | 116 |
| Total | 1000 | 1000 |
| Classes (N) | Class Size | Accuracy (, 100 Hz) | Accuracy (, 300 Hz) |
|---|---|---|---|
| 20 | 9° | ≈91% | ≈95% |
| 30 | 6° | ≈89% | ≈92% |
| 45 | 4° | ≈81% | ≈91% |
| 60 | 3° | ≈69% | ≈87% |
| 90 | 2° | ≈52% | ≈77% |
| 180 | 1° | ≈23% | ≈57% |
| Classes (N) | Class Size | Accuracy (, 10 Hz) | Accuracy (, 100 Hz) | Accuracy (, 300 Hz) |
|---|---|---|---|---|
| 20 | 9° | ≈84% | ≈97% | ≈98% |
| 30 | 6° | ≈76% | ≈96% | ≈97% |
| 45 | 4° | ≈63% | ≈95% | ≈96% |
| 60 | 3° | ≈52% | ≈93% | ≈95% |
| 90 | 2° | ≈40% | ≈89% | ≈93% |
| 180 | 1° | ≈20% | ≈79% | ≈86% |
| Class Size | () | Accuracy () | () | Accuracy () |
|---|---|---|---|---|
| 10° | 18 | ≈93% | 9 | ≈91% |
| 5° | 36 | ≈84% | 18 | ≈79% |
| 3° | 60 | ≈69% | 30 | ≈58% |
| 2° | 90 | ≈56% | 45 | ≈52% |
| 1° | 180 | ≈29% | 90 | ≈36% |
| Class Size | () | Accuracy () | () | Accuracy () |
|---|---|---|---|---|
| 10° | 18 | ≈79% | 9 | ≈99% |
| 5° | 36 | ≈58% | 18 | ≈99% |
| 3° | 60 | ≈41% | 30 | ≈97% |
| 2° | 90 | ≈26% | 45 | ≈96% |
| 1° | 180 | ≈13% | 90 | ≈91% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joshi, A.; Hickey, J.-P. Deep Learning-Based Low-Frequency Passive Acoustic Source Localization. Appl. Sci. 2024, 14, 9893. https://doi.org/10.3390/app14219893
Joshi A, Hickey J-P. Deep Learning-Based Low-Frequency Passive Acoustic Source Localization. Applied Sciences. 2024; 14(21):9893. https://doi.org/10.3390/app14219893
Chicago/Turabian StyleJoshi, Arnav, and Jean-Pierre Hickey. 2024. "Deep Learning-Based Low-Frequency Passive Acoustic Source Localization" Applied Sciences 14, no. 21: 9893. https://doi.org/10.3390/app14219893
APA StyleJoshi, A., & Hickey, J.-P. (2024). Deep Learning-Based Low-Frequency Passive Acoustic Source Localization. Applied Sciences, 14(21), 9893. https://doi.org/10.3390/app14219893








