Abstract
Topological defects are a key concern in numerous branches of physics. It is meaningful to exploit the topological defect evolutions during the phase transitions of condensed matter. Here, via varying the initial azimuthal orientation of the square alignment lattice in a hybrid cell, the topological defect evolution of liquid crystal during the nematic (N)–smectic A (SmA) phase transition is investigated. The director fields surrounding ±1 point defects are manipulated by predesigning the initial azimuthal orientation. When further cooled to the SmA phase, spiral toric focal conic domain (TFCD) arrays are formed as a result of twisted deformation suppression and unique symmetry breaking after the phase transition. The variation in the azimuthal orientation causes the TFCDs to degenerate from infinite rotational symmetry to quadruple rotational symmetry, thus releasing new textures for the SmA phase. Landau–de Gennes numerical modeling is adopted to reproduce the director distributions in the N phase and reveal the evolution of the topological defects. This work enriches the knowledge on the self-organization of soft matter, enhances the capability for the manipulations of topological defects, and may inspire new intriguing applications.
1. Introduction
Topological defects are discontinuities or nontrivial regions in physical systems that cannot be eliminated through continuous symmetry operations [1]. They are distinguished by topology and play vital roles in various fields of physics, including condensed matter physics [2], cosmology [3], and quantum field theory [4], determining corresponding properties and behaviors. Topological defects inevitably arise during the phase transition of condensed matter because of a spontaneous symmetry breaking process [5]. Thus, it is meaningful to exploit the behaviors and mechanisms of topological defect transformations across the phase transitions. Liquid crystals (LCs) provide an ideal platform for such investigations owing to their unique combination of fluidity, stimuli-responsive optical anisotropy, and abundance of phases and topological defects [6].
The constituent rod-like molecules in the nematic phase (N) of LCs spontaneously orient along a dominant direction, referred to as the director n, where n and −n are physically equivalent [7]. NLCs usually exhibit point defects, line defects, and wall defects. The topological charge s is a conserved quantity characterizing the number of rotations of the director around the defect core, and is considered as a key property of topological defects [7]. The value of s is infinite in theory; however, topological defects with ±1 and ±1/2 are usually observed experimentally. The spatial dimension is another feature of topological defects [8]. For example, point defects can be classified into bulk point defects (three-dimensional) and surface point defects (two-dimensional). The former is usually formed in spherical nematic droplets with perpendicular anchoring surfaces and uniformly aligned NLCs embedded with spherical particles of vertical alignment [9,10,11,12]. The latter has been more extensively investigated due to its ability to freely generate and manipulate under external stimuli such as electric fields [13,14], magnetic fields [15], topographically patterned mechanical scrubbing [16], and preprogrammed photopatterning [17]. Across the N–smectic A (SmA) phase transition, one-dimensional positional order is further introduced in addition to long-range directional order. Accordingly, the LC molecules arrange into parallel layers with nanometer thicknesses. Under hybrid anchoring conditions, these layers are periodically wrapped to generate toric focal conic domains (TFCDs) [18,19]. TFCDs exhibit perfect rotational symmetry and can focus light like a microlens due to their radially gradient refractive index change [20]. Moreover, their specific director distribution enables the transportation of functional nanoparticles to the central singularity [21] and this unique topographic feature facilitates the manufacture of artificial superhydrophobic surfaces [22]. Recently, ordered TFCDs were converted from NLCs with predesigned point defects during the N-S phase transition [23,24]. Up until now, the LC orientation around point defects has been restricted to the radial condition, hindering the behaviors of the corresponding structures. New architectures with unprecedented properties can be released if one can overcome the infinite rotational symmetry limitation.
In this work, we investigate the topological defect evolution of LCs across the N-SmA phase transition in a hybrid cell via presetting different azimuthal orientations of a square alignment lattice. The square lattice of the radial alignment is imprinted on the substrate by photoalignment, while a perpendicular alignment is set on the superstrate. When the LC is filled with such a cell, a ±1 point defect array is achieved in the N phase when it is slowly cooled from the isotropic phase. Via varying the initial azimuthal orientation of each alignment unit, the transformations of both the point defects and the surrounding director fields occur correspondingly. The evolution of ordered TFCDs is generated during the N-SmA phase transition due to the inheritance of orientational order. The Landau–de Gennes theory is utilized to model the director distributions of point defects in the N phase, revealing how topological defect profiles change in response to variations in the azimuthal orientation. This work extends the understanding of orientational order control and may release more creative architectures of soft matter.
2. Materials and Methods
The LC device is formed by an LC layer [8CB (NCLCP, Nanjing, China), isotropic—40.5 °C-N–33.5 °C-SmA] sandwiched between a photoalignment agent [SD1 (NCLCP, Nanjing, China), dissolving in dimethylformamide (DMF) at a concentration of 0.3 wt.%.]-covered substrate and a PDMS (Polydimethylsiloxane, Dow Corning, Midland, MI, USA) layer coated with a superstrate [Figure 1a; the molecular structures of SD1, PDMS, and LC 8CB are shown in Figure 1b]. The former gives planar anchoring, while the latter provides homeotropic alignment, and they work together to generate a hybrid alignment. The specific sample fabrication and characterization are presented in Appendix A. A periodic square lattice of +1 and −1 defects is imposed in the SD1 layer using a multistep partly overlapping photoalignment technique [25], with directors varying gradually among adjacent defects (Figure 1), and the detailed processes are given in Appendix B. The director field is depicted as follows [26]:
where topological charge is set as si = ±1, (x0i, y0i) are the coordinates of the singularities, and α0 (the angle between the easy axis and the x-axis) is the initial azimuthal orientation. Here, the cell gap is fixed as h = 8.5 μm, and the lattice constant is set as l = 30 μm. The LC director follows the guidance of the photopatterned substrate, and the undefined director orientation on the alignment singularities leads to the generation of ±1 point defects. α0 can be freely varied owing to the flexibility of photoalignment. Figure 1a–d show the lattices with α0 = 0°, 30°, 60°, and 90°, respectively. The director fields surrounding the alignment singularities change according to the variance of α0.
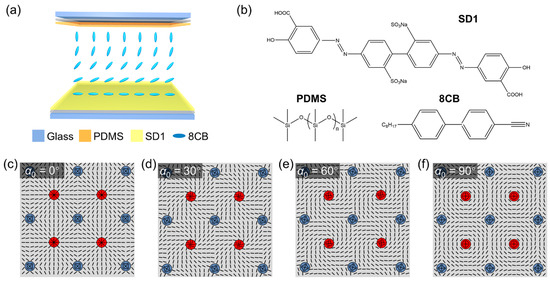
Figure 1.
(a) Schematic illustration of the hybrid cell. (b) Molecular structures of SD1, PDMS, and 8CB. The square lattice of alignment singularities defined on the substrate with (c) α0 = 0°, (d) α0 = 30°, (e) α0 = 60°, and (f) α0 = 90°. Each lattice contains four singularities—two +1 (red dots) and two −1 (blue dots).
3. Results and Discussions
When the infilled 8CB is cooled from the isotropic state to the N phase at a rate of −0.3 °C/min, the LC directors follow the local alignment of SD1 on the substrate and gradually turn to a uniform vertical alignment toward the superstrate. Figure 2 reveals the generated N textures observed under polarization optical microscopy (POM). When α0 = 0°, a square lattice of Maltese crosses is exhibited (Figure 2a). When the polarizers are rotated, the Maltese crosses around +1 point defects rotate in the same direction, whereas those around −1 point defects rotate in the opposite direction. The above phenomena indicate that +1 and −1 point defects are located exactly on the predesigned +1 and −1 alignment singularities. Similar textures are observed in samples with α0 = 30°, 60°, and 90°, except for obvious rotations of Maltese crosses at the corresponding anchoring angles. The bright field images shown in the insets of Figure 2 further confirm the consistency of point defects on alignment singularities. Cyan and magenta interference colors are simultaneously observed in Maltese crosses around adjacent +1 point defects. These differences are caused by the distinct phase retardations induced by the different tilt angles of the adjacent domains. To more precisely determine the director field around the point defects, a first-order retardation plate (λ = 530 nm) is inserted between the sample and the analyzers. Magenta is observed when n is parallel and vertical to the polarizers, and cyan blue and yellow colors appear when n is parallel and vertical to the slow axis of the λ-plate, respectively [27]. As shown in the bottom images of Figure 2a, cyan blue and magenta emerge twice alternatively in each unit, suggesting n rotates accordingly. The bottom images of Figure 2b–d show the cases with α0 = 30°, 60°, and 90°, respectively. The square lattices are maintained, while the interference colors change with varying α0. The interference color variations are consistent with the presetting local alignments α(x,y).
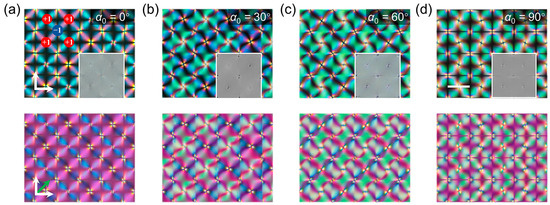
Figure 2.
POM micrographs of the samples in the N phase at 34.0 °C with (a) α0 = 0°, (b) α0 = 30°, (c) α0 = 60°, and (d) α0 = 90° (top row), as well as corresponding micrographs observed with a λ plate (bottom row). Insets show bright field images. The white arrows denote the directions of a pair of crossed polarizers. The green arrow denotes the direction of the λ-plate. The scale bar indicates 30 μm for all images.
The Landau–de Gennes theory is further utilized to reproduce the NLC director distribution and investigate the point defect evolution [28]. A traceless and symmetric tensor is adopted to describe the director field; this is expressed as , where S is the uniaxial scalar order parameter. The total free energy F of the NLC is defined as follows:
The bulk energy fbulk describes the degree of nematic order, which is given as follows:
Here, A = A0(T − T*), where T* defines the supercooling temperature of the nematic phase; A0, B, and C are defined as constants. For Equation (3), the uniaxial scalar order parameter of the bulk equilibrium can be calculated as , and it depends on the temperature T. felastic is used to describe the contribution of anisotropic elastic free energy, including the all-spatial gradient of tensor Q, which is given as follows:
where the coefficients Li (i = 1, 2, 4, 24) represent the splay (k11), twist (k22), bend (k33), and saddle-splay (k24) elastic constants of Frank theory, and the relationships of them can be defined as follows:
The second integral in Equation (2) is the anchoring energy, which includes the homeotropic anchoring energy of the superstrate covered with a PDMS layer and the planar anchoring contribution of the substrate covered with an SD1 layer. The calculation of homeotropic anchoring energy is defined by the Rapini-Papoular expression: . Wh represents the anchoring strength and Qs is the priority tensor of the surface. The planar anchoring energy is calculated using the following equation: , where , using the projection operator: , . Here, the tensor Pij will subtract the normal of the Q tensor, and v represents the normal of the substrate. The total free energy of the LCs is further minimized based on the Euler–Lagrange equation, and is solved by a finite difference method. Here, the parameters in the simulations are selected as A = −0.172 × 106 J/m3, B = 2.12 × 106 J/m3, and C = 1.73 × 106 J/m3; thus, the scalar order parameter is Seq = 0.533 [28]. The homeotropic anchoring strength of the PDMS superstrate is Wh = 6 × 10−6 J/m2 and the planar anchoring strength of the SD1 substrate is Wp = 1 × 10−4 J/m2 [29]. For the elastic constants, we choose k11 = k33 = 2k22 = 9.5 × 10−12 N and k24 = k22. Finally, our simulation is conducted on a cubic lattice with periodic boundary conditions along two lateral directions.
Figure 3 reveals the simulated LC directors of samples with different α0. The director n distributions of three typical cross sections are further selected to study the defect evolution along with the variation in α0. They are the middle layers in the x-y cross section (top images in Figure 3), and the x-z cross section passing through −1 (y = 0) and +1 (y = l/2) point defects with y = 0 (middle images in Figure 3) and y = l/2 (bottom images in Figure 3), respectively. Here, φ is defined as the azimuthal angle between the director n and the x-axis. Figure 3a shows the φ distributions and director fields in the three cross sections for the sample with α0 = 0°. The top image reveals that the director n is radially distributed within each unit due to the guidance of the preset alignment. The middle image in Figure 3a reveals the variation of directors in the z dimension. According to the simulation, a +1 point defect is classified into two types: (1) +1 converging type (+1c), in which the director field will converge toward the z axis; (2) +1 diverging type (+1d), in which the director field will diverge from the z axis. Moreover, for the −1 defect point, the converging and diverging director fields coexist in orthogonal planes, resulting in only one type. The cross section passing through the center of the +1 point defects (bottom image in Figure 3a) proves that there is no azimuth rotation for the +1 point defects, differing from the case of the −1 point defects; the calculated director distribution is consistent with the interference color in the POM image (Figure 2a). The director fields and φ distributions of samples with α0 = 30° (Figure 3b), α0 = 60° (Figure 3c), and α0 = 90° (Figure 3d) are also simulated, indicating that the directors rotate with increasing α0, which is consistent with the experimental interference colors. In the x-z cross sections with y = 0 (middle images), the variation in the director field astride the −1 point defect indicates a transformation from the convergent type to the divergent type. The bottom images indicate that the type of +1 point defect remains unchanged, whereas slight deformation occurs due to the increase in the azimuthal component of the surrounding directors as α0 increases. Thus, the variation of α0 leads to an azimuthal rotation of the director fields.
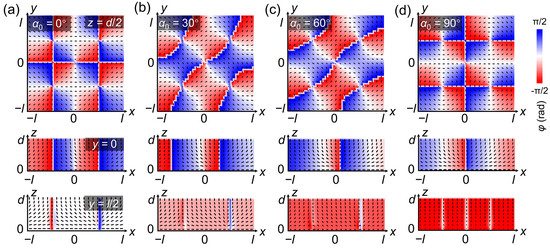
Figure 3.
Simulated director fields and calculated φ distributions in three cross sections of samples with (a) α0 = 0°, (b) α0 = 30°, (c) α0 = 60°, and (d) α0 = 90°. The top images are the middle layers in the x-y cross sections, and the middle and bottom images are the x-z cross sections passing through the −1 and +1 point defect with y = 0 and y = l/2, respectively.
When the sample is further cooled to the SmA phase, the LC molecules locally arrange into parallel layers and form TFCDs. In each domain, the LC layers are wrapped around a defect pair (red) of a straight line and a circle (the inset in Figure 4a). As reported previously [24], when α0 = 0°, TFCDs are generated only at +1c point defects due to the conforming converging director fields. Moreover, +1d point defects change to domains with positive Gaussian curvatures and are alternatively embedded into the TFCDs, resulting in a square TFCD array with a lattice constant of (top image in Figure 4a). In this case, the TFCD exhibits infinite rotational symmetry, which is further verified by the circular contour in the bright field image of each TFCD (bottom image in Figure 4a). For the case of α0 = 30°, TFCDs are still formed, but are rotationally distorted. The distortion is attributed to the azimuthal twist of the LC director fields guided by the anchoring (top image in Figure 4b). Due to the inheritance of orientational order across the N-SmA phase transition, distortion induces the deformation of the LC layers. As a result, TFCDs are split into four partial lobes, whose boundaries are clearly observed as dark curves in bright field images (bottom image in Figure 4b). In this case, spiral TFCDs exhibiting chirality are formed due to symmetry breaking. Accordingly, the TFCD units degenerate from infinite rotational symmetry to quadruple rotational symmetry. Notably, the core of the spiral TFCD is enlarged compared with that of the standard TFCD, while the diameters remain . We find that the integrity of the spiral TFCD remains until α0 > 45°. When α0 = 60°, the spiral unit is divided into four individual parts and forms a windmill-like texture (Figure 4c). When α0 = 90°, a new texture is formed. Thus, via changing α0, the infinite rotational symmetry of the TFCD is broken and the shape of the repeatable unit is varied, which enriches the self-assembly of SmA hierarchical architectures.

Figure 4.
TFCDs and split TFCDs in the S phase observed at 33.0 °C (top) and corresponding bright field images (bottom) when (a) α0 = 0°, (b) α0 = 30°, (c) α0 = 60°, and (d) α0 = 90°. The bottom right inset in (a) shows the layered configuration and director distribution of a single TFCD. The yellow lines mark the evolution of the TFCD units. The white arrows denote the directions of a pair of crossed polarizers. The scale bar indicates 30 μm for all images.
Via reasonably predesigning the initial azimuthal orientation of the alignment lattices, the mechanisms and behaviors of topological defect evolutions during the N-SmA phase transition are investigated. In previous research, the direction fields of the TFCD transformed from +1 point defects were restricted to a radial distribution. Here, through programming the photoalignment patterns, the infinite rotational symmetry restriction is broken, and new SmA textures are generated. Here, topological defect evolutions occur at the millisecond scale to the second scale. This approach significantly enhanced the direct observation of these evolutions, which is unachievable in quantum physics and cosmology. New properties and applications can be reasonably expected as new ordered LC textures are fabricated. It also brings about new possibilities for existing diffraction elements, particle assembly, and asymmetric imaging.
4. Conclusions
The topological defect evolutions of LCs are investigated via varying the initial azimuthal orientation of the square alignment lattice in a hybrid cell. As α0 increases from 0° to 90°, the twist deformations of the director n lead to significant director field variations surrounding +1 and −1 point defects. The Landau–de Gennes theory is adopted to analyze the director distributions and defect transformations. The simulations indicate that the directors rotate with increasing α0, and there is no azimuth rotation for the +1 point defect, while the −1 point defects exist. Further theoretical analysis reveals that the −1 point defect changes from a convergent type to a divergent type, while the type of +1 point defect remains unchanged. Although twisted deformation is suppressed in the SmA phase, discontinuous LC layers are formed due to the inheritance of orientation order of the above textures. This results in various spiral TFCDs when α0 ≤ 45°. For larger α0, the unit is divided into four individual lobes. TFCDs degenerate from infinite rotational symmetry to quadruple rotational symmetry, and the shape of the repeatable unit drastically changes with the variance of α0. This work enriches the fundamental understanding on the self-organization of soft matter systems and may open the door for advanced applications of topological defects.
Author Contributions
Y.S. and J.W. (Jinbing Wu) contributed equally to the work. Y.S., J.W. (Jinbing Wu), and W.H. designed the research; Y.S. and J.W. (Jinbing Wu) performed the research; Y.S., J.W. (Jinbing Wu), J.W. (Jingge Wang), S.W., and W.H. analyzed the data; Y.S., J.W. (Jinbing Wu), and W.H. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (2022YFA1203703), the National Natural Science Foundation of China (NSFC) (62035008 and 13001281), and the University Research Project of Guangzhou Education Bureau (202235053).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no competing interests.
Appendix A
Sample preparation: The glass substrates were first treated with ultrasonic bathing, and then cleaned with UV-ozone. SD1 were spin-coated onto a substrate and cured at 100 °C for 10 min. The substrate covered with an SD1 layer was then exposed under a dynamic polarization microlithography system (Digi Optron-120, NCLCP, Nanjing, China) to record the predesigned alignment patterns. The other substrate was spin-coated with a thin PDMS layer mixed with a small amount of initiator and then baked at 120 °C for 20 min for curing. UV glue doped with spacers is adopted to separate these two substrates from forming a hybrid cell. Finally, LC 8CB was injected into the above cell using capillary action at 70 °C and cooled to the N and SmA phases successively using a heating stage (LTS 120, Linkam, Redhill, UK).
Characterization: microscopy was characterized using a polarized optical microscope (50i, Nikon, Tokyo, Japan) with a pair of crossed polarizers, and a CCD camera was adopted to capture all micrographs (DS-Ri1, Nikon, Tokyo, Japan).
Appendix B
The multi-step partly overlapping exposure process was performed to carry out the predesigned alignment patterns through a digital micro-mirror device (DMD)-based dynamic micro-lithography system. The LC director distribution of each pattern is calculated based on Equation (1). The directors of every period region changing from 0 to 180° are divided equally into 36 subregions. Each subregion is assigned a uniform director value, from 0° to 175° in intervals of 5°. Five adjacent subregions are simultaneously exposed at a dose of ~1 J/cm2, which is insufficient to achieve a stable reorientation of SD1. Subsequently, as the polarizer rotates synchronously by 5 °, the exposure of the subregion shifts by one subregion. Finally, after completing one exposure cycle, each subregion will be exposed five times, and the total exposure dose is ~5 J/cm2. This is enough to redirect the SD1 molecules and achieve a quasi-continuous space variant orientation. When the LC 8CB is capillarily injected, the predesigned director distribution of the LC is achieved.
References
- de Gennes, P.G.; Prost, J. Physics of Liquid Crystals; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Elshaari, A.W.; Pernice, W.; Srinivasan, K.; Benson, O.; Zwiller, V. Hybrid integrated quantum photonic circuits. Nat. Photonics 2020, 14, 285–298. [Google Scholar] [CrossRef] [PubMed]
- Chuang, I.; Durrer, R.; Turok, N.; Yurke, B. Cosmology in the laboratory: Defect dynamics in liquid crystals. Science 1991, 251, 1336–1342. [Google Scholar] [CrossRef] [PubMed]
- Chiu, C.K.; Teo, J.C.Y.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef]
- Lavrentovich, O.D. Topological defects in dispersed words and worlds around liquid crystals, or liquid crystal drops. Liq. Cryst. 1998, 24, 117–126. [Google Scholar] [CrossRef]
- Collings, P.; Patel, J. Handbook of Liquid Crystal Physics; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Kleman, M.; Lavrentovich, O.D. (Eds.) Soft Matter Physics: An Introduction; Springer: New York, NY, USA, 2003. [Google Scholar]
- Cladis, P.E.; Kleman, M. Non-singular disclinations of strength S = +1 in nematics. J. Phys. France 1972, 33, 591–598. [Google Scholar] [CrossRef]
- Souléab, E.R.; Rey, A.D. Hedgehog defects in mixtures of a nematic liquid crystal and a non-nematogenic component. Soft Matter 2012, 8, 1395–1403. [Google Scholar] [CrossRef]
- Svetec, M.; Slavinec, M. Structural transition of nematic liquid crystal in cylindrical capillary as a result of the annihilation of two point defects. J. Chem. Phys. 2008, 128, 084704. [Google Scholar] [CrossRef]
- Poulin, P.; Cabuil, V.; Weitz, D. Direct measurement of colloidal forces in an anisotropic solvent. Phys. Rev. Lett. 1997, 79, 4862. [Google Scholar] [CrossRef]
- Lubensky, T.C.; Pettey, D.; Currier, N.; Stark, H. Topological defects and interactions in nematic emulsion. Phys. Rev. E 1997, 57, 610. [Google Scholar] [CrossRef]
- Sasaki, Y.; Jampani, V.S.R.; Tanaka, C.; Sakurai, N.; Sakane, S.; Le, K.V.; Araoka, F.; Orihara, H. Large-scale self-organization of reconfigurable topological defect networks in nematic liquid crystals. Nat. Commun. 2016, 7, 13238. [Google Scholar] [CrossRef]
- Sasaki, Y.; Ueda, M.; Le, K.V.; Amano, R.; Sakane, S.; Fujii, S.; Araoka, F.; Orihara, H. Polymer-stabilized micropixelated liquid crystals with tunable optical properties fabricated by double templating. Adv. Mater. 2017, 29, 1703054. [Google Scholar] [CrossRef]
- Migara, L.K.; Song, J.K. Standing wave-mediated molecular reorientation and spontaneous formation of tunable, concentric defect arrays in liquid crystal cells. NPG Asia Mater. 2018, 10, e459. [Google Scholar] [CrossRef]
- Kim, J.H.; Yoneya, M.; Yokoyama, H. Tristable nematic liquid-crystal device using micropatterned surface alignment. Nature 2002, 420, 159–162. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Jiang, M.; Peng, C.H.; Sun, K.; Yaroshchuk, O.; Lavrentovich, O.D.; Wei, Q.H. High-resolution and high-throughput plasmonic photopatterning of complex molecular orientations in liquid crystals. Adv. Mater. 2016, 28, 2353. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.M.; MacLachlan, S.; Atherton, T.J.; Farrell, P.E. Structural landscapes in geometrically frustrated smectics. Phys. Rev. Lett. 2021, 126, 177801. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.B.; Wu, S.B.; Cao, H.M.; Chen, Q.M.; Lu, Y.Q.; Hu, W. Electrically tunable microlens array enabled by polymer-stabilized smectic hierarchical architectures. Adv. Opt. Mater. 2022, 10, 2201015. [Google Scholar] [CrossRef]
- Ma, L.L.; Wu, S.B.; Hu, W.; Liu, C.; Chen, P.; Qian, H.; Wang, Y.D.; Chi, L.F.; Lu, Y.Q. Self-assembled asymmetric microlenses for four-dimensional visual imaging. ACS Nano 2019, 13, 13709–13715. [Google Scholar] [CrossRef]
- Yoon, D.K.; Choi, M.C.; Kim, Y.H.; Kim, M.W.; Lavrentovich, O.D.; Jung, H.T. Internal structure visualization and lithographic use of periodic toroidal holes in liquid crystals. Nat. Mater. 2007, 6, 866–870. [Google Scholar] [CrossRef]
- Kim, Y.H.; Yoon, D.K.; Jeong, H.S.; Kim, J.H.; Yoon, E.K.; Jung, H.T. Fabrication of a superhydrophobic surface from a smectic liquid-crystal defect array. Adv. Funct. Mater. 2009, 19, 3008–3013. [Google Scholar] [CrossRef]
- Gim, M.J.; Beller, D.A.; Yoon, D.K. Morphogenesis of liquid crystal topological defects during the nematic-smectic A phase transition. Nat. Comm. 2017, 8, 15453. [Google Scholar] [CrossRef]
- Wu, S.B.; Wu, J.B.; Cao, H.M.; Lu, Y.Q.; Hu, W. Topological defect guided order evolution across the nematic-smectic phase transition. Phys. Rev. Lett. 2023, 130, 078101. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Ge, S.J.; Duan, W.; Wei, B.Y.; Cui, G.X.; Hu, W.; Lu, Y.Q. Digitalized geometric phases for parallel optical spin and orbital angular momentum encoding. ACS Photonics 2017, 4, 1333–1338. [Google Scholar] [CrossRef]
- Murray, B.S.; Pelcovits, R.A.; Rosenblatt, C. Creating arbitrary arrays of two-dimensional topological defects. Phys. Rev. E 2014, 90, 052501. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.B.; Wu, S.B.; Hu, W. Azimuthal orientation guided topological defect evolution across the nematic-smectic phase transition. Phys. Rev. B 2023, 108, 224107. [Google Scholar] [CrossRef]
- Ravnik, M.; Zumer, S. Landau–de Gennes modelling of nematic liquid crystal colloids. Liq. Cryst. 2009, 36, 1201–1214. [Google Scholar] [CrossRef]
- Akiyama, H.; Kawara, T.; Takada, H.; Takatsu, H.; Chigrinov, V.; Prudnikova, E.; Kozenkov, V.; Kwok, H. Synthesis and properties of azo dye aligning layers for liquid crystal cells. Liq. Cryst. 2002, 29, 1321. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).