Comparison Between InterCriteria and Correlation Analyses over sEMG Data from Arm Movements in the Horizontal Plane
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Protocol
- MT 1: Calm position. The subject was sitting on a chair. He took the position described above and kept it for one minute. This record aimed to follow the reliability of all the signals of the six muscles and the angle.
- MT 2: Evoking of maximal isometric contractions. The examiner passively moved the subject’s upper limb into six different starting positions. A contraction began in the musculature from these positions. The subject opposed the examiner’s controlled resistance, applied in the distal part of the bones. As a result, there was a maximum rise in muscle tension without allowing movement in the joints. Thus, instead of isotonic, the muscle contraction became isometric.
- -
- The first phase was elbow flexion—flexion was limited to the point when the thumb touched the opposite shoulder.
- -
- The second phase was a posture, i.e., the final flexed position was retained.
- -
- The third phase was elbow extension—the arm moved from the flexed position until the arm was extended straight ahead.
- -
- The fourth phase was again a pose—the final extended position was held.
- MT 3: Flexions and extensions in the horizontal plane—active phases lasting 10 s, denoted in the paper as fH10 and eH10.
- MT 4: Flexions and extensions in the horizontal plane—active phases lasting 6 s, denoted here as fH6 and eH6.
- MT 5: Flexions and extensions in the horizontal plane—active phases lasting 2 s, denoted here as fH2 and eH2.
- MT 6: Flexions and extensions in the horizontal plane—active phases lasting 1 s, denoted here as fH1 and eH1.
- MT LOAD 7: Flexions and extensions in the horizontal plane with the attached weight. The active phases lasted 10 s (denoted in this paper as eH10w and eH10w).
- MT LOAD 8: Flexions and extensions in the horizontal plane with the attached weight. The active phases lasted 6 s (eH6w and eH6w).
- MT LOAD 9: Flexions and extensions in the horizontal plane with the attached weight. The active phases lasted 2 s (eH2w and eH2w).
- MT LOAD 10: Flexions and extensions in the horizontal plane with the attached weight. The active phases lasted 1 s (eH1w and eH1w).
2.2. ICrA Analysis
| Obj1 | … | Objk | … | Objn | |
| Cr1 | eCr1,Obj1 | … | eCr1,Objk | … | eCr1,Objn |
| … | … | … | … | … | … |
| Cri | eCri,Obj1 | … | eCri,Objk | … | eCri,Objn |
| … | … | … | … | … | … |
| Crm | eCrm,Obj1 | … | eCrm,Objk | … | eCrm,Objn |
| Cr1 | … | Cri | … | Crm | |
| Cr1 | 〈1, 0〉 | … | … | ||
| … | … | … | … | … | … |
| Cri | … | 〈1, 0〉 | … | ||
| … | … | … | … | … | … |
| Crm | … | … | 〈1, 0〉 |
2.3. Correlation Analyses of Pearson and Spearman
- 0.00 and 0.09, there is a negligible correlation;
- 0.10 and 0.39, there is a weak correlation;
- 0.40 and 0.69, there is a significant correlation;
- 0.70 and 0.89, there is a strong correlation;
- 0.90 and 1.00, there is a very strong correlation.
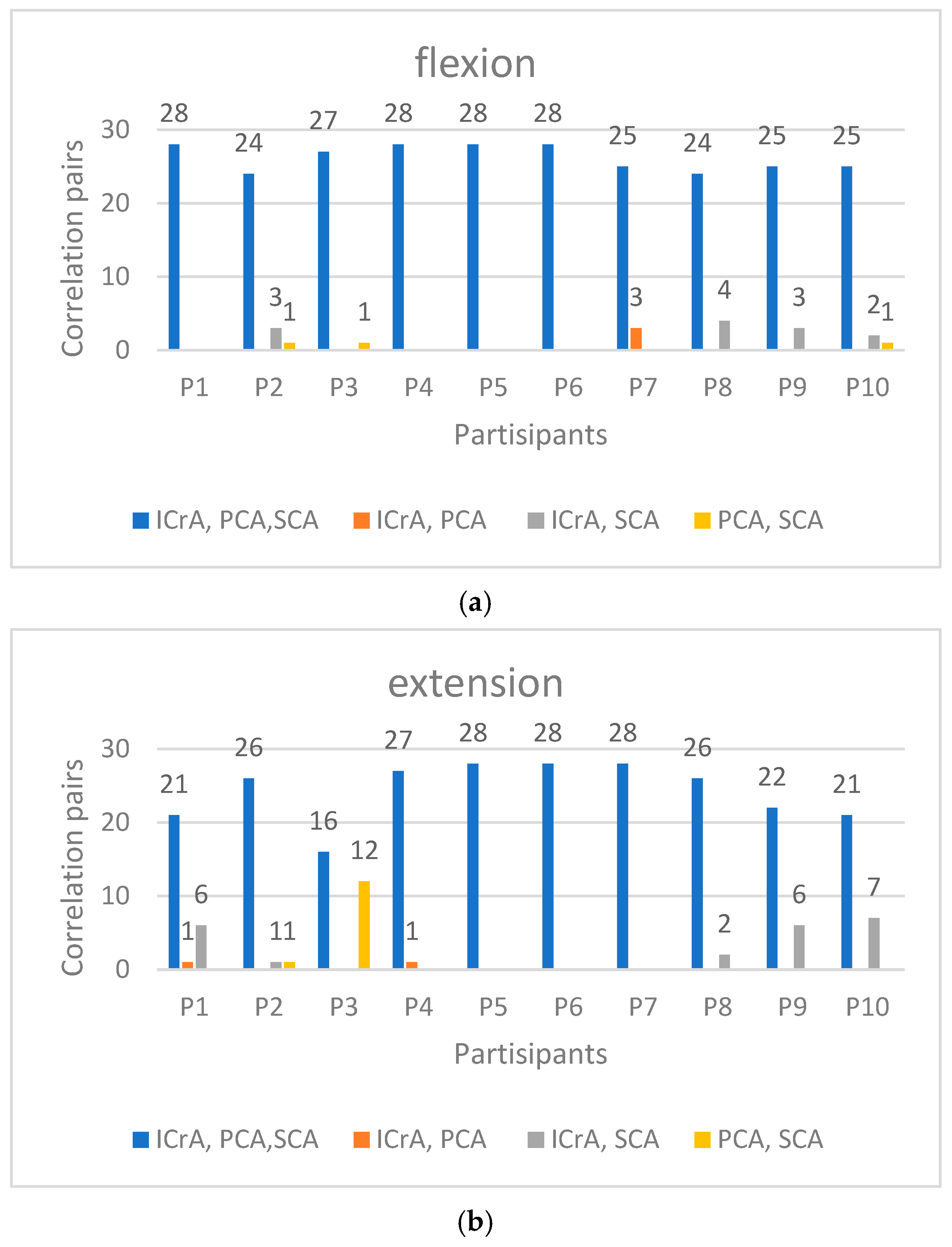
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Atanassov, K.; Mavrov, D.; Atanassova, V. Intercriteria Decision Making: A New Approach for Multicriteria Decision Making. Based on Index Matrices and Intuitionistic Fuzzy Sets. Issues Intuitionistic Fuzzy Sets Gen. Nets 2014, 11, 1–8. [Google Scholar]
- D’Avella, A.; Portone, A.; Fernandez, L.; Lacquaniti, F. Control of Fast-Reaching Movements by Muscle Synergy Combinations. J. Neurosci. 2006, 26, 7791–7810. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, T.S.; Rovai, G.P.; Rymer, W.Z. Strategies for muscle activation during isometric torque generation at the human elbow. J. Neurophysiol. 1989, 62, 1201–1212. [Google Scholar] [CrossRef]
- Jamison, J.C.; Caldwell, G.E. Muscle synergies and isometric torque production: Influence of supination and pronation level on elbow flexion. J. Neurophysiol. 1993, 70, 947–960. [Google Scholar] [CrossRef]
- Angelova, S.; Angelova, M.; Raikova, R. Estimating Surface EMG Activity of Human Upper Arm Muscles Using InterCriteria Analysis. Math. Comput. Appl. 2024, 29, 8. [Google Scholar] [CrossRef]
- Angelova, M.; Angelova, S.; Raikova, R. How to Optimize the Experimental Protocol for Surface EMG Signal Measurements Using the InterCriteria Decision-Making Approach. Appl. Sci. 2024, 14, 5436. [Google Scholar] [CrossRef]
- Antonov, A. Dependencies between Model Indicators of the Basic and the Specialized Speed in Hockey Players Aged 13–14. Trak. J. Sci. 2020, 18, 647–657. [Google Scholar] [CrossRef]
- Ilkova, T.; Petrov, M. InterCriteria Analysis For Evaluation of The Pollution of The Struma River in The Bulgarian Section. Notes IFSs 2016, 22, 120–130. [Google Scholar]
- Georgieva, V.; Angelova, N.; Roeva, O.; Pencheva, T. Intercriteria Analysis of Wastewater Treatment Quality. J. Int. Sci. Publ. Ecol. Saf. 2016, 10, 365–376. [Google Scholar]
- Danailova-Veleva, S.; Doukovska, L.; Vassilev, P. InterCriteria Analysis of the Global Competitiveness Report for the Financial System EU Countries. In Proceedings of the 2022 IEEE 11th International Conference on Intelligent Systems (IS), Warsaw, Poland, 12–14 October 2022; pp. 1–5. [Google Scholar]
- Danailova-Veleva, S.; Doukovska, L.; Dukovski, A. InterCriteria Analysis of the Supervisory Statistic Data for Selected 8 EU Countries During the Period 2020–2021. In Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 793, pp. 129–137. [Google Scholar]
- Angelova, M. InterCriteria Analysis of Control Parameters Relations in Artificial Bee Colony Algorithm. WSEAS Trans. Math. 2019, 18, 123–128. [Google Scholar]
- Fidanova, S.; Roeva, O.; Luque, G.; Paprzycki, M. InterCriteria analysis of different hybrid ant colony optimization algorithms for workforce planning. In Recent Advances in Computational Optimization. Studies in Computational Intelligence; Fidanova, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 838, pp. 61–81. [Google Scholar]
- Mucherino, A.; Fidanova, S.; Ganzha, M. Ant Colony Optimization with environment changes: An application to GPS surveying. In Proceedings of the 2015 Federated Conference on Computer Science and Information Systems (FedCSIS), Lodz, Poland, 13–16 September 2015; Volume 5, pp. 495–500. [Google Scholar]
- Traneva, V.; Tranev, S. The InteCriteria Analysis (ICrA)—An Innovative Tool for Optimization the Evaluation of Human resources. Bulg. El. Sc. J. Econ. Manag. 2021, 1, 82–89. Available online: https://spisanie-su.eu (accessed on 10 October 2024). (In Bulgarian).
- Todinova, S.; Mavrov, D.; Krumova, S.; Marinov, P.; Atanassova, V.; Atanassov, K.; Taneva, S. Blood Plasma Thermograms Dataset Analysis by Means of InterCriteria and Correlation Analyses for the Case of Colorectal Cancer. Int. J. Bioautom. 2016, 20, 115–124. [Google Scholar]
- Krumova, S.; Todinova, S.; Mavrov, D.; Marinov, P.; Atanassova, V.; Atanassov, K.; Taneva, S. Intercriteria Analysis of Calorimetric Data of Blood Serum Proteome. Biochim. Biophys. Acta–Gen. Subj. 2017, 1861, 409–417. [Google Scholar] [CrossRef] [PubMed]
- Vassilev, P.; Todorova, L.; Popov, E.; Georgieva, R.; Slavov, C.; Atanassov, K. Two New Modifications of the InterCriteria Analysis. Comptes Rendus De L’academie Bulg. Des Sci. 2023, 76, 23–34. [Google Scholar] [CrossRef]
- Basmajian, J.V.; De Luca, C.J. Muscles Alive: Their Function Revealed by Electromyography; Williams & Wilkens: Baltimore, MD, USA, 1985. [Google Scholar]
- Enoka, R.M. Neuromechanics of Human Movement, 4th ed.; Human Kinetics: Champaign, IL, USA, 2008. [Google Scholar]
- Farina, D. Interpretation of the surface electromyogram in dynamic contractions. Exerc. Sport Sci. Rev. 2006, 34, 121–127. [Google Scholar] [CrossRef]
- Lamontagne, M. Application of Electromyography in Sport Medicine. In Rehabilitation of Sports Injuries; Puddu, G., Giombini, A., Selvanetti, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Kotov-Smolenskiy, A.M.; Khizhnikova, A.E.; Klochkov, A.S.; Suponeva, N.A.; Piradov, M.A. Surface EMG: Applicability in the Motion Analysis and Opportunities for Practical Rehabilitation. Hum. Physiol. 2021, 47, 237–247. [Google Scholar] [CrossRef]
- Luzheng, B.; Feleke, A.G.; Guan, C. A review on EMG-based motor intention prediction of continuous human upper limb motion for human-robot collaboration. Biomed. Signal Process. Control 2019, 51, 113–127. [Google Scholar]
- Mao, Z.; Hosoya, M.; Maeda, S. Flexible Electrohydrodynamic Fluid-Driven Valveless Water Pump via Immiscible Interface. Cyborg Bionic Syst. 2024, 5, 91. [Google Scholar] [CrossRef]
- Mao, Z.; Bai, X.; Peng, Y.; Shen, Y. Design, modeling, and characteristics of ring-shaped robot actuated by functional fluid. J. Intell. Mater. Syst. Struct. 2024. [Google Scholar] [CrossRef]
- Nogueira-Neto, G.; Scheeren, E.; Krueger, E.; Nohama, P.; Lúcia, V.; Button, S.N. The Influence of Window Length Analysis on the Time and Frequency Domain of Mechanomyographic and Electromyographic Signals of Submaximal Fatiguing Contractions. Open J. Biophys. 2013, 3, 3. [Google Scholar] [CrossRef]
- Kim, K.T.; Park, S.; Lim, T.H.; Lee, S.J. Upper-Limb Electromyogram Classification of Reaching-to-Grasping Tasks Based on Convolutional Neural Networks for Control of a Prosthetic Hand. Front. Neurosci. 2021, 12, 733359. [Google Scholar] [CrossRef] [PubMed]
- Curado, M.R.; Cossio, E.G.; Broetz, D.; Agostini, M.; Cho, W.; Brasil, F.L.; Yilmaz, O.; Liberati, G.; Lepski, G.; Birbaumer, N.; et al. Residual Upper Arm Motor Function Primes Innervation of Paretic Forearm Muscles in Chronic Stroke After Brain-Machine Interface (BMI) Training. PLoS ONE 2015, 10, e0140161. [Google Scholar] [CrossRef] [PubMed]
- de Vargas Ferreira, V.M.; Varoto, R.; Cacho, Ê.W.A.; Cliquet, A. Relationship Between Function, Strength and Electromyography of Upper Extremities of Persons with Tetraplegia. Spinal Cord. 2012, 50, 28–32. [Google Scholar] [CrossRef] [PubMed]
- Fraser, G.D.; Chan, A.D.C.; Green, J.R.; MacIsaac, D.T. Biosignal Quality Analysis of Surface EMG Using a Correlation Coefficient Test for Normality. Interna-Tional Symposium on Medical Measurements and Applications (MeMeA). In Proceedings of the 2013 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Gatineau, QC, Canada, 4–5 May 2013; pp. 196–200. [Google Scholar]
- Aoyama, T.; Kohno, Y. Temporal and Quantitative Variability in Muscle Electrical Activity De-Creases as Dexterous Hand Motor Skills Are Learned. PLoS ONE 2020, 15, e0236254. [Google Scholar] [CrossRef]
- Caillet, A.H.; Phillips, A.T.M.; Modenese, L.; Farina, D. NeuroMechanics: Electrophysiological and computational methods to accurately estimate the neural drive to muscles in humans in vivo. J. Electromyogr. Kinesiol. 2024, 76, 102873. [Google Scholar] [CrossRef]
- Guidance on Assessing and Minimizing Risk in Human Research, and When They Are Prolonged, the Risk Rises. Available online: https://irb.unm.edu/library/documents/guidance/assessing-and-minimizing-risk-in-human-research.pdf (accessed on 18 March 2024).
- Attracting Life Science Investments in Europe. Fourth Edition. 2023. Available online: https://www.europabio.org/wp-content/uploads/2023/10/Life-Science-Attractiveness-2023-October-22-Final.pdf (accessed on 21 March 2024).
- Available online: http://www.seniam.org/ (accessed on 4 October 2024).
- Martinek, R.; Ladrova, M.; Sidikova, M.; Jaros, R.; Behbehani, K.; Kahankova, R.; Kawala-Sterniuk, A. Advanced Bioelectrical Signal Processing Methods: Past, Present, and Future Approach—Part III: Other Biosignals. Sensors 2021, 21, 6064. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Atanassova, V.K.; Gluhchev, G. InterCriteria analysis: Ideas and problems. Notes Int. Fuzzy Sets 2015, 21, 81–88. [Google Scholar]
- Ikonomov, N.; Vassilev, P.; Roeva, O. ICrAData—Software for InterCriteria analysis. Int. J. Bioautom. 2018, 22, 1–10. [Google Scholar] [CrossRef]
- Available online: https://www.aimj.ir/article_125464.html?lang=en (accessed on 20 August 2024).
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- De Luca, C.J.; Mambrito, B. Voluntary control of motor units in the human antagonist muscles: Coactivation and reciprocal activation. J. Neurophysiol. 1987, 58, 525–542. [Google Scholar] [CrossRef]
- Standring, S. GRAY’S Anatomy: The Anatomical Basis of Clinical Practice, 41st ed.; Elsevier Limited: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Park, S.; Marino, H.; Charles, S.; Sternad, D.; Hogan, N. Moving Slowly is Hard for Humans: Limitations of Dynamic Primitives. J. Neurophysiol. 2017, 118, 69–83. [Google Scholar] [CrossRef]


| Flexion | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|
| fH10–fH6 | 0.93 | 0.47 | 1.00 | 1.00 | 1.00 | 1.00 | 0.93 | 1.00 | 0.87 | 0.80 |
| fH10–fH2 | 0.93 | 0.40 | 0.73 | 0.93 | 0.93 | 0.93 | 0.93 | 0.93 | 0.47 | 0.67 |
| fH10–fH1 | 0.93 | 0.33 | 0.67 | 0.93 | 1.00 | 0.93 | 0.87 | 0.93 | 0.80 | 0.80 |
| fH10–fH10w | 0.93 | 0.27 | 0.73 | 1.00 | 0.93 | 0.93 | 0.87 | 1.00 | 0.83 | 0.67 |
| fH10–fH6w | 0.93 | 0.33 | 0.73 | 0.87 | 1.00 | 1.00 | 0.87 | 0.93 | 0.53 | 0.60 |
| fH10–fH2w | 0.93 | 0.40 | 0.73 | 0.87 | 1.00 | 0.93 | 0.87 | 0.93 | 0.80 | 0.67 |
| fH10–fH1w | 0.87 | 0.40 | 0.60 | 0.80 | 1.00 | 0.93 | 0.87 | 0.93 | 0.93 | 0.80 |
| fH6–fH2 | 1.00 | 0.93 | 0.73 | 0.93 | 0.93 | 0.93 | 0.87 | 0.93 | 0.60 | 0.87 |
| fH6–fH1 | 1.00 | 0.87 | 0.67 | 0.93 | 1.00 | 0.93 | 0.80 | 0.93 | 0.93 | 0.87 |
| fH6–fH10w | 1.00 | 0.80 | 0.73 | 1.00 | 0.93 | 0.93 | 0.80 | 1.00 | 0.67 | 0.60 |
| fH6–fH6w | 1.00 | 0.87 | 0.73 | 0.87 | 1.00 | 1.00 | 0.80 | 0.93 | 0.67 | 0.53 |
| fH6–fH2w | 1.00 | 0.80 | 0.73 | 0.87 | 1.00 | 0.93 | 0.80 | 0.93 | 0.93 | 0.60 |
| fH6–fH1w | 0.93 | 0.67 | 0.60 | 0.80 | 1.00 | 0.93 | 0.80 | 0.93 | 0.93 | 0.73 |
| fH2–fH1 | 1.00 | 0.93 | 0.80 | 1.00 | 0.93 | 1.00 | 0.93 | 1.00 | 0.53 | 0.87 |
| fH2–fH10w | 1.00 | 0.87 | 1.00 | 0.93 | 0.87 | 0.87 | 0.93 | 0.93 | 0.93 | 0.60 |
| fH2–fH6w | 1.00 | 0.80 | 1.00 | 0.93 | 0.93 | 0.93 | 0.93 | 1.00 | 0.93 | 0.67 |
| fH2–fH2w | 1.00 | 0.87 | 1.00 | 0.80 | 0.93 | 1.00 | 0.93 | 1.00 | 0.67 | 0.60 |
| fH2–fH1w | 0.93 | 0.73 | 0.87 | 0.87 | 0.93 | 1.00 | 0.93 | 1.00 | 0.53 | 0.73 |
| fH1–fH10w | 1.00 | 0.93 | 0.80 | 0.93 | 0.93 | 0.87 | 1.00 | 0.93 | 0.60 | 0.73 |
| fH1–fH6w | 1.00 | 0.87 | 0.80 | 0.93 | 1.00 | 0.93 | 0.87 | 1.00 | 0.60 | 0.67 |
| fH1–fH2w | 1.00 | 0.93 | 0.80 | 0.80 | 1.00 | 1.00 | 0.87 | 1.00 | 0.87 | 0.73 |
| fH1–fH1w | 0.93 | 0.80 | 0.93 | 0.87 | 1.00 | 1.00 | 1.00 | 1.00 | 0.87 | 0.87 |
| fH10w–fH6w | 1.00 | 0.93 | 1.00 | 0.87 | 0.93 | 0.93 | 0.87 | 0.93 | 0.87 | 0.93 |
| fH10w–fH2w | 1.00 | 0.87 | 1.00 | 0.87 | 0.93 | 0.87 | 0.87 | 0.93 | 0.60 | 1.00 |
| fH10w–fH1w | 0.93 | 0.73 | 0.87 | 0.80 | 0.93 | 0.87 | 1.00 | 0.93 | 0.60 | 0.87 |
| fH6w–fH2w | 1.00 | 0.80 | 1.00 | 0.87 | 1.00 | 0.93 | 1.00 | 1.00 | 0.73 | 0.93 |
| fH6w–fH1w | 0.93 | 0.67 | 0.87 | 0.93 | 1.00 | 0.93 | 0.87 | 1.00 | 0.60 | 0.80 |
| fH2w–fH1w | 0.93 | 0.87 | 0.87 | 0.80 | 1.00 | 1.00 | 0.87 | 1.00 | 0.87 | 0.87 |
| strong positive consonance | strong dissonance | |||||||||
| positive consonance | dissonance | |||||||||
| weak positive consonance | weak dissonance | |||||||||
| pair in positive consonance | ||||||||||
| Extension | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|
| eH10–eH6 | 1.00 | 0.87 | 1.00 | 1.00 | 0.93 | 1.00 | 0.93 | 0.93 | 0.87 | 1.00 |
| eH10–eH2 | 0.93 | 0.87 | 0.73 | 1.00 | 1.00 | 1.00 | 1.00 | 0.93 | 0.60 | 0.87 |
| eH10–eH1 | 0.93 | 0.47 | 0.73 | 1.00 | 1.00 | 1.00 | 0.87 | 0.93 | 0.80 | 0.93 |
| eH10–eH10w | 0.80 | 0.73 | 0.73 | 1.00 | 0.93 | 1.00 | 0.87 | 1.00 | 1.00 | 0.80 |
| eH10–eH6w | 1.00 | 0.80 | 0.73 | 0.93 | 0.93 | 1.00 | 0.87 | 0.93 | 0.60 | 0.73 |
| eH10–eH2w | 1.00 | 0.67 | 0.73 | 1.00 | 0.93 | 0.93 | 1.00 | 0.87 | 0.93 | 0.87 |
| eH10–eH1w | 0.93 | 0.60 | 0.73 | 0.87 | 0.87 | 1.00 | 0.93 | 0.93 | 0.93 | 0.93 |
| eH6–eH2 | 0.93 | 0.87 | 0.73 | 1.00 | 0.93 | 1.00 | 0.93 | 1.00 | 0.60 | 0.87 |
| eH6–eH1 | 0.93 | 0.60 | 0.73 | 1.00 | 0.93 | 1.00 | 0.93 | 1.00 | 0.80 | 0.93 |
| eH6–eH10w | 0.80 | 0.87 | 0.73 | 1.00 | 0.87 | 1.00 | 0.93 | 0.93 | 0.87 | 0.80 |
| eH6–eH6w | 1.00 | 0.80 | 0.73 | 0.93 | 0.87 | 1.00 | 0.93 | 0.87 | 0.73 | 0.73 |
| eH6–eH2w | 1.00 | 0.80 | 0.73 | 1.00 | 0.87 | 0.93 | 0.93 | 0.93 | 0.93 | 0.87 |
| eH6–eH1w | 0.93 | 0.73 | 0.73 | 0.87 | 0.80 | 1.00 | 0.87 | 1.00 | 0.93 | 0.93 |
| eH2–eH1 | 1.00 | 0.60 | 1.00 | 1.00 | 1.00 | 1.00 | 0.87 | 1.00 | 0.67 | 0.93 |
| eH2–eH10w | 0.73 | 0.73 | 1.00 | 1.00 | 0.93 | 1.00 | 0.87 | 0.93 | 0.60 | 0.67 |
| eH2–eH6w | 0.93 | 0.80 | 1.00 | 0.93 | 0.93 | 1.00 | 0.87 | 0.87 | 0.73 | 0.60 |
| eH2–eH2w | 0.93 | 0.80 | 1.00 | 1.00 | 0.93 | 0.93 | 1.00 | 0.93 | 0.67 | 0.87 |
| eH2–eH1w | 0.87 | 0.73 | 1.00 | 0.87 | 0.87 | 1.00 | 0.93 | 1.00 | 0.67 | 0.93 |
| eH1–eH10w | 0.73 | 0.73 | 1.00 | 1.00 | 0.93 | 1.00 | 0.87 | 0.93 | 0.80 | 0.73 |
| eH1–eH6w | 0.93 | 0.67 | 1.00 | 0.93 | 0.93 | 1.00 | 0.87 | 0.87 | 0.67 | 0.67 |
| eH1–eH2w | 0.93 | 0.80 | 1.00 | 1.00 | 0.93 | 0.93 | 0.87 | 0.93 | 0.87 | 0.93 |
| eH1–eH1w | 0.87 | 0.87 | 1.00 | 0.87 | 0.87 | 1.00 | 0.80 | 1.00 | 0.87 | 1.00 |
| eH10w–eH6w | 0.80 | 0.93 | 1.00 | 0.93 | 0.87 | 1.00 | 1.00 | 0.93 | 0.60 | 0.93 |
| eH10w–eH2w | 0.80 | 0.93 | 1.00 | 1.00 | 0.87 | 0.93 | 0.87 | 0.87 | 0.93 | 0.67 |
| eH10w–eH1w | 0.73 | 0.87 | 1.00 | 0.87 | 0.93 | 1.00 | 0.80 | 0.93 | 0.93 | 0.73 |
| eH6w–eH2w | 1.00 | 0.87 | 1.00 | 0.93 | 1.00 | 0.93 | 0.87 | 0.80 | 0.67 | 0.73 |
| eH6w–eH1w | 0.93 | 0.80 | 1.00 | 0.80 | 0.93 | 1.00 | 0.80 | 0.87 | 0.67 | 0.67 |
| eH2w–eH1w | 0.93 | 0.93 | 1.00 | 0.87 | 0.93 | 0.93 | 0.93 | 0.93 | 1.00 | 0.93 |
| strong positive consonance | strong dissonance | |||||||||
| positive consonance | dissonance | |||||||||
| weak positive consonance | weak dissonance | |||||||||
| pair in positive consonance | ||||||||||
| Flexion | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|
| fH10–fH6 | 1.00 | 0.43 | 0.81 | 0.98 | 1.00 | 1.00 | 0.99 | 0.97 | 0.96 | 0.74 |
| fH10–fH2 | 0.99 | 0.27 | 0.36 | 0.99 | 0.98 | 0.96 | 1.00 | 0.84 | −0.07 | 0.70 |
| fH10–fH1 | 0.99 | −0.02 | 0.39 | 0.99 | 0.99 | 0.90 | 0.99 | 0.66 | 0.68 | 0.90 |
| fH10–fH10w | 0.99 | 0.42 | 0.44 | 0.95 | 0.94 | 0.99 | 0.98 | 0.93 | 0.43 | 0.36 |
| fH10–fH6w | 0.98 | 0.28 | 0.44 | 0.93 | 0.96 | 0.90 | 0.98 | 0.93 | 0.60 | 0.00 |
| fH10–fH2w | 0.98 | −0.21 | 0.44 | 0.78 | 0.99 | 0.87 | 0.99 | 0.56 | 0.94 | 0.42 |
| fH10–fH1w | 0.92 | −0.16 | 0.38 | 0.91 | 0.99 | 0.86 | 0.98 | 0.66 | 0.94 | 0.67 |
| fH6–fH2 | 1.00 | 0.97 | −0.22 | 0.99 | 0.99 | 0.97 | 1.00 | 0.91 | −0.08 | 0.90 |
| fH6–fH1 | 0.99 | 0.77 | −0.18 | 0.99 | 0.99 | 0.92 | 0.98 | 0.77 | 0.83 | 0.68 |
| fH6–fH10w | 0.99 | 0.97 | −0.16 | 0.97 | 0.90 | 0.99 | 0.99 | 0.98 | 0.41 | 0.21 |
| fH6–fH6w | 0.98 | 0.96 | −0.15 | 0.95 | 0.93 | 0.92 | 0.99 | 0.93 | 0.67 | −0.07 |
| fH6–fH2w | 0.99 | 0.59 | −0.15 | 0.81 | 0.97 | 0.89 | 1.00 | 0.67 | 0.99 | 0.38 |
| fH6–fH1w | 0.92 | 0.56 | −0.20 | 0.92 | 0.97 | 0.89 | 0.97 | 0.78 | 0.93 | 0.51 |
| fH2–fH1 | 0.99 | 0.88 | 0.96 | 0.97 | 0.98 | 0.98 | 0.99 | 0.96 | −0.38 | 0.76 |
| fH2–fH10w | 1.00 | 0.91 | 0.97 | 0.98 | 0.93 | 0.98 | 1.00 | 0.98 | 0.87 | −0.02 |
| fH2–fH6w | 1.00 | 0.94 | 1.00 | 0.98 | 0.93 | 0.98 | 0.99 | 0.99 | 0.66 | −0.17 |
| fH2–fH2w | 1.00 | 0.69 | 0.97 | 0.88 | 0.97 | 0.96 | 1.00 | 0.91 | −0.18 | 0.21 |
| fH2–fH1w | 0.95 | 0.68 | 0.96 | 0.95 | 0.97 | 0.95 | 0.98 | 0.96 | −0.27 | 0.46 |
| fH1–fH10w | 0.98 | 0.75 | 0.96 | 0.95 | 0.88 | 0.95 | 0.98 | 0.88 | 0.20 | 0.43 |
| fH1–fH6w | 0.98 | 0.81 | 0.96 | 0.94 | 0.93 | 0.99 | 0.97 | 0.94 | 0.40 | 0.25 |
| fH1–fH2w | 0.99 | 0.92 | 0.97 | 0.80 | 0.97 | 0.99 | 0.98 | 0.99 | 0.86 | 0.58 |
| fH1–fH1w | 0.93 | 0.90 | 1.00 | 0.95 | 0.97 | 0.98 | 1.00 | 1.00 | 0.77 | 0.84 |
| fH10w–fH6w | 1.00 | 0.99 | 0.98 | 0.98 | 0.96 | 0.96 | 1.00 | 0.98 | 0.90 | 0.88 |
| fH10w–fH2w | 0.99 | 0.66 | 1.00 | 0.92 | 0.97 | 0.93 | 1.00 | 0.81 | 0.30 | 0.96 |
| fH10w–fH1w | 0.96 | 0.60 | 0.98 | 0.94 | 0.94 | 0.94 | 0.98 | 0.89 | 0.24 | 0.83 |
| fH6w–fH2w | 1.00 | 0.73 | 0.98 | 0.93 | 0.99 | 1.00 | 1.00 | 0.88 | 0.60 | 0.88 |
| fH6w–fH1w | 0.98 | 0.66 | 0.96 | 0.97 | 0.99 | 1.00 | 0.96 | 0.95 | 0.43 | 0.72 |
| fH2w–fH1w | 0.96 | 0.96 | 0.98 | 0.86 | 0.99 | 1.00 | 0.97 | 0.98 | 0.92 | 0.93 |
| perfect correlation | significant correlation | |||||||||
| very strong correlation | weak correlation | |||||||||
| strong correlation | negligible correlation | |||||||||
| pair in strong correlation | no correlation | |||||||||
| Extension | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|
| eH10–eH6 | 0.99 | 0.95 | 0.99 | 1.00 | 0.97 | 0.98 | 0.99 | 0.99 | 0.97 | 0.97 |
| eH10–eH2 | 0.85 | 0.95 | 0.17 | 0.98 | 0.98 | 0.98 | 1.00 | 0.94 | 0.16 | 0.92 |
| eH10–eH1 | 0.77 | 0.17 | 0.12 | 0.99 | 0.98 | 0.96 | 0.98 | 0.88 | 0.86 | 0.92 |
| eH10–eH10w | 1.00 | 0.89 | 0.17 | 0.98 | 0.98 | 0.99 | 0.98 | 0.95 | 1.00 | 0.82 |
| eH10–eH6w | 1.00 | 0.78 | 0.18 | 0.96 | 0.99 | 0.99 | 0.99 | 0.90 | 0.88 | 0.84 |
| eH10–eH2w | 0.81 | 0.63 | 0.19 | 0.89 | 0.99 | 0.93 | 1.00 | 0.80 | 0.95 | 0.85 |
| eH10–eH1w | 0.65 | 0.34 | 0.23 | 0.94 | 0.96 | 0.99 | 1.00 | 0.90 | 0.94 | 0.90 |
| eH6–eH2 | 0.87 | 0.97 | 0.08 | 0.98 | 0.99 | 1.00 | 0.99 | 0.97 | 0.19 | 0.99 |
| eH6–eH1 | 0.81 | 0.39 | 0.04 | 0.99 | 0.99 | 0.99 | 1.00 | 0.93 | 0.94 | 0.99 |
| eH6–eH10w | 0.98 | 0.97 | 0.07 | 0.99 | 0.92 | 0.99 | 1.00 | 0.94 | 0.98 | 0.73 |
| eH6–eH6w | 0.99 | 0.90 | 0.09 | 0.97 | 0.95 | 0.99 | 1.00 | 0.86 | 0.93 | 0.74 |
| eH6–eH2w | 0.82 | 0.82 | 0.01 | 0.89 | 0.94 | 0.97 | 0.99 | 0.87 | 0.99 | 0.82 |
| eH6–eH1w | 0.67 | 0.60 | 0.14 | 0.95 | 0.90 | 0.99 | 0.99 | 0.95 | 0.99 | 0.83 |
| eH2–eH1 | 0.99 | 0.35 | 0.98 | 0.94 | 1.00 | 1.00 | 0.98 | 0.98 | 0.26 | 1.00 |
| eH2–eH10w | 0.80 | 0.93 | 0.96 | 0.97 | 0.94 | 0.98 | 0.98 | 0.84 | 0.11 | 0.66 |
| eH2–eH6w | 0.84 | 0.85 | 0.97 | 0.98 | 0.97 | 0.98 | 0.99 | 0.73 | 0.54 | 0.66 |
| eH2–eH2w | 0.99 | 0.75 | 0.95 | 0.96 | 0.95 | 0.95 | 1.00 | 0.90 | 0.20 | 0.79 |
| eH2–eH1w | 0.94 | 0.54 | 0.98 | 0.89 | 0.94 | 0.99 | 1.00 | 0.98 | 0.21 | 0.77 |
| eH1–eH10w | 0.72 | 0.51 | 0.99 | 0.98 | 0.96 | 0.97 | 0.99 | 0.79 | 0.87 | 0.69 |
| eH1–eH6w | 0.76 | 0.61 | 0.99 | 0.93 | 0.96 | 0.97 | 0.99 | 0.65 | 0.92 | 0.70 |
| eH1–eH2w | 0.98 | 0.77 | 0.98 | 0.83 | 0.95 | 0.96 | 0.99 | 0.95 | 0.98 | 0.83 |
| eH1–eH1w | 0.96 | 0.87 | 0.99 | 0.95 | 0.94 | 0.98 | 0.98 | 0.99 | 0.98 | 0.81 |
| eH10w–eH6w | 1.00 | 0.98 | 1.00 | 0.98 | 0.95 | 1.00 | 1.00 | 0.97 | 0.86 | 0.99 |
| eH10w–eH2w | 0.77 | 0.91 | 1.00 | 0.90 | 0.97 | 0.97 | 0.99 | 0.81 | 0.95 | 0.91 |
| eH10w–eH1w | 0.59 | 0.72 | 0.97 | 0.95 | 0.98 | 1.00 | 0.98 | 0.84 | 0.95 | 0.94 |
| eH6w–eH2w | 0.81 | 0.95 | 1.00 | 0.96 | 0.99 | 0.97 | 0.99 | 0.65 | 0.93 | 0.93 |
| eH6w–eH1w | 0.65 | 0.79 | 0.98 | 0.90 | 0.96 | 1.00 | 0.99 | 0.71 | 0.93 | 0.97 |
| eH2w–eH1w | 0.97 | 0.94 | 0.97 | 0.77 | 0.98 | 0.96 | 1.00 | 0.96 | 1.00 | 0.98 |
| perfect correlation | significant correlation | |||||||||
| very strong correlation | weak correlation | |||||||||
| strong correlation | negligible correlation | |||||||||
| pair in strong correlation | no correlation | |||||||||
| Flexion | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|
| fH10–fH6 | 0.94 | −0.20 | 1.00 | 1.00 | 1.00 | 1.00 | 0.94 | 1.00 | 0.83 | 0.77 |
| fH10–fH2 | 0.94 | −0.26 | 0.43 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | −0.09 | 0.43 |
| fH10–fH1 | 0.94 | −0.37 | 0.31 | 0.94 | 1.00 | 0.94 | 0.83 | 0.94 | 0.77 | 0.77 |
| fH10–fH10w | 0.94 | −0.43 | 0.43 | 1.00 | 0.94 | 0.94 | 0.83 | 1.00 | −0.03 | 0.31 |
| fH10–fH6w | 0.94 | −0.37 | 0.43 | 0.89 | 1.00 | 1.00 | 0.89 | 0.94 | 0.20 | 0.09 |
| fH10–fH2w | 0.94 | −0.31 | 0.43 | 0.83 | 1.00 | 0.94 | 0.89 | 0.94 | 0.77 | 0.31 |
| fH10–fH1w | 0.89 | −0.31 | 0.09 | 0.71 | 1.00 | 0.94 | 0.83 | 0.94 | 0.94 | 0.66 |
| fH6–fH2 | 1.00 | 0.94 | 0.43 | 0.94 | 0.94 | 0.94 | 0.83 | 0.94 | 0.09 | 0.83 |
| fH6–fH1 | 1.00 | 0.83 | 0.31 | 0.94 | 1.00 | 0.94 | 0.66 | 0.94 | 0.94 | 0.89 |
| fH6–fH10w | 1.00 | 0.77 | 0.43 | 1.00 | 0.94 | 0.94 | 0.66 | 1.00 | 0.14 | 0.31 |
| fH6–fH6w | 1.00 | 0.83 | 0.43 | 0.89 | 1.00 | 1.00 | 0.77 | 0.94 | 0.37 | 0.20 |
| fH6–fH2w | 1.00 | 0.66 | 0.43 | 0.83 | 1.00 | 0.94 | 0.77 | 0.94 | 0.94 | 0.31 |
| fH6–fH1w | 0.94 | 0.37 | 0.09 | 0.71 | 1.00 | 0.94 | 0.66 | 0.94 | 0.94 | 0.54 |
| fH2–fH1 | 1.00 | 0.94 | 0.77 | 1.00 | 0.94 | 1.00 | 0.94 | 1.00 | 0.03 | 0.89 |
| fH2–fH10w | 1.00 | 0.83 | 1.00 | 0.94 | 0.89 | 0.89 | 0.94 | 0.94 | 0.94 | 0.43 |
| fH2–fH6w | 1.00 | 0.77 | 1.00 | 0.94 | 0.94 | 0.94 | 0.94 | 1.00 | 0.94 | 0.49 |
| fH2–fH2w | 1.00 | 0.83 | 1.00 | 0.71 | 0.94 | 1.00 | 0.94 | 1.00 | 0.14 | 0.43 |
| fH2–fH1w | 0.94 | 0.60 | 0.83 | 0.83 | 0.94 | 1.00 | 0.94 | 1.00 | −0.03 | 0.60 |
| fH1–fH10w | 1.00 | 0.94 | 0.77 | 0.94 | 0.94 | 0.89 | 1.00 | 0.94 | 0.09 | 0.54 |
| fH1–fH6w | 1.00 | 0.83 | 0.77 | 0.94 | 1.00 | 0.94 | 0.89 | 1.00 | 0.26 | 0.49 |
| fH1–fH2w | 1.00 | 0.94 | 0.77 | 0.71 | 1.00 | 1.00 | 0.89 | 1.00 | 0.89 | 0.54 |
| fH1–fH1w | 0.94 | 0.71 | 0.94 | 0.83 | 1.00 | 1.00 | 1.00 | 1.00 | 0.89 | 0.83 |
| fH10w–fH6w | 1.00 | 0.94 | 1.00 | 0.89 | 0.94 | 0.94 | 0.89 | 0.94 | 0.89 | 0.94 |
| fH10w–fH2w | 1.00 | 0.89 | 1.00 | 0.83 | 0.94 | 0.89 | 0.89 | 0.94 | 0.09 | 1.00 |
| fH10w–fH1w | 0.94 | 0.60 | 0.83 | 0.71 | 0.94 | 0.89 | 1.00 | 0.94 | 0.09 | 0.83 |
| fH6w–fH2w | 1.00 | 0.71 | 1.00 | 0.83 | 1.00 | 0.94 | 1.00 | 1.00 | 0.43 | 0.94 |
| fH6w–fH1w | 0.94 | 0.37 | 0.83 | 0.94 | 1.00 | 0.94 | 0.89 | 1.00 | 0.26 | 0.77 |
| fH2w–fH1w | 0.94 | 0.89 | 0.83 | 0.77 | 1.00 | 1.00 | 0.89 | 1.00 | 0.83 | 0.83 |
| perfect correlation | significant correlation | |||||||||
| very strong correlation | weak correlation | |||||||||
| strong correlation | negligible correlation | |||||||||
| pair in strong correlation | ||||||||||
| Extension | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|
| eH10–eH6 | 1.00 | 0.83 | 1.00 | 1.00 | 0.94 | 1.00 | 0.94 | 0.94 | 0.89 | 1.00 |
| eH10–eH2 | 0.94 | 0.83 | 0.43 | 1.00 | 1.00 | 1.00 | 1.00 | 0.94 | 0.09 | 0.89 |
| eH10–eH1 | 0.94 | −0.14 | 0.43 | 1.00 | 1.00 | 1.00 | 0.89 | 0.94 | 0.77 | 0.94 |
| eH10–eH10w | 0.77 | 0.60 | 0.43 | 1.00 | 0.94 | 1.00 | 0.89 | 1.00 | 1.00 | 0.77 |
| eH10–eH6w | 1.00 | 0.71 | 0.43 | 0.94 | 0.94 | 1.00 | 0.89 | 0.94 | 0.43 | 0.66 |
| eH10–eH2w | 1.00 | 0.49 | 0.43 | 1.00 | 0.94 | 0.94 | 1.00 | 0.83 | 0.94 | 0.83 |
| eH10–eH1w | 0.94 | 0.26 | 0.43 | 0.83 | 0.89 | 1.00 | 0.94 | 0.94 | 0.94 | 0.94 |
| eH6–eH2 | 0.94 | 0.89 | 0.43 | 1.00 | 0.94 | 1.00 | 0.94 | 1.00 | 0.09 | 0.89 |
| eH6–eH1 | 0.94 | 0.31 | 0.43 | 1.00 | 0.94 | 1.00 | 0.94 | 1.00 | 0.66 | 0.94 |
| eH6–eH10w | 0.77 | 0.83 | 0.43 | 1.00 | 0.89 | 1.00 | 0.94 | 0.94 | 0.89 | 0.77 |
| eH6–eH6w | 1.00 | 0.77 | 0.43 | 0.94 | 0.83 | 1.00 | 0.94 | 0.83 | 0.60 | 0.66 |
| eH6–eH2w | 1.00 | 0.77 | 0.43 | 1.00 | 0.83 | 0.94 | 0.94 | 0.94 | 0.94 | 0.83 |
| eH6–eH1w | 0.94 | 0.66 | 0.43 | 0.83 | 0.77 | 1.00 | 0.89 | 1.00 | 0.94 | 0.94 |
| eH2–eH1 | 1.00 | 0.31 | 1.00 | 1.00 | 1.00 | 1.00 | 0.89 | 1.00 | 0.31 | 0.94 |
| eH2–eH10w | 0.60 | 0.71 | 1.00 | 1.00 | 0.94 | 1.00 | 0.89 | 0.94 | 0.09 | 0.49 |
| eH2–eH6w | 0.94 | 0.77 | 1.00 | 0.94 | 0.94 | 1.00 | 0.89 | 0.83 | 0.66 | 0.37 |
| eH2–eH2w | 0.94 | 0.77 | 1.00 | 1.00 | 0.94 | 0.94 | 1.00 | 0.94 | 0.14 | 0.83 |
| eH2–eH1w | 0.89 | 0.60 | 1.00 | 0.83 | 0.89 | 1.00 | 0.94 | 1.00 | 0.14 | 0.94 |
| eH1–eH10w | 0.60 | 0.60 | 1.00 | 1.00 | 0.94 | 1.00 | 0.89 | 0.94 | 0.77 | 0.66 |
| eH1–eH6w | 0.94 | 0.43 | 1.00 | 0.94 | 0.94 | 1.00 | 0.89 | 0.83 | 0.49 | 0.60 |
| eH1–eH2w | 0.94 | 0.77 | 1.00 | 1.00 | 0.94 | 0.94 | 0.89 | 0.94 | 0.83 | 0.94 |
| eH1–eH1w | 0.89 | 0.83 | 1.00 | 0.83 | 0.89 | 1.00 | 0.77 | 1.00 | 0.83 | 1.00 |
| eH10w–eH6w | 0.77 | 0.94 | 1.00 | 0.94 | 0.89 | 1.00 | 1.00 | 0.94 | 0.43 | 0.94 |
| eH10w–eH2w | 0.77 | 0.94 | 1.00 | 1.00 | 0.89 | 0.94 | 0.89 | 0.83 | 0.94 | 0.60 |
| eH10w–eH1w | 0.60 | 0.89 | 1.00 | 0.83 | 0.94 | 1.00 | 0.77 | 0.94 | 0.94 | 0.66 |
| eH6w–eH2w | 1.00 | 0.89 | 1.00 | 0.94 | 1.00 | 0.94 | 0.89 | 0.77 | 0.49 | 0.66 |
| eH6w–eH1w | 0.94 | 0.77 | 1.00 | 0.66 | 0.94 | 1.00 | 0.77 | 0.83 | 0.49 | 0.60 |
| eH2w–eH1w | 0.94 | 0.94 | 1.00 | 0.83 | 0.94 | 0.94 | 0.94 | 0.94 | 1.00 | 0.94 |
| perfect correlation | significant correlation | |||||||||
| very strong correlation | weak correlation | |||||||||
| strong correlation | negligible correlation | |||||||||
| pair in strong correlation | ||||||||||
| ICrA | Pearson’s CA | Spearman’s CA | |||
|---|---|---|---|---|---|
| Flexion | Extension | Flexion | Extension | Flexion | Extension |
| fH1–fH1w fH10w–fH6w fH2w–fH1w | eH10–eH6 eH1–eH2w eH1–eH1w eH2w–eH1w | fH1–fH1w fH10w–fH6w fH2w–fH1w | eH10–eH6 eH1–eH2w eH1–eH1w eH10w–eH6w eH10w–eH2w eH2w–eH1w | fH1–fH1w fH10w–fH6w fH2w–fH1w | eH10–eH6 eH1–eH2w eH1–eH1w eH2w–eH1w |
| Full EP | Runtime [min] | I Optimized EP | Runtime [min] | II Optimized EP | Runtime [min] |
|---|---|---|---|---|---|
| MT 1 | 1 | MT 1 | 1 | MT 1 | 1 |
| MT 2 | 1 | MT 2 | 1 | MT 2 | 1 |
| MT 3 | 1 | MT 3 | 1 | MT 3 | 1 |
| MT 4 | 1 | MT 4 | 1 | MT 4 | 1 |
| MT 5 | 1 | MT 5 | 1 | MT 5 | 1 |
| MT 6 | 1 | MT 6 | 1 | - | - |
| MT LOAD 7 | 1 | MT LOAD 7 | 1 | MT LOAD 7 | 1 |
| MT LOAD 8 | 1 | MT LOAD 8 | 1 | MT LOAD 8 | 1 |
| MT LOAD 9 | 1 | MT LOAD 9 | 1 | - | - |
| MT LOAD 10 | 1 | - | - | MT LOAD 10 | 1 |
| Total runtime, [min] | 10 | Total runtime, [min] | 9 | Total runtime, [min] | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angelova, M.; Raikova, R.; Angelova, S. Comparison Between InterCriteria and Correlation Analyses over sEMG Data from Arm Movements in the Horizontal Plane. Appl. Sci. 2024, 14, 9864. https://doi.org/10.3390/app14219864
Angelova M, Raikova R, Angelova S. Comparison Between InterCriteria and Correlation Analyses over sEMG Data from Arm Movements in the Horizontal Plane. Applied Sciences. 2024; 14(21):9864. https://doi.org/10.3390/app14219864
Chicago/Turabian StyleAngelova, Maria, Rositsa Raikova, and Silvija Angelova. 2024. "Comparison Between InterCriteria and Correlation Analyses over sEMG Data from Arm Movements in the Horizontal Plane" Applied Sciences 14, no. 21: 9864. https://doi.org/10.3390/app14219864
APA StyleAngelova, M., Raikova, R., & Angelova, S. (2024). Comparison Between InterCriteria and Correlation Analyses over sEMG Data from Arm Movements in the Horizontal Plane. Applied Sciences, 14(21), 9864. https://doi.org/10.3390/app14219864







