Irregular Eccentric Wellbore Cementing: An Equivalent Circulation Density Calculation and Influencing Factors Analysis
Abstract
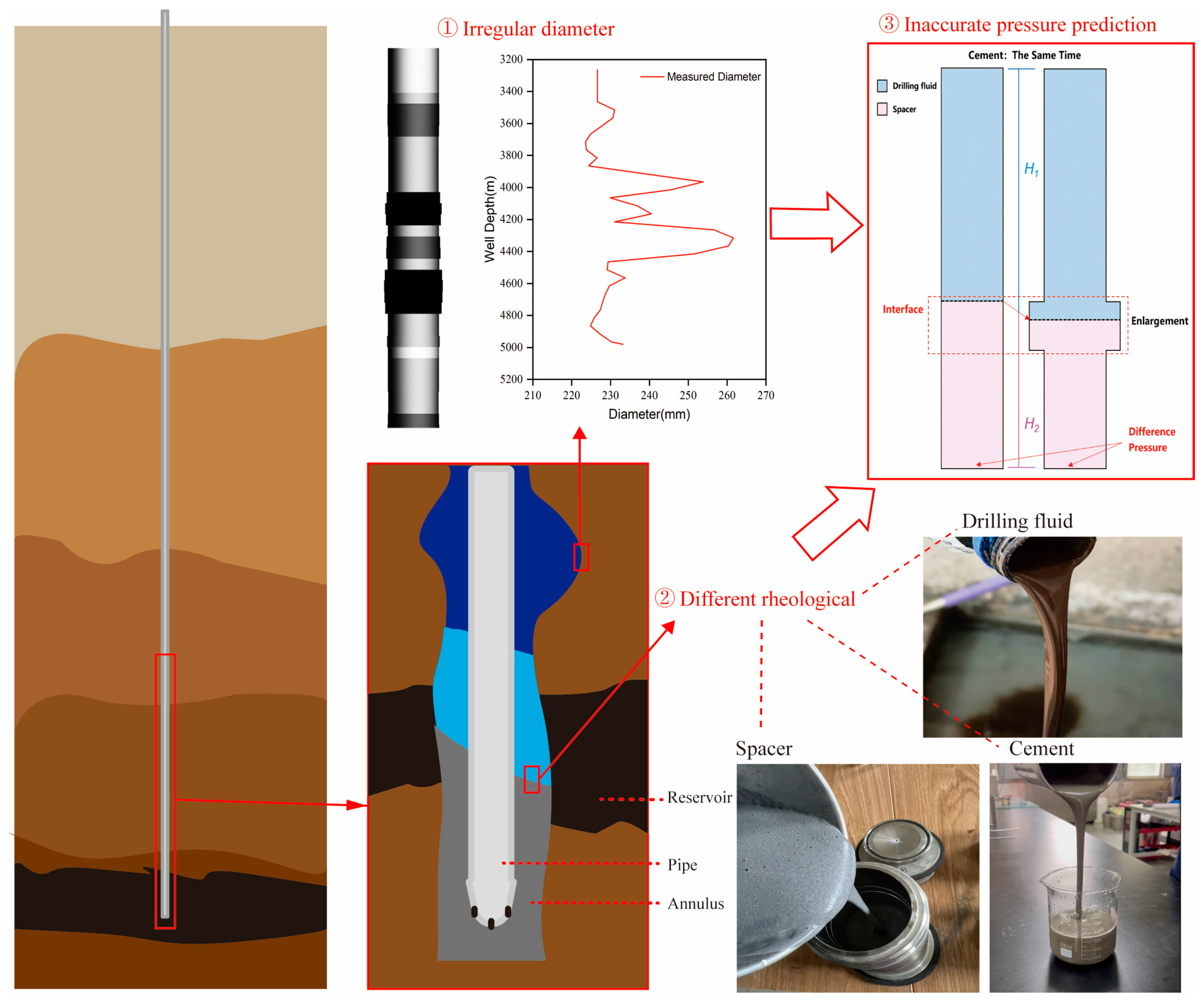
1. Introduction
2. Study on the Irregular Eccentric Shaft Model
2.1. Physical Parameters of the Wellbore Model
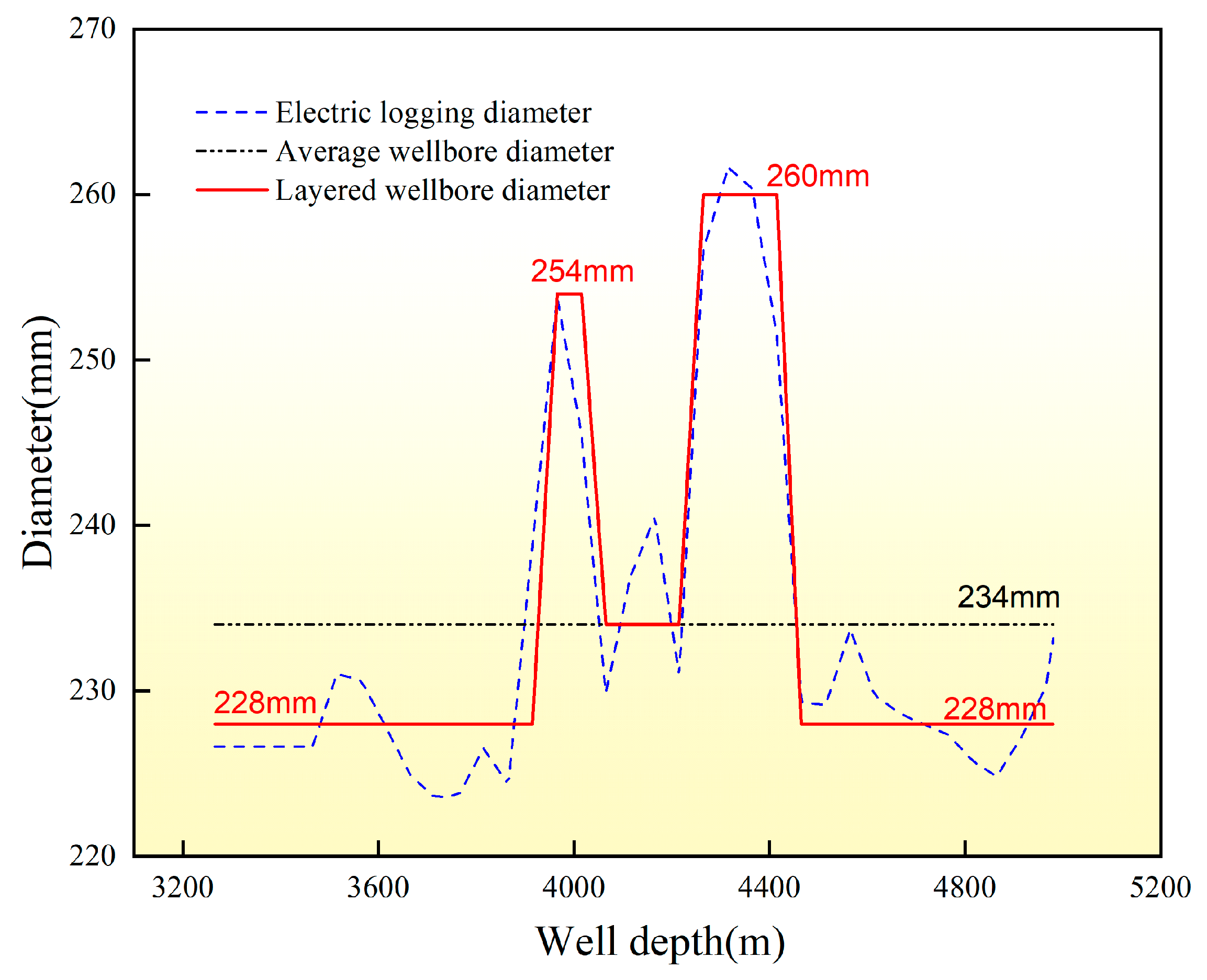
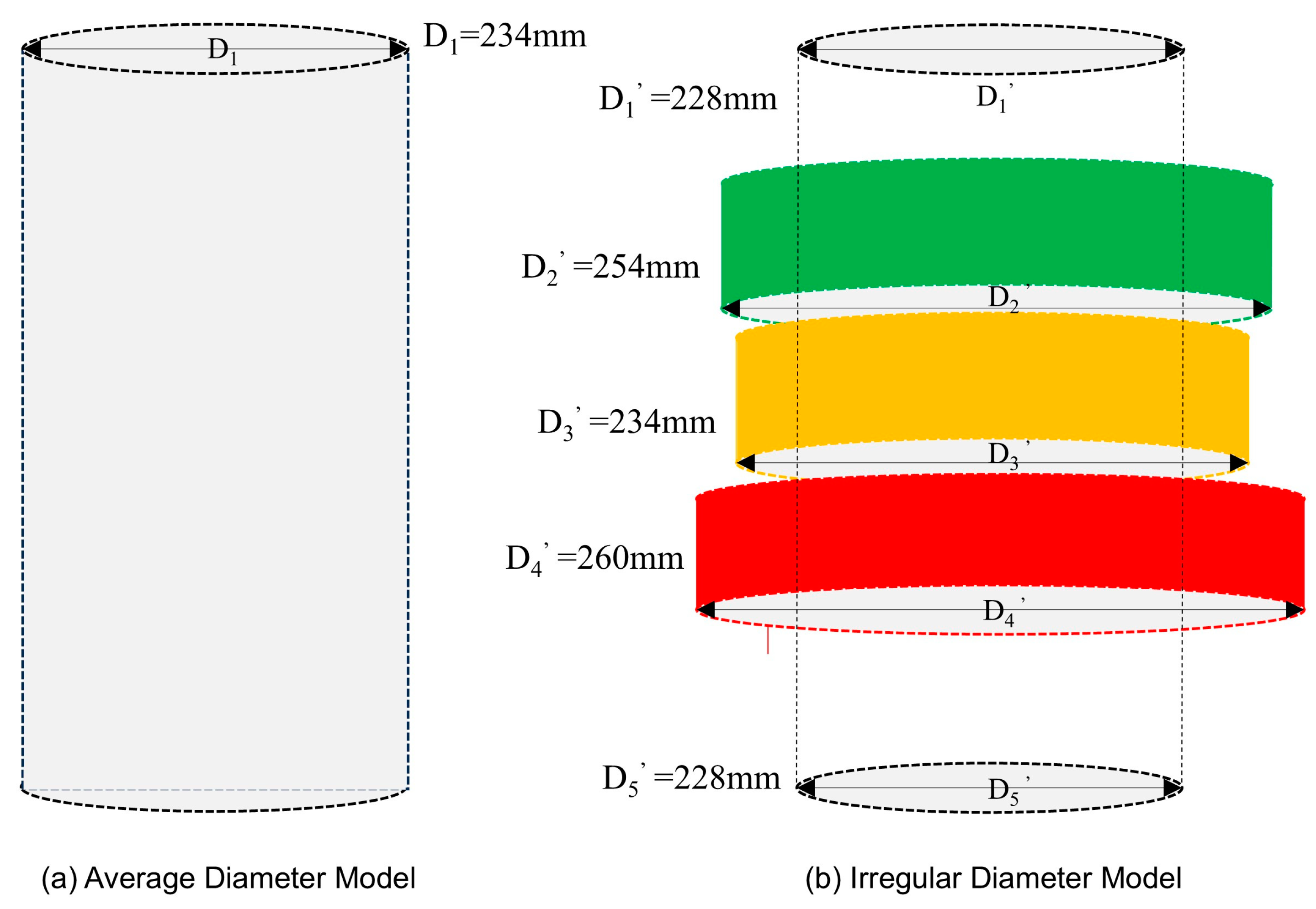
2.1.1. Well Diameter
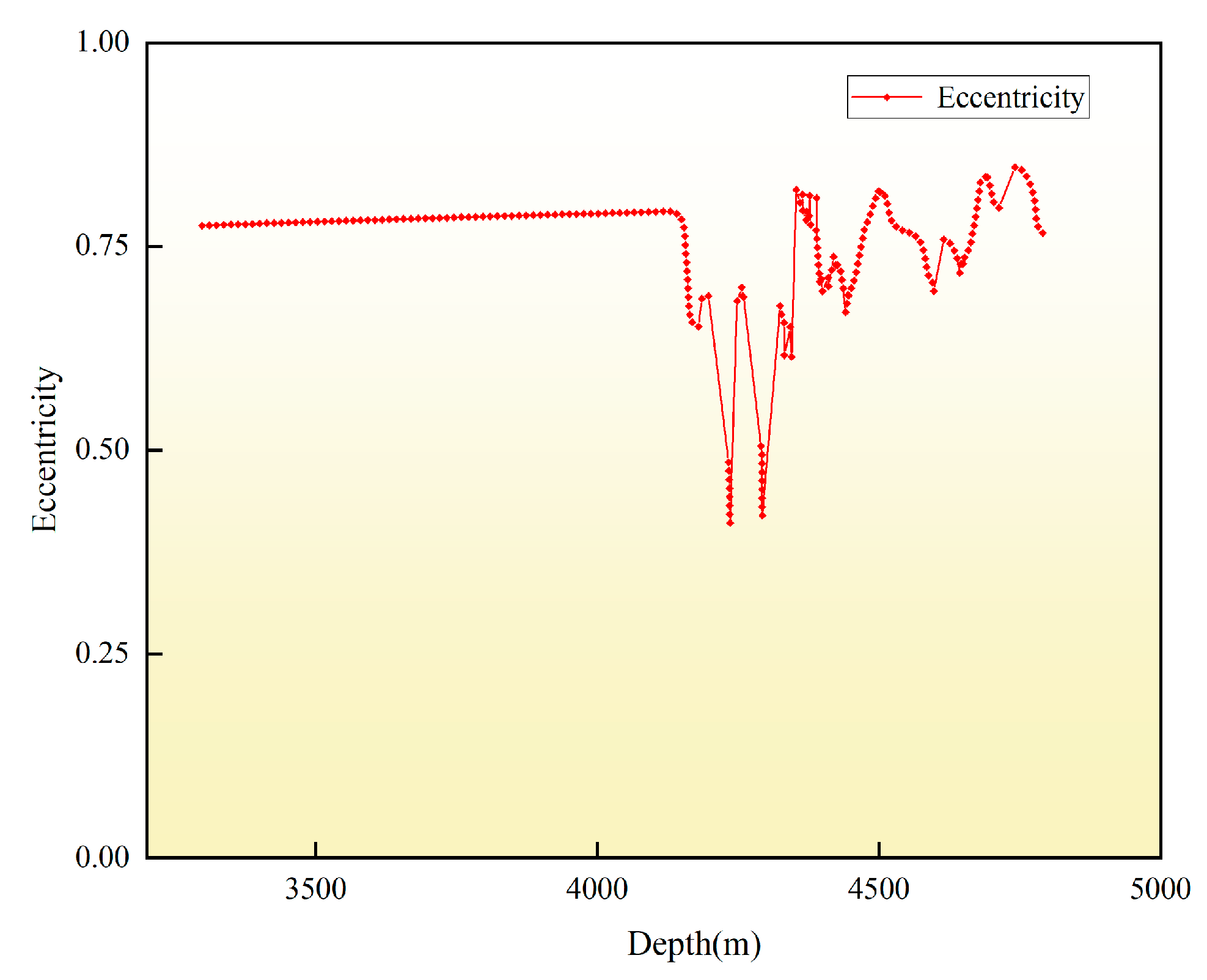
2.1.2. Eccentricity
2.2. Physical Parameters of Wellbore Fluids
2.2.1. Density Under High Temperature and High Pressure
- ρD is the predicted drilling fluid density, kg/m3;
- ρd is the test drilling fluid density, kg/m3;
- ρS is the predicted spacer density, kg/m3;
- ρs is the test spacer density, kg/m3;
- T is the downhole temperature, °C;
- T0 is the test temperature, °C;
- P is the downhole pressure, MPa;
- P0 is the test pressure, MPa.
2.2.2. Rheology Under High Temperature and High Pressure
- α1…α7 are the fitting coefficients, dimensionless;
- τ is the shear stress, Pa;
- τ0 is the dynamic shear stress, Pa;
- n is the fluidity index, dimensionless;
- k is the consistency coefficient, Pa·sn.
3. Study on the ECD Model of the Irregular Eccentric Wellbore
3.1. Temperature Field
3.1.1. Wellbore Model
- The radial temperature gradient within the drilling fluid is neglected;
- The vertical heat conduction along the drill string and the formation is neglected;
- The thermal conductivity of the formation is assumed to be constant.
3.1.2. Governing Equation
- (1)
- Inside the casing:
- Qc is energy generated by friction pressure drop of drilling fluid per unit length of casing, W/m;
- ρ1 is the density of the working fluid inside the casing, kg/m3;
- q is the discharge rate of the drilling fluid, m3/s;
- C1 is the specific heat capacity of the drilling fluid, W/(m·K);
- Tc is the temperature of the drilling fluid inside the casing, °C;
- Tw is the temperature of the casing column, °C;
- rci is the inner diameter of the casing, m;
- hci is the convective heat transfer coefficient between the fluid inside the casing and the casing, W/(m·K).
- (2)
- Casing string:
- ρ2 is the density of the casing string, kg/m3;
- C2 is the specific heat capacity of the casing string, J/(kg·K);
- λ2 is the thermal conductivity of the casing, W/(m·K);
- rci is the inner diameter of the casing, m;
- rco is the outer diameter of the casing, m;
- hci is the convective heat transfer coefficient between the fluid inside the casing and the casing itself, W/(m2·K);
- hco is the convective heat transfer coefficient between the annular fluid and the casing, W/(m2·K);
- Ta is the temperature of the annular fluid, °C.
- (3)
- Annular fluid:
- Tf1 is the temperature of the wellbore wall, °C;
- rb is the radius of the barehole annulus, m;
- rco is the outer diameter of the casing, m;
- hb is the convective heat transfer coefficient between the formation and the drilling fluid in the annulus, W/(m·K);
- hco is the convective heat transfer coefficient between the annular drilling fluid and the casing, W/(m·K);
- Qa is the heat generated by the frictional pressure drop of the drilling fluid in the annulus per unit length and per unit time, W.
- (4)
- The formation and the wellbore wall:
- r is the radial distance, m;
- ρe is the density of the formation rock, kg/m3;
- ce is the specific heat capacity of the formation rock, J/(kg·K);
- λe is the thermal conductivity of the formation, W/(m·K).
3.1.3. Initial and Boundary Conditions
- Formation temperature: the initial temperature of the drilling fluid in the drill string and the annulus and each element in the formation;
- Casing inlet boundary: The inlet temperature of the drilling fluid can usually be measured in practice. T(z = 0, t) = Tin, Tin is known;
- Annulus inlet boundary: at the bottom of the well (z = Hmax), the temperature of the fluid inside the drill string is approximately equal to that in the annulus;
- Formation boundary: Te(z,r→∞,t) is equal to the geothermal gradient.
3.2. ECD Calculation Model
3.2.1. Hydrostatic Pressure Calculation
- i is the layer, dimensionless;
- Ri is the layer’s annular radius, m;
- h is the well layer’s depth, m;
- Pc is the wellhead back pressure, Pa;
- ρ(Ti) is the fluid density at the layer’s temperature, kg/m3;
- Pf(T,Ri) is the frictional pressure drop at the layer’s radius and temperature, Pa.
3.2.2. Frictional Pressure Drop Calculation
- α is the angle, °;
- R1 is the annular inner radius, m;
- R2 is the annular outer radius, m.
- Pf is friction pressure drop, Pa;
- e is the eccentric distance, m.
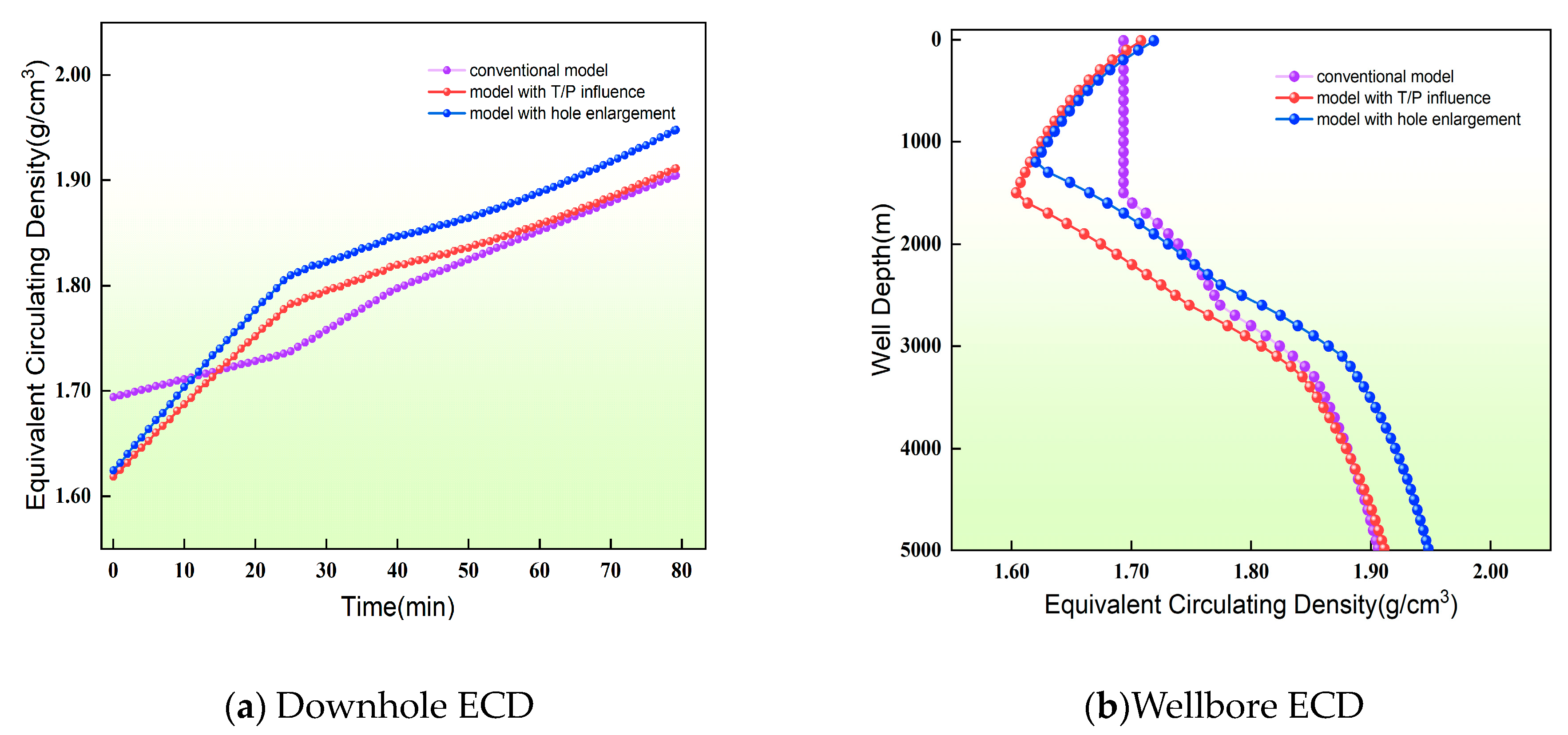
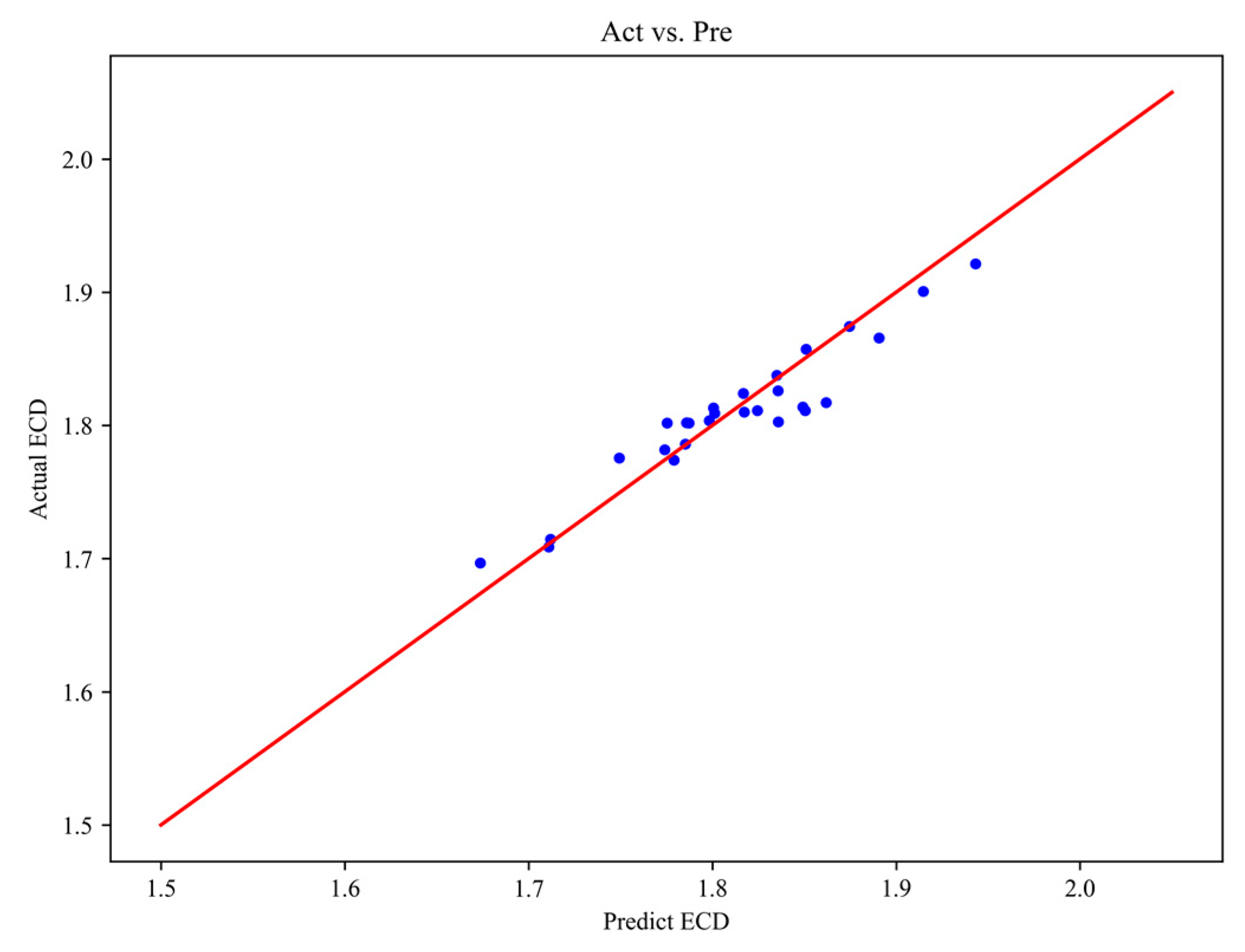
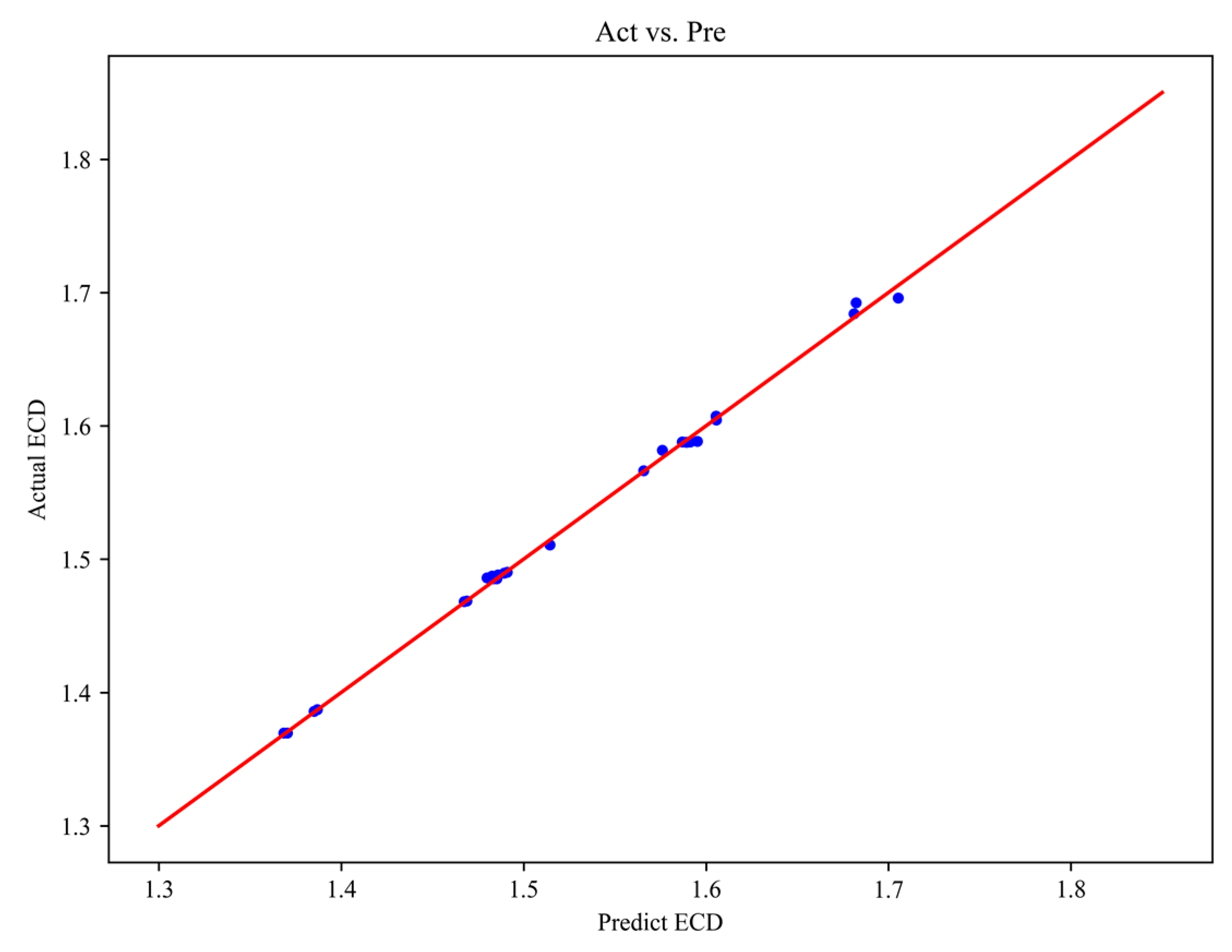
3.3. Validation of Computational Results
4. Based on the Random Forest Algorithm for Irregular Wellbore Diameter Weight Analysis
4.1. Random Forest Model and Related Parameters
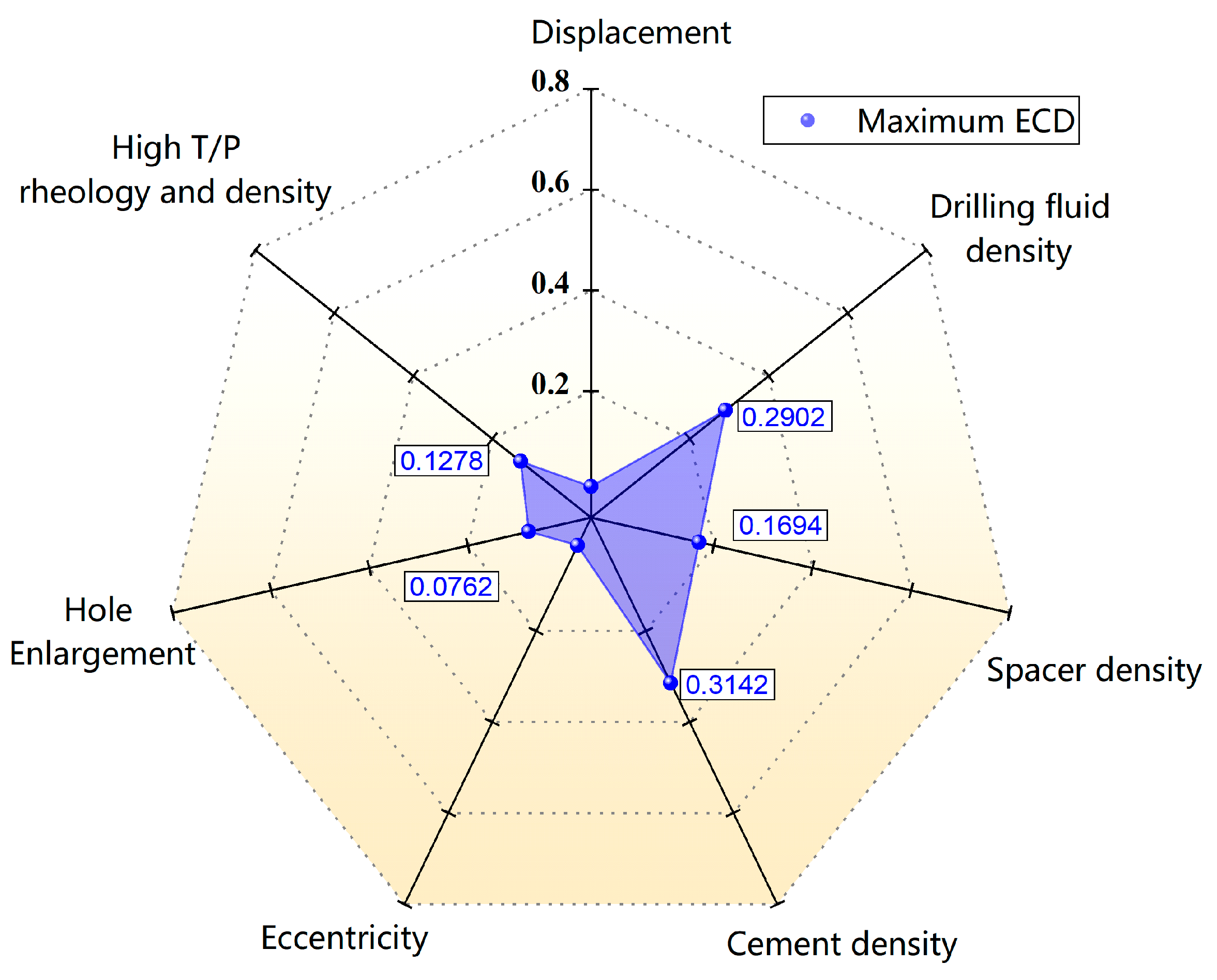
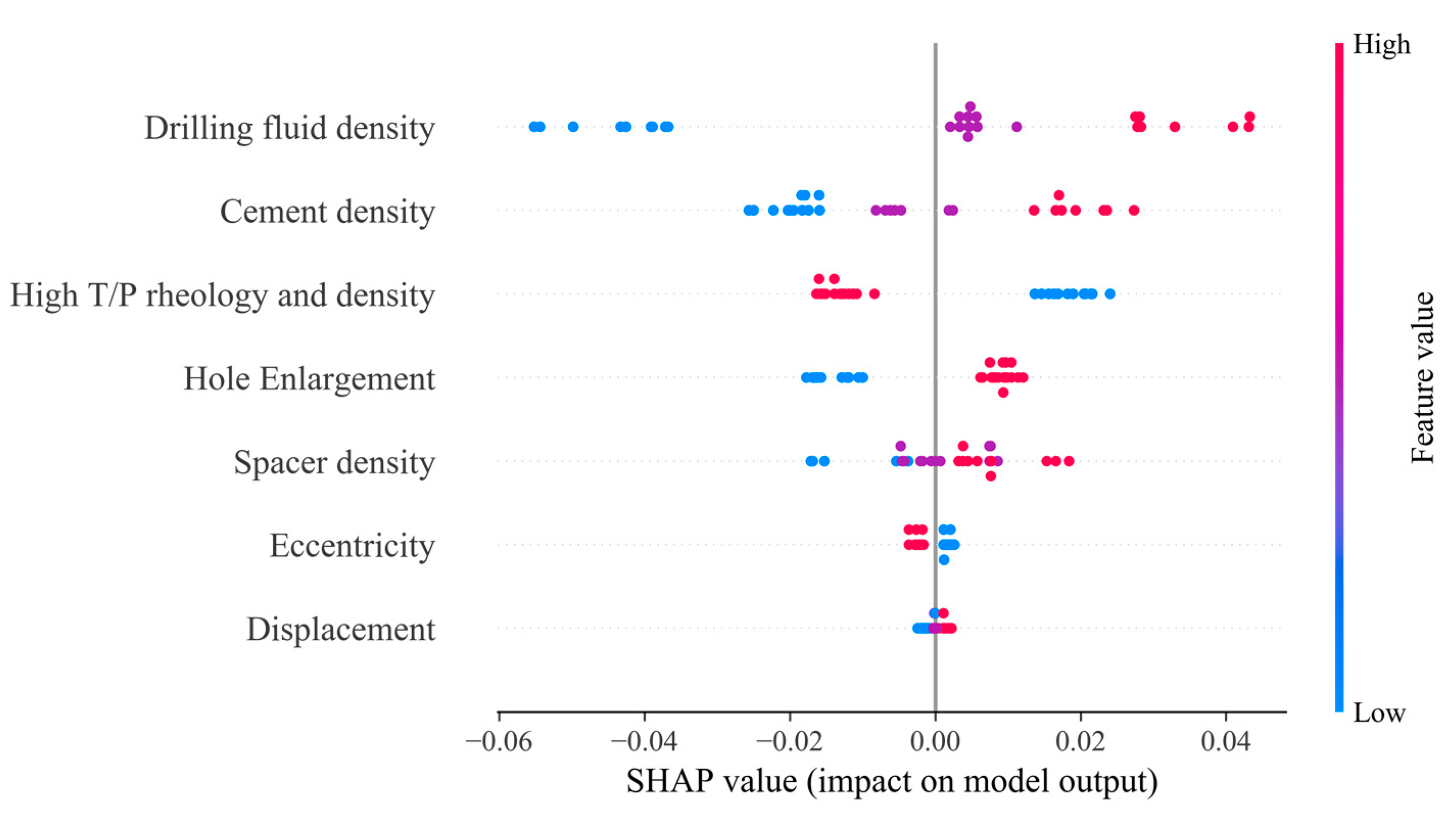
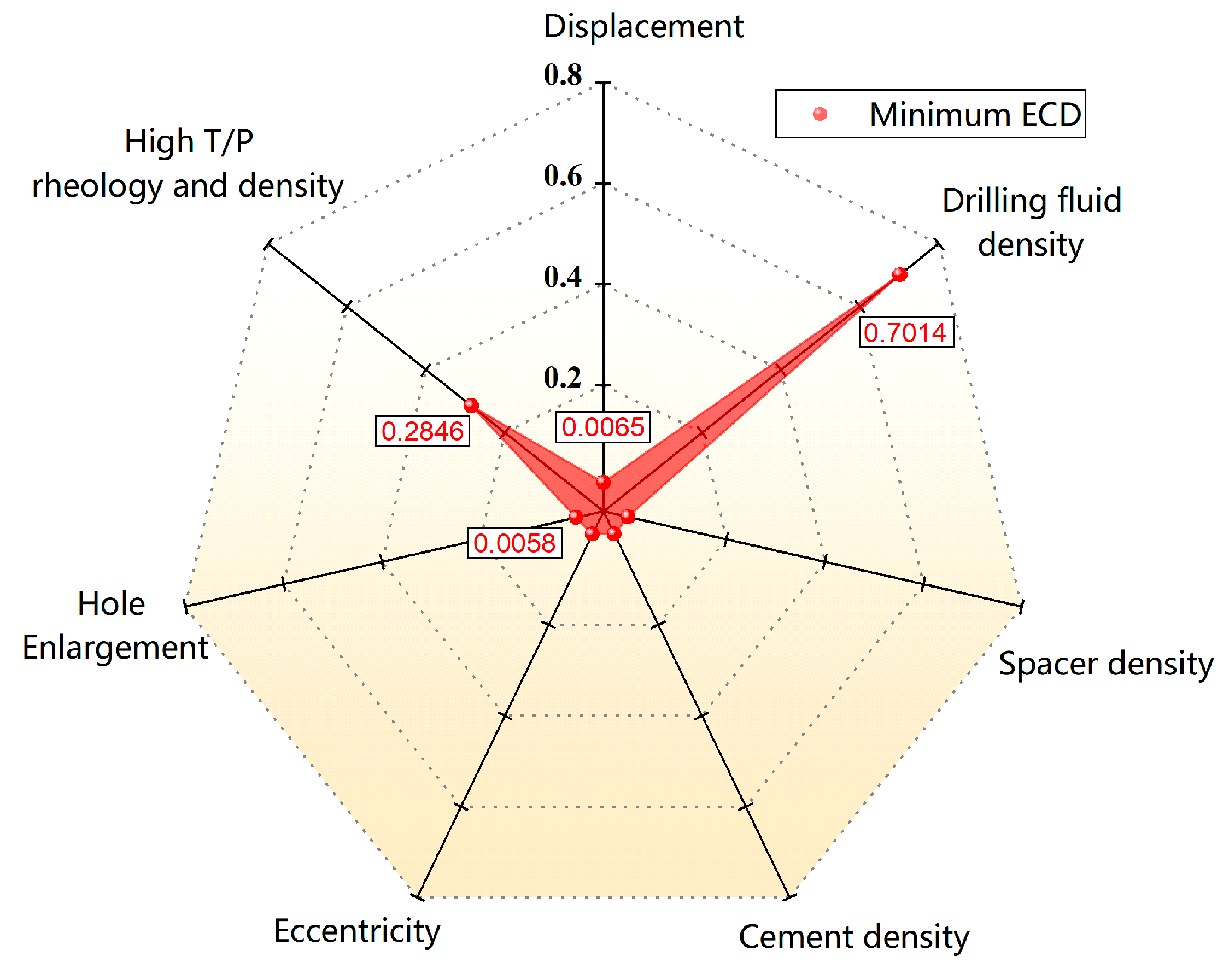
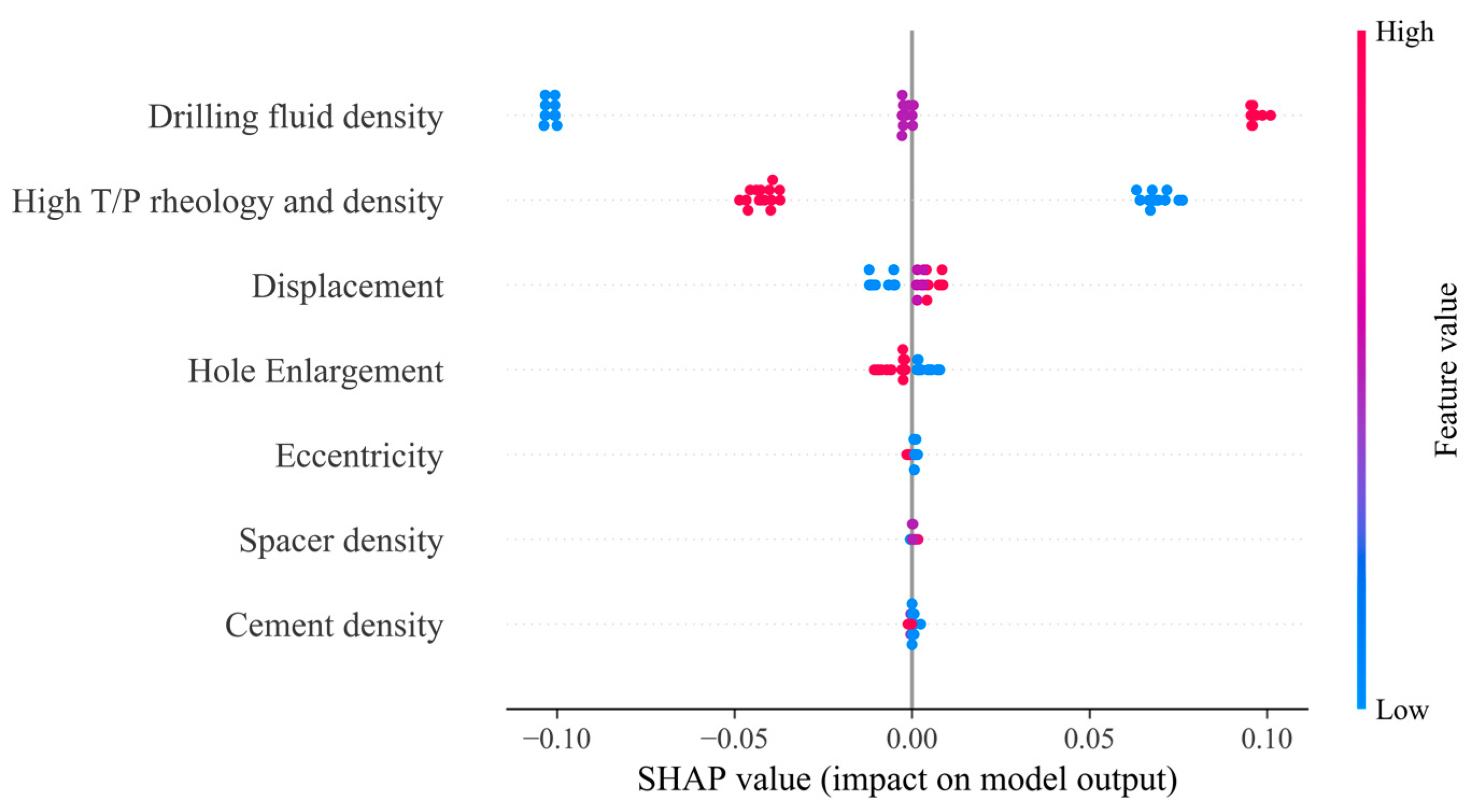
4.2. The Maximum/Minimum ECD Multifactor Weight Analysis During Cementing Operations
5. Conclusions
- In view of the narrow density window problem faced by deep well drilling and cementing operations, this study establishes a new calculation model for cementing ECD. This new model does not adopt the assumption of a uniform wellbore but instead establishes a multi-layer structure of the wellbore based on an irregular wellbore, further clarifying the impact of irregular well diameter factors on both the downhole and wellbore ECD. The comparison between the model calculation results and the conventional, temperature, and pressure models proves that an irregular well diameter significantly impacts the downhole and wellbore ECD and provides new ideas for the study of deep well ECD control methods.
- Based on the random forest method, a quantitative analysis of the calculation results of the new model found that the density of cement slurry and drilling fluid has the most significant impact on the maximum ECD, with the impact reaching 0.3142 and 0.2902, respectively. Moreover, the impact of spacer fluid density, rheological changes, and irregular well diameter cannot be ignored. The main factors that affect the minimum ECD are the density and rheological changes in the drilling fluid, reaching 0.7014 and 0.2846.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hou, Z.; Luo, J.; Xie, Y.; Wu, L.; Huang, L.; Xiong, Y. Carbon Circular Utilization and Partially Geological Sequestration: Potentialities, Challenges, and Trends. Energies 2023, 16, 324. [Google Scholar] [CrossRef]
- Xie, Y.; Qi, J.; Zhang, R.; Jiao, X.; Shirkey, G.; Ren, S. Toward a Carbon-Neutral State: A Carbon–Energy–Water Nexus Perspective of China’s Coal Power Industry. Energies 2022, 15, 4466. [Google Scholar] [CrossRef]
- Barbosa, C.; Felipe, L.; Iqbal, J. Novel Shear Dependent Cement Slurry System, Tailored to Rescue and Cure Losses when ECD Management and LCM Pills Failed—A Case Study from Southern Iraq. In Proceedings of the Middle East Oil, Gas and Geosciences Show, Manama, Bahrain, 19–21 February 2023. [Google Scholar]
- Wu, X.; Li, Z.; Hou, Z.; Liu, J.; Huang, S.; Su, D.; Li, J.; Cao, C.; Wu, L.; Song, W. Analytical Perspectives on Cement Sheath Integrity: A Comprehensive Review of Theoretical Research. ACS Omega 2024, 9, 17741–17759. [Google Scholar] [CrossRef]
- Wu, X.; Liu, J.; Li, Z.; Song, W.; Liu, Y.; Shi, Q.; Chen, R. Failure Analysis of Cement Sheath Mechanical Integrity Based on the Statistical Damage Variable. ACS Omega 2023, 8, 2128–2142. [Google Scholar] [CrossRef] [PubMed]
- Annis, M. High-Temperature Flow Properties of Water-Base Drilling Fluids. J. Pet. Technol. 1967, 19, 1074–1080. [Google Scholar] [CrossRef]
- Zhao, J.; Pillai, S.; Pilon, L. Rheology of colloidal gas aphrons (microfoams) made from different surfactants. Colloids Surf. A Physicochem. Eng. Asp. 2009, 348, 93–99. [Google Scholar] [CrossRef][Green Version]
- Gokdemir, M.G.; Erkekol, S.; Dogan, H.A. Investigation of High Pressure Effect on Drilling Fluid Rheology. In Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Ye, Y.; Fan, H.; Liu, Y. A New Approach for Predicting the Rheological Properties of Oil-Based Drilling Fluids under High Temperature and High Pressure Based on a Parameter-Free Method. Appl. Sci. 2023, 13, 8592. [Google Scholar] [CrossRef]
- Hashemian, Y.; Yu, M.; Shirazi, S.; Ahmed, R. Accurate Predictions of Velocity Profiles and Frictional Pressure Losses in Annular YPL-Fluid Flow. J. Can. Pet. Technol. 2014, 6, 355–363. [Google Scholar] [CrossRef]
- Dokhani, V.; Ma, Y.; Li, Z.; Geng, T.; Yu, M. Effects of drill string eccentricity on frictional pressure losses in annuli. J. Pet. Sci. Eng. 2020, 187, 106853. [Google Scholar] [CrossRef]
- Heshamudin, N.S.; Katende, A.; Rashid, H.A.; Ismail, I.; Sagala, F.; Samsuri, A. Experimental investigation of the effect of drill pipe rotation on improving hole cleaning using water-based mud enriched with polypropylene beads in vertical and horizontal wellbores. J. Petrol. Sci. Eng. 2019, 179, 1173–1185. [Google Scholar] [CrossRef]
- Katende, A.; Segar, B.; Ismail, I.; Sagala, F.; Saadiah, H.H.A.R.; Samsuri, A. The effect of drill–pipe rotation on improving hole cleaning using polypropylene beads in water-based mud at different hole angles. J. Pet. Explor. Prod. Technol. 2020, 10, 1253–1262. [Google Scholar] [CrossRef]
- Yeu, W.J.; Katende, A.; Sagala, F.; Ismail, I. Improving hole cleaning using low density polyethylene beads at different mud circulation rates in different hole angles. J. Nat. Gas. Sci. Eng. 2019, 61, 333–343. [Google Scholar] [CrossRef]
- Babu, D.R. Effect of P–ρ–T behavior of muds on lossrgain during high-temperature deep-well drilling. J. Petrol. Sci. Eng. 1998, 20, 49–62. [Google Scholar] [CrossRef]
- Yuan, B.; Li, J.; Xu, B.; Su, Y.; Li, B.; Yang, L. Managed wellhead backpressure during waiting setting of managed pressure cementing. J. Petrol. Sci. Eng. 2021, 207, 109158. [Google Scholar] [CrossRef]
- Liang, H.; Liu, G.; Zou, J.; Bai, J.; Jiang, Y. Research on calculation model of bottom of the well pressure based on machine learning. Future Gener. Comput. Syst. 2021, 124, 80–90. [Google Scholar] [CrossRef]
- Kumar, A.; Ridha, S.; Ganet, T.; Vasant, P.; Ilyas, S.U. Machine Learning Methods for Herschel–Bulkley Fluids in Annulus: Pressure Drop Predictions and Algorithm Performance Evaluation. Appl. Sci. 2020, 10, 2588. [Google Scholar] [CrossRef]
- Binger, Z.M.; Achilli, A. Surrogate modeling of pressure loss & mass transfer in membrane channels via coupling of computational fluid dynamics and machine learning. Desalination 2023, 548, 116241. [Google Scholar] [CrossRef]
- McMordie, W.C., Jr.; Bland, R.G.; Hauser, J.M. Effect of Temperature and Pressure on the Density of Drilling Fluids. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 26–29 September 1982. [Google Scholar]
- Osman, E.A. Determination of Drilling Mud Density Change with Pressure and Temperature Made Simple and Accurate by ANN. In Proceedings of the Middle East Oil Show, Manama, Bahrain, 9–12 June 2003. [Google Scholar]
- Alade, O.; Mahmoud, M.; Al-Nakhli, A. Rheological studies and numerical investigation of barite sag potential of drilling fluids with thermochemical fluid additive using computational fluid dynamics (CFD). J. Petrol. Sci. Eng. 2023, 220, 111179. [Google Scholar] [CrossRef]
- Dokhani, V.; Ma, Y.; Yu, M. Determination of equivalent circulating density of drilling fluids in deepwater drilling. J. Nat. Gas. Sci. Eng. 2016, 34, 1096–1105. [Google Scholar] [CrossRef]
- Yang, M.; Luo, D.; Chen, Y.; Li, G.; Tang, D.; Meng, Y. Establishing a practical method to accurately determine and manage wellbore thermal behavior in high-temperature drilling. Appl. Energy 2019, 238, 1471–1483. [Google Scholar] [CrossRef]
- Flayh, S.J.; Sultan, H.S.; Alshara, A.K. Numerical study of drilling fluids pressure drop in wellbores with pipe rotation. IOP Conf. Ser. Mater. Sci. Eng. 2019, 518, 32037. [Google Scholar] [CrossRef]
- Meng, Y.; Yang, M.; Liu, S.; Mou, Y.; Peng, C.; Zhou, X. Quantitative Assessment of the Importance of Bio-physical Drivers of Land Cover Change. Ecol. Inform. 2020, 61, 101204. [Google Scholar] [CrossRef]



| Fluid | Parameters | The Fitted Equation | R2 |
|---|---|---|---|
| Drilling fluid | k | k = 0.623 − 0.006 × (T − T0) − 0.004 × (P − P0) | 0.982 |
| n | n = 0.769 | ||
| τ | tau = 1.784 + 0.015 × (T − T0) + 0.017 × (P − P0) | ||
| Spacer | k | k = 0.69 − 0.001 × (T − T0) | 0.998 |
| n | n = 0.573 | ||
| τ | tau = 18.514 − 0.013 × (T − T0) | ||
| Cement slurry | k | k = 0.992 − 0.003 × (T − T0) | 0.999 |
| n | n = 0.739 | ||
| τ | tau = 1.698 + 0.005 × (T − T0) |
| Inlet Velocity (m/s) | Model Calculation (Pa) | Experimental Result (Pa) | Deviation (%) |
|---|---|---|---|
| 0.18 | 24,043.35 | 21,858.351 | 9.09 |
| 0.3 | 27,829.73 | 26,313.37 | 5.45 |
| 0.4 | 30,270.05 | 29,501.259 | 2.54 |
| 0.5 | 32,334.30 | 32,301.236 | 0.1 |
| Item Number | Type of Fluid | Injection Flow Rate (m3/min) | Injection Volume (m3) |
|---|---|---|---|
| 1 | Spacer | 1.8 | 30 |
| 2 | Leading cement | 1.0 | 18.0 |
| 3 | Tailing cement | 1.0 | 34.0 |
| 4 | Displacement fluid 1 | 1.2 | 4.8 |
| 5 | Displacement fluid 2 | 1.2 | 43 |
| Item | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| Annulus parameters | Drill bit size, m | 0.2159 | Inlet mud temperature, °C | 29.4 |
| Pipe size, m | 0.1397 | Geothermal gradient, °C/100 m | 4.9 | |
| Pipe depth, m | 4971 | Wellbore depth, m | 4980 | |
| fluid parameters | Rheology of fluid | Refer to Table 1 | ||
| Density of drilling fluid and spacer, g/cm3 | Refer to Equations (1) and (2) | |||
| Density of cement, g/cm3 | Leading: 2.05/tailing: 1.90 | |||
| Displacement and replacement time | Refer to Table 3 | |||
| Labels | Classification | Labels | Classification |
|---|---|---|---|
| Drilling fluid density | 1.4/1.5/1.6 | Eccentricity | 0.4/0.8 |
| Spacer density | 1.6/1.7/1.8 | Irregular wellbore diameter | Presence = 1/absence = 0 |
| Cement slurry density | 1.8/1.9/2.0 | ||
| Flow rate | 0.5/1.2/1.8 | Rheology | Presence = 1/absence = 0 |
| Labels | Importance | SHAP Value | Labels | Importance | SHAP Value |
|---|---|---|---|---|---|
| Flow rate | 0.0111 | 0.001 | Eccentricity | 0.0111 | 0.0021 |
| Drilling fluid density | 0.2902 | 0.0266 | High T/P rheology and density | 0.1278 | 0.0156 |
| Spacer density | 0.1694 | 0.0072 | |||
| Cement slurry density | 0.3142 | 0.0159 | Hole enlargement | 0.0762 | 0.0109 |
| Labels | Importance | SHAP Value | Labels | Importance | SHAP Value |
|---|---|---|---|---|---|
| Flow rate | 0.0065 | 0.0059 | Eccentricity | 0.0006 | 0.0009 |
| Drilling fluid density | 0.7015 | 0.0633 | High T/P rheology and density | 0.2846 | 0.0542 |
| Spacer density | 0.0007 | 0.0004 | |||
| Cement slurry density | 0.0003 | 0.0004 | Hole enlargement | 0.0058 | 0.0046 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Sun, J.; Luo, H.; Shi, Y.; Zhang, J.; Li, Z. Irregular Eccentric Wellbore Cementing: An Equivalent Circulation Density Calculation and Influencing Factors Analysis. Appl. Sci. 2024, 14, 9573. https://doi.org/10.3390/app14209573
Yang F, Sun J, Luo H, Shi Y, Zhang J, Li Z. Irregular Eccentric Wellbore Cementing: An Equivalent Circulation Density Calculation and Influencing Factors Analysis. Applied Sciences. 2024; 14(20):9573. https://doi.org/10.3390/app14209573
Chicago/Turabian StyleYang, Fujie, Jinfei Sun, Hanlin Luo, Yue Shi, Jingyan Zhang, and Zaoyuan Li. 2024. "Irregular Eccentric Wellbore Cementing: An Equivalent Circulation Density Calculation and Influencing Factors Analysis" Applied Sciences 14, no. 20: 9573. https://doi.org/10.3390/app14209573
APA StyleYang, F., Sun, J., Luo, H., Shi, Y., Zhang, J., & Li, Z. (2024). Irregular Eccentric Wellbore Cementing: An Equivalent Circulation Density Calculation and Influencing Factors Analysis. Applied Sciences, 14(20), 9573. https://doi.org/10.3390/app14209573






