State of Charge Estimation for Lithium-Ion Batteries Using Optimized Model Based on Optimal HPPC Conditions Created Using Taguchi Method and Multi-Objective Optimization

Abstract

This study proposes a comprehensive methodology for accurate State of Charge (SOC) estimation in lithium-ion batteries by optimizing equivalent circuit model (ECM) parameters under varying temperature conditions using the Taguchi method. Analysis of Variance (ANOVA) was employed to evaluate the influence of these parameters on ECM accuracy. Experiments were conducted at −10 °C, 25 °C, and 40 °C to evaluate the effects of pulse time gap, discharge pulse time, and C-rate on SOC estimation accuracy. A genetic algorithm-based multi-objective optimization technique was employed to minimize RMSE in the extended Kalman filter (EKF) SOC estimation process. The results showed that temperature significantly impacts SOC prediction, with deviations most pronounced at low (−10 °C) and high (40 °C) temperatures. When assessments are conducted for different SOC levels (SOC90, SOC50, SOC30), the key results highlight the substantial influence of pulse time gap and discharge pulse time on model accuracy. Also, it was observed that there is a significant reduction in RMSE, indicating improved performance under optimized conditions. The findings are particularly relevant for real-time applications, such as electric vehicles, where accurate SOC estimation is crucial for battery management.

1. Introduction

The electric vehicle (EV) market is witnessing rapid expansion, with sales exceeding 10 million units in 2022. This surge represented 14% of all new car sales, a significant jump from around 9% in 2021 and less than 5% in 2020. The momentum in electric vehicle sales is projected to maintain its strength throughout 2023, with forecasts indicating that sales could reach 14 million by the end of the year, accounting for 18% of total car sales for the entire year [1]. Recently, the power battery, which is a crucial component of EVs, has garnered significant attention.

To improve battery performance, extend battery life, and optimize behaviour in applications, the implementation of a battery management system (BMS) is crucial. The BMS plays an essential role in monitoring and managing various aspects of the battery’s operation, ensuring efficient performance and protecting against potential issues, thereby enhancing the overall reliability of the system [2]. For the BMS to perform these functions effectively, a precise evaluation of the battery’s state is necessary, including parameters like the State of Charge (SOC). This level of accuracy is facilitated using a battery model. Battery models are typically divided into four categories: data-driven models (including extreme learning machine models, support vector machine models, and neural networks), empirical models (such as the Nernst model, Unnewehr universal model, and Shepherd model), electrochemical models (like the single particle model and pseudo-2D model), and equivalent circuit models (including the Thevenin model, dual-polarization model, and Rint model). These models provide the necessary frameworks to accurately assess and manage battery performance [3].

The equivalent circuit model (ECM) has become widely utilized in practical applications due to its straightforward parameterization, effective representation of Li-ion battery characteristics, and cost-effectiveness [4]. ECM models are highly effective in estimating the nonlinear behaviour of batteries and in parameterizing model variables based on factors, such as temperature, State of Charge (SOC), State of Health (SOH), and C-rate. The influence of these factors on battery performance can differ significantly depending on the specific chemistry and manufacturing processes of the battery [3]. Since ECM parameters are not physical attributes and cannot be measured directly, they must be identified through an optimization algorithm once the battery model is established. There are two principal methods for this identification: offline and online. Offline identification involves determining the parameters based on the State of Charge (SOC) through controlled experiments under specific operational conditions. Various testing profiles can be employed for this parameter identification, including the pulse test [5], hybrid pulse power characterization (HPPC) test [6], and drive cycle test [7,8]. Before using the HPPC test for ECM parameter identification, it is crucial to analyse the correlation between each HPPC parameter and the model’s accuracy. This analysis is essential to understand the impact of each parameter on the overall accuracy of the model. However, there is limited research in this field. Li et al. [8] explored how various HPPC profiles affect identification accuracy, specifically examining the pulse width of the simulating current and the rest time. Tran et al. [4] examined how the State of Health (SOH) impacts the parameters of the equivalent circuit model (ECM) utilized for lithium-ion batteries. Bialon et al. [9] identified the parameters of the equivalent circuit using the particle swarm optimization (PSO) algorithm for a lithium-ion battery cell using the results obtained from HPPC tests. Zhang et al. [10] assessed the impact of different test profiles on ECM accuracy by comparing various pulse test lengths, two identification methods, and a combination of pulse and drive cycle tests, finding that application optimization yields the highest accuracy. Waag et al. [11] explored how ECM parameters depend on the frequency characteristics of the load current and suggested a method for application-specific parameterization based on the frequency spectrum of the load. Additionally, the effects of the load current profile on ECM parameters were examined by Tang et al. [12]. Sharma et al. [13] incorporated C-rate-dependent resistance into the ECM to account for slow kinetics and the impact of C-rates on diffusivity, which becomes more pronounced at temperatures below 0 °C. Their research demonstrated that this enhanced ECM could be integrated into battery management systems to accurately forecast cell behaviour under various low-temperature operating conditions.

The offline identification method, due to its reliance on specific experimental conditions, often requires a significant number of tests, leading to lengthy development cycles and increased costs. In this context, Design of Experiments (DOE) methods are crucial for efficiently investigating and understanding the effects of multiple variables in a system. By structuring experiments to systematically vary these variables, DOE helps identify which factors significantly impact outcomes, reduces the resources needed for research, and improves the reliability of results. Sun et al. [14] investigated the impact of four HPPC parameters—positive and negative pulse height, pulse length, and relaxation length—on the performance of the equivalent circuit model (ECM) under various application conditions. They employed the Taguchi method to analyse the effects of these parameters, revealing that a decline in SOH leads to increased ohmic and polarization resistance, as well as decreased polarization capacitance. Mathew et al. [15] developed an electro-thermal model for electric vehicles by leveraging a Design of Experiments (DOE) approach to enhance the efficiency and accuracy of battery management systems (BMSs). They focused on lithium-ion batteries, particularly modelling the effects of temperature and State of Charge (SOC) on the equivalent circuit model parameters. Their methodology included software-in-the-loop (SIL) and hardware-in-the-loop (HIL) testing to simulate battery pack behaviours under various scenarios. They stated that this method allowed for precise statistical analysis to identify significant model parameters and validate the model through comparison with traditional approaches, proving that fewer experimental runs could achieve similar accuracy. Amanor-Boadu et al. [16] investigated the effects of pulse charging parameters on the life cycle characteristics of lithium-ion batteries. They utilized a DOE approach, specifically Taguchi orthogonal arrays, to systematically study and optimize these parameters. Key factors such as pulse frequency, duty cycle, and charging temperature were analysed to determine their impact on battery performance. Their findings suggested that optimized pulse charging can significantly enhance battery life and efficiency compared to standard constant current–constant voltage charging methods. Zhang et al. [17] introduced a new DoE approach that combines partial and deep discharge tests for battery evaluation, significantly enhancing ECM precision by reducing the root mean square error by nearly 70%.

The data-driven method is considered a “black box” approach, relying heavily on the quality of input data, training, and hyperparameter selection [18]. Despite the theoretical challenges, model-driven methods like the Kalman filter (KF), a prevalent state estimation technique, are used to estimate the optimal posterior SOC based on ECM [19]. Within this framework, the extended Kalman filter (EKF) uses a first-order Taylor expansion to linearize nonlinear systems’ evolution and measurement functions, enhancing SOC estimation accuracy [20]. Yuan et al. [21] addressed the challenges in SOC estimation caused by factors affecting the accuracy of extended Kalman filters. The authors aimed to improve voltage simulation and estimation techniques to reduce errors. Ge et al. [22] introduced an algorithm to improve the real-time performance of SOC estimation filters by solving for suboptimal fading factors, crucial for maintaining filter effectiveness under varying conditions. Duan et al. [23] proposed a novel approach combining maximum correntropy criterion (MCC) with EKF, called C-WLS-EKF. Experimental results show that the C-WLS-EKF significantly reduces SOC estimation errors compared to traditional EKF methods, achieving a mean square error (MSE) reduction from 1.361% to 0.512%. The authors stated the importance of accurate SOC estimation in electric vehicles for battery protection, efficiency, and longevity.

In the current literature, various approaches have been proposed for SOC estimation and ECM parameter identification for lithium-ion batteries. These methods typically focus on specific optimization techniques and limited test profiles, often without considering the combined effect of multiple variables like temperature, SOC levels, and operational conditions. While the literature provides significant insights into battery modelling and estimation methods, it lacks comprehensive studies that address the following gaps. Li et al. [8] and Zhang et al. [17] focused on the impact of pulse width or rest time during HPPC tests. They explored how pulse width and rest time affect identification accuracy but did not comprehensively examine the effects of multiple HPPC parameters, such as pulse time gap, discharge pulse time, and C-rate, under various conditions. Also, the simultaneous effects of multiple HPPC parameters on ECM performance under different environmental conditions (e.g., low and high ambient temperatures) were not investigated by the researchers. While temperature is recognized as a critical factor affecting lithium-ion battery performance, studies such as those by Tang et al. [12] and Sharma et al. [13] generally focused on low or high temperatures without considering intermediate conditions. They rarely explore how temperature interacts with SOC and C-rate to influence the overall model accuracy. There is limited research on the combined effects of temperature, SOC, and operational variables (e.g., C-rate) on ECM parameterization and SOC estimation accuracy. Most of the existing work, such as Bialon et al. [9] and Waag et al. [11], focused on single-objective optimization techniques for ECM parameter identification. While these methods improve certain aspects of model accuracy (e.g., reducing RMSE for specific SOC levels), they may fail to balance competing objectives, such as minimizing RMSE at different SOC levels and temperatures simultaneously.

To fill these research gaps, this study examines varying levels of four widely utilized HPPC parameters, specifically focusing on discharge parameters: pulse time gap, discharge pulse time, discharge pulse C-rate, and rest time. In this context, the Taguchi method (DoE) was applied to set the research plan, and a statistical analysis (ANOVA) was performed to evaluate the results. This investigation includes conducting HPPC tests at different operating temperatures (−10 °C, 25 °C, 40 °C) and obtaining equivalent circuit models (ECMs) for diverse combinations of these parameters. The selection of the most suitable parameters for each test was facilitated by employing RMSE (root mean square error) values. These values, computed from the differences between experimental and simulated data, functioned as quality metrics in the evaluation process. Analysing the effect of each parameter variation on model performance offers valuable insights, aiding in the selection of optimal parameters for a generic ECM. Additionally, after the parameters were determined based on the model that minimizes the RMSE value, the EKF algorithm was utilized for SoC estimation, which optimizes the model accuracy and the estimation performance with simultaneous iterations.

2. Materials and Methods

2.1. Experimental Setup

The selected battery cell in this research is a 2.9 Ah, cylindrical 18650 lithium-ion battery cell (Aspilsan INR18650A28), incorporating a nickel manganese cobalt oxide (NMC) cathode and a graphite anode. The detailed specifications of the cell are provided in

Table 1. Specifications of the lithium-ion cell used in the experiments.

Properties	Value
Diameter (mm)	18.30 + 0.1/−0.2
Height (mm)	65 ± 0.2
Weight (g)	44.5 ± 0.7
Discharge Capacity (mAh)	2950 (Maximum) 2900 (Typical) 2850 (Minimum)
Nominal Voltage (V)	3.68
Energy Density (Wh/kg)	244
Standard Charge Current (mA)	1450
Max. Continuous Charge Current (mA)	4000 (10–50 °C)
Charge Cutoff Current (mA)	140
Charge End Voltage (V)	4.25
Standard Discharge Current (mA)	580
Max. Continuous Discharge Current (mA)	25,000
Discharge End Voltage (V)	2.5

.

In this study, the charge and discharge tests were conducted using a QPX 1200SP programmable DC power supply and a PRODIGIT 3117 programmable DC electronic load device and the control of these devices, and the data acquisition process were carried out with the LabVIEW 2020SP1 software. To maintain the consistency of experimental data and to provide several different temperatures, all tests were carried out within a climate chamber, depicted in Figure 1.

To ensure the battery’s capacity is accurately measured and validated, it is essential to test the maximum available capacity. The testing process is conducted at three different ambient temperatures of −10 °C, 25 °C, and 40 °C, beginning with charging the battery using a constant current. The temperatures −10 °C, 25 °C, and 40 °C were selected to represent a wide range of environmental conditions that lithium-ion batteries commonly experience in real-world applications. Each temperature is chosen to simulate different operational scenarios, enabling a comprehensive understanding of how temperature impacts battery performance, model accuracy, and SOC estimation. At low temperatures, such as −10 °C, lithium-ion batteries experience significant increases in internal resistance and decreases in ionic conductivity, leading to voltage drops and reduced capacity. This condition was chosen to represent extreme cold environments, which are commonly encountered in regions with cold climates or during winter operations. The impact of low temperatures on battery performance is critical for applications like electric vehicles in cold weather, where reduced battery efficiency and energy loss can affect driving range and power availability. Studying the model’s performance under these conditions helps improve SOC estimation and overall battery management in low-temperature environments. A temperature of 25 °C was chosen as the reference temperature because it represents standard laboratory conditions and is generally considered the optimal operating temperature for lithium-ion batteries. Under this temperature, the battery’s electrochemical reactions are stable, internal resistance is minimal, and overall performance is predictable. Testing at this temperature provides a baseline for comparing battery performance and SOC estimation under more extreme conditions. Additionally, many industrial and consumer battery applications (e.g., electronics, stationary energy storage systems) operate at or near room temperature, making this an essential condition for model validation. High temperatures, such as 40 °C, were selected to simulate hot environments where lithium-ion batteries may experience thermal stress due to accelerated electrochemical reactions and increased thermal degradation. These conditions are common in tropical regions or during high-intensity battery use in applications like electric vehicles, renewable energy storage, and portable electronics. Operating at elevated temperatures can lead to faster aging, increased self-discharge rates, and potential safety risks. Studying battery performance and SOC estimation at 40 °C helps understand how to mitigate thermal effects and optimize battery management under high-temperature conditions [24].

Once the battery’s terminal voltage reaches 4.2 V, the charging mode is switched to constant voltage, and charging continues until the current drops to 0.01C or less. After charging, the battery is allowed to rest for a minimum of 30 min before being discharged at a constant current until it reaches the cutoff voltage. The experiment is repeated three times, and if the deviation between the three test results and the mean is within 2%, the average of the three test results is taken as the maximum available capacity of the battery.

To obtain parameters under different SOC conditions, an HPPC test should be conducted on the battery, varying the SOC values throughout the discharge process. In this context, varying levels of four widely utilized HPPC parameters were investigated, specifically focusing on discharge parameters: pulse time gap, discharge pulse time, discharge pulse C-rate, and rest time. Firstly, the current is drawn in the time period determined according to the set discharge current (discharge pulse C-rate and discharge pulse time); then, the time period between the pulses (discharge pulse and sweep discharge pulse) is awaited (pulse time gap), and then the step is drawn in the time period determined according to the sweep current (180 s 1C); finally the rest time process is started and the process is repeated. The Taguchi orthogonal arrays were applied as DoE method to set the research plan, and all tests were repeated at different constant ambient temperatures (−10 °C, 25 °C, 40 °C).

2.2. Design of Experiments Using Taguchi Orthogonal Arrays and ANOVA Analysis

An experimental design is typically employed to assess the impact of different parameters on the system’s output. Taguchi orthogonal array (OA) is a DOE technique commonly used for robust experimental design. It employs an OA to systematically design and analyse experiments involving multiple factors and levels [25]. In Taguchi OA, different factors at various levels are given equal weight. This ensures that every level of each factor appears an equal number of times, and all possible combinations of different levels of any two factors occur equally often. This approach eliminates interference between factors, allowing the method to effectively assess the sensitivity of system output to different levels of various factors [14]. Taguchi OA is typically denoted as LA(BC), where L represents the orthogonal design, A indicates the number of experiments, B denotes the number of levels of each factor, and C refers to the number of factors [26]. The partial factorial design used in Taguchi OA necessitates significantly fewer experiments compared to the full factorial design. Despite the reduced number of experiments, the OA design yields results comparable to those of the full factorial design [27].

In the widely used standard HPPC test, that can be controlled in the HPPC profile include the discharge pulse C-rate, the charge pulse C-rate, the pulse time, and the rest time between charge and discharge pulses, and the values of these parameters are 1C, 0.75C, 10 s and 40 s, respectively [14].

In this study, for an accurate comparison with the standard test, HPPC profile parameters will be adjusted based on the standard parameters. In this context, two additional higher values for the discharge pulse C-rate (2C and 3C) are used to further investigate their effect on model performance.

It has been stated in the literature that the discharge pulse duration should be limited to a maximum of 200 s since the HPPC test is to be performed in a range of 0 to 100% SOC [14]. This prevents the battery voltage from being outside the permissible operating voltage range for long periods of time. Therefore, in this study, the discharge pulse time values were selected as 50 s, 125 s, and 200 s, respectively.

The pulse time gap, which is the interval between the discharge pulse and the sweep discharge pulse, significantly impacts battery performance. A longer pulse time gap may enhance energy efficiency by allowing the battery to stabilize between pulses, potentially reducing energy losses and extending battery life by minimizing thermal stress and material degradation. Conversely, shorter pulse time gaps can lead to increased power output but might cause performance instability and greater wear on the battery due to more frequent charge–discharge cycles. Additionally, adequate pulse time gaps contribute to effective thermal management by facilitating heat dissipation, influence charge redistribution within battery cells, and affect internal resistance and overall cycling performance. Thus, optimizing the pulse time gap is crucial for maintaining battery efficiency, longevity, and performance. Therefore, in this study, the pulse time gap values were selected as 50 s, 125 s, and 200 s, respectively.

The performance of the ECM may also be influenced by the rest time. To evaluate this effect, the rest time was set to three levels: 60, 120, and 180 s. The Taguchi design is beneficial in this case because it allows for the determination of the effects of individual factor levels on model performance without needing to evaluate all possible combinations of factor levels. Given that there are four control factors, each at three levels, the Taguchi OA L9 (34) was selected, as detailed in

Table 2. L9 (34) orthogonal array in this study.

Case	Pulse Time Gap (s)	Discharge Pulse Time (s)	Discharge Pulse C-Rate	Rest Time (s)
1	50	50	1C	60
2	50	125	2C	120
3	50	200	3C	180
4	125	50	2C	180
5	125	125	3C	60
6	125	200	1C	120
7	200	50	3C	120
8	200	125	1C	180
9	200	200	2C	60

.

The impact of control factors on the quality function is referred to as factor effects. Typically, the output response of the experimental design is evaluated using the signal-to-noise ratio (S/N), which is the method most commonly used for analysing factor effects in Taguchi’s orthogonal array (OA). In this study, as mentioned earlier, Taguchi OA is employed to assess how HPPC parameters influence ECM performance. The inputs are the pulse time gap, discharge pulse time, discharge pulse C-rate, and rest time. The root mean square error (RMSE) of the error between the ECM’s voltage response and the measured value under each different validation test condition is to be evaluated as the control factor. The experimental data were converted into a signal-to-noise ratio (S/N) to measure the deviation of parameter quality from the desired values. The Taguchi method involves analysing three types of performance characteristics: the larger the better, the smaller the better, and the nominal-the-better [28].

Deviations from the optimal value depend on result dispersion in the optimization process. Therefore, the analysis of variance (ANOVA) is based on the mean and variance of each test. ANOVA identifies sources of dispersion within a dataset and measures the contribution of each data point to the total variance. This technique assesses the significance of effects compared to random error, also known as noise. For the variance analysis of RMSE, the “smaller-the-better” criterion was chosen, and the signal-to-noise ratio (S/N) was calculated using Equation (1) as follows [26]:

$$S/N=-10\log \left({\displaystyle \frac{1}{n}}\right)\sum y^2$$

(1)

where y represents the response variable, and n denotes the number of experiments.

Following the experiments, analysis of variance (ANOVA) was carried out to calculate the variance of the errors. Furthermore, the contribution ratio of the variable factors to the output parameters was assessed. The sum of squares for both within-group and between-group variations was calculated to establish the contribution rate. Equation (2) represents the sum of squares within the group, while Equation (3) depicts the sum of squares between groups. Here, l denotes the number of parameter levels, j is the level number of the specific parameter p, and (${\left(S/N\right)}_j^2$ is the sum of the S/N ratios for the j level and parameter p. t denotes the number of repetitions for each level of parameter p, m signifies the total number of experiments, and ${\left(S/N\right)}_i$ refers to the S/N ratio for the ith experiment. The percentage contribution (Pc) of the factors is determined by the ratio of the sum of squares within the group to the sum of squares between the groups, as shown in Equation (4) [29].

$${SS}_p=\sum _{j=1}^l{\displaystyle \frac{{\left(S/N\right)}_j^2}{t}}-{\displaystyle \frac{1}{m}}{\left[\sum _{i=1}^m{\left(S/N\right)}_i\right]}^2$$

(2)

$${SS}_T=\sum _{i=1}^m{\left(S/N\right)}_i^2-{\left[\sum _{i=1}^m{\left(S/N\right)}_i\right]}^2$$

(3)

$$P_C={\displaystyle \frac{{SS}_p}{{SS}_T}}\ast 100$$

(4)

2.3. Battery Modelling Using Equivalent Circuit Model

The equivalent circuit model (ECM) is a widely used approach to simulate the electrical behaviour of lithium-ion batteries. The ECM abstracts the complex internal electrochemical processes of the battery into simpler electrical components, such as resistors, capacitors, and voltage sources. Among the various ECM configurations, the 2-loop model, also known as the 2RC model, is particularly effective in capturing the dynamic behaviour of lithium-ion batteries under different operating conditions. The structure of the 2RC model is depicted in Figure 2.

To identify the model parameters more easily, the equations of the 2RC model can be written in discrete form as follows:

$$U_{cell,i}\left(t\right)=U_{OCV}\left(t\right)-R_{int}{I}_{cell,i}\left(t\right)-U_{1,i}\left(t\right)-U_{2,i}\left(t\right)$$

(5)

$$U_{1,i+1}(t+1)=e^{{\displaystyle \frac{-∆t}{R_1{C}_1}}}{U}_{1,i}(t)+\left(1-e^{{\displaystyle \frac{∆t}{R_1{C}_1}}}\right)R_1{I}_i(t)$$

(6)

$$U_{2,i+1}(t+1)=e^{{\displaystyle \frac{-∆t}{R_2{C}_2}}}{U}_{2,i}(t)+\left(1-e^{{\displaystyle \frac{∆t}{R_2{C}_2}}}\right)R_2{I}_i(t)$$

(7)

In these equations (Equations (5)–(7)), $U_{cell}$ is the terminal voltage, $U_{OCV}$ is the open circuit voltage, $I_{cell,i}$ is the battery current, and $R_{int}$ is the internal ohmic resistance. U₁ and U₂ are the voltages of the two RC networks, with the subscript i indicating the discrete time index for the time step. Δt, R₁C₁ and R₂C₂ are the time constants of those RC networks. This ECM allows for the simulation of the terminal voltage using only the battery current.

The State of Charge (SoC) of battery is used to define the remaining capacity of the lithium-ion battery and is expressed between 0% and 100% by the following equation:

$$SoC={SoC}_{initial}+\int {\displaystyle \frac{I_{cell}}{Q_{max}}}dt SOC\left(t\right)$$

(8)

where ${SoC}_{initial}$ is the initial SoC of the battery cell; $Q_{max}$ is the maximum cell charge value.

Accurate parameter identification is crucial for the reliability of the 2-loop equivalent circuit model. In the equivalent circuit network model, the input parameter of the model is current $I_{cell}\left(t\right)$, while battery terminal voltage is the output parameter time step $t$. The parameters $R_{int}$ R₁, R₂, C₁ and C₂ are typically obtained through experimental techniques such as Electrochemical Impedance Spectroscopy (EIS) and Hybrid Pulse Power Characterization (HPPC). The $U_{OCV}\left(t\right)$ parameter is determined as a function of SoC and the battery temperature. SOC-OCV curve is calculated based on test results obtained at different temperatures such as −10 °C, 25 °C, and 40 °C.

The battery equivalent circuit model in (5)–(7) must be expressed in an explicit state-space form to estimate the SoC value using extended Kalman Filter (KF).

$$\begin{gathered} \mathit{x}\left(k+1\right)={\mathit{A}}_{\mathit{s}\mathit{y}\mathit{s}}\mathit{x}\left(k\right)+{\mathit{B}}_{\mathit{s}\mathit{y}\mathit{s}}u\left(k\right) \\ z\left(k\right)={\mathit{C}}_{\mathit{s}\mathit{y}\mathit{s}}\mathit{x}\left(k\right)+{\mathit{D}}_{\mathit{s}\mathit{y}\mathit{s}}u\left(k\right) \end{gathered}$$

(9)

where $z\left(k\right)ϵ{\mathbb{R}}^m$ and $u\left(k\right)ϵ{\mathbb{R}}^p$ are output and input of the system, respectively. The system input is $u\left(k\right)=I_{cell}\left(k\right),$ and output is $z\left(k\right)=U_{cell}\left(k\right)$. $\mathit{x}\left(k+1\right)ϵ{\mathbb{R}}^n$ is the state vector at time $\left(k+1\right);$ the state variables in this study are $\mathit{x}=\left[\begin{array}{ccc}\mathit{S}\mathit{o}\mathit{C}& {\mathit{V}}_{\mathbf{1}}& {\mathit{V}}_{\mathbf{2}}\end{array}\right]$. ${\mathit{A}}_{\mathit{s}\mathit{y}\mathit{s}}ϵ{\mathbb{R}}^{nxn}$, ${\mathit{B}}_{\mathit{s}\mathit{y}\mathit{s}}ϵ{\mathbb{R}}^{nxp}$, ${\mathit{C}}_{\mathit{s}\mathit{y}\mathit{s}}ϵ{\mathbb{R}}^{mxn}$ and ${\mathit{D}}_{\mathit{s}\mathit{y}\mathit{s}}ϵ{\mathbb{R}}^{mxp}$ are system matrices and expressed in the following form.

$$\begin{gathered} {\mathit{A}}_{\mathit{s}\mathit{y}\mathit{s}}=\left[\begin{array}{ccc}1& 0& 0\\ 0& e^{{\displaystyle \frac{∆t}{R_1{C}_1}}}& 0\\ 0& 0& e^{{\displaystyle \frac{-∆t}{R_2{C}_2}}}\end{array}\right], {\mathit{B}}_{\mathit{s}\mathit{y}\mathit{s}}=\left[\begin{array}{c}{\displaystyle \frac{{-I}_{cell}∆t}{Q_{max}}}\\ \left(1-e^{{\displaystyle \frac{∆t}{R_1{C}_1}}}\right)R_1\\ (1-e^{{\displaystyle \frac{∆t}{R_2{C}_2}}})R_2\end{array}\right] \\ {\mathit{C}}_{\mathit{s}\mathit{y}\mathit{s}}=\left[\begin{array}{ccc}1{\displaystyle \frac{\partial U_{OCV}}{\partial SoC}}& -1& -1\end{array}\right], {\mathit{D}}_{\mathit{s}\mathit{y}\mathit{s}}=-R_{int} \end{gathered}$$

(10)

As stated before, the HPPC test involves applying a series of charge and discharge pulses to the battery and measuring the corresponding voltage response. The data obtained from these tests are then used to fit the model parameters using optimization algorithms. The Taguchi method, as mentioned in Section 2.2, is a robust Design of Experiments technique that can be used to optimize the HPPC parameters, ensuring accurate and repeatable parameter identification.

The validity of the 2RC equivalent circuit model is verified by comparing the simulated voltage response with experimental data under various operating conditions, such as different current rates and temperatures. The model’s ability to accurately predict the voltage response under these conditions demonstrates its effectiveness in representing the dynamic behaviour of lithium-ion batteries.

2.4. Extended Kalman Filter

The State of Charge (SoC) of the battery is significantly affected by factors such as environmental temperature and current profile changes. Therefore, the dynamics of lithium batteries exhibit a highly nonlinear behaviour. In this study, the extended Kalman filter (EKF) is introduced as a solution to address challenges in state estimation problems in nonlinear systems, representing an improvement over the traditional Kalman filter algorithm. The EKF algorithm is given in

Table 3. Extended Kalman filter algorithm.

Summary of EKF
1: Initialization: $\mathit{x}\left(\mathbf{0}\right)=\mathit{E}\left[\mathit{x}\left(\mathbf{0}\right)\right]$ Error Definition: ${\tilde{\mathit{x}}}_{\mathbf{0}}={\mathit{x}}_{\mathbf{0}}-{\widehat{\mathit{x}}}_{\mathbf{0}}$ Covariance matrix: $\mathit{P}\left(\mathbf{0}\right)=\mathit{E}\left[\left({\mathit{x}}_{\mathbf{0}}-{\widehat{\mathit{x}}}_{\mathbf{0}}\right){\left({\mathit{x}}_{\mathbf{0}}-{\widehat{\mathit{x}}}_{\mathbf{0}}\right)}^{\mathit{T}}\right]=\mathit{E}\left[{\tilde{\mathit{x}}}_{\mathbf{0}}{{\tilde{\mathit{x}}}_{\mathbf{0}}}^{\mathit{T}}\right]$ 2: Predicting the one state estimation:             $\widehat{\mathit{x}}(\mathit{k}+\mathbf{1}|\mathit{k})=\mathit{A}{\widehat{\mathit{x}}\left(\mathit{k}\right|\mathit{k})}^{+}+\mathit{B}\mathit{u}(\mathit{k})$
3: Error covariance one step ahead:         $\mathit{P}(\mathit{k}+\mathbf{1}|\mathit{k})=\mathit{A}(\mathit{k}\left|\mathit{k}\right)\mathit{P}\left(\mathit{k}\right|\mathit{k}\left){\mathit{A}}^{\mathit{T}}\right(\mathit{k}\left|\mathit{k}\right)+\mathit{Q}\left(\mathit{k}\right)$
4: Calculating the Kalman Filter Gain:    $\mathit{K}=\mathit{P}(\mathit{k}+\mathbf{1}|\mathit{k}){\mathit{C}}^{\mathit{T}}{\widehat{\mathit{x}}(\mathit{k}+\mathbf{1}|\mathit{k}\left)\right[\mathit{C}\widehat{\mathit{x}}(\mathit{k}+\mathbf{1}|\mathit{k}\left)\mathit{P}\right(\mathit{k}+\mathbf{1}\left|\mathit{k}\right){\mathit{C}}^{\mathit{T}}\widehat{\mathit{x}}(\mathit{k}+\mathbf{1}|\mathit{k})+\mathit{R}(\mathit{k}\left)\right]}^{-\mathbf{1}}$
5: Updating the estimate with measurement:       $\mathit{x}(\mathit{k}+\mathbf{1}|\mathit{k}+\mathbf{1})=\mathit{x}(\mathit{k}+\mathbf{1}\left|\mathit{k}\right)+\mathit{K}(\mathit{k}+\mathbf{1})\left[\mathit{z}\right(\mathit{k})-\mathit{C}\widehat{\mathit{x}}(\mathit{k}+\mathbf{1}\left|\mathit{k}\right)]$
6: Error covariance measurement update:        $\mathit{P}(\mathit{k}+\mathbf{1}|\mathit{k}+\mathbf{1})=[\mathit{I}-\mathit{K}(\mathit{k}+\mathbf{1})\mathit{C}\left(\widehat{\mathit{x}}\right(\mathit{k}+\mathbf{1}\left|\mathit{k}\right)\left)\right]\mathit{P}(\mathit{k}+\mathbf{1}|\mathit{k})$
7: Repeating Step 2 to 6

as follows for discrete systems.

2.5. Selection of Optimal Model-Based Genetic Algorithm-Based Multi-Objective Approach

Genetic algorithms (GAs), which are derived from the principles of natural selection and genetics, constitute a highly effective optimization technique for solving complex, multi-objective problems, such as the optimization of engineering systems. The fundamental approach of GAs is to enhance a population of potential solutions, with the goal of identifying outcomes that are either optimal or near-optimal results.

The main operators of a GA include selection, crossover, and mutation operators. A random population is initially generated in the GA optimization process. The fitness function, which evaluates the quality of each population member, is calculated to transfer the randomly generated individuals. Subsequently, the selection operator is employed to select new individuals according to fitness function value. New offspring are then generated using the crossover operator, and the fitness function is recalculated for each offspring. This iterative process is repeated until criterion is met.

During this study, the determination of optimal battery ECM model parameters (pulse time gap, discharge pulse time, C-rate, and rest time) is considered as a multi-objective optimisation problem with constraints. The purpose of the optimisation process is to minimize total RMSE errors between real and simulation model data corresponding to 30%, 50%, and 90% SoC values under different environmental conditions.

Three objective functions were defined in MATLAB 2023a Software, and GAMULTIOBJ function was utilized to achieve the Pareto optimal solution set. These functions are given as follows.

$$\begin{gathered} f_{90\mathrm{\%}\mathit{SoC}\mathit{RMSE}\mathit{val}.}=\mathrm{m}\mathrm{i}\mathrm{n}.\sum _{i=1}^N{PTG}_i,{DPT}_i,{Crate}_i,{RT}_i \\ {f}_{50\mathrm{\%}\mathit{SoC}\mathit{RMSE}\mathit{val}.}=\mathrm{m}\mathrm{i}\mathrm{n}.\sum _{i=1}^N{PTG}_i,{DPT}_i,{Crate}_i,{RT}_i \\ {f}_{30\mathrm{\%}\mathit{SoC}\mathit{RMSE}\mathit{val}.}=\mathrm{m}\mathrm{i}\mathrm{n}.\sum _{i=1}^N{PTG}_i,{DPT}_i,{Crate}_i,{RT}_i \\ -10\le T_{env.}\le 40w \end{gathered}$$

(11)

where $PTG, DPT, Crate,$ and $RT$ are the pulse time gap, discharge pulse time, C-rate, and rest time, respectively. The subscript $i$ demonstrates the number of cases. $T_{env.}$ is the environmental temperature.

A simplified diagram illustration of used experimental methods and all other models is presented in Figure 3.

3. Results and Discussion

The evaluation of the results in this study is divided into two parts. In the first part, experimental results for current and voltage parameters were evaluated for different ambient temperatures (−10 °C, 25 °C, 40 °C), and a statistical analysis (ANOVA) was performed to evaluate the results. The accuracy of the selected parameters in predicting the output points of the battery at different SOC points (SOC 90, SOC 50, SOC 30) was examined and shown statistically by taking RMSE values into consideration. In the second part, the model with the highest accuracy was determined by ANOVA analysis, and then the most suitable model was determined by the genetic algorithm obtaining equivalent circuit models (ECMs) for diverse combinations of these parameters. After the parameters were determined based on the model that minimizes the RMSE value, the EKF algorithm was utilized for SoC estimation; then, this model was tested in real time, and comparisons were made by making SOC predictions.

3.1. Model Validation and ANOVA Results

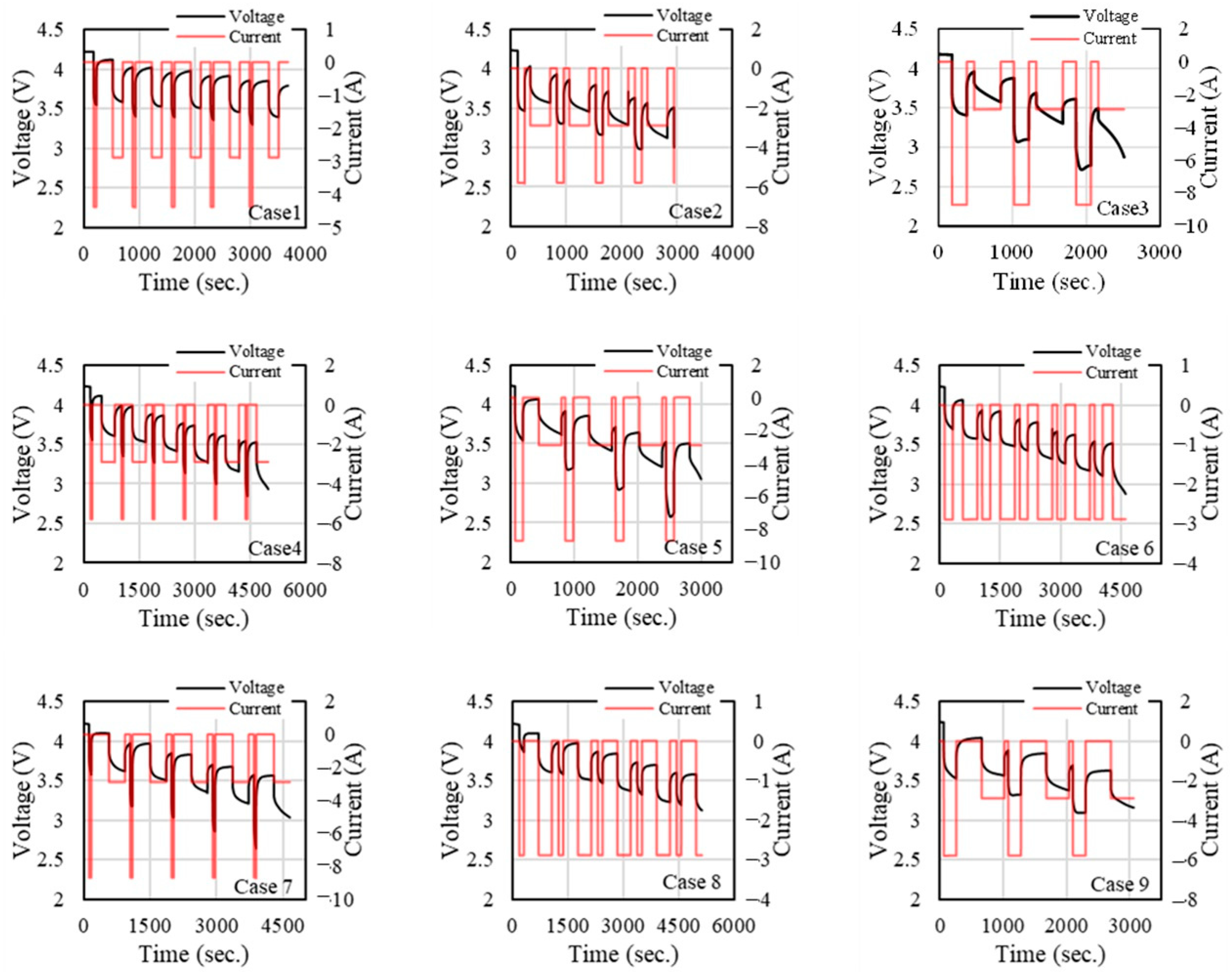
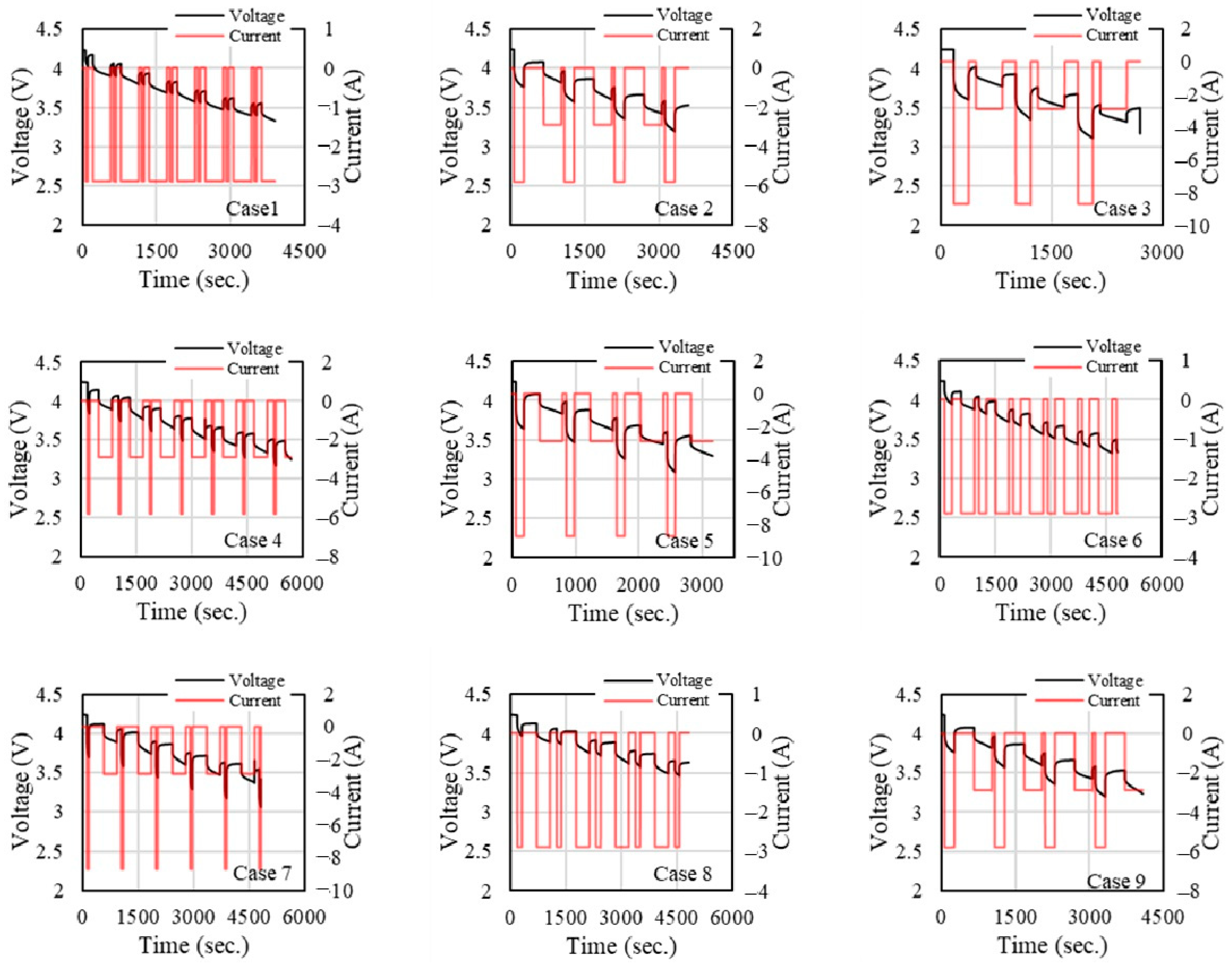
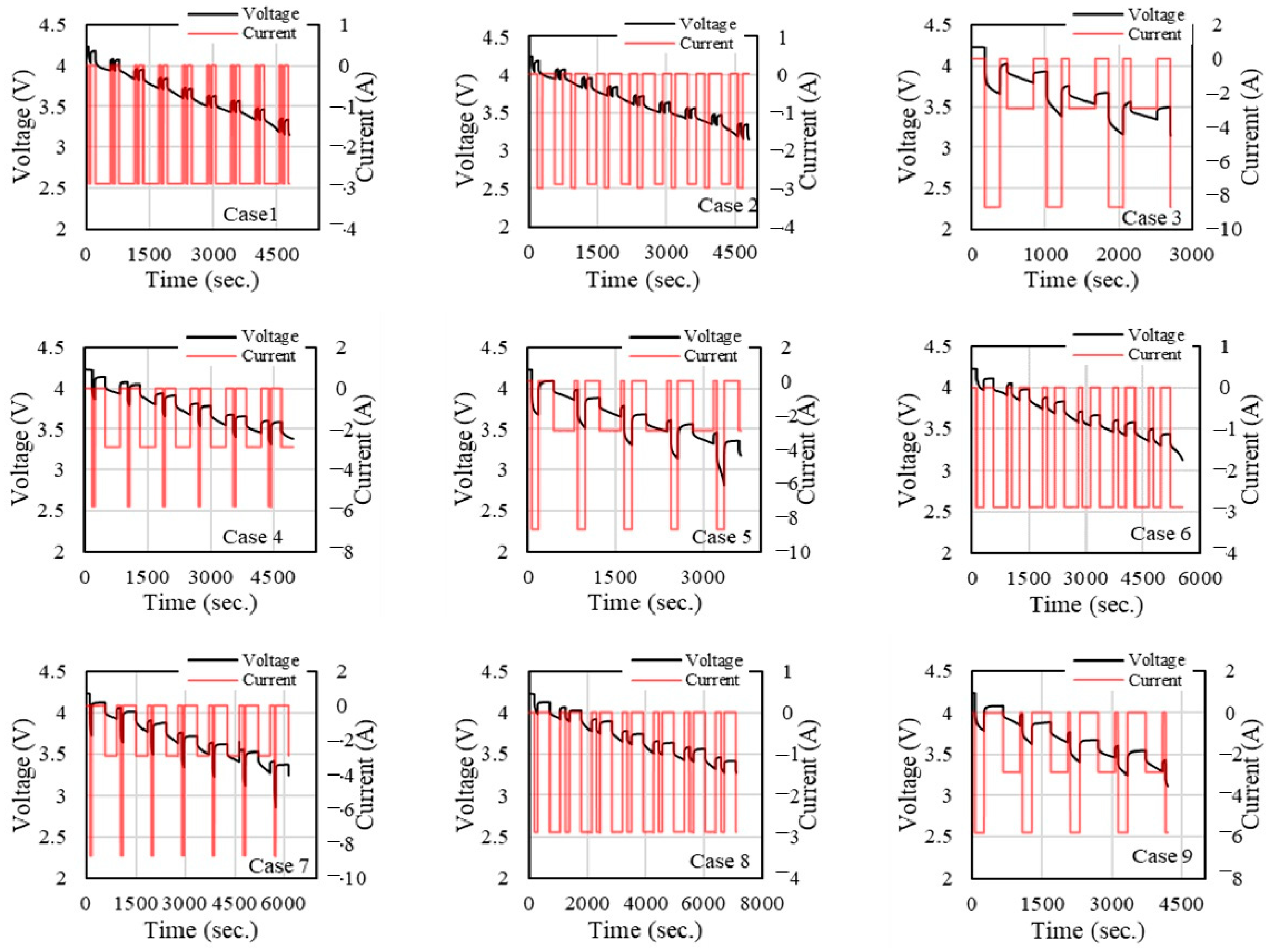
Figure 4, Figure 5 and Figure 6 show the current and voltage response over time under various ambient temperatures (−10 °C, 25 °C and 40 °C) across different cases for each temperature condition. In Figure 4, the voltage remains within the range of approximately 2 to 4.5 V, while the current shows varied patterns of charging and discharging with spikes and drops. The different cases appear to be set up to observe the battery’s response to distinct operating conditions. The voltage profiles seem relatively stable, albeit with small fluctuations, whereas the current profiles exhibit more pronounced variations. In all cases, the voltage generally stays within a narrow band between 3 V and 4.2 V, which is typical for lithium-ion batteries. The relatively stable voltage profiles across all cases indicate that the battery’s State of Charge is being maintained effectively without severe voltage drops, which would suggest significant capacity depletion or over-discharge.

The current profiles are more variable than the voltage profiles, with distinct spikes and drops corresponding to charging and discharging cycles. These variations are likely due to different load conditions applied in each case. Cases 3, 5, and 9 exhibit more extreme current behaviours, with higher peaks or deeper discharges. This could indicate more aggressive charging or discharging scenarios, putting the battery under higher stress. Cases 1 and 7 appear to be more moderate in terms of current fluctuations, which could represent standard or baseline testing conditions where the battery is not overly stressed.

At a lower temperature, the voltage drop becomes more abrupt and steeper across most cases compared to 40 °C. Cold temperatures affect the internal resistance and kinetics of the battery, causing higher voltage drop-offs. This is especially evident in Case 3 and Case 7, where voltage drops sharply after each pulse. The current shows a similar pattern to 25 °C and 40 °C, but the voltage is less stable.

Figure 5 illustrates the current and voltage results for different cases at an ambient temperature of 25 °C. In this condition, the voltage behaviour stabilizes compared to −10 °C. The voltage curves still show stepwise declines, but they are smoother than at lower temperatures. Case 3 and Case 7, with larger current pulses, continue to show significant drops in voltage after current pulses. The current pulses resemble those at 40 °C, but the voltage response is more stable. This suggests that 25 °C may represent a more optimal operating temperature for the battery, where the performance is more predictable, and less stress is imposed on the voltage.

In Figure 6, for all cases, the voltage shows a gradual decline, but there are consistent steps or reductions following each pulse in the current. Cases with lower current magnitudes (such as Case 2, Case 4, and Case 6) exhibit a smoother voltage drop, while others with higher or more varied current show more abrupt declines (e.g., Case 3 and Case 7). The current has a pulse-type waveform, with various amplitudes. The more significant current pulses (e.g., Case 7, Case 3) correspond to more pronounced voltage drops. Some cases show a lower magnitude of current pulses (e.g., Case 1), indicating a less aggressive charging/discharging profile, while others have alternating positive and negative current pulses, signifying charge/discharge cycling.

While evaluating the temperature effects on voltage response, the experimental results clearly show that temperature plays a critical role in the battery’s voltage response and overall performance. At −10 °C, the sharp voltage drops at this temperature, especially during discharge pulses, are directly tied to a possible increase in internal resistance. These voltage fluctuations demonstrate the difficulty the battery faces in maintaining stable power output under cold conditions, which also increases the RMSE in the SOC estimation. At 40 °C, the electrochemical reactions occur more rapidly, and due to a possible increase in the internal resistance beng lower, the battery is prone to thermal degradation. The results show a smoother voltage curve compared to −10 °C, but over time, high temperatures can lead to faster capacity fading and side reactions within the battery. These thermal effects increase the stress on the system, affecting long-term performance and the accuracy of SOC estimation models.

While discussing the impact of pulse time gap and discharge pulse time, both pulse time gap and discharge pulse time significantly influence the battery’s behaviour across different temperatures. A longer pulse time gap allows the battery to rest and recover, enabling thermal dissipation and charge redistribution within the cells. At low temperatures like −10 °C, this recovery period is crucial as it helps mitigate the effects of high internal resistance, leading to more stable voltage profiles and reduced errors in the SOC estimation. Conversely, at higher temperatures, a longer pulse time gap also helps manage thermal runaway by allowing the battery to cool down between pulses.

At low temperatures, shorter discharge pulses are preferable because longer pulses exacerbate voltage drops due to increased internal resistance. Also, at low temperatures, extended discharge pulses lead to larger deviations in the voltage curve, highlighting the physical strain on the battery’s electrochemical system. At 40 °C, longer discharge pulses also increase the risk of overheating, as shown by the gradual voltage degradation over time in the charts.

The effect of input parameters (pulse time gap, discharge pulse time, discharge pulse C-rate, and rest time) on RMSE values for different ambient temperatures is evaluated in Figure 7. This figure shows the main effect plot for signal-to-noise (S/N) ratios, using the “Smaller is better” criterion. At the ambient temperature of −10 °C (Figure 7a), the S/N ratio decreases slightly as the pulse time gap increases from 50 to 200 s, indicating that a larger pulse time gap may not significantly enhance the signal-to-noise performance of the system. However, the decrease is relatively small, suggesting that the influence of pulse time gap on battery parameter identification is minor. The S/N ratio fluctuates in relation to discharge pulse time, initially decreasing from 50 to 125 s but then increasing slightly. This suggests that an optimal discharge pulse time exists, likely between 100 and 150 s. Beyond this range, the performance degrades, possibly due to thermal or internal resistance effects in the battery. While evaluating the discharge pulse C-rate, a decreasing trend is shown from a C-rate of 2.9 to 8.7. This means that higher C-rates negatively affect the signal-to-noise ratio. A lower C-rate is preferable for minimizing parameter variance during identification, likely because high C-rates introduce larger thermal effects and voltage drops, which reduce the precision of parameter estimates. The most significant variation in S/N ratios is observed in the rest time. The ratio drops to its lowest at 120 s and then dramatically increases at 180 s. This indicates that inadequate rest time can degrade the performance of the parameter identification, but beyond a critical rest period, the signal-to-noise ratio improves significantly. A rest time around 180 s appears to provide the best conditions for battery relaxation and more accurate parameter extraction. From the ANOVA, it can be said that rest time has the most pronounced effect on the signal-to-noise ratio, with 180 s offering the best performance. Lower C-rates and moderate discharge pulse times (between 100 and 150 s) are also beneficial. Overall, adjusting the rest time and C-rate can substantially improve the accuracy of battery parameter identification based on the “Smaller is better” criterion.

At an ambient temperature of 25 °C (Figure 7b), the S/N ratio increases significantly from 50 to 200 s, indicating that increasing the pulse time gap improves the system’s performance. The discharge pulse time has a marked effect on the S/N ratio, as shown by the peak at 125 s. There is a significant rise from 50 to 125 s, followed by a sharp decrease at 200 s. This suggests that the optimal discharge pulse time for achieving better signal-to-noise performance is around 125 s. Any further increase in discharge time might introduce negative effects, such as thermal instability, which degrade the precision of parameter estimation. The C-rate parameter has a relatively flat trend, but there is a slight decline in the S/N ratio as the C-rate increases. In terms of rest time, there is an increase in the S/N ratio from 60 to 120 s, followed by a slight decrease at 180 s.

At an ambient temperature of 40 °C (Figure 7c), there is a sharp increase in the S/N ratio from 50 s to 125 s, indicating that increasing the pulse time gap significantly improves the precision of the parameter identification. However, after this peak at 125 s, the S/N ratio decreases sharply at 200 s. This suggests that while a pulse time gap of 125 s yields the best performance, extending the pulse time gap to 200 s may introduce detrimental effects, such as reduced accuracy or increased variability. The discharge pulse time exhibits a fluctuating trend. The S/N ratio increases slightly at 125 s, then drops at 200 s. The C-rate shows a relatively flat trend, with only minor variations in the S/N ratio. A slight increase can be observed between 2.9 and 5.8, followed by a decrease at 8.7. The rest time has a similar trend to the previous graphs, showing a drop in the S/N ratio at 120 s and a recovery at 180 s.

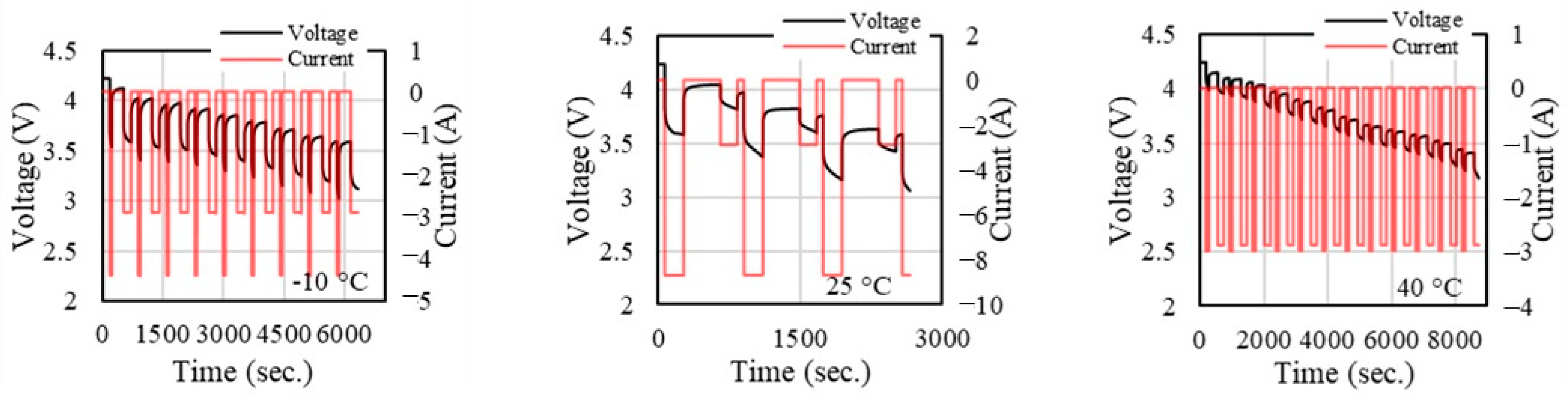
Figure 8 presents the voltage and current profiles of a battery under varying ambient temperatures (−10 °C, 25 °C, and 40 °C), highlighting the optimal experimental parameters under these conditions. At an ambient temperature of −10 °C, both voltage and current experience fluctuations, indicating a performance degradation at low temperatures. At 25 °C, the voltage remains relatively stable, but current fluctuations are more pronounced, with sharp peaks and troughs that may correspond to the optimal operation range under standard conditions. At 40 °C, there is a steady decline in voltage over time, while the current oscillates periodically.

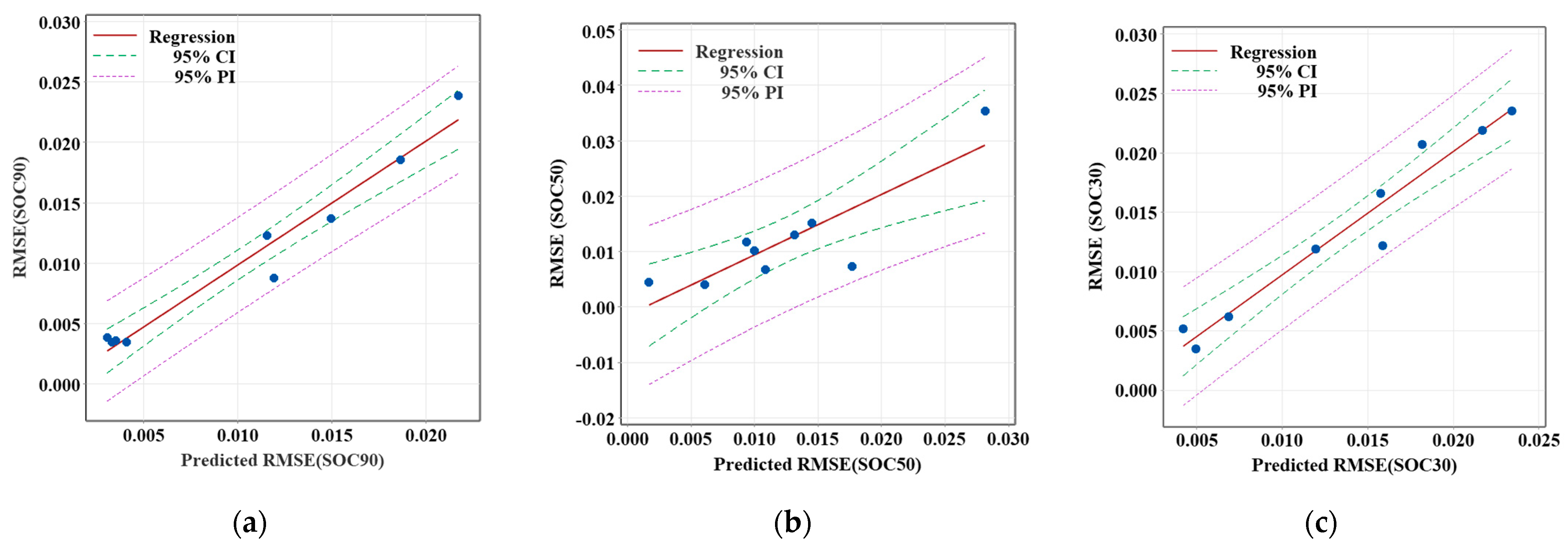
Figure 9 illustrates the regression analysis of the root mean square error (RMSE) for different SOC values at an ambient temperature of −10 °C. The regression lines, along with the 95% confidence intervals (CIs) and 95% prediction intervals (PIs), provide the relationship between the predicted and observed RMSE values for SOC at various stages of the battery’s discharge cycle: SOC90, SOC50, and SOC30. All three issues demonstrate a positive correlation between the predicted and observed RMSE, with the data points generally clustering along the regression lines. The regression model results demonstrated that the SOC estimation method is most reliable in the early stages of discharge at −10 °C but faces challenges in the later stages, where estimation errors increase.

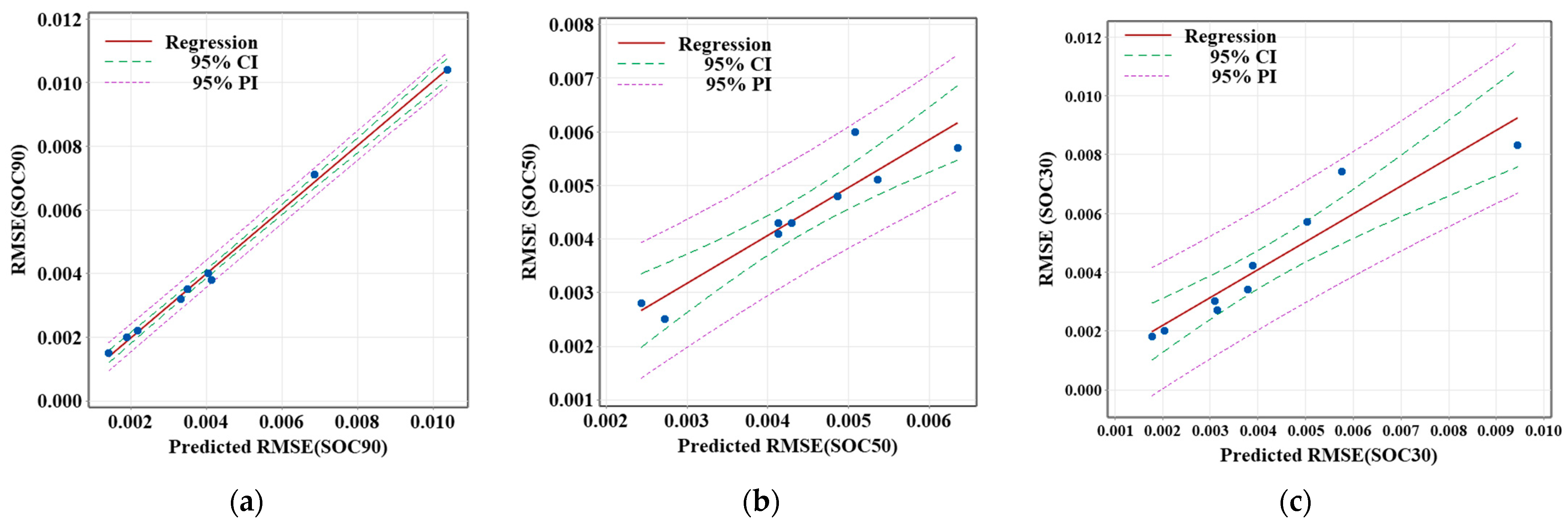
The RMSE values of different SOC values (SOC90, SOC50, and SOC30) at an ambient temperature of 25 °C are shown in Figure 10. The regression models display positive correlations between the predicted and observed RMSE in all three plots, reflecting consistent model performance across different SOC levels. However, as seen in the −10 °C analysis, variability increases in the later stages of the discharge process, indicated by the widening of confidence and prediction intervals. In summary, the SOC estimation model demonstrates high accuracy at the beginning of the discharge process at 25 °C, but its performance declines in the later stages, particularly as the battery approaches deeper discharge.

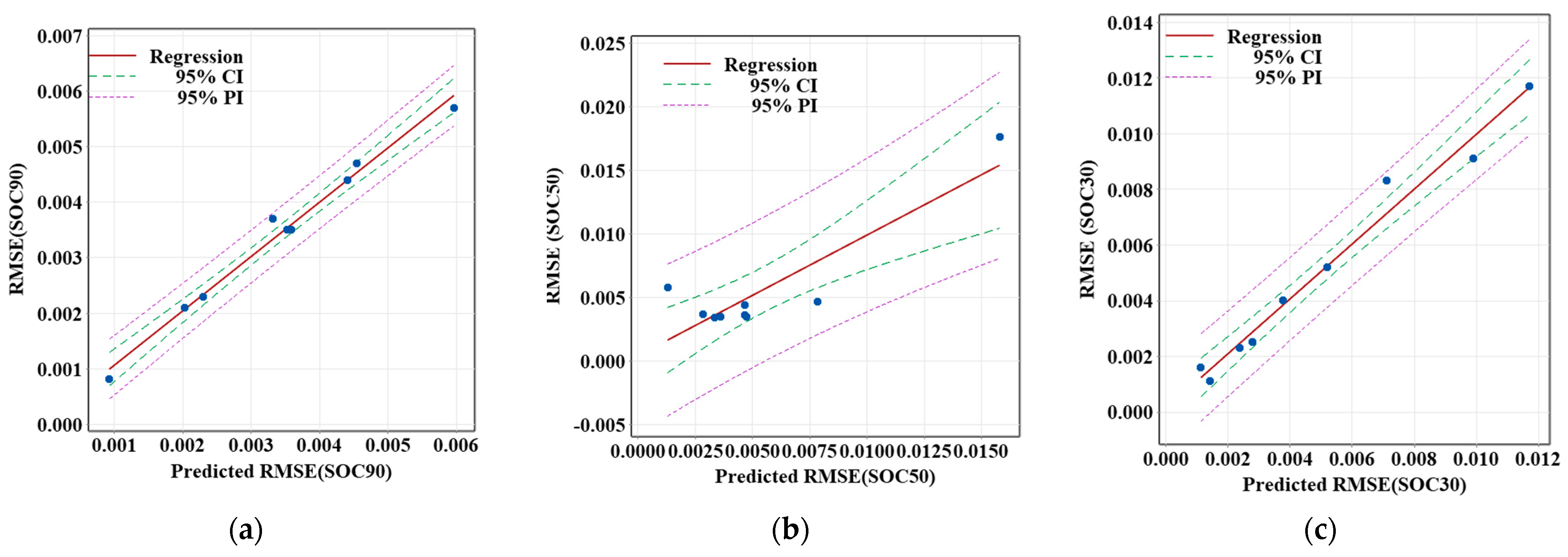
The RMSE values for various SOC values at an ambient temperature of 40 °C are given in Figure 11. Across all stages (SOC90, SOC50, and SOC30), the data points generally follow a positive correlation, with some scatter. The 95% confidence and prediction intervals show that the accuracy of the SOC estimation decreases slightly as the battery approaches lower charge levels. However, the overall model performance remains nearly stable.

Briefly, at −10 °C, the RMSE is higher due to the increased internal resistance and more pronounced voltage drops. At 40 °C, the RMSE remains relatively low in the early stages but increases as the battery heats up, highlighting the need to account for thermal effects in the model. At lower SOC levels, this resistance increases, causing larger voltage deviations and higher RMSE, which emphasizes the importance of accurate SOC estimation models at different SOC levels.

Table 4. ANOVA results of RMSE for the different ambient temperatures.

Ambient Temperature	Source	SOC90	SOC50	SOC30
−10 °C	Regression	98.72%	90.42%	98.85%
	Pulse time gap (s)	40.73%	39.83%	66.35%
	Discharge pulse time (s)	37.05%	17.59%	3.00%
	Discharge pulse C-rate	1.02%	7.49%	8.49%
	Rest time	0.01%	0.17%	2.16%
	Other parameters	19.91%	25.34%	18.85%
25 °C	Regression	99.91%	99.16%	97.66%
	Pulse time gap (s)	49.48%	71.71%	39.80%
	Discharge pulse time (s)	10.49%	3.70%	21.43%
	Discharge pulse C-rate	12.91%	7.05%	6.73%
	Rest time	1.22%	1.69%	8.07%
	Other parameters	25.81%	15.01%	21.63%
40 °C	Regression	99.79%	91.74%	99.27%
	Pulse time gap (s)	55.50%	31.55%	56.91%
	Discharge pulse time (s)	18.70%	36.55%	0.06%
	Discharge pulse C-rate	11.69%	15.57%	7.41%
	Rest time	0.41%	5.83%	0.01%
	Other parameters	13.49%	2.24%	34.88%

illustrates the ANOVA results for RMSE across different stages of battery discharge (SOC90, SOC50, SOC30) under three distinct ambient temperatures: −10 °C, 25 °C, and 40 °C. Each SOC value is analysed with respect to multiple sources of variation, including regression, pulse time gap, discharge pulse time, C-rate, rest time, and other parameters. The table indicates the percentage contribution of each source to the total variance in RMSE. The regression model consistently contributes the highest percentage to the variance in RMSE across all ambient temperatures and SOC levels, ranging from 90.42% to 99.79%, indicating that the model is the primary driver of SOC estimation accuracy. As the ambient temperature increases from −10 °C to 40 °C, the regression contribution becomes slightly higher in most cases, reflecting better model performance under higher temperatures. This suggests that the estimation model is more stable and accurate at warmer temperatures, particularly at 40 °C. The results also showed that pulse time gap and discharge pulse time significantly affect the RMSE, especially at low and high ambient temperatures (−10 °C and 40 °C). The contribution of these parameters (pulse time gap and discharge pulse time) also varies based on the battery’s SOC levels. At higher SOC levels (SOC 90%), the battery voltage is closer to its maximum, and the electrochemical reactions are more stable. In this state, the battery is less sensitive to changes in pulse time gap and discharge pulse time. However, at extreme temperatures, especially at −10 °C, even at high SOC, increased internal resistance causes the battery to struggle with large pulse durations, resulting in higher RMSE values. At mid SOC levels (SOC 50%), the battery begins to experience more significant voltage drops as the available charge decreases. The effects of both pulse time gap and discharge pulse time become more pronounced in this range, especially at low temperatures, where voltage drops due to increased resistance can be severe if the pulse duration is too long or the time gap between pulses is too short. Similarly, at high temperatures, extended discharge times at mid SOC can cause thermal runaway, impacting RMSE. At low SOC levels (SOC 30%), the battery voltage is already near its cutoff threshold, and any additional stress due to inappropriate pulse durations or insufficient recovery time between pulses can cause sharp voltage drops, increasing the RMSE. At low temperatures, the battery becomes more susceptible to issues with voltage predictions as a result of its elevated internal resistance. Similarly, at high temperatures, the increased electrochemical activity makes the battery more sensitive to pulse time changes.

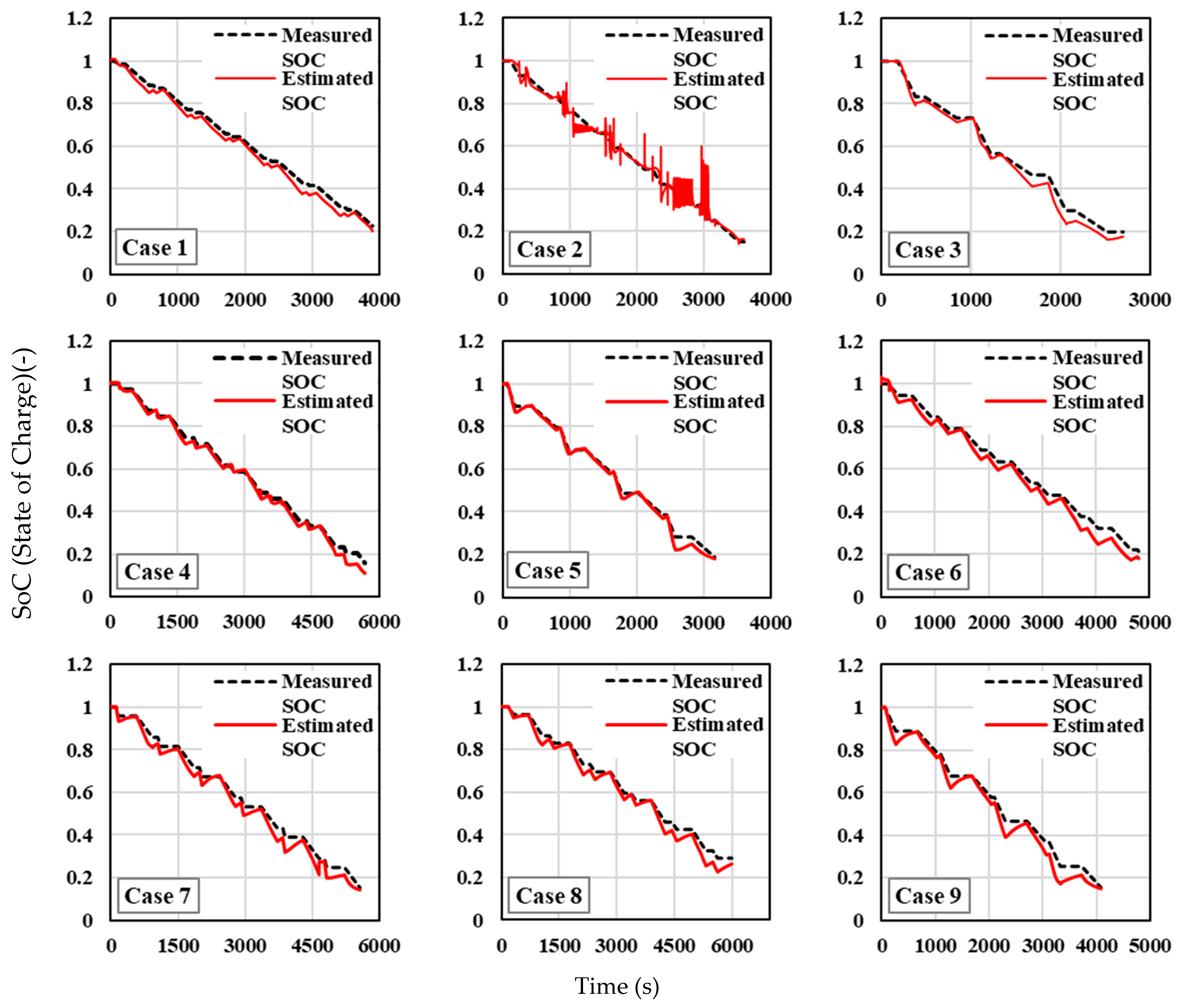
3.2. SOC Estimation Results

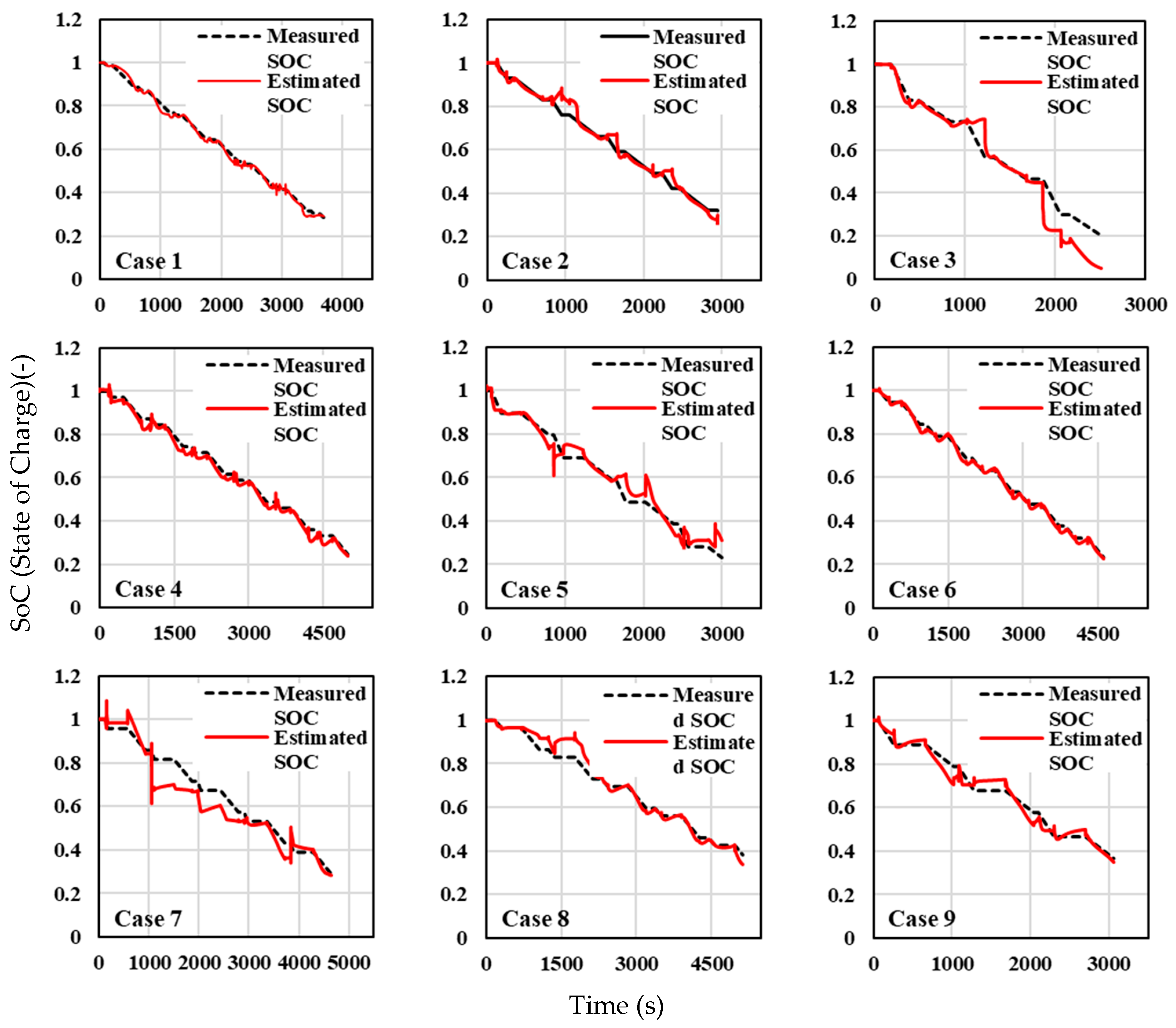
Figure 12, Figure 13 and Figure 14 show the SOC estimation compared against the measured SOC values for different test cases under ambient temperatures of −10 °C, 25 °C, and 40 °C, respectively. At an ambient temperature of −10 °C (Figure 12), across all cases, both the measured and estimated SOC curves display a downward trend as time progresses, indicating that the SOC decreases steadily, consistent with battery discharge behaviour under cold conditions. The estimated SOC generally tracks the measured SOC, though there are deviations in some cases that need closer inspection. The SOC estimation methodology performs reasonably well for the majority of cases, with minimal deviations between the estimated and measured values in many instances, especially at the beginning and middle stages of the discharge process. However, cases, such as Case 2, Case 3, Case 5, and Case 7, exhibit more significant deviations, particularly in the middle and later stages of the discharge cycle, highlighting potential weaknesses in the parameter identification or the effects of extreme temperatures (−10 °C) on battery performance. The recurring deviations at the end of the discharge cycles across several cases suggest that the model’s accuracy could be improved with better handling of SOC dynamics during the final phase of the battery’s discharge.

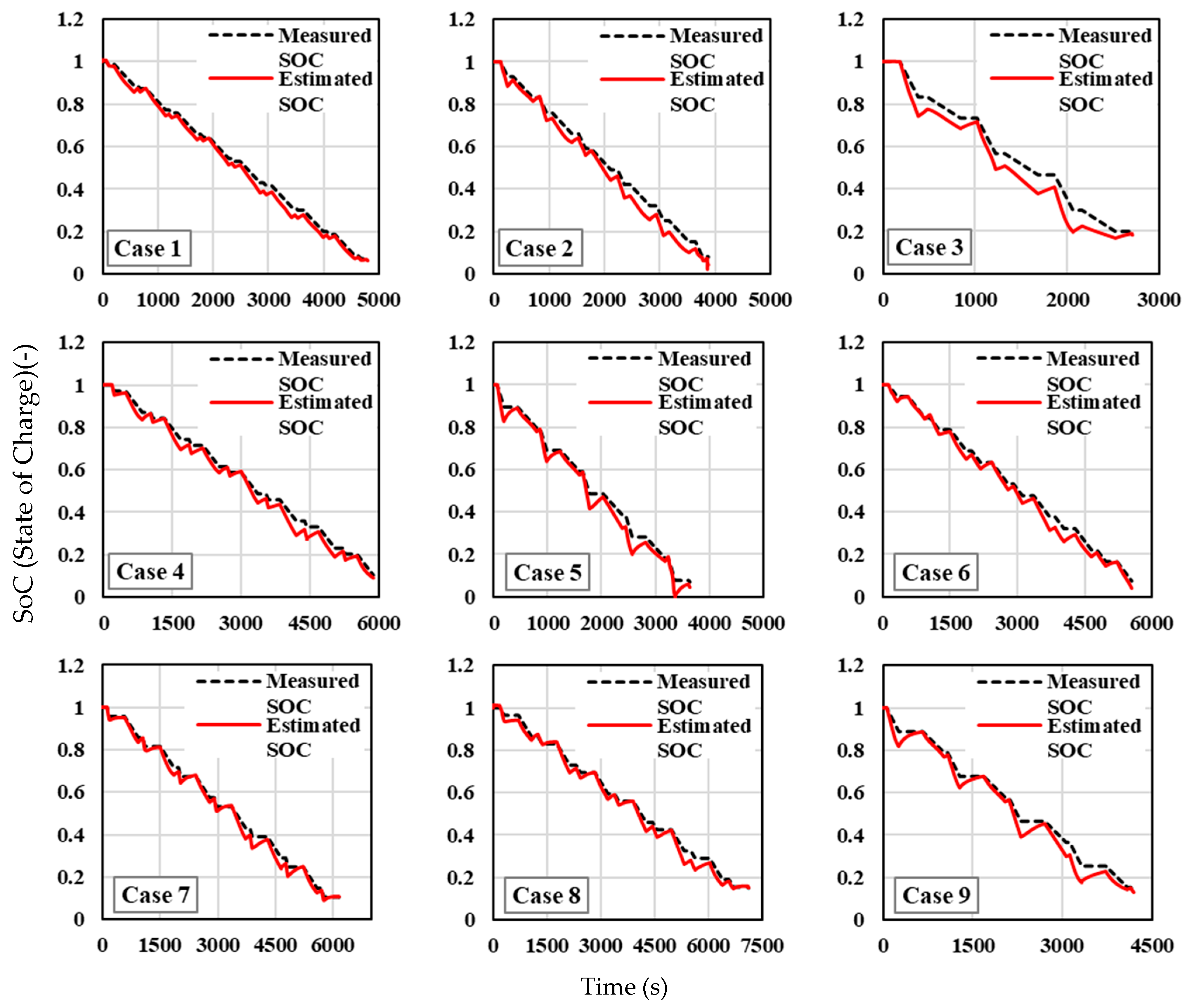
The estimated SOC against the measured SOC for different cases at an ambient temperature of 25 °C is given in Figure 13. This represents a more moderate, favourable operating temperature for lithium-ion batteries compared to the previous analysis at −10 °C and, as a result, the SOC estimation performance under these conditions is expected to improve due to more stable electrochemical activity in the cells. The estimated SOC curves in most cases are more closely aligned with the measured SOC values, indicating that the parameter identification process is more reliable under these moderate-temperature conditions. However, deviations still exist in certain cases, particularly in dynamic operating conditions. Case 1, Case 4, and Case 5 exhibit nearly perfect SOC tracking, suggesting that the model performs optimally in these scenarios. Case 2 presents an exception, with significant noise or instability in the middle of the discharge process, which may indicate an issue with the sensor data or a model mismatch under certain dynamic operating conditions. For the other cases, the SOC estimation is accurate during the earlier and middle stages, with some deviations towards the end of the discharge cycle.

High ambient temperatures generally accelerate electrochemical reactions in lithium-ion batteries, potentially leading to faster discharge and increased errors in SOC estimation models due to thermal effects. At an ambient temperature of 40 °C, the SOC estimation curves still follow the measured SOC closely, but there are instances where the deviation between the estimated and measured SOC increases, particularly in cases involving significant dynamic variations (Figure 14).

The SOC estimation model generally performs well, though the higher temperature appears to introduce more noticeable deviations in some cases, particularly during the middle and later stages of the discharge process. Case 1, Case 4, and Case 7 maintain high accuracy throughout the discharge cycle, indicating that the SOC estimation model is robust under high-temperature conditions for certain battery dynamics. Case 2, Case 5, Case 6, and Case 9 show deviations that become more pronounced in the later stages of the discharge. In Case 3, the model shows overprediction, reflecting that thermal effects at 40 °C are not fully accounted for, leading to increased errors during periods of dynamic battery behaviour.

Briefly, during the middle and later stages of discharge, the battery experiences a possible increase in internal resistance due to the polarization of active material. This phenomenon is more pronounced in certain cases where the discharge pulses are more aggressive (e.g., higher C-rates, longer discharge pulse times). As the discharge progresses, especially at lower SOC levels, the accumulation of polarization effects creates voltage drops, which lead to deviations between the measured and estimated SOC values. Additionally, as the SOC decreases, the battery approaches its cutoff voltage, and charge transfer resistance increases. This contributes to the observed deviations in the voltage response during the final discharge stages. The operating temperature plays a significant role in the accuracy of SOC estimation, as said before. In cases where the battery is tested at extreme temperatures (e.g., −10 °C or 40 °C), thermal effects lead to deviations. At low temperatures, the battery’s ionic mobility is reduced, leading to slower reaction kinetics and higher internal resistance, particularly during the final stages of discharge when the battery is already under stress. These combined effects cause the battery voltage to deviate more significantly from the expected behaviour. At high temperatures (40 °C), the battery experiences faster electrochemical reactions and potential thermal degradation, which can cause voltage drifts or inconsistencies in the SOC estimation. The deviations in these cases during the final stages can be attributed to accelerated capacity loss and self-discharge at elevated temperatures. Also, the deviations in cases can also be linked to the rest time allowed between pulses. During rest periods, the battery undergoes charge redistribution and voltage recovery as it equilibrates after a high-power discharge. In cases where the rest time is too short, the battery does not fully recover, leading to deviations in the SOC estimation due to an incomplete relaxation of the battery’s voltage.

Table 5. RMSE values of SOC estimation using EKF for each case under different temperature conditions.

Cases	−10 °C	25 °C	40 °C
1	0.0202	0.0273	0.0248
2	0.0299	0.0322	0.0419
3	0.0802	0.0329	0.0611
4	0.022	0.0211	0.0301
5	0.0417	0.0207	0.0361
6	0.0167	0.0371	0.0275
7	0.0643	0.0341	0.0231
8	0.0354	0.0324	0.0246
9	0.0321	0.0409	0.0384

presents the variation in the measured property across distinct temperature levels (−10 °C, 25 °C, and 40 °C). At −10 °C, the recorded values span from 0.0167 to 0.0802, with Case 3 exhibiting the highest value, implying a greater sensitivity to lower temperatures. At 25 °C, the range becomes narrower, between 0.0207 and 0.0371, indicating more stable behaviour at moderate temperatures. At 40 °C, a moderate increase in variability is noted, with values ranging from 0.0231 to 0.0611, where once again, Case 3 registers the highest measurement.

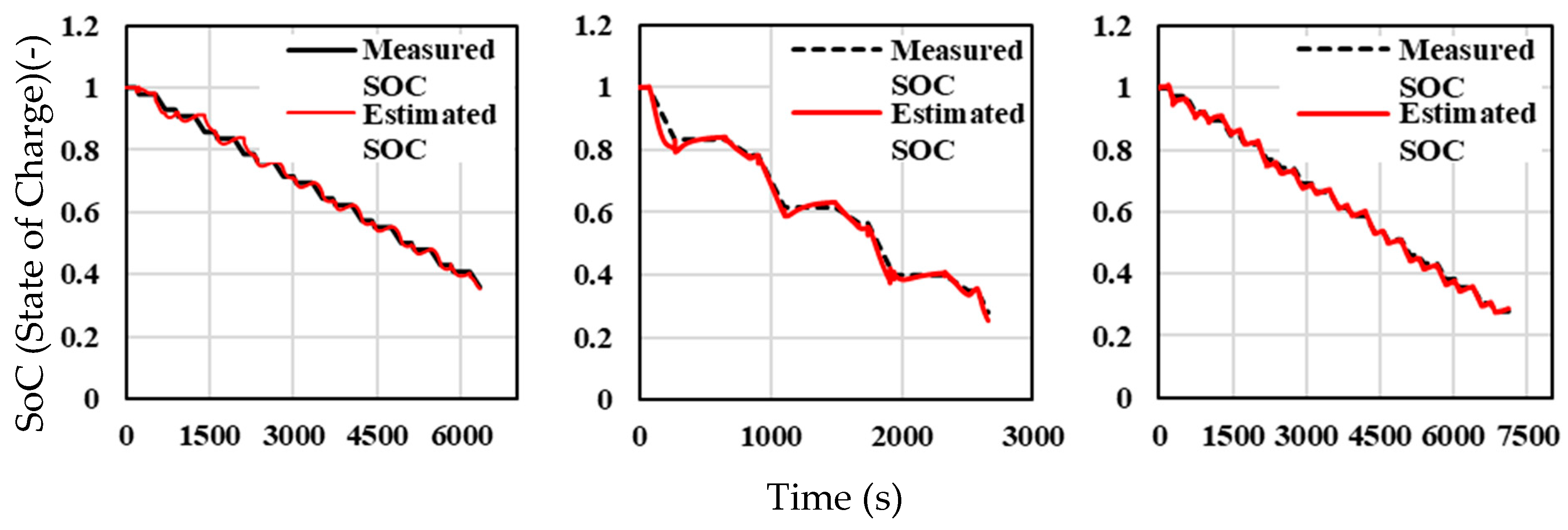
Figure 15 presents the SOC estimation performance under optimal input conditions at three distinct ambient temperatures. Across all three temperature conditions, the SOC estimation follows the general trend of the measured SOC with good alignment. The SOC estimation model performs optimally at 40 °C, with strong alignment between the estimated and measured SOC. This suggests that the model functions well under conditions where the battery experiences higher levels of electrochemical activity.

The RMSE values corresponding to the three temperature levels (−10 °C, 25 °C, and 40 °C) are presented in

Table 6. RMSE values of SoC estimation using EKF for each case under different temperature conditions.

	−10 °C	25 °C	40 °C
RMSE	0.0144	0.0197	0.0105

. The data reveal that the error is lower at −10 °C (0.0144) and 40 °C (0.0105), with a moderate increase observed at 25 °C (0.0197). In comparison with the results shown in Table 5, there is a significant reduction in RMSE, indicating improved performance under optimized conditions. This reduction in error underscores the enhanced reliability of the system across varying temperature conditions following optimization. These findings highlight the critical role of optimization in minimizing fluctuations and improving the overall stability of the system.

The SOC estimation model developed for a single lithium-ion cell can be scaled to battery packs, which are composed of many cells connected in series and parallel configurations. However, larger battery packs introduce non-uniformities between individual cells, which can affect SOC accuracy. These non-uniformities arise due to differences in cell aging, temperature gradients, and manufacturing tolerances, leading to deviations in the performance of individual cells within the pack. If the SOC estimation model is applied without accounting for cell balancing and cell-to-cell variability, the SOC predictions at the pack level may be inaccurate. For example, under dynamic loading conditions or extreme temperatures, certain cells within the pack may experience higher internal resistance or capacity fade than others, causing the pack-level SOC estimation to deviate from the true state of the individual cells. Temperature gradients are more pronounced in larger battery packs because cells in the centre of the pack may heat up more quickly due to limited cooling, while cells near the edges may stay cooler. As temperature significantly affects the internal resistance, polarization, and overall electrochemical behaviour of lithium-ion cells, this introduces additional complexities in maintaining accurate SOC estimation across the pack. Also, cell balancing becomes more crucial in large battery packs to maintain consistent SOC across all cells. Passive and active balancing strategies can be employed to equalize the SOC and voltage drift between cells. If the SOC estimation model and HPPC parameters are scaled up without considering the balancing mechanisms, the deviations between individual cells’ SOC values can accumulate, leading to inaccurate pack-level SOC predictions.

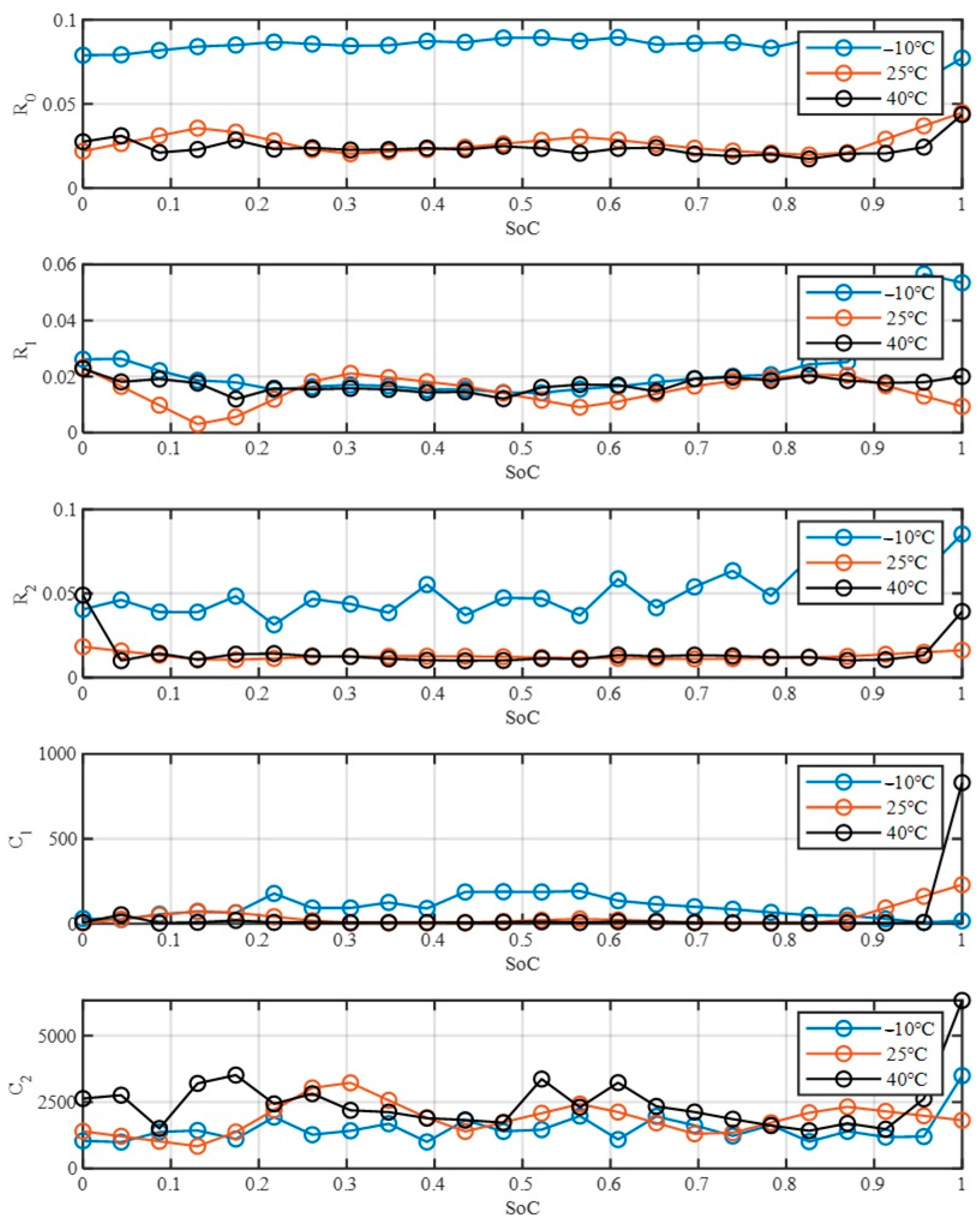
Figure 16 illustrates the variation in electrical parameters (R₀, R₁, R₂, C₁, and C₂) of ECM as a function of SoC for three different temperature conditions: −10 °C, 25 °C, and 40 °C. It is evident from the plots that temperature significantly affects the parameters, particularly at lower SoC levels, with R₀ and R₁ demonstrating more pronounced fluctuations under different temperatures. The capacitive components, C₁ and C₂, exhibit relatively larger magnitudes but appear to be less sensitive to temperature variations compared to the resistive components.

4. Conclusions

This study demonstrated that using the Taguchi method and ANOVA for optimizing the HPPC profile significantly improves the accuracy of SOC estimation for lithium-ion batteries. In this context, the impact of four HPPC parameters (pulse time gap, discharge pulse time, discharge pulse C-rate, and rest time) on ECM performance at different operating temperatures (−10 °C, 25 °C, 40 °C) was examined. The main findings showed the following:

• All four parameters have an impact on the accuracy of the parameters’ identification.
• Lower temperatures (i.e., −10 °C) lead to higher internal resistance and more significant voltage drops, particularly in cases with higher current pulses. The battery is more stable at 25 °C, with less voltage degradation compared to extreme temperatures (cold or hot).
• Certain cases (e.g., Case 3 and Case 7) consistently show larger voltage drops across all temperatures, indicating that high current amplitudes and rapid cycling are more detrimental to battery health under extreme conditions.
• Conversely, cases with lower current profiles (e.g., Case 1 and Case 2) are less affected by temperature changes.
• Higher currents correlate with sharper voltage declines, particularly at colder temperatures. This is critical for battery management strategies, as it highlights the need for controlled current profiles in sub-optimal temperature environments.
• When evaluation is made for different SOC values (SOC90, SOC50, SOC30), key findings include the significant impact of pulse time gap and discharge pulse time on model accuracy, with optimal values reducing RMSE between experimental and simulated data.
• The application of EKF further enhances SOC estimation, allowing for real-time adjustments based on varying battery conditions.
• The genetic algorithm-based multi-objective approach proves effective in selecting the optimal ECM parameters, especially under different temperature conditions.
• The validation results indicate that the proposed methodology achieves high precision across a wide range of SOC and operating temperatures, confirming its robustness.
• It was found that there is a significant reduction in RMSE, indicating improved performance under optimized conditions.

The findings of this study offer significant potential for various practical applications. The optimized SOC estimation model can be integrated into EV battery management systems to enhance real-time monitoring, extend driving range, and improve energy management across diverse temperatures and SOC levels. This will prevent over-discharge, increase charging efficiency, and ensure safer operation, leading to more reliable electric vehicles with longer battery life. Furthermore, the model can be applied to lithium-ion energy storage systems in renewable energy grids to optimize charge/discharge cycles and improve grid stability. Additionally, it has applications in consumer electronics, improving battery life predictions and performance. The model’s versatility also makes it suitable for industrial, military, and aerospace applications, where reliable energy management is crucial, especially in extreme conditions.

For highly nonlinear operating conditions, such as low SOC or high C-rate at extreme temperatures, more advanced filtering techniques such as the Unscented Kalman Filter (UKF) or Particle Filters may be more appropriate. These methods are designed to handle nonlinearities more accurately but come at the cost of increased computational complexity. In future work, exploring nonlinear estimation techniques like the UKF or machine learning-based SOC estimation could further improve model accuracy, especially in dynamic or extreme environments.

While this study focuses on NMC-based lithium-ion batteries, future research should validate the proposed methodology across a wider range of battery chemistries (e.g., LFP, NCA) and form factors (e.g., pouch cells, prismatic cells). Although the current study focuses on short-term experiments under controlled conditions, future research could investigate the long-term effects of battery aging and degradation on SOC estimation accuracy. Incorporating State of Health (SOH) into the optimization model and SOC estimation would help account for capacity fade, internal resistance growth, and other aging factors, making the model more practical for real-world applications with aging batteries. Also, the HPPC profile optimized in this study is designed to reflect the behaviour of a single cell. When scaling up for a larger battery pack, adjustments to the HPPC parameters may be required to reflect the pack’s dynamics. Future research should focus on developing multi-scale models that integrate cell-level SOC estimation with pack-level dynamics. These models should account for cell-to-cell variability, thermal gradients, and balancing algorithms to ensure accurate SOC prediction at the pack level.