A Redactable Blockchain Scheme Supporting Quantum-Resistance and Trapdoor Updates
Abstract
1. Introduction
1.1. Problem and Motivation
- How to balance variability and security;
- How to balance decentralization and assigning edit permissions;
- How to consider the compatibility between variability and existing blockchain systems.
1.2. Related Work
1.3. Contributions
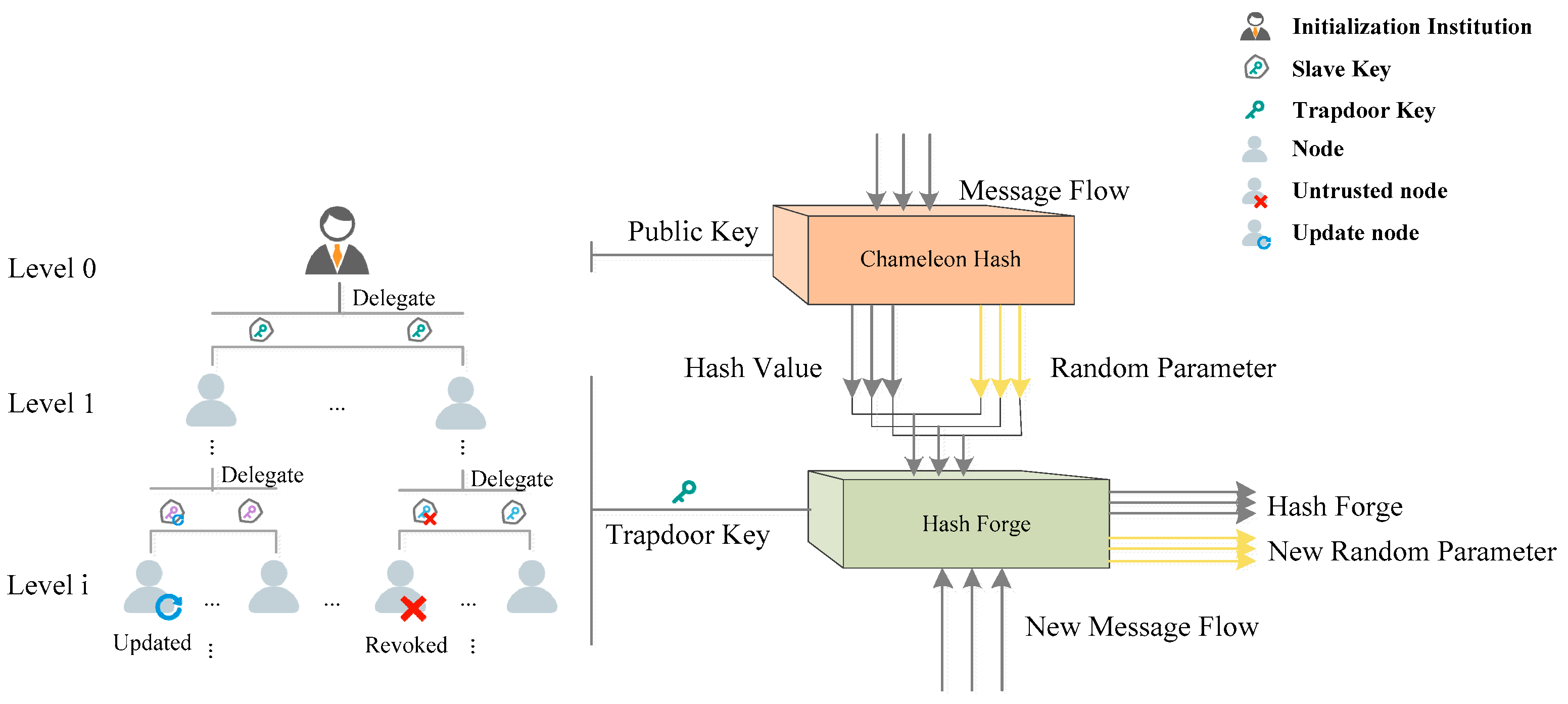
- Hierarchical identity-based chameleon hash: To regulate edit permissions and facilitate trapdoor management, this paper employed hierarchical identity for the decentralized delegation of trapdoors. Simultaneously, we introduced the concept of a slave key algorithm within hierarchical identity to avoid parent nodes that can deduce child nodes’ keys and the key dimensions increasing during the key delegation process. This integration imparted the revocable subkey mechanism’s delegation attributes.
- Redactable scheme with quantum resistance and revocability: We used a lattice-based cryptographic scheme to support more secure editing operations. In the redactable scheme, we also implemented the method of withdrawing the edit operation by saving the edit history.
- Private data were edited and managed by the individual user: We cryptographically verified private data to protect the security and privacy of the redactable blockchain.
- Addressing consistency, traceability, and accountability problems: In Section 4, we present three algorithms to illustrate how to achieve consistency, traceability, and accountability. For this, we advocate caching modify transactions with consensus authority nodes before their final commitment. The block number recording the edit history is stored in the redactable transaction to prove whether the transaction was modified. Demonstrating the viability of our redactable scheme, we opted for the Hyperledger Fabric platform, a widely embraced federated blockchain solution, to implement the scheme.
2. Preliminaries
2.1. Concepts of Lattices
2.2. Hierarchical Identity-Based Chameleon Hashing
3. Hierarchical Identity-Based Chameleon Hash with Revocable Subkey
3.1. Syntax of HIBCH-RS
- Formally, if message and identity , it has , where the experiment is described as below:
- Run
- Run
- Run
- Run
- If : return 1.
- The is defined as following:
- If :
- return 1; otherwise: return 0.
- For any , if it satisfies , , and when is invertible, , . At the same time, the system can still effectively recover, update, or disable disclosed trapdoor keys when malicious users are present. This security requirement proves that the old trapdoor key does not work properly.
- . For any PPT adversary , if , the chameleon hash algorithm construct of the HIBCH-RS model is collision-resistant under active attacks. The experiment is described as follows:
- Run ,
- Run ;
- Run ;
- Define ;
- Run ;
- Define , ;
- If and :
- return 1; otherwise: return 0.
- The is defined as follows:
- If run
- if : define
- return .
- The is defined as follows:
- If : return 1.
- If : run , define , return 1. otherwise: return 0.
- For users and messages with identity ID, if it holds that , then the construction of HIBCH-RS satisfies forgery indistinguishability.
3.2. Construction of HIBCH-RS
- Given a security parameter and any integer , let . Run algorithm such that . Generate randomly compute such as . Finally, algorithm output public parameter master key
- Randomly sample from , and an error from . Compute Randomly choose and H-tag , then . Finally, algorithm output and .
- At level , is a -dimensional vector. Let where is chosen randomly from . For tag at level is generated and sent by , and . Evaluate to obtain a trapdoor for . Generate personal key for . Finally, algorithm output .
- : If the key is found to be exposed or an illegitimate edit request, then the algorithm is executed to update the key for the edit member. The parent node updates a reversible tag by the algorithm of [32] 6.1. Then, the slave key pair is updated to and and the ID of the revoked key is appended to , so . The algorithm outputs new tag and to generate a new key for the user.
- : Input public parameter and message , compute chameleon hash and verification pair. If a transaction is identified as public-modifiable, then we use PP to calculate the hash value. Let where , sample , compute the chameleon hash of message as: ; . If a transaction is identified as belonging to an individual, then we give editing rights to the individual. Suppose this transaction belongs to , then calculates an extra verification pair and fills them into the block. In other words, select randomly ,, and , then , Algorithm output hash value , collision string and verification pair . We illustrate the operation of the algorithm in Algorithm 1 in a simple code language.
| Algorithm 1 Chameleon hash function. |
| and if is public: else if is private: // Hash map of identity ID , , , , return |
- Input the public key and the trapdoor key of , finding the collisions of chameleon hash. For personal data, the ability of users to decrypt is verified to determine whether they have the permission to edit the private data, and the hash collision is calculated if the verification is passed, and the editing request is rejected if it is not passed. provides the decryption key Then, compute . If , output True; otherwise output False. If , output True; otherwise output False. For public transaction data or personal data with successful verification, users can easily calculate hash collisions. Let . Then, sample from such that . Output the collision . We illustrate the operation of the algorithm in Algorithm 2 in a simple code language.
| Algorithm 2 Chameleon hash forge function. |
| If new message is private: // Decryption key of user ID: if [( and ) or () and ]: // Hash map of message return . return . |
3.3. Security Analysis
3.3.1. Parameters
3.3.2. Security
- In [36], is also a trapdoor for with tag for any , as long as is invertible modulo q. At this point, the old trapdoor is still available even after updating the public key. However, this useful feature does not apply to HIBCH-RS. To prove the above, we have with a tag and ID. From the algorithm, we know that . We now assume that there is an invertible tag such that . So, if is also a trapdoor , then should be equal to . While currently . However, it is obvious that .
- Any , First of all, we assume , . We also know , . Then, , so we can derive that . In other words, we want to confirm a trapdoor of the form . Since is the random vector that came from , we can also represent as , a form that comes from the definition [36]. We also have is a vector whose row is 1, and the other rows are 0 with the probability of . In this ideal case, is constant. However, in practice, when the key pair is updated, is a matrix of changes. Therefore, it is possible to forge a that satisfies this situation with the probability of .
- First, when a malicious user exists in a child node, its parent node can disable the child node trapdoor by updating the slave key information as well as the tag information, and at the same time add the child node’s identity to the revocation list and remove its edit permissions. Secondly, if a malicious user delegates illegitimate trapdoor information to other users, we can update its trapdoor information by assigning its child node to other legitimate nodes and then updating its trapdoor information. If a malicious user makes a request to modify other private data or non-editable transactions, the regulator may be able to automatically lock the malicious user’s edit permissions. Furthermore, if a malicious user refuses to cooperate in revoking an insecure trapdoor key, we can add the user to the revocation list, restrict its edit permissions, and then update the trapdoor information. For the above cases, the illegal behavior of malicious users can be fully considered and measures can be taken to ensure the overall security of the system. □
- Generate .
- Sample .
- Generate ,
- and .
- and send to .
- Second, query:
- , and .
- Generate ().
- Then, the challenger executes the following:
- Sample
- if , and , return ;
- otherwise, continue.
- Generate ;
- Send to and .
- For the Forgery group , the challenger calculates:
- with , and .
- Finally, if the above condition is satisfied, then return 1.
- Thus, through the above process, we can calculate . □
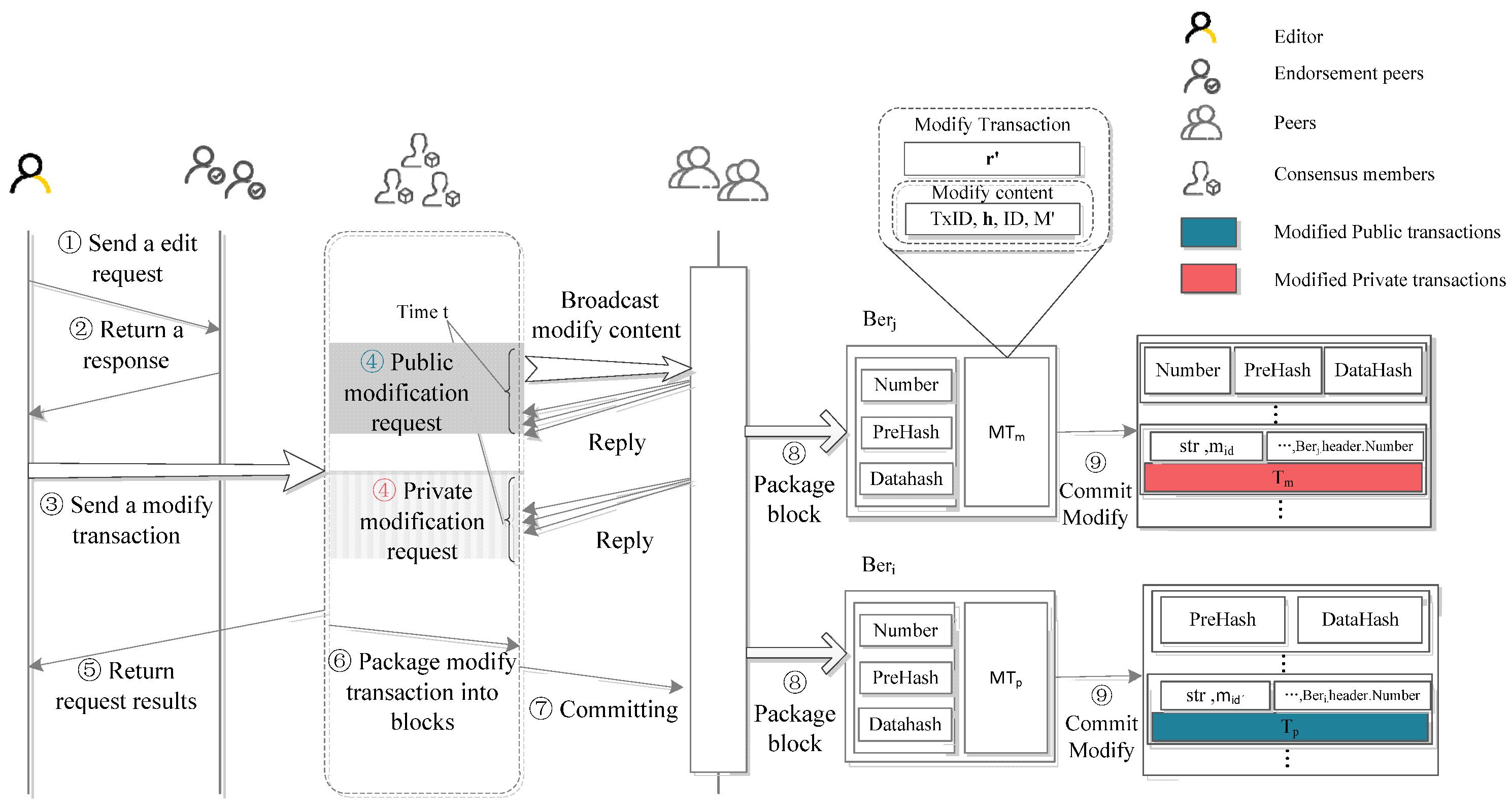
4. Redactable Programs
4.1. Editorial Role
4.2. Editorial Process
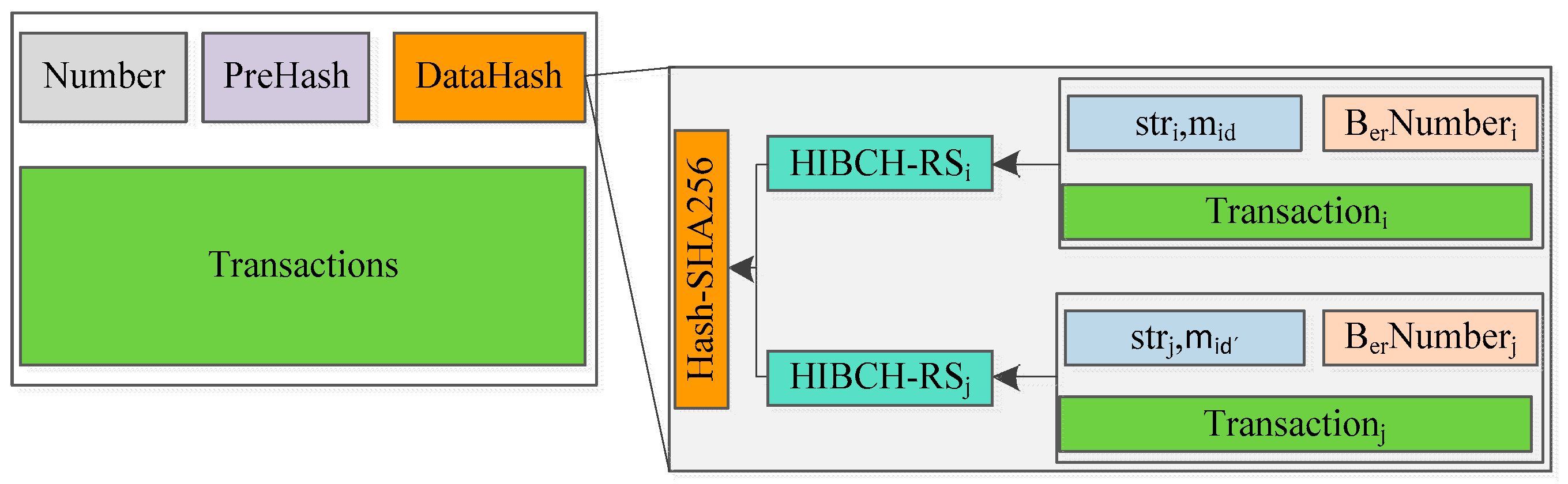
- Modified content (MC): MC encompasses several elements, including the transaction ID (TxID) of the transaction being revised, the hash value of the transaction, the identification of the member initiating the edit request, and the new content. If we would like to delete illegal information, the new content will be defined as empty.
- Key parameter (KP): The KP encompasses the hash collision . Importantly, this component determines the ability to accurately modify the transaction within the block in a physical sense. Notably, the field related to KP remains concealed from all parties until the completion of the request submission process.
- Public transaction data: In scenarios involving public transaction data, the consensus body disseminates MC to a randomly selected subset of n members. These members assess the content and respond with a agree message if they approve. Conversely, a reject message is transmitted if they disagree. The validation process hinges on accumulating a specific number of agree responses, indicating the legitimacy and consistency of the edit request.
- Personal transaction data: For personal data, which is confidential, nodes have restricted access to MC. Rather, nodes provide feedback solely on whether they consent to the block modification.
- The originator of the request initiates a withdrawal. Upon this decision, the consensus body eliminates the edit request from local records.
- Illegal requests. Before submission, the edit request undergoes verification by the nodes through broadcast. If the edit is determined to be unlawful or if the regulatory entity identifies the modifier’s identity as illicit, or if verification of the personal data modifier’s identity fails, the consensus body eliminates the request from local records. The regulator exercises the authority to decide whether to incorporate the edit requestor’s identity into the revocation list, contingent upon the severity of the violation.
- If no response is received within a designated timeframe, the edit request is discarded.
| Algorithm 3 Block redact. |
| Input: The new content , transaction ID of , redactor identity , and revocation list . Output: The redacted block and block and edit request transaction . Extract block by , output . if then: send to nodes for do: //consistency if then: if and then: return , |
4.3. Accountability and Traceability
| Algorithm 4 Trace edit history. |
| Input: The redacted transaction . Output: The edit history list . Extract by . for do: Extract edit block by . return |
| Algorithm 5 Accountability for edit request. |
| Input: Illegal edit request and revocation list . Output: The revocation list . Send to verifiers nodes Receive if do: Delete return . |
| Algorithm 6 Rollback the edit operation. |
| Input: The redacted transaction , the number of rollback times , and identity ID. Output: The rollback block . Extract by ; Extract by ; ; for do: Extract by Delete return |
5. Experiments and Results Analysis
5.1. Performance of HIBCH-RS
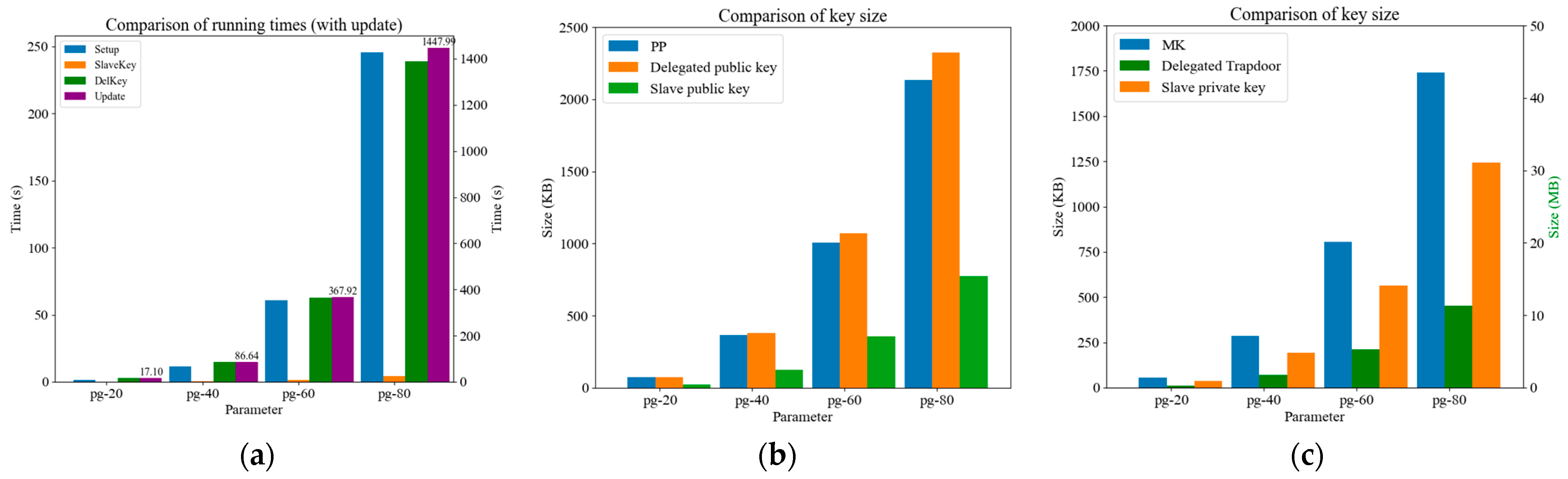
5.1.1. Evaluation Time and Size of the Hierarchical Model
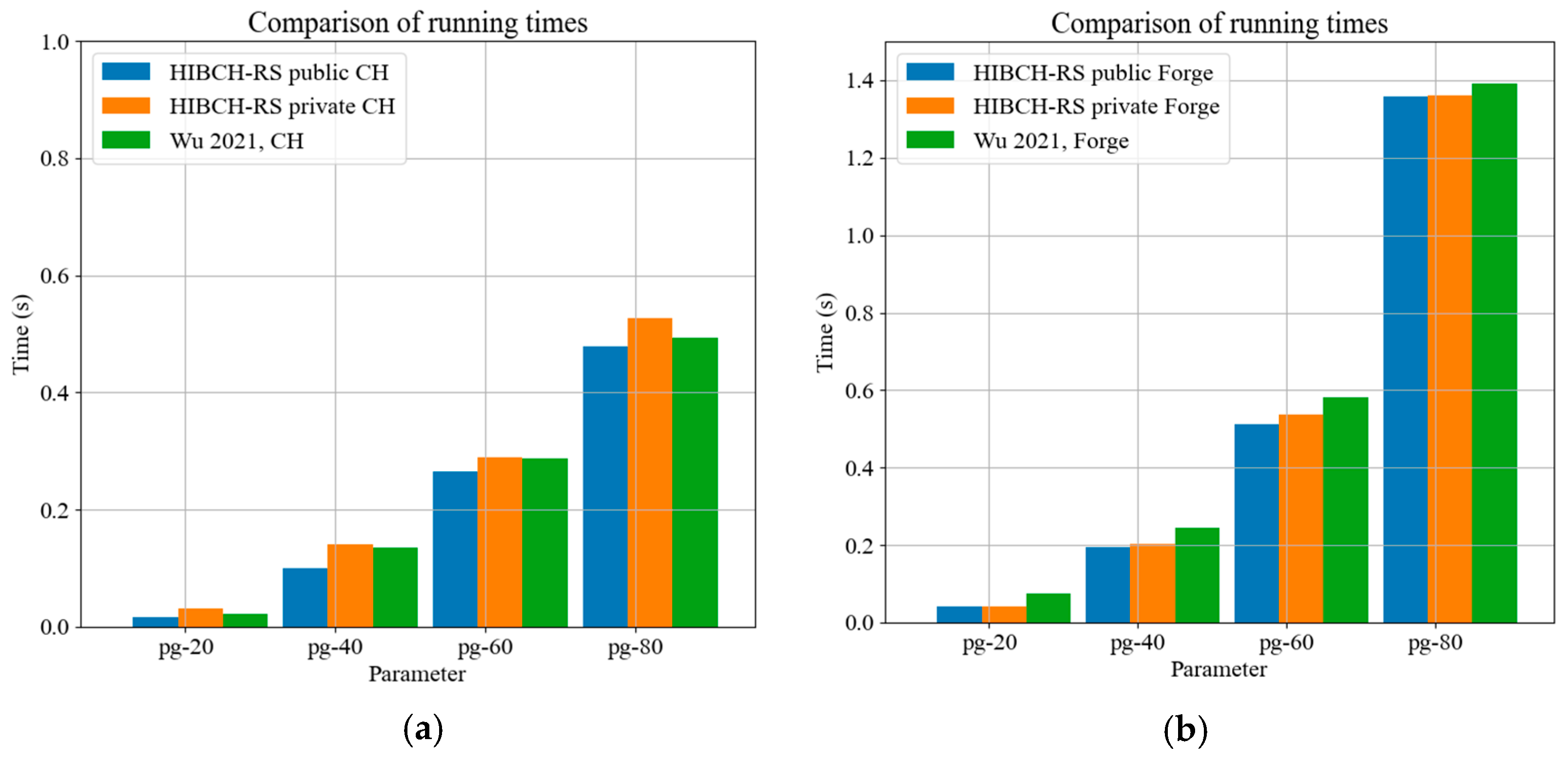
5.1.2. Comparison of Time to Compute Chameleon Hash and Find Collisions
5.1.3. Scalability
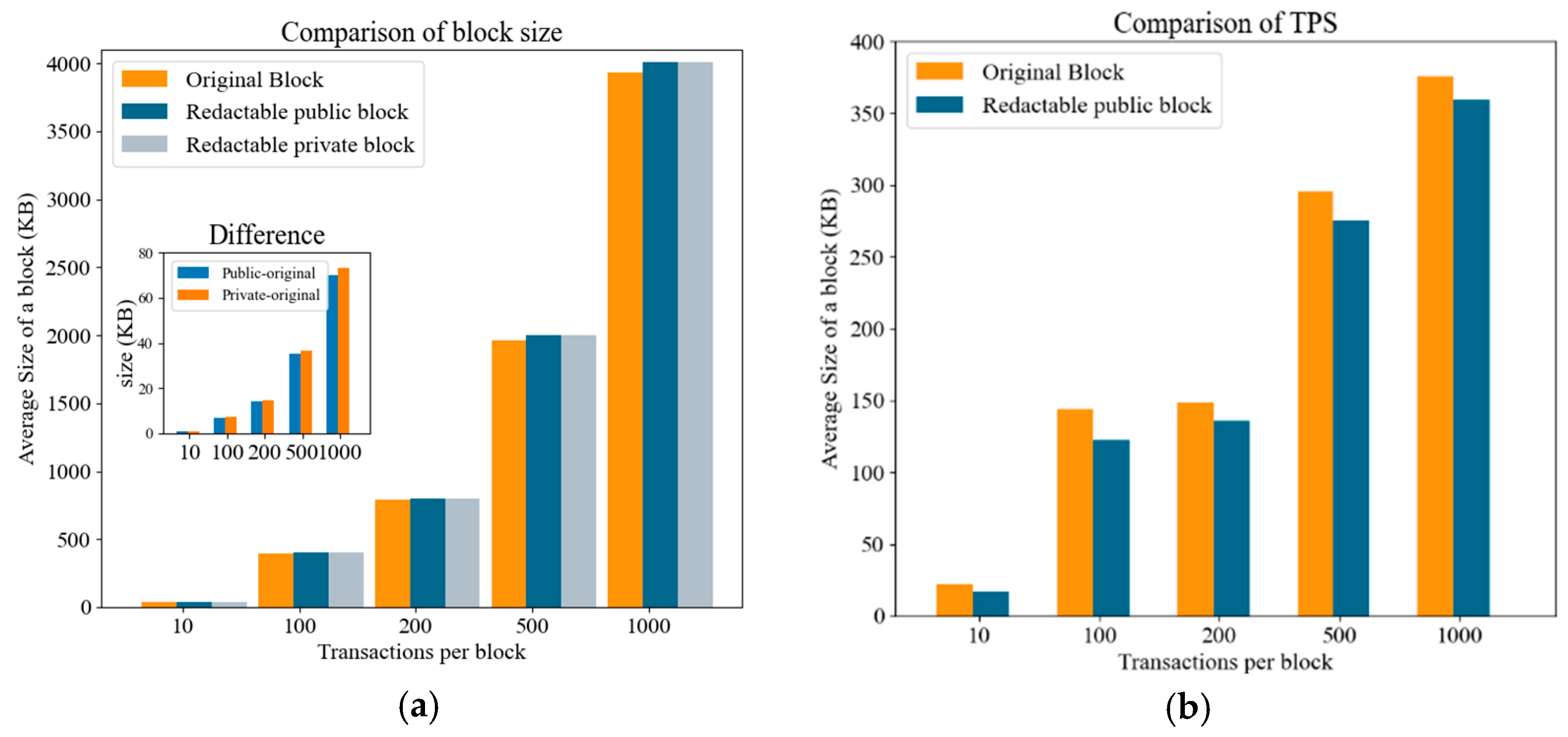
5.2. Performance of HIBCH-RS-Based Redactable Blockchain
Redactable Hyperledger Fabric
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Jaroodi, J.; Mohamed, N. Blockchain in industries: A survey. IEEE Access 2019, 7, 36500–36515. [Google Scholar] [CrossRef]
- Saad, M.; Spaulding, J.; Njilla, L.; Kamhoua, C.; Shetty, S.; Nyang, D.; Mohaisen, D. Exploring the attack surface of blockchain: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 1977–2008. [Google Scholar] [CrossRef]
- Wang, Y.; He, J.; Zhu, N.; Yi, Y.; Zhang, Q.; Song, H.; Xue, R. Security enhancement technologies for smart contracts in the blockchain: A survey. Trans. Emerg. Telecommun. Technol. 2021, 32, e4341. [Google Scholar] [CrossRef]
- Velliangiri, S.; Karthikeyan, P. Blockchain technology: Challenges and security issues in consensus algorithm. In Proceedings of the 2020 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 22–24 January 2020; pp. 1–8. [Google Scholar]
- Chou, I.T.; Su, H.H.; Hsueh, Y.L.; Hsueh, C.W. Bc-store: A scalable design for blockchain storage. In Proceedings of the 2nd International Electronics Communication Conference, Singapore, 8–10 July 2020; pp. 33–38. [Google Scholar]
- Chan, W.K.; Chin, J.J.; Goh, V.T. Simple and scalable blockchain with privacy. J. Inf. Secur. Appl. 2021, 58, 102700. [Google Scholar] [CrossRef]
- Matzutt, R.; Kalde, B.; Pennekamp, J.; Drichel, A.; Henze, M.; Wehrle, K. How to securely prune bitcoin’s blockchain. In Proceedings of the 2020 IFIP Networking Conference (Networking), Paris, France, 22–26 June 2020; pp. 298–306. [Google Scholar]
- Azbeg, K.; Ouchetto, O.; Andaloussi, S.J. BlockMedCare: A healthcare system based on IoT, Blockchain and IPFS for data management security. Egypt. Inform. J. 2022, 23, 329–343. [Google Scholar]
- Athanere, S.; Thakur, R. Blockchain based hierarchical semi-decentralized approach using IPFS for secure and efficient data sharing. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1523–1534. [Google Scholar]
- Liu, Y.; Liu, J.; Salles, M.A.V.; Zhang, Z.; Li, T.; Hu, B.; Henglein, F.; Lu, R. Building blocks of sharding blockchain systems: Concepts, approaches, and open problems. Comput. Sci. Rev. 2022, 46, 100513. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, J.; Wang, H.; Shu, J. Framework of decentralized multi-chain data management for power systems. CSEE J. Power Energy Syst. 2019, 6, 458–468. [Google Scholar]
- Xu, J.; Xue, K.; Tian, H.; Hong, J.; Wei, D.S.; Hong, P. An identity management and authentication scheme based on redactable blockchain for mobile networks. IEEE Trans. Veh. Technol. 2020, 69, 6688–6698. [Google Scholar]
- Yeh, L.Y.; Hsu, W.H.; Shen, C.Y. GDPR-Compliant Personal Health Record Sharing Mechanism with Redactable Blockchain and Revocable IPFS. IEEE Trans. Dependable Secur. Comput. 2023. [Google Scholar] [CrossRef]
- Fernandez-Carames, T.M.; Fraga-Lamas, P. Towards post-quantum blockchain: A review on blockchain cryptography resistant to quantum computing attacks. IEEE Access 2020, 8, 21091–21116. [Google Scholar] [CrossRef]
- Wu, C.; Ke, L.; Du, Y. Quantum resistant key-exposure free chameleon hash and applications in redactable blockchain. Inf. Sci. 2021, 548, 438–449. [Google Scholar]
- Ateniese, G.; Magri, B.; Venturi, D.; Andrade, E. Redactable blockchain-or-rewriting history in bitcoin and friends. In Proceedings of the 2017 IEEE European Symposium on Security and Privacy (EuroS&P), Paris, France, 26–28 April 2017; pp. 111–126. [Google Scholar]
- Wan, Z.; Liu, W.; Cui, H. HIBEChain: A hierarchical identity-based blockchain system for large-scale IoT. IEEE Trans. Dependable Secur. Comput. 2022, 20, 1286–1301. [Google Scholar]
- Pavithran, D.; Al-Karaki, J.N.; Shaalan, K. Edge-based blockchain architecture for event-driven IoT using hierarchical identity based encryption. Inf. Process. Manag. 2021, 58, 102528. [Google Scholar]
- Khalili, M.; Dakhilalian, M.; Susilo, W. Efficient chameleon hash functions in the enhanced collision resistant model. Inf. Sci. 2020, 510, 155–164. [Google Scholar] [CrossRef]
- Derler, D.; Samelin, K.; Slamanig, D. Bringing order to chaos: The case of collision-resistant chameleon-hashes. In Proceedings of the Public-Key Cryptography–PKC 2020: 23rd IACR International Conference on Practice and Theory of Public-Key Cryptography, Edinburgh, UK, 4–7 May 2020; pp. 462–492. [Google Scholar]
- Ateniese, G.; de Medeiros, B. Identity-Based Chameleon Hash and Applications. In Financial Cryptography, Proceedings of the 8th International Conference, FC 2004, Key West, FL, USA, 9–12 February 2004; Lecture Notes in Computer Science; Juels, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 164–180. [Google Scholar]
- Bao, F.; Deng, R.H.; Ding, X.; Lai, J.; Zhao, Y. Hierarchical identity-based chameleon hash and its applications. In Proceedings of the Applied Cryptography and Network Security: 9th International Conference, Nerja, Spain, 7–10 June 2011; pp. 201–219. [Google Scholar]
- Derler, D.; Samelin, K.; Slamanig, D.; Striecks, C. Fine-grained and controlled rewriting in blockchains: Chameleon-hashing gone attribute-based. IACR Cryptol. ePrint Arch. 2019, 2019, 406. [Google Scholar]
- Ma, J.; Xu, S.; Ning, J.; Huang, X.; Deng, R.H. Redactable blockchain in decentralized setting. IEEE Trans. Inf. Forensics Secur. 2022, 17, 1227–1242. [Google Scholar] [CrossRef]
- Wei, J.; Zhu, Q.; Li, Q.; Nie, L.; Shen, Z.; Choo, K.K.R.; Yu, K. A redactable blockchain framework for secure federated learning in industrial Internet of Things. IEEE Internet Things J. 2022, 9, 17901–17911. [Google Scholar]
- Jia, Y.; Sun, S.F.; Zhang, Y.; Liu, Z.; Gu, D. Redactable blockchain supporting supervision and self-management. In Proceedings of the 2021 ACM Asia Conference on Computer and Communications Security, Hong Kong, China, 7–11 June 2021; pp. 844–858. [Google Scholar]
- Jia, M.; Chen, J.; He, K.; Du, R.; Zheng, L.; Lai, M.; Wang, D.; Liu, F. Redactable Blockchain from Decentralized Chameleon Hash Functions. IEEE Trans. Inf. Forensics Secur. 2022, 17, 2771–2783. [Google Scholar] [CrossRef]
- Peng, C.; Xu, H.; Li, P. Redactable Blockchain Using Lattice-based Chameleon Hash Function. In Proceedings of the 2022 International Conference on Blockchain Technology and Information Security, Huaihua, China, 15–17 July 2022; pp. 94–98. [Google Scholar]
- Puddu, I.; Dmitrienko, A.; Capkun, S. μchain: How to Forget without Hard Forks. IACR Cryptol. ePrint Arch. 2017, 2017, 106. [Google Scholar]
- Marsalek, A.; Zefferer, T. A correctable public blockchain. In Proceedings of the 2019 18th IEEE International Conference on Trust, Security And Privacy in Computing and Communications/13th IEEE International Conference on Big Data Science and Engineering, Rotorua, New Zealand, 5–8 August 2019; pp. 554–561. [Google Scholar]
- Deuber, D.; Magri, B.; Thyagarajan, S.A.K. Redactable blockchain in the permissionless setting. In Proceedings of the 2019 IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 19–23 May 2019; pp. 124–138. [Google Scholar]
- Nejatollahi, H.; Dutt, N.; Ray, S.; Regazzoni, F.; Banerjee, I.; Cammarota, R. Post-quantum lattice-based cryptography implementations: A survey. ACM Comput. Surv. 2019, 51, 1–41. [Google Scholar] [CrossRef]
- Ajtai, M.; Dwork, C. A public-key cryptosystem with worst-case/average-case equivalence. In Proceedings of the Twenty-Ninth Annual ACM Symposium on Theory of Computing, El Paso, TX, USA, 4–6 May 1997; pp. 284–293. [Google Scholar]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM 2009, 56, 1–40. [Google Scholar]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; pp. 197–206. [Google Scholar]
- Vershynin, R. Introduction to the non-asymptotic analysis of random matrices. arXiv 2010, arXiv:1011.3027. [Google Scholar]
- Micciancio, D.; Peikert, C. Trapdoors for lattices: Simpler, tighter, faster, smaller. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 700–718. [Google Scholar]
- Agrawal, S.; Boneh, D.; Boyen, X. Efficient lattice (H) IBE in the standard model. In Proceedings of the Advances in Cryptology–EUROCRYPT 2010: 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Riviera, French, 30 May–3 June 2010. [Google Scholar]
- Dutta, P.; Jiang, M.; Duong, D.H.; Susilo, W.; Fukushima, K.; Kiyomoto, S. Hierarchical identity-based puncturable encryption from lattices with application to forward security. In Proceedings of the 2022 ACM on Asia Conference on Computer and Communications Security, Nagasaki, Japan, 30 May–3 June 2022; pp. 408–422. [Google Scholar]
- Van Nguyen, N.A.; Pham, M.T.T. Quantum-safe Anonymous Hierarchical Identity-Based Encryption with Traceable Identities. Comput. Stand. Interfaces 2023, 84, 103695. [Google Scholar] [CrossRef]
- Micciancio, D.; Regev, O. Worst-case to average-case reductions based on Gaussian measures. SIAM J. Comput. 2007, 37, 267–302. [Google Scholar]
| Mode | References | Grain | Self Management | Security Model 4 | Features | Edit Permissions |
|---|---|---|---|---|---|---|
| Non-CH | [29] | Ts 1 | Y 2 | - | C 3&T 3 | Sender/Recipient/User/Smart Contract |
| CH | [16] | Bs 1 | N 2 | ROM/SM | C | Central/Users Set |
| [26] | Ts | Y | ROM | C&R 3&A 3 | Personal and Regulator | |
| [24] | Ts | N | IND-CCA | C&A 3 | Controlled Multiple | |
| Lattice-CH | [15] | Ts | N | GGM/ROM | - | Central/Multiple/(Any/Subset) |
| [28] | Bs | N | - | C | Any | |
| Ours | Ts | Y | ROM | T&A&C&R | Multiple |
| Symbols | Description |
|---|---|
| A random variable from a certain distribution | |
| Security parameter | |
| The matrix is denoted in bold and capitals | |
| The vector is denoted in bold and lowercase | |
| , | The transpose of the matrix or vector |
| Positive integer | |
| The set of integers of modulus | |
| The upper limit | |
| LWE | Learning with errors |
| ISIS | Inhomogeneous small integer solution |
| The identity of level | |
| The parent of identity at level |
| Parameter Group | n | m | w |
|---|---|---|---|
| Group 1 | 20 | 920 | 460 |
| Group 2 | 40 | 2080 | 1040 |
| Group 3 | 60 | 3480 | 1740 |
| Group 4 | 80 | 5120 | 2560 |
| Model | Size (Public Key) | Size (Trapdoor) | Parameter |
|---|---|---|---|
| HIBCH-RS | |||
| HIBPE | |||
| AHIBET |
| Exp1 | Exp2 | Exp3 | Exp4 | Exp5 | |
|---|---|---|---|---|---|
| Transaction per block | 10 | 100 | 200 | 500 | 1000 |
| Send transaction number | 400 | 4000 | 8000 | 20,000 | 40,000 |
| Public Transactions Data | Private Transactions Data | |
|---|---|---|
| Time(s) | 4.66 | 8.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chen, Y.; Zhu, X.; Li, C.; Fang, K. A Redactable Blockchain Scheme Supporting Quantum-Resistance and Trapdoor Updates. Appl. Sci. 2024, 14, 832. https://doi.org/10.3390/app14020832
Wang X, Chen Y, Zhu X, Li C, Fang K. A Redactable Blockchain Scheme Supporting Quantum-Resistance and Trapdoor Updates. Applied Sciences. 2024; 14(2):832. https://doi.org/10.3390/app14020832
Chicago/Turabian StyleWang, Xiayu, Yineng Chen, Xinghui Zhu, Cheng Li, and Kui Fang. 2024. "A Redactable Blockchain Scheme Supporting Quantum-Resistance and Trapdoor Updates" Applied Sciences 14, no. 2: 832. https://doi.org/10.3390/app14020832
APA StyleWang, X., Chen, Y., Zhu, X., Li, C., & Fang, K. (2024). A Redactable Blockchain Scheme Supporting Quantum-Resistance and Trapdoor Updates. Applied Sciences, 14(2), 832. https://doi.org/10.3390/app14020832






