Determining Digital Representation and Representative Elementary Volume Size of Broken Rock Mass Using the Discrete Fracture Network–Discrete Element Method Coupling Technique
Abstract
1. Introduction
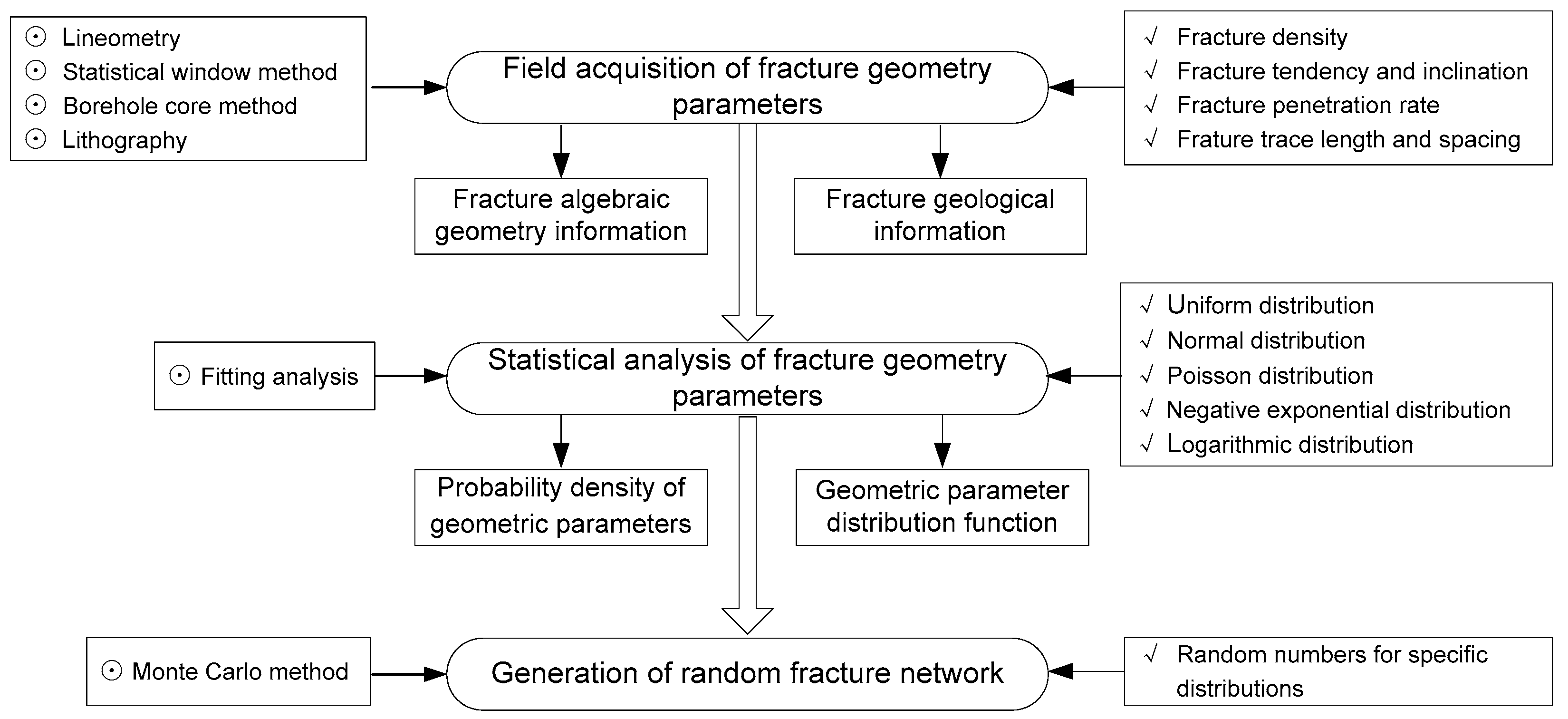
2. Characterization of Random Fracture Networks in Broken Rock Masses
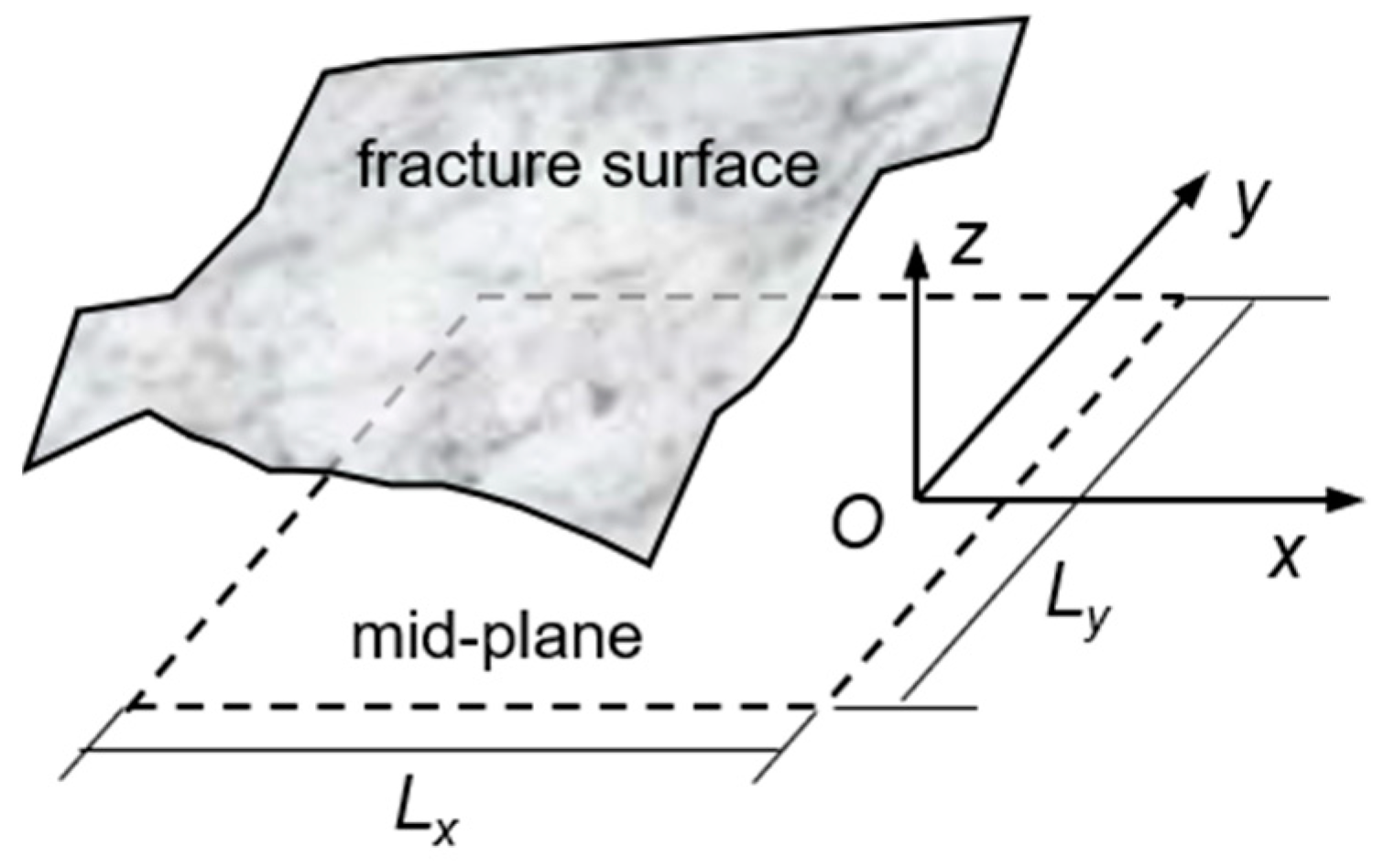
2.1. On-Site Research of Structural Surface
2.2. Mathematical Description of Stochastic Model for Geometric Parameters of Structural Surfaces
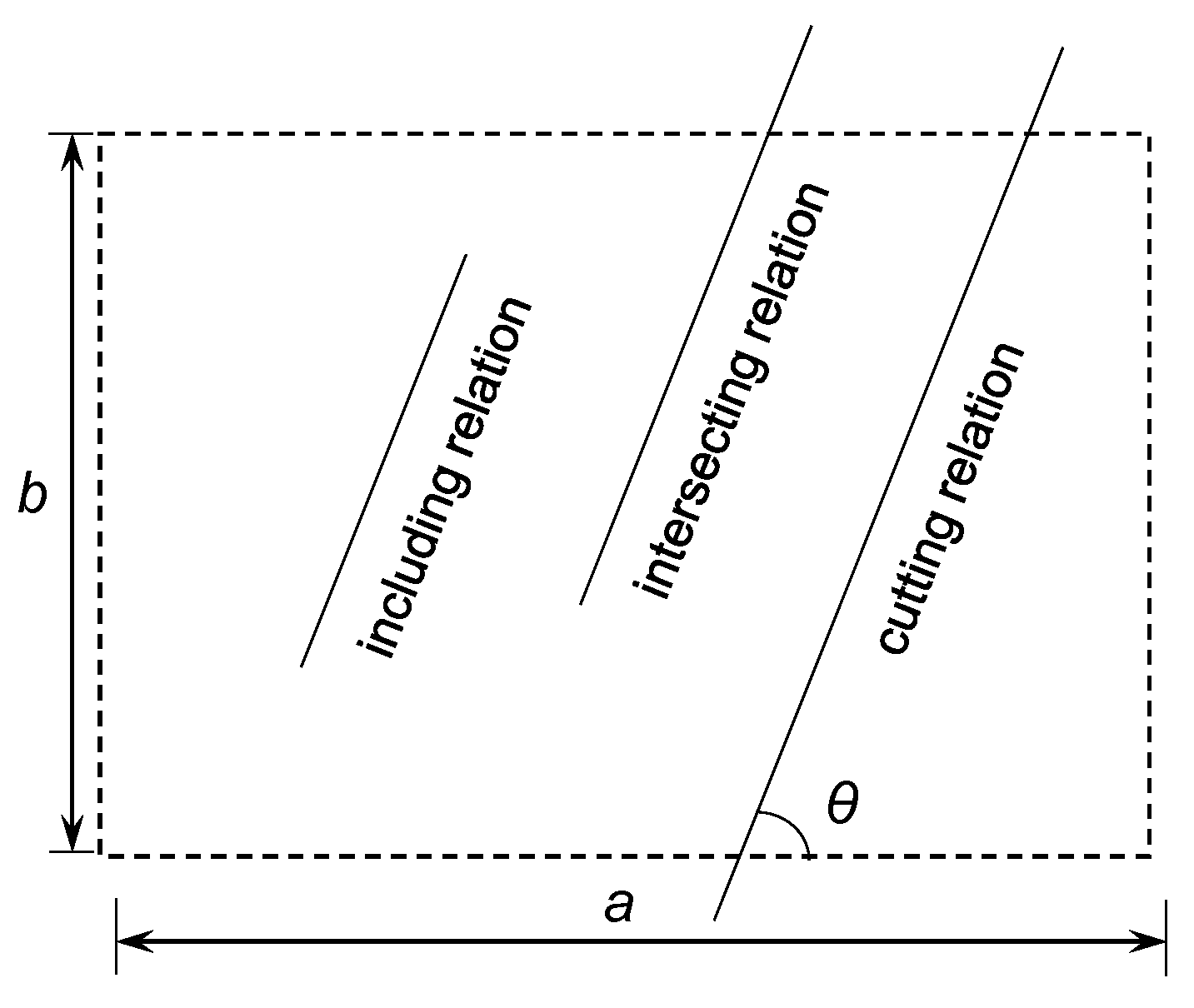
2.2.1. Shape and Size of Structural Surfaces
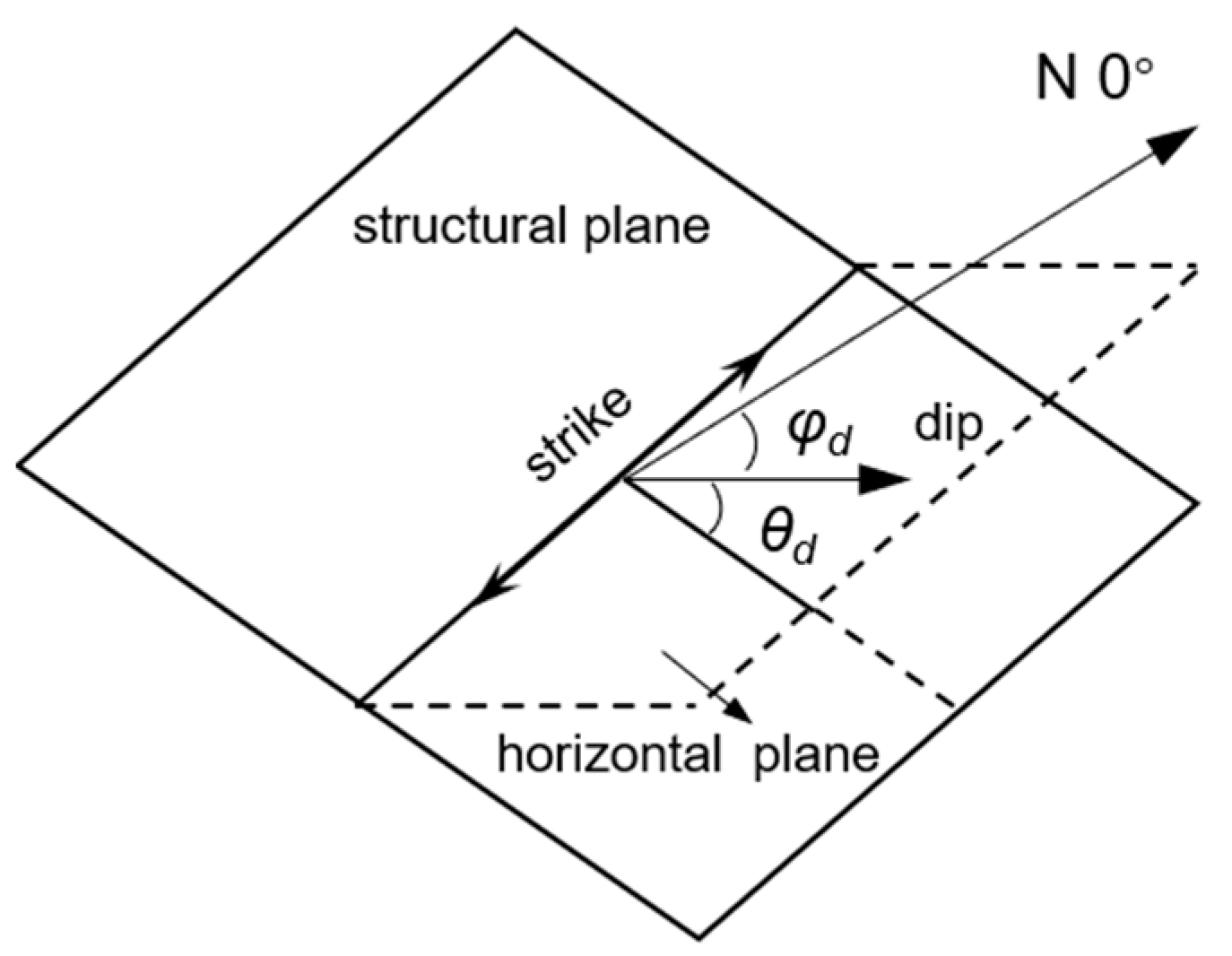
2.2.2. Occurrence of Structural Planes
2.2.3. Density of Structural Planes
2.2.4. Center Point and Vertex of a Rectangular Structural Surface
2.2.5. Degree of Aperture of a Structural Plane
2.3. Generation of Random Fracture Network Model
3. Modeling of Broken Rock Masses Based on the Coupled DFN–DEM Approach
3.1. Statistics of Structural Plane Geometric Parameters
3.2. Construction of Discrete Fracture Networks
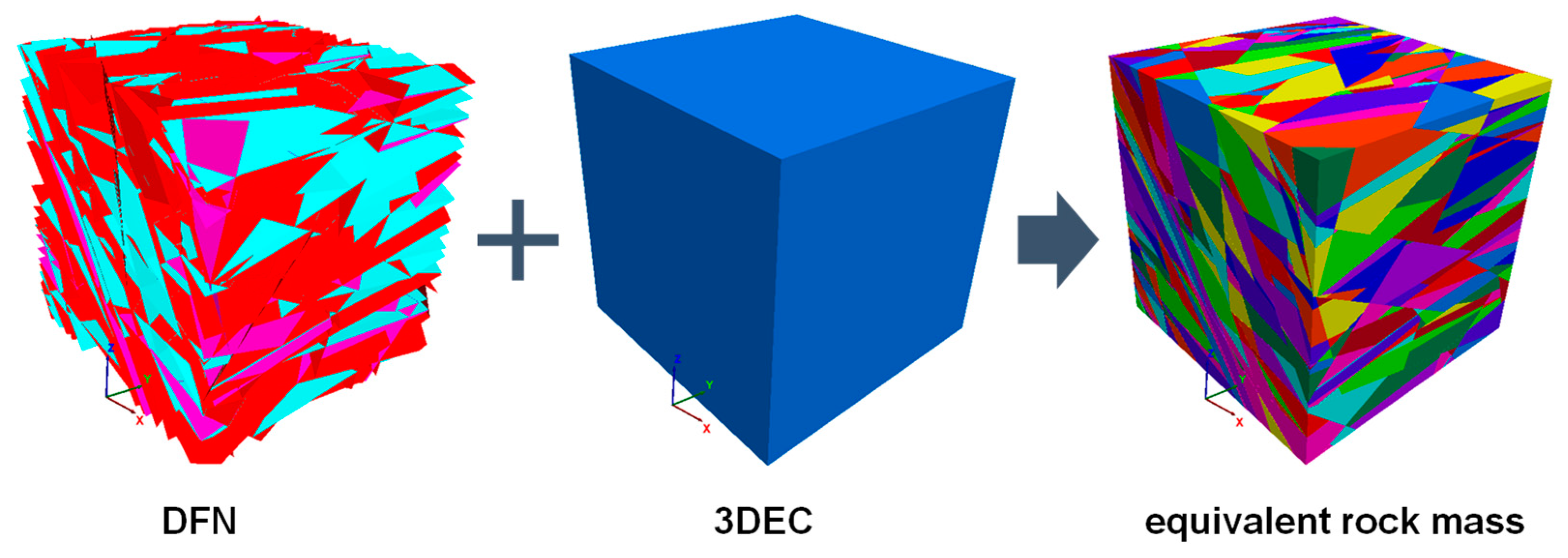
3.3. Construction of Equivalent Rock Mass Models Using DFN–DEM Coupling Technique
4. REV Size of Broken Rock Mass
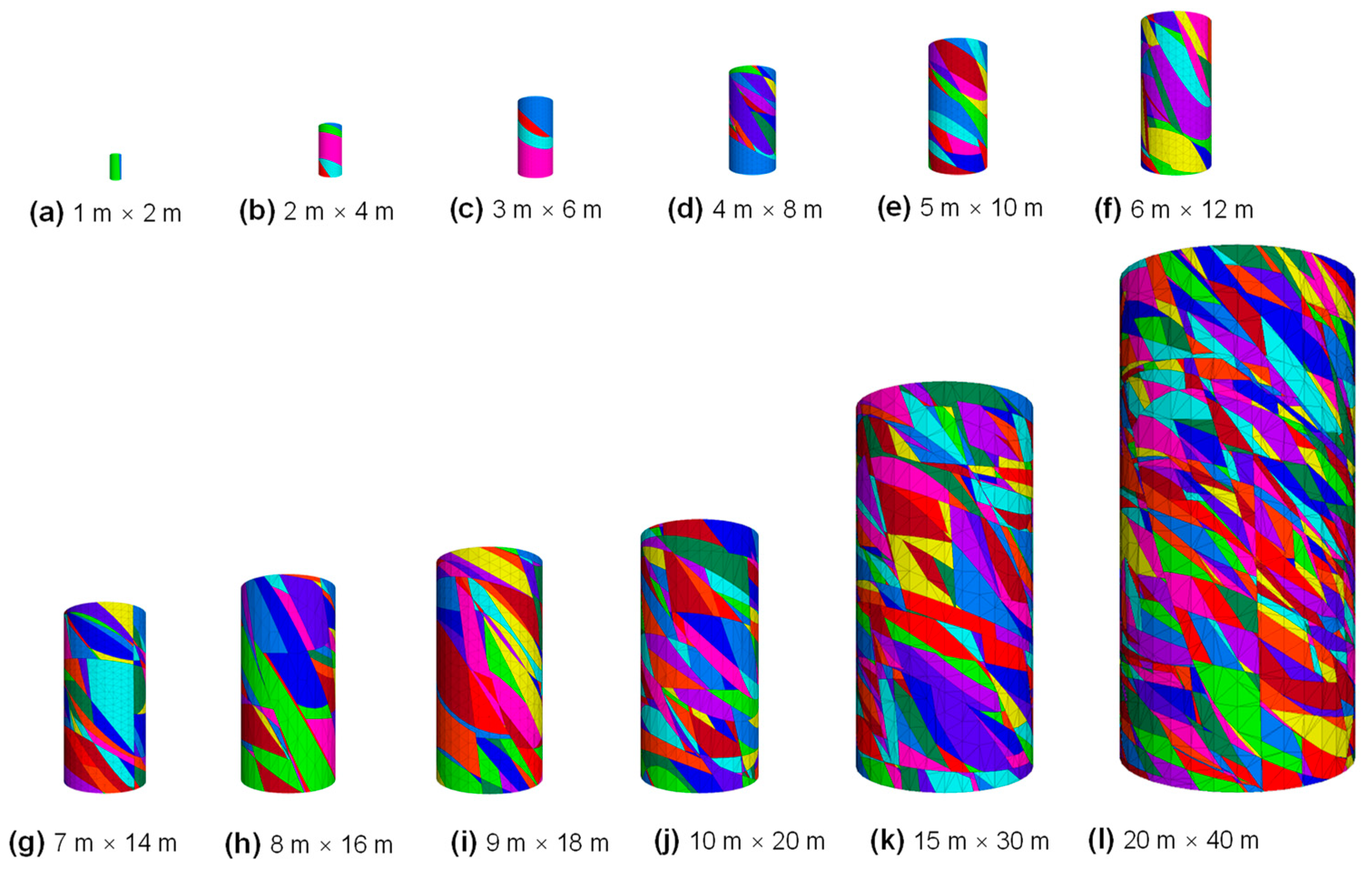
4.1. Establishment of Numerical Models
4.2. Determination of REV
5. Conclusions
- (1)
- The average and variance values of the structural plane in the surrounding rock of the main powerhouse are 4.30 m and 3.45 m2, respectively, and the average and variance of the structural plane dip angles are 51.42° and (27.93°)2, respectively. The count and length of fractures per unit area of the rock masses are 0.23 and 0.97 m−1, respectively; the number of fractures per unit length of the rock is 0.58 m−1; and the fracture area per unit length is 1.87 m−1.
- (2)
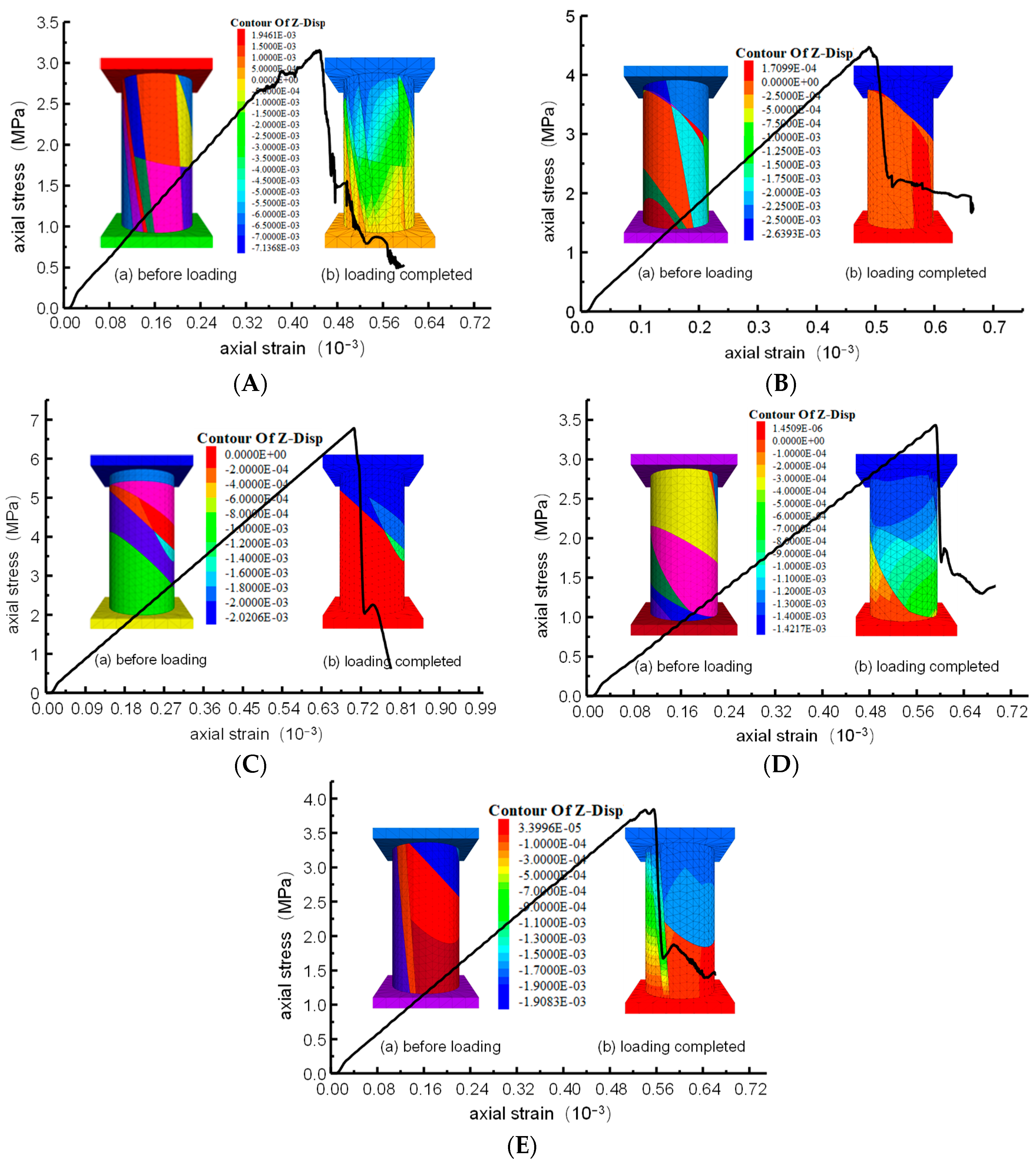
- The mechanical parameters evaluated from five cylindrical models generated using the proposed approach are quite close, which suggests good stability and effectiveness of the method.
- (3)
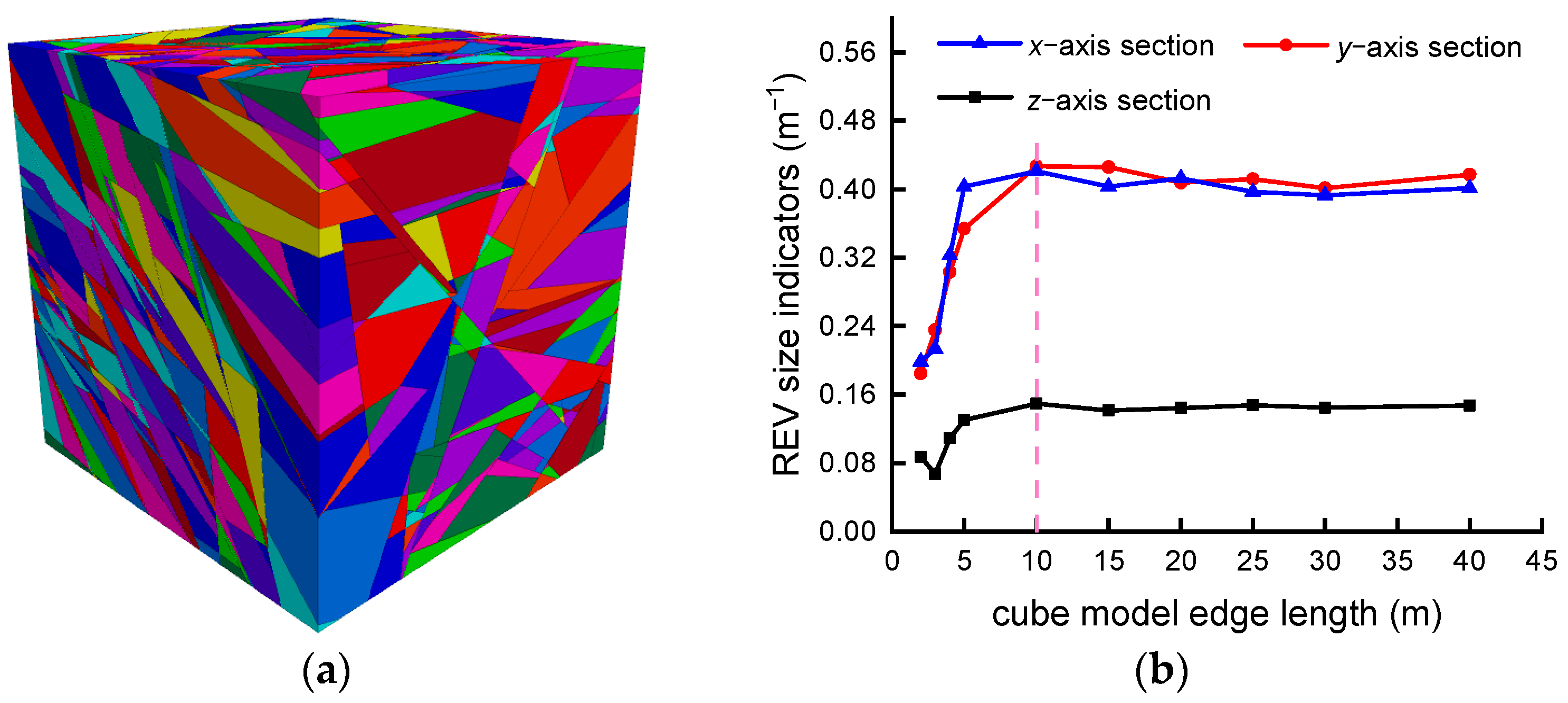
- The REV size of the rock masses determined using the proposed approach is 5 m × 10 m for the cylindrical rock models. This result is consistent with the REV size estimated by the RMSI method using cubic rock models, which demonstrates the validity of using cylindrical models to evaluate the REV size of broken rock masses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, L.; Liu, S. A conceptual model to characterize and model compaction behavior and permeability evolution of broken rock mass in coal mine gobs. Int. J. Coal Geol. 2017, 172, 60–70. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, Y.; Xie, Y.; Cheng, Q.; Deng, K. Multiscale effects caused by the fracturing and fragmentation of rock blocks during rock mass movement: Implications for rock avalanche propagation. Nat. Hazard. Earth Sys. Sci. 2022, 22, 639–657. [Google Scholar] [CrossRef]
- Ardeshiri-Lajimi, S.; Yazdani, M.; Langroudi, A.A. Control of fault lay-out on seismic design of large underground caverns. Tunn. Undergr. Space Technol. 2015, 50, 305–316. [Google Scholar] [CrossRef]
- Dong, J.; Zhao, Y.; Liu, H.; Zhao, J.; Zhang, Z.; Chi, Q.; Yang, J. Creep Characteristics of a Strongly Weathered Argillaceous Sandstone Sliding Zone and the Disaster Evolution Mechanism of the Huaipa Landslide, China. Appl. Sci. 2023, 13, 8579. [Google Scholar] [CrossRef]
- Tan, W.H.; Sun, Z.H.; Li, N.; Jiang, X.H. Stochastic Three-Dimensional Joint Geometry Model and the Properties of REV for a Jointed Rock Mass. Adv. Mater. Res. 2015, 1079, 266–271. [Google Scholar] [CrossRef]
- Huang, H.; Shen, J.; Chen, Q.; Karakus, M. Estimation of REV for fractured rock masses based on Geological Strength Index. Int. J. Rock Mech. Min. Sci. 2020, 126, 104179. [Google Scholar] [CrossRef]
- Regassa, B.; Xu, N.; Mei, G. An equivalent discontinuous modeling method of jointed rock masses for DEM simulation of mining-induced rock movements. Int. J. Rock Mech. Min. Sci. 2018, 108, 1–14. [Google Scholar] [CrossRef]
- Xu, N.Z.; Liu, C.Q.; Su, C.; Zhou, T. Study on the Size and Occurrence Effects of Equivalent Elasticity Modulus of Orthogonal Random Jointed Rock Masses. Front. Earth Sci. 2022, 10, 888551. [Google Scholar]
- Niazmandi, M.M.; Binesh, S.M. A DFN–DEM Approach to Study the Influence of Confinement on the REV Size of Fractured Rock Masses. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 587–601. [Google Scholar] [CrossRef]
- Samaniego, A. Simulation of Fluid in Fractured Rock. Ph.D. Thesis, Imperial College, University of London, London, UK, 1984. [Google Scholar]
- Grenon, M.; Bruneau, G.; Kalala, I.K. Quantifying the impact of small variations in fracture geometric characteristics on peak rock mass properties at a mining project using a coupled DFN–DEM approach. Comput. Geotech. 2014, 58, 47–55. [Google Scholar] [CrossRef]
- Ivars, D.M.; Pierce, M.E.; Darcel, C.; Reyes-Montes, J.; Potyondy, D.O.; Young, R.P.; Cundall, P.A. The synthetic rock mass approach for jointed rock mass modelling. Int. J. Rock Mech. Min. Sci. 2011, 48, 219–244. [Google Scholar] [CrossRef]
- Wang, Z.; Li, W.; Bi, L.; Liu, J. Estimation of the REV Size and Equivalent Permeability Coefficient of Fractured Rock Masses with an Emphasis on Comparing the Radial and Unidirectional Flow Configurations. Rock Mech. Rock Eng. 2018, 51, 1457–1471. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, J.; Liu, R.; Li, S.; Liu, D.; Wang, X. Estimation of the representative elementary volume of three-dimensional fracture networks based on permeability and trace map analysis: A case study. Eng. Geol. 2022, 309, 106848. [Google Scholar] [CrossRef]
- Xia, L.; Zheng, Y.; Yu, Q. Estimation of the REV size for blockiness of fractured rock masses. Comput. Geotech. 2016, 76, 83–92. [Google Scholar] [CrossRef]
- Ni, P.; Wang, S.; Wang, C.; Zhang, S. Estimation of REV Size for Fractured Rock Mass Based on Damage Coefficient. Rock Mech. Rock Eng. 2017, 50, 555–570. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Chen, J.; Song, S.; Zhan, J.; Han, X. Determination of Geometrical REVs Based on Volumetric Fracture Intensity and Statistical Tests. Appl. Sci. 2018, 8, 800. [Google Scholar] [CrossRef]
- Ni, H.; Xu, W.; Wang, W.; Lu, B.; Shi, A.; Zou, L. Statistical analysis of scale effect on equivalent elastic modulus of jointed rock masses. Arab. J. Geosci. 2016, 9, 206. [Google Scholar] [CrossRef]
- Castelli, M.; Saetta, V.; Scavia, C. Numerical Study of Scale Effects on the Stiffness Modulus of Rock Masses. Int. J. Geomech. 2003, 3, 160–169. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Hydraulic properties of fractured rock masses with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2007, 44, 704–719. [Google Scholar] [CrossRef]
- Khani, A.; Baghbanan, A.; Hashemolhosseini, H. Numerical investigation of the effect of fracture intensity on deformability and REV of fractured rock masses. Int. J. Rock Mech. Min. Sci. 2013, 63, 104–112. [Google Scholar] [CrossRef]
- Li, G.; Tang, C.A. A statistical meso-damage mechanical method for modeling trans-scale progressive failure process of rock. Int. J. Rock Mech. Min. Sci. 2015, 74, 133–150. [Google Scholar] [CrossRef]
- Cordero, S.; Rojas, F.; Riccardo, J.L. Simulation of Three-Dimensional Porous Networks. Colloid. Surf. A 2001, 187, 425–438. [Google Scholar] [CrossRef]
- Warburton, P.M. A computer program for reconstructing blocky rock geometry and analyzing single block stability. Comput. Geosci.-UK 1985, 11, 707–712. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Wu, T.H. Estimation of mean trace length of discontinuities. Rock Mech. Rock Eng. 1984, 17, 215–232. [Google Scholar] [CrossRef]
- Zhao, Y.S.; Feng, Z.C.; Dong, Y.; Liang, W.G.; Feng, Z.J. Three-dimensional fractal distribution of the number of rock-mass fracture surfaces and its simulation technology. Comput. Geotech. 2015, 65, 136–146. [Google Scholar]
- Hekmatnejad, A.; Crespin, B.; Vallejos, J.A.; Opazo, A.; Adoko, A.C. A hybrid predictive model of unstable rock blocks around a tunnel based on estimated volumetric fracture intensity and circular variance from borehole data sets. Tunn. Undergr. Space Technol. 2021, 111, 103865. [Google Scholar] [CrossRef]
- Cruden, D.M. Describing the size of discontinuities. Int. J. Rock Mech. Min. 1977, 14, 133–137. [Google Scholar] [CrossRef]
- Villaescusa, E.; Brown, E.T. Maximum likelihood estimation of joint size from trace length measurements. Rock Mech. Rock Eng. 1992, 25, 67–87. [Google Scholar] [CrossRef]
- Feng, G.L.; Feng, X.T.; Chen, B.R.; Xiao, Y.X.; Zhao, Z.N. Effects of structural planes on the microseismicity associated with rockburst development processes in deep tunnels of the Jinping-II Hydropower Station, China. Tunn. Undergr. Space Technol. 2019, 84, 273–280. [Google Scholar] [CrossRef]
- Kulatilake, P.H.S.W.; Wu, T.H. The density of discontinuity traces in sampling windows. Int. J. Rock Mech. Min. Sci. 1984, 21, 345–347. [Google Scholar] [CrossRef]
- Mauldon, M. Intersection probabilities of impersistent joints. Int. J. Rock Mech. Min. Sci. 1994, 31, 107–115. [Google Scholar] [CrossRef]
- Hudson, J.A.; Priest, S.D. Discontinuity frequency in rock masses. Int. J. Rock Mech. Min. Sci. 1983, 20, 73–89. [Google Scholar] [CrossRef]
- François, M.; Grosges, T.; Barchiesi, D.; Erra, R. Pseudo-random number generator based on mixing of three chaotic maps. Commun. Nonlinear Sci. 2014, 19, 887–895. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive large scale movements in blocky rock systems. In Proceedings of the Symposium of the International Society for Rock Mechanics; Society for Rock Mechanics (ISRM): Nancy, France, 1971. [Google Scholar]
- Sistaninia, M.; Sistaninia, M. Theoretical and experimental investigations on the mode II fracture toughness of brittle materials. Int. J. Mech. Sci. 2015, 98, 1–13. [Google Scholar] [CrossRef]
- Ovalle, C.; Frossard, E.; Dano, C.; Hu, W.; Maiolino, S.; Hicher, P.Y. The effect of size on the strength of coarse rock aggregates and large rockfill samples through experimental data. Acta. Mech. 2014, 225, 2199–2216. [Google Scholar] [CrossRef]
- Wang, W. Research on Construction Technology of Large Section Tailwater Tunnel under Unfavorable Geological Conditions. Ph.D. Thesis, Shenyang Agricultural University, Shenyang, China, 2018. [Google Scholar]
- Zhang, G.K.; Xu, W.Y. Simulation of Fracture Networks and Research on REV Scale. Rock Soil Mech. 2008, 29, 1675–1680. [Google Scholar]
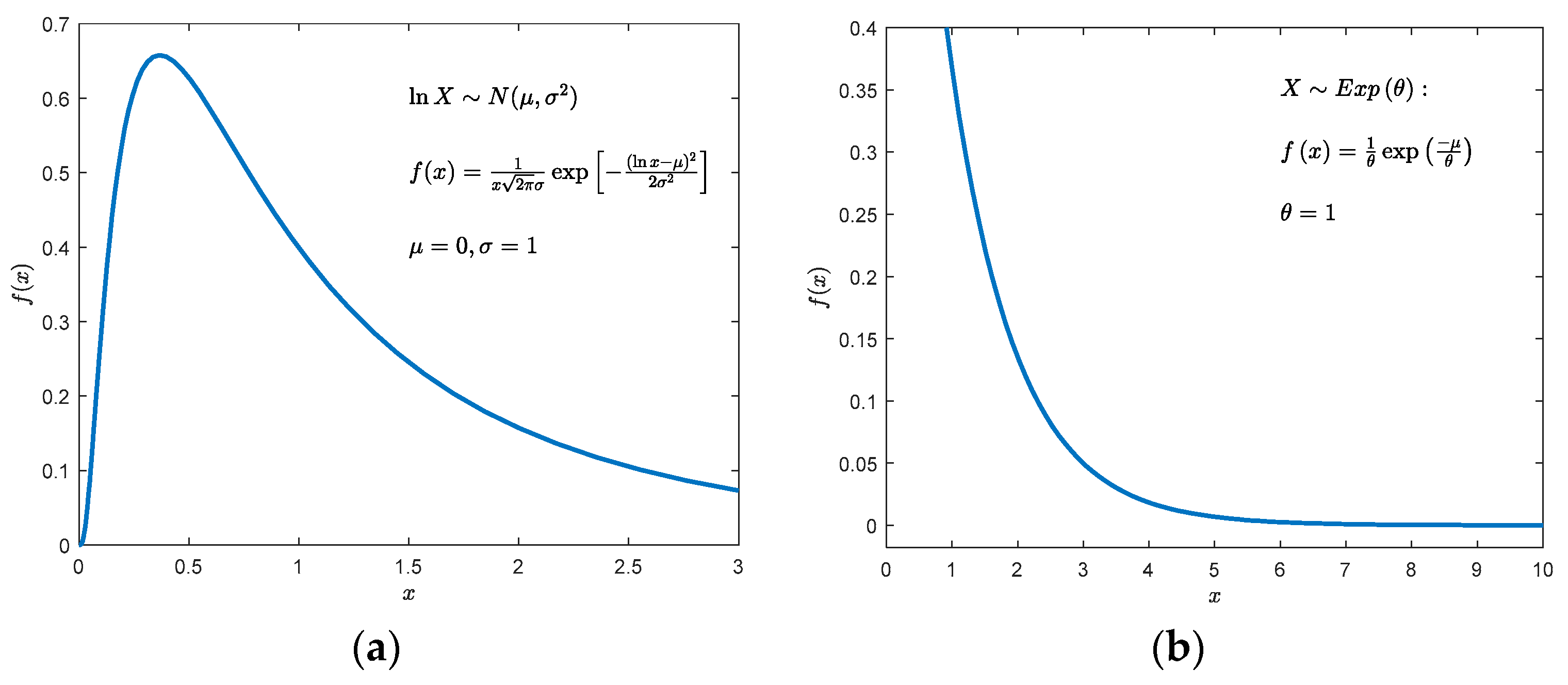

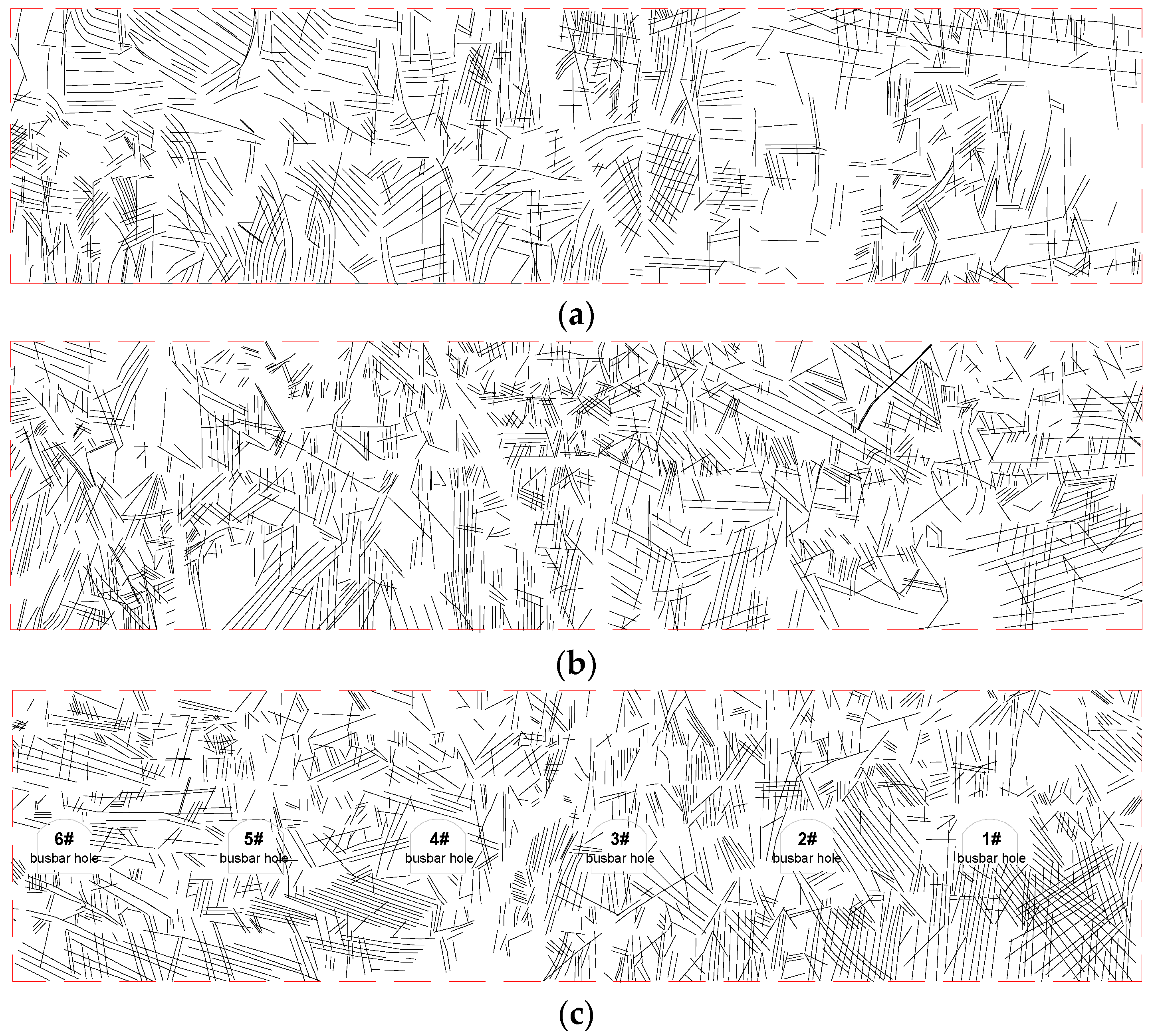



| Distribution Type | Probability Density Function | Random Numbers | Fissure Applications |
|---|---|---|---|
| Uniform distribution | Midpoint location | ||
| Negative exponents distribution | Trace length | ||
| Fisher distribution | Dip angle | ||
| Log-normally distributed | Trace length/Aperture | ||
| Poisson distribution | Density | ||
| Normal distribution | Aperture |
| Geologic Statistics Window Locations | Roof Arch | Upstream Wall | Downstream Wall | Average |
|---|---|---|---|---|
| Number of structural faces/strips | 1049 | 1238 | 1421 | 1236 |
| Average trace length of fractures/m | 4.99 | 3.76 | 4.15 | 4.30 |
| Trace length variance/m2 | 4.00 | 2.85 | 3.50 | 3.45 |
| Fracture average dip angle/° | 43.26 | 56.32 | 54.69 | 51.42 |
| Dip angle variance/(°)2 | 29.76 | 27.01 | 27.02 | 27.93 |
| Quantity areal density (number of fractures per unit area)/m−2 | 0.15 | 0.29 | 0.26 | 0.23 |
| Fracture density (length of fracture per unit area)/m−1 | 0.75 | 1.07 | 1.10 | 0.97 |
| Fracture line density (number of fractures per unit length)/m−1 | 0.31 | 0.87 | 0.55 | 0.58 |
| Three-dimensional fracture density (fracture area per unit volume)/m−1 | 2.40 | 1.22 | 1.99 | 1.87 |
| Density /g·cm−3 | Bulk Modulus /GPa | Shear Modulus /GPa | Cohesion /MPa | Internal Friction Angle/° | Tensile Strength /MPa |
|---|---|---|---|---|---|
| 2600 | 24.6 | 12.5 | 11.3 | 50 | 3.58 |
| Normal Stiffness/GPa | Tangential Stiffness/GPa | Tensile Strength/MPa | Cohesion/MPa | Tensile Strength /MPa |
|---|---|---|---|---|
| 30 | 15 | 0.3 | 1.1 | 30 |
| Density/g·cm−3 | Bulk Modulus/GPa | Shear Modulus/GPa |
|---|---|---|
| 7800 | 300 | 250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Li, S.; Jin, J.; Shi, C. Determining Digital Representation and Representative Elementary Volume Size of Broken Rock Mass Using the Discrete Fracture Network–Discrete Element Method Coupling Technique. Appl. Sci. 2024, 14, 606. https://doi.org/10.3390/app14020606
Huang X, Li S, Jin J, Shi C. Determining Digital Representation and Representative Elementary Volume Size of Broken Rock Mass Using the Discrete Fracture Network–Discrete Element Method Coupling Technique. Applied Sciences. 2024; 14(2):606. https://doi.org/10.3390/app14020606
Chicago/Turabian StyleHuang, Xiao, Siyuan Li, Jionghao Jin, and Chong Shi. 2024. "Determining Digital Representation and Representative Elementary Volume Size of Broken Rock Mass Using the Discrete Fracture Network–Discrete Element Method Coupling Technique" Applied Sciences 14, no. 2: 606. https://doi.org/10.3390/app14020606
APA StyleHuang, X., Li, S., Jin, J., & Shi, C. (2024). Determining Digital Representation and Representative Elementary Volume Size of Broken Rock Mass Using the Discrete Fracture Network–Discrete Element Method Coupling Technique. Applied Sciences, 14(2), 606. https://doi.org/10.3390/app14020606






