A bi-Gamma Distribution Model for a Broadband Non-Gaussian Random Stress Rainflow Range Based on a Neural Network
Abstract
1. Introduction
2. Non-Gaussian Stress
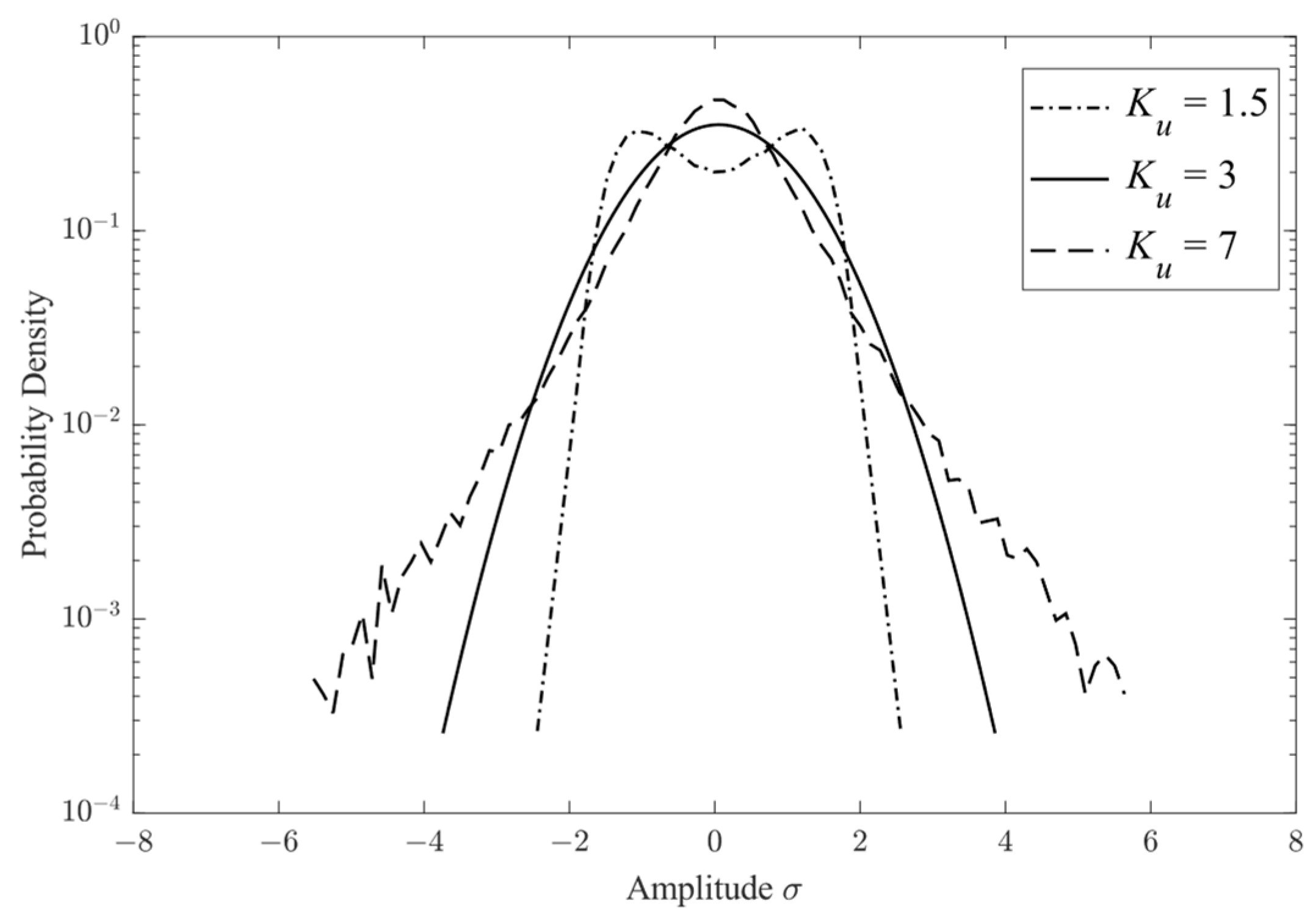
2.1. Definition of Kurtosis
2.2. Stress PSD
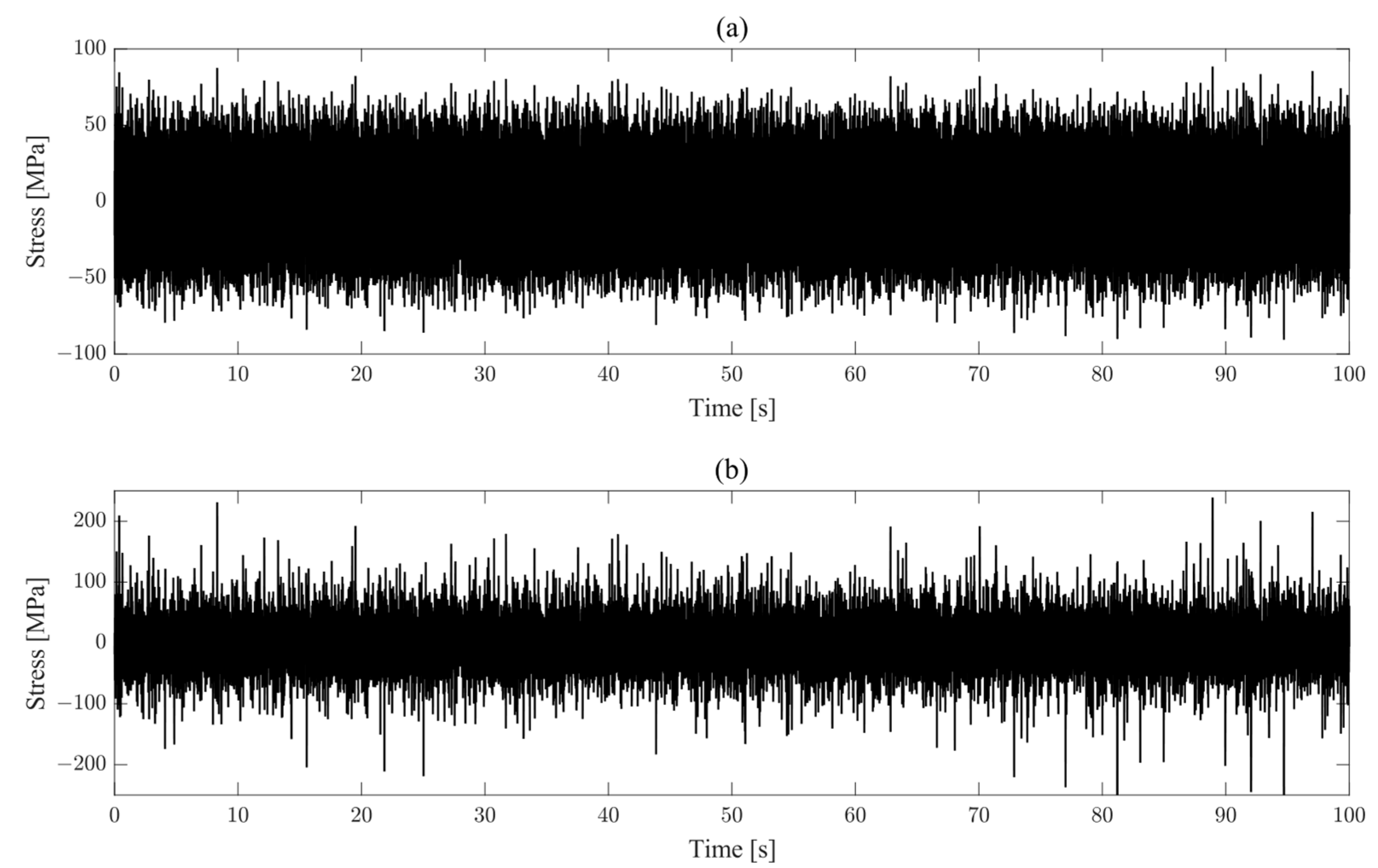
2.3. Generating of Non-Gaussian Stresses
3. Fatigue Life Calculation in Frequency Domain
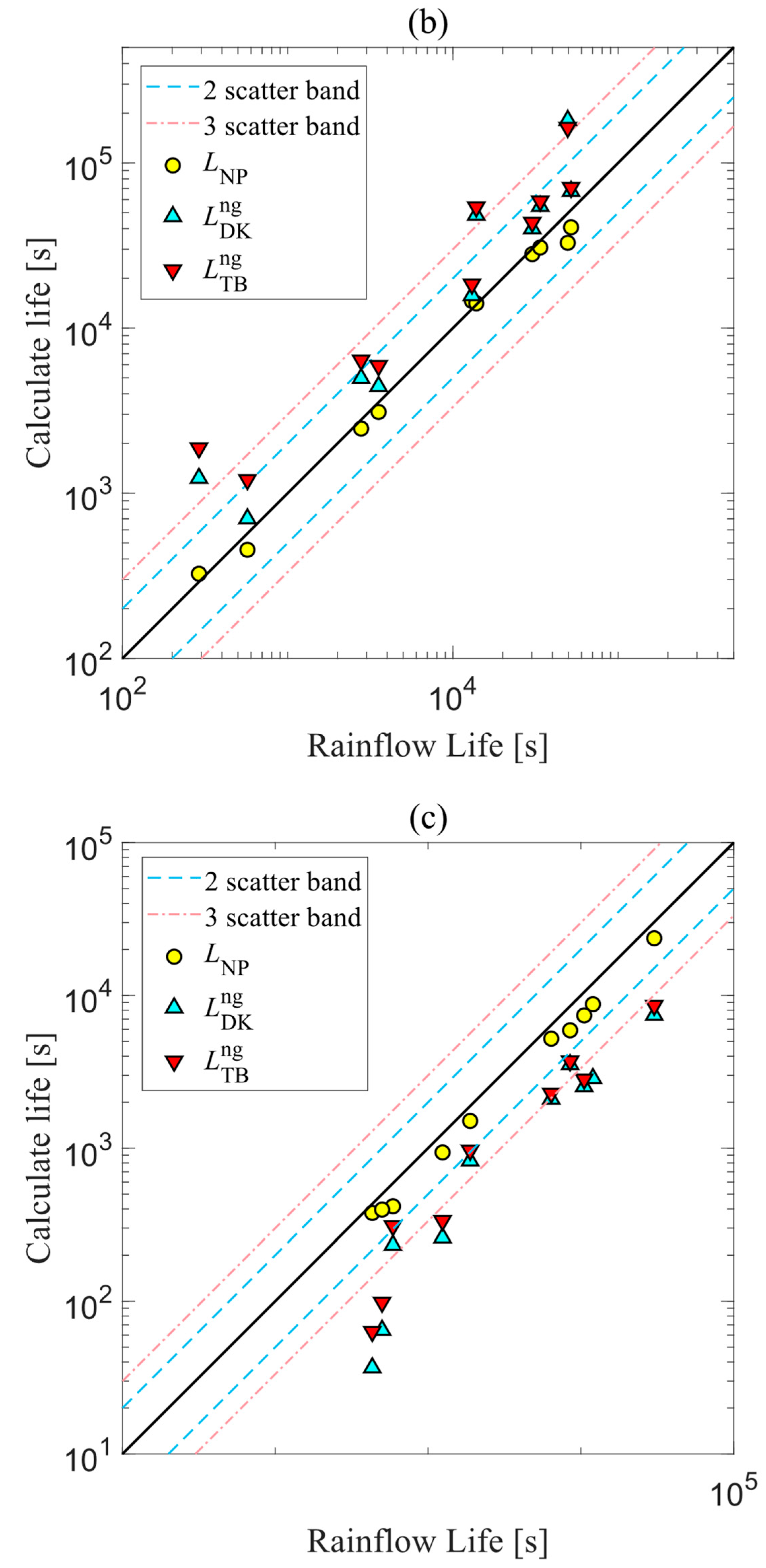
3.1. Fatigue Life Calculation
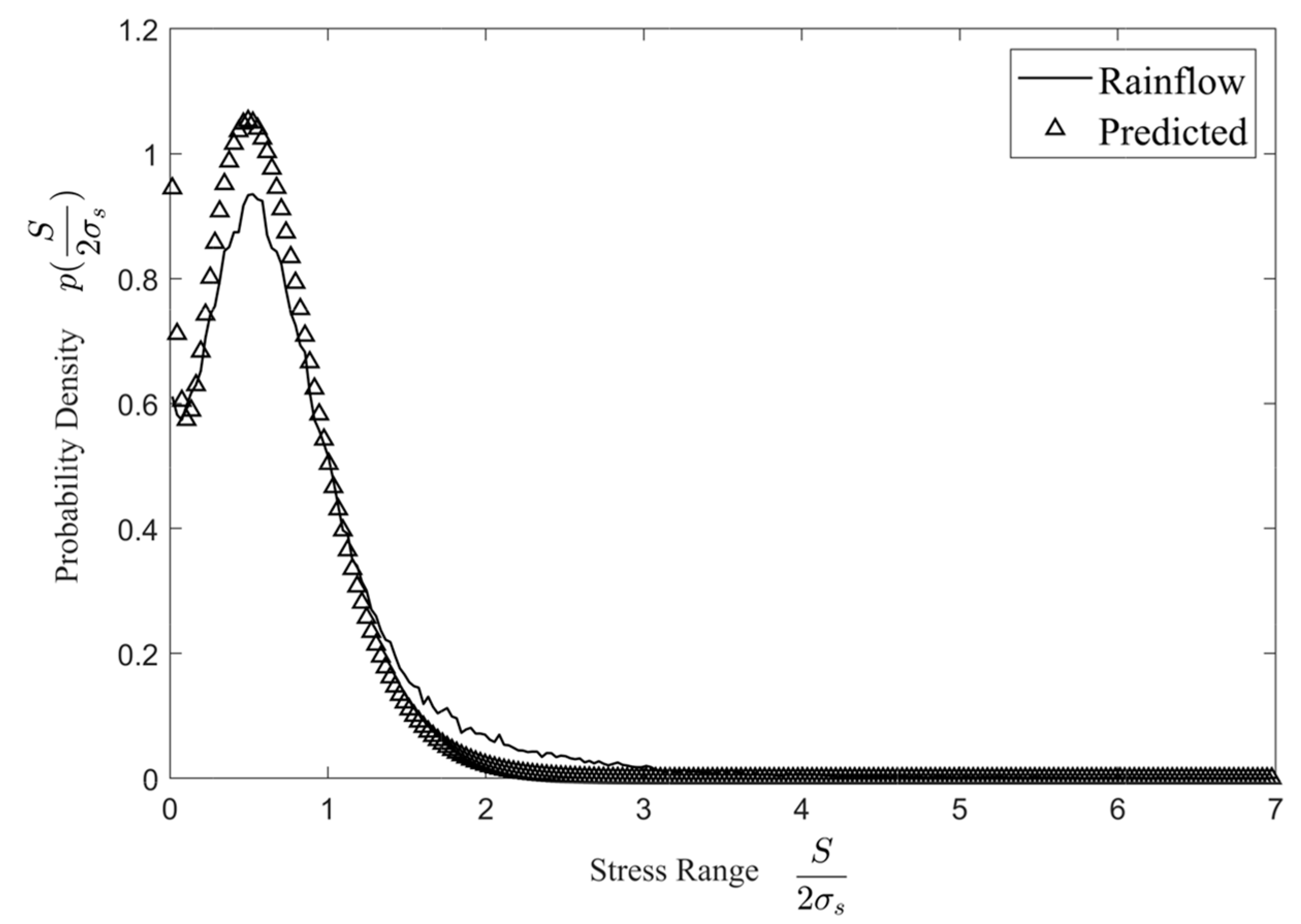
3.2. Stress Rainflow Range PDF Model
- (1)
- Dirlik model for Gaussian case
- (2)
- Tovo–Benasciutti model for Gaussian case
- (3)
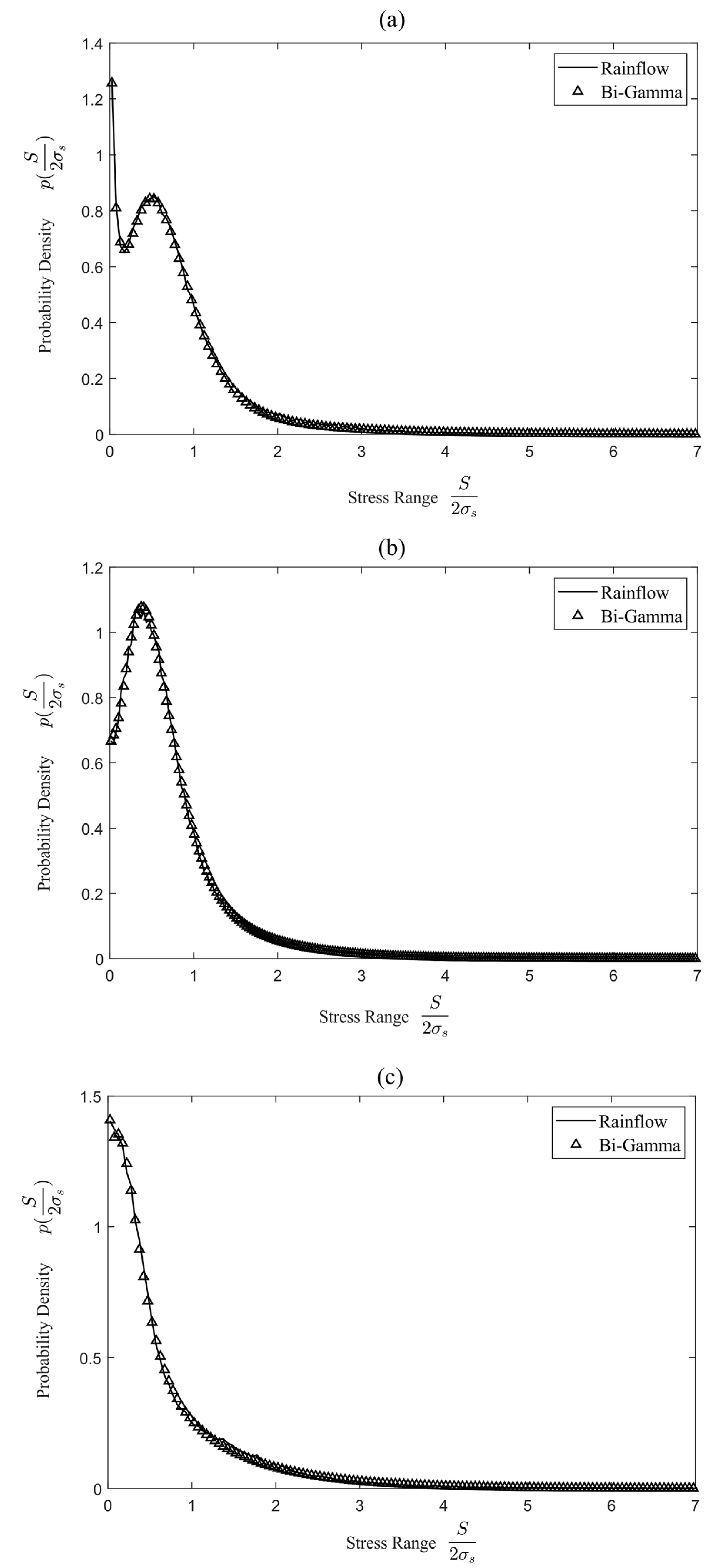
- Bi-Gamma model for non-Gaussian case
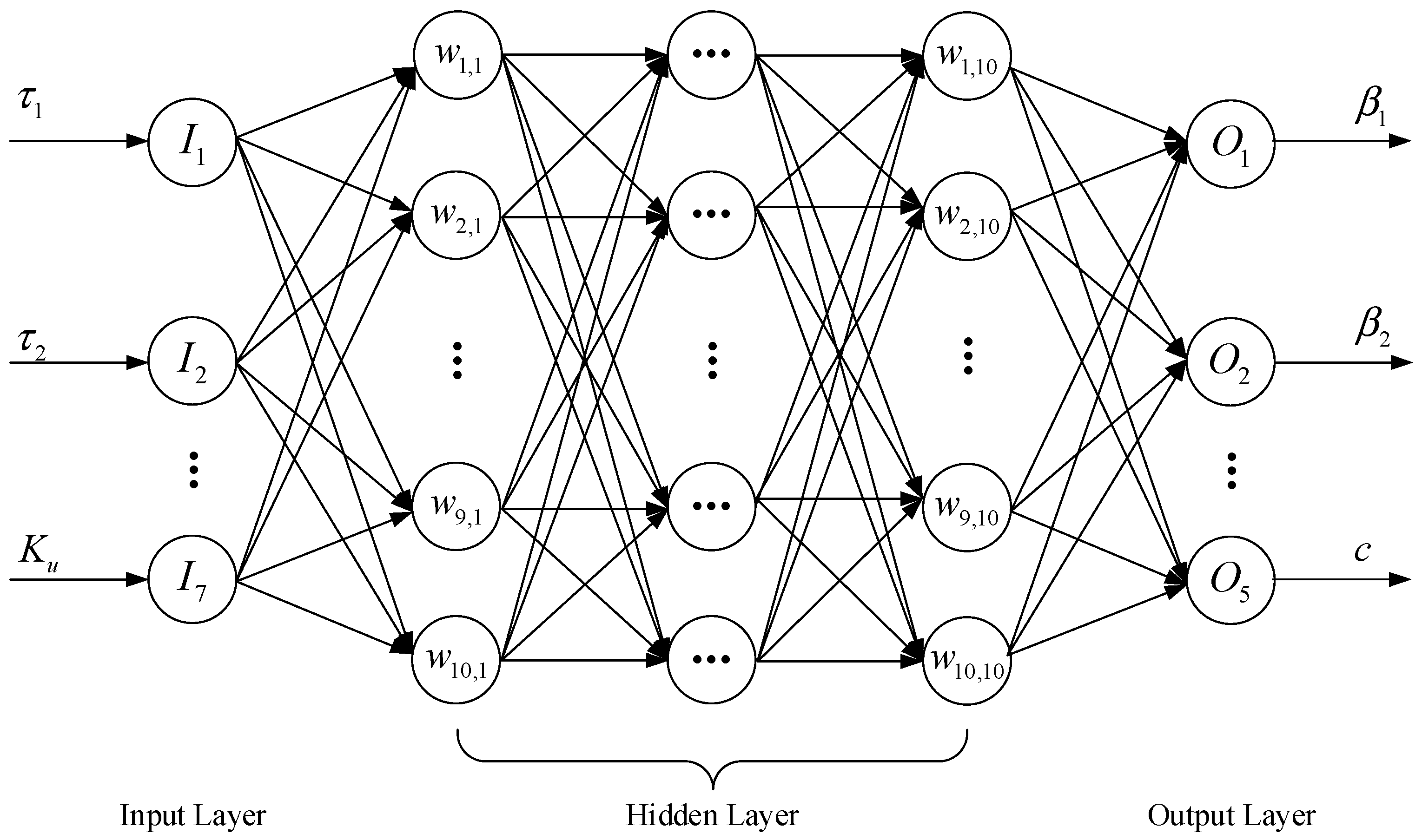
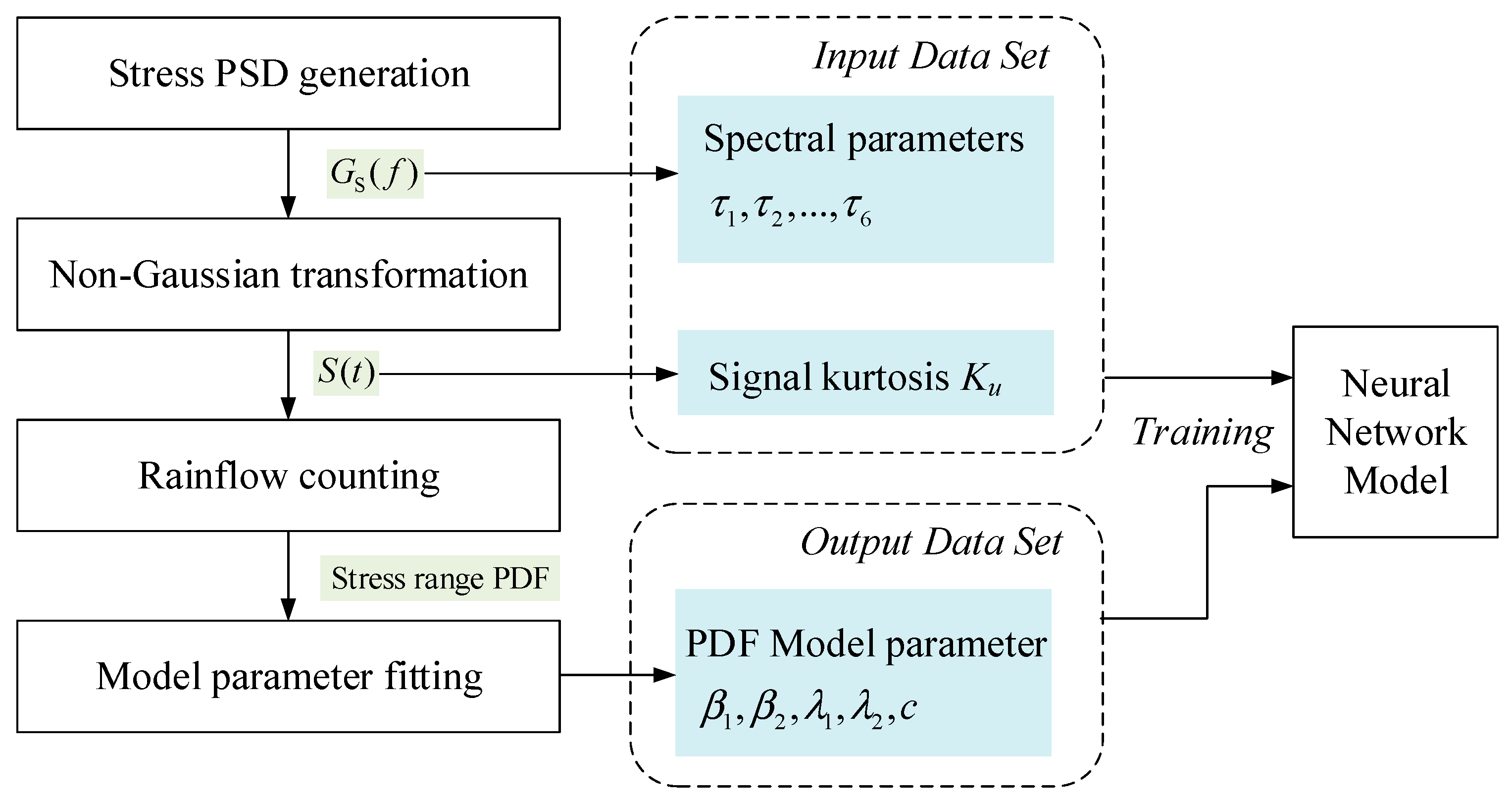
4. Neural Network Prediction Model
4.1. PDF bi-Gamma Model
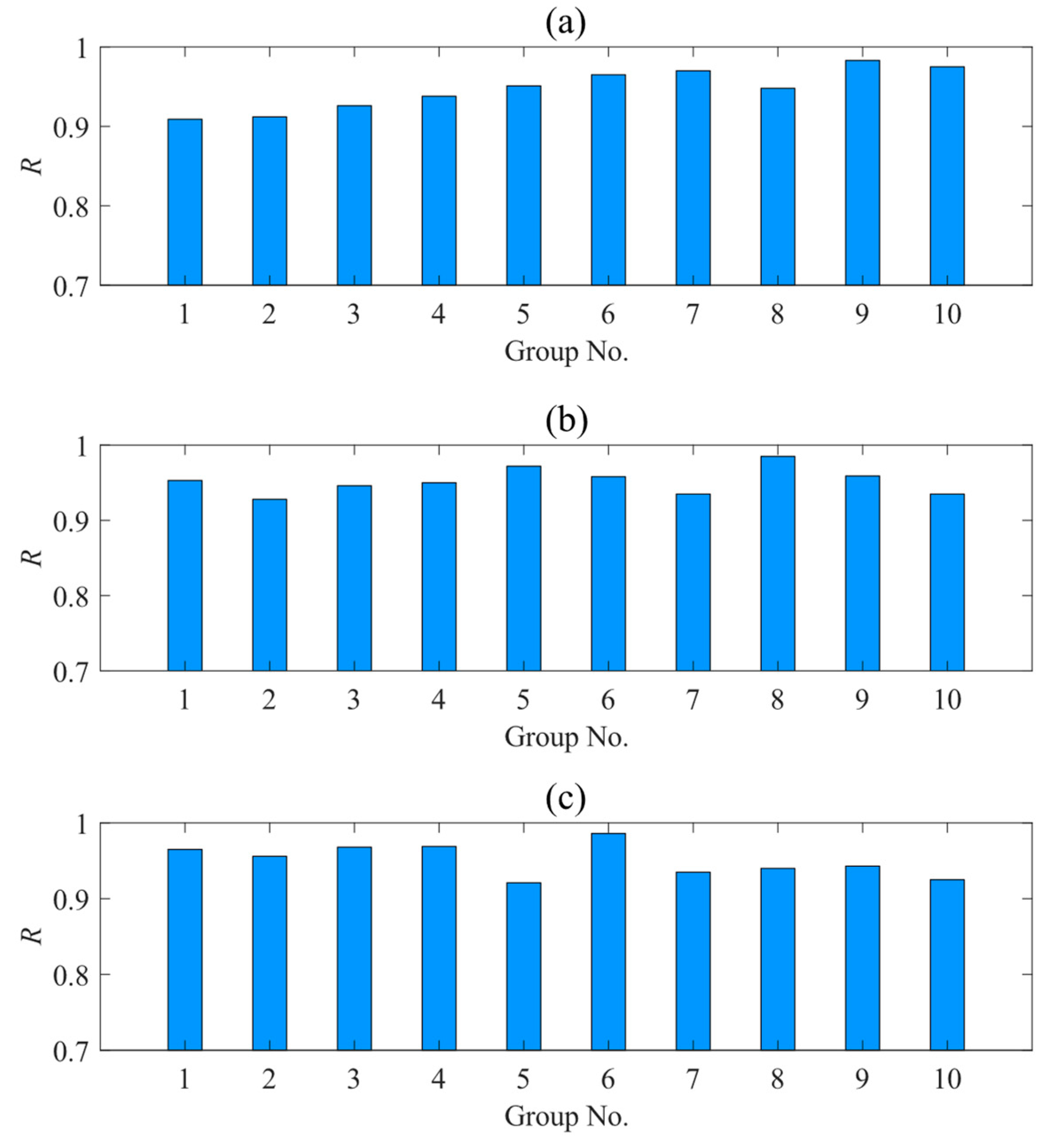
4.2. Dataset Generation and Establishment of Neural Network Model
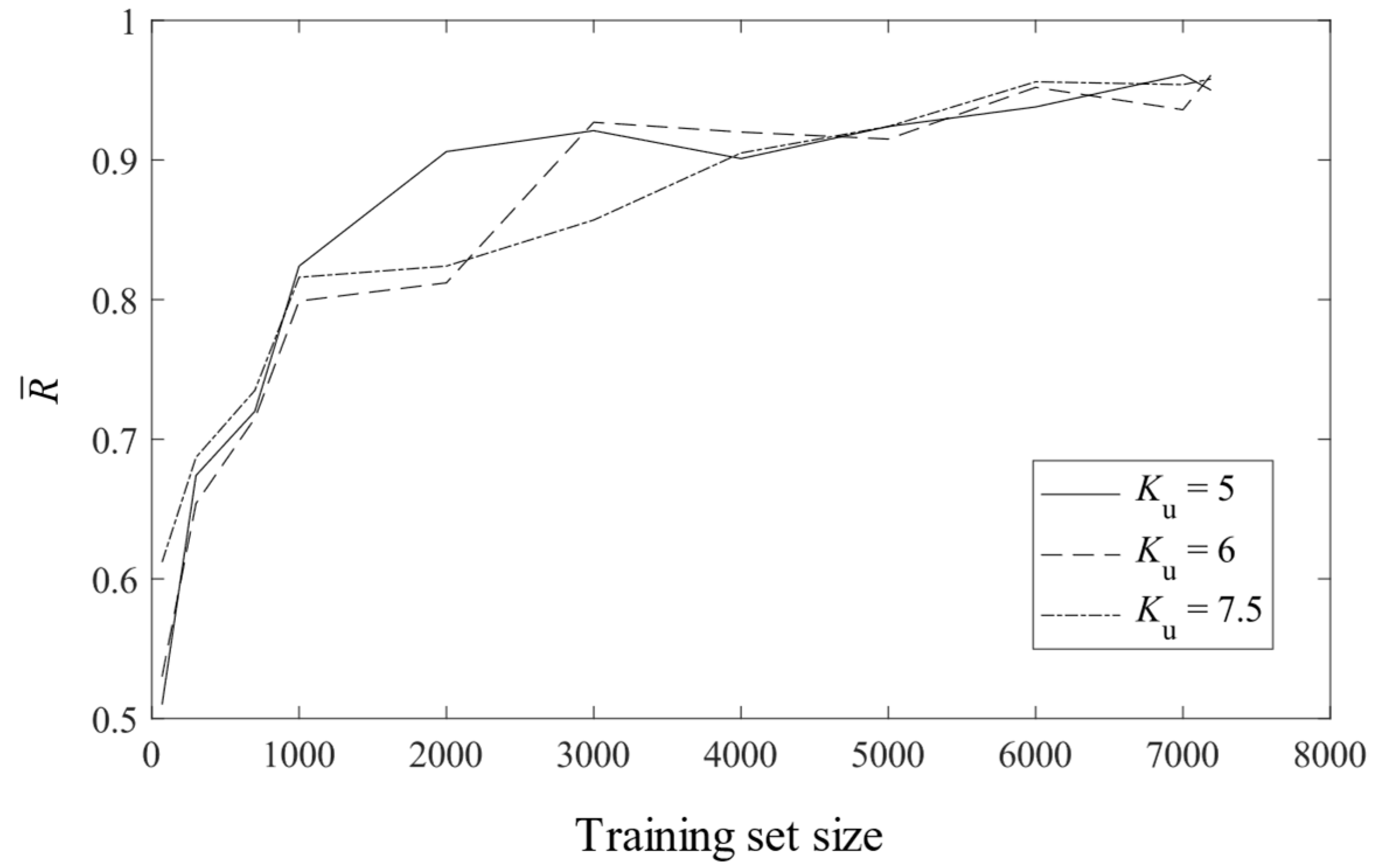
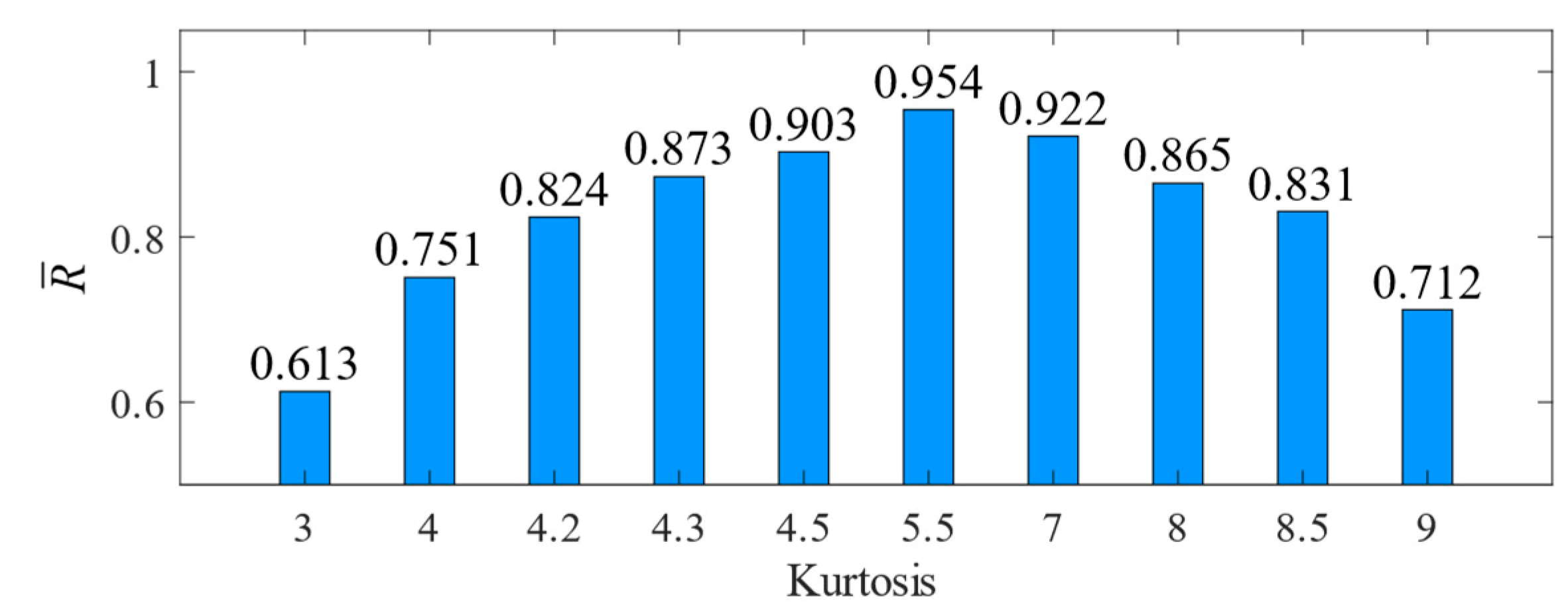
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dirlik, T. Application of Computers in Fatigue Analysis; University of Warwick: Coventry, UK, 1985. [Google Scholar]
- Lee, Y.-L. (Ed.) Fatigue Testing and Analysis: Theory and Practice; Elsevier Butterworth-Heinemann: Amsterdam, The Netherlands; Boston, MA, USA, 2005; ISBN 978-0-7506-7719-6. [Google Scholar]
- Slavic, J.; Boltezar, M.; Mrsnik, M.; Cesnik, M.; Javh, J. Vibration Fatigue by Spectral Methods: From Structural Dynamics to Fatigue Damage: Theory and Experiments; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 978-0-12-822190-7. [Google Scholar]
- Zheng, R.; Chen, H.; He, X. Control Method for Multiple-Input Multiple-Output Non-Gaussian Random Vibration Test. Packag. Technol. Sci. 2017, 30, 331–345. [Google Scholar] [CrossRef]
- Palmieri, M.; Česnik, M.; Slavič, J.; Cianetti, F.; Boltežar, M. Non-Gaussianity and Non-Stationarity in Vibration Fatigue. Int. J. Fatigue 2017, 97, 9–19. [Google Scholar] [CrossRef]
- Cianetti, F.; Palmieri, M.; Slavič, J.; Braccesi, C.; Morettini, G. The Effort of the Dynamic Simulation on the Fatigue Damage Evaluation of Flexible Mechanical Systems Loaded by Non-Gaussian and Non Stationary Loads. Int. J. Fatigue 2017, 103, 60–72. [Google Scholar] [CrossRef]
- ASTM E1049-85; Standard Practices for Cycle Counting in Fatigue Analysis. ASTM: West Conshohocken, PA, USA, 2017.
- Benasciutti, D.; Tovo, R. Spectral Methods for Lifetime Prediction under Wide-Band Stationary Random Processes. Int. J. Fatigue 2005, 27, 867–877. [Google Scholar] [CrossRef]
- Benasciutti, D.; Tovo, R. Comparison of Spectral Methods for Fatigue Analysis of Broad-Band Gaussian Random Processes. Probabilistic Eng. Mech. 2006, 21, 287–299. [Google Scholar] [CrossRef]
- Banvillet, A. Fatigue Life under Non-Gaussian Random Loading from Various Models. Int. J. Fatigue 2004, 26, 349–363. [Google Scholar] [CrossRef]
- Benasciutti, D.; Tovo, R. Fatigue Life Assessment in Non-Gaussian Random Loadings. Int. J. Fatigue 2006, 28, 733–746. [Google Scholar] [CrossRef]
- Braccesi, C.; Cianetti, F.; Lori, G.; Pioli, D. The Frequency Domain Approach in Virtual Fatigue Estimation of Non-Linear Systems: The Problem of Non-Gaussian States of Stress. Int. J. Fatigue 2009, 31, 766–775. [Google Scholar] [CrossRef]
- Sun, H.; Qiu, Y.; Li, J. A Novel Artificial Neural Network Model for Wide-Band Random Fatigue Life Prediction. Int. J. Fatigue 2022, 157, 106701. [Google Scholar] [CrossRef]
- Yang, J.; Kang, G.; Liu, Y.; Kan, Q. A Novel Method of Multiaxial Fatigue Life Prediction Based on Deep Learning. Int. J. Fatigue 2021, 151, 106356. [Google Scholar] [CrossRef]
- Plets, J.; Bouckaert, Q.; Ahmed, B.; De Waele, W.; Hectors, K. Neural Network Based Fatigue Lifetime Prediction of Metals Subjected to Block Loading. Int. J. Fatigue 2024, 183, 108283. [Google Scholar] [CrossRef]
- Bai, Y.; Xie, C.; Zhou, X. AI-Based Macro Model Learning for High Cycle Fatigue Assessment of Welded Joints in Large-Span Steel Structures. Int. J. Fatigue 2024, 184, 108321. [Google Scholar] [CrossRef]
- Susmel, L. Estimating Notch Fatigue Limits via a Machine Learning-Based Approach Structured According to the Classic Kf Formulas. Int. J. Fatigue 2024, 179, 108029. [Google Scholar] [CrossRef]
- Wang, B.; Xie, L.; Song, J.; Zhao, B.; Li, C.; Zhao, Z. Curved Fatigue Crack Growth Prediction under Variable Amplitude Loading by Artificial Neural Network. Int. J. Fatigue 2021, 142, 105886. [Google Scholar] [CrossRef]
- Kamiyama, M.; Shimizu, K.; Akiniwa, Y. Prediction of Low-Cycle Fatigue Crack Development of Sputtered Cu Thin Film Using Deep Convolutional Neural Network. Int. J. Fatigue 2022, 162, 106998. [Google Scholar] [CrossRef]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight Uncertainty in Neural Networks 2015. In Proceedings of the 32nd International Conference on International Conference on Machine Learning - Volume 37 (ICML’15), Lille, France, 6–11 July 2015. [Google Scholar]
- Arunakumara, P.C.; Sagar, H.N.; Gautam, B.; George, R.; Rajeesh, S. A Review Study on Fatigue Behavior of Aluminum 6061 T-6 and 6082 T-6 Alloys Welded by MIG and FS Welding Methods. Mater. Today Proc. 2023, 74, 293–301. [Google Scholar] [CrossRef]
- Moreira, P.M.G.P.; Richter-Trummer, V.; de Castro, P.M.S.T. Fatigue Behaviour of FS, LB and MIG Welds of AA6061-T6 and AA6082-T6. In Multiscale Fatigue Crack Initiation and Propagation of Engineering Materials: Structural Integrity and Microstructural Worthiness; Sih, G.C., Ed.; Springer: Dordrecht, The Netherlands, 2008; pp. 85–111. [Google Scholar]


| Kurtosis | RMS | |
|---|---|---|
| Gaussian signal | 3.0246 | 20.1679 |
| Non-Gaussian signal | 7.5988 | 20.1679 |
| β1 | β2 | λ1 | λ2 | c | |
|---|---|---|---|---|---|
| f1 = 8 Hz, f2 = 91 Hz | 0.6107 | 4.0269 | 0.8114 | 5.3480 | 0.4984 |
| f1 = 19 Hz, f2 = 192 Hz | 1.0773 | 4.0521 | 1.4323 | 6.8156 | 0.5895 |
| f1 = 42 Hz, f2 = 153 Hz | 0.8112 | 2.4348 | 0.9951 | 7.3505 | 0.7691 |
| Group No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| f1 [Hz] | 33 | 15 | 13 | 44 | 10 | 33 | 13 | 33 | 21 | 15 |
| f2 [Hz] | 80 | 111 | 150 | 108 | 161 | 71 | 196 | 172 | 72 | 76 |
| Parameter | C | k |
|---|---|---|
| Value | 5.899 × 1026 | 9.842 |
| No. | Gaussian Stress Ku = 3 | Non-Gaussian Stress Ku = 7.5 | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2.4666 × 106 | 1.6156 × 106 | 2.1526 × 106 | 589.2192 | 232.5485 | 309.8470 | 416.4163 |
| 2 | 2.6203 × 107 | 2.4503 × 107 | 2.5823 × 107 | 8.5049 × 103 | 3.5269 × 103 | 3.7170 × 103 | 5.9124 × 103 |
| 3 | 1.6319 × 107 | 1.4576 × 107 | 1.5879 × 107 | 6.4004 × 103 | 2.0981 × 103 | 2.2856 × 103 | 5.2125 × 103 |
| 4 | 4.9295 × 105 | 2.5516 × 105 | 4.3926 × 105 | 431.5450 | 36.7281 | 63.2274 | 376.7941 |
| 5 | 2.2346 × 107 | 1.9906 × 107 | 2.1365 × 107 | 1.1993 × 104 | 2.8653 × 103 | 3.0753 | 8.7648 × 103 |
| 6 | 2.6646 × 106 | 1.8067 × 106 | 2.3256 × 106 | 1.2440 × 103 | 260.0622 | 334.74 | 938.0734 |
| 7 | 7.9882 × 106 | 5.7403 × 106 | 6.7135 × 106 | 1.8858 × 103 | 826.2697 | 966.3466 | 1.5082 × 103 |
| 8 | 7.8686 × 106 | 4.4939 × 105 | 6.8265 × 105 | 500.2461 | 64.6857 | 98.2612 | 396.3677 |
| 9 | 2.0573 × 107 | 1.7607 × 107 | 1.9657 × 107 | 1.0515 × 104 | 2.5344 × 103 | 2.8294 × 103 | 7.4056 × 103 |
| 10 | 6.3115 × 107 | 5.1605 × 107 | 5.9634 × 107 | 3.0222 × 104 | 7.4280 × 103 | 8.5838 × 103 | 2.3686 × 104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Chen, H. A bi-Gamma Distribution Model for a Broadband Non-Gaussian Random Stress Rainflow Range Based on a Neural Network. Appl. Sci. 2024, 14, 8376. https://doi.org/10.3390/app14188376
Wang J, Chen H. A bi-Gamma Distribution Model for a Broadband Non-Gaussian Random Stress Rainflow Range Based on a Neural Network. Applied Sciences. 2024; 14(18):8376. https://doi.org/10.3390/app14188376
Chicago/Turabian StyleWang, Jie, and Huaihai Chen. 2024. "A bi-Gamma Distribution Model for a Broadband Non-Gaussian Random Stress Rainflow Range Based on a Neural Network" Applied Sciences 14, no. 18: 8376. https://doi.org/10.3390/app14188376
APA StyleWang, J., & Chen, H. (2024). A bi-Gamma Distribution Model for a Broadband Non-Gaussian Random Stress Rainflow Range Based on a Neural Network. Applied Sciences, 14(18), 8376. https://doi.org/10.3390/app14188376






