Quantitative Assessment of Rock Burst Risk in Roadway Tunneling Considering Variation of Coal Mass Parameters

Abstract

To investigate the influence of varied mechanical parameters of coal mass on rock burst occurrence during deep roadway tunneling, the surrounding coal and rock mass of a deep roadway were taken as the research objects. A geometric model of roadway tunneling was developed using 3DEC numerical simulation software, and the failure characteristics of the coal mass in the roadway side were analyzed based on the rock burst mechanism and stress difference gradient theory for deep mining. The risk of rock burst during roadway tunneling was quantitatively assessed using the change rate of the stress difference gradient (D_gc), thereby elucidating the burst failure patterns of the deep roadway under the influence of varied mechanical parameters. The findings indicate that the coal mass in the roadway side zone is more prone to burst failure due to stress disturbances during deep excavation compared to the coal and rock mass in the roof and floor zones, and that the released kinetic energy and the risk of burst failure are positively correlated with the magnitude of the ground stress. The variation of the mechanical properties of coal mass has a significant effect on the rock burst risk during roadway tunneling. The variation of both internal friction angle and cohesion significantly affects rock burst, with cohesion exerting a greater influence. Conversely, the elastic modulus does not significantly impact the risk. The tendency of bursting in the coal mass is positively correlated with the coefficient of variation (COV) in cohesion and negatively correlated with the COV in internal friction angle. These research findings offer valuable insights for the quantitative assessment of rock burst risk during roadway tunneling.

1. Introduction

Coal has always served as the predominant energy source in China. As the intensity of coal mining has escalated, dynamic disasters, such as rock burst, have become increasingly frequent, posing a substantial threat to the safety of coal production. Rock burst is a dynamic phenomenon characterized by sudden instability and violent destruction of coal mass under high ground stress conditions, typically occurring during deep coal mining [1,2,3]. Effective monitoring and early warning measures, coupled with appropriate prevention and control strategies, can mitigate the risk of rock burst during mining operations. Presently, rock burst risk assessment primarily relies on the intrinsic properties of the coal and rock mass, utilizing specific indicators to gauge the risk of destructive potential. However, due to the variation in the mechanical properties of coal and rock mass, accurate characterization of coal bursting liability through mechanical parameters remains challenging. Furthermore, the identification of rock burst risk during roadway tunneling necessitates further refinement. Therefore, a quantitative assessment of rock burst risk during roadway tunneling is essential for mitigating the occurrence of typical dynamic disasters in coal mines [4,5].

Scholars from all over the world have conducted extensive research on the factors that induce rock burst during roadway tunneling, yielding significant insights into the mechanisms. Gu et al. [6] employed UDEC 7.0 software to simulate a laboratory-scale double shear test, discovering that unstable slip damage at the coal–rock interface can trigger sudden unconfinement, potentially causing destabilizing sidewall damage. Wu et al. [7] used UDEC to reveal the mechanism of roadway rock burst damage under dynamic loads, finding a correlation between dynamic load distances and rock burst damage. Zhao et al. [8] analyzed factors affecting rock burst and concluded that greater three-way stress differences within the coal and rock mass increase its susceptibility to damage from external disturbances. Wang et al. [9] studied the impact law of coal and rock mass under dynamic and static load coupling, demonstrating that coal and rock mass is more vulnerable to bursting under dynamic load waves in high ground stress environments. Zuo et al. [10] suggested that the surrounding rock of the roadway undergoes a transition from “three-way stress → bi-directional stress → approximate uniaxial stress”, with the formation of a stress gradient around the roadway leading to rock burst damage. Liu et al. [11] proposed that the change rate of the three-way stress difference gradient, D_gc, indicates the mechanism of rock burst damage in the surrounding rock. Zhang et al. [12] indicated that a higher stress concentration in the elastic area of isolated coal mass increases the likelihood of rock burst. These studies collectively enhance the understanding of the factors contributing to rock burst and provide critical insights into the mechanisms of roadway rock burst damage.

The evaluation of rock burst risk in coal seams is essential for effectively mitigating risks and quantitatively inducing threats. Based on previous research into rock burst mechanisms, scholars have developed several novel methods for roadway rock burst risk assessment. Agrawal et al. [13] proposed a probabilistic risk assessment framework to model rock burst and gas outburst in heterogeneous coal seams with a consideration of variations in the mechanical properties of coal and rock mass due to lithological diversity. Wojtecki et al. [14] employed machine learning algorithms, such as neural networks (ANN), decision trees (DT), random forest (RF), gradient boosting (GB), and extreme gradient boosting (XGB), to assess the risk of rock burst in a coal mine situated in the Upper Silesian Coal Basin. Zhang et al. [15] employed on-site microseismic monitoring data, acoustic emission, electromagnetic radiation, and other monitoring data to propose a multi-parametric coupling method for identifying hazardous areas of rock burst. Wang et al. [16] analyzed the characteristics of microseismic waveforms and spectra at various energy levels to establish prediction indices and set thresholds for rock burst. Han et al. [17] proposed a comprehensive warning system that integrates medium- and long-term dynamic warnings of mining-induced seismic activity with short-term spatial and temporal warnings of rock burst deformation energy. Wu et al. [18] assessed the rock burst risk in tunnel boring by examining the deformation damage and energy evolution characteristics of the surrounding rock after boring. Guo et al. [19] developed a quantitative rock burst risk assessment method using the plastic zone morphology coefficient as an index. Jaiswal et al. [20] combined motion thermogram data from laboratory rock burst monitoring with an advanced deep neural network approach employing a regional convolutional network (Mask R-CNN). Askaripour et al. [21] noted that current empirical methods for rock burst prediction predominantly depend on the geomechanical parameters of rocks. These methods are crucial in understanding and predicting rock burst events. Qi et al. [22] advanced this research by investigating additional factors and techniques that can enhance the accuracy and reliability of rock burst prediction.

The above research findings have a guiding role in monitoring and preventing rock burst in coal mining activities. However, the inducing factors of rock burst in coal mines are complex and diverse. Most studies based on the analysis of the mechanism of rock burst occurrence, and energy dissipation characteristics cannot meet the requirements of the quantitative assessment of roadway rock burst risk under the influence of varied mechanical parameters in coal and rock mass.

Based on the variation characteristics of coal mass parameters, this paper considers the essence of rock burst phenomena as an extreme manifestation driven by the stress difference gradient within continuous unit bodies in coal. The change rate of the stress difference gradient is employed to characterize its ability to resist stress-driven deformation, thereby quantitatively assessing the rock burst risk during roadway tunneling. The research findings could have theoretical and practical significance for the prevention and control of rock burst in coal roadways.

2. Engineering Cases and Discrete Element Modeling

This study identifies a specific coal mine in the Xuzhou mining area of China as its research context, with a primary focus on the 7# coal seam. The average thickness of this coal seam measures approximately 4.76 m, exhibiting a dip angle that ranges from 16.1° to 20.7°. Although generally characterized by stability, noticeable variations in thickness are observed in proximity to fault zones. Specifically, this research investigates the 8101 working face located within the 7# coal seam, positioned at an approximate depth of approximately 1124 m along the transportation roadway. The roof of the roadway predominantly comprises sandy mudstone, with local variations transitioning into fine-grained sandstone. The immediate roof has an average thickness of 6.7 m and contains a few slip planes. The upper roof is gray-white medium-grained sandstone, primarily composed of quartz and feldspar. The immediate bottom is mudstone, which contains carbonaceous material and minor yellow pyrite films, with plant fossils present. From the western to the eastern side of the working face, the immediate bottom gradually transitions from mudstone to sandy mudstone, with the thickness increasing progressively. The working face extends approximately 40 m in length. In 20 August 2018, a total of three instances of rock burst accidents occurred in the vicinity of the aforementioned working face during tunneling operations [23].

Based on field observation and laboratory test data, this paper establishes a numerical model specifically focused on the roadway tunneling of that working face. The dimensions of the model measure 60 m in length, 40 m in height, and 4 m in width. The distribution of rock and coal strata within the model is depicted in Figure 1. The comprehensive model consists of two strata as the top plate, two as the bottom plate, and a vertically oriented coal seam situated centrally. During the modeling process, a from-geometry approach was employed to randomly partition a central area measuring 20 m in length and 16 m in width into triangular sections, each with a side length of 1 m.

The outer perimeter rock was segmented into irregular hexagonal blocks under Voronoi model, each possessing a side length of 2 m. The model adheres to Mohr–Coulomb principal relationship, encompassing specific boundary conditions. Vertical and horizontal displacements are constrained by supports at the bottom; horizontal displacements are restricted by simple supports at the left and right boundaries, while vertical stress is applied at the upper boundary. Ground stress is calculated based on the depth of the working face, with a horizontal lateral pressure coefficient of 1.25. The parameters for surrounding rock joints are derived from geological data relevant to coal mine engineering, as shown in

Table 1. Mechanical parameters of rock and coal mass.

Height/m	The Name of the Rock Formation	Density/ (kg/m3)	Modulus of Elasticity/ GPa	Shear Modulus/ GPa	Bulk Modulus/ GPa	Poisson’s Ratio
10	upper roof	2560	27.5	11.08	18.41	0.26
6.4	immediate roof	2500	9.6	3.87	8.2	0.28
9.6	coal seam	1400	3.1	1.25	3.02	0.31
4	immediate bottom	2500	9.6	3.87	8.2	0.28
10	basic bottom	2560	27.5	11.08	18.41	0.26

and

Table 2. Mechanical parameters of perimeter rock joints.

The Name of the Rock Formation	Normal Stiffness/ GPa	Tangential Stiffness/ GPa	Internal Friction Angle/°	Adhesion/ MPa	Tensile Strength/ MPa
upper roof	5100	2100	25	10.2	5.6
immediate roof	3200	1400	20	8.1	3.2
coal seam	2000	800	18	3.0	1.1
immediate bottom	3200	1400	20	8.1	3.2
basic bottom	5100	2100	25	10.2	5.6

.

3. Variation of Mechanical Parameters in the Coal Mass

Coal mass exhibits inherent non-homogeneity, which can be characterized using a normal distribution function with a coefficient of variation to relate it to mechanical properties [24]. In this study, a coefficient of variation of 0.15 is applied to the mechanical parameters. The standard deviation for each selected parameter—elastic modulus, internal friction angle, and cohesion—is calculated based on the original coal seam parameters, as detailed in

Table 3. Statistical characteristics of three mechanical parameters.

Mechanical Parameter	Mean μ	Standard Deviation σ	Coefficient ν
Elastic modulus $c$/GPa	3.1	0.465	0.15
Internal friction angle $\phi$/(°)	18	2.7	0.15
Cohesion $E$/kPa	3.0	0.45	0.15

.

Assuming a normal distribution, parameters are selected within the range of (μ − 3σ, μ + 3σ) for ten distinct sets of parameter groups (a~j), as detailed in

Table 4. Ten varied parameter groups of coal mass based on 3σ criterion.

Parameter Group	(μ − 3σ, μ + 3σ)	Elastic Modulus	Internal Friction Angle	Cohesion
a	(−3, 3, −3)	1.705	9.9	1.65
b	(−3, −3, 0)	1.705	9.9	3.0
c	(−3, −3, 3)	1.705	9.9	4.35
d	(−3, 0, −3)	1.705	18	1.65
e	(−3, 3, −3)	1.705	26.1	1.65
f	(0, −3, −3)	3.1	9.9	1.65
g	(3, −3, −3)	4.495	9.9	1.65
h	(0, 0, 0)	3.1	18	3.0
i	(3, 3, 3)	4.495	26.1	4.35
j	(0, 3, 3)	3.1	26.1	4.35

[25]. By employing the stochastic response surface methodology, calculations are performed to ascertain the necessary number of required matching points for the ten parameter sets. Adjustments are implemented to align with the 3σ criterion, with a particular focus on the tenth parameter group.

Finally, a functional relationship is established between variations in mechanical parameters of coal mass and the results obtained from numerical modeling of coal tunneling processes. This methodology offers valuable insights into the manner in which variability in the mechanical properties of coal mass affects roadway stability.

4. Results of Roadway Tunneling Simulation

4.1. Determination of Burst-Prone Area around the Roadway

To gain deeper insights into the factors influencing rock burst during roadway tunneling, different groups of coal mass parameters were employed based on various parameter schemes, and tunneling simulations were conducted using 3DEC 7.0 software. Real-time monitoring of the surrounding rock was carried out to analyze the zones that were prone to rock burst near the roadway.

Considering the stress conditions at various positions during the tunneling process, monitoring points were established in the center of the roadway’s roof and floor, designated as A and C, respectively. Additionally, another monitoring point was positioned at the center of the left roadway side, designated as B. The real-time displacement changes in the surrounding rock at the monitoring points throughout the tunneling process were recorded. The locations of the roadway monitoring points are depicted in Figure 2.

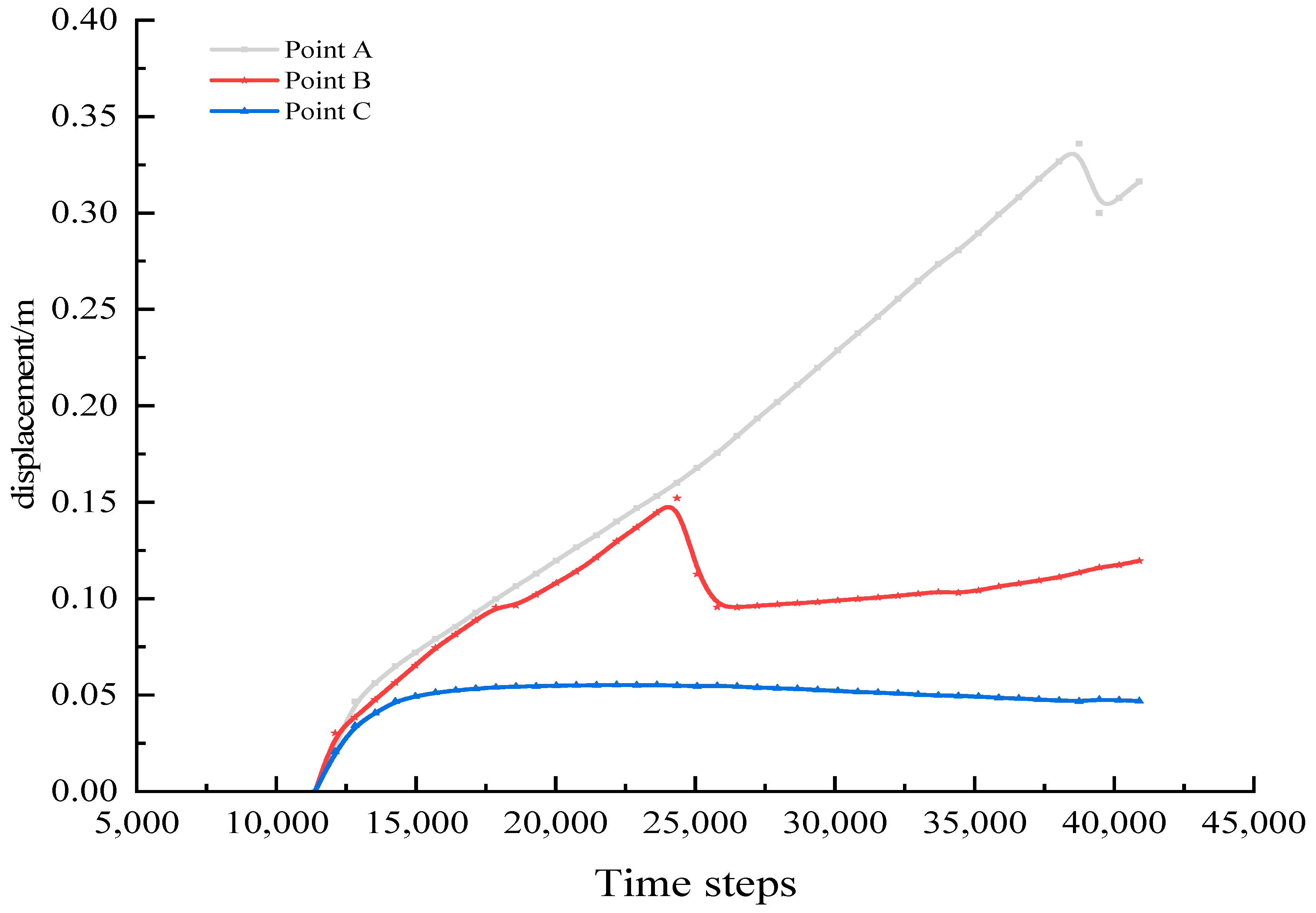
4.1.1. Displacement Analysis of Coal and Rock Mass during Roadway Tunneling

To characterize the roadway failure during the tunneling process through displacement, data from three monitoring points on the coal and rock mass were analyzed, as illustrated in Figure 3. The displacement curves at the monitoring points reveal that the coal-and-rock mass in the roof, floor, and roadway side areas have simultaneous displacement with comparable initial changes. As the time steps increase, the displacements of the three points continue to grow. The displacement at point C on the floor reaches a peak of 0.05 m before stabilizing. In contrast, the displacements at the roof and roadway side show an approximately linear increase until about 25,000 steps. Subsequently, the displacement at point B suddenly drops, while at point A, the displacement continues to increase. After that sudden drop at point B, the displacement increases again, although at a reduced rate, until the end of the model solution. Additionally, point A exhibits minor fluctuations towards the final stage of the model equilibrium.

By comparing these three displacement curves, the likelihood of rock burst at those points can be ranked as B > A > C. The patterns of the three curves indicate that the roof is prone to collapsing under stress disturbances caused by tunneling, while the floor is less likely to experience block displacement. The coal mass at the roadway side shows the most significant displacement changes under stress disturbances.

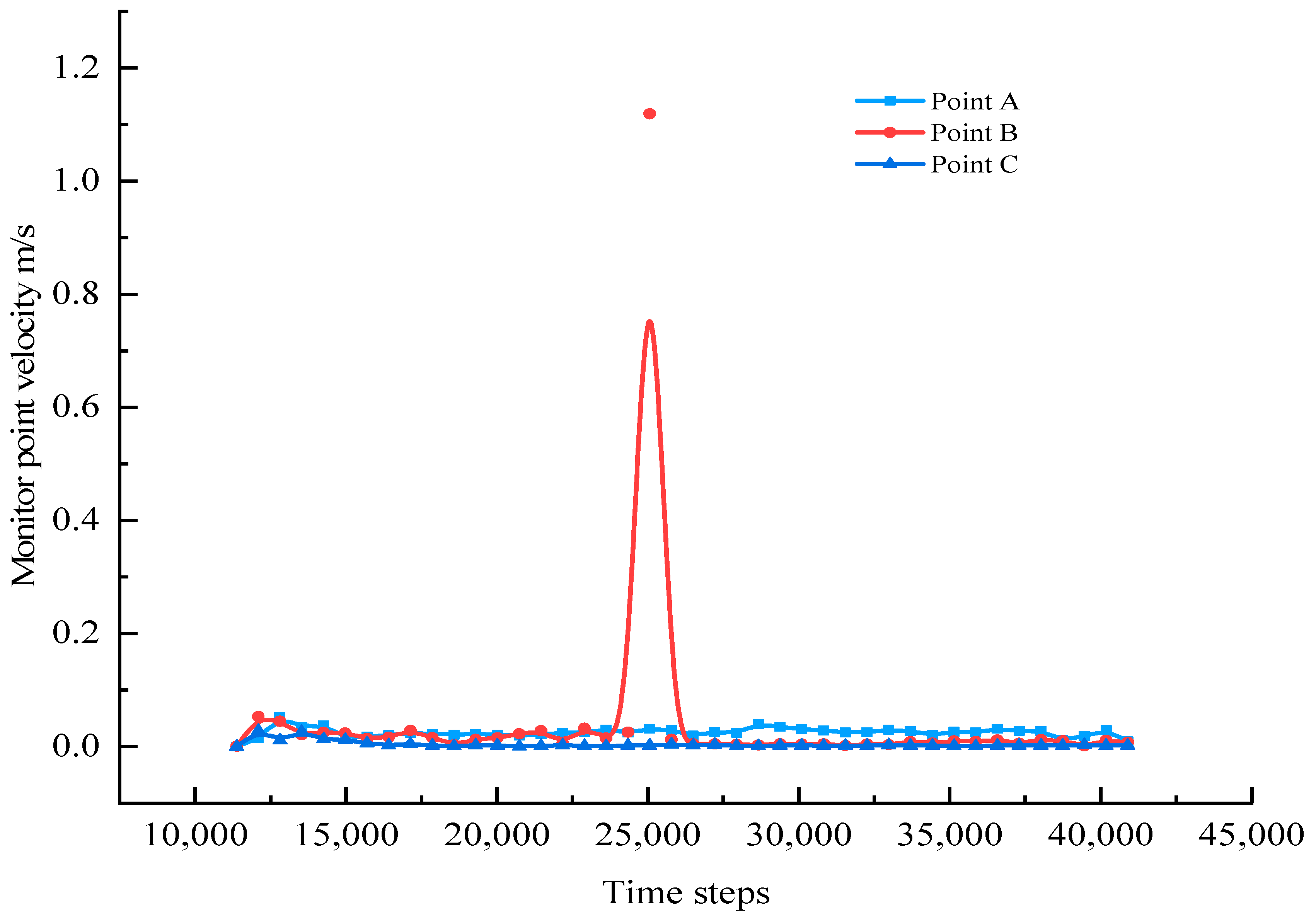
4.1.2. Velocity Analysis of Coal and Rock Mass during Roadway Tunneling

Based on a previous displacement analysis, a comprehensive analysis was conducted under the combination of velocity and displacement to examine the movement of the coal and rock mass throughout the roadway tunneling process. Figure 4 illustrates the curves of the coal and rock mass velocity recorded at the monitoring points. The velocity curves of the coal and rock mass at points A, B, and C exhibit distinct differences. The velocity curves at points A and C are relatively stable compared to point B. The velocities of the coal mass in the vicinity of the three points demonstrates slight fluctuations, predominantly around 0.02 m/s. During the middle stage of the roadway tunneling, the velocity at point B suddenly increased, rising to 1.12 m/s, and then a rapid decline ensued within a brief time interval.

A comparison with Figure 3 in the previous section shows that a sudden drop in displacement at point B was accompanied by a significant change in its velocity. This observation suggests that the coal mass at the roadway side continuously accumulates elastic strain energy until a state of dynamic instability arises. The rapid release of the strain energy propels the coal mass from the roadway side, leading to the movement of the coal mass during rock burst events. In contrast, the velocity at point A demonstrates no significant variations during displacement fluctuations, indicating a static failure phenomenon, with no eruptions. Based on the results derived from Figure 3 and Figure 4, it can be concluded that during the tunneling process, although large coal rock blocks detach from both the roof (A) and the floor (C), no ejection of blocks occurs. Therefore, the coal mass in the roadway side region is most likely to undergo failure and burst due to stress disturbances.

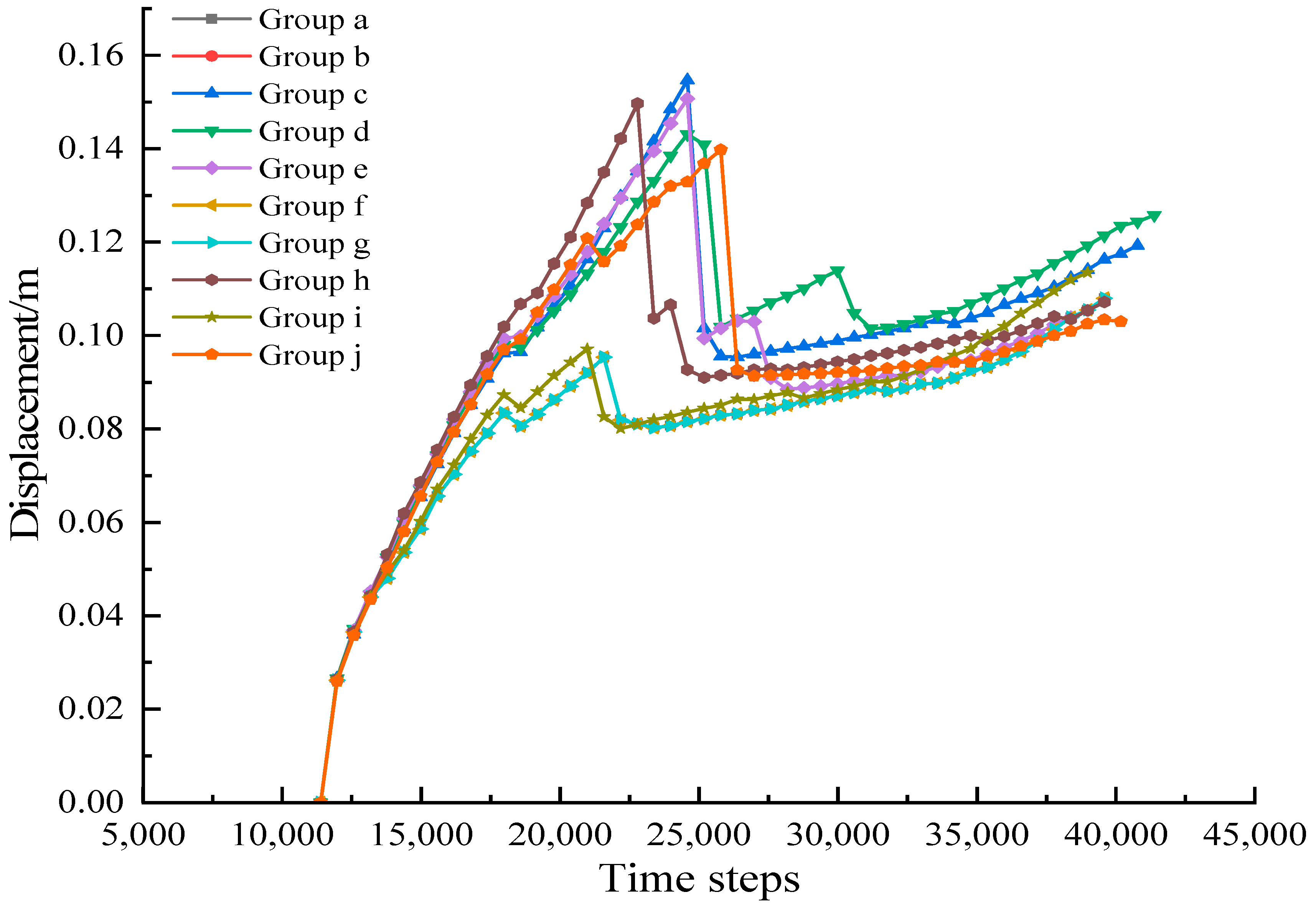
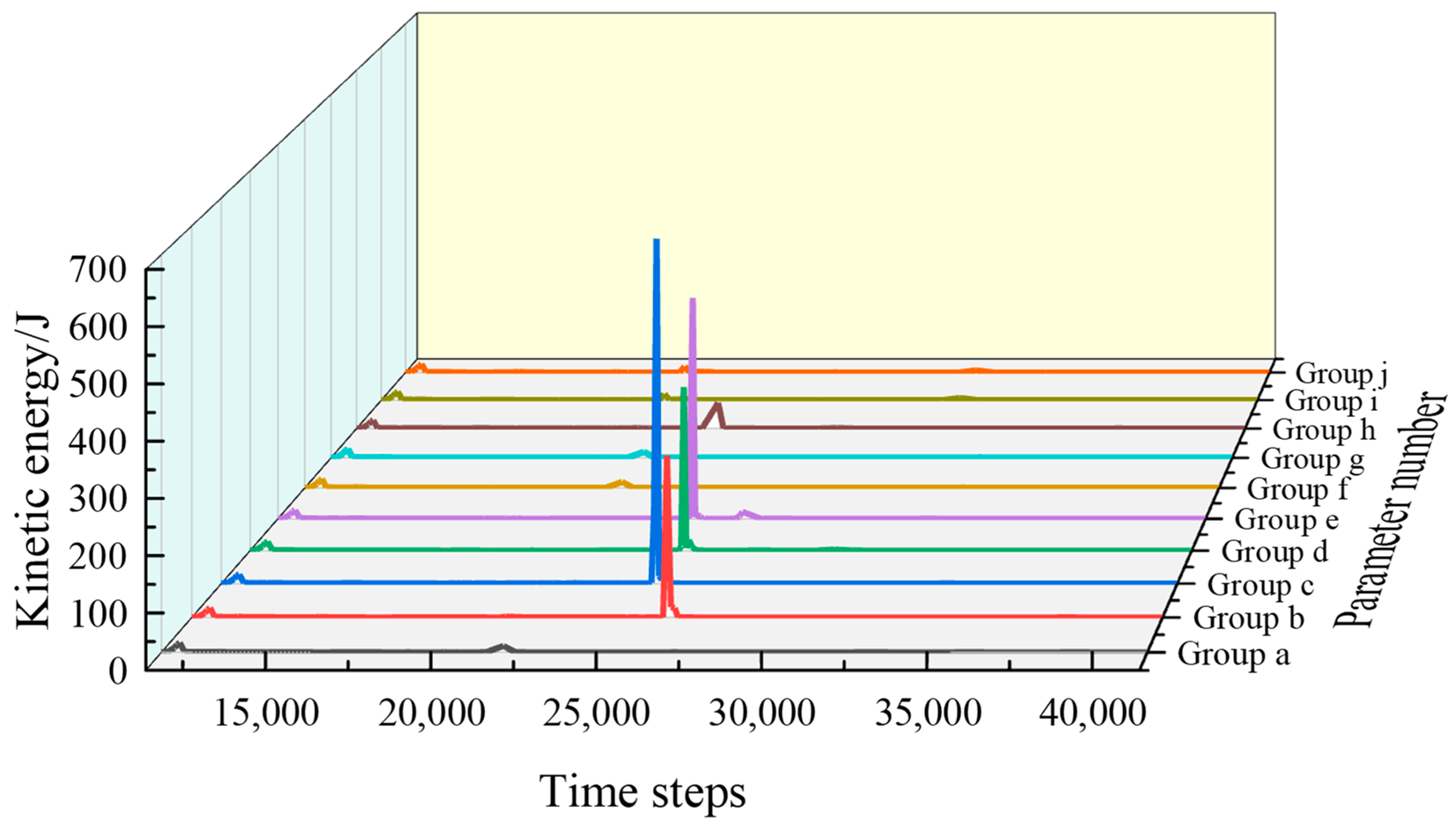
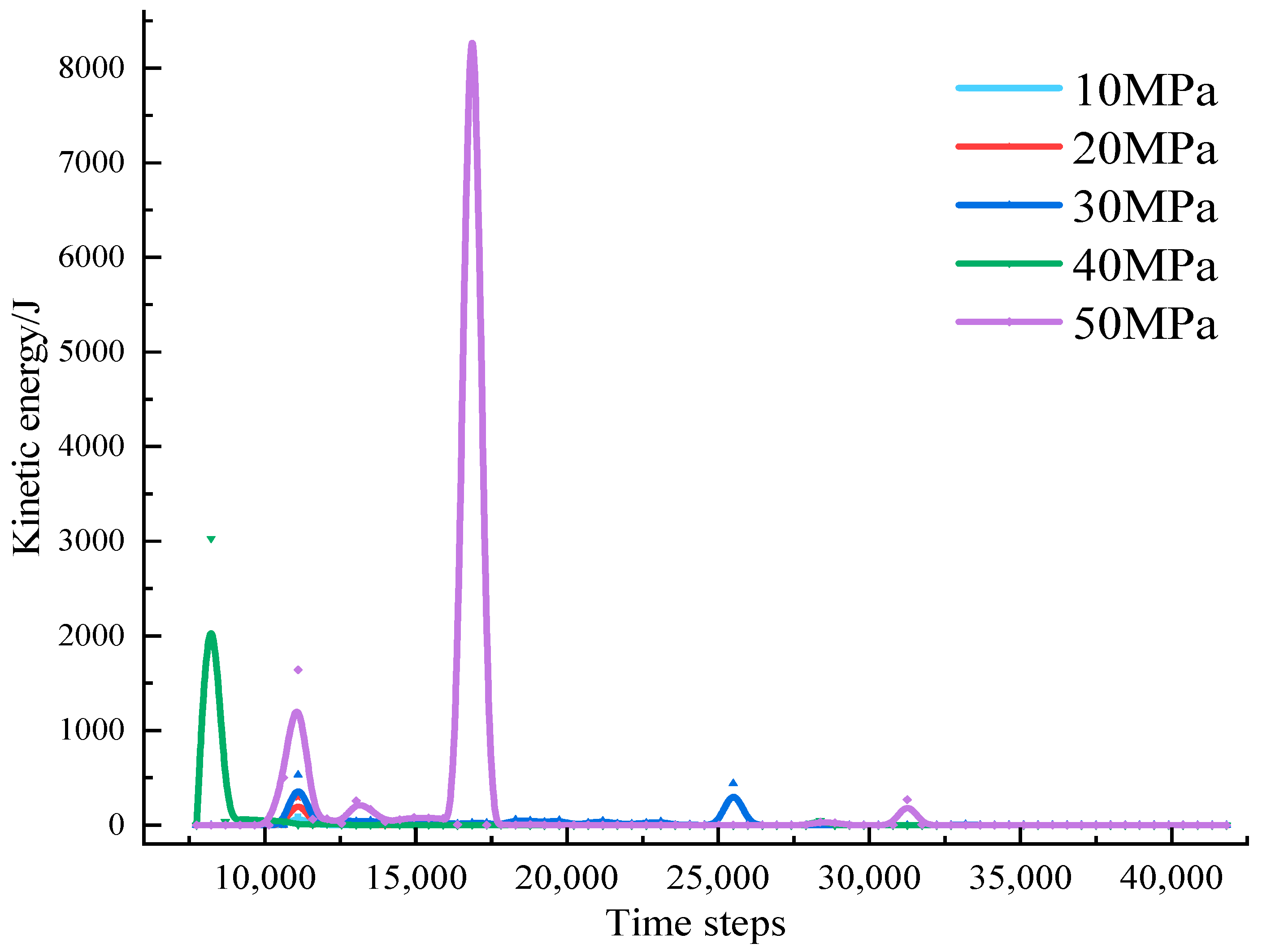
4.2. Energy Analysis of Coal Mass under Parameter Variation

In order to predict the associated risks during roadway tunneling, the distribution of stress and deformation energy within the surrounding coal mass were examined. The main energy types involved in rock burst include elastic strain energy, plastic strain energy, and kinetic energy. Real-time monitoring of surrounding coal mass velocities can be realized by 3DEC, and the kinetic energy for individual coal units can be calculated.

Based on the analysis in Section 4.1, the roadway side area is particularly vulnerable to stress disturbances during tunneling. Figure 5 depicts the displacement change curves for the coal mass under varied parameter conditions discussed in Section 3.

The observations from Figure 5 reveal that displacement on the roadway side is significantly influenced by variations in the mechanical parameters in the coal seam. Notably, during the middle stage of roadway tunneling, coal mass displacements experience sudden decreases over short periods. However, the total trends of the displacement curves for different parameter sets remain similar, suggesting that mechanical parameter variations do not drastically alter coal mass movement characteristics on the roadway side.

The plotted curves can be classified into two categories, according to their peak displacements at inflection points: Category 1 (b~e, h, j) exhibits peak displacements above 0.14 m, whereas Category 2 (a, f, g, i) exhibits displacements below 0.1 m. Furthermore, the magnitude of the displacement decreases also show differences between the two groups.

In summary, variations in coal seam parameters could affect peak displacements in the roadway side area during roadway tunneling, demonstrating the importance of parameter variation for predicting and managing rock burst hazards effectively.

The kinetic energy of the coal mass is determined using Equation (1) in the simulation process. The velocity change data of coal blocks at the roadway side position are recorded under parameter variation. Concurrently, considering the density of the coal mass and the model size calculation, the mass of an irregular coal block with a side length of 1 m is approximately 1 ton. The kinetic energies for ten groups of coal blocks are illustrated in Figure 6, below:

$$U_V={\displaystyle \frac{1}{2}}\sum _{i=0}^n{m}_i{v}_i^2$$

(1)

where U_V is the kinetic energy of the coal mass; m_i is the mass of the ith coal block; and V_i is the velocity at the center of ith coal block.

Figure 6 demonstrates substantial changes in the kinetic energy of the coal block under varied parameter conditions. For Category 1, the peak kinetic energy values range from 290 to 626 J, with Group c displaying the highest value and Group b the lowest. Conversely, the kinetic energy values for Category 2 do not exceed 100 J. Group h reaches a peak of 50.3 J, whereas the other groups fluctuate around 17 J, showing no significant differences in peak values. A comparative analysis of Groups b to e reveals that the increase in both the internal friction angle and the cohesion enhance the kinetic energy of coal blocks along the roadway side, with cohesion having a particularly pronounced effect.

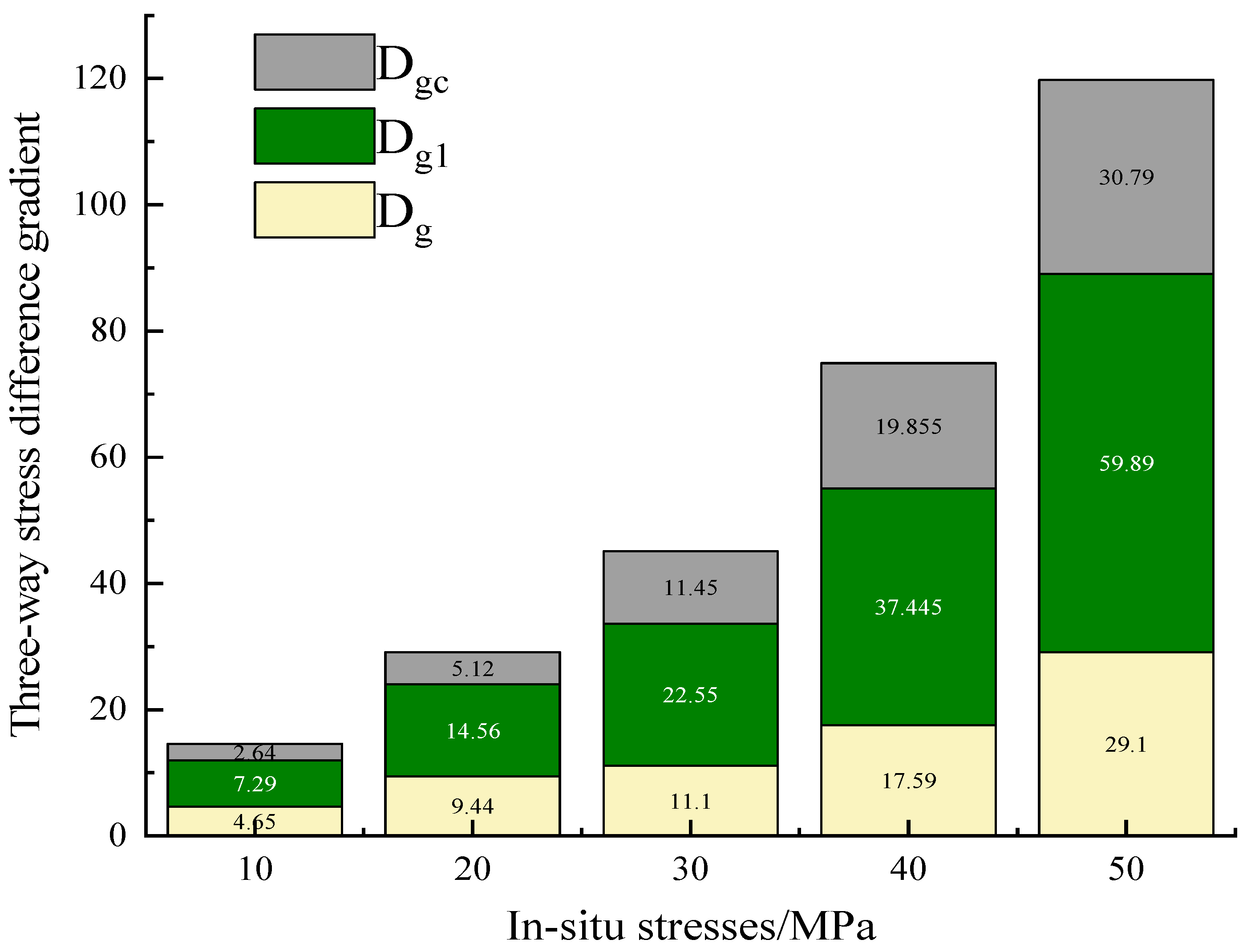
4.3. Analysis of Rock Burst Damage Energy under Different Ground Stresses

Ground stress constitutes a fundamental factor affecting the damage to surrounding coal and rock in mining engineering, especially during the tunneling of deep coal roadways under substantial disturbance. The intricate conditions of ground stress and intense mining activities may precipitate dynamic disasters, like rock burst events.

Considering the relationship between the ground stress, the burial depth of the roadway, and the working face in coal mining, five levels of ground stress—10 MPa, 20 MPa, 30 MPa, 40 MPa, and 50 MPa— were examined while maintaining a constant coefficient of horizontal lateral pressure.

Figure 7 illustrates the kinetic energy of the coal block at the monitoring point on the roadway side.

As depicted in Figure 7, the kinetic energy of the coal block at the roadway side increases from 86.93 J to 12,400 J as the ground stress rises from 10 MPa to 50 MPa. This demonstrates a clear positive correlation between the ground stress and the kinetic energy of the coal block. Higher initial ground stress results in the greater accumulation of elastic strain energy within the coal mass, making it more susceptible to bursting and damage from stress disturbance by mining activities [26].

5. Quantitative Assessment of Roadway Rock Burst Risk

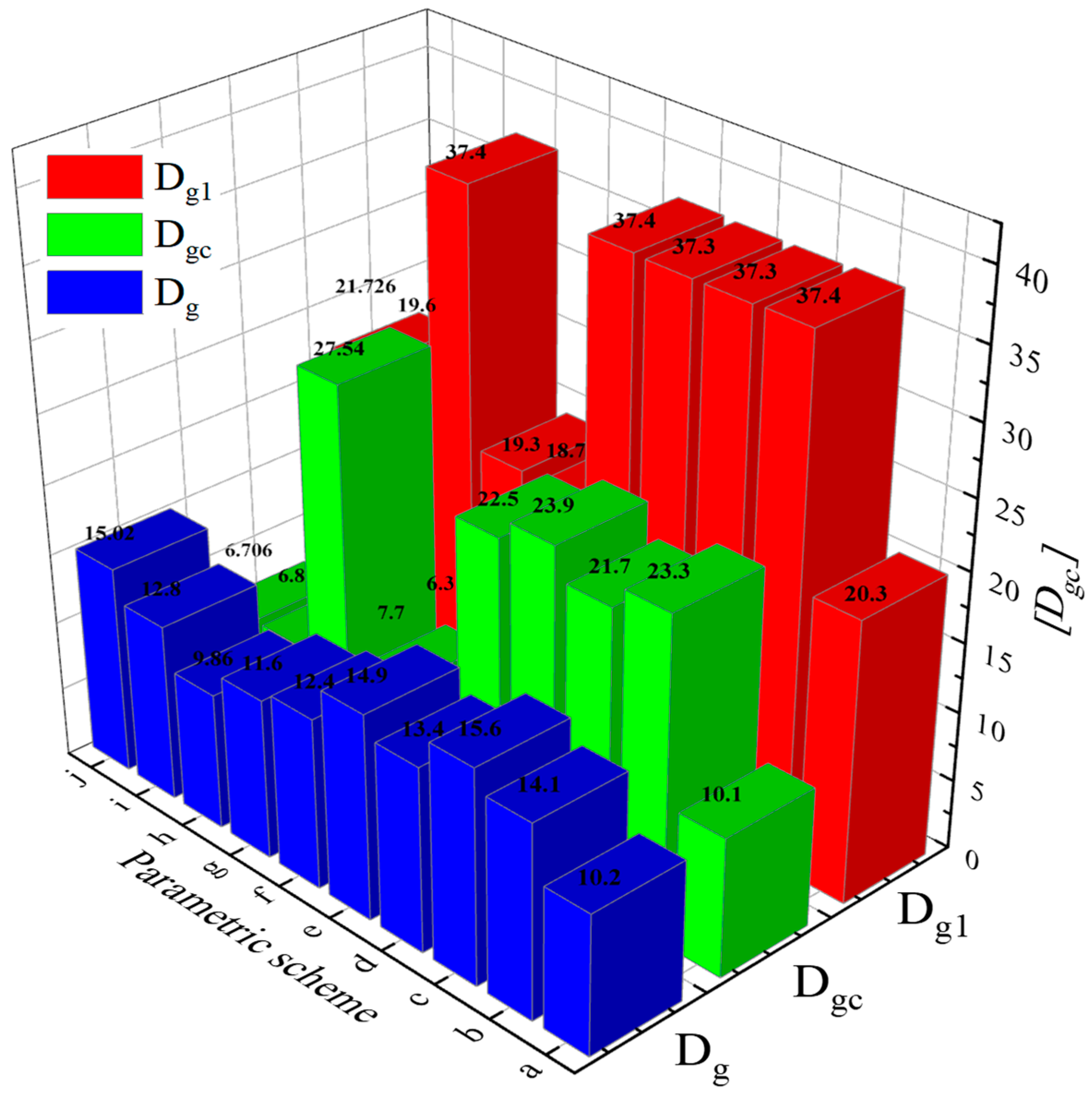
5.1. Discrimination Parameters for Roadway Rock Burst Risk

In practical tunneling operations, monitoring the difference between maximum and minimum principal stresses, as well as changes in horizontal stress, facilitates the implementation of effective preventive and control measures against rock burst. Three parameters can be employed for quantitative evaluation. The parameter D_g illustrates the stress difference gradient of coal mass, and D_g1 means the D_g value of coal mass at a depth of 1 m within the roadway side, and the change rate of the stress difference gradient can be expressed as D_gc, which can be calculated from D_g and D_g1 [11].To investigate the influence of mechanical properties on coal mass burst during tunneling, the D_g1 at the roadway sides is compared with D_g in the elastic–plastic boundary region of the roadway under varied parameters.

From engineering experience and case studies of rock burst accidents, the critical condition for rock burst occurrence is D_gc ≥ [D_gc], where [D_gc] is semi-quantitatively calculated. Considering the simulated elevated zone depth of the roadway (D_gmax) and the influence of the coal seam parameters on [D_gc], a specific value of 13 is established for [D_gc] in this paper.

Figure 8 depicts the gradient of the three-way stress difference with respect to the number of time steps during roadway tunneling under different ground stress environments. It can be observed that the gradient rate of change of the three-way stress approaches critical levels for rock burst damage under a vertical stress of 30 MPa (at a burial depth of approximately 1100 m). Moreover, the rate of change in this gradient is linearly correlated with stress levels. This suggests that rupture surfaces in coal-and-rock mass in deep mining parallel to the maximum principal stress direction can be generated through controlled blasting, with accumulated energy released, thereby preemptively reducing the likelihood of rock burst damage.

As depicted in Figure 9, several groups denoted as b~e and h, show D_gc values significantly higher than the critical threshold, and dynamic rock burst damage can occur. Conversely, the remaining groups have D_gc values below the critical condition, indicating a proximately static failure rather than rock burst damage.

It can be noted form Figure 5, Figure 6 and Figure 9 that the analysis of D_gc under different coal mass parameters is correlated with changes in the kinetic energy and displacement curves. For instance, although Group j shows a displacement curve similar to the groups with burst damage, its kinetic energy change is more aligned with the groups with static failure. For Group h, the D_gc value surpasses the critical condition despite the peak kinetic energy being significantly lower than in other groups with burst damage. Therefore, its energy dissipation and coal rock motion characteristics still satisfy the rock burst occurrence criteria.

Therefore, the stress difference gradient can be a powerful factor in predicting and mitigating coal and rock mass burst hazard within roadway sides, which could provide guidance for roadway stability evaluations under varied geotechnical conditions.

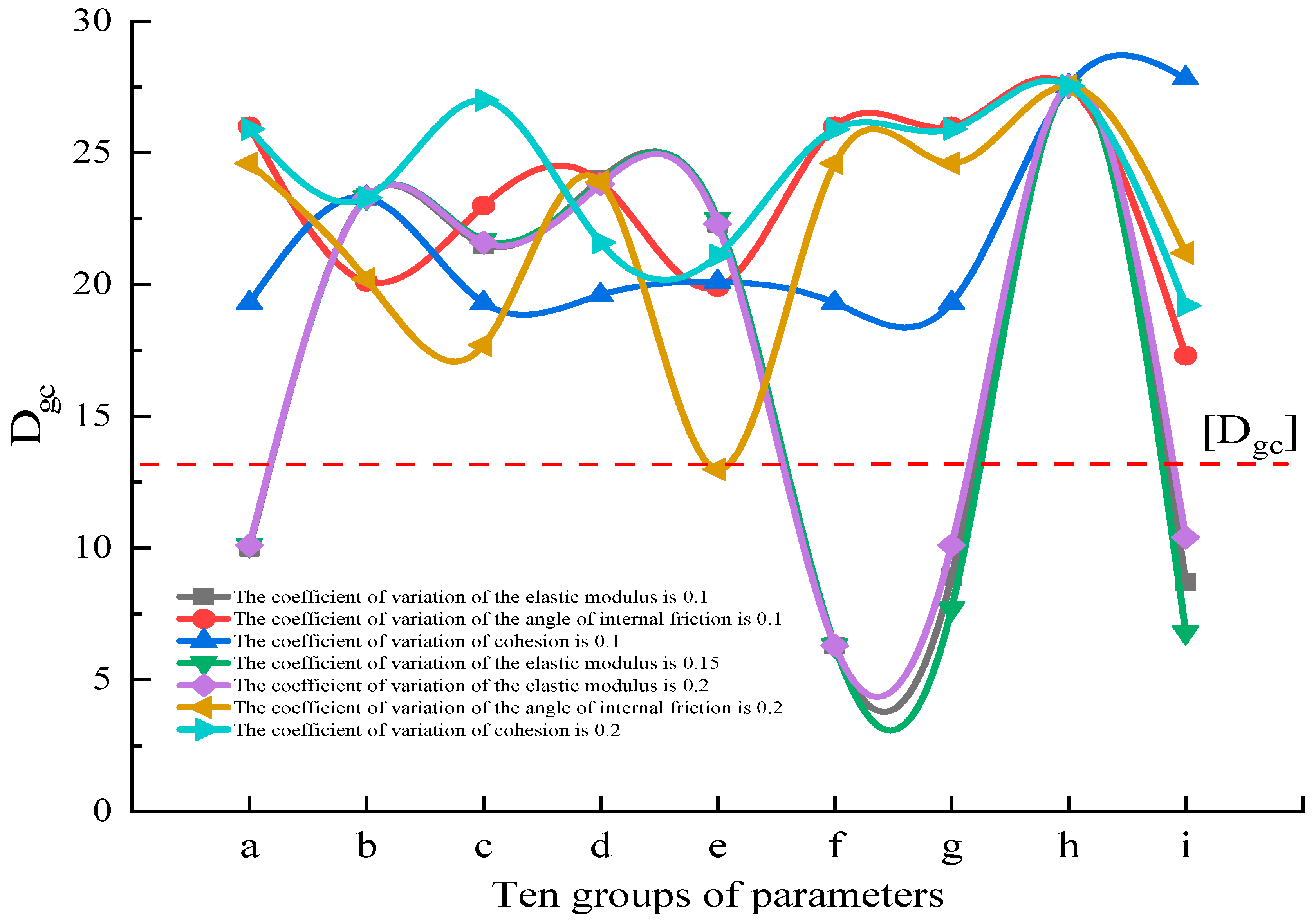
5.2. Quantitative Analysis of Roadway Rock Burst Risk

Based on the above simulation results from 10 groups of parameters for roadway tunneling, a quantitative analysis of rock burst risk was conducted using critical expression (2), based on the method for the stress difference gradient change rate. The coefficients of variation (COV) for the mechanical parameters of coal mass were adjusted to 0.1 and 0.2.

$$f_{\left(c,\phi ,E\right)}=\left[D_{gc}\right]-D_{gc\left(c,\phi ,E\right)}$$

(2)

where $f_{\left(c,\phi ,E\right)}$ is the index of coal mass burst risk; [D_gc] is the critical value of the change rate of the stress difference gradient under engineering experience, where the value 13 is employed; and $D_{gc\left(c,\phi ,E\right)}$ is the change rate of the stress difference gradient for coal seams with different groups of parameters.

When $f_{\left(c,\phi ,E\right)} <$ 0, rock burst damage occurs; by contrast, when $f_{\left(c,\phi ,E\right)} \ge$ 0, there is no rock burst damage, and other mine pressure phenomena, such as instability or the static failure of coal mass, may apply under specific [D_gc] values determined by similar engineering project.

Figure 10 presents the gradient value curves for the stress difference in the coal mass of the roadway side, considering different elastic moduli, internal friction angles, and cohesion values under various COVs. It can be noted that the D_gc trends obtained are different. Despite the COVs for the internal friction angle and cohesion change, D_gc surpasses the critical value across various parameter sets, suggesting that both factors exert a comparable influence on D_gc. Conversely, the D_gc curves under varied COV for the elastic modulus nearly overlap, indicating that the variation of the elastic modulus has a minimal burst effect on D_gc.

It can be concluded from Figure 10 that as the COV for the internal friction angle increases, the curves of D_gc decline with the amplitude fluctuation. In contrast, the curves for the cohesion rise with an increase in the COV, and amplitude fluctuation also exists. The relationship between the COV and D_gc suggests that the cohesion and the internal friction angle of the coal mass exert opposing effects on the burst tendency in the roadway side. An increased COV for cohesion is more likely to induce significant deformation in the surrounding coal and rock during roadway tunneling, thereby increasing the risk of rock burst. Therefore, in practical roadway tunneling, it is crucial to monitor the variation trends of cohesion in coal seams across different sections and to implement appropriate measures to mitigate the occurrence of rock burst.

6. Conclusions

This study proposes a method for assessing the rock burst risk associated with roadway tunneling by incorporating variation in the mechanical parameters of the surrounding rock using 3DEC numerical simulations and the principle of stress gradient difference. The main conclusions are as follows:

• Rock burst risk can occur even with relatively low kinetic energy within the coal mass, according to the analysis of the displacement and kinetic energy patterns in the roadway side during tunneling. Areas adjacent to the side of the roadway exhibit a higher susceptibility to stress disturbances induced by tunneling, leading to an increased stress gradient difference in the coal mass near the side zone, thereby resulting in burst phenomena. The released kinetic energy and rock burst risk are associated with the ground stress change.
• With the consideration of the effects of variation in the mechanical parameters of coal mass on rock burst, a relationship between coal mass mechanical properties and rock burst is established. This relationship elucidates the connection between rock burst risk during roadway tunneling and the mechanical parameters of coal mass, indicating that the varied values of these parameters significantly influence the induction of rock burst risk.
• A clear linear relationship exists between the coefficient of variation (COV) of coal- mass parameters and the occurrence of rock burst in roadway sides. The variation of the COV in the internal friction angle and cohesion exhibits positive and negative correlations with burst risk, respectively. An increased COV in cohesion heightens the likelihood of significant deformation in the side during roadway tunneling, which, consequently, elevates the rock burst risk.

However, the study did not carry out an in-depth investigation of roadway damage or eruption under more complex geological conditions in the surrounding coal and rock variation. Future investigations should incorporate stochastic field theory to quantitatively evaluate rock burst risk and conduct reliability analyses of tunneling processes influenced by the variable spatial parameters of coal seams. This methodology has the potential to yield theoretical and technical insights for the early warning and prevention of dynamic hazards associated with deep mining.