Abstract
In recent years, deep-learning methods have significantly improved the classification results in the field of plant-leaf recognition. However, limited by the model input, the original image needs to be compressed to a certain size before it can be input into the convolutional neural network. This results in great changes in the shape and texture information of some samples, thus affecting the classification accuracy of the model to a certain extent. Therefore, a minimum enclosing quadrate (MEQ) method is proposed to standardize the sample datasets. First, the minimum enclosing rectangle (MER) of the leaf is obtained in the original image, and the target area is clipped. Then, the minimum enclosing quadrate of the leaf is obtained by extending the short side of the rectangle. Finally, the sample is compressed to fit the input requirements of the model. In addition, in order to further improve the classification accuracy of plant-leaf recognition, an EC-ResNet50 model based on transfer-learning strategy is proposed and further combined with the MEQ method. The Swedish leaf, Flavia leaf, and MEW2012 leaf datasets are used to test the performance of the proposed methods, respectively. The experimental results show that using the MEQ method to standardize datasets can significantly improve the classification accuracy of neural networks. The Grad-CAM visual analysis reveals that the convolutional neural network exhibits a higher degree of attention towards the leaf surface features and utilizes more comprehensive feature regions during recognition of the leaf samples processed by MEQ method. In addition, the proposed MEQ + EC-ResNet50 method also achieved the best classification results among all the compared methods. This experiment provides a widely applicable sample standardization method for leaf recognition research, which can avoid the problem of sample deformation caused by compression processing and reduce the interference of redundant information in the image to the classification results to a certain degree.
1. Introduction
Plants are an integral part of the Earth’s ecosystem, play an important role in the global balance of nature, and are closely related to human life. It is estimated that there are more than 420,000 species of plants in the world [1]. It is difficult for the average person to accurately identify these species, and this difficulty is not conducive to the conservation of plant diversity. Hence, it is necessary to use computer technology to realize the automatic classification of plant species.
Identification of plants is often based on their leaves, which can be described by texture, color, and shape. In recent years, many scholars have carried out in-depth research according to the above characteristics and achieved certain results. Chengzhuan Yang et al. [2] adopted the proposed multiscale triangle descriptor (MTD) to describe the shape information and used the local binary pattern histogram Fourier (LBP-HF) as the texture feature to identify plant leaves. The classification accuracy of the proposed method on the Flavia leaf, Swedish leaf, and MEW2012 leaf datasets reached 99.16%, 98.48%, and 95.64%, respectively. Xiang Zhang et al. [3] used Margin Feature (MF) to represent the outline and edge of leaves and used Global Shape Feature (GSF) to represent the global shape of leaves. Based on the above features, a series of multi-grained fusion (MGF) methods were proposed to capture the global shape and margin details of the leaves effectively. After experimental comparison, the classification accuracy of the proposed method on Swedish leaf dataset reached 95.82%. Xin Chen et al. [4] proposed a method to describe the shape of leaves called histogram of Gaussian convolution vectors (HoGCV). By convolving the contour vector functions with Gaussian functions of different widths and calculating the spatial distribution of the resulting Gaussian convolution vectors, a multiscale, invariant, and discriminative shape descriptor, HoGCV, was obtained. The classification accuracy of this method on the Flavia leaf dataset reached 96.56%. Rolla Almodfer et al. [5] proposed a new descriptor for plant-leaf classification called the Pyramid Blurred Shape Model (PBSM). The PBSM algorithm used a pyramid structure to capture leaf features. With the transformation of the pyramid level from coarse to fine, the extracted features also change from global information to high-level local features. Then, a sequential feature fusion method was used to fuse the shape and texture features of each pyramid level to form a new descriptor. In addition, to avoid extracting redundant and unimportant features from leaf images, feature selection based on grey wolf optimization (GWO) was adopted. This method can effectively determine the leaf features that are conducive to recognition and avoid the waste of computing resources. The experimental results show that the classification accuracy of the proposed method on Flavia leaf, Swedish leaf, and MEW2012 leaf datasets reached 96.34%, 96.89%, and 94.14%, respectively. Wu et al. [6] proposed a novel leaf-contour representation method called local triangle feature (LTF) and constructed a composite descriptor based on this approach. This composite descriptor incorporates two fusion schemes: one captures low-level contour features and integrates them with low-level appearance features using the LTF method, followed by the identification of plant species using Hausdorff distance; and the other employs Fisher vector to transform these aforementioned low-level features into high-level representations, which are then merged and differentiated using Euclidean distance for distinguishing between leaves. Experimental results demonstrate that this method achieves an accuracy of 98.75% on the CVIP100 dataset, surpassing existing manual feature-based methods for plant-leaf recognition. Although these methods based on geometric features have achieved good research results and classification effects, their limitations have become apparent with the increase in species. These low-level visual features are not sufficient to effectively represent high-level semantics, thus limiting the performance of plant-leaf recognition.
Deep learning is a new research direction in the field of machine learning. Deep convolutional neural networks can learn autonomously and represent the high-level semantic information of plant leaves well. With the great breakthrough of the AlexNet model proposed by Geoffrey Hinton in the field of image recognition, the academic circle has set off a wave of deep-learning research based on convolutional neural network (CNN). Zhu et al. [7] proposed a two-way attention model combined with deep CNN for plant-leaf recognition. It has two types of attention: family-first attention and max-sum attention. The experiment results show that the proposed method achieved good classification results on several challenging datasets. Xu et al. [8] proposed the Attentional Pyramid Network (APN) for the recognition of Chinese herbal medicine, as it combines competitive attention and spatial collaborative attention. On the self-established Chinese herbal-medicine dataset, the accuracy of this method reached 94.90%. Quach, Dinh, et al. [9] proposed a novel method to solve the leaf recognition problem. Firstly, the leaves were preprocessed to extract texture features, Fourier descriptors, and vein images. These properties were then transformed into a better representation by a neural network-based encoder. To this end, the authors designed a simple and effective 2D convolutional encoder. The proposed model extracted features from the processed color image by stacking convolutional layers and then used a fully connected layer for encoding. And, finally, the support vector machine (SVM) model was used to classify different leaves. The recognition accuracy of this method on the Flavia leaf dataset reached 99.58%. Sun, Xu, et al. [10] designed several composite models to improve the accuracy of tree species identification. In contrast to previous deep-learning recognition algorithms, the authors integrated three models with distinct classifiers as the decision model and further employed the k-fold cross-validation (k-fold cv) method to mitigate overfitting issues. The composite model design facilitates efficient feature extraction across different plant organs based on their respective preferences for feature extraction. Moreover, a leaf sample dataset that aligns closely with tree-growth characteristics was constructed in order to evaluate the proposed model’s performance. This dataset comprises images showcasing multiple branches and leaves, effectively demonstrating diverse leaf-arrangement patterns on branches. Experimental results demonstrate that the MixNet XL CNN model combined with the K-nearest neighbor (KNN) classifier achieves an exceptional classification rate of 99.86%, surpassing other classical CNN algorithms. Wu et al. [11] combined leaf-shape features with convolutional features extracted from deep-learning models for the classification of plant species. Firstly, aiming at tackling the issue of the lack of internal salient points in common leaf-shape descriptors, the multi-scale triangle descriptor was improved. Then, the classical VGG16 model was used to accumulate convolutional features of different depths. Finally, the shape features and convolution features were fused for plant-leaf recognition. Experimental results demonstrate that this proposed method achieves an impressive 99.47% classification accuracy on the Swedish leaf dataset and also performs well on several other commonly used leaf datasets. These findings highlight the complementary nature of high-level convolutional information and low-level visual characteristics in leaf recognition.
The above results prove the effectiveness of the deep-learning method in the field of leaf recognition. However, the disadvantage of this approach is that it requires a large number of samples to train the network models. Therefore, more and more scholars adopt the strategy of transfer learning to avoid the long-term training of network models. Transfer learning is a method of reapplying pre-trained convolutional neural networks to new problems. Currently, mature CNNs (e.g., AlexNet, ResNet, VGG16, etc.) are pre-trained on large-scale annotated natural image datasets (e.g., ImegeNet, which includes 15 million images) and then used to solve cross-domain image classification problems. Zhu et al. [12] proposed a leaf-recognition method that combines Deep Convolutional Generative Adversarial Networks (DCGANs) and transfer learning. First, DCGAN was used to expand the sample database, and then the pre-trained Inception V3 network was applied to image data processing. The experimental results show that the classification rate of the proposed method on Swedish leaf dataset reached 96.57%. Isik et al. [13] proposed a method for leaf recognition based on transfer learning. Based on the number of categories in the Flavia leaf and Swedish leaf datasets, the fully connected layer of the Inception-v3 model was retuned and trained. In addition, data enhancement was used to suppress overfitting and underfitting. The experimental results show that the classification accuracy of the proposed method on the above two datasets reached 98.95% and 99.11%, respectively. Krishnamoorthy et al. [14] proposed an improved InceptionResNetV2 model for the classification of rice-leaf diseases. In this classification task, the authors compared the proposed method to a simple model without transfer learning. The experimental results show that the transfer-learning method has a better classification performance. Thangaraj et al. [15] proposed a CNN model based on transfer learning to identify tomato-leaf diseases. Moreover, adaptive moment estimation (Adam), stochastic gradient descent (SGD), and RMSprop optimizers were used to evaluate the performance of the proposed model. The experimental results show that the Modified-Xception model based on Adam optimizer had the best performance, and the classification rate of this method reached 99.55%. Zhang et al. [16] proposed an improved CNN model based on mixed activation functions for plant-leaf recognition. The five activation functions with good performance were combined in pairs to replace the ReLU activation functions at different positions in the original model. The experimental results show that the ELU-Swish1 model has the best performance among the 20 combinations proposed. Furthermore, the classification rate of the method on the Flava leaf and Swedish leaf reached 99.30% and 99.39%, respectively. The authors, Zhou et al. [17], employed multiple pre-trained CNN models to achieve efficient recognition of plant leaves. Initially, three pre-trained networks were utilized as feature-extraction models to capture advanced leaf features. Subsequently, attention weights were employed for recalibrating and emphasizing valid features. Ultimately, the fusion of spatial and channel features was accomplished through element multiplication, followed by classification using SVM. This approach effectively leverages the complementary information from different CNNS and achieves an impressive 99.97% accuracy in classifying the Swedish leaf dataset. However, employing multiple models with a large number of parameters as feature extractors leads to excessive utilization of computing resources, thus hindering practical applicability. The abovementioned results fully prove the superiority of transfer learning in the field of leaf recognition. In comparison to manual feature-recognition methods and deep-learning approaches that necessitate model retraining, transfer learning is more apt for practical applications. This is due to its ability not only to conserve substantial computing resources but also to significantly enhance tree species-identification accuracy.
Although the current methods of species identification have reached an unprecedented level, there are still certain limitations. Influenced by shooting techniques, equipment, and other factors, noticeable variations exist in the size and background of sample images across different datasets. Moreover, due to the CNN model’s restriction on input sample size, the shape and texture features of most samples undergo significant changes after compression. Consequently, such irregularly shaped leaves’ feature extraction unavoidably impacts the model’s attention allocation and distorts the classification results obtained through the CNN algorithm. It is worth noting that current deep-learning methods do not focus on the impact of the abovementioned factors on classification. In this case, this paper proposes the method of using minimum enclosing quadrate (MEQ) to standardize the sample datasets. The main contributions of this method lie in its ability to prevent the alteration of fundamental information during sample compression, thereby reducing the interference caused by redundant information on the model and ultimately enhancing classification accuracy. In addition, based on the transfer-learning strategy, the EC-ResNet50 model is proposed and combined with the MEQ method. Experimental results show that the proposed fusion method achieves the best classification results in all comparative experiments and can be used as a feasible scheme for plant-leaf recognition.
2. Materials and Methods
2.1. Minimum Enclosing Quadrate Treatment of Leaf Samples
In the classification and recognition of plants, the shape and texture features of leaves are particularly important. However, asymmetric compression operations are often detrimental to maintaining the normativity of these features. As shown in Figure 1, the original sample image is shown on the left, and the compressed image of this sample is shown on the right. In the process of compression, its size is changed from 2544 × 1205 to 224 × 224. It can be clearly seen that the basic characteristics of the leaves have been greatly changed. Obviously, this phenomenon is not conducive to the classification and recognition of the CNN models. It can also be seen that there is a lot of redundant information in the original sample, which will also affect the classification accuracy of the models.

Figure 1.
Comparison of a leaf-sample image before and after compression.
In order to avoid the influence of the abovementioned problems on the classification results, the MEQ method is proposed to standardize the leaf-sample datasets.
Firstly, the RGB image of the leaf sample is converted into a grayscale image by eliminating the hue and saturation information while maintaining the brightness. In this process, RGB values are converted to gray values by calculating the weighted sum of R, G, and B components. The calculation method is given in Equation (1).
where Gray represents the transformed gray value; and R, G, and B separately represent the red, green, and blue components.
Secondly, the gray image is converted into a binary image to show the leaf contour more clearly. Before that, the Otsu [18] method is used to calculate the global threshold of the grayscale image. Otsu is an algorithm to determine the threshold of image binarization segmentation, and Otsu is used in this experiment to select the optimal threshold that minimizes the within-class variance of the thresholded black-and-white pixels. The principle of finding the best threshold, , is as follows.
Let the gray level of a given image be denoted by , and there exists a threshold, , to classify the pixels in the image into 2 classes: class and class . The pixels of class have gray levels of (1, …, ), and the gray level of class pixels is (, …, ).
The within-class variance, , and between-class variance, , are expressed as follows:
where and are the probabilities of occurrence of class and , respectively; denotes the variance of class ; and denotes the variance of class . In addition, and , respectively, represent the average gray values of the two categories, and represents the total average level of the grayscale image.
Since is always true (where is the total variance), the sum of the within-class variance and the between-class variance is fixed, which means that the maximum between-class variance is the minimum within-class variance. So, the optimal threshold, , should satisfy the following equation:
And the search for the maximum, , can be restricted to the following:
Here,
and
where and are the zeroth- and the first-order cumulative moments of the histogram up to the th level, respectively. And denotes the probability that a pixel with gray value appears in the image.
Therefore, according to the obtained optimal threshold, , all values greater than the threshold in the grayscale image are replaced with 1 (white), and all other values are set to 0 (black) to obtain the binary image of the sample.
After that, the next work is to find the minimum enclosing quadrate of the sample. To do this, we need to find the minimum enclosing rectangle (MER) of the sample. MER refers to the maximum extent of some 2D shape (e.g., points, lines, and polygons) represented in 2D coordinates, that is, a rectangle bounded by the maximum abscissa, minimum abscissa, maximum ordinate, and minimum ordinate of each vertex of a given 2D shape. However, due to the interference of the image background and redundant information, directly calculating the MER of sample binary images cannot achieve the desired effect. Consequently, in this paper, the method of finding the maximum connected component of the image is adopted to obtain the MER of the leaf. We take the area of each object (connected component) in the image and create a rectangle parallel to the axis in 2D coordinates. As shown in Figure 2, is defined as a rectangular four-element vector (expressed in data units). The point represents the lower-right corner of the rectangle and is used to determine its position. The and denote the length and width of the rectangle, respectively, and are used to determine the dimensions of the rectangle. Then, the four-element vector of the rectangle with the largest area in the image is recorded, which is the MER of the leaf. The search for the rectangle, , can be determined according to the following expression:
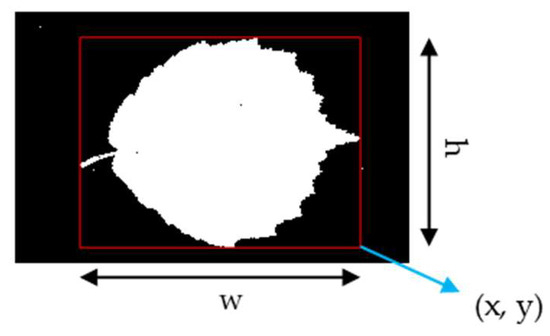
Figure 2.
The four-element vector of the minimum enclosing rectangle of the leaf.
Finally, according to the recorded coordinate data, the target area is cropped out in the original color sample image. The shorter side of the rectangle is symmetrically extended on both sides, transforming it into a square. It should be mentioned that, considering the importance of leaf edge information, we retain part of the background information of leaf edges.
Figure 3 shows the standardization process of a sample, and Figure 4 shows the compressed images of the standardized sample and the original sample, which is from the MEW2012 leaf dataset. From Figure 3, it can be found that the sample processed by the MEQ method not only fully retains the main characteristics of the leaf but also eliminates most of the redundant information in the image. It can also be clearly seen from Figure 4 that the characteristics of the original sample have changed greatly after direct compression. Different from them, the MEQ method ensures the standardization of the sample features, and the texture information of the leaf also becomes clearer, which is very helpful for the feature extraction of the CNN models.
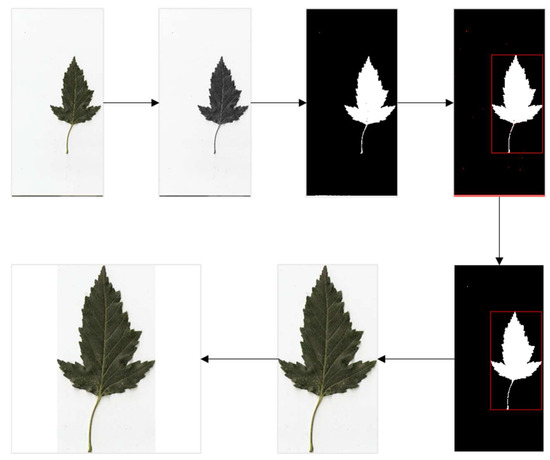
Figure 3.
An example of the standardization process for the sample.

Figure 4.
Comparison of compressed images of the standardized sample and the original sample.
2.2. Residual Network
In recent years, with the development of computer vision technology and artificial intelligence technology, deep learning has been widely used in the field of image recognition. Theoretically, the deeper the depth of the network model, the more advanced the features extracted and the better the performance. But deeper neural networks are also harder to train and expose a degradation problem: as the network gets deeper, it saturates with accuracy and then rapidly degrades. In 2015, He Kaiming et al. [19] proposed a deep residual network (ResNet) for image recognition, which solved the degradation problem to a certain extent. It is a convolutional neural network that introduces the shortcut connections. Shortcut connections are those that skip one or more layers. This skip connection makes the network easier to learn and leads to a better performance [20]. As shown in Figure 5, there are two types of residual blocks used in a residual network. The residual structure used by the ResNet50 model is shown in Figure 5b, where the 1 × 1 layers are responsible for reducing and then increasing dimensions, making the 3 × 3 layers a bottleneck with smaller input/output dimensions [19]. And the complete structure of the ResNet50 model is shown in Figure 6.
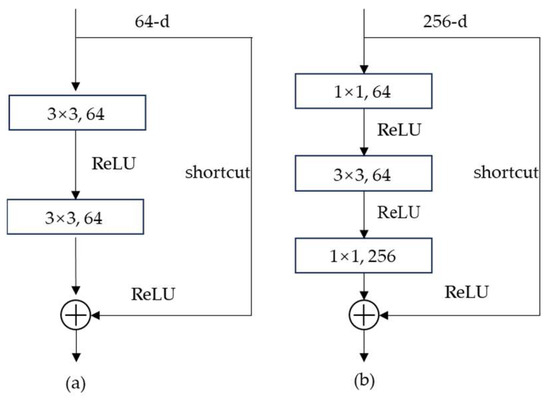
Figure 5.
The residual blocks of ResNet. (a) lists the residual block in the shallow residual networks, including ResNet18 and ResNet34. (b) shows the residual block in the ResNet50 model or deeper residual networks.
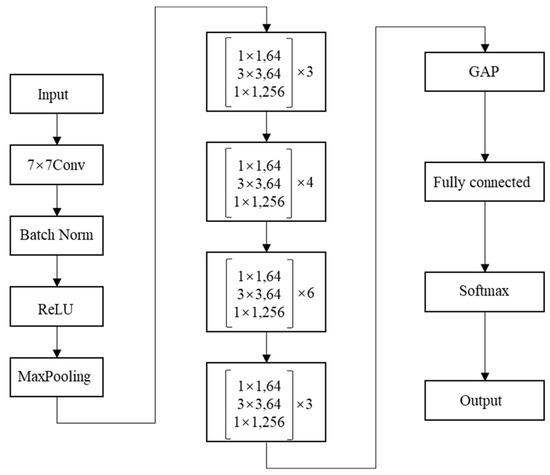
Figure 6.
The structure of the ResNet50 network model.
2.3. Improved ResNet50 Model and Transfer Learning
Activation functions can promote deep neural networks by introducing nonlinearities into the learning process, enabling them to learn complex patterns. Some studies have proved that the activation function has a certain impact on the classification results of convolutional neural network models [16,21,22]. In consequence, the role of the activation function is crucial. As a kind of unsaturated activation function, ReLU is widely used in computer vision tasks because of its simple and efficient characteristics [23]. But its negative input is identical to zero, leading to the problem of neuronal death. Therefore, in many cases, the ReLU activation function may not be the best choice to improve the performance of the CNN model. Furthermore, the size of the convolution kernel directly impacts the feature-extraction efficacy of a CNN model. Smaller kernel sizes result in reduced receptive fields, facilitating the identification of smaller targets and local details. Conversely, larger sizes lead to expanded acceptance fields, enabling the enhanced extraction of global information. Considering that most CNN models use a small-sized 3 × 3 convolution kernel, this may limit the model’s ability to fully capture the global information of the sample. Hence, the ResNet50 model is improved from two aspects, one is to replace the original activation function, and the other is to expand the convolution kernel size of the last residual structure. And the standardized Flavia leaf dataset is utilized to investigate the impact of different activation functions and convolution kernel sizes on the enhanced ResNet50 model (the dataset used is detailed in Section 3.3). Subsequently, a series of exploratory experiments are conducted, with validation accuracy serving as the benchmark for evaluating models.
2.3.1. Comparison of Several Excellent Activation Functions
The experiments test the performance of several commonly used activation functions on the improved model; they are ReLU, LeakyReLU, ELU, and Swish. The following is a brief introduction to these activation functions. And Figure 7 shows an image of them.
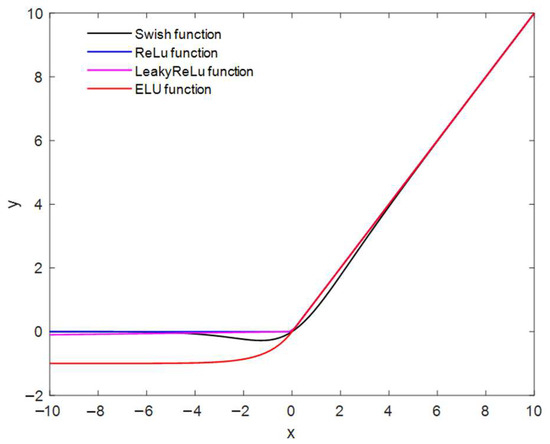
Figure 7.
The graph of the activation functions.
ReLU is the most widely used activation function, which enhances the sparsity of the network by forcing negative inputs to zero, but it also causes the problem of neuronal death [23]. It is defined as the following expression:
LeakyReLU solves the problem of neuron death [24], and its expression is as follows:
where is the initialization constant, usually .
The ELU activation function [24] can accelerate the learning of deep neural networks and effectively alleviate the problem of gradient vanishing. It is defined as follows:
where is also used as an initialization constant, usually .
Swish is a variable non-monotonic activation function [24]. It is defined as the following expression:
where is a constant or trainable parameter. When , Swish is equivalent to Sigmoid-Weighted Linear Unit (SiL). When , Swish becomes a linear function, . As , Swish approximates the ReLU activation function. In this experiment, .
The abovementioned four activation functions with excellent performance were used to test the improvement of ResNet50 model, and the evaluation results are shown in Table 1. The enhanced model utilizing the ELU activation function demonstrates a superior classification performance, potentially attributed to the heightened learning capability inherent in the ELU activation function. ELU has negative values compared to ReLU, thus allowing it to push the mean unit activation closer to zero. The shifts of the mean to zero can make the normal gradient closer to the unit natural gradient and thus accelerate the learning [25]. While LeakyReLU also has a negative value, it does not guarantee a robust deactivation state in the presence of noise. The Swish activation function has good generalization capabilities. However, there is evidence [26] that it outperforms ReLU only in deeper networks, and for those that are not deep enough, their results are very similar. The experimental results in this paper also confirm this phenomenon, and it can be seen that they are exactly the same in terms of validation accuracy. Moreover, from the perspective of model training time, the model that uses the ReLU activation function before improvement takes the shortest time, while the model improved with the LeakyReLU, Swish, and ELU activation functions takes more time successively. Although the time consumption of the improved model using ELU is significantly increased compared with that before the improvement, this trade-off is evidently justified by the observed performance enhancement. Therefore, it can be proved that ELU is more suitable for the improved model proposed in this paper.

Table 1.
Performance comparison of different activation functions on standardized Flavia leaf dataset.
2.3.2. Comparison on the Size of Convolution Kernels
We tested the effect of different convolution kernel sizes in the improved model. Table 2 lists the results of five convolution kernel sizes that perform relatively well for improvements to the ResNet50 model. The training results of leaf classification recognition indicate that the validation accuracy of the model exhibits fluctuations as the convolution kernel size increases, and it reaches its highest point when a kernel size of 11 × 11 is utilized. Simultaneously, it can be seen that, with the enlargement of the convolution kernel size, the training time consumption of the model shows an increasing trend, but the growth rate is small. The experimental results demonstrate the viability of utilizing larger convolution kernels to enhance the classification performance of the model. However, it is imperative to emphasize that selecting the appropriate convolution kernel is crucial.

Table 2.
Performance comparison of different convolution kernel sizes on standardized Flavia leaf dataset.
To sum up, the specific improvement schemes of the ResNet50 network model are as follows:
- The ELU activation function was used to replace the ReLU of the original model;
- A larger convolution kernel (11 × 11) was used to replace the smaller convolution kernel (3 × 3) in the last residual block of the original model;
- A new fully connected layer was added, and the parameters were adjusted.
2.3.3. Transfer Learning
Transfer learning refers to the transfer and reuse of knowledge from one domain to another. There are two commonly used transfer-learning strategies, one is feature extraction and the other is fine-tuning [27]. Feature extraction is to add a simple classifier after the pre-trained network structure, take the pre-trained network on the source task as the feature extractor of the target task, and only train the parameters of the newly added classifier. Fine-tuning is using a pre-trained network to initialize the network model and using new data to train part or the entire network. Due to the fact that the datasets used in this paper are all composed of a small number of samples, retraining network models from scratch not only requires a lot of time but also easily leads to the problem of overfitting. Hence, the transfer-learning strategy is adopted to reduce the training time and improve the convergence effect of the model.
Firstly, the ResNet50 model is pre-trained on the ImageNet dataset, and then most of the pre-trained parameters are transferred to improve the convergence effect of the model. Secondly, the ELU activation function with better performance is used to promote network learning, and the convolutional layer of the last residual block of the model is subsequently replaced. Finally, a global average pooling (GAP) layer is used to reduce the parameters, and a new fully connected layer is added for the classification of the target dataset. Since the improved model uses ELU activation function and a larger convolution kernel size, it is named EC-ResNet50. The specific process of transfer learning for the EC-ResNe50 network is shown in Figure 8.
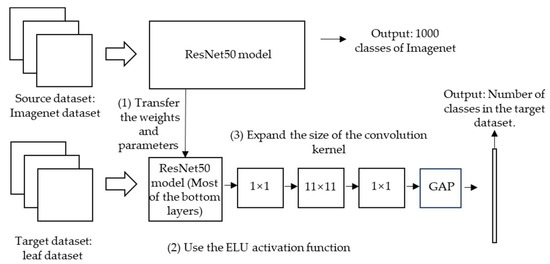
Figure 8.
The transfer-learning process of the EC-ResNet50 network.
3. Results and Discussions
In this study, we tested the classification performance of the proposed approach using the Swedish leaf, Flavia leaf, and MEW2012 leaf datasets, respectively. First, six classical CNN models were selected to evaluate the performance of MEQ method. In these experiments, AC values represent the classification accuracy obtained by the model on the original datasets, and MAC values represent the classification accuracy obtained by the model on the standardized datasets. Then, the classification performance of MEQ combined with EC-ResNet50 was tested and compared with that of the recognition methods of other scholars.
3.1. Experimental Configuration and Parameters
The experimental platform used in this study is as follows: the hardware environment is a Intel Core i5-12500h processor (Santa Clara, CA, USA), NVIDIA RTX3050 4 G graphics card (Santa Clara, CA, USA), 16 G memory, and 64-bit operating system. The software environment is WIN11 system, MatlabR2021a.
For all datasets used in this experiment, the ratio of training set and verification set was 7:3, the size of the input image was 224 × 224 pixels, the epoch was set to 6, the mini-batch was set to 10, and the learning rate was set to 0.0001.
3.2. Tests on the Swedish Leaf Dataset
3.2.1. Introduction to Swedish Leaf Dataset
The first dataset selected for the experiment was the Swedish leaf dataset [28], which originated at Linkoping University in Sweden and is widely used to evaluate the performance of recognition methods. The dataset has 15 categories, each with 75 images. Figure 9a–c, separately, show some original sample images, input images obtained by direct compression, and input images obtained by MEQ standardization. It can be found that, compared with the direct compression of leaf samples, the MEQ method can retain the basic information of these samples more completely and make the shape and texture characteristics of the leaves more normalized. In addition, it is obvious that the leaf samples in this dataset all have similar colors, and some samples have little difference in shape and texture, such as Class 7 and Class 15.

Figure 9.
The original image of the Swedish leaf sample (a), input images obtained by direct compression (b), and input images obtained by MEQ standardization (c).
3.2.2. Performance Test of MEQ Method on Swedish Leaf Dataset
In this section, six commonly used CNN models were used to test the performance of MEQ methods. Table 3 lists the classification results of these six models on the standardized Swedish leaf and the original Swedish leaf. And their validation accuracy and validation loss are shown in Figure 10. It can be seen that the classification performance of almost all tested models has a certain degree of improvement in the standardized dataset. Among them, the MAC values of ResNet18 and ResNet50 models both reach 99.39%. In addition, the MAC values of AlexNet and ResNet101 models both reach 99.70%. Compared with the AC values obtained on the original dataset, their classification results are improved by about 0.30%. For the VGG16 and GoogLeNet models, although their classification results are not significantly improved, it is not difficult to find from Figure 9 that these networks have lower validation loss values on the standardized dataset. Moreover, it can also be found from Figure 10 that the proposed method reduces the fluctuation of the validation accuracy curve of these models during the training process to some extent. Therefore, the above experimental results can prove that using the MEQ method to standardize the dataset is beneficial to the classification and recognition of the CNN model.

Table 3.
Comparison of classification results of CNN models on the original and standardized Swedish leaf datasets.
Figure 10.
Validation accuracy and validation loss of CNN models on the original and standardized Swedish leaf datasets. (a–f) enumerate the validation result curves of AlexNet, GoogLeNet, VGG16, ResNet18, ResNet50, and ResNet101 in turn.
3.2.3. Performance Test of the Fusion Method on Swedish Leaf Dataset
The classification performance of the proposed combination method is evaluated and compared with alternative methods in this experiment. Table 4 shows the classification results of these methods on the Swedish leaf dataset. It can be seen that the classification accuracy obtained by the MEQ + EC-ResNet50 method reaches 100%, which is higher than that of all other compared methods. More concretely, the accuracy of the fusion method is 1.52% higher than that of the shape-and-texture-based MTD + LBP-HF method. Moreover, the classification accuracy of the MEQ + EC-ResNet50 method is 3.17% and 2.46% higher than that of the HGO-CNN and Deep-Plant methods, respectively. Among other leaf-recognition methods, the accuracy of the IMTD + relu5_2 method on the Swedish leaf dataset reaches 99.47%, but it is still about 0.5% lower than that of the MEQ + EC-ResNet50 method. The abovementioned comparison results are sufficient to prove that the MEQ + EC-ResNet50 method has a better classification performance.

Table 4.
Comparison of classification results of different methods on the Swedish leaf dataset.
3.3. Experiments on the Flavia Leaf Dataset
3.3.1. Introduction to Flavia Leaf Dataset
The second dataset used to evaluate the performance of the proposed methods is the Flavia leaf dataset [35]. The dataset consists of 32 categories, each ranging from 50 to 77 images, for a total of 1907 leaf images. Figure 11a–c, respectively, show some original sample images, input images obtained by direct compression, and input images obtained by MEQ standardization. It can be found that, different from other datasets, the samples in this dataset do not have petioles, and their background is white, which is more conducive to feature extraction. In addition, since the shape and texture features of the leaves in this dataset are very similar, which increases the difficulty of classification, it is widely used in experiments by researchers.

Figure 11.
Partial original sample images of the Flavia leaf dataset (a), input images obtained by direct compression (b), and input images obtained by MEQ standardization (c).
3.3.2. Performance Evaluation of the MEQ Method on Flavia Leaf Dataset
In this classification task, six typical network models were again used to evaluate the effect of the MEQ method. The background of the sample image in this dataset contains fewer redundant features, thus enabling it to better demonstrate the impact of sample image deformation on the classification performance of the model. Table 5 enumerates the experimental results of these models on the Flavia leaf dataset. And their verification accuracy and verification loss comparison are shown in Figure 12. From the experimental results, it can be found that the MAC value of GoogLeNet reaches 99.30%, which is 0.17% higher than the classification result on the original dataset. At the same time, the classification results of ResNet50 and ResNet101 models are both improved by more than 0.30%. In addition, the classification performance of the VGG16 model is also significantly improved, and its MAC value reached 99.48%. As can be seen from the results in Figure 12, although the effective accuracy of the AlexNet and ResNet18 models on the two datasets before and after MEQ processing remains unchanged, the network convergence velocity becomes faster, and the training process is more stable on the standardized dataset. The abovementioned experimental results show that the MEQ method can also have a positive impact on the classification and recognition of the network model when the dataset has a unified background.

Table 5.
Comparison of classification results of CNN models on original and standardized Flavia leaf datasets.
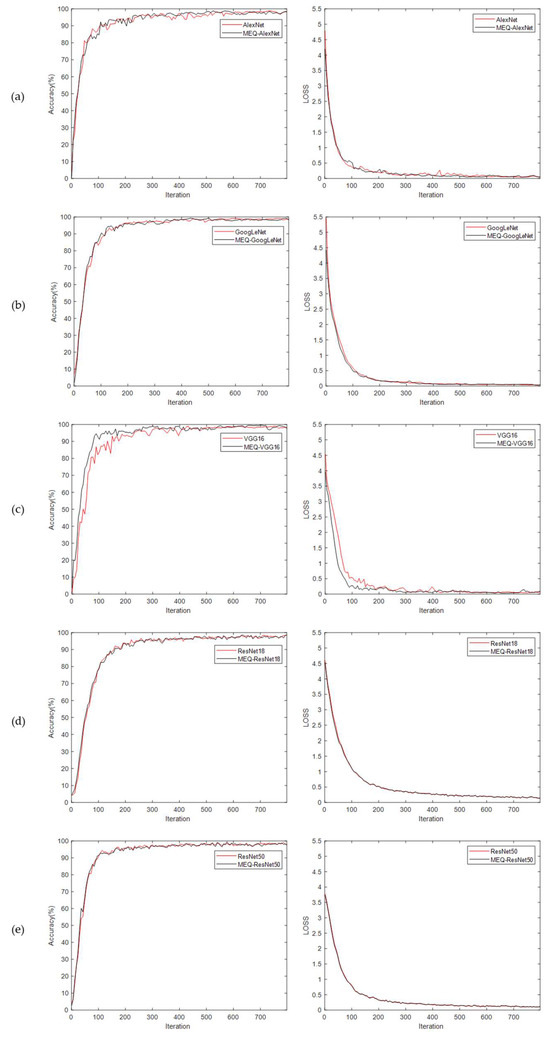
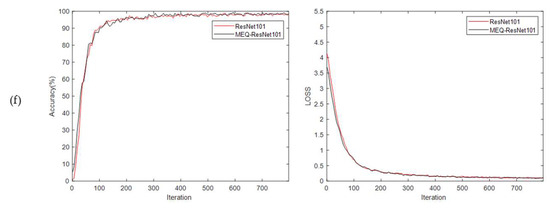
Figure 12.
Validation accuracy and validation loss of CNN models on original and standardized Flavia leaf datasets. The validation result curves of AlexNet, GoogLeNet, VGG16, ResNet18, ResNet50, and ResNet101 are sequentially presented in (a–f).
The comparison models and methods employed in the experiment are identical to those utilized in Section 3.2.3. Detailed comparison results of these methodologies are presented in Table 6. It can be distinctly seen from the table that the classification accuracy of the MEQ + EC-ResNet50 method on this dataset reaches 99.83%, which is better than all the compared methods. The proposed MEQ + EC-ResNet50 method exhibits a superior classification accuracy of 0.67% compared to the newly proposed MTD + LBP-HF method based on manual features. Furthermore, the MEQ + EC-ResNet50 algorithm also exhibits significant advantages when compared to other leaf-recognition methods integrated with deep-learning techniques. Specifically, the recognition accuracy of the MEQ + EC-ResNet50 method surpasses that of the Dual-Path CNN method and Deep-Plant method by 0.55% and 1.61%, respectively. The recognition accuracy of our method on this dataset is approximately 0.2% higher compared to that of the recently proposed IMTD + relu5 algorithm, thereby further substantiating the advantages derived from the integration of sample standardization and transfer-learning algorithms. All of these experimental results show that the MEQ + EC-ResNet50 method still has excellent performance on monochromatic-background leaf datasets with less redundant information.

Table 6.
Comparison of classification results of different methods on the Flavia leaf dataset.
3.4. Tests on the MEW2012 Leaf Dataset
3.4.1. Introduction to MEW2012 Leaf Dataset
The proposed method was evaluated on the MEW2012 leaf dataset [36], which is a more complex dataset consisting of 153 species of trees and shrubs from Central Europe. Each category contains between 50 and 99 images, resulting in a total of 9745 leaf images. Figure 13a–c, respectively, depict a portion of the original sample images from the MEW2012 leaf dataset, the input images obtained through direct compression processing, and the input images acquired via MEQ standardization processing. The analysis of this dataset reveals that directly compressing the original sample results in more severe leaf deformation and adversely affects the recognition efficacy of the CNN model. Furthermore, due to the high similarity in shape and color among certain leaf samples, accurately identifying these tree species poses a significant challenge.

Figure 13.
Partial original sample images from the MEW2012 leaf dataset (a), the input images obtained by direct compression of the original samples (b), and the input images obtained by MEQ standardization (c).
3.4.2. Performance Examination of the MEQ Method on MEW2012 Leaf Dataset
This experiment further evaluated the performance of the MEQ method on the MEW2012 leaf dataset. The specific test results of six commonly used CNN models are presented in Table 7. Figure 14 shows the validation accuracy and validation loss of these CNN models on the original and standardized MEW2012 datasets. It can be clearly seen that, except for AlexNet, the other five network models have achieved better classification results on the standardized MEW2012 dataset. Specifically, the MAC value of the ResNet18 model reaches 96.47%, which is 0.24% higher than the AC value obtained on the original dataset. Meanwhile, the MAC values of the ResNet50 and ResNet101 models are also slightly higher than their AC values. In the remaining two models, the MAC value of VGG16 is 0.14% higher than the AC value obtained on the original dataset, and the test result of GoogLeNet is also improved by 0.24%. The above comparison results can prove that the MEQ method is still effective even in more difficult classification tasks. Furthermore, it is also evident from Figure 14 that almost all models obtain lower loss values on the standardized MEW2012 leaf dataset. This also provides strong evidence for the performance effectiveness of the MEQ method.

Table 7.
Comparison of classification results of CNN models on original and standardized MEW2012 leaf datasets.
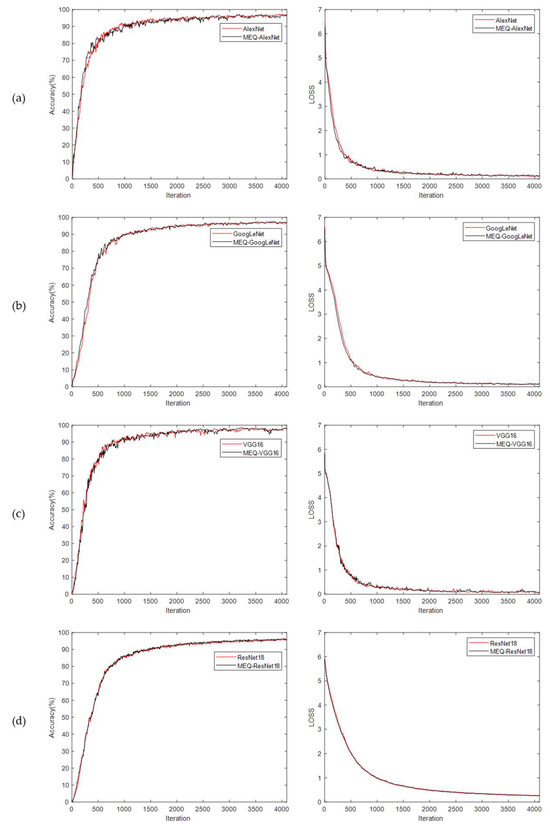
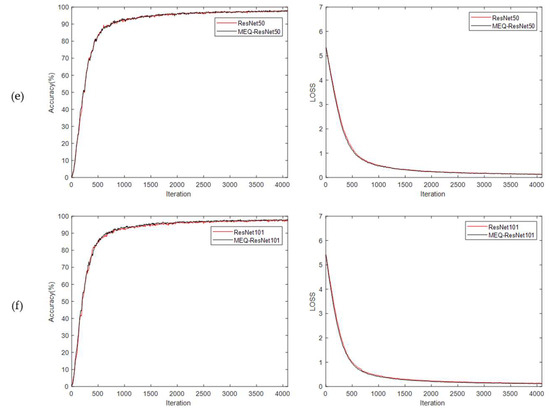
Figure 14.
Validation accuracy and validation loss of CNN models on original and standardized MEW2012 leaf datasets. Where (a–f) list the validation result curves of AlexNet, GoogLeNet, VGG16, ResNet18, ResNet50, and ResNet101, respectively.
3.4.3. Performance Examination of the Fusion Method on MEW2012 Leaf Dataset
The classification performance of the MEQ + EC-ResNet50 algorithm on the MEW2012 dataset with a greater variety of leaf species was evaluated using the same comparison models and methods as described in Section 3.2.3. The specific results of these comparisons are listed in Table 8. It can be seen that the MEQ + EC-ResNet50 method again obtains the best classification results. On this dataset, the classification accuracy of MEQ + EC-ResNet50 fusion algorithm finally reaches 99.25%, which is 0.16% higher than that of IMTD + relu5_2 method based on shape and convolutional features. Among various deep-learning methods, MaskCOV demonstrated a superior performance, with a classification accuracy of 98.32%, which is still slightly lower by 0.93% compared to that of MEQ + EC-ResNet50. In addition, the classification accuracy of our method is 1.19% higher than that of the VGG16 + relu5_2 algorithm, indicating that the performance of MEQ + EC-ResNet50 algorithm is better than that of existing leaf-recognition schemes combined with deep learning. Similarly, the classification accuracy of the MEQ + EC-ResNet50 method is better than those classification methods based on manual features. The comparison results presented above provide compelling evidence that our MEQ + EC-ResNet50 method continues to exhibit a superior performance when applied to larger leaf datasets.

Table 8.
Comparison of classification results of different methods on the MEW2012 leaf dataset.
3.5. Grad-CAM Visual Analysis
Gradient-Weighted Class Activation Mapping (Grad-CAM) is a class-discriminative localization technique used to generate ‘visual explanations’ for decisions from a large class of CNN-based models, making them more transparent and interpretable. The gradient information from the last convolutional layer, which is fed into the CNN, is utilized to assign significance values to individual neurons for a specific decision of interest. The detailed principle of the Grad-CAM technique can be found in the literature [37]. Considering that there are differences in shape and texture information between the standardized samples and the directly compressed original samples, this may lead to changes in the regions of interest of the CNN models. Hence, the Grad-CAM technique is used to visualize the significant regions of interest for the above six models in high-resolution detail. Figure 15 shows the Grad-CAM images of input samples from the Swedish leaf dataset and the standardized Swedish leaf dataset, where the samples in Figure 15a are from class 5, and the samples in Figure 15b are from class 1.
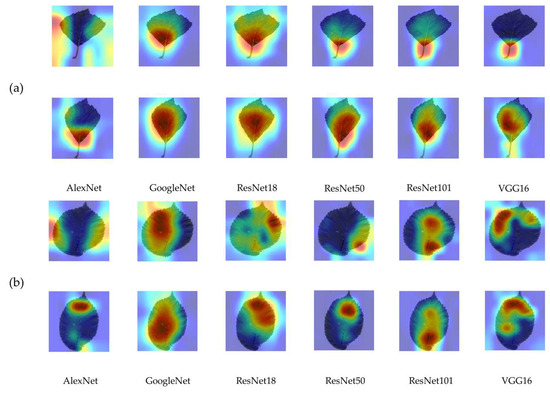
Figure 15.
The Grad-CAM images of directly compressed and MEQ-standardized samples. (a) Sample with petiole and (b) sample without petiole. In both (a,b), the upper section displays the Grad-CAM image of the directly compressed sample, whereas the lower section showcases the Grad-CAM image of the MEQ standardized sample.
As expected, the six models showed significant changes in the areas of attention on both the original and standardized leaf samples. As can be seen from Figure 15a, in the case of direct compression of the original sample, all models primarily focus on the petiole and its surrounding background. The AlexNet model, in particular, focuses almost exclusively on the background of the image. This indicates that even if the model can correctly classify such samples when training on specific datasets, it may not achieve ideal results in practical applications. The Grad-CAM images of standardized sample, however, did not exhibit a similar phenomenon. Conversely, the regions of interest for all models during the recognition process were predominantly concentrated on the leaf surface. Additionally, to enhance the demonstration of the MEQ method’s effectiveness, a Grad-CAM image of a petiole-free sample was utilized for comparative analysis, as depicted in Figure 15b. The significant changes can still be observed in this case, and for the directly compressed original sample, the model’s attention is primarily focused on the leaf’s edge. However, for standardized samples, their area of interest remains concentrated on the leaf surface. These experimental results demonstrate the efficacy of the MEQ method in eliminating redundant information from images, thereby facilitating more accurate extraction of texture and shape features by convolutional models.
Furthermore, it can be found that the AlexNet network appears to exhibit greater susceptibility to sample deformation, and its attention primarily focused on the background and leaf edges of the sample image. These may be the reasons for the unsatisfactory performance of the model on the standardized MEW2012 leaf dataset. Many species of leaf samples in this dataset come from the same genus, resulting in a high degree of similarity in their leaf shape and texture features, which undoubtedly increases the difficulty of classification recognition. The inevitable variations in the acquisition time and illumination of different types of sample data in the dataset result in differences in background and size among different types of samples. Directly compressing these samples may diminish the similarity between highly similar ones. Moreover, the disparities caused by background differences further amplify the dissimilarities among these similar leaves to a certain extent. Consequently, the classification results obtained under such circumstances are evidently inaccurate.
Based on the above analysis, it can be concluded that the MEQ leaf sample-standardization method can effectively mitigate the interference caused by redundant information in sample images, enhance the CNN network’s focus on internal texture details of leaves, and consequently improve the accuracy of model classification results.
4. Conclusions
The present paper introduces a novel sample-standardization method, namely MEQ, for the purpose of plant-leaf recognition. Firstly, the minimum enclosing rectangle of the leaf sample is obtained by finding the maximum connected component in the image. Then, the target area of the original sample image is cropped according to the coordinates of the rectangle. Finally, the rectangle is further expanded into a square and compressed to meet the input requirements of the models. The proposed method can effectively avoid the issue of leaf deformation caused by asymmetric sample compression due to the input limitation of the CNN model, while simultaneously maximizing the removal of redundant information in the image. In addition, an improved ResNet50 model is proposed and used in combination with MEQ methods. The main advantages of this model lie in the utilization of the ELU activation function, which exhibits superior learning capabilities compared to the original ReLU, and the incorporation of a larger convolution kernel size within the specific residual block for enhanced extraction of global leaf features. The results of the transfer-learning experiment on six typical CNN models using various original leaf datasets and MEQ standardized datasets demonstrate that the utilization of the MEQ method significantly enhances the classification accuracy of CNN models when applied to leaf datasets. This validates the universal applicability of the proposed sample standardization method and introduces a new idea for plant-leaf recognition research. Simultaneously, the validation accuracy of the MEQ + EC-ResNet50 algorithm on Swedish, Flavia, and MEW2012 leaf datasets, respectively, reached 100%, 99.83%, and 99.25%, and it also obtained the best results among all comparison methods and can be used as a feasible scheme for plant-leaf recognition.
Additionally, the proposed MEQ algorithm can serve as an exceptional preprocessing method for image samples in various other fields of image classification. By bringing the samples closer to their natural state, it significantly enhances the training and practical application of recognition algorithms. However, the current standardization method for samples falls short when dealing with image backgrounds, as it still requires retaining a portion of background information to prevent the loss of blade-edge details. Moving forward, we will continue refining the MEQ algorithm and optimizing the approach to processing sample background information.
Author Contributions
Conceptualization, G.L. and H.N.; methodology, G.L.; software, G.L. and R.Z.; formal analysis, G.L.; investigation, G.L.; resources, H.N.; data curation, G.L. and H.N.; writing—original draft preparation, G.L.; writing—review and editing, G.L., R.Z. and H.N.; visualization, G.L. and H.N.; supervision, D.Q.; project administration, D.Q. and H.N.; funding acquisition, H.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities (No. 2572022BC03), the Innovation Training program for the college students at Northeast Forestry University (No. 202110225485), and the Project of National Natural Science Foundation of China (No. 31570712).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Scotland, R.W.; Wortley, A.H. How many species of seed plants are there? Taxon 2003, 52, 101–104. [Google Scholar] [CrossRef]
- Yang, C.Z. Plant leaf recognition by integrating shape and texture features. Pattern Recognit. 2021, 112, 107809. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, W.Q.; Luo, H.Z.; Chen, L.; Peng, J.Y.; Fan, J.P. Plant recognition via leaf shape and margin features. Multimed. Tools Appl. 2019, 78, 27463–27489. [Google Scholar] [CrossRef]
- Chen, X.; Wang, B. Invariant leaf image recognition with histogram of Gaussian convolution vectors. Comput. Electron. Agric. 2020, 178, 105714. [Google Scholar] [CrossRef]
- Almodfer, R.; Mudhsh, M.; Zhao, J.F. Pyramided and optimized blurred shape model for plant leaf classification. IET Image Process. 2023, 17, 2838–2854. [Google Scholar] [CrossRef]
- Wu, H.; Fang, L.C.; Yu, Q.; Yang, C.Z. Composite descriptor based on contour and appearance for plant species identification. Eng. Appl. Artif. Intell. 2024, 133, 108291. [Google Scholar] [CrossRef]
- Zhu, Y.X.; Sun, W.M.; Cao, X.Y.; Wang, C.Y.; Wu, D.Y.; Yang, Y.; Ye, N. TA-CNN: Two-way attention models in deep convolutional neural network for plant recognition. Neurocomputing 2019, 365, 191–200. [Google Scholar] [CrossRef]
- Xu, Y.X.; Wen, G.H.; Hu, Y.; Luo, M.N.; Dai, D.; Zhuang, Y.S.; Hall, W. Multiple attentional pyramid networks for Chinese herbal recognition. Pattern Recognit. 2021, 110, 107558. [Google Scholar] [CrossRef]
- Quach, B.M.; Dinh, V.C.; Pham, N.; Huynh, D.; Nguyen, B.T. Leaf recognition using convolutional neural networks based features. Multimed. Tools Appl. 2023, 82, 777–801. [Google Scholar] [CrossRef]
- Sun, X.B.; Xu, L.; Zhou, Y.F.; Shi, Y.J. Leaves and Twigs Image Recognition Based on Deep Learning and Combined Classifier Algorithms. Forests 2023, 14, 1083. [Google Scholar] [CrossRef]
- Wu, H.; Fang, L.C.; Yu, Q.; Yuan, J.R.; Yang, C.Z. Plant leaf identification based on shape and convolutional features. Expert Syst. Appl. 2023, 219, 119626. [Google Scholar] [CrossRef]
- Zhu, L.; Yan, M.; Huang, J. Plant Leaf Recognition Method With New Convolution Neural Network. J. Northeast. For. Univ. 2020, 48, 50–53. [Google Scholar] [CrossRef]
- Isik, S.; Ozkan, K. Overview of handcrafted features and deep learning models for leaf recognition. J. Eng. Res. 2021, 9, 12. [Google Scholar] [CrossRef]
- Krishnamoorthy, N.; Prasad, L.V.N.; Kumar, C.S.P.; Subedi, B.; Abraha, H.B.; Sathishkumar, V.E. Rice leaf diseases prediction using deep neural networks with transfer learning. Environ. Res. 2021, 198, 111275. [Google Scholar] [CrossRef]
- Thangaraj, R.; Anandamurugan, S.; Kaliappan, V.K. Automated tomato leaf disease classification using transfer learning-based deep convolution neural network. J. Plant Dis. Prot. 2021, 128, 73–86. [Google Scholar] [CrossRef]
- Zhang, R.L.; Zhu, Y.J.; Ge, Z.S.J.; Mu, H.B.; Qi, D.W.; Ni, H.M. Transfer Learning for Leaf Small Dataset Using Improved ResNet50 Network with Mixed Activation Functions. Forests 2022, 13, 2072. [Google Scholar] [CrossRef]
- Zhou, D.X.; Ma, X.T.; Feng, S. An Effective Plant Recognition Method with Feature Recalibration of Multiple Pretrained CNN and Layers. Appl. Sci. 2023, 13, 4531. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Shafiq, M.; Gu, Z.Q. Deep Residual Learning for Image Recognition: A Survey. Appl. Sci. 2022, 12, 8972. [Google Scholar] [CrossRef]
- Kilicarslan, S.; Celik, M. RSigELU: A nonlinear activation function for deep neural networks. Expert Syst. Appl. 2021, 174, 114805. [Google Scholar] [CrossRef]
- Bawa, V.S.; Kumar, V. Linearized sigmoidal activation: A novel activation function with tractable non-linear characteristics to boost representation capability. Expert Syst. Appl. 2019, 120, 346–356. [Google Scholar] [CrossRef]
- Jiang, Y.Y.; Xie, J.Y.; Zhang, D. An Adaptive Offset Activation Function for CNN Image Classification Tasks. Electronics 2022, 11, 3799. [Google Scholar] [CrossRef]
- Ying, Y.; Su, J.L.; Shan, P.; Miao, L.G.; Wang, X.L.; Peng, S.L. Rectified Exponential Units for Convolutional Neural Networks. IEEE Access 2019, 7, 101633–101640. [Google Scholar] [CrossRef]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar] [CrossRef]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2018, arXiv:1710.05941. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, F.; Cao, R. Research on recognition method of leaf diseases of woody fruit plants based on transfer learning. Sci. Rep. 2022, 12, 15385. [Google Scholar] [CrossRef]
- Söderkvist, O. Computer Vision Classification of Leaves from Swedish Trees. Master’s Thesis, Linköping University, Linköping, Sweden, 2001. [Google Scholar]
- Shah, M.P.; Singha, S.; Awate, S.P. Leaf classification using marginalized shape context and shape+texture dual-path deep convolutional neural network. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 860–864. [Google Scholar] [CrossRef]
- Lee, S.H.; Chan, C.S.; Remagnino, P. Multi-Organ Plant Classification Based on Convolutional and Recurrent Neural Networks. IEEE Trans. Image Process. 2018, 27, 4287–4301. [Google Scholar] [CrossRef]
- Lee, S.H.; Chan, C.S.; Mayo, S.J.; Remagnino, P. How deep learning extracts and learns leaf features for plant classification. Pattern Recognit. 2017, 71, 1–13. [Google Scholar] [CrossRef]
- Yang, C.Z.; Yu, Q. Multiscale Fourier descriptor based on triangular features for shape retrieval. Signal Process. Image Commun. 2019, 71, 110–119. [Google Scholar] [CrossRef]
- Yu, X.H.; Zhao, Y.; Gao, Y.S.; Xiong, S.W. MaskCOV: A random mask covariance network for ultra-fine-grained visual categorization. Pattern Recognit. 2021, 119, 108067. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Wu, S.G.; Bao, F.S.; Xu, E.Y.; Wang, Y.X.; Chang, Y.F.; Xiang, Q.L. A Leaf Recognition Algorithm for Plant Classification Using Probabilistic Neural Network. In Proceedings of the 2007 IEEE International Symposium on Signal Processing and Information Technology, Giza, Egypt, 15–18 December 2007; pp. 11–16. [Google Scholar] [CrossRef]
- Novotny, P.; Suk, T. Leaf recognition of woody species in Central Europe. Biosyst. Eng. 2013, 115, 444–452. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).