Abstract
Traditional drilling methods often face difficulty meeting the demand for efficient and accurate coring under complex geological conditions. Cordless coring is an advanced technology that uses hydraulic lifting to carry out coring, which can achieve automation and automated and intelligent drilling operations. In this research, a new type of hydraulic lifting cordless coring drilling tool is designed. Moreover, a numerical simulation model of the fluid flow in the annulus between the spearhead and spool of the cordless coring drilling tool was established. Orthogonal simulation tests are carried out, and according to the orthogonal test data, a numerical prediction model of the spool annulus fluid field based on the Backpropagation Neural Network (BP neural network) is established. The prediction of the flow rate of the drilling fluid and the spool back-pressure ratio was obtained when the structural parameters of the spearhead and the spool annulus were different. A multi-objective optimization of the annulus flow structure of the cordless core drilling tool has been carried out. The optimization objectives include deciding the back pressure ratio of the spool overcoming the spring and the flow rate of the drilling fluid. According to the established nonlinear optimization model and based on the improved Non-dominated Sorting Genetic Algorithm II (NSGA-II) multi-objective optimization algorithm, it is verified that the convergence speed and diversity of the improved algorithm are better than those before the improvement. The simulation and experimental validation are carried out. It is verified that the flow rate of drilling fluid increased by 33.56% after optimization, and the force ratio was lowered by 5.825%. Finally, based on the simulation and optimization results, the φ96 cordless core drilling tool was manufactured on a trial basis, and on-site concrete drilling, coring, and hydraulic lifting operations were conducted for smooth coring and lifting. This study could provide an important scientific basis and technical support for the application and development of hydraulic lifting cordless coring technology.
1. Introduction
With the advancement in oil and gas exploration and development, traditional coring methods are facing multiple challenges, including low operational efficiency, high cost, and operational safety issues. Under complex geological conditions, traditional drilling methods often face difficulty meeting the demand for efficient and accurate coring. Therefore, it is particularly important to develop a new technology that can improve coring efficiency and reduce operation costs. Cordless coring is an advanced technology that uses hydraulic lifting for coring, which can be automated and intelligently perform drilling operations and improve drilling efficiency as well as safety. The cordless coring drilling tool can improve the coring efficiency and reduce the operation cost [1,2,3]. In the design and development of this drilling tool, the annular fluid flow structure plays a key role in the performance, and by optimizing the annular fluid flow structure, the coring efficiency can be significantly improved and energy consumption can be reduced [4,5].
Rope coring is the most widely used non-lift drilling coring method at present [6,7,8]. For horizontal holes or large inclined holes drilling, the salvager lowering is a difficult and time-consuming operation process [9,10,11,12]. For the circulating liquid flow structure, Ma et al. [13] designed the structure of a rope coring reverse circulation drilling tool and carried out numerical simulation analysis and research on the flow field of the jet reverse circulation channel using fluent software (FLUENT 14.0). Zhao et al. [14] proposed a new type of combined rotary flow borehole purification scheme. The CFD-EDEM coupling method was used to visualize the flow field and particle movement law in the borehole. Shi et al. [15] designed a large-diameter modular drill bit according to the structure of the rope coring tool. The computational fluid dynamics (CFD) method was used to establish the simulation model of the modular drill bit in the simulation environment. Based on the theory of multi-objective optimization, Wang et al. [16,17] designed the water passage system of a bottom-sprayed diamond bit according to the operation of the seafloor drilling rig and stratigraphic characteristics. To improve drilling efficiency and core recovery, Wang et al. [18] proposed a subsea drill bit design combining the characteristics of subsea formations within 300 m. Cao et al. [19] developed a retractable drill bit for casing while drilling, and the orthogonal design method was used to optimize the bit structure. You et al. [20] used the fluid simulation software FLUENT (Fluent 2022R1) to numerically simulate the bottomhole flow field. Li et al. [21] established a three-dimensional model of a laser-mechanical drill bit with the goal of improving the chip removal performance of the drill bit and numerically simulated the chip removal process using the EDEM-Fluent coupling method. Wang et al. [22] used CFD to study the influence of different wellbore parameters on the rock-carrying capacity and obtained the relevant flow law. The design and optimization of the liquid flow structure in the annulus of cordless coring tools are crucial for improving the coring efficiency, ensuring the sampling quality, and ensuring the stable operation of the system [23,24,25,26]. In terms of optimization methods, Verma et al. [27] analyzed the modifications in NSGA-II and discussed the various performance evaluation techniques. Kumar et al. [28] proposed a multi-criteria web optimization algorithm based on NSGA-II, which is capable of generating multiple web object sequences. Elarbi et al. [29] used benchmark problems involving up to 20 objectives. The enhanced algorithm labeled NSGA-II with reference-point-based superiority over the four recently proposed decomposition-based multi-objective evolutionary algorithms has been statistically proven to be competitive and yields better results. Pawar et al. [30] used NSGA-II to obtain the optimal values of process variables such as wheel speed, workpiece speed, dressing depth, and dressing lead in order to improve process performances such as production cost, productivity, and surface finish. Wang et al. [31] proposed a novel multi-objective optimization algorithm for wind turbine blades, which has a good advantage in dealing with turbine multi-objective optimization with better performance.
The objective of this study is to perform a multi-objective optimization of the annulus fluid flow structure of the cordless core drilling tool while optimizing the back pressure ratio of the spool to overcome the spring and the drilling fluid flow rate, as well as to obtain a low back pressure ratio and a high drilling fluid flow rate in hard rock formations to ensure high-quality core samples. In this work, at first, the structural parameters of the spearhead and spool are simulated, followed by designing orthogonal experiments to derive the spool back pressure and drilling fluid flow rate under different structural parameters. Secondly, a prediction model is also established to achieve the prediction of spool back pressure and drilling fluid flow rate under different structural parameters. A mathematical model of the relationship between decision variables and optimization objectives is then fitted by the BP neural network. Then, the optimal spool back pressure and drilling fluid flow rate in hard rock formation, as well as the solution space of structural parameters of spearhead and spool, are derived from the established nonlinear optimization model and the solution of the improved NSGA-II multi-objective optimization algorithm [32,33,34,35]. Finally, simulation and experimental verification are carried out to verify the multi-objective optimization results and achieve the improvement of coring efficiency and coring quality, as well as the reduction of energy consumption.
2. Structural Design and Principles of Hydraulic Lifting Cordless Coring Drilling Tool
The hydraulic lifting cordless coring tool includes an outer assembly and an inner assembly, of which the outer assembly includes the coring bit, the support ring, the outer pipe, and the adapter. The inner assembly includes the annular fluid flow structure, the single-acting mechanism, the valve gland, and the core pipe. The structure of the hydraulic lifting cordless coring tool is shown in Figure 1. The annular fluid flow structure is a crucial channel for achieving core recovery and debris removal, and it includes components such as the fishing spear, spool, valve body, and spring.
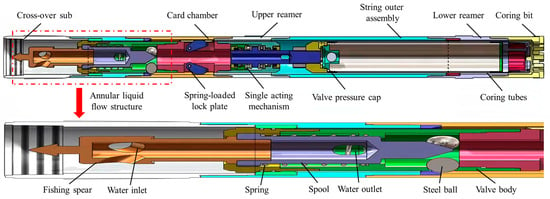
Figure 1.
Hydraulic lift cordless core drilling tool structure.
Before coring, the drilling fluid enters the spearhead and spool from the inner and outer pipe inlets and then enters the gap between the spool and the valve body from the outlet. As the drilling fluid is pumped in, it fills the gap. As a result, the pressure at the bottom of the spool increases. When the pressure increases to the spring pressure, it starts to push the spool inward. When the spool’s outlet moves to a certain position, the spring can no longer be compressed, and the spool stops moving inward. At this time, the spool pushes the steel ball to block the outlet of the valve body, and the drilling fluid continues to flow into the gap between the inner and outer tubing rings to the vicinity of the drill bit, forming a circulating channel between the outer tubing and the wall of the well. As a result, slag drainage and wall protection circulation could be achieved. After the sampling is completed, positive circulation is stopped, and the spring returns to its normal state. Following this, the circulation channel between the inner and outer assemblies is closed, and the reverse circulation is opened. During the reverse circulation, the mud is injected through the outer pipe, and the mud returns to the well wall to push the inner assembly and lift it to the wellhead.
3. Numerical Simulation and Calculation of Fluid Flow in Spearhead and Spool Annulus of Cordless Core Drilling Tools
3.1. Numerical Simulation Model of Spearhead and Spool Flow
In the positive circulation process, the mud flows out through the mud pump, flows into the inlet of the spearhead through the internal channel of the drill pipe, and then enters the inlet of the spearhead to form the back pressure through the internal flow channel, so that the spearhead moves to form the path. In this process, the loss along the way and the internal energy loss of the spearhead are taken into account. Ansys Fluent can accurately simulate laminar flow, turbulence, chemical reactions, multiphase flow, and other complex flow phenomena because of its rich model, powerful processing capability, and software compatibility. The establishment of the spearhead and spool fluid simulation model is shown in Figure 2.
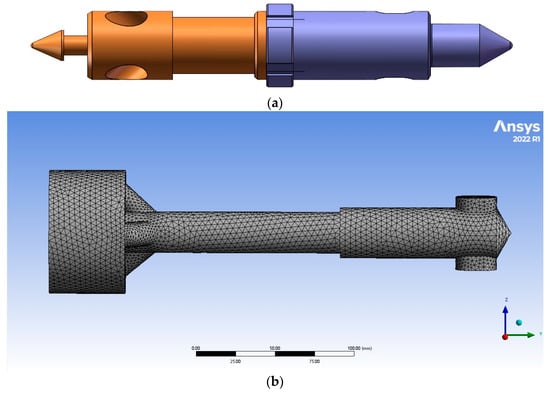
Figure 2.
Fluid simulation model of spearhead and spool valve. (a) Spearhead and spool assembly diagram annular liquid flow structure. (b) Mesh delineation model of the flow channel of an annular liquid flow structure.
By using the FLUENT Meshing pre-processing tool, the extracted flow channel is meshed. In numerical simulation, the mesh not only serves as the carrier of the finite element volume method but also as the geometric representation of the analytical computational fluid dynamics model. The mesh can be divided into two types. One is unstructured mesh, and the other is structured mesh. As the flow rules of the internal flow field of the flow channel are chaotic and dominated by turbulent flow, the mesh is mainly divided into unstructured meshes in this simulation. In finite element calculation, the quality of mesh division has a significant influence on the accuracy of the calculation results and the efficiency of the calculation. A triangular face mesh is used to mesh the flow channel. The boundary expansion is added, and the number of layers is 5. To complete the mesh division of the flow channel model, the triangular face mesh structure is divided into a total of 83,193. The steady-state solution is selected, and the k-epsilon double equation model (k-ε model) is chosen as the turbulence model, where k is the turbulent pulsation kinetic energy. The larger the k, the higher the length and time scale of the turbulent pulsation. The energy dissipation rate of the pulsation is expressed in terms of the energy diffusion coefficient ε, with a larger ε indicating a smaller length and time scale of the turbulent pulsation.
3.2. Orthogonal Test Design
Through the orthogonal test, the primary and secondary factors affecting the flow field of the drilling tool annulus under the effect of the factors are analyzed. The factors considered were the number of spearhead inlet ports (A), the diameter of spearhead inlet ports (B), the number of spool outlet ports (C), the diameter of outlet ports (D), and the distance between the centers of the two circular holes in the elongated outlet port (E). The optimal combination of the parameters A, B, C, D, and E was determined to optimize the structure of the spearhead and spool. A prediction model is established to predict the spool back pressure and drilling fluid flow rate under different structural parameters. Multi-objective optimization is carried out at the same time to complete the optimization of the ratio of fluid back pressure to spring force pressure and the drilling fluid flow rate.
The test indexes are the characteristic quantities used to evaluate the results of the orthogonal tests, which are selected according to different test purposes. There is at least one test index for each test. The ratio of fluid back pressure to spring force pressure (Y1) and the drilling fluid flow rate (Y2) are used as experimental indicators. Test factors refer to the factors that may affect the test indexes. Factors such as the number of inlet ports of spearhead A, the diameter of the inlet ports of spearhead B, the number of spool outlets C, the diameter of the outlet ports D, and the center distance between the two outlet ports of the oblong holes E are selected as test factors. Considering the overall size of the drilling tools, the installation location, and the difficulty of achieving a comprehensive analysis of a number of factors, the orthogonal test factors and their levels are formulated as shown in Table 1.

Table 1.
Factors and level setting of mixed orthogonal test table.
The table shows that there are five structural parameters to be analyzed. Among these, two parameters have two levels each, one parameter has six levels, and two parameters have nine levels each. Therefore, 81 experiments are required for the simulation. According to the number of factors and their decided levels, the SPSS software (SPSS2022) is used to generate a hybrid orthogonal test table. According to the test table, the simulation test is carried out in FLUENT fluid simulation software (Fluent 2022R1). The test program and results are shown in Appendix A.
3.3. Numerical Prediction Model of Spool Annular Flow Field Based on BP Neural Network
Suitable spool back pressure and drilling fluid flow rate have a large impact on coring quality and coring operation efficiency. Due to the complexity of the actual drilling conditions, it is difficult to accurately predict the flow field performance of the spool under different structural parameters only through experience or simple models. Therefore, it is important to establish an accurate prediction model. The prediction model can predict the spool back pressure and drilling fluid flow rate based on the existing design parameters and operation data, improve the coring quality and drilling fluid flow efficiency, and reduce energy consumption and cost. The effects of different structural parameters on spool back pressure and flow rate are analyzed by orthogonal experimental methods, which provide a training basis for the model based on the obtained data.
The BP Neural Network is a common artificial neural network with good nonlinear mapping capability. It usually consists of an input layer, one or more hidden layers, and an output layer [36,37,38,39,40]. The neural network learns the patterns in the data by adjusting the weights. The specific process is as follows: First, forward propagation: the input data were passed through the input layer, layer by layer, to the hidden layer and the output layer to get the predicted output. Second, error calculation: the error between the predicted output and the actual output is calculated, in which the error calculation formula is shown in Equation (1);
where is the total error, is the predicted output, is the actual output, and is the number of output nodes.
Then, back-propagation: the error is passed backward from the output layer layer by layer, and the weights of each layer are adjusted by calculating the gradient. Finally, weight update: the weights are updated according to the gradient of the error to reduce the error, and the weight update formula is shown in Equation (2). The whole process is repeated until the error of the network is reduced to an acceptable range or reaches the preset number of training times.
where is the value after weight update, is the current weight value, is the learning rate, is the partial derivative of the error with respect to the weight.
During the training process using the BP neural network, 70% of them are used as training data for network training and 30% as test data for testing the fitting performance of the network. According to the nonlinear functional relationship between the structural parameters and the composition of the optimization objective, the structure of the BP neural network was set to be 5-10-2, with 5 nodes in the input layer, 10 nodes in the hidden layer, and 2 nodes in the output layer. The BP neural network was randomly initialized, and the relevant network parameter configurations were configured, in which the number of iterations was 1000, the error threshold was set to 1 × 10−6, and the learning rate was 0.01. Figure 3 shows the function of the correlation between the dependent variable, the ratio of the fluid back pressure and the spring force pressure, and the independent variables, the number of spearhead intakes, the diameter of spearhead intakes, the number of spool outlets, the diameter of outlets, and the distance between the two centers of the two circles of the outlet oblong hole. The fitting situation, recorded as model I, has a correlation coefficient of R = 0.94. R is the correlation coefficient. The larger the R, the higher the fitting accuracy.
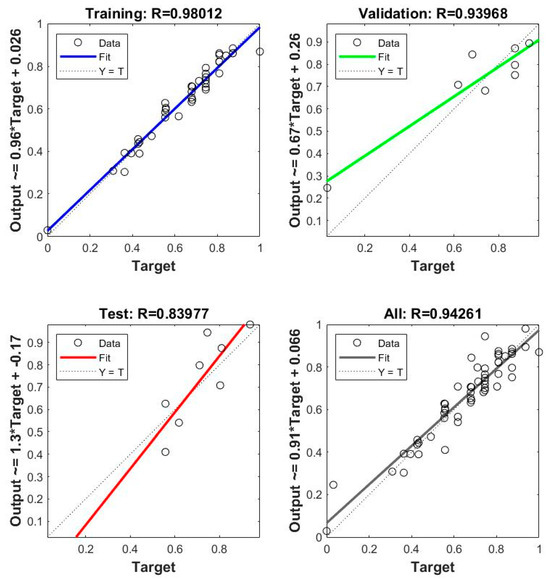
Figure 3.
Model I training results.
Figure 4 shows the function fitting of the dependent variable drilling fluid flow rate to the independent variables of the number of spearhead inlets, the diameter of spearhead inlets, the number of spool outlets, the diameter of spool outlets, and the distance between the centers of the two circles of spool outlet long holes, which is denoted as Model II, with a correlation coefficient of R = 0.92. Based on the numerical prediction model of the spool annulus flow field established with the BP neural network, the fluid backpressure to spring force pressure ratio and the flow rate of the spool outlet can be derived for the design of the cordless coring tool with different annulus flow structures. This prediction model also serves as an input for multi-objective optimization. Fluid back pressure to spring force pressure ratio and drilling fluid flow rate can provide references for the design of the annulus flow structure when drilling in different formations. This prediction model is also used as an input for multi-objective optimization to obtain the values of the parameters of the annulus flow structure of the cordless coring tool under the optimal objective.
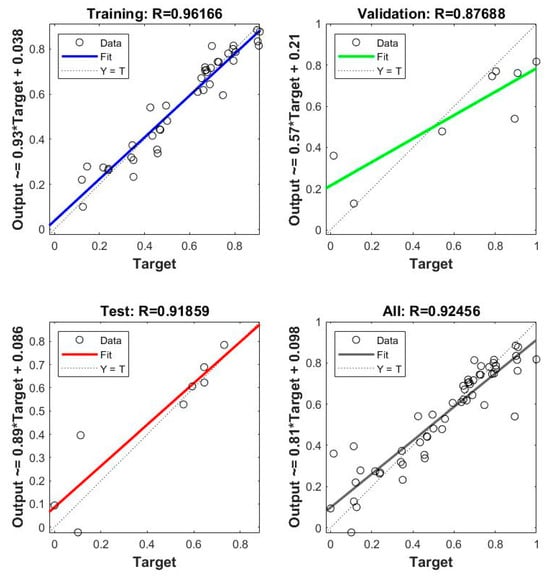
Figure 4.
Model II training results.
4. Optimization of Structural Dimensions of an Annular Hollow Fluid Flow Runner Based on Improved NSGA-II Algorithm
4.1. Principles of the Improved NSGA-II Algorithm
The NSGA-II algorithm is a widely used evolutionary algorithm for multi-objective optimization. The four criteria of NSGA-II include non-dominated sorting, elite retention strategy, congestion calculation, and race selection, the core of which lies in fast non-dominated sorting and congestion comparison. Multi-objective optimization is the process of finding a vector of decision variables that satisfy the constraints and assigning appropriate values to all objective functions. Such a problem produces a set of optimal solutions, i.e., a set of Pareto optimal solutions, rather than a single solution. The multi-objective problem can be formulated as:
where is the value of the objective function and is the set of equality and inequality constraints.
In this study, for a desired set of fluid back pressure to spring force pressure ratio and drilling fluid flow rate, the number of spearhead inlets, diameter of spearhead inlets, number of spool outlets, diameter of spool outlets, and distance between the centers of the two circles of the spool outlet oblong holes are used as the decision variables. The objective function is the output of the BP neural network. The improved NSGA-II algorithm is improved in terms of fitness allocation, environment selection mechanism, crossover, and mutation operation. The execution steps are as follows:
Step 1: Population initialization and fitness calculation: an initial population is randomly generated, and the objective function value of each individual is calculated. Then the fitness calculation is performed, which is based on the position of each individual on its dominance frontier. The fitness of an individual is related to its dominance level (Pareto rank) and crowding distance. The fitness calculation formula is:
where denotes the Pareto rank; a low rank indicates that an individual dominates fewer individuals and denotes the crowding distance. The crowding distance between individuals on the same frontier is used to maintain the diversity of the solution set.
Step 2: Fast, non-dominated sorting (Algorithm 1) to sort the population and assign Pareto rank. The following steps are followed to compute the dominance relationships and Pareto ranks of individuals:
- (1)
- For each individual p, its objective function value is compared with other individuals in the population;
- (2)
- The set of individuals Sp is determined, dominated by individual p, and the number of dominated individuals np;
- (3)
- Dominance relationships are used to stratify the population, which is not dominated by any individual belonging to the first frontier.
| Algorithm 1: Fast Non-Dominated Sorting |
| Input: Population P |
| Output: Sorted fronts F and Pareto ranks R |
| 1: Initialize empty lists F and R |
| 2: for each individual p in P do |
| 2.1: Initialize empty list Sp and set np = 0 |
| 2.2: for each individual q in P do |
| 2.2.1: if p dominates q then |
| 2.2.1.1: Add q to Sp |
| 2.2.2: else if q dominates p then |
| 2.2.2.1: Increment np by 1 |
| 2.3: if np == 0 then |
| 2.3.1: Set rank of p to 1 |
| 2.3.2: Add p to the first front F1 |
| 3: Set i = 1 |
| 4: while Fi is not empty do |
| 4.1: Initialize empty list Q |
| 4.2: for each individual p in Fi do |
| 4.2.1: for each individual q in Sp do |
| 4.2.1.1: Decrement nq by 1 |
| 4.2.1.2: if nq == 0 then |
| 4.2.1.2.1: Set rank of q to i + 1 |
| 4.2.1.2.2: Add q to Q |
| 4.3: Increment i by 1 |
| 4.4: Add Q to F |
| 5: Return F and R |
Step 3: Crowding distance calculation within the same Pareto front and calculating the crowding distance between individuals for maintaining population diversity (Algorithm 2). The improved crowding distance calculation considers not only the target space but also the similarity in the decision space to increase the efficiency of the algorithm in dealing with highly correlated variables. The formula for the improved crowding distance, di, is:
where is the number of objective functions, is the m-th objective function, is the parameter of the trade-off between the decision variable and the objective function, is the decision variable, and is the number of decision variables.
| Algorithm 2: Crowding Distance Calculation |
| Input: Front F |
| Output: Crowding distances D |
| 1: Initialize D with zeros for all individuals in F |
| 2: for each objective function m do |
| 2.1: Sort the individuals in F based on objective m |
| 2.2: Set the crowding distance of boundary points to infinity |
| 2.3: for i = 2 to |F| − 1 do |
| 2.3.1: Calculate the distance using the m-th objective: |
| D[i] += (f_m[i + 1] − f_m[i − 1])/(f_m_max − f_m_min) |
| 3: for each decision variable j do |
| 3.1: Sort the individuals in F based on decision variable j |
| 3.2: for i = 2 to |F| − 1 do |
| 3.2.1: Calculate the distance using the j-th decision variable: |
| D[i] += (x_j[i + 1] − x_j[i − 1])/(x_j_max − x_j_min) |
| 4: Return D |
Step 4: Selection operation: binary tournament. Selecting parent individuals based on Pareto rank and crowding distance. Comparing two randomly selected individuals and selecting the one with a low Pareto rank. If the ranks are the same, the one with the highest crowding distance is selected.
Step 5: Crossover and Mutation Operations. Simulated Binary Crossover (SBX) and Polynomial Mutation are widely used in genetic algorithms. The crossover and mutation parameters and control the distribution of offspring. Where the crossover formula is:
where is the first child individual, is the second child individual, is the first parent individual, is the second parent individual. is a parameter that controls the crossover operation, which is used to regulate the generation of new individuals. It is calculated based on the crossover probability and crossover parameter .
The mutation formula is:
where is the individual after the mutation, is the original individual before the mutation, and is used as the offset of the mutation.
Where the uniformly distributed random number in the interval [0, 1] < 0.5,
When ≥ 0.5,
The improved crossover and variation parameters can be dynamically adjusted to balance exploration and utilization according to the diversity of populations.
where t denotes the current number of iterations and T denotes the maximum number of iterations of the Algorithm 3.
| Algorithm 3: Genetic Operators |
| Input: parent1, parent2, p_c, p_m, eta_c, eta_m, lower_bound, upper_bound |
| Output: child1, child2 |
| 1: Initialize child1 and child2 with parent1 and parent2 |
| 2: // Simulated Binary Crossover (SBX) |
| 3: if random(0, 1) < p_c then |
| 4: for i = 1 to number_of_variables do |
| 5: if abs(parent1[i] − parent2[i]) > EPS then |
| 6: y1 = min(parent1[i], parent2[i]) |
| 7: y2 = max(parent1[i], parent2[i]) |
| 8: rand = random(0, 1) |
| 9: beta = 1.0 + (2.0 * (y1 − lower_bound[i])/(y2 − y1)) |
| 10: alpha = 2.0 − (1.0/((1.0 + beta)^(eta_c + 1.0))) |
| 11: if rand <= (1.0/alpha) then |
| 12: beta_q = (rand * alpha)^(1.0/(eta_c + 1.0)) |
| 13: else |
| 14: beta_q = (1.0/(2.0 − rand * alpha))^(1.0/(eta_c + 1.0)) |
| 15: end if |
| 16: child1[i] = 0.5 * ((y1 + y2) − beta_q * (y2 − y1)) |
| 17: child2[i] = 0.5 * ((y1 + y2) + beta_q * (y2 − y1)) |
| 18: // Ensure children are within bounds |
| 19: child1[i] = min(max(child1[i], lower_bound[i]), upper_bound[i]) |
| 20: child2[i] = min(max(child2[i], lower_bound[i]), upper_bound[i]) |
| 21: end if |
| 22: end for |
| 23: end if |
| 24: // Polynomial Mutation |
| 25: for i = 1 to number_of_variables do |
| 26: if random(0, 1) < p_m then |
| 27: delta = if random(0, 1) < 0.5 then (2.0 * random(0, 1))^(1.0/(eta_m + 1.0)) − 1.0 |
| 28: else 1.0 − (2.0 * (1.0 − random(0, 1)))^(1.0/(eta_m + 1.0)) |
| 29: child1[i] += delta * (upper_bound[i] − lower_bound[i]) |
| 30: child2[i] += delta * (upper_bound[i] − lower_bound[i]) |
| 31: // Ensure children are within bounds |
| 32: child1[i] = min(max(child1[i], lower_bound[i]), upper_bound[i]) |
| 33: child2[i] = min(max(child2[i], lower_bound[i]), upper_bound[i]) |
| 34: end if |
| 35: end for |
| 36: return child1, child2 |
4.2. Multi-Objective Optimization of Annular-Air Liquid Flow Structure
In order to verify the effectiveness of the improvement strategy proposed in this paper for the NSGA-II algorithm, the algorithm performance testing experiments could be carried out using the multi-objective test function ZDT3, which could be used to evaluate the convergence and diversity of the improved NSGA-II algorithm by comparing it with the NSGA-II algorithm. The test function is a two-objective optimization problem, which is suitable for performance testing and comparison of multi-objective optimization algorithms since its true optimal solution set is known. ZDT3 [41] test function, first objective function:
The second objective function is:
where is a function computed from the 2nd to the 30th element of the vector :
In the test function, , the decision variable .
Inverse Generation Distance (IGD) is used to evaluate the convergence and diversity of the solved Pareto approximate solution set. The calculation of IGD needs to obtain a set of solution sets uniformly sampled on the real Pareto Front (PF) in advance. The formula is defined as follows:
where is the set of real PF sampling solutions, is the set of PF approximation solutions obtained by the algorithm.
The improved NSGA-II algorithm and the normal NSGA-II algorithm are tested using the aforementioned ZDT3 test function, and the Pareto frontiers obtained are shown in Figure 5a and Figure 5b, respectively. Considering the comparison diagram of Pareto frontiers, the Pareto frontiers of the improved NSGA-II algorithm have a more uniform and wider distribution in general, while the ordinary NSGA-II algorithm has the phenomenon of stacking and overlapping of individuals in some regions and discontinuities in some regions. Intuitively, the improved NSGA-II algorithm is significantly better than the ordinary NSGA-II algorithm when considering the diversity of solution distribution.
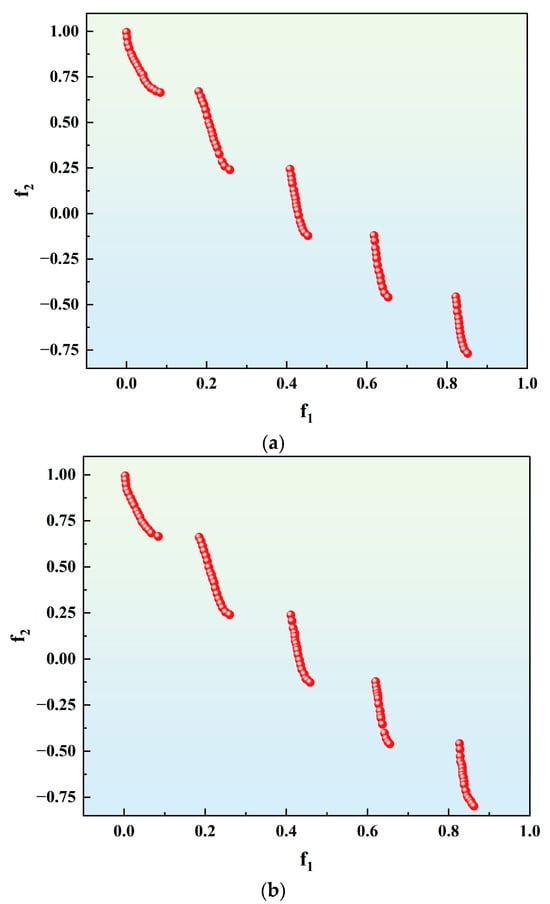
Figure 5.
Comparison of ZDT3 test function algorithms. (a) Improved NSGA-II Algorithm Pareto Frontier. (b) Ordinary NSGA-II algorithm Pareto Frontier.
To obtain more accurate experimental results, this section uses the evaluation metric IGD to quantitatively analyze the algorithms. Each algorithm is run 20 times independently for each test problem. The IGD index values obtained from each run are recorded, and the mean and standard deviation are calculated. The results are shown in Table 2. The experimental results show that the improved NSGA-II algorithm is better than the NSGA-II algorithm in terms of convergence and distribution diversity.

Table 2.
Mean and variance of IGD indexes of two algorithms.
Using 500 iterations of the improved NSGA-II algorithm program, the solution set of the Pareto optimal solutions of the five structural parameters of the hydraulic lift cordless coring tool with respect to the drilling fluid flow rate, the fluid back pressure, and the spring force pressure ratio in the parameter range, the Pareto front, is obtained (Figure 6). As shown in Figure 6, it is known from the concept of the Pareto solution set that any point of the blue color in the figure satisfies the optimal solution of the objective function. The difference lies in the different weights of the two response objectives, determined by the positions of the different points. The five structural parameters of the hydraulic lift cordless core drilling tool corresponding to the optimal solution set can be obtained by inverse normalization of the obtained points.
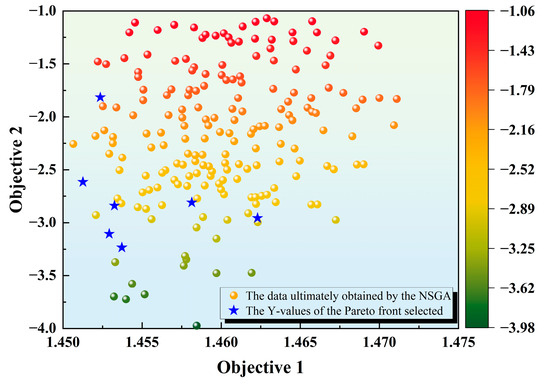
Figure 6.
The Pareto frontier graph shows the optimal two key objectives.
4.3. Numerical Simulation Verification of the Optimised Annular Fluid Flow Structure
A set of optimized structural parameters is selected, which is suitable for hard rock strata to be set in the numerical simulation model of the spearhead and spool. Tests are carried out to obtain the simulation results, as shown in Figure 7 and Figure 8. The number of spearhead inlets corresponding to the optimization target is 3, the diameter of the spearhead inlet is 16.92 mm, the number of spool outlet ports is 2, the diameter of the outlet port is 16.69 mm, the center distance between the two circles of outlet port oblong holes is 14.79 mm, the outlet flow rate is 3.286 m/s, and the ratio of fluid backpressure to spring force pressure is 1.454. It can be concluded that the flow rate of drilling fluid after optimization is 33.56% higher than that before optimization, and the force ratio is 5.825% lower.
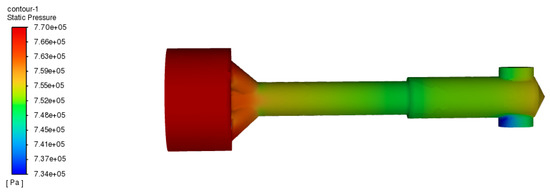
Figure 7.
Pressure cloud of optimisation result.
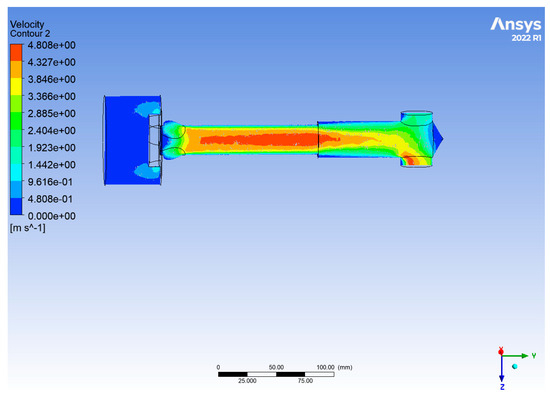
Figure 8.
Velocity vector diagram of optimization results.
5. Field Trial Study Conclusion
According to the optimized dimensions of the designed annular fluid flow structure, the processing of the φ96 cordless coring drilling tool is completed, and trial production is carried out in terms of material selection, processing, assembly, and debugging. After the assembly is completed, the valve body spool, popping card mechanism, suspension mechanism, and single-action mechanism are functionally debugged and adapted to the outer pipe assembly. The gap between the card spring seat and the inner step of the drill bit is adjusted. The gap of the φ96 drilling tool is in the range of 8–10 mm, and the physical drawing of the φ96 hydraulic lift cordless coring drilling tool is shown in Figure 9.

Figure 9.
A physical drawing of φ96 hydraulic lift cordless core drilling tool.
A total of 12 well-entry tests were carried out successively. According to the test conditions, six coring tests with φ96 drilling tools (divided into two tests) and two hydraulic salvage tests with φ96 drilling tools were carried out. In order to simulate the rock stratum coring, the test holes were fully drilled, filled with high-grade cement, and hardened three times. The test was carried out with an XY-5 vertical shaft core drilling rig, and a 250 triplex single-acting horizontal mud pump was selected. The drilling fluid consisted of clean water due to the wall protection of the borehole pipe and cement hardening. The combination of drilling tools was φ96 diamond drill bit + φ96 cordless core drilling tool + adapter joint + φ89 rope drill pipe + active drill pipe. The test drilling pressure was 14–18 KN, the rotating speed was 260 rpm, the pumping volume was 145 L/min, and the pumping pressure was 0.3–0.5 Mpa. A complete coring was achieved. The entire test system, as shown in Figure 10a, enabled the switching between normal and reverse circulation through ball valves 1# and 2#. As shown in Figure 10c, the coring test was conducted for the φ96 drilling tool.
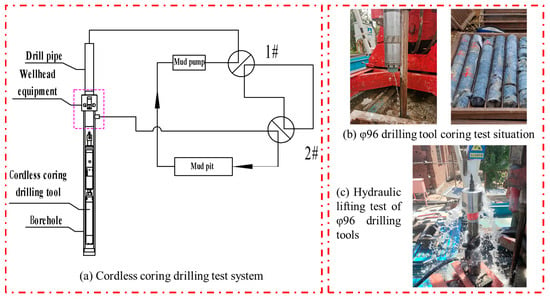
Figure 10.
Field tests for coring and hydraulic lifting using the cordless coring drilling tool.
The hydraulic salvage test of the φ96 drilling tool was carried out two times, mainly to verify the feasibility of hydraulic lifting and salvage under the condition of a small annular space gap in the stratum of slight leakage (small leakage or ordinary seepage). Due to the limited test conditions, only the hydraulic salvage test was carried out for the vertical holes. The visualization bench test was carried out for the large inclined holes or the horizontal holes at a later time. The hydraulic salvage test and the core drilling test used the same mud pump with a pump volume of 145 L/min and a pump pressure of 0.1–0.2 MPa when pushing the salvage in reverse circulation. Due to the shallow depth of the well, which was only less than 20 m, the assembly in the drilling tool was pushed to the hole in 40–50 s. The hydraulic lifting test of the φ96 drilling tool on site is shown in Figure 10c.
6. Conclusions and Discussion
In this research, a new type of hydraulic lifting cordless core drilling tool was designed, and a numerical simulation model of the liquid flow in the annulus of the spearhead and spool of the cordless core drilling tool was established. Moreover, an orthogonal test was carried out, and according to the results of the orthogonal test, a numerical prediction model of the annulus of the spool based on the BP neural network was established. The NSGA-II algorithm was optimized, and multi-objective optimization was carried out for the annulus of the cordless core drilling tool. According to the parameters of the optimized structure, the φ96 cordless core drilling tool was developed, and finally, the simulation and field test were carried out. Optimized structural parameters and the φ96 cordless coring drilling tool were developed. Finally, simulation and field tests were carried out. The following conclusions could be drawn:
(1) According to the established numerical simulation model of spearhead and spool, different parameters such as the number of spearhead inlets, the diameter of spearhead inlets, the number of spool outlets, the diameter of spool outlets, and the center distance between the two circles of spool outlets could affect the ratio of fluid back pressure to spring force pressure and the flow rate of the drilling fluid. The numerical prediction model of the spool’s annular fluid field with a BP neural network was established, which demonstrates the effect on the flow rate of the drilling fluid when the parameters of the structure of the spearhead and spool were different. The numerical prediction model of the BP neural network of the spool annulus flow field was established to predict the drilling fluid flow rate and spool back pressure ratio at different parameters of the spearhead and spool annulus flow structure. The average correlation coefficient of the prediction was R = 0.93, which provided a basis for the design of hydraulic lift cordless coring drilling tools for drilling in different formations.
(2) The NSGA-II algorithm was optimized. The Pareto front of the improved NSGA-II algorithm has a more uniform and wider distribution in general. The mean and variance of the IGD indexes have been reduced by 46.4% and 83.2%, respectively, compared to that of the ordinary NSGA-II algorithm [42,43]. Based on the multi-objective optimization results, the solution sets of the Pareto optimal solutions for the five structural parameters of the hydraulic lift cordless core drilling tool with respect to the drilling fluid flow rate, fluid backpressure, and spring force pressure ratio in the parameter range were obtained. The results of the multi-objective optimization were simulated and verified. It was concluded that the drilling fluid flow rate increased by 33.56% and the force ratio was reduced by 5.825% compared to before the optimization.
(3) According to the design and multi-objective optimization of the annular fluid flow structure of the cordless coring tool, the machining trial production of the φ96 cordless coring tool was completed. The coring test of the φ96 drilling tool was conducted six times (divided into two tests) to achieve complete coring. The hydraulic salvage test of the φ96 drilling tool was conducted two times, and the assembly of the drilling tool was pushed to the hole in 40–50 s at the 20 m test well depth.
The designed and developed hydraulic lifting cordless coring tool can achieve effective coring and hydraulic lifting after the field test, which can improve the coring efficiency and quality. At the same time, it can reduce the operation cost and energy consumption, providing a new technical solution for drilling operations under complex geological conditions.
Author Contributions
Conceptualization, Z.Z.; methodology, F.H., Y.Z. and H.W.; software, F.H. and C.L.; validation, Y.S.; formal analysis, M.J.; investigation, G.L., Y.S. and M.J.; data curation, Y.Z. and G.L.; writing—original draft preparation, Z.Z. and C.L.; writing—review and editing, H.W.; project administration, Z.Z. and H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the open project of the Key Laboratory of Drilling and Mining Technology for Complex Conditions of the Ministry of Natural Resources and Jinshi Drilling (Tangshan) Company Limited (FZJS230203); the National Key Research and Development Program of China (2023YFC2813102; 2023YFC3007003) and Geological Survey Project of China Geological Survey (DD20242850).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
Authors thanks to Jiuquan Wang and Jinshi Drilltech Co., Ltd. for the project funding and the provision of the test site.
Conflicts of Interest
Author Fan Huang was employed by the company Changjiang Geotechnical Engineering Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare that this study received funding from Jinshi Drilling (Tangshan) Company Limited. The funder had the following involvement with the study: methodology.
Appendix A

Table A1.
Orthogonal test table and simulation results.
Table A1.
Orthogonal test table and simulation results.
| Serial Number | Number of Water Inlets (pcs) | Inlet Diameter (mm) | Number of Water Outlets (pcs) | Outlet Diameter (mm) | Distance between the Centres of the Two Circles of the Outlet (mm) | Ratio of Fluid Back Pressure to Spring Force Pressure | Drilling Fluid Flow Rate (m/s) |
|---|---|---|---|---|---|---|---|
| 1 | 3.00 | 18.50 | 3.00 | 18.00 | 10.00 | 1.461 | 2.14 |
| 2 | 4.00 | 19.50 | 3.00 | 16.50 | 16.00 | 1.463 | 2.215 |
| 3 | 3.00 | 19.50 | 3.00 | 17.00 | 14.00 | 1.463 | 2.205 |
| 4 | 3.00 | 16.50 | 3.00 | 20.00 | 12.00 | 1.459 | 1.96 |
| 5 | 3.00 | 19.50 | 2.00 | 20.00 | 10.00 | 1.461 | 2.59 |
| 6 | 3.00 | 16.00 | 2.00 | 17.50 | 14.00 | 1.449 | 2.775 |
| 7 | 3.00 | 20.00 | 2.00 | 20.00 | 14.00 | 1.465 | 2.48 |
| 8 | 3.00 | 18.00 | 3.00 | 17.50 | 14.00 | 1.461 | 2.19 |
| 9 | 4.00 | 16.50 | 2.00 | 18.00 | 10.00 | 1.46 | 3.155 |
| 10 | 4.00 | 20.00 | 2.00 | 19.00 | 12.00 | 1.455 | 2.91 |
| 11 | 3.00 | 17.00 | 2.00 | 16.50 | 10.00 | 1.4386 | 3.295 |
| 12 | 3.00 | 17.50 | 2.00 | 16.50 | 10.00 | 1.451 | 3.075 |
| 13 | 3.00 | 19.00 | 3.00 | 16.50 | 12.00 | 1.463 | 2.21 |
| 14 | 3.00 | 20.00 | 2.00 | 18.50 | 10.00 | 1.4589 | 2.685 |
| 15 | 3.00 | 20.00 | 2.00 | 18.00 | 12.00 | 1.461 | 2.77 |
| 16 | 3.00 | 16.50 | 2.00 | 17.00 | 16.00 | 1.455 | 2.66 |
| 17 | 3.00 | 18.50 | 2.00 | 19.50 | 14.00 | 1.457 | 2.12 |
| 18 | 4.00 | 18.00 | 3.00 | 18.00 | 18.00 | 1.467 | 1.45 |
| 19 | 3.00 | 18.00 | 3.00 | 18.50 | 10.00 | 1.459 | 2.185 |
| 20 | 3.00 | 16.00 | 3.00 | 19.00 | 18.00 | 1.455 | 1.209 |
| 21 | 3.00 | 19.00 | 2.00 | 19.50 | 14.00 | 1.4589 | 2.27 |
| 22 | 3.00 | 19.00 | 2.00 | 19.00 | 10.00 | 1.457 | 2.76 |
| 23 | 3.00 | 17.00 | 2.00 | 18.50 | 12.00 | 1.451 | 2.64 |
| 24 | 4.00 | 18.50 | 2.00 | 19.00 | 16.00 | 1.463 | 2.695 |
| 25 | 3.00 | 18.00 | 2.00 | 16.00 | 16.00 | 1.453 | 3.005 |
| 26 | 4.00 | 18.50 | 2.00 | 16.00 | 14.00 | 1.45 | 2.89 |
| 27 | 4.00 | 17.50 | 2.00 | 20.00 | 10.00 | 1.464 | 3.175 |
| 28 | 3.00 | 19.50 | 2.00 | 17.50 | 10.00 | 1.4589 | 3.351 |
| 29 | 3.00 | 19.50 | 3.00 | 16.00 | 12.00 | 1.459 | 2.95 |
| 30 | 3.00 | 17.00 | 3.00 | 20.00 | 16.00 | 1.459 | 1.48 |
| 31 | 3.00 | 18.50 | 2.00 | 20.00 | 12.00 | 1.4589 | 2.81 |
| 32 | 3.00 | 16.00 | 2.00 | 16.50 | 20.00 | 1.449 | 3.14 |
| 33 | 3.00 | 16.00 | 2.00 | 16.00 | 10.00 | 1.4376 | 3.16 |
| 34 | 3.00 | 17.50 | 3.00 | 17.50 | 16.00 | 1.461 | 1.52 |
| 35 | 4.00 | 16.50 | 2.00 | 16.50 | 12.00 | 1.459 | 2.905 |
| 36 | 4.00 | 16.00 | 2.00 | 18.50 | 16.00 | 1.461 | 2.41 |
| 37 | 3.00 | 16.50 | 3.00 | 19.00 | 10.00 | 1.457 | 1.725 |
| 38 | 3.00 | 20.00 | 2.00 | 19.50 | 16.00 | 1.4628 | 2.025 |
| 39 | 3.00 | 16.00 | 2.00 | 18.00 | 12.00 | 1.4473 | 2.77 |
| 40 | 4.00 | 16.00 | 2.00 | 17.00 | 12.00 | 1.459 | 2.93 |
| 41 | 4.00 | 19.00 | 2.00 | 18.50 | 14.00 | 1.469 | 2.89 |
| 42 | 4.00 | 16.00 | 3.00 | 20.00 | 14.00 | 1.463 | 1.47 |
| 43 | 3.00 | 17.00 | 3.00 | 19.50 | 12.00 | 1.457 | 1.72 |
| 44 | 4.00 | 17.00 | 2.00 | 16.00 | 18.00 | 1.456 | 3.125 |
| 45 | 3.00 | 16.50 | 2.00 | 18.50 | 14.00 | 1.4512 | 2.43 |
| 46 | 3.00 | 20.00 | 3.00 | 17.00 | 18.00 | 1.461 | 1.96 |
| 47 | 4.00 | 17.00 | 3.00 | 19.00 | 14.00 | 1.461 | 1.69 |
| 48 | 4.00 | 18.00 | 2.00 | 16.50 | 14.00 | 1.463 | 2.652 |
| 49 | 4.00 | 19.50 | 2.00 | 18.00 | 14.00 | 1.465 | 2.93 |
| 50 | 3.00 | 17.00 | 2.00 | 18.00 | 20.00 | 1.449 | 2.5915 |
| 51 | 3.00 | 17.50 | 3.00 | 18.00 | 14.00 | 1.455 | 1.94 |
| 52 | 3.00 | 19.00 | 3.00 | 16.00 | 20.00 | 1.461 | 1.452 |
| 53 | 4.00 | 17.50 | 2.00 | 17.00 | 20.00 | 1.465 | 2.685 |
| 54 | 3.00 | 18.00 | 2.00 | 19.00 | 12.00 | 1.4589 | 2.605 |
| 55 | 4.00 | 19.00 | 2.00 | 20.00 | 18.00 | 1.465 | 2.64 |
| 56 | 4.00 | 19.00 | 3.00 | 17.00 | 10.00 | 1.465 | 2.28 |
| 57 | 3.00 | 19.00 | 2.00 | 18.00 | 16.00 | 1.4589 | 2.85 |
| 58 | 3.00 | 17.50 | 2.00 | 19.50 | 18.00 | 1.461 | 2.37 |
| 59 | 3.00 | 18.50 | 2.00 | 16.50 | 18.00 | 1.4608 | 2.86 |
| 60 | 4.00 | 18.50 | 3.00 | 17.50 | 12.00 | 1.465 | 1.95 |
| 61 | 3.00 | 20.00 | 3.00 | 16.50 | 14.00 | 1.459 | 1.9 |
| 62 | 3.00 | 18.00 | 2.00 | 17.00 | 12.00 | 1.457 | 2.85 |
| 63 | 4.00 | 20.00 | 3.00 | 16.00 | 10.00 | 1.461 | 2.57 |
| 64 | 4.00 | 17.50 | 3.00 | 18.50 | 12.00 | 1.465 | 1.96 |
| 65 | 3.00 | 17.00 | 2.00 | 17.00 | 14.00 | 1.4551 | 2.705 |
| 66 | 3.00 | 16.50 | 2.00 | 16.00 | 14.00 | 1.4531 | 3.115 |
| 67 | 3.00 | 16.50 | 2.00 | 17.50 | 18.00 | 1.4589 | 2.625 |
| 68 | 3.00 | 18.50 | 2.00 | 17.00 | 10.00 | 1.4589 | 3.135 |
| 69 | 3.00 | 17.50 | 2.00 | 19.00 | 14.00 | 1.4551 | 2.625 |
| 70 | 4.00 | 17.00 | 2.00 | 17.50 | 10.00 | 1.465 | 2.885 |
| 71 | 3.00 | 18.00 | 2.00 | 20.00 | 20.00 | 1.4551 | 1.6735 |
| 72 | 3.00 | 16.00 | 3.00 | 19.50 | 10.00 | 1.451 | 2.18 |
| 73 | 3.00 | 19.50 | 2.00 | 19.00 | 20.00 | 1.4628 | 2.15 |
| 74 | 3.00 | 19.00 | 2.00 | 17.50 | 12.00 | 1.4551 | 3.15 |
| 75 | 4.00 | 19.50 | 2.00 | 19.50 | 12.00 | 1.467 | 2.91 |
| 76 | 4.00 | 18.00 | 2.00 | 19.50 | 10.00 | 1.461 | 2.66 |
| 77 | 3.00 | 19.50 | 2.00 | 18.50 | 18.00 | 1.4608 | 2.3995 |
| 78 | 3.00 | 18.50 | 3.00 | 18.50 | 20.00 | 1.4599 | 1.425 |
| 79 | 4.00 | 20.00 | 2.00 | 17.50 | 20.00 | 1.4599 | 2.65 |
| 80 | 4.00 | 16.50 | 3.00 | 19.50 | 20.00 | 1.465 | 1.241 |
| 81 | 3.00 | 17.50 | 2.00 | 16.00 | 12.00 | 1.4512 | 3.315 |
References
- Linnenberg, C.; Reimeir, B.; Eberle, R.; Weidner, R. The Influence of Circular Physical Human–Machine Interfaces of Three Shoulder Exoskeletons on Tissue Oxygenation. Appl. Sci. 2023, 13, 10534. [Google Scholar] [CrossRef]
- Mena-Álvarez, J.; Ruiz-Barrio, M.; Quispe-López, N.; de Pedro-Muñoz, A.; Rico-Romano, C. Comparative Analysis of Temperature Variation with Three Continuous Wave Obturation Systems in Endodontics: An In Vitro Study. Appl. Sci. 2022, 12, 6229. [Google Scholar] [CrossRef]
- Adeyemo, A.T.; Olaleye, B.M.; Saliu, M.A. Correlating wave velocities of some basement complex rock types with their in situ and laboratory determined penetration rates in North Central Nigeria. J. Emerg. Trends Eng. Appl. Sci. 2018, 9, 271–274. [Google Scholar]
- He, W.; Zhang, H. Application of rope core drilling technology in the construction of horizontal holes of pit drilling in Yunnan Hongniu Copper Mine. World Non-Ferr. Met. 2021, 5, 174–175. [Google Scholar]
- Li, B.; Zou, R.; Guo, C. Application of rope coring technology in overburden drilling. Coalf. Geol. Explor. 2019, 47, 217–222. [Google Scholar]
- Wang, S. Application of rope coring technology in geotechnical drilling construction. World Non-Ferr. Met. 2019, 5, 226–228. [Google Scholar]
- Wen, Y.; Zhang, G.; Xie, H.; Gao, M.; Zhang, X.; Wang, Y.; Li, C. Design and dynamic analysis of the wire-line coring robot for deep lunar rocks. Appl. Sci. 2023, 13, 1722. [Google Scholar] [CrossRef]
- Wang, L. Application of rope coring technology in parametric well exploration for coalbed methane in Liupanshui. Inn. Mong. Petrochem. 2021, 47, 55–58. [Google Scholar]
- Li, Z. Research and Application of Deep Hole Rope Coring Drilling Process in Water Sensitive Complex Formation. Geol. Equip. 2024, 25, 43–48. [Google Scholar]
- Pan, X. Application of rope core drilling technology in Persimmon Flower Tree Mine, Guizhou. Energy Environ. 2023, 4, 50–52. [Google Scholar]
- Chen, X.; Jin, E. Study on the application of rope core drilling technology in the slope survey of copper, silver and molybdenum mine. Constr. Technol. Dev. 2023, 50, 4–6. [Google Scholar]
- Roman, M.D.; Fleacă, S.R.; Mohor, C.I.; Bacila, C.; Bratu, D.; Teodoru, A.; Bocea, B.; Boicean, A.G. Extraction of Broken Interlocking Tibial Nails: A Review of Surgical Techniques and Practical Management. Appl. Sci. 2023, 13, 1645. [Google Scholar] [CrossRef]
- Ma, Z. Structure Design of Reverse Circulation with Wire-Line CoringTool and Numerical Simulation Study on Flow Field of the Bottom of the Hole. Master’s Thesis, Jilin University, Changchun, China, 2014. [Google Scholar]
- Zhao, J. Numerical simulation study of downhole cyclone wellbore purification tool. M.S. 2022. [Google Scholar]
- Shi, Y.; Li, C. Flow field simulation of a hydrogeological exploration drill bit for switching coring drilling and non-coring drilling. Appl. Sci. 2023, 14, 4893. [Google Scholar] [CrossRef]
- Wang, J.; Qian, D.; Sun, Y.; Peng, F. Design of diamond bits water passage system and simulation of bottom hole fluid are applied to seafloor drill. J. Mar. Sci. Eng. 2021, 9, 1100. [Google Scholar] [CrossRef]
- Wang, J.; Chen, C.; Qian, D.; Peng, F.; Yu, M.; Sun, Y.; Peng, D. Design and flow field analysis of impregnated diamond bit for seafloor drill in soft-hard interlaced strata. J. Eng. Appl. Sci. 2022, 69, 84. [Google Scholar] [CrossRef]
- Wang, J.; Qian, D.; Sun, Y.; Peng, F. Surface-set Diamond Bit Design for Deep-Sea Operating Environment of Seafloor Drill and Hole-Bottom Flow Field Analysis. Int. J. Fluid Mach. Syst. 2022, 15, 158–168. [Google Scholar] [CrossRef]
- Cao, P.; Cui, G.; Qi, B.; Yao, S.; Zheng, Z.; Bo, K. Investigation on the cuttings carrying capacity of a novel retractable drill bit used in casing while drilling with air reverse circulation. J. Pet. Sci. Eng. 2022, 219, 111079. [Google Scholar] [CrossRef]
- You, Z.; Chen, L.; Li, C.; Liu, G.; Ye, B.; Shi, X. Cutting Migration and Core Disturbance Caused by the Hydraulic Structure of Pressure-and Gas-Maintaining Coring Bits. Geofluids 2022, 2022, 9728046. [Google Scholar] [CrossRef]
- Li, Q.; Lei, Y.; Sun, H.; Dai, M.; Chen, K. Study on the flow field and chip removal performance of laser-mechanical drilling bit at the bottom of well based on EDEM-Fluent coupling. J. Eng. Des. 2023, 30, 521–530. [Google Scholar]
- Wang, X.; Liao, Z.; Wang, Y.; Ma, C.; Du, M. A Fluent-based study of wellbore annulus chip-carrying pattern. Energy Environ. Prot. 2017, 39, 217–222. [Google Scholar]
- Xi, B. Experimental Study on The Characteristics of Water Hammer on Annular Space in Petroleum Engineering. Ph.D. Thesis, Northeast Petroleum University, Daqing, China, 2015. [Google Scholar]
- Chen, J. Study on the Application of Diamond Rope Core Drilling Process Technology in Jiulongchuan Well Field. Energy Environ. 2013, 5, 44–45. [Google Scholar]
- Liu, G. Diamond drilling with rope core drilling. Prospect. Eng. 1982, 3, 62–64. [Google Scholar]
- Jia, C. Coalbed methane exploration and coring technology in Baiyangling coal mine, Xiyang, Shanxi. Prospect. Eng. (Geotech. Drill. Excav. Eng.) 2009, 36, 25–28. [Google Scholar]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Kumar, T.V.; Dilip, K. Multi-criteria website optimisation using NSGA-II. Int. J. Bus. Inf. Syst. 2016, 21, 418–438. [Google Scholar] [CrossRef]
- Elarbi, M.; Bechikh, S.; Gupta, A.; Said, L.B.; Ong, Y. A new decomposition-based NSGA-II for many-objective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1191–1210. [Google Scholar] [CrossRef]
- Pawar, P.J.; Rai-Kalal, D.P. Multi-objective optimisation of grinding process parameters using NSGA-II. Int. J. Metaheuristics 2013, 2, 123–140. [Google Scholar] [CrossRef]
- Wang, L.; Wang, T.; Luo, Y. Improved non-dominated sorting genetic algorithm (NSGA)-II in multi-objective optimization studies of wind turbine blades. Appl. Math. Mech. 2011, 32, 739–748. [Google Scholar] [CrossRef]
- Hamdani, T.M.; Won, J.; Alimi, A.M.; Karray, F. Multi-objective feature selection with NSGA-II, Adaptive and Natural Computing Algorithms. In 8th International Conference, ICANNGA 2007, Warsaw, Poland, 11–14 April 2007, Proceedings, Part I 8; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Li, Z.; Liu, J.; Jin, H.; Wang, J.; Liu, L. A multi-objective optimisation method for coking coal allocation with improved NSGA-II. Manuf. Autom. 2024, 46, 103–108. [Google Scholar]
- Wang, X. Research on multi-objective optimisation of machinery green manufacturing system based on improved NSGA-II algorithm. Agric. Mach. Use Maint. 2023, 9, 72–75. [Google Scholar]
- Li, J.; Cheng, J.; Shi, J.; Huang, F. Brief introduction of back propagation (BP) neural network algorithm and its improvement. In Advances in Computer Science and Information Engineering; Springer: Berlin/Heidelberg, Germany, 2012; Volume 2. [Google Scholar]
- Jin, W.; Li, Z.J.; Wei, L.S.; Zhen, H. The improvements of BP neural network learning algorithm. In WCC 2000-ICSP 2000. 2000 5th International Conference on Signal Processing Proceedings. 16th World Computer Congress 2000; IEEE: New York, NY, USA, 2000. [Google Scholar]
- Zhao, Y. Research and application on BP neural network algorithm. In Proceedings of the 2015 International Industrial Informatics and Computer Engineering Conference, Xi’an, China, 10–11 January 2015; Atlantis Press: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Xie, R.; Wang, X.; Li, Y.; Zhao, K. Research and application on improved BP neural network algorithm. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications, Taichung, Taiwan, 15–17 June 2010; IEEE: New York, NY, USA, 2010. [Google Scholar]
- Li, X.; Qi, B.; Wang, L. A new improved BP neural network algorithm. In Proceedings of the 2009 Second International Conference on Intelligent Computation Technology and Automation, Zhangjiajie, China, 10–11 October 2009; IEEE: New York, NY, USA, 2009. [Google Scholar]
- Michalak, K. Improving the NSGA-II performance with an external population. In Intelligent Data Engineering and Automated Learning–IDEAL 2015: 16th International Conference, Wroclaw, Poland, 14–16 October 2015, Proceedings 16; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Khodadadi, N.; Abualigah, L.; Al-Tashi, Q.; Mirjalili, S. Multi-objective chaos game optimization. Neural Comput. Appl. 2023, 35, 14973–15004. [Google Scholar] [CrossRef]
- Pan, J.; Zhang, A.; Chu, S.; Zhao, J.; Snášel, V. An activity level based surrogate-assisted evolutionary algorithm for many-objective optimization. Appl. Soft. Comput. 2024, 164, 111967. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).