Abstract
Cross-domain cooperative task allocation is a complex and challenging issue in the field of multi-agent task allocation that requires urgent attention. This paper proposes a task allocation method based on the multi-strategy improved dung beetle optimization (MSIDBO) algorithm, aiming to solve the problem of fully distributed multi-agent cross-domain cooperative task allocation. This method integrates two key objective functions: target allocation and control allocation. We propose a target allocation model based on the optimal comprehensive efficiency, cluster load balancing, and economic benefit maximization, and a control allocation model leveraging the radar detection ability and control data link connectivity. To address the limitations of the original dung beetle optimization algorithm in solving such problems, four revolutionary strategies are introduced to improve its performance. The simulation results demonstrate that our proposed task allocation algorithm significantly improves the cross-domain collaboration efficiency and meets the real-time requirements for multi-agent task allocation on various scales. Specifically, our optimization performance was, on average, 32.5% higher compared to classical algorithms like the particle swarm optimization algorithm and the dung beetle optimization algorithm and its improved forms. Overall, our proposed scheme enhances system effectiveness and robustness while providing an innovative and practical solution for complex task allocation problems.
1. Introduction
With the development of intelligent collaboration technology, multi-agent systems with the characteristics of low cost and replaceability are being increasingly used for complex task allocation [1]. The problem of task allocation is fundamental in the field of military operation research. Its primary purpose is to provide an optimal or quasi-optimal cooperative allocation scheme for multi-agents. This is achieved by fully understanding the intention of decision makers, so as to assist them in formulating action plans and maximizing the overall efficiency.
Traditional multi-agent task allocation is mostly based on single-space domains such as land, sea, and air. The increasing adoption of cross-domain cooperation and the integration of new technologies to leverage their complementary advantages facilitate omnidirectional interactions. Thus, there is a need to address the challenges associated with large-scale cross-domain cooperative tasking, especially in dynamic and uncertain environments. This has become a key research direction in the field of task allocation [2,3]. Cross-domain cooperative task allocation involves transferring the control of the load agent between multi-dimensional sea and air platforms through the handover and relay of the control of the surface agent and the air relay control agent in the cluster to the target beyond the line of sight, on the basis of sharing situation data. By comprehensively utilizing the internal resources of the cluster, this approach can compensate for the shortcomings of single-platform sensors in terms of detection, signal control distance, and accuracy. It maximizes the range capability and concealment of the load agent, thereby ensuring the safety of the delivery platform. In an actual task scenario, the number of targets is large, the density is large, the timeliness is strong, the load resources and the delivery platform resources are limited, and the command and control constraints are very complex; therefore, an assessment of the real-time performance of task allocation is greatly required [4,5]. At present, the multi-agent system of decision making and control is developing towards network distribution. Various devices can serve as nodes within the information fusion center, which features a distributed network structure without a central node. This configuration enhances the system’s decision-making capabilities and addresses the limitations of centralized task allocation algorithms, such as high communication demands, elevated computational complexity, poor fault tolerance, and limited system scalability. This decision mode requires that the decision control center receives support from each agent system to fully mobilize all the resources, comprehensively analyze the global situation, hierarchically develop the global task plan, and realize the maximization of global revenue. Simultaneously, the decision control center must inject the global initial optimal plan into each agent before it makes autonomous decisions. This process guides the agent in adjusting the task plan according to its own characteristics and completing autonomous actions [6]. In this research, we examined multi-agent task allocation methods under the background of distributed cross-domain cooperation, combined with the latest task allocation ideas.
The existing research on task allocation methods has mainly focused on optimizing the mathematical model of task allocation and improving the solving algorithm of the model [7].
In order to ensure the achievement of goals, the traditional mathematical model of task allocation often considers task efficiency to be the primary index of goal allocation, and transforms the constraint function by constructing a penalty function. This makes the solution space of the model extremely complex, which can easily lead to allocation failure or oversaturation due to an unreasonable threshold setting for the efficiency index, leading to a waste of resources [8]. Peng et al. [9] established the target optimization mathematical model according to the weighted sum of UAV distance fuel consumption and the latest task completion time. The allocation results fully considered the actual work of the UAV carrier and the completion advantage of the attack, reconnaissance, warnings, and other tasks, but they did not start from the perspective of the carrier’s actual task goal; therefore, the model did not achieve optimal comprehensive efficiency for the task. Zhang et al. [10] established a fire allocation model based on the minimum waste of fire, which took into account the target damage requirements and the oversaturation problem of fire allocation. Their model enhanced the rationality of the allocation. Tan et al. [11] deeply studied the target task allocation optimization model under the background of specified tasks, but they only considered the allocation of a single task or a single target, and did not consider the workload-balancing ability of heterogeneous multi-load and multi-target platforms in collaborative action from the perspective of the comprehensive performance indicators of the actual surface platform cluster. The above scholars have established models based on the requirements of a single target under the background of a specific task, but the problem of the unified allocation of the multi-task targets involved in cross-domain collaboration has not been solved so far.
After decades of development, multiple research branches on solving algorithms for task allocation models have been formed and applied in various fields of engineering technology. Since Manne’s work [12] in ballistic missile defense strategy optimization research in 1958, the proposed missile allocation problem (MAP) and the weapon target allocation (WTA) problem have been widely considered typical NP-complete combinatorial optimization problems [13]. After decades of development, the research [14] on the WTA problem can be divided into static WTAs [15,16] and dynamic WTAs [17], and into centralized WTAs and distributed WTAs [18,19] in terms of decision-making power. In terms of modeling methods, they can be divided into traditional algorithms, such as integer programming, dynamic programming [20], and graph theory, and innovative algorithms, such as game theory [21] and multi-agent theory. In terms of optimization methods, they can be divided into traditional exact algorithms, heuristic algorithms, and hybrid intelligent algorithms that combine multiple intelligent algorithms. The existing task allocation algorithms are summarized in Figure 1 below. The traditional algorithms have high accuracy but experience difficulty overcoming the real-time requirements of large-scale task allocation problems. Intelligent algorithms such as genetic algorithms and heuristic algorithms have been widely used to simplify the problem scale and the time complexity of solutions at the cost of a certain level of accuracy. At present, various intelligent optimization algorithms, such as the particle swarm optimization algorithm [22], the ant colony algorithm [23], and the chimpanzee algorithm [24], have difficulty solving the intractable problem of cross-domain collaborative task allocation with complex constraints, a huge scale, and high timeliness requirements. The dung beetle optimizer (DBO) is a new metaheuristic swarm intelligence search algorithm proposed by Xue et al. [25] that imitates the survival behaviors of dung beetles, such as ball bowling, dancing, foraging, stealing, and reproduction, as its basic principle. It has attracted attention due to its strong evolutionary ability, fast convergence speed, and strong optimization ability [26,27]. It has been successfully applied to path planning [28], underwater wireless sensor network (UWSN) coverage [29], and feature selection [30]. In order to better solve the problems [31] of integer programming in the cross-domain collaborative task allocation model, which easily falls into the local optimum and has many constraints, this research proposes a multi-strategy improved dung beetle optimization algorithm, MSIDBO, that integrates multiple strategies.
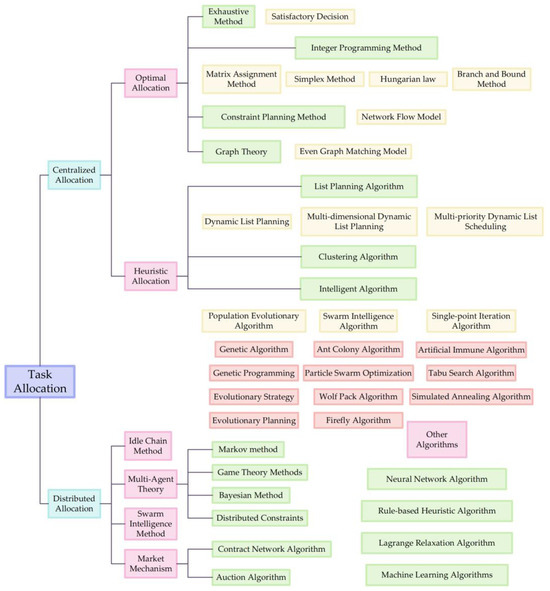
Figure 1.
Tree diagram of existing algorithms for the WTA problem.
In the realm of cross-domain cooperative task allocation, the challenges of mathematical modeling and algorithm solving persist. This research aims to address these challenges by developing a distributed dung beetle population inspired by the concept of massively parallel processing. By employing a bottom-up analysis strategy within multi-agent theory, this study innovatively optimizes the decision-coding model to ensure that each decision matrix satisfies the constraints. The core contribution of this paper lies in the presentation of a task allocation model tailored for large-scale complex systems, which seamlessly integrates multi-agent target allocation with the control allocation of the load agent. Furthermore, the improved multi-strategy dung beetle optimization algorithm, MSIDBO, is also proposed.
The enhanced dung beetle optimization algorithm, incorporating multi-strategy fusion, demonstrates a rapid ability to escape local optima and significantly accelerates optimization convergence. Additionally, it guarantees high solution accuracy and effectively addresses cross-domain collaborative task allocation challenges. The improved algorithm can obtain the solution for tasks on various scales stably and efficiently, which has broad application prospects. The benchmarks used in this study include traditional optimization algorithms and their latest enhanced versions, as detailed in Table 1.

Table 1.
Benchmarking algorithms.
2. Cross-Domain Collaborative Task Allocation Model
Traditional models, constrained by single domains, struggle to address the multifaceted challenges of cross-domain collaboration. The advent of cross-domain cooperation necessitates novel models that integrate diverse platforms and dynamically adapt to shifting battlefield dynamics. We introduce a comprehensive cross-domain collaborative task allocation model, encompassing two pillars: target allocation and control allocation. It ensures precise matching of load agents to targets and seamless transfer of control between platforms.
2.1. Problem Description
The cross-domain cooperative task introduces the air cooperative control platform as the child node of task allocation. Consequently, it was necessary to consider not only the control and guidance function for the middle and late stages of the load, but also the relay control process and the control channel allocation problem. According to the functional process, this task was divided into two parts: target allocation and control allocation. The target allocation commences at the sensor boot time of the surface platform and is concluded in the data center of the surface platform, in accordance with the battlefield fusion situation. The control allocation commences at the moment that the surface platform launches the load agent in accordance with the target allocation result. The surface platform is responsible for guiding the early and middle stages of the flight process, and then the control allocation is completed according to the detection and data link advantages of the air platform. In the final phase of the flight, the control is transferred to the air platform.
It is assumed that the multi-agent cross-domain cooperative task allocation includes four basic types of agent units: a surface agents, forming the set ; b air relay control agents, forming the set ; c target agents, forming the set ; and d load agents, forming the set . Among them, the nth surface agent is responsible for the launch and pre-middle-stage guidance tasks of the ith load agent , and the kth air relay control agent is responsible for the end-stage guidance task of the ith load agent . The two agents cooperate with each other and connect in an orderly manner. From the functional process, the cross-domain collaborative task can be divided into two stages: target allocation and control allocation. The former mainly solves the target allocation problem of the load agent to the target platform , and the latter solves the control allocation problem of the relay control platform to the load agent . In summary, in the multi-agent cross-domain collaborative task, the key is to obtain the optimal or quasi-optimal task allocation scheme of the target allocation matrix and the control allocation matrix , where and are decision variables; a value of 1 means that the load agent is assigned to the target agent or the air relay control agent , and a value of 0 means that the load agent is not assigned.
In order to reduce the time complexity of the task allocation solution and meet the actual task requirements, the following assumptions were made:
- There was no redistribution problem in the load agent, and the matching relationship between the load and the target was no longer changed by the control allocation after the target allocation was completed. It was assumed that the target allocation and the control allocation were independent of each other, and the optimal solution of the target allocation was the premise in the control allocation;
- The number of load agents participating in the allocation exceeded the number of target agents or air relay control agents;
- Each load agent was independent of the others, and the corresponding damage probability was calculated in advance without considering its type selection problem;
- The air relay control agent had a unique type. In order to ensure the safety and reliability of the communication between it and the load agent, an attitude change was not allowed, and the flight was always level. In the calculation of the relay control agent’s detection ability, the detection performance of the radar transmitter, receiver, and antenna was the same and was only affected by the relative position of the sensor and the detection target;
- Each load agent could only be delivered by a single surface agent, so the target allocation problem was equivalent to the fire channel allocation problem of multiple surface agents to multiple target agents ;
- The possible time for the control handover of the load agent in the context of cross-domain cooperation was as follows: (a) When the load agent reached the set control handover distance, the air relay control agent obtained control of the load agent. (b) If the surface agent was seriously threatened or the control signal was disturbed, it was forced to transfer control to the air relay control agent. (c) When a new target appeared or according to a real-time situation judgment, control was handed over to the air relay control agent.
2.2. Encoder–Decoder Scheme
Cross-domain collaborative task allocation represents a typical NP-complete combinatorial optimization problem characterized by a discrete solution space with variable intervals. The presence of numerous constraints within the model significantly hampers search efficiency and limits the applicability of the initial population. If the penalty function method is used to judge all of the constraints, and the constraint judgment factor is set to make the fitness function diverge when the constraints are not satisfied, the search efficiency will be greatly affected [37,38]. To adapt to the constraints of metaheuristic intelligent algorithms on operators, this research designs a decision variable encoding and decoding scheme for integer programming problems. This scheme achieves a readable solution space for task allocation and equal-interval continuous encoding. This scheme was successfully applied to various metaheuristic intelligent optimization algorithms.
Integer matrix coding can intuitively display the results of task allocation and realize the parallel calculation of various groups in the swarm intelligence algorithm. In this research, the allocation matrix was defined based on the idea of the Hungarian algorithm to realize the continuous movement of each operator and establish the initial population that is in line with the constraints through matrix coding. The updated decision matrix was guaranteed to meet the constraints. Then, each allocation matrix was transformed and decoded into a 0–1 planning allocation problem to obtain the allocation scheme. In the task allocation scenario, six surface agents transport twelve load agents to execute an attack on four target agents , under the relay of six aerial relay control agents . The specific coding scheme and the corresponding decoded decision matrix are presented in Figure 2 and Equation (1).
where ; ; ; and denote the ith target allocation or control allocation scheme; and represent the coding value corresponding to the ith load agent in the jth allocation scheme; and indicate the decision variable values corresponding to the decision pairs and in the ith allocation scheme, respectively.
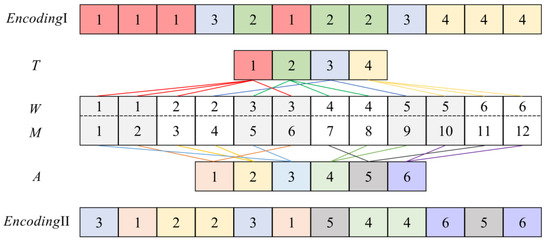
Figure 2.
Integer encoding model.
2.3. Mathematical Model of Target Allocation
In the process of cross-domain collaborative task allocation, the load agents and target agents are heterogeneous. The value expectations of different targets vary, the cost of the load is proportional to its penetration capability, and the value of the target is proportional to its defense capability. Therefore, the optimization objective of the target allocation model depends on various aspects, such as the comprehensive effectiveness, the time cost, and the cluster load.
2.3.1. Based on Comprehensive Optimizing Effectiveness
Most traditional task allocation models use the task success probability as the objective function [39]. According to the task allocation scenario setting, combined with the performance index of the load agent and the characteristics of the target agent, the probability of the load agent damaging the target agent is given and its damage probability is taken as the optimization goal of the model. After reviewing and summarizing the actual task results, it is evident that ensuring the task’s sustainability and cost-effectiveness is essential. To achieve this, the efficiency/cost ratio and threat level of each task must be incorporated into the objective function, along with the overall efficiency and cluster workload. The economic benefit of cross-domain collaborative tasks mainly depends on the value of the target agent. Therefore, the coefficient of the target value and target threat degree was introduced to make more rational use of the resources and enhance the practical significance of the allocation scheme. The objective function was mainly determined by the damage probability of the load agent to the target agent, the threat degree, and the economic value of the target agent, as shown in Equation (2):
where is the damage probability of the load agent to the target agent ; is the threat coefficient of the target agent ; is the number of load agents in the cluster; and is the amount of value of the target agent .
2.3.2. Based on the Greatest Distance Advantage
In practical applications, the flight time of the loads affects the timeliness of task allocation to a certain extent, and the distance advantage is also an important factor in the cluster target allocation scenario. Hence, inspired by the concept of the Traveling Salesman Problem, we incorporated the optimization function pertaining to flight time cost as a pivotal evaluation metric for task allocation. Subsequently, the formulation of this time cost optimization function was established, as detailed in Equation (3), offering a quantitative basis for assessing and enhancing operational efficiency.
where is the distance between the load agent and the target agent , and when the decision variable is 0, it is also set to 0; is the average flight speed of the load agent .
2.3.3. Based on Cluster Load Balancing
In consideration of the varying abilities of each surface agent to transport the load within the cluster, we introduce the concept of load capacity balancing for the target distribution channel optimization in this model. To establish the target distribution channel cluster load model, we employ the root mean square of the workload in the target distribution channel on each platform, represented by Equation (4):
where is the number of available target allocation channels for the water surface agent and the channel workload is assigned to the target of the water surface agent .
Among them, the target allocation channel workload formed by various allocation schemes for an agent in the cluster can be expressed as Equation (5):
where is the internal workload of the water surface agent , that is, the number of target allocation channels assigned to the main targets of the agent. In a target allocation scheme, a water surface agent primarily focuses on attacking four main targets using loads, while considering other targets as cooperative targets. The cooperative workload of the water surface agent, denoted as , represents the number of target allocation channels assigned to the cooperative targets. Additionally, represents the weight coefficient of the internal workload of the cluster within the total workload. In this research, the value of was taken as 0.3 during the simulation calculation, as the collaborative workload typically requires more resources and is generally not greater than 0.5. If each water surface agent has 16 available target allocation channels, the cluster workload is 1 when there is no cooperation or full cooperation, corresponding to being equal to 1 or 0, respectively. In the case of local cooperation (), the cluster workload is less than 1.
2.3.4. Mathematical Model Construction of Target Allocation
Objective assignment is a multi-objective combinatorial optimization problem. Because the above three objective functions have different dimensions and orders of magnitude, in order to unify the data scale and increase the speed of model convergence, the data correlation must be eliminated by data normalization methods. Firstly, the min–max normalization method was used to process the objective function value of each objective assignment scheme. Then, the analytic hierarchy process (AHP) was used to weight each objective function value according to the importance of the elements and expert experience, and the linear weighted sum method was used to combine the above three preprocessed objective function values to obtain the fitness of each objective allocation scheme.
The mathematical model and the constraint conditions of the constructed objective allocation are shown in Equation (6), respectively:
where ① indicates that the total number of load agents in each allocation scheme is limited to no more than ; ② indicates that each load agent can only be assigned to one target in an allocation; ③ indicates that each target agent is limited to be hit by, at most, load agents at the same time to prevent a waste of resources. In the actual calculation process, combined with the attack ability of our load agent, was taken as 15; ④ indicates that the distance between the load agent and the target agent is less than the theoretical maximum range of the load agent.
2.4. Mathematical Model of Control Allocation
Analyzing the control handover process and simulation results [40,41] reveals three key factors influencing control right allocation in cross-domain cooperation. These factors include the radar detection capability of the air relay control agent, the connectivity of the control data link, and the connectivity of the return data link between the air relay control agent and the load agent. To ensure reliable handover and stable control guidance, this study developed a mathematical model for control allocation based on these three aspects.
2.4.1. The Advantages of Radar Detection Capability
The detection capability of the air relay control agent mainly depended on the airborne detection radar, which was affected by sea clutter, hydrometeorology, the target characteristics, and other factors. The signal-to-noise ratio (SNR) of the airborne radar was as follows (Equation (7)):
where is the peak transmission power of the radar; is the antenna main lobe gain; is the wavelength; is the target RCS; is the radar environmental factor; is the energy intensity of the sea clutter; is the radar noise power; and is the target slant range.
The aerial relay control agent was always maneuvering at a high speed and the relative position between the target and the target agent changed constantly, resulting in a changing angle of the view of the target relative to the airborne detection radar. Therefore, the Swerling type I was used to characterize the RCS fluctuation in the target, and the detection probability of the Swerling I target [42] was used to characterize the radar detection ability advantage. The detection probability of the Swerling I target was used to characterize the radar detection ability advantage as Equations (8) and (9).
where is the detection probability of the target agent by the aerial relay control agent controlling the load agent .
where is the number of accumulated radar pulses; is the signal-to-noise ratio of the airborne radar; is the detection threshold; is an incomplete function .
2.4.2. The Advantage of Control Data Chain Connectivity
The directional gain of airborne radar will affect the power of the echo signal in different enemy or foe situations, so it was necessary to modify the traditional control data link model to receive the power of the data link. For this radar, the antenna gain as a function of the scanning angle and the direction angle was as shown in Equation (10):
where is the antenna gain function of each directional angle and is the gain in the normal direction of the antenna array.
In the control data link, the received power of the load agent is shown in Equation (11):
where is the receiving gain of the load agent data link antenna; and are the transmission gain and transmission power of the air relay control agent data link antenna, respectively; is the loss factor.
In the back-transmission data link, the received power of the air relay control agent is shown by Equation (12):
where is the receiving gain of the data link antenna of the air relay control agent; and are the transmission gain and transmission power of the load agent data link antenna, respectively; is the loss factor.
It can be seen from Equation (10) that the angle and distance will affect the communication ability of the air relay control agent when communicating with the load agent. Therefore, the target detection probability of the Swerling 0 model [34] was used to represent the connectivity advantage of the data link.
The connectivity advantage of the control data link was as shown in Equation (13):
where , , and are the Gram–Charlier series coefficients, which usually vary with the type of target fluctuation.
The connectivity advantage of the backhaul data link was as shown in Equation (14):
2.4.3. Mathematical Model Construction of Control Allocation
The radar detection capability, control, and backhaul data link connectivity were the key indicators used to determine the success or failure of the control allocation task. Since the three capability indicators are probability-based and share similar dimensions and magnitudes, the radar detection capability advantage in Equation (8) and the control/backhaul data link connectivity advantage in Equations (13) and (14) were combined using the method outlined in Equation (15). Subsequently, the mathematical model and constraint conditions for control allocation in load agents were derived as presented in Equation (15):
where ① indicates that the total number of load agents in each control allocation scheme is limited to no more than ; ② indicates that each load agent can only be controlled by one air relay control agent in a distribution; ③ indicates that each air relay control agent can stably control at most load agents at the same time. In the actual calculation process, combined with the data communication processing capacity of our air relay control agent, was set to 25.
2.5. Establishment of Constrained Objective Functions for Cross-Domain Collaborative Task Allocation
In the context of the cross-domain cooperative task, the air relay control agent had an extremely high maneuverability, and the relay control load agent hit the target as the core task. In the actual task process, after developing the control allocation scheme of the load agent, the air relay control agent had enough time to reach the predetermined position. Therefore, in order to simplify the model architecture, the optimal scheme of target allocation was used as the precondition of control allocation, and the control allocation results were considered to converge in all the feasible solution sets of target allocation.
The cross-domain collaborative task allocation model is shown in Equation (16).
According to the importance of each element in the model and expert experience, the AHP method was used to assign weights to each objective function value in the objective allocation. Specifically, the weights were assigned as follows: . The overall model framework incorporates multiple criteria decision-making methods to achieve balanced and optimized task allocation.
3. Multi-Strategy Improved Dung Beetle Optimization Algorithm
Before delving deeply into the principles and enhancement strategies of the MSIDBO algorithm, it is important to acknowledge that this paper is developed on the foundation of the groundbreaking work conducted by Xue Jiankai et al. [25]. This chapter begins with a detailed exposition of the principles and formulations of the original DBO algorithm. Subsequently, in response to the limitations observed when applying the DBO algorithm to solve complex large-scale optimization problems, several targeted strategies are introduced to further expand and update some key formulations of the DBO algorithm. Based on these modifications, the MSIDBO algorithm is proposed.
3.1. Dung Beetle Optimization Algorithm
The dung beetle optimization algorithm updates the position of a dung beetle by imitating dung beetle behavior, resulting in the global optimal solution being found. Combined with the task background of this research, the principle of the original dung beetle algorithm can be briefly described as follows:
- 1.
- Population initialization: An initial dung beetle population of size is randomly generated, which is composed of four types of dung beetles, namely rolling beetles, new beetles, small beetles, and thieves. Each individual dung beetle in the population represents a target allocation or control allocation decision scheme, and the initial population is shown in Equation (17):where represents the position of the ith dung beetle, that is, the code of the ith allocation scheme. Additionally, represents the dimensional position of the ith dung beetle, for which is the coding value corresponding to the ith load agent in the jth allocation scheme.
- 2.
- Ball-rolling behavior: The position update formula of the dung beetle’s rolling ball is shown in Equation (18), which guides the allocation plan to achieve optimization in the direction that deviates from the illumination, that is, the current global worst position.where represents the current iteration number; is the position of the ith dung beetle after the tth iteration; is the deflection control variable direction of the dung beetle, where means no deviation at that time and means deviation from the original direction at that time; is the deflection coefficient; is the light intensity coefficient; is the global worst dung beetle position; and is the simulated light, which is negatively correlated with the light intensity.
- 3.
- Dancing behavior: When an individual dung beetle encounters an obstacle, it stops marching and uses dancing to reposition itself. The position update of the dancing behavior is shown in Equation (19):where the rolling direction and the position were not updated; .
- 4.
- Reproductive behavior: In order to optimize the spawning position of female dung beetles, the spawning boundary was set as shown in Equation (20):where and represent the lower and upper bounds of the spawning area, respectively; represents the current local optimal dung beetle position; , is the set maximum number of iterations; and and denote the lower and upper bounds of the breeding region, respectively.As the number of iterations increases, the spawning position will be dynamically updated, as shown in Equation (21):where represents the position of the ith dung beetle egg in the tth iteration and and are random vectors with a size of .
- 5.
- Foraging behavior: The optimal foraging area for small dung beetles will be updated iteratively, as shown in Equation (22):where is the global optimal dung beetle position and and represent the lower and upper bounds of the optimal foraging area, respectively.The position of the small dung beetle is updated as shown in Equation (23):where and are two independent random numbers; the former follows a normal distribution and the latter ranges from 0 to 1.
- 6.
- Stealing behavior: When a thief dung beetle steals other dung beetles’ dung balls, its position is updated in the manner shown in Equation (24):where is a constant value and is a random vector with a size of that obeys a normal distribution.
3.2. Algorithm Improvement Strategy for Cross-Domain Collaborative Task Allocation Problem
To meet the solving requirements of the large-scale cross-domain collaborative task allocation model, several strategies were employed to enhance the original dung beetle algorithm. These strategies also aimed to improve the efficiency and performance of the algorithm in addressing complex optimization problems. Specifically, the Fuch chaotic map and opposition-based learning strategies are first introduced in the initialization process of the random population. This is followed by the adaptive rolling dung beetle population decreasing strategy in the dung beetle’s rolling behavior, the spiral search strategy in the dung beetle’s reproduction behavior, and the convex lens imaging opposition-based learning and optimal value guidance strategies in the dung beetle’s foraging behavior. These strategies work together in different stages of the algorithm and can effectively improve the search efficiency, convergence speed, and solution accuracy of the algorithm. The process of the MSIDBO algorithm is shown in Figure 3.
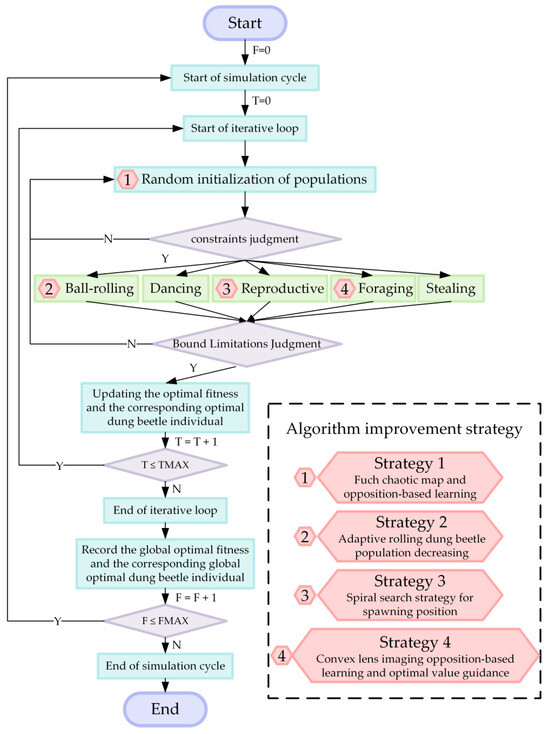
Figure 3.
Process of MSIDBO algorithm.
3.2.1. Fuch Chaotic Mapping and Opposition-Based Learning Strategy Fusion
The quality of the initial dung beetle population will have a huge impact on the calculation results of the model, and an uneven distribution or poor diversity of the population will lead to the convergence of the calculation results in advance, leading to the calculation falling into the local optimum [43]. Therefore, improved Fuch chaotic mapping was used to determine the initial position of the dung beetle population, and Equation (17) was substituted into Equation (25):
where is the randomly generated initial position of the dung beetle population and is the population of dung beetles obtained via chaotic mapping.
In order to further expand the search space and improve the quality of the initial population, opposition-based learning was performed on the initial population obtained by applying Equation (25), as shown in Equation (26):
where and represent the lower and upper bounds of the dung beetle distribution space, respectively; represents the inverse scheme corresponding to each initial decision scheme; and is a random number ranging from 0 to 1.
Finally, in order to unify the initial population size, the fitness corresponding to the initial population generated using Equation (25) and the inverse population generated using Equation (26) was sorted, and the first half of the population with better fitness was taken as the initial population.
3.2.2. Adaptive Rolling Dung Beetle Population Decreasing Strategy
In the initial iteration of the dung beetle optimization algorithm, a dung beetle with a strong global search ability could quickly find the optimal solution and accelerate the convergence speed. In the later iteration stage, the global search was basically completed and turned into the local search stage. In order to reduce the search step size and improve the ability of the algorithm to jump out of the local optimal solution, an adaptive decreasing strategy of the number of rolling beetles was introduced to dynamically adjust the proportion of rolling beetles. The updated formula for the number of rolling beetles is shown in Equation (27):
where and represent the maximum value and minimum value of the proportion of rolling beetles in the dung beetle population, respectively.
Let and ; as the number of iterations increases, the proportions of all types of dung beetles undergo a corresponding change, as illustrated in Figure 4.
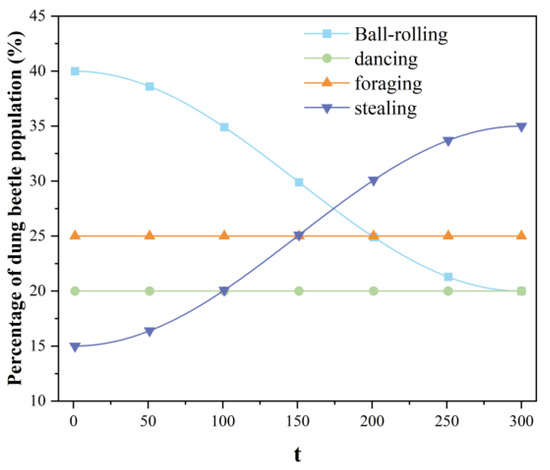
Figure 4.
Adaptive strategy for decreasing the number of rolling dung beetles.
3.2.3. Spiral Search Strategy for Spawning Position
In Equation (21), female dung beetles gather in the spawning area to produce eggs, which can make the population converge rapidly, but at the same time, this will increase the probability of being trapped in the local optimum. The behavior of the head whale population when hunting prey inspired the spiral search strategy in the whale algorithm [44]. This strategy was incorporated to update the position relationship between the spawning position and the global optimal position, ensuring faster convergence and enhancing individual diversity. The spiral search strategy was improved, as shown in Equation (28):
where is the dynamic spiral search shape parameter and is a random number whose value ranges from −1 to 1.
3.2.4. Fusion of Convex Lens Imaging Opposition-Based Learning and Optimal Value Guidance Strategies
In Equation (23), the foraging behavior of small dung beetles was always aimed at the global optimal position , and the position was updated by two random numbers, and . The lack of adaptive mechanisms, simple and random strategies, and a weak global search ability seriously restricted the convergence speed and accuracy of the algorithm. The implementation of an opposition-based learning strategy, rooted in the principles of convex lens imaging, was employed to introduce perturbations within the population. By incorporating the current global optimal position as a guiding mechanism for the generation of novel candidate solutions, this approach significantly enhanced the diversity of the population. This, in turn, enabled smaller dung beetles occupying suboptimal foraging positions to promptly escape from their current limitations. Ultimately, this led to a substantial improvement in both the convergence speed and accuracy of the algorithm.
The initial foraging position of small dung beetles improved through the convex lens imaging opposition-based learning strategy, as shown in Equation (29):
where is the adaptive opposition-based learning control factor.
The position update formula for the foraging behavior of small dung beetles after introducing the optimal value guidance strategy is shown in Equation (30):
where is the optimal value-guiding factor.
4. Experimental Verification and Results Analysis
In the preceding sections, we systematically introduced the MSIDBO algorithm to address the multi-agent cross-domain collaborative task allocation problem, and established corresponding mathematical models for target and control allocation. To verify the effectiveness and superiority of these theoretical models and the MSIDBO algorithm in practical applications, this section provides detailed experimental verification and analysis. By designing cross-domain collaborative task scenarios of varying scales and simulating the task allocation process in real-world environments, we compare the performance of the MSIDBO algorithm with other classical and improved algorithms. This section focuses on key performance indicators such as convergence speed, solution accuracy, and real-time performance. Through comprehensive and detailed experimental validation, we aim to demonstrate the significant advantages of the MSIDBO algorithm in solving cross-domain collaborative task allocation problems, analyze its optimization mechanisms, and identify applicable scenarios, thereby providing strong support for subsequent practical applications.
4.1. Simulation of Environment Construction and Parameter Settings
This experiment used the Windows 10 operating system and the MATLAB R2023b simulation platform to verify the rationality of the task allocation model in this research and the performance of the MSIDBO algorithm in solving multi-agent multi-constraint allocation problems. As shown in Table 2, three task scenarios were assumed and simulated. These scenarios encompassed a wide range of complexities and cross-domain collaborations, spanning from simple tasks involving minimal interaction between agents to highly complex scenarios requiring extensive coordination and communication across multiple domains. By comparing the simulation results of each algorithm across these varying scales of cross-domain collaborative tasks, we were able to comprehensively evaluate the performance of the MSIDBO algorithm in diverse situations. The simulation results of each algorithm on different scales of cross-domain collaborative tasks were compared.

Table 2.
Task scenario parameters on different scales.
Based on the existing agent performance index and experience, the scenario and intelligent algorithm parameters were preconceived as follows:
- Basic parameter assumptions: The population size of dung beetles was set to n = 200, the number of iterations of the algorithm was set to T = 300, and the number of simulations was set to F = 100. In the control allocation, the number of radar accumulation pulses was set to = 5; the probability of radar false alarms was set to , which was corresponding number of false alarms .
- Load agent performance index scenario: The average flight speed of the load agent was set as km/h, and a random number in (0, 0.5) was randomly selected as the damage probability of each load agent to each target platform. With an increase in the scale of the task scene and the number of load agents, the regularity of the damage ability distribution of the load agents gradually increased and continued to approach a normal distribution. This is shown in Figure 5; Ncd is the total number of samples, which is obtained by multiplying the number of target agents and the number of load agents.
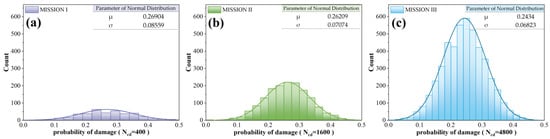 Figure 5. Statistics of damage capability of the load agent. (a) Mission I. (b) Mission II. (c) Mission III.
Figure 5. Statistics of damage capability of the load agent. (a) Mission I. (b) Mission II. (c) Mission III. - Calculation of threat coefficient of target agent: The threat degree of the target agent was determined by many quantitative and qualitative factors, including quantitative indicators, such as the target’s speed, distance, and relative position, and qualitative indicators, such as the target’s threat type, defense capability, etc. In order to eliminate the dimension and magnitude differences between various factors, the quantitative factors of the quantitative and qualitative indicators were obtained by combining the analytic hierarchy process and the entropy weight method. Then, the factors that affected the threat degree were normalized to obtain the membership degree of each factor. The characteristic information of the four types of targets is shown in Table 3.
 Table 3. Target feature information.
Table 3. Target feature information.
According to the characteristic information of each target in Table 3, the target membership matrix can be given as follows:
Combined with the analytical hierarchy process and entropy weight method, the weight coefficient matrix of each index was obtained as follows:
Using the comprehensive weight, the threat degree coefficient matrix of various targets was calculated as follows:
- 4.
- Task allocation situation scenario: The task allocation situation was determined by the relative position relationship of each agent platform. According to the performance index and historical experience statistics of the load agent, the water agent and the target agent were scattered in two rectangular areas, respectively. The vertex coordinates of the rectangle were (75, 0), (125, 0), (125, 25), (75, 25) and (0, 300), (200, 300), (200, 400), (0, 400). The aerial relay control agents were distributed in the irregular sector area; the vertex coordinates of the sector were (65.5672, 0), (−79.0625, 420.0352), (279.0625, 420.0352), (134.4328, 0); the center of the circle was (100, −100); the radius was 550; the coordinate position unit was km; and the angle was 38°. According to the simulation scene parameters and situation scenarios in Table 2, the situation graphs of three kinds of scale mission scenarios were randomly generated, as shown in Figure 6.
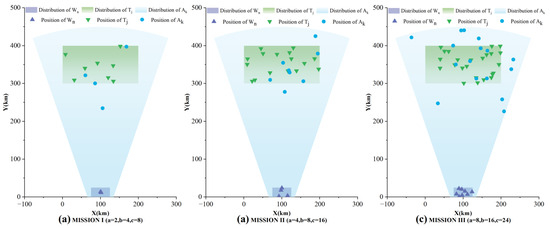 Figure 6. Diagrams of mission scenarios.
Figure 6. Diagrams of mission scenarios.
4.2. Comparative Analysis of Simulation Results
To evaluate the performance of the improved dung beetle optimization algorithm in the cross-domain cooperative task allocation model proposed in this study, several classical metaheuristic algorithms were utilized as benchmarks. These algorithms included particle swarm optimization (PSO) [34], sparrow search algorithm (SSA) [35], and gray wolf optimizer (GWO) [36]. By comparing the results obtained from these algorithms with the improved dung beetle optimization algorithm, the effectiveness and efficiency of the proposed approach could be assessed. Additionally, the original dung beetle optimizer (DBO) and its many newer and original improved forms (for example, Original MODBO, MSADBO [32], and IDBO [33]) were used as comparison algorithms to verify the superiority of MSIDBO. The parameters of these methods are shown in Table 4 below.

Table 4.
Simulation parameter settings of each comparison algorithm.
In Table 4, and denote the upper limit and starting proportion of the rolling dung beetles; , , and represent the maximum and minimum values of the variable inertia weight coefficient of the MSADBO algorithm and the coefficient of variation of Gaussian disturbance, respectively; , , , , and are the proportions of rolling balls, newborns, young, and thieves in the population and the constant coefficient of thieves in the DBO algorithm, respectively; , , , and are the inertia weight coefficient of the PSO algorithm, the acceleration coefficient of personal cognition, the acceleration coefficient of social cognition, and the limit speed proportion coefficient; and is the main population proportion coefficient of the SSA.
In a task allocation simulation calculation, the performance of each algorithm was greatly affected by the initial random search; the objective function value changed sharply, the performance of each algorithm fluctuated with an increase in the number of iterations, and a regularity conclusion could not be determined. In order to visually display the performance of each algorithm, the average value of 100 Monte Carlo simulation results was used, and the change curve for the mean value of the fitness of each algorithm in solving the task allocation model with an increase in the number of iterations was plotted, as shown in Figure 7 and Figure 8.
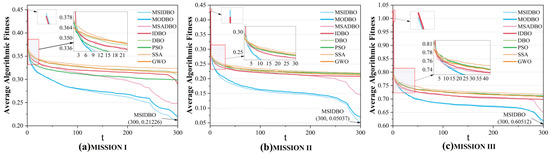
Figure 7.
Comparison of average fitness of algorithms for target allocation.
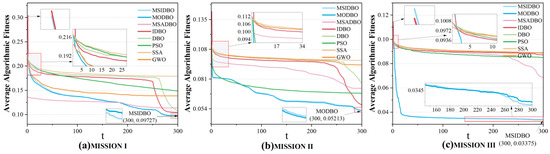
Figure 8.
Comparison of average fitness of algorithms for control allocation.
The convergence index and fitness function were used to describe the convergence effect of the algorithm, as shown in Figure 9 and Figure 10.
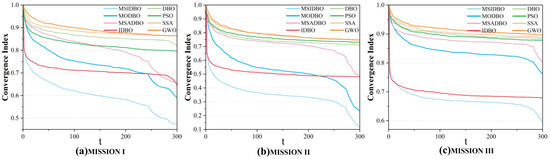
Figure 9.
Convergence index change in target allocation.
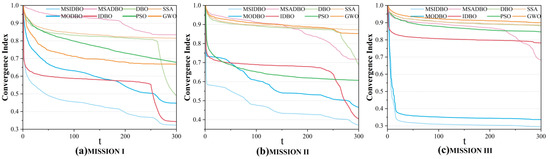
Figure 10.
Convergence index change in control allocation.
In order to evaluate and verify the significant differences between different target allocation schemes to enhance the reliability of the results, the average running time and global optimal solution of each algorithm are given in Table 5; the LSD significance test was conducted, and statistical analysis box plots of the results were drawn. The letters above each algorithm denote the LSD significance test results, and the different letters of the two algorithms indicate significant differences, as shown in Figure 11 and Figure 12.

Table 5.
Simulation performance of each algorithm.

Figure 11.
LSD significance test of target allocation and statistical analysis of results.

Figure 12.
LSD significance test for control allocation and statistical analysis of results.
After deeply analyzing and comparing a variety of task allocation algorithms, we pay special attention to the performance of the MSIDBO algorithm in cross-domain collaborative task allocation problems. By comparing the MSIDBO algorithm with other classical and improved algorithms in terms of optimization performance, running time and convergence, the advantages of the MSIDBO algorithm can be comprehensively assessed. By comparing and analyzing the data in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 and Table 5, the following conclusions can be drawn:
- Optimization performance: As can be seen from the data in Figure 7 and Figure 8 and Table 5, the solving performance of the MSIDBO algorithm for the control allocation model was close to that of MODBO, but the solving time was greatly shortened. Figure 12 shows that there were no significant differences between the two algorithms. In other task scenarios, the performance of the MSIDBO algorithm was significantly better than that of other algorithms, which indicates that the MSIDBO algorithm has significant advantages when solving cross-domain collaborative task allocation problems. For small-, medium-, and large-scale task scenarios, the optimization performance of the MSIDBO algorithm was 28.9–55.8%, 22.7–77%, and 14.6–62.4% higher than that of classical algorithms such as PSO, and 3.5–31.4%, 8.5–76.1%, and 2.1–62.1% higher than that of the original DBO algorithm and other existing improved forms, among which the index of the MODBO algorithm was not counted in the control allocation.
- Running time: It can be seen from Figure 7, Figure 8, Figure 9 and Figure 10 that, with an increase in the problem scale, the time for each algorithm to fall into the local optimal solution increased, and the number of iterations required to jump out of the local optimal solution increased continuously. The average running time of MSIDBO was close to that of DBO, PSO, SSA, and GWO and much lower than that of MODBO, MSADBO, IDBO, and other improved dung beetle algorithms, which indicates that MSIDBO has high computational efficiency.
- Convergence: It can be seen from Figure 7, Figure 8, Figure 9 and Figure 10 that the initial function value of the MSIDBO algorithm was large; it converged rapidly in the early iterations and the convergence index dropped sharply. This indicates that the solution space of the initial allocation scheme generated by the algorithm was uniform and had strong diversity, and the introduced fusion Fuch chaotic mapping and reverse learning strategy had obvious effects. In the middle iteration, the time to fall into the local optimal solution was less than that of other algorithms, indicating that the algorithm can quickly jump out of the local optimal solution and balance the contradiction between a global search and a local search.
In summary, compared with other algorithms, the MSIDBO algorithm generates an initial population with a uniform distribution and strong diversity in the early iteration of the algorithm; it can quickly jump out of the local optimal solution in the middle of the algorithm; and it can obtain the global optimal solution with the lowest fitness at the end of the algorithm. The MSIDBO algorithm can adapt to task allocation problems of different scales, and can better balance global optimization and efficient calculations. The LSD significance test and a comparative analysis showed that the MSIDBO algorithm has significant advantages in solving cross-domain collaborative task allocation problems, and the solution obtained has a good convergence and distribution. The real-time performance of the algorithm is also strong, and the solution speed is significantly better than that of other improved algorithms. Finally, an effective and feasible task allocation scheme was obtained.
Although the MSIDBO algorithm demonstrated superior performance, it still has the following problems:
- Computational Resource Utilization: The MSIDBO algorithm needs to replace the beetle population that exceeds the constraint boundary when updating the position in each iteration, and the fitness function is called frequently, which occupies a large amount of system computing resources and increases the iteration time cost. In practical tasks, the replacement set of dung beetle individuals should be generated in advance, and the replacement should be called in order.
- Parameter Tuning Challenges: In the adaptive rolling dung beetle population reduction strategy, we have innovatively designed the proportion of rolling dung beetles to decrease as the number of iterations increases. Consequently, the proportion of the other three types of dung beetles also varies. To determine the upper and lower bounds of the variations in the number of rolling dung beetles and other dung beetles, extensive experiments were needed to compare the algorithm’s performance with different parameters and .
5. Conclusions and Prospects
In the context of cross-domain collaborative task allocation, and acknowledging interdependencies among subtasks, this study divides the task into two components: target allocation and control allocation. We propose the MSIDBO algorithm, which integrates parallel solving, adaptive adjustment mechanisms, opposition-based learning, and an optimal value guidance strategy to effectively address the model. Through sufficient simulations and a comparative analysis, it was observed that the multi-agent cross-domain cooperative task allocation method based on the multi-strategy improved dung beetle optimization algorithm proposed in this research can be used to obtain the optimal task allocation scheme while meeting timeline requirements. The superior performance of the MSIDBO algorithm, as compared to classical and other improved DBO algorithms, underscores its potential for practical applications.
Moreover, this research not only validates the feasibility of the MSIDBO algorithm in solving a single-wave cross-domain cooperative task allocation problem but also opens up new avenues for future exploration. Recognizing the complexity and dynamic nature of real-world multi-wave scenarios, we aim to extend our work by investigating the effectiveness of the MSIDBO algorithm in handling such problems. This includes exploring strategies to adapt the algorithm for scenarios with varying task waves, optimizing the parameter tuning process, and integrating additional mechanisms to handle uncertainties and disruptions. Additionally, we plan to evaluate the algorithm’s scalability and robustness in larger-scale systems to further solidify its practical significance.
In conclusion, this research presents a significant advancement in the field of cross-domain collaborative task allocation, and MSIDBO algorithm offers a promising solution. On average, our optimization performance was 32.5% higher than traditional algorithms and their enhanced versions. The identified gaps and future directions outlined above provide a roadmap for continuing this important work and pushing the boundaries of what is possible in this challenging domain.
Author Contributions
Conceptualization, Y.Z. and F.L.; methodology, Y.Z.; software, Y.Z. and L.W.; validation, F.L., Y.Z. and J.X.; resources, J.X.; writing—original draft preparation, Y.Z.; writing—review and editing, L.W.; project administration, F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Technical Area Fund of the 173 Program of the Military Science and Technology Commission, grant number 2023-JCJQ-JJ-0388.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, C.; Zhao, J.; Sun, N. A review of collaborative air-ground robots research. J. Intell. Robot. Syst. 2022, 106, 60. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, L.; Xu, X. Cooperative targets assignment based on multi-agent reinforcement learning. Syst. Eng. Electron. 2023, 45, 2793–2801. [Google Scholar] [CrossRef]
- Jiang, B.T.; Wen, G.H.; Zhou, J.L.; Zheng, D.Z. Cross-Domain Cooperative Technology of Intelligent Unmanned Swarm Systems: Current Status and Prospects. Srategic Study CAE 2024, 26, 117–126. [Google Scholar] [CrossRef]
- Song, G.; Qiang, Y.; Liu, T.; Liu, Z. The present situation and progress of dynamic weapon target assignment. J. Ordnance Equip. Eng. 2022, 43, 83–88. [Google Scholar] [CrossRef]
- Li, M.; Chang, X.; Shi, J.; Chen, C.; Huang, J.; Liu, Z. Developments of weapon target assignment: Models, algorithms, and applications. Syst. Eng. Electron. 2023, 45, 1049–1071. [Google Scholar] [CrossRef]
- Li, G.; He, G.; Zheng, M.; Zheng, A. Uncertain Sensor–Weapon–Target Allocation Problem Based on Uncertainty Theory. Symmetry 2023, 15, 176. [Google Scholar] [CrossRef]
- Chakraa, H.; Guérin, F.; Leclercq, E.; Lefebvre, D. Optimization techniques for Multi-Robot Task Allocation problems: Review on the state-of-the-art. Robot. Auton. Syst. 2023, 168, 104492. [Google Scholar] [CrossRef]
- Guo, W.; Lu, T.; Wang, S.; Yan, Y. Firepower Allocation of Missile Group under Variable Communication Conditions. J. Command Control 2024, 10, 106–111. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, X.; Li, H.; Hu, S. UAV cooperative mission planning based on improved wolf packalgorithm. Comput. Eng. 2024, 1–13. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, K. Optimal Firepower Distribution Based on Minimum Firepower Waste. Electron. Opt. Control 2020, 27, 55–59. [Google Scholar] [CrossRef]
- Tan, G. Research on Decision and Coordinated Control Method of Multi-type Unmanned Surface Vehicle Swarm. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2024. [Google Scholar]
- Manne, A.S. A target-assignment problem. Oper. Res. 1958, 6, 346–351. [Google Scholar] [CrossRef]
- Lloyd, S.P.; Witsenhausen, H.S. Weapons allocation is NP-complete. In Proceedings of the 1986 Summer Computer Simulation Conference, Reno, NV, USA, 28–30 July 1986; pp. 1054–1058. [Google Scholar]
- Kline, A.; Ahner, D.; Hill, R. The Weapon-Target Assignment Problem. Comput. Oper. Res. 2019, 105, 226–236. [Google Scholar] [CrossRef]
- Kline, A.G.; Ahner, D.K.; Lunday, B.J. A heuristic and metaheuristic approach to the static weapon target assignment problem. J. Global Optim. 2020, 78, 791–812. [Google Scholar] [CrossRef]
- Hughes, M.S.; Lunday, B.J. The Weapon Target Assignment Problem: Rational Inference of Adversary Target Utility Valuations from Observed Solutions. Omega-Int. J. Manag. Sci. 2022, 107, 102562. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; Wang, Y.; Yu, Y.; Guo, L.; Gao, Y.; Chen, Y.; Zhang, F. A Time-Driven Dynamic Weapon Target Assignment Method. IEEE Access 2023, 11, 129623–129639. [Google Scholar] [CrossRef]
- Li, W.; Lyu, Y.; Dai, S.; Chen, H.; Shi, J.; Li, Y. A Multi-Target Consensus-Based Auction Algorithm for Distributed Target Assignment in Cooperative Beyond-Visual-Range Air Combat. Aerospace 2022, 9, 486. [Google Scholar] [CrossRef]
- Hendrickson, K.; Ganesh, P.; Volle, K.; Buzaud, P.; Brink, K.; Hale, M. Decentralized Weapon-Target Assignment Under Asynchronous Communications. J. Guid. Control Dyn. 2023, 46, 312–324. [Google Scholar] [CrossRef]
- Summers, D.S.; Robbins, M.J.; Lunday, B.J. An approximate dynamic programming approach for comparing firing policies in a networked air defense environment. Comput. Oper. Res. 2020, 117, 104890. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, L.; Wang, C.; Zheng, X.; Wang, Q. An Evolutionary Game-Theoretic Approach to Unmanned Aerial Vehicle Network Target Assignment in Three-Dimensional Scenarios. Mathematics 2023, 11, 4196. [Google Scholar] [CrossRef]
- Liu, S.; Liu, W.; Huang, F.; Yin, Y.; Yan, B.; Zhang, T. Multitarget allocation strategy based on adaptive SA-PSO algorithm. Aeronaut. J. 2022, 126, 1069–1081. [Google Scholar] [CrossRef]
- Cao, M.; Fang, W. Swarm Intelligence Algorithms for Weapon-Target Assignment in a Multilayer Defense Scenario: A Comparative Study. Symmetry 2020, 12, 824. [Google Scholar] [CrossRef]
- She, W.; Niu, W.; Kong, D.; Tian, Z. Weapon Target Assignment Optimization Algorithm Based on Particle Swarm Genetic Taboo. J. Zhengzhou Univ. (Nat. Sci. Ed.) 2023, 55, 1–10. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Z.; Zhao, Y.; Sun, F. Multi-Strategy Fusion Improved Dung Beetle Optimization Algorithm and Engineering Design Application. IEEE Access 2024, 12, 97771–97786. [Google Scholar] [CrossRef]
- Zilong, W.; Peng, S. A Multi-Strategy Dung Beetle Optimization Algorithm for Optimizing Constrained Engineering Problems. IEEE Access 2023, 11, 98805–98817. [Google Scholar] [CrossRef]
- He, J.; Fu, L. Robot path planning based on improved dung beetle optimizer algorithm. J. Braz. Soc. Mech. Sci. 2024, 46, 235. [Google Scholar] [CrossRef]
- Lei, F.; Ji, W. 3D UWSN coverage method for marine ranching based on improved Dung beetle optimization algorithm. ACTA Sci. Nat. Univ. Sunyatseni 2024, 63, 115–122. [Google Scholar] [CrossRef]
- Jun, L.; Qin, X. Improved dung beetle optimization for feature selection tasks. Electron. Meas. Technol. 2024, 47, 79–86. [Google Scholar] [CrossRef]
- Zhu, F.; Li, G.; Tang, H.; Li, Y.; Lv, X.; Wang, X. Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems. Expert. Syst. Appl. 2024, 236. [Google Scholar] [CrossRef]
- Pan, J.; Li, S.; Zhou, P.; Yang, G.; Lv, D. Dung Beetle Optimization Algorithm Guided by Improved Sine Algorithm. Comput. Eng. Appl. 2023, 59, 92–110. [Google Scholar] [CrossRef]
- Li, Y.; Sun, K.; Yao, Q.; Wang, L. A dual-optimization wind speed forecasting model based on deep learning and improved dung beetle optimization algorithm. Energy 2024, 286, 129604. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Kong, L.; Wang, J.; Zhao, P. Solving the Dynamic Weapon Target Assignment Problem by an Improved Multiobjective Particle Swarm Optimization Algorithm. Appl. Sci. 2021, 11, 9254. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Zhao, S.; Zhang, J.; Wang, X. Research on Air Combat Decision-making Problems Based on Particle Swarm Optimization Algorithm. Fire Control Command Control 2023, 48, 66–73. [Google Scholar] [CrossRef]
- Nam, C.; Shell, D.A. Assignment Algorithms for Modeling Resource Contention in Multirobot Task Allocation. IEEE Trans. Autom. Sci. Eng. 2015, 12, 889–900. [Google Scholar] [CrossRef]
- Zhang, A.; Xu, S.; Bi, W.; Xu, H. Weapon-target Assignment and Guidance Sequence Optimization in Air-to-Ground Multi-target Attack. ACTA Armamentarii 2023, 44, 2233–2244. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, R.; Wu, Y.; Xu, Y.; Deng, Y. Research on Guidance Superiority Model in Cooperative Air Combat. Fire Control Command Control 2020, 45, 19–24. [Google Scholar] [CrossRef]
- Mahafza, B.R. Radar Systems Analysis and Design Using MATLAB, 3rd ed.; CRC Press, Inc.: Boca Raton, FL, USA, 2016; pp. 372–379. ISBN 978-7-121-26001-8. [Google Scholar]
- Chen, J.; Liu, L.; Guo, K.; Liu, S.; He, D. Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models. Appl. Sci. 2024, 14, 5966. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).