Effect of Wettability and Permeability on Pore-Scale of CH4–Water Two-Phase Displacement Behavior in the Phase Field Model
Abstract
1. Introduction
2. Theoretical and Numerical Scheme
2.1. Control Equations
2.2. Phase Field Equations
2.3. Numerical Scheme
3. Results and Discussion
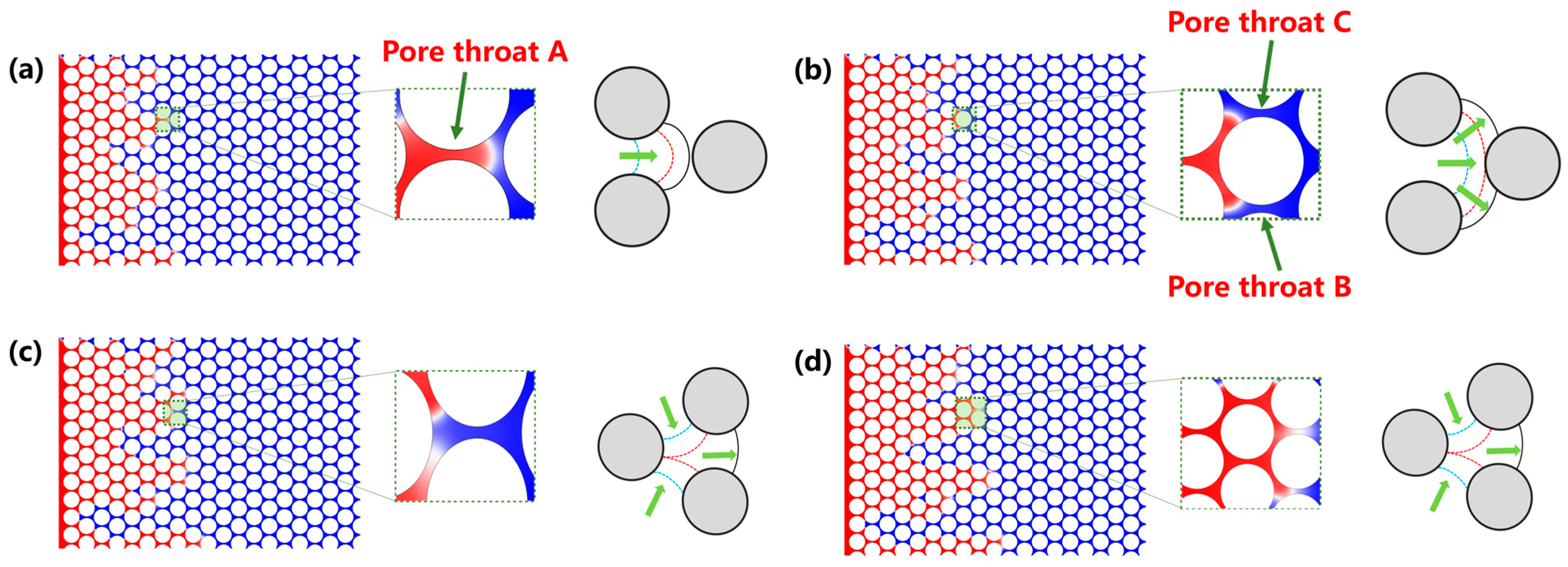
3.1. Analysis of Local Flow Patterns
3.2. Effect of Viscosity (M) and Capillary Force (Ca) on Flow in Porous Media
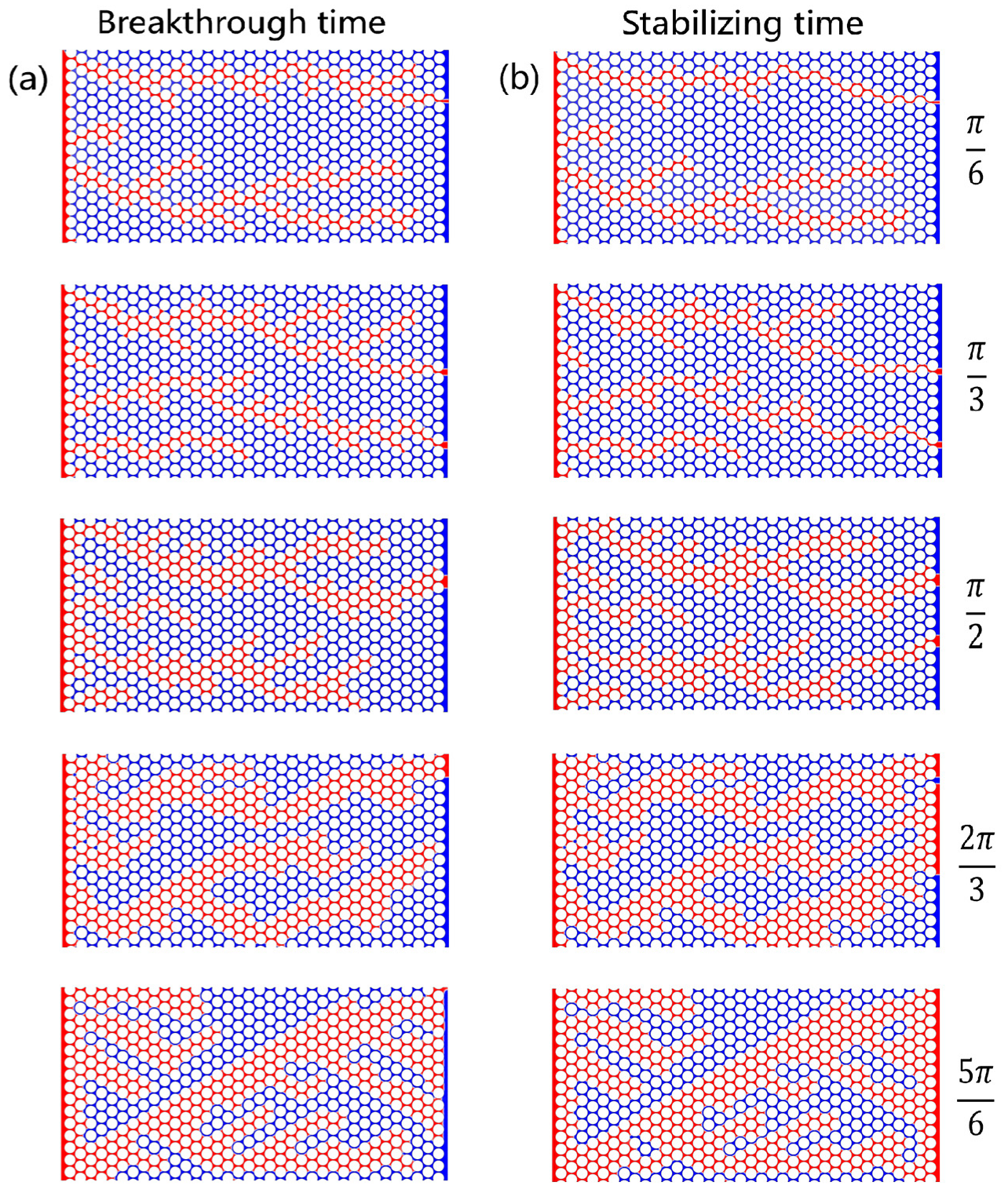
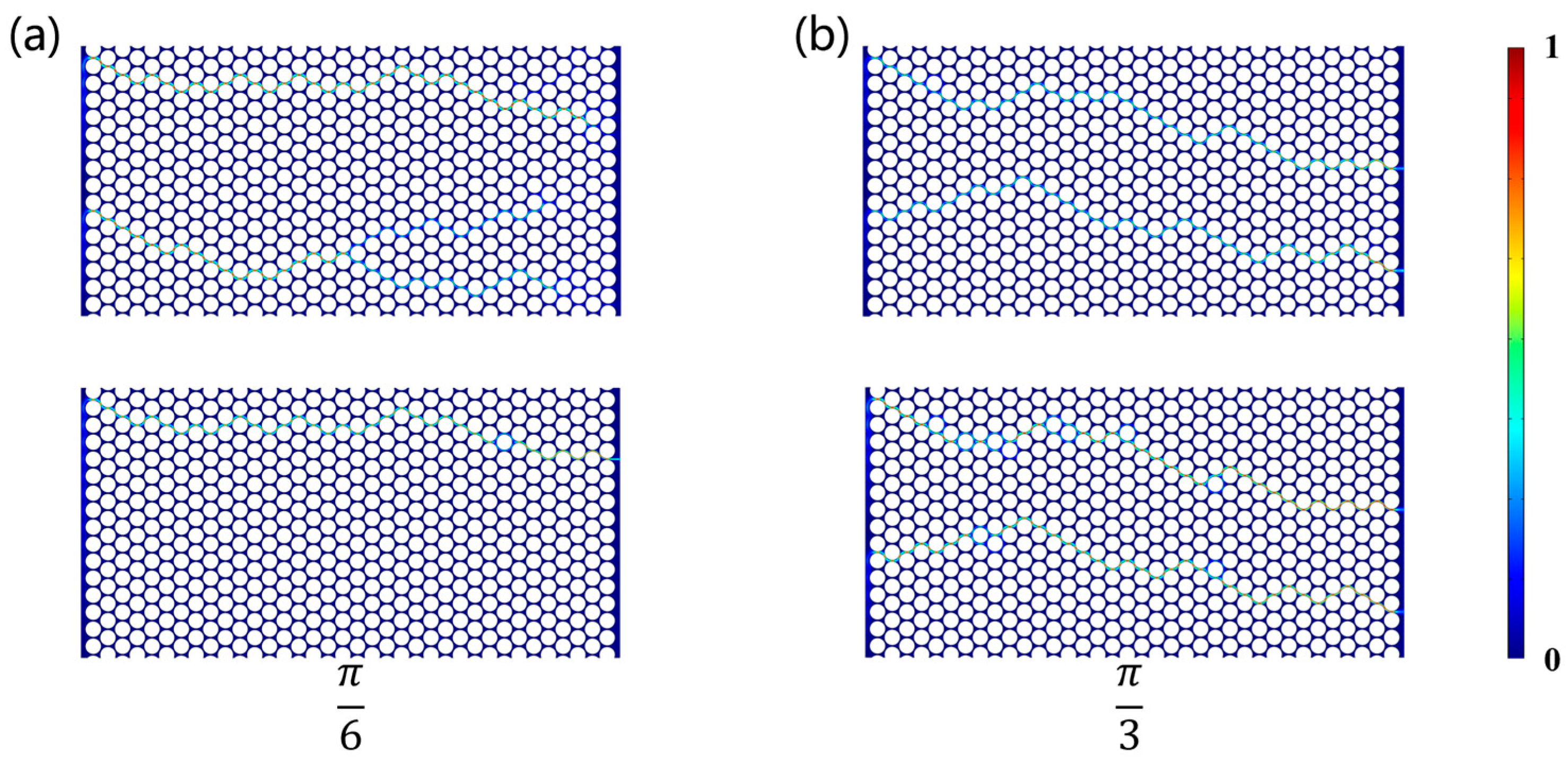
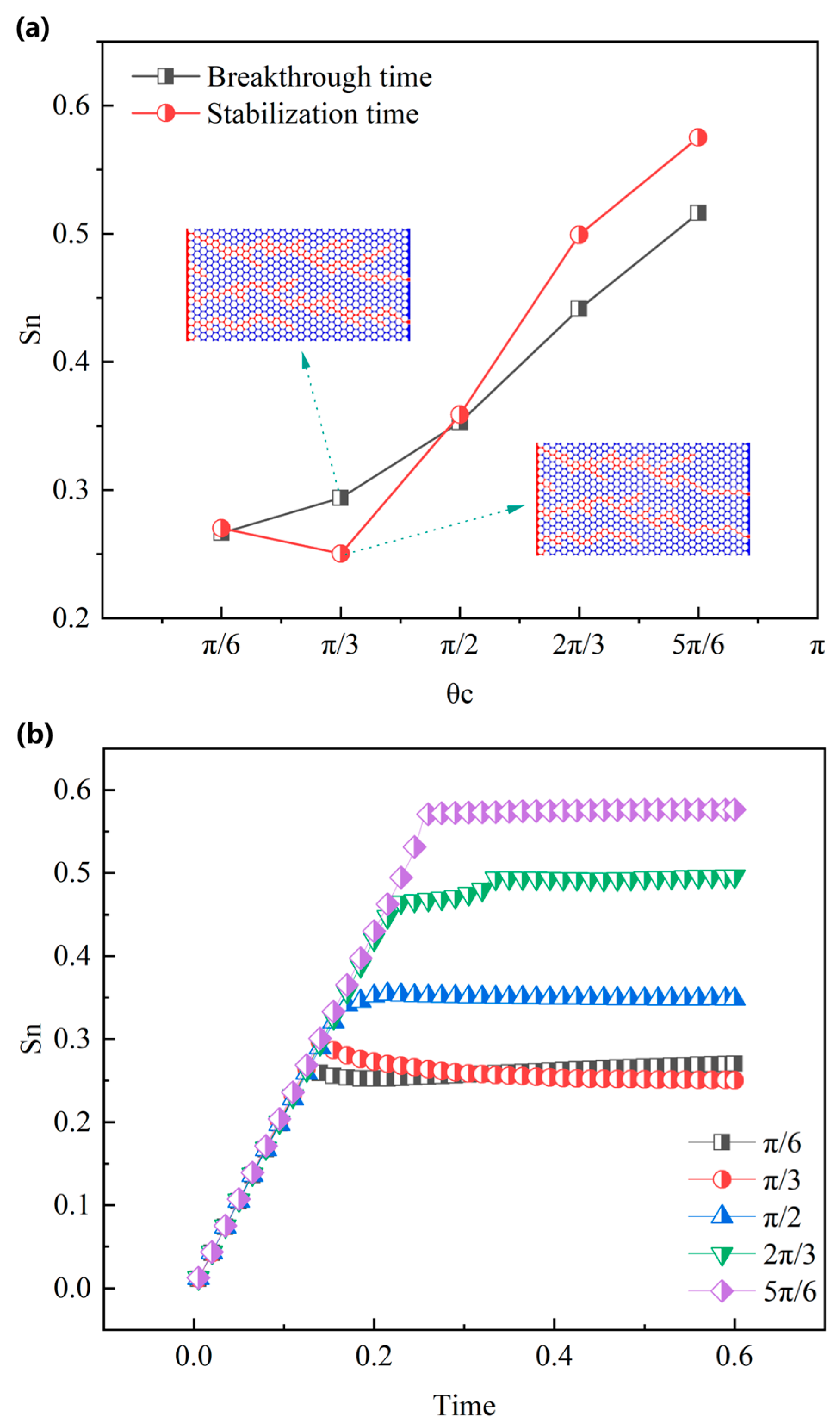
3.3. Effect of Wettability on Flow in Pore Media
3.4. Effect of Permeability and Inhomogeneity on Flow in Pore Media
4. Conclusions
- (1)
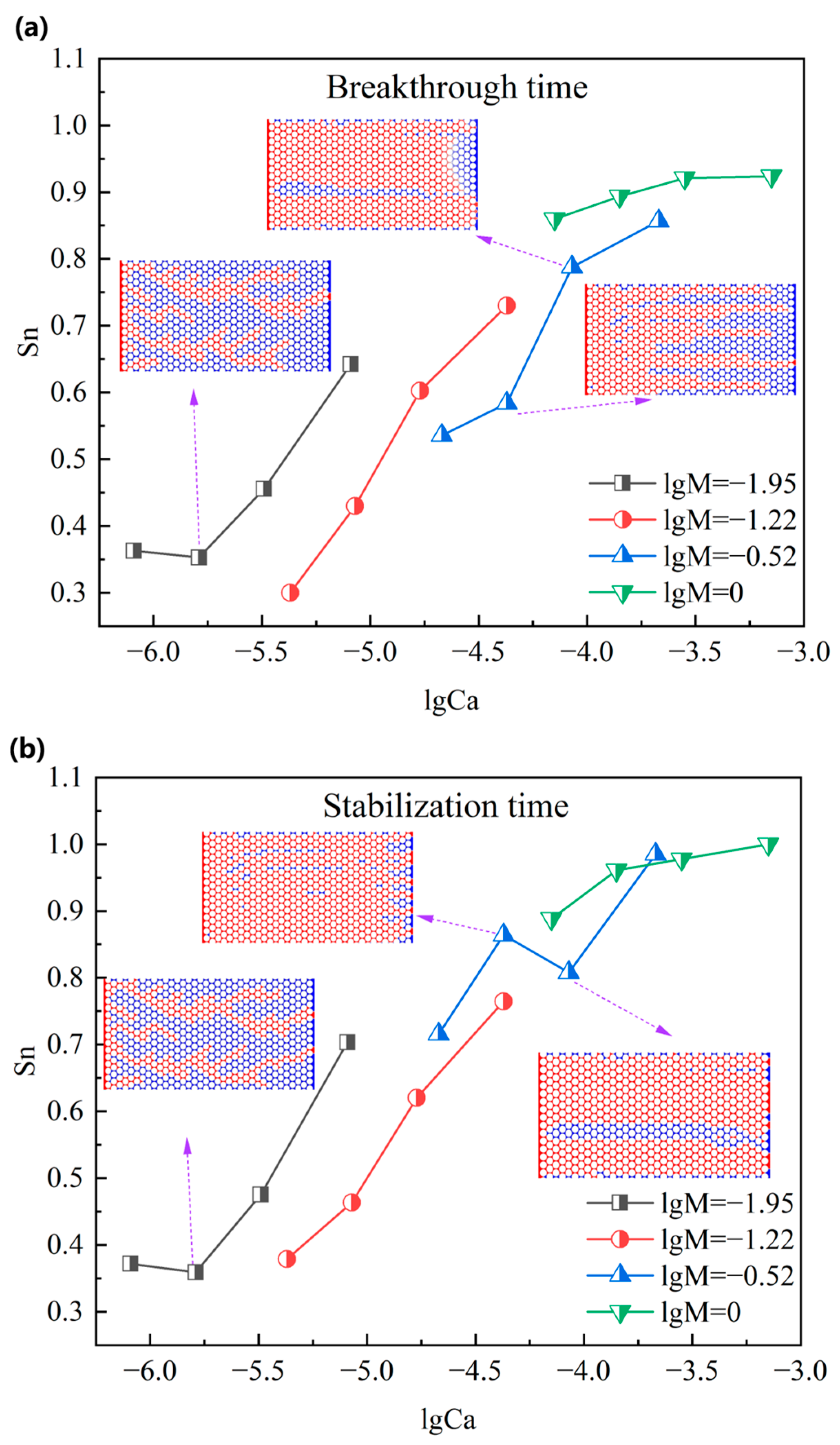
- It is found that during the CH4–water displacement process, fingering phenomena are very pronounced when lgCa < −4.37. The boundary between capillary fingering and viscous fingering is approximately determined to be at lgM = −1.22, lgCa = −4.77, while the boundary between viscous fingering and stable displacement is approximately at lgM = −0.52, lgCa = −4.07.
- (2)
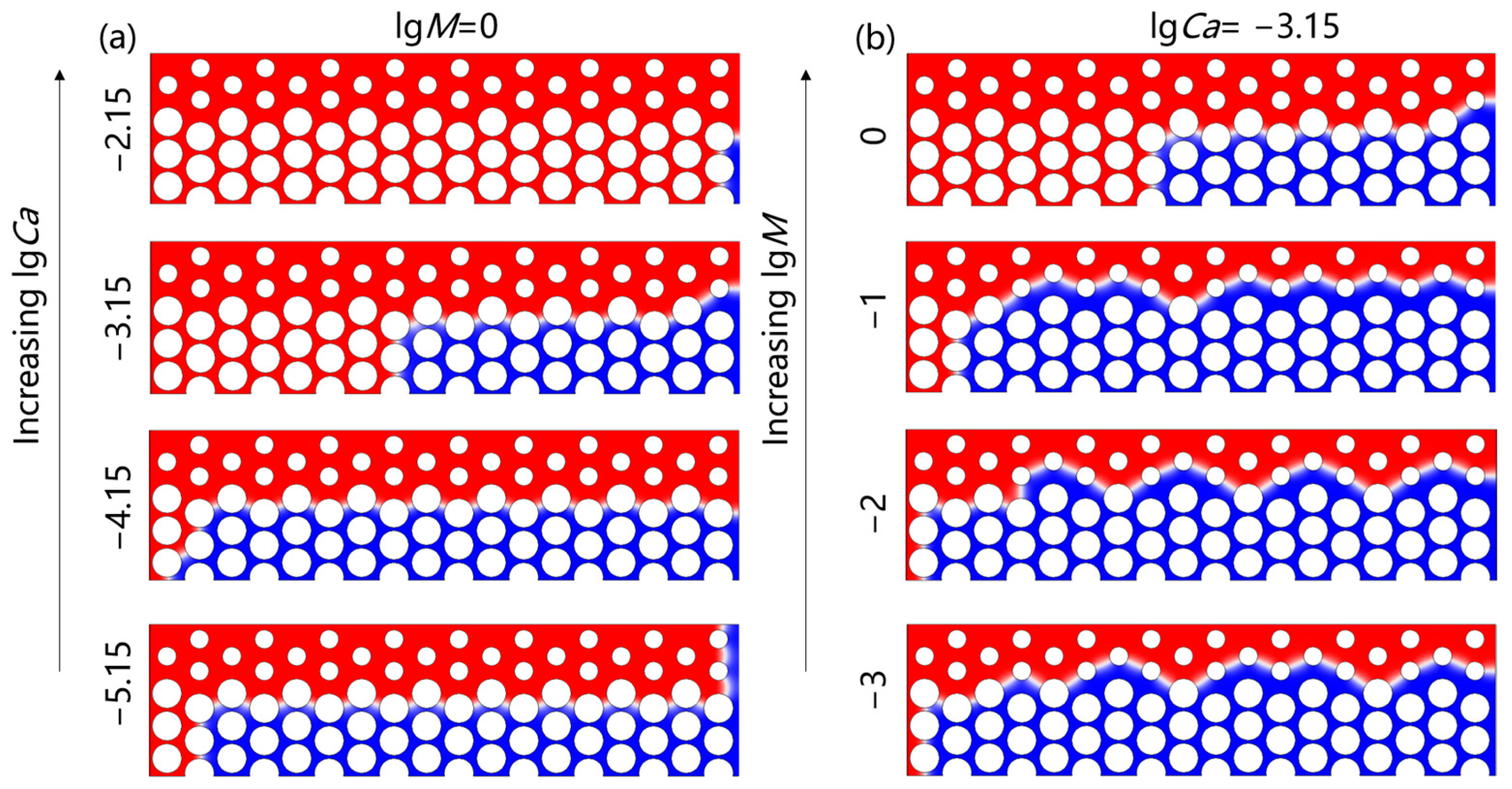
- The CH4–water two-phase flow patterns and invading phase (CH4) saturation are quantitatively analyzed under different capillary forces (Ca) and viscous forces (M). As Ca and M increased, the invading CH4 gradually transitioned from capillary fingering to viscous fingering and eventually to stable displacement, with higher displacement efficiency. The saturation of invading CH4 at breakthrough and stability is compared. At lgM = −0.52 and lgCa = −4.37, displacement efficiency decreases due to the appearance of preferential paths.
- (3)
- By changing the wettability angle of the porous media, the CH4–water two-phase flow in hydrophilic, neutral, and hydrophobic coal bodies is simulated. The backflow occurs only under hydrophilic conditions and that drainage efficiency increases significantly with increasing wettability angle.
- (4)
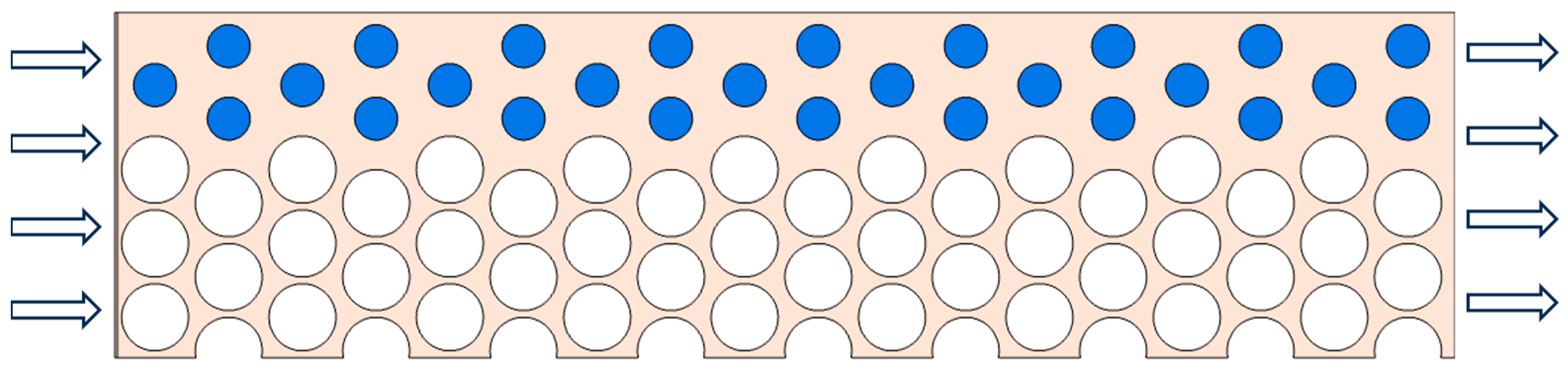
- A dual permeability model is constructed under different Ca and M values to simulate the effect of varying local permeability on two-phase displacement in real coal seams. CH4 preferentially invaded high-permeability regions, and displacement efficiency in low-permeability regions increases with unfavorable viscosity ratios (lgM < 0, lgCa = −3.15) and increasing lgCa.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kang, H.; Gao, F.; Xu, G.; Ren, H. Mechanical Behaviors of Coal Measures and Ground Control Technologies for China’s Deep Coal Mines—A review. J. Rock Mech. Geotech. Eng. 2023, 15, 37–65. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Zhao, J.; Ju, M.; De Silva, R.V.S.; Rathnaweera, T.D.; Bandara, A.K.M.S. Opportunities and Challenges in Deep Mining: A Brief Review. Engineering 2017, 3, 546–551. [Google Scholar] [CrossRef]
- Li, P.; Cai, M. Challenges and New Insights for Exploitation of Deep Underground Metal Mineral Resources. Trans. Nonferrous Met. Soc. China 2021, 31, 3478–3505. [Google Scholar] [CrossRef]
- Xie, H.; Zhao, J.W.; Zhou, H.W.; Ren, S.H.; Zhang, R.X. Secondary Utilizations and Perspectives of Mined Underground Space. Tunn. Undergr. Space Technol. 2020, 96, 103129. [Google Scholar] [CrossRef]
- Ershadnia, R.; Wallace, C.D.; Soltanian, M.R. CO2 Geological Sequestration in Heterogeneous Binary Media: Effects of Geological and Operational Conditions. Adv. Geo-Energy Res. 2020, 4, 392–405. [Google Scholar] [CrossRef]
- Shabani Afrapoli, M.; Alipour, S.; Torsaeter, O. Fundamental Study of Pore Scale Mechanisms in Microbial Improved Oil Recovery Processes. Transp. Porous Media 2011, 90, 949–964. [Google Scholar] [CrossRef]
- Veld, K.V.; Phillips, O.R. The Economics of Enhanced Oil Recovery: Estimating Incremental Oil Supply and CO2 Demand in the Powder River Basin. Energy J. 2010, 31, 31–56. [Google Scholar] [CrossRef]
- Li, G.; Zhan, L.; Yun, T.; Dai, S. Pore-Scale Controls on the Gas and Water Transport in Hydrate-Bearing Sediments. Geophys. Res. Lett. 2020, 47, e2020GL086990. [Google Scholar] [CrossRef]
- Chang, C.; Kneafsey, T.J.; Wan, J.; Tokunaga, T.K.; Nakagawa, S. Impacts of Mixed-Wettability on Brine Drainage and Supercritical CO2 Storage Efficiency in a 2.5-D Heterogeneous Micromodel. Water Resour. Res. 2020, 56, e2019WR026789. [Google Scholar] [CrossRef]
- Yang, W.; Chang, Y.; Cheng, J.; Wang, Z.; Li, X.; Lv, P.; Zhang, B.; Liu, B.; Song, Y. Gravity Effects on Oil–Water Two-Phase Displacement in Homogeneous Porous Media. Phys. Fluids 2021, 33, 102003. [Google Scholar] [CrossRef]
- Løvoll, G.; Jankov, M.; Måløy, K.J.; Toussaint, R.; Schmittbuhl, J.; Schäfer, G.; Méheust, Y. Influence of Viscous Fingering on Dynamic Saturation—Pressure Curves in Porous Media. Transp. Porous Media 2011, 86, 305–324. [Google Scholar] [CrossRef]
- Lenormand, R. Flow Through Porous Media: Limits of Fractal Patterns. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1989, 423, 159–168. [Google Scholar] [CrossRef]
- Lenormand, R.; Zarcone, C.; Sarr, A. Mechanisms of the Displacement of One Fluid by Another in a Network of Capillary Ducts. J. Fluid Mech. 1983, 135, 337–353. [Google Scholar] [CrossRef]
- He, S.; Kahanda, G.L.M.K.S.; Wong, P. Roughness of Wetting Fluid Invasion Fronts in Porous Media. Phys. Rev. Lett. 1992, 69, 3731–3734. [Google Scholar] [CrossRef] [PubMed]
- Frey, S.; Scheller, S.; Karadimitriou, N.; Lee, D.; Reina, G.; Steeb, H.; Ertl, T. Visual Analysis of Two-Phase Flow Displacement Processes in Porous Media. Comput. Graph. Forum 2022, 41, 243–256. [Google Scholar] [CrossRef]
- Holtzman, R. Effects of Pore-Scale Disorder on Fluid Displacement in Partially-Wettable Porous Media. Sci. Rep. 2016, 6, 36221. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.B.; Browne, C.A.; Amchin, D.B.; Nunes, J.K.; Datta, S.S. Controlling Capillary Fingering Using Pore Size Gradients in Disordered Media. Phys. Rev. Fluids 2019, 4, 084303. [Google Scholar] [CrossRef]
- Pak, T.; Rabbani, H.S.; Raeini, A.Q.; Shokri, N. Effects of the Pore Morphology on Multiphase Fluid Displacement in Porous Media—A High-Resolution Modeling Investigation. ACS Omega 2023, 8, 3889–3895. [Google Scholar] [CrossRef] [PubMed]
- Lenormand, R.; Touboul, E.; Zarcone, C. Numerical Models and Experiments on Immiscible Displacements in Porous Media. J. Fluid Mech. 1988, 189, 165–187. [Google Scholar] [CrossRef]
- Zhang, C.; Oostrom, M.; Wietsma, T.W.; Grate, J.W.; Warner, M.G. Influence of Viscous and Capillary Forces on Immiscible Fluid Displacement: Pore-Scale Experimental Study in a Water-Wet Micromodel Demonstrating Viscous and Capillary Fingering. Energy Fuels 2011, 25, 3493–3505. [Google Scholar] [CrossRef]
- Amiri, H.A.A.; Hamouda, A.A. Pore-Scale Modeling of Non-Isothermal Two Phase Flow in 2D Porous Media: Influences of Viscosity, Capillarity, Wettability and Heterogeneity. Int. J. Multiph. Flow 2014, 61, 14–27. [Google Scholar] [CrossRef]
- Chen, K.; Liu, P.; Wang, W.; Chen, Y.; Bate, B. Effects of Capillary and Viscous Forces on Two-Phase Fluid Displacement in the Microfluidic Model. Energy Fuels 2023, 37, 17263–17276. [Google Scholar] [CrossRef]
- Singh, K.; Jung, M.; Brinkmann, M.; Seemann, R. Capillary-Dominated Fluid Displacement in Porous Media. Annu. Rev. Fluid Mech. 2019, 51, 429–449. [Google Scholar] [CrossRef]
- Gong, W.; Liu, J. Effect of Wettability Heterogeneity on Water-Gas Two-Phase Displacement Behavior in a Complex Pore Structure by Phase-Field Model. Energies 2022, 15, 7658. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, H.; He, Z.; Liu, X.; Chen, L.; Tao, W.-Q. Effects of Cassie-Wenzel Wetting Transition on Two-Phase Flow in Porous Media. Int. Commun. Heat Mass Transf. 2023, 146, 106931. [Google Scholar] [CrossRef]
- Zhao, B.; MacMinn, C.W.; Juanes, R. Wettability Control on Multiphase Flow in Patterned Microfluidics. Proc. Natl. Acad. Sci. USA 2016, 113, 10251–10256. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Lv, P.; Liu, Y.; Jiang, L.; Tetsuya, S.; Song, Y.; Wu, B.; Liu, S. CO2/Water Two-Phase Flow in a Two-Dimensional Micromodel of Heterogeneous Pores and Throats. RSC Adv. 2016, 6, 73897–73905. [Google Scholar] [CrossRef]
- Chen, R.; Xu, W.; Chen, Y.; Hu, Y.; Li, J.; Zhuang, D.; Bate, B. Modeling Pore-Scale CO2 Plume Migration with a Hypergravity Model. Geoenergy Sci. Eng. 2023, 231, 212294. [Google Scholar] [CrossRef]
- Dlotko, T. Navier-Stokes-Cahn-Hilliard System of Equations. J. Math. Phys. 2022, 63, 111511. [Google Scholar] [CrossRef]
- Jacqmin, D. Contact-Line Dynamics of a Diffuse Fluid Interface. J. Fluid Mech. 2000, 402, 57–88. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, G. A Blowup Criterion for Nonhomogeneous Incompressible Navier–Stokes–Landau–Lifshitz System in 2-D. Math. Methods Appl. Sci. 2023, 46, 2500–2516. [Google Scholar] [CrossRef]
- Yang, J.; Ju, Q. Existence of Global Weak Solutions for Navier-Stokes-Poisson Equations with Quantum Effect and Convergence to Incompressible Navier-Stokes Equations. Math. Methods Appl. Sci. 2015, 38, 3629–3641. [Google Scholar] [CrossRef]
- Yang, J.; Wang, S. Convergence of Compressible Navier-Stokes-Maxwell Equations to Incompressible Navier-Stokes Equations. Sci. China Math. 2014, 57, 2153–2162. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Q. Cahn-Hilliard vs Singular Cahn-Hilliard Equations in Phase Field Modeling. Commun. Comput. Phys. 2010, 7, 362–382. [Google Scholar] [CrossRef]
- Basirat, F.; Yang, Z.; Niemi, A. Pore-Scale Modeling of Wettability Effects on CO2—Brine Displacement during Geological Storage. Adv. Water Resour. 2017, 109, 181–195. [Google Scholar] [CrossRef]
- Jacqmin, D. Calculation of Two-Phase Navier–Stokes Flows Using Phase-Field Modeling. J. Comput. Phys. 1999, 155, 96–127. [Google Scholar] [CrossRef]
- Yue, P.; Zhou, C.; Feng, J.J.; Ollivier-Gooch, C.F.; Hu, H.H. Phase-Field Simulations of Interfacial Dynamics in Viscoelastic Fluids Using Finite Elements with Adaptive Meshing. J. Comput. Phys. 2006, 219, 47–67. [Google Scholar] [CrossRef]
- Erbil, H.Y. Surface Chemistry: Of Solid and Liquid Interfaces, 1st ed.; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-1-4051-1968-9. [Google Scholar]
- Cieplak, M.; Robbins, M.O. Dynamical Transition in Quasistatic Fluid Invasion in Porous Media. Phys. Rev. Lett. 1988, 60, 2042–2045. [Google Scholar] [CrossRef] [PubMed]
- Cieplak, M.; Robbins, M.O. Influence of Contact Angle on Quasistatic Fluid Invasion of Porous Media. Phys. Rev. B 1990, 41, 11508–11521. [Google Scholar] [CrossRef]
- Lan, T.; Hu, R.; Guo, W.; Wei, G.; Chen, Y.; Zhou, C. Direct Prediction of Fluid-Fluid Displacement Efficiency in Ordered Porous Media Using the Pore Structure. Water Resour. Res. 2022, 58, e2021WR031875. [Google Scholar] [CrossRef]
- Hu, R.; Lan, T.; Wei, G.-J.; Chen, Y.-F. Phase Diagram of Quasi-Static Immiscible Displacement in Disordered Porous Media. J. Fluid Mech. 2019, 875, 448–475. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, C.; Chen, M.; Chi, Y.; Zhang, Y.; Zhao, J. Pore-Scale Visualization Study on CO2 Displacement of Brine in Micromodels with Circular and Square Cross Sections. Int. J. Greenh. Gas Control. 2020, 95, 102958. [Google Scholar] [CrossRef]
- Brown, C.E.; Neustadter, E.L. The Wettability of Oil/Water/Silica Systems with Reference to Oil Recovery. J. Can. Pet. Technol. 1980, 19, PETSOC-80-03-06. [Google Scholar] [CrossRef]





| Invading Fluid | Defending Fluid | σ (mN/m) | Contact Angle | Flow Rate U (m/s) | lgM | lgCa |
|---|---|---|---|---|---|---|
| CH4 | water | 70 | 90° | 0.005, 0.01, 0.02, 0.05 | −1.95 | −6.09,−5.79,−5.49,−5.09 |
| −1.22 | −5.37, −5.07, −4.77, −4.37 | |||||
| −0.52 | −4.67, −4.37, −4.07, −3.67 | |||||
| 0 | −4.15, −3.85, −3.55, −3.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Guo, C.; Liu, N.; Fan, K.; Zhang, X.; Liu, T. Effect of Wettability and Permeability on Pore-Scale of CH4–Water Two-Phase Displacement Behavior in the Phase Field Model. Appl. Sci. 2024, 14, 6815. https://doi.org/10.3390/app14156815
Wang Z, Guo C, Liu N, Fan K, Zhang X, Liu T. Effect of Wettability and Permeability on Pore-Scale of CH4–Water Two-Phase Displacement Behavior in the Phase Field Model. Applied Sciences. 2024; 14(15):6815. https://doi.org/10.3390/app14156815
Chicago/Turabian StyleWang, Zedong, Chang Guo, Nan Liu, Kai Fan, Xiangliang Zhang, and Ting Liu. 2024. "Effect of Wettability and Permeability on Pore-Scale of CH4–Water Two-Phase Displacement Behavior in the Phase Field Model" Applied Sciences 14, no. 15: 6815. https://doi.org/10.3390/app14156815
APA StyleWang, Z., Guo, C., Liu, N., Fan, K., Zhang, X., & Liu, T. (2024). Effect of Wettability and Permeability on Pore-Scale of CH4–Water Two-Phase Displacement Behavior in the Phase Field Model. Applied Sciences, 14(15), 6815. https://doi.org/10.3390/app14156815







