Interleaved Modified SEPIC Converters with Soft Switching and High Power Factor for LED Lighting Appliance
Abstract
1. Introduction
2. Proposed LED Driver and Analysis of Steady-State Operation
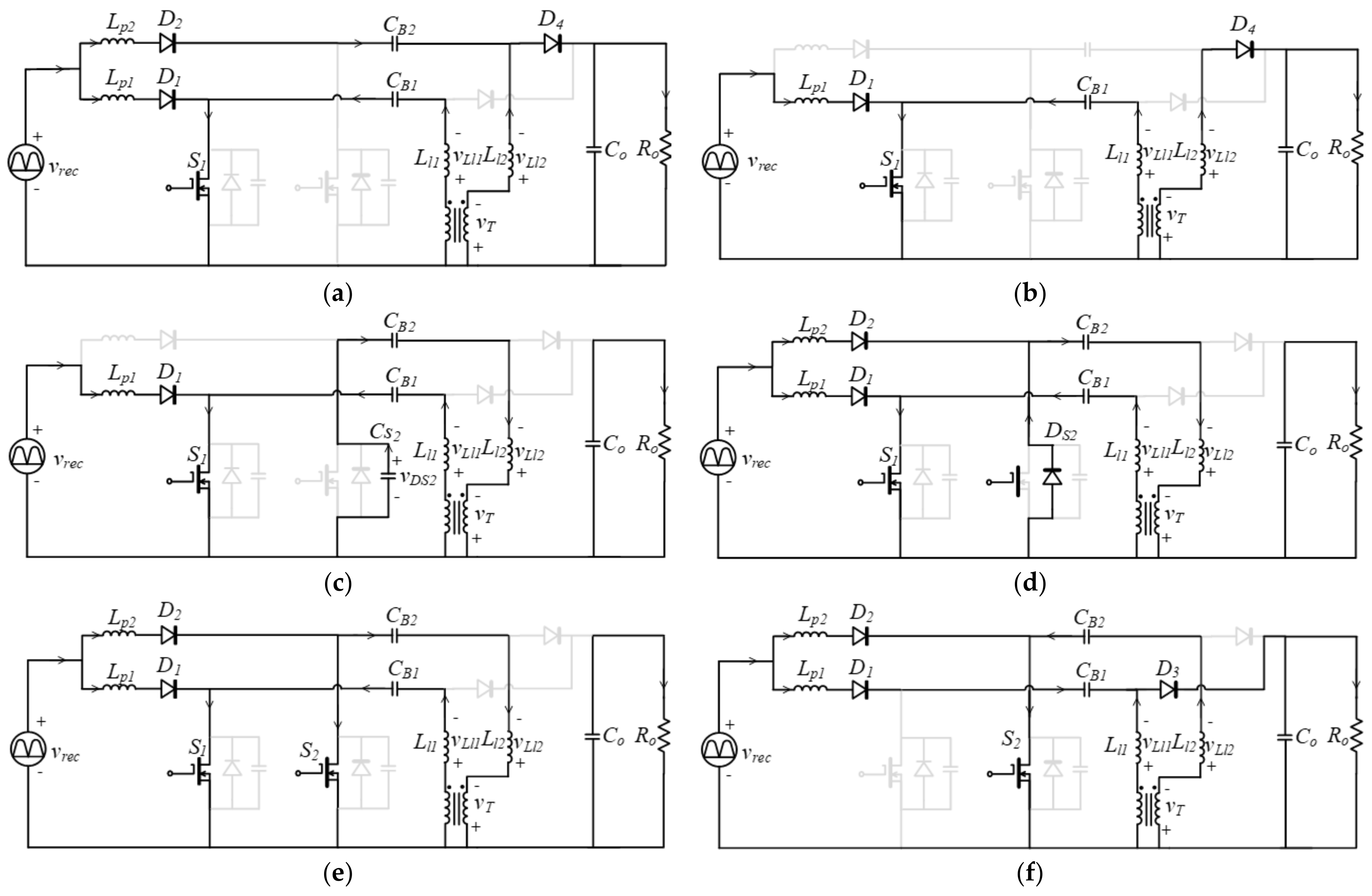
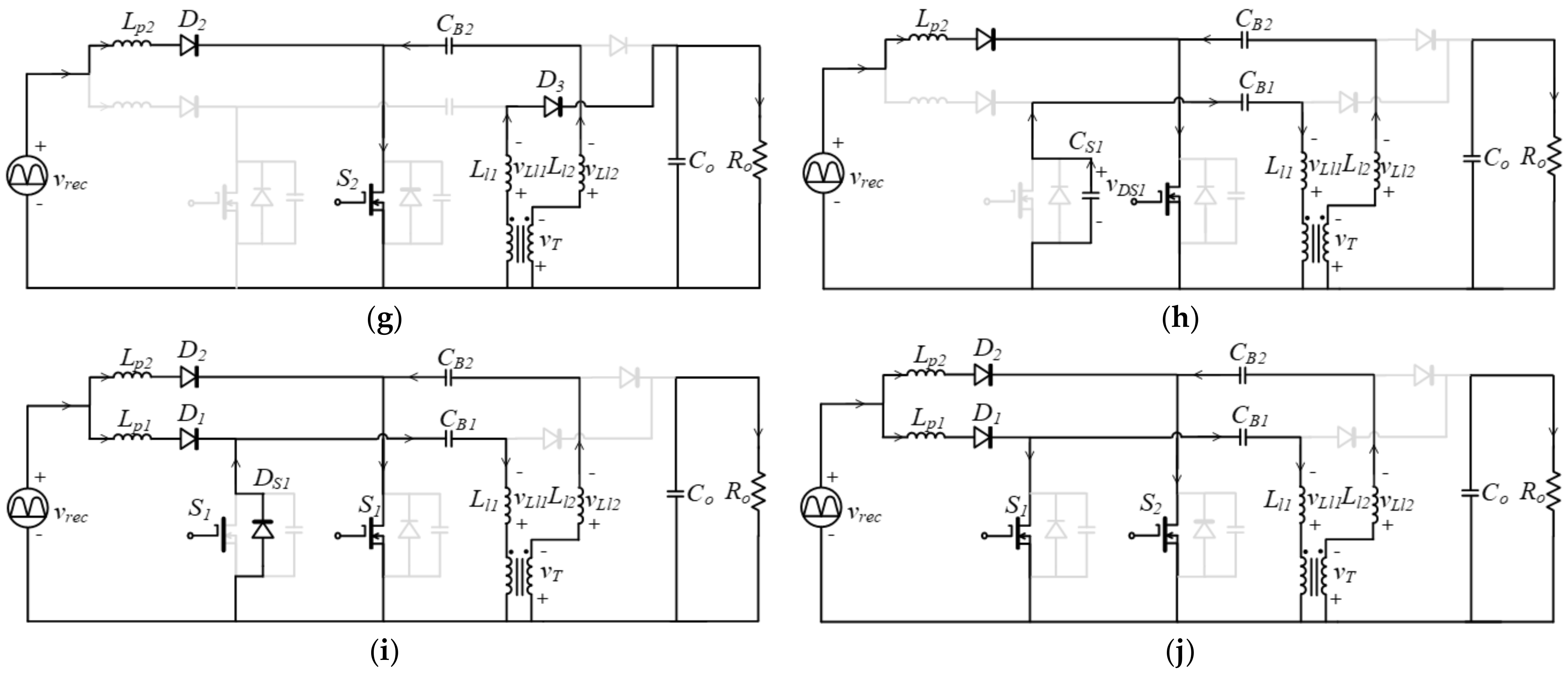
2.1. Circuit Topology
2.2. Analysis of Operation Mode
- (1)
- In order to ensure ZCS operation for all diodes, the currents of Lp1 and Lp2 are designed to operate in discontinuous-current mode (DCM), and the winding currents of T1 are all designed to decrease to zero amps.
- (2)
- All components are considered ideal except for the parasitic capacitance (CS1 and CS2) and intrinsic diodes (DS1 and DS2) of the S1 and S2.
- (3)
- The two SCPIC circuits are identical with Lp1 = Lp2 = Lp, CB1 = CB2 = CB, VB1 = VB2 = VB.
- (4)
- Capacitors CB1, CB2, and Co are large enough that the voltages across them (VB1, VB2, and VO) can be regarded as constant.
- (5)
- The winding resistance and iron loss of T1 are neglected. The leakage inductance in the primary and secondary windings are equal (Ll1 = Ll2 = Ll), and the mutual inductance Lm is large enough so that the mutual inductance current is regarded as a constant ILm.
- (6)
- S1 and S2 are turned on and off at a high frequency (fs) well above the input line frequency (fL). Therefore, the rectified input voltage can be regarded as a constant value in each high-frequency cycle.
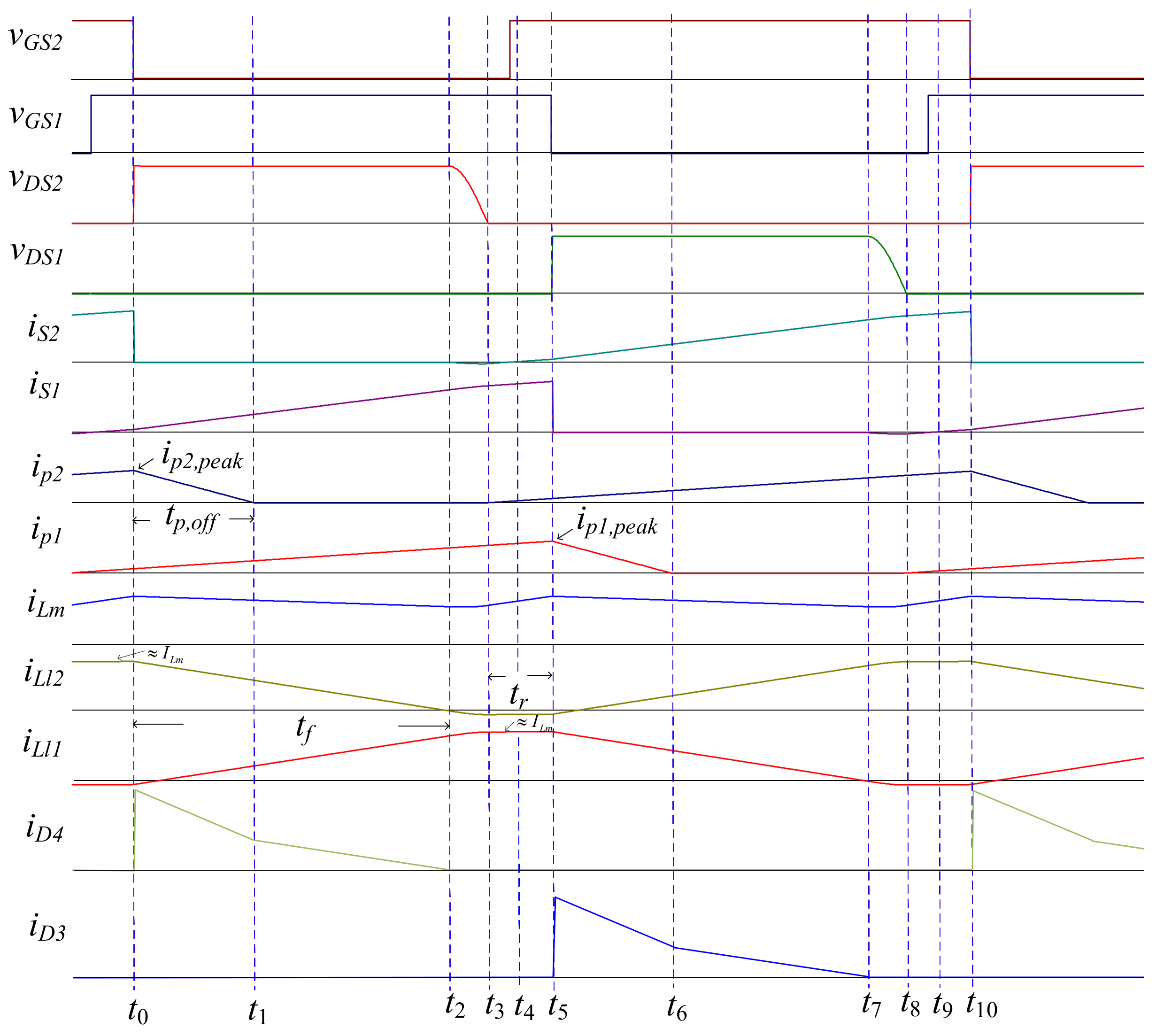
2.2.1. Operation Mode 1 (t0 < t < t1)
2.2.2. Operation Mode 2 (t1 < t < t2)
2.2.3. Operation Mode 3 (t2 < t < t3)
2.2.4. Operation Mode 4 (t3 < t < t4)
2.2.5. Operation Mode 5 (t4 < t < t5)
2.2.6. Operation Mode 6 (t5 < t < t6) ~ Operation Mode 10 (t9 < t < t10)
3. Mathematical Equations for Parameters Design
3.1. Boost-Typed PFC Converter
3.2. Buck–Boost Converter
4. Parameters Design and Experimental Results
4.1. Parameters Design
- A.
- Choose duty ratio and dc-link voltage.
- B.
- Calculate PFC inductance.
- C.
- Determine the leakage inductance and the mutual inductance of T1.
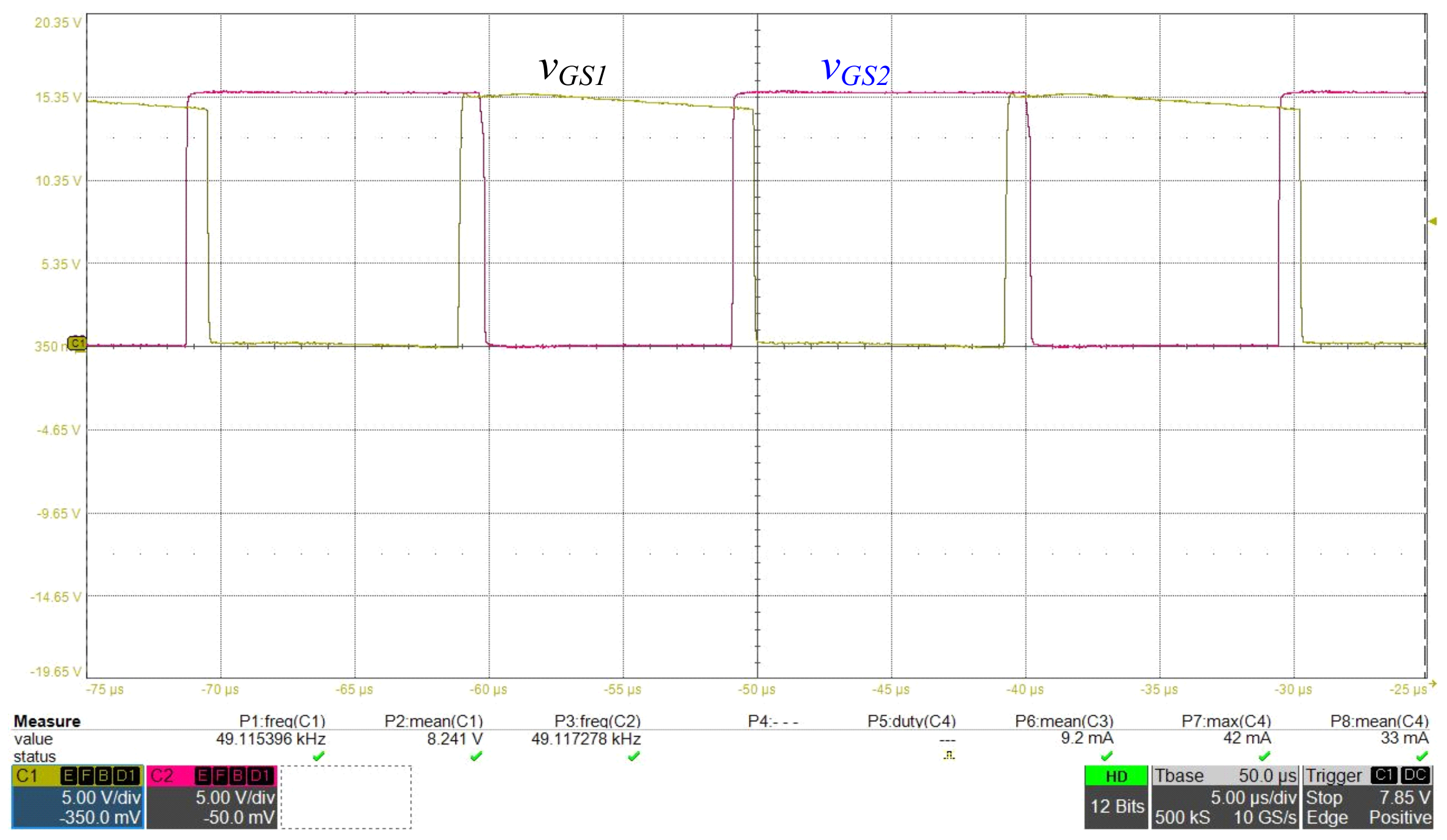
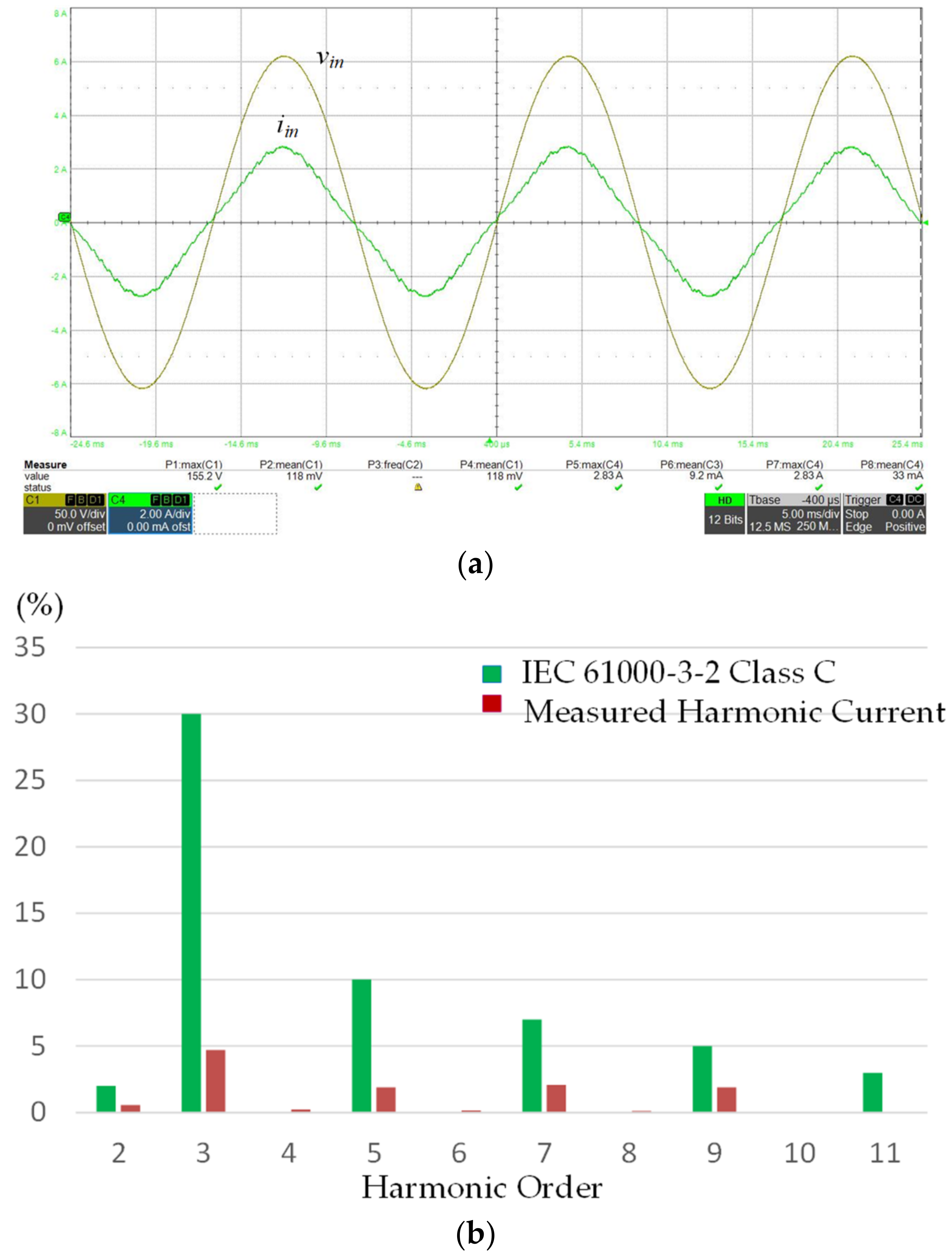
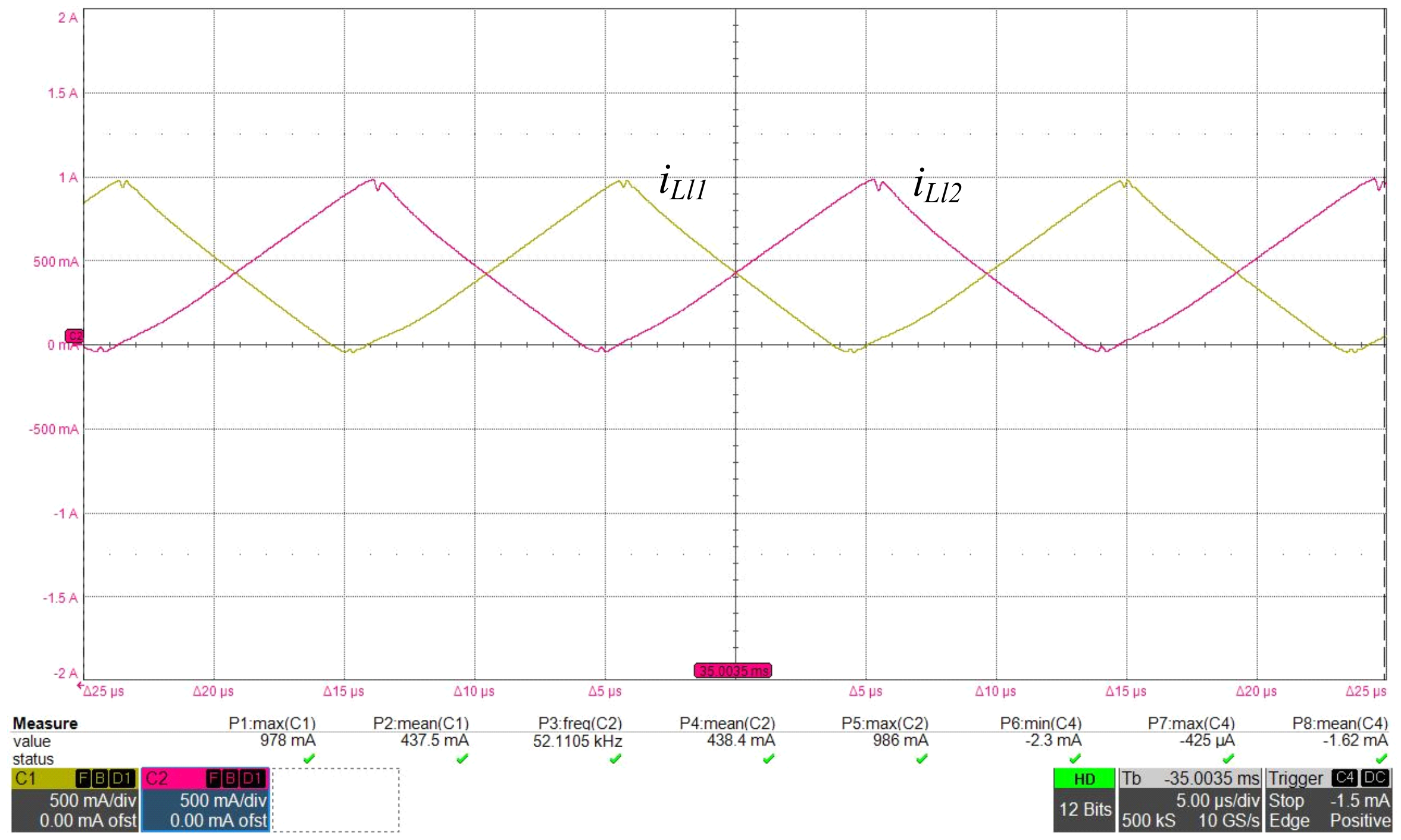
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhan, X.; Chung, H.; Zhang, R. Investigation into the use of single inductor for driving multiple series-connected LED channels. IEEE Trans. Power Electron. 2017, 32, 3034–3050. [Google Scholar] [CrossRef]
- Cheng, C.A.; Lee, C.M.; Chang, E.H.; Hou, S.H.; Lan, L.F.; Lin, C.K. A novel integrated electronic lighting driver circuit for supplying an LED projection lamp with high power factor and soft switching characteristics. Electronics 2023, 12, 4642. [Google Scholar] [CrossRef]
- Esteki, M.; Khajehoddin, S.A.; Safaee, A.; Li, Y. LED system applications and LED driver topologies: A review. IEEE Access 2023, 11, 38324–38358. [Google Scholar] [CrossRef]
- Abdelmessih, G.Z.; Alonso, J.M.; Dalla Costa, M.A. Analysis, design, and experimentation of the active hybrid-series-parallel PWM dimming scheme for high-efficient off-line LED drivers. IET Power Electron. 2019, 12, 1697–1705. [Google Scholar] [CrossRef]
- Subjak, J.S.; Mcquilkin, J.S. Harmonics-causes, effects, measurements, and analysis: An update. IEEE Trans. Ind. Appl. 1990, 26, 1034–1042. [Google Scholar] [CrossRef]
- IEC 61000-3-2:2018/AMD2:2024; Amendment 2—Electromagnetic compatibility (EMC)—Part 3-2: Limits—Limits for Harmonic Current Emissions (Equipment Input Current ≤ 16 A Per Phase). International Electrotechnical Commission (IEC): Geneva, Switzerland, 2024. Available online: https://webstore.iec.ch/en/publication/77736 (accessed on 24 July 2024).
- IEEE 519-2022; IEEE Standard for Harmonic Control in Electric Power Systems. Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2022. Available online: https://standards.ieee.org/ieee/519/10677 (accessed on 24 July 2024).
- Arseneau, R.; Ouellette, M. The effects of supply harmonics on the performance of compact fluorescent lamps. IEEE Trans. Power Deliv. 1993, 8, 473–479. [Google Scholar] [CrossRef]
- Christiansen, R. Effect of high levels of harmonics from lighting equipment and system. In Proceedings of the Conference Record of the 1991 IEEE Industry Applications Society Annual Meeting, Dearborn, MI, USA, 28 September–4 October 1991; pp. 1859–1862. [Google Scholar]
- Camponogara, D.; Ferreira, G.F.; Campos, A.; Dalla Costa, M.A.; Garcia, J. Offline LED driver for street lighting with an optimized cascade structure. IEEE Trans. Ind. Appl. 2013, 49, 2437–2443. [Google Scholar] [CrossRef]
- Cheng, H.L.; Chang, Y.N.; Cheng, C.A.; Chang, C.H.; Lin, Y.H. High-power-factor dimmable LED driver with low-frequency pulse-width modulation. IET Power Electron. 2016, 9, 2139–2146. [Google Scholar] [CrossRef]
- Cheng, C.A.; Cheng, H.L.; Chung, T.Y. A novel single-stage high-power-factor LED street-lighting driver with coupled inductors. IEEE Trans. Ind. Appl. 2014, 50, 2821–2826. [Google Scholar] [CrossRef]
- Gacio, D.; Alonso, J.M.; Calleja, A.J.; García, J.; Rico-Secades, M. A universal-input single-stage high-power-factor power supply for HB-LEDs based on integrated buck-flyback converter. IEEE Trans. Ind. Electron. 2011, 58, 589–599. [Google Scholar] [CrossRef]
- Alonso, J.M.; Viña, J.; Vaquero, D.G.; Martínez, G.; Osório, R. Analysis and design of the integrated double buck-boost converter as a high-power-factor driver for power-LED lamps. IEEE Trans. Ind. Electron. 2012, 59, 1689–1697. [Google Scholar] [CrossRef]
- Li, Y.C.; Chen, C.L. A novel primary-side regulation scheme for single-stage high-power-factor AC–DC LED driving circuit. IEEE Trans. Ind. Electron. 2013, 60, 4978–4986. [Google Scholar] [CrossRef]
- Cheng, C.A.; Chang, C.H.; Cheng, H.L.; Chang, E.C.; Lin, Y.R.; Lan, L.F. A novel light-emitting diode streetlight driver circuit applied to a direct current-input voltage source. Sustainability 2023, 15, 10934. [Google Scholar] [CrossRef]
- Moon, S.C.; Koo, G.B.; Moon, G.W. A new control method of interleaved single-stage flyback AC-DC converter for outdoor LED lighting systems. IEEE Trans. Power Electron. 2013, 28, 4051–4062. [Google Scholar] [CrossRef]
- Lam, C.W.; Jain, P.K. A high power factor, electrolytic capacitor-less AC-input LED driver topology with high frequency pulsating output current. IEEE Trans. Power Electron. 2015, 30, 943–955. [Google Scholar] [CrossRef]
- Wang, S.; Ruan, X.; Yao, K.; Tan, S.C.; Yang, Y.; Ye, Z. A flicker free electrolytic capacitor-less AC-DC LED driver. IEEE Trans. Power Electron. 2012, 27, 4540–4548. [Google Scholar] [CrossRef]
- Zhang, F.; Ni, J.; Yu, Y. High power factor AC–DC LED driver with film capacitors. IEEE Trans. Power Electron. 2013, 28, 4831–4840. [Google Scholar] [CrossRef]
- Yu, X.; Su, J.; Guo, S.; Zhong, S.; Shi, Y.; Lai, J. Properties and synthesis of lossless snubbers and passive soft-switching PWM converters. IEEE Trans. Power Electron. 2020, 35, 3807–3826. [Google Scholar] [CrossRef]
- Lee, J.H.; Yu, D.H.; Kim, J.G.; Kim, Y.H.; Shin, S.C.; Jung, D.Y.; Jung, Y.C.; Won, C.Y. Auxiliary switch control of a bidirectional soft-switching dc/dc converter. IEEE Trans. Power Electron. 2013, 28, 5446–5457. [Google Scholar] [CrossRef]
- Yun, J.J.; Choe, H.J.; Hwang, Y.H.; Park, Y.K.; Kang, B. Improvement of power-conversion efficiency of a dc-dc boost converter using a passive snubber circuit. IEEE Trans. Ind. Electron. 2012, 59, 1808–1814. [Google Scholar] [CrossRef]
- Lo, Y.K.; Chiu, H.J.; Lin, J.Y.; Wang, C.F.; Lin, C.Y.; Gu, B. Single-stage interleaved active-clamping forward converter employing two transformers. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 1898–1905. [Google Scholar]
- Wang, Y.; Guan, Y.; Huang, J.; Wang, W.; Xu, D. A single-stage LED driver based on interleaved buck–boost circuit and LLC resonant converter. IEEE J. Emerg. Sel. Topics Power Electron. 2015, 3, 732–741. [Google Scholar] [CrossRef]
- Ma, H.; Lai, J.S.; Zheng, C.; Sun, P. A high-efficiency quasi-single-stage bridgeless electrolytic capacitor-free high-power AC–DC driver for supplying multiple LED strings in parallel. IEEE Trans. Power Electron. 2016, 3, 5825–5836. [Google Scholar] [CrossRef]
- Liu, J.; Tian, H.; Liang, G.; Zeng, J. A bridgeless electrolytic capacitor free LED driver based on series-resonant converter with constant frequency control. IEEE Trans. Power Electron. 2019, 34, 2712–2725. [Google Scholar] [CrossRef]
- Filho, O.C.D.S.; Tofoli, F.; Barreto, L.H.S.C.; Oliveira, D.D.S. Single-phase isolated AC–AC symmetrical full-bridge converter. IEEE J. Emerg. Sel. Topics Power Electron. 2022, 10, 846–855. [Google Scholar] [CrossRef]
- Cheng, H.L.; Hwang, L.C.; Chang, H.H.; Wang, Q.Y.; Cheng, C.A. High-efficiency flicker-free LED driver with soft-switching feature. Micromachines 2022, 13, 797. [Google Scholar] [CrossRef]
- Liu, K.H.; Lin, Y.L. Current waveform distortion in power factor correction circuits employing discontinuous-mode boost converters. In Proceedings of the IEEE Power Electronics Specialists Conference, Milwaukee, WI, USA, 26–29 June 1989; pp. 825–829. [Google Scholar]






| Item | Value |
|---|---|
| Input voltage, Vin | 110 ± 10% Vrms, 60 Hz |
| Output voltage, VLED | 216 V (60 × 3.6 V) |
| Output current, VLED | 0.84 A (3 × 0.28 A) |
| Output power, Po | 180 W |
| Switching frequency, fs (at rated power) | 50 kHz |
| Item | Value |
|---|---|
| Low-pass filter Lf, Cf | Lf = 0.5 mH, Cf = 2 µF |
| Diodes Dr1–Dr4 | MUR460 |
| Diodes D1–D2 | C3D10060A |
| PFC inductance Lp1, Lp2 | 0.58 mH |
| DC-link capacitance CB1, CB2 | 100 µF |
| Mutual inductance Lm | 16.54 mH |
| Leakage inductance Ll1, Ll2 | 1.84 mH |
| Output capacitance Co | 100 µF |
| Active switches S1, S2 | IPW65R080CFD |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.-L.; Cheng, C.-A.; Chang, C.-H.; Chang, E.-C.; Hwang, L.-C.; Hung, Y.-C. Interleaved Modified SEPIC Converters with Soft Switching and High Power Factor for LED Lighting Appliance. Appl. Sci. 2024, 14, 6656. https://doi.org/10.3390/app14156656
Cheng H-L, Cheng C-A, Chang C-H, Chang E-C, Hwang L-C, Hung Y-C. Interleaved Modified SEPIC Converters with Soft Switching and High Power Factor for LED Lighting Appliance. Applied Sciences. 2024; 14(15):6656. https://doi.org/10.3390/app14156656
Chicago/Turabian StyleCheng, Hung-Liang, Chun-An Cheng, Chien-Hsuan Chang, En-Chih Chang, Lain-Chyr Hwang, and Yi-Chan Hung. 2024. "Interleaved Modified SEPIC Converters with Soft Switching and High Power Factor for LED Lighting Appliance" Applied Sciences 14, no. 15: 6656. https://doi.org/10.3390/app14156656
APA StyleCheng, H.-L., Cheng, C.-A., Chang, C.-H., Chang, E.-C., Hwang, L.-C., & Hung, Y.-C. (2024). Interleaved Modified SEPIC Converters with Soft Switching and High Power Factor for LED Lighting Appliance. Applied Sciences, 14(15), 6656. https://doi.org/10.3390/app14156656










