Groundwater Discharge Limits of Mountain Tunnels Based on the Normal Growth of Typical Herbaceous Plants
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Preparation and Implementation
2.2. Effects of Different Groundwater Depths on Plant Growth
3. The Variation Law of Groundwater during Tunnel Construction
3.1. Numerical Model
- (1)
- The surrounding rock is considered as an isotropic material using the Mohr Coulomb elastoplastic model.
- (2)
- The tunnel excavation uses the step method, with the construction sequence and times as follows:
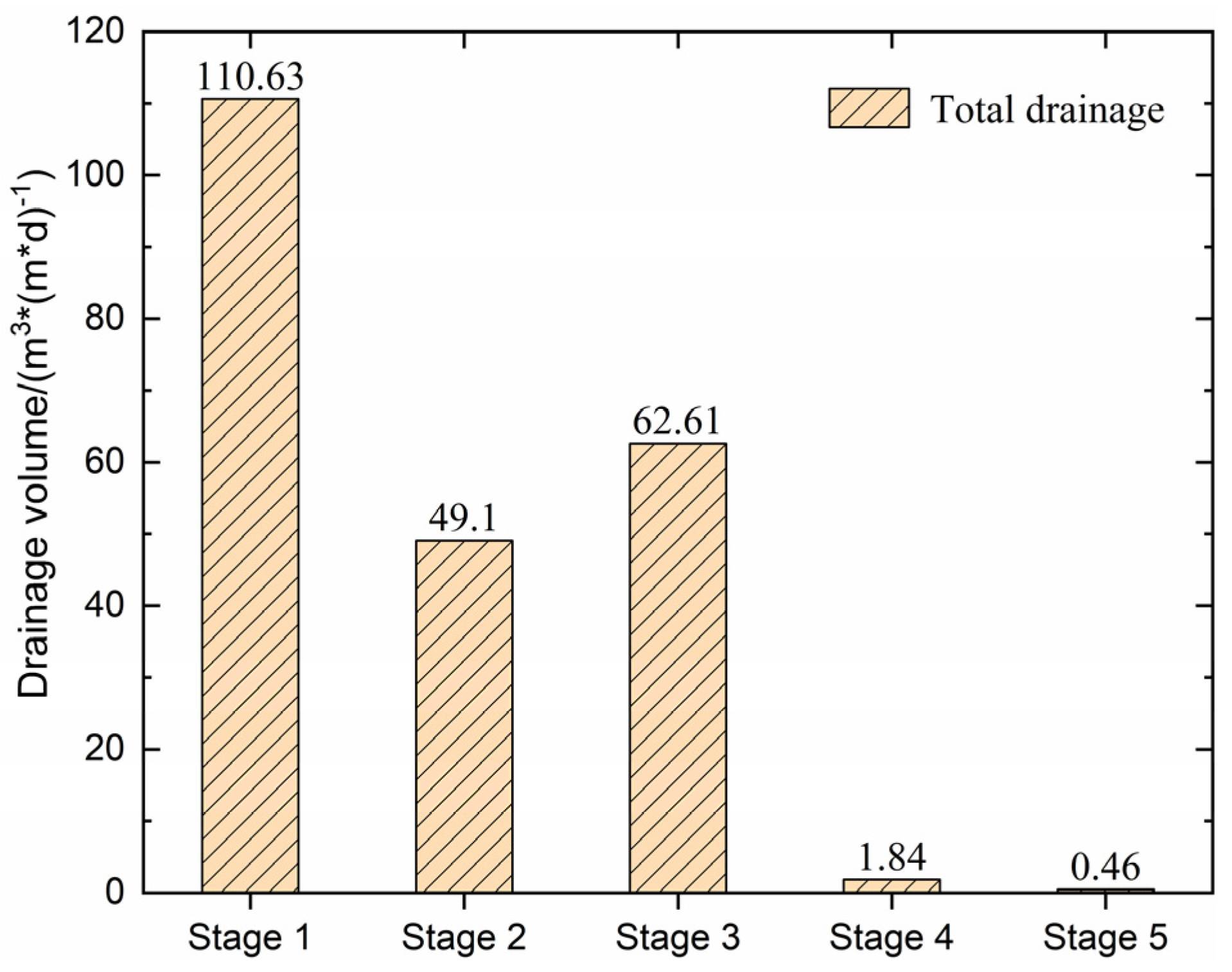
- Stage 1: Upper step excavation (3 h);
- Stage 2: Initial support for upper steps (6 h);
- Stage 3: Lower bench excavation (9 h);
- Stage 4: Initial support for descending steps (12 h);
- Stage 5: Construction of secondary lining (steady-state analysis).
3.2. Tunnel Drainage Volume
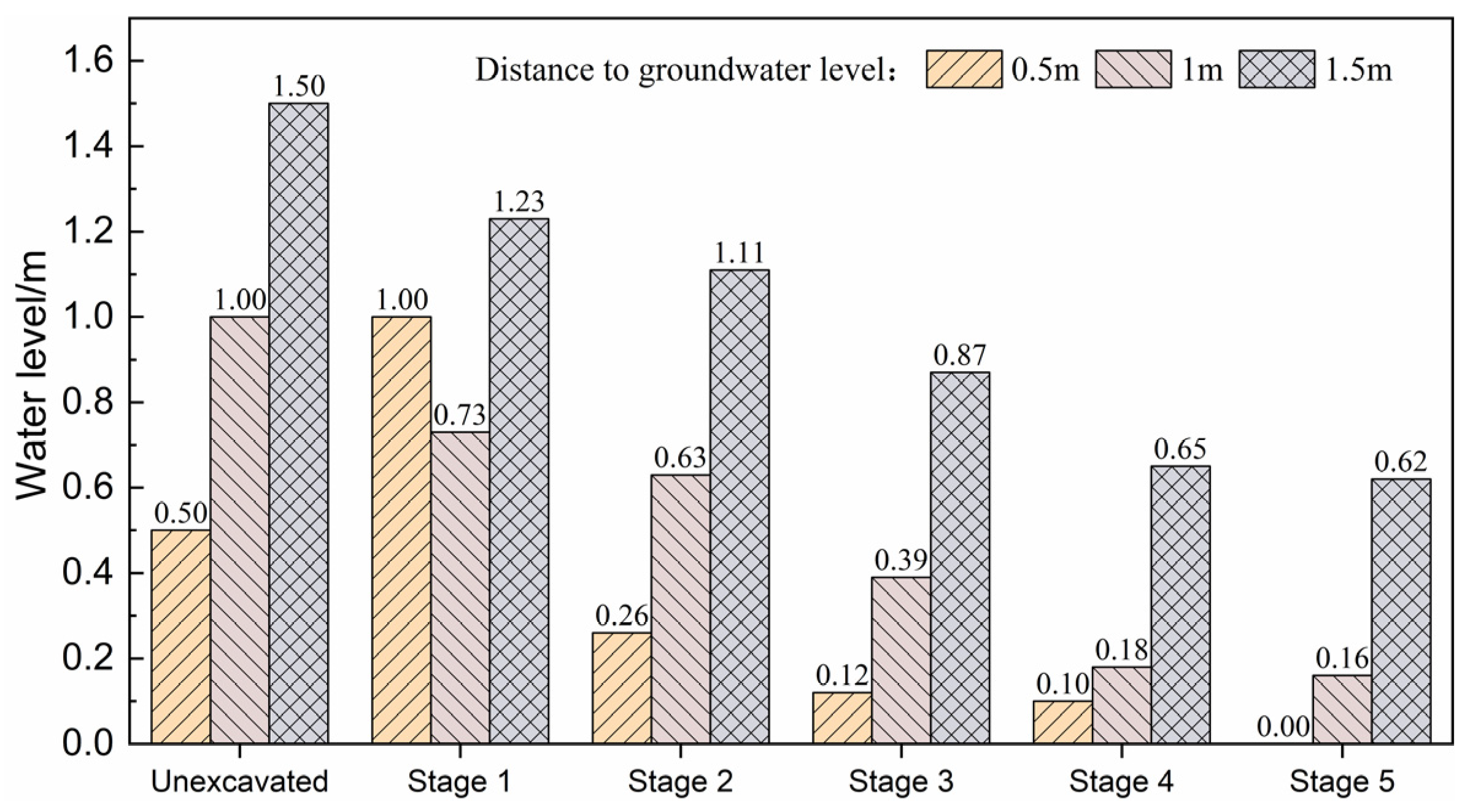
3.3. Groundwater Level
4. The Influence of Different Waterproofing and Drainage Measures on the Underground Water Level in the Tunnel
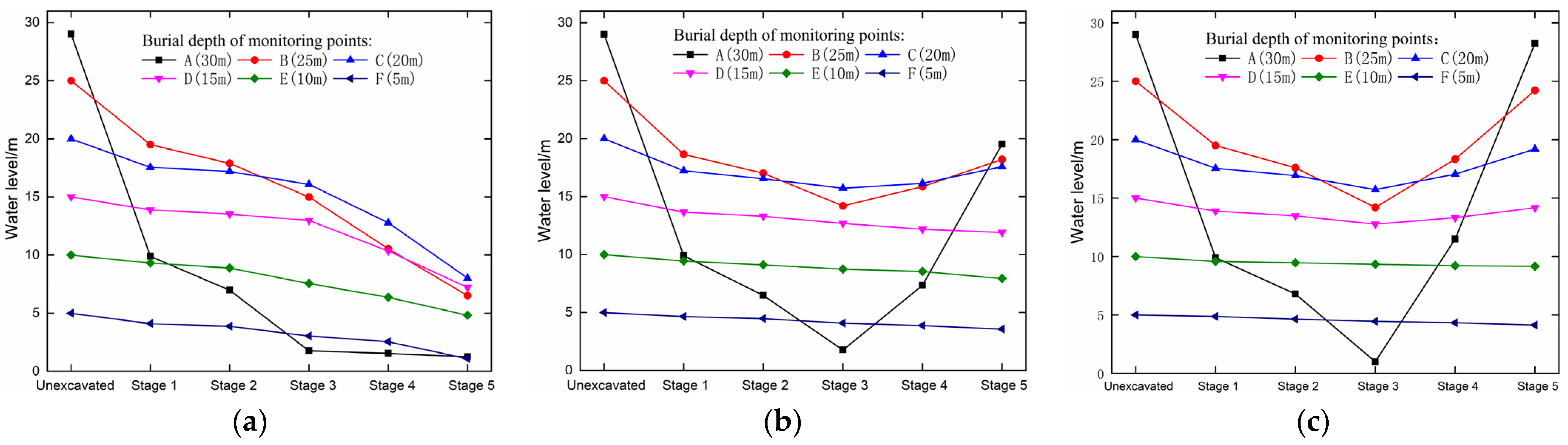
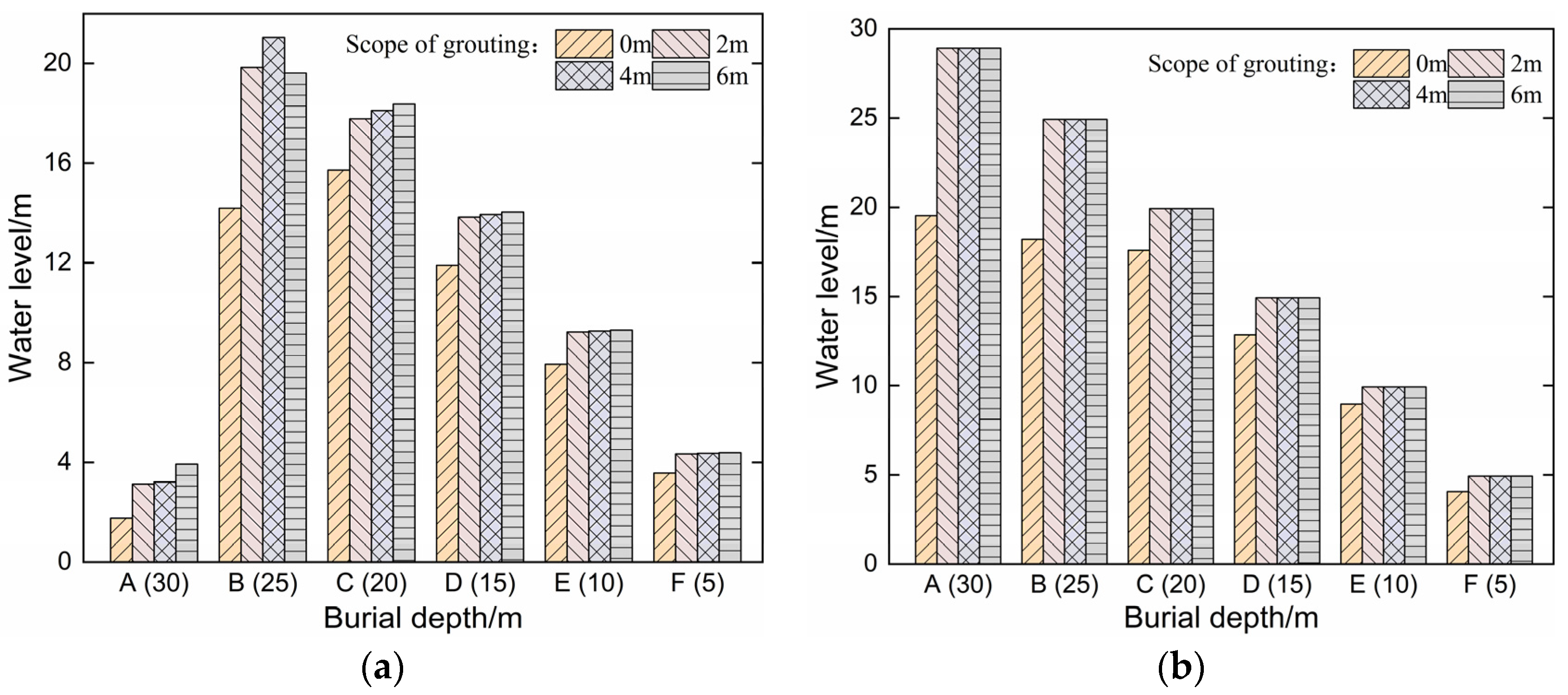
4.1. Influence of Tunnel Drainage Mode on Groundwater Level
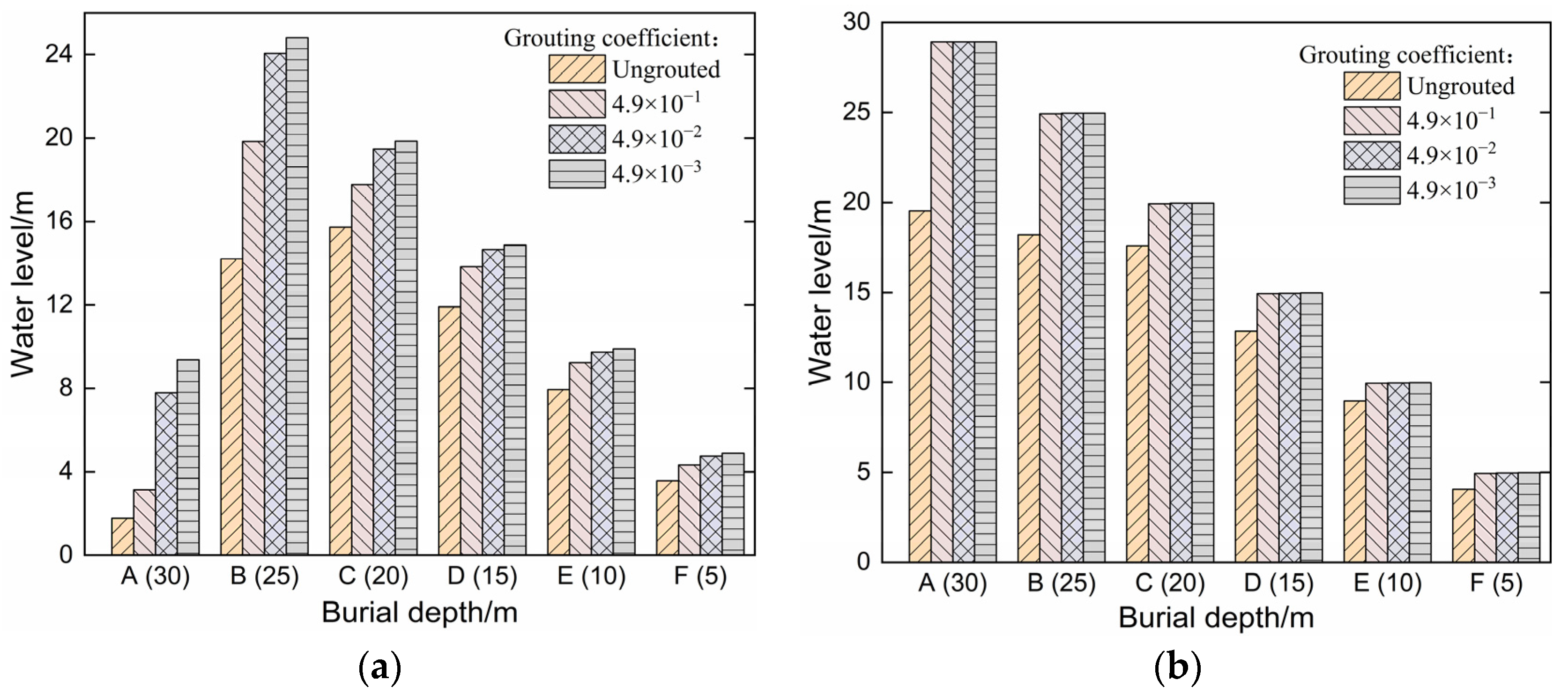
4.2. The Influence of the Thickness of the Water Blocking Grouting Circle on the Groundwater Level of the Tunnel
4.3. The Influence of Permeability Coefficient of Water-Blocking Grouting Circle on Tunnel Groundwater Level
5. Tunnel Limited Discharge Values Based on Vegetation Protection
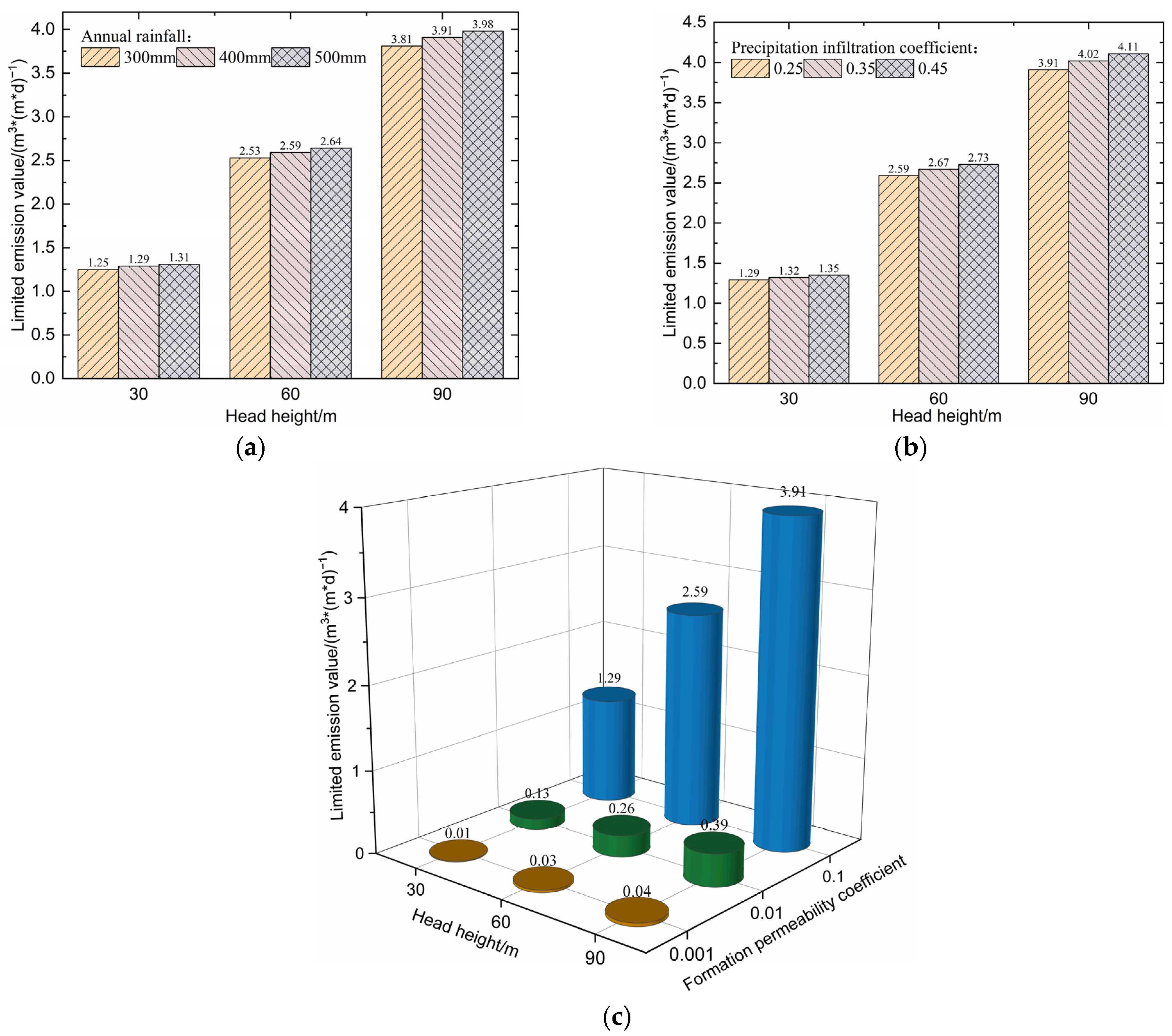
5.1. Calculation Method for Limited Discharge Values
5.2. Calculation Example of Limited Discharge Values
6. Discussion
6.1. The Relationship between Normal Growth of Different Plants and Groundwater Buried Depth
6.2. Research on Grouting Parameters for Tunnels
7. Conclusions
- (1)
- The transplant experiments showed that Artemisia annua grew 4 cm taller than before the experiment when soil moisture content was 30% and groundwater depth was 80 cm. Stipa grew 2.5 cm taller than before the experiment when soil moisture content was 25% and groundwater depth was 80 cm. These increments of growth were the largest. Artemisia annua and Stipa grew well also when groundwater depth was 60 cm. Thus, it is suggested that groundwater depth be controlled between 0.6 m and 0.8 m to protect the normal growth of herbaceous plants.
- (2)
- Based on ensuring the normal growth of herbaceous plants around the tunnel, a grouting circle with a thickness of 2 m and a permeability coefficient of 4.9 × 10−3 m/d are proposed. In tunnel construction, groundwater level decline was between 0.02 m and 0.66 m. After the secondary lining construction, the water level gradually recovered. These grouting parameters ensure that the recovery degree of water level can exceed 90%. When these grouting parameters were used, these herbaceous plants were able to normally grow in the construction of Longzang Mountain No. 1 Tunnel.
- (3)
- Based on the hydrology, meteorology, and geology information of Longzang Mountain No. 1 Tunnel, the results of the empirical formula calculation showed that when the groundwater discharge limit was 0.2~4.0 m3/(m·d), the groundwater level decline was less than 0.8 m. In this situation, herbaceous plants in Qinghai’s alpine grasslands were able to normally grow. This research offers guidance and support for managing groundwater discharge during tunnel construction in ecologically fragile areas, such as the Three Rivers Source in Qinghai.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xin, G.; Wang, B.; Zheng, H.; Zeng, L.; Yang, X. Study on Water Inrush Characteristics of Hard Rock Tunnel Crossing Heterogeneous Faults. Appl. Sci. 2024, 14, 2536. [Google Scholar] [CrossRef]
- Chen, Z.; He, C.; Zhang, Y.; Xu, Z.; Li, Z.; Yu, B. The impact of formation heterogeneity on water discharge and groundwater depletion of an excavated tunnel. J. Hydrol. 2023, 627, 130403. [Google Scholar] [CrossRef]
- Jiang, T.; Pei, X.; Wang, W.; Li, L.; Guo, S. Effects of the Excavation of a Hydraulic Tunnel on Groundwater at the Wuyue Pumped Storage Power Station. Appl. Sci. 2023, 13, 5196. [Google Scholar] [CrossRef]
- Lv, Y.; Jiang, J.; Chen, L.; Hu, W.; Jiang, Y. Elaborate simulation and predication of the tunnel drainage effect on karst groundwater field and discharge based on Visual MODFLOW. J. Hydrol. 2022, 612, 128023. [Google Scholar] [CrossRef]
- Chen, Y.N.; Chen, Y.P.; Xu, C.C.; Ye, Z.X.; Li, Z.Q.; Zhu, C.G.; Ma, X.D. Effects of ecological water conveyance on groundwater dynamics and riparian vegetation in the lower reaches of Tarim River, China. Hydrol. Process. 2010, 24, 170–177. [Google Scholar] [CrossRef]
- Fu, A.; Chen, Y.; Li, W. Water use strategies of the desert riparian forest plant community in the lower reaches of Heihe River Basin, China. Sci. China (Earth Sci.) 2014, 57, 1293–1305. [Google Scholar] [CrossRef]
- Stirzaker, R.J.; Passioura, J.B.; Wilms, Y. Soil structure and plant growth: Impact of bulk density and biopores. Plant Soil 1996, 185, 151–162. [Google Scholar]
- Behzad, H.M.; Jiang, Y.J.; Arif, M.; Wu, C.; He, Q.F.; Zhao, H.J.; Lv, T. Tunneling induced groundwater depletion limits long-term growth dynamics of forest trees. Sci. Total Environ. 2022, 811, 152375. [Google Scholar] [CrossRef]
- Talebnejad, R.; Sepaskhah, A.R. Effect of different saline groundwater depths and irrigation water salinities on yield and water use of quinoa in lysimeter. Agric. Water Manag. 2015, 148, 177–188. [Google Scholar] [CrossRef]
- Du, J.; Wang, X.; Huo, Z.; Guan, H.; Xiong, Y.; Huang, G. Response of shelterbelt transpiration to shallow groundwater in arid areas. J. Hydrol. 2021, 592, 125611. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, J.; Zhou, X.; Li, F. Effects of shallow groundwater table and fertilization level on soil physico-chemical properties, enzyme activities, and winter wheat yield. Agric. Water Manag. 2018, 208, 307–317. [Google Scholar] [CrossRef]
- Wang, D.; Yu, Z.; Peng, G.; Zhao, C.; Ding, J.; Zhang, X. Water use strategies of Populus euphratica seedlings under groundwater fluctuation in the Tarim River Basin of Central Asia. Catena 2018, 166, 89–97. [Google Scholar] [CrossRef]
- Xu, H.; Li, X.; Gokdemir, C. Modeling and assessing the impact of tunnel drainage on terrestrial vegetation. Tunn. Undergr. Space Technol. 2021, 116, 104097. [Google Scholar] [CrossRef]
- Gu, J.; Guo, J.; Chen, F.; Li, J. Evolution Law and Grouting Treatment of Water Inrush in Hydraulic Tunnel Approaching Water-Rich Fault: A Case Study. Appl. Sci. 2024, 14, 3407. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, H.; Ge, W.; Zhang, J. Investigation of the emergency water supply schemes for youkou groundwater source field in Nanchang using a simulation–optimization model. Sci. Rep. 2024, 14, 2610. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhou, X.; Wang, B.; Cheng, X.; Wei, W. Methodology for the Prediction of Water Gushing in Tunnels in Igneous Fracture Tectonic Zones: A Case Study of a Tunnel in Guangdong Province, China. Appl. Sci. 2022, 12, 10438. [Google Scholar] [CrossRef]
- Zhang, N.; Niu, M.; Wan, F.; Lu, J.; Wang, Y.; Yan, X.; Zhou, C. Hazard Prediction of Water Inrush in Water-Rich Tunnels Based on Random Forest Algorithm. Appl. Sci. 2024, 14, 867. [Google Scholar] [CrossRef]
- Fu, H.; An, P.; Cheng, G.; Wen, S.; Li, J. Calculation of the Allowable Drainage of Parallel Tunnels Based on Ecological Environment Protection. KSCE J. Civ. Eng. 2022, 26, 2420–2427. [Google Scholar] [CrossRef]
- Gokdemir, C.; Li, Y.D.; Rubin, Y.; Li, X.J. Stochastic modeling of groundwater drawdown response induced by tunnel drainage. Eng. Geol. 2022, 297, 106529. [Google Scholar] [CrossRef]
- Huang, D.W.; Zhao, Z.Q.; Xu, C.J.; Luo, W.J.; Geng, D.X.; Shi, Y.F. Experimental study on influences of side grouting on deformation of shield tunnels under loads. Chin. J. Geotech. Eng. 2024, 46, 510–518. [Google Scholar]
- Liu, Y.C.; Yuan, Z.Y.; Cheng, X.S.; Li, G.; Zhang, T.X.; Li, Q.H. Experimental study on plugging effect of different grouting materials for water and sand leakage of tunnels. Chin. J. Geotech. Eng. 2021, 43, 249–252. [Google Scholar]
- Zheng, L.; Lian, X.; Huang, D.; Li, X.; Zou, J. Research on Seepage of Jointed Rock Mass of Tunnel and Limited Discharge of Grouting. Water 2022, 14, 104. [Google Scholar] [CrossRef]
- Ma, X.; Li, W.; Zhu, C.; Chen, Y. Spatio-temporal variation in soil moisture and vegetation along the lower reaches of Tarim River, China. Acta Ecol. Sin. 2010, 30, 4035–4045. [Google Scholar]
- Cheng, P.; Li, L.; Zou, J.F.; Zhao, L.H.; Luo, W. Determination Method for Water Discharge of Tunnel Based on the Ecological Water Requirement of Vegetation. J. China Railw. Soc. 2013, 35, 107–113. [Google Scholar]
- Shi, C.H.; Peng, L.M.; Zhao, D. Calculation of stratum deformation caused by tunnel excavation and dewatering. China Civ. Eng. J. 2008, 12, 91–96. [Google Scholar]
- Pagnozzi, M.; Coletta, G.; Leone, G.; Leone, G.; Catani, V.; Esposito, L.; Fiorillo, F. A steady-state model to simulate groundwater flow in unconfined aquifer. Appl. Sci. 2020, 10, 2708. [Google Scholar] [CrossRef]
- Xue, Y.Q. A Discussion on the Stable Well Flow Model and Dupuit Formula—Reply to Professor Chen Chongxi’s “Discussion”. J. Hydraul. Eng. 2011, 42, 1252–1256. [Google Scholar]
- Zhu, D.; Li, Q. Prediction of outflow in tunnel based on exper-imental permeating coefficient of precipitation. J. Railw. Eng. Soc. 1995, 1, 100–102. [Google Scholar]
- Liu, S.; Roberts, D.A.; Chadwick, O.A.; Still, C.J. Spectral responses to plant available soil moisture in a Californian grassland. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 31–44. [Google Scholar] [CrossRef]
- Siteng, Z.; Xueyong, Z.; Yulin, L. Relationship between the trait response of aboveground and belowground parts of dominant plant species to groundwater depth change in Horqin Sandy Land, eastern China. Ecol. Indic. 2023, 156, 111001. [Google Scholar]
- Dai, Y.; Wang, H.W.; Shi, Q.D. Contrasting plant water-use responses to groundwater depth from seedlings to mature trees in the Gurbantunggut Desert. J. Hydrol. 2022, 610, 127986. [Google Scholar] [CrossRef]
- Chang, L.N.; Zhao, X.Q. Multi-Functional Management and Natural Protected Area Construction of Grassland in Three-River Source National Park. Nat. Prot. Areas 2022, 2, 1–8. [Google Scholar]
- Han, Z.; Song, W.; Deng, X.; Xu, X. Grassland ecosystem responses to climate change and human activities within the Three-River Headwaters region of China. Sci. Rep. 2018, 8, 9079. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.M. Study on Eroded Environment and lts Soil and Water Loss Characteristics During Expressway Construction. J. Soil Water Conserv. 2006, 2, 5–9. [Google Scholar]
- Lei, D.; Zhang, Y.; Ran, Y.; Gao, L.; Li, J.; Li, Z.; Mo, J.; Liu, X. Assessment of ecosystem health based on landscape pattern in ecologically fragile regions at different spatial scales: A case study of Dianchi Lake basin, China. Front. Environ. Sci. 2023, 11, 1076344. [Google Scholar] [CrossRef]
- Zhang, C.P.; Zhang, D.; Wang, M.; Xiang, Y. Study on appropriate parameters of grouting circle for tunnels with limiting discharge lining in high water pressure and water-enriched region. Chin. J. Rock Mech. Eng. 2007, 26, 2270–2276. [Google Scholar]
- Hua, T.; Liu, S.; Zhang, X.; Meng, L.; Wang, P. Numerical analysis of grouting of water-enriched karst highway tunnel based on critical water-enriched height. Processes 2023, 11, 149. [Google Scholar] [CrossRef]
- Hongpeng, L.; Yongli, X.; Xiaohua, Y. Treatment effect analysis of shallow-buried crushed surrounding rocks under unsymmetrical pressure reinforced with surface pregrouting technology in highway tunnel. Chin. J. Rock Mech. Eng. 2008, 27, 2309–2315. [Google Scholar]
- Liu, J.; Chen, W.; Yuan, J.; Li, C.; Zhang, Q.; Li, X. Groundwater control and curtain grouting for tunnel construction in completely weathered granite. Bull. Eng. Geol. Environ. 2018, 77, 515–531. [Google Scholar] [CrossRef]



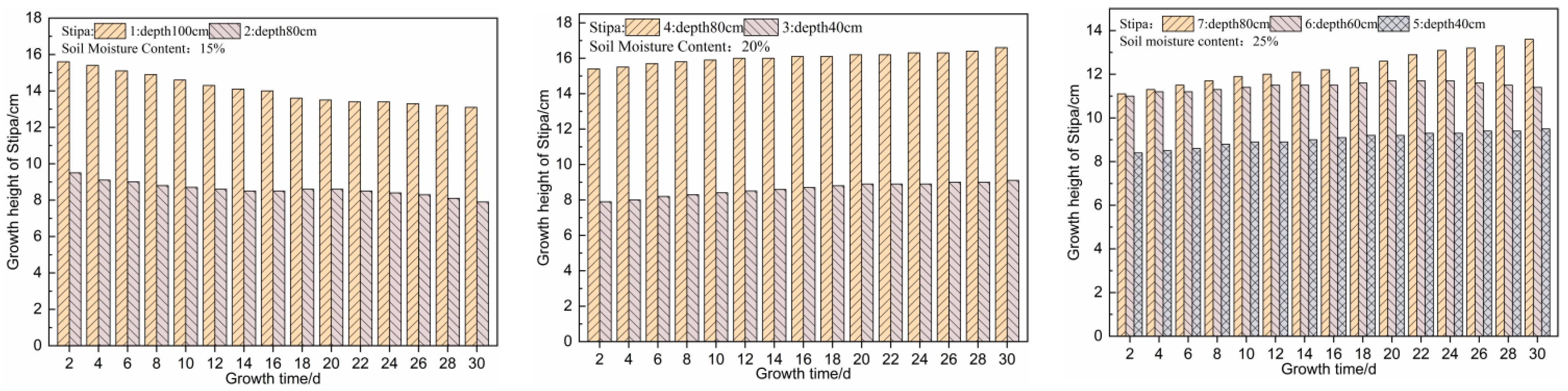


| Device Number | Depth of Groundwater Burial (cm) | Artemisia Plant Number | Actual Measured Soil Moisture Content | Stipa Plant Number | Actual Measured Soil Moisture Content |
|---|---|---|---|---|---|
| 1 | 100 | 1 | 15.2% | 1 | 15.0% |
| 2 | 80 | 2 | 17.5% | 2 | 16.1% |
| 3 | 60 | 3 | 26.0% | Plant death | / |
| 4 | 40 | 4 | 30.8% | 3 | 20.3% |
| 5 | 80 | 5 | 24.6% | 4 | 22.1% |
| 6 | 60 | Plant death | / | 5 | 24.1% |
| 7 | 40 | Plant death | / | 6 | 24.1% |
| 8 | 100 | 6 | 25.3% | Plant death | / |
| 9 | 80 | 7 | 30.5% | 7 | 24.0% |
| 10 | 60 | 8 | 30.5% | Plant death | / |
| Material | Bulk Density (kN/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesive Force (MPa) | Internal Friction Angle (°) | Permeability Coefficient (m/d) | Porosity |
|---|---|---|---|---|---|---|---|
| Wall rock | 22 | 3.90 | 0.30 | 0.3 | 30 | 4.3 × 10−2 | 0.32 |
| Initial support | 24 | 28 | 0.25 | 3.0 × 10−7 | 0.21 | ||
| Secondary lining | 26 | 32 | 0.20 | 3.0 × 10−8 | 0.25 |
| Number | Research Region | Species | Plant Type | Precipitation | Groundwater Depth/m | Reference |
|---|---|---|---|---|---|---|
| 1 | Qinghai | Herbaceous | Artemisia annua, Stipa | Low | 0.6~0.8 | [32,33] |
| 2 | Inner Mongolia | Herbaceous, Shrub | Pennisetum centrasiaticum Artemisia halodendron | Low | 0.5~2.0 | [30] |
| 3 | Xinjiang | Arbor | Haloxylon ammodendron | Low | 4.6~11 | [31] |
| Name | Tunnel Type | Surrounding Rock Type | Grouting Thickness/m | Grouting Permeability Coefficient/(m/d) |
|---|---|---|---|---|
| Longzang Mountain Tunnel No. 1 | Mountain tunnel | The surrounding rock is relatively complete | 2 | 4.9 × 10−3 |
| Yuanliangshan tunnel [36] | Water-rich karst tunnel | Broken surrounding rock | 5 or 8 | 8.64 × 10−4 |
| Liaoshan Tunnel [37] | Water-rich karst tunnel | The surrounding rock is relatively complete | 1 | / |
| Guangfu Tunnel [38] | Shallow buried bias pressure tunnel | Broken surrounding rock | 2–8 | / |
| Cenxi Tunnel [39] | Fully weathered granite tunnel | Broken surrounding rock | 6 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Zhang, X.; Liu, Y.; Yang, Y. Groundwater Discharge Limits of Mountain Tunnels Based on the Normal Growth of Typical Herbaceous Plants. Appl. Sci. 2024, 14, 6561. https://doi.org/10.3390/app14156561
Zhou Y, Zhang X, Liu Y, Yang Y. Groundwater Discharge Limits of Mountain Tunnels Based on the Normal Growth of Typical Herbaceous Plants. Applied Sciences. 2024; 14(15):6561. https://doi.org/10.3390/app14156561
Chicago/Turabian StyleZhou, Yuanfu, Xuefu Zhang, Yuanpeng Liu, and Yuanguang Yang. 2024. "Groundwater Discharge Limits of Mountain Tunnels Based on the Normal Growth of Typical Herbaceous Plants" Applied Sciences 14, no. 15: 6561. https://doi.org/10.3390/app14156561
APA StyleZhou, Y., Zhang, X., Liu, Y., & Yang, Y. (2024). Groundwater Discharge Limits of Mountain Tunnels Based on the Normal Growth of Typical Herbaceous Plants. Applied Sciences, 14(15), 6561. https://doi.org/10.3390/app14156561






