Comparative Analysis of the Irradiation with Medium Fluences of High-Energy Electrons and Pr Doping on the Fluctuation Conductivity of YBa2Cu3O7–δ Single Crystals
Abstract
1. Introduction
2. Experimental Methods
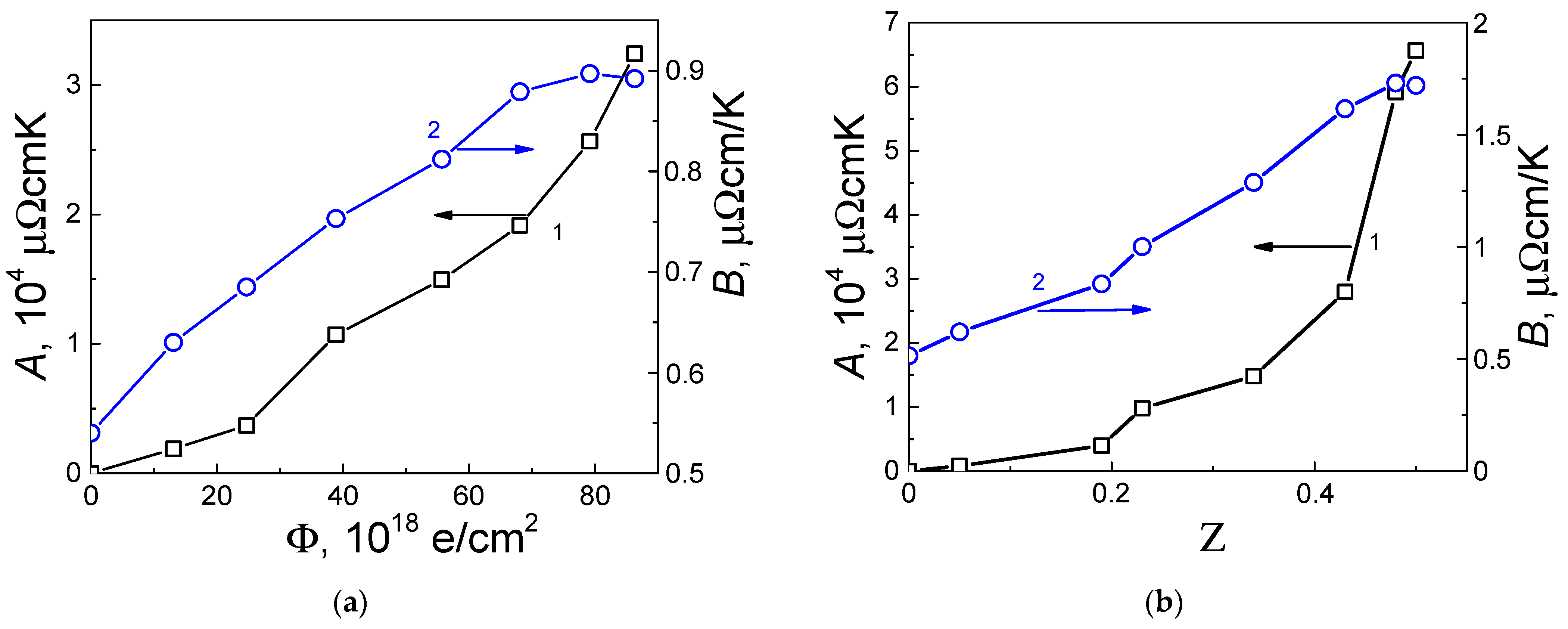
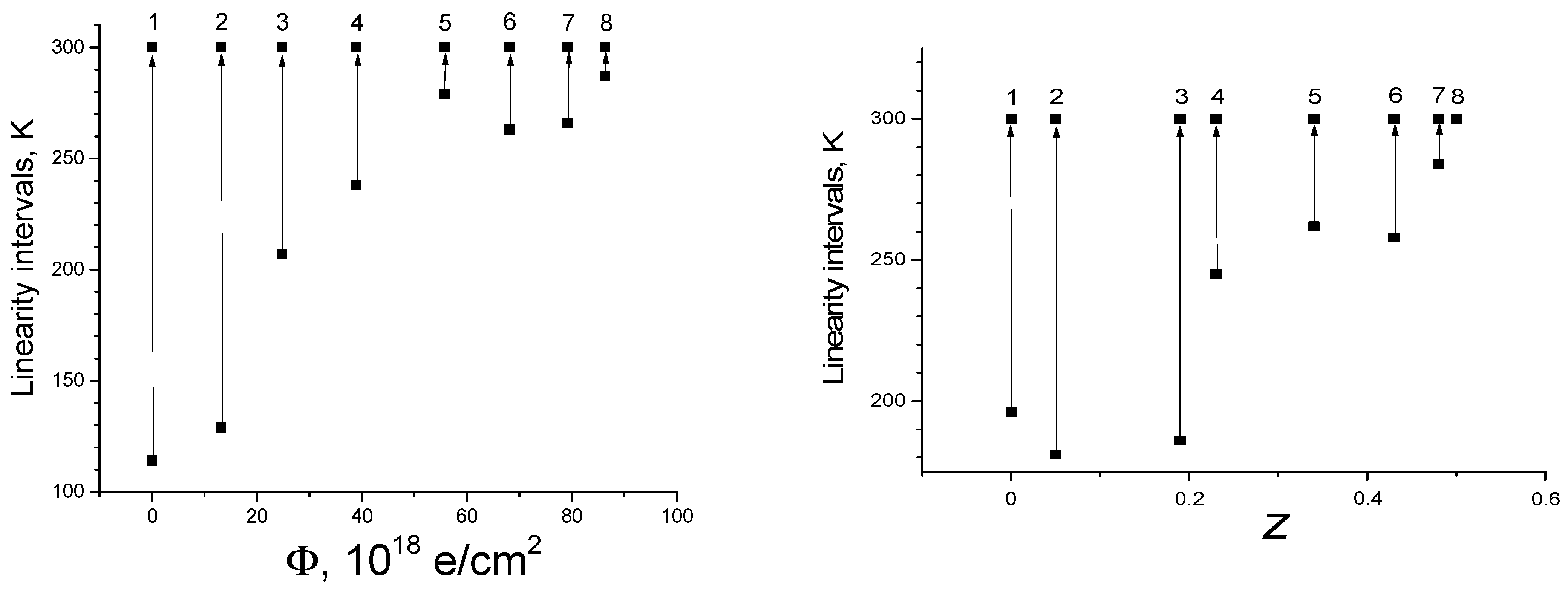
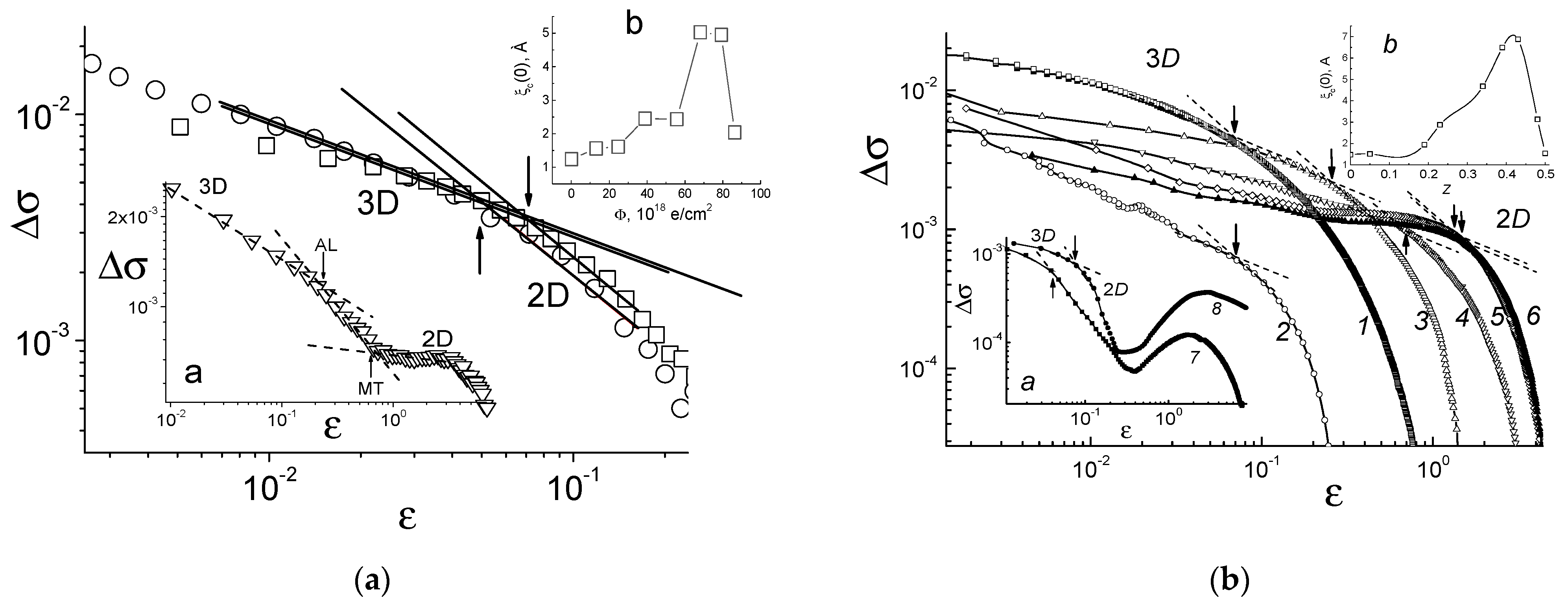
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vovk, R.V.; Solovyov, A.L. Electric transport and the pseudogap in the 1-2-3 HTSC system, under all-around compression (Review Article). Low Temp. Phys. 2018, 44, 111–153. [Google Scholar] [CrossRef]
- Friedman, T.A.; Rice, J.P.; Giapintzakis, J.; Ginzberg, D.M. In-plane paraconductivity in a single crystal of superconducting YBa2Cu3O7−x. Phys. Rev. B 1989, 39, 4258–4266. [Google Scholar] [CrossRef]
- Jorgensen, D.; Pes, S.; Lightfoot, P.; Shi, H.; Paulikas, A.P.; Veal, B.W. Time-dependent structural phenomena at room temperature in quenched YBa2Cu3O6.41: Local oxygen ordering and superconductivity. Phys. C 1990, 17, 571–578. [Google Scholar] [CrossRef]
- Mendonca Ferreira, L.; Pureur, P.; Borges, H.A.; Lejay, P. Effects of pressure on the fluctuation conductivity of YBa2Cu3O7. Phys. Rev. B 2004, 69, 212505. [Google Scholar] [CrossRef]
- Petrusenko, Y.T.; Neklyudov, I.M.; Sleptsov, A.N.; Yakovlev, V.F.; Bondarenko, A.V.; Obolensky, M.A. Recovery processes in YBa2Cu3O7−x single crystals after low-temperature irradiation. Phys. B Condens. Matter 1991, 169, 711–712. [Google Scholar] [CrossRef]
- Borges, H.A.; Continentino, M.A. Pressure study of the paraconductivity of high Tc superconductors. Solid State Commun. 1991, 80, 197–199. [Google Scholar] [CrossRef]
- Solovjov, A.L.; Omelchenko, L.V.; Vovk, R.V.; Dobrovolskiy, O.V.; Kamchatnaya, S.N.; Sergeyev, D.M. Peculiarities in the pseudogap behavior in optimally doped YBa2Cu3O7−δ single crystals under pressure up to 1 GPa. Curr. Appl. Phys. 2016, 16, 931–938. [Google Scholar] [CrossRef]
- Solovjov, A.L.; Habermeier, H.-U.; Haage, T. Fluctuation conductivity in YBa2Cu3O7−y films with different oxygen content. I. Optimally and lightly doped YBCO films. Low Temp. Phys. 2002, 28, 17–24. [Google Scholar] [CrossRef]
- Vovk, R.V.; Vovk, N.R.; Khadzhai, G.Y.; Goulatis, I.L.; Chroneos, A. Effect of high pressure on the electrical resistivity of optimally doped YBa2Cu3O7−δ single crystals with unidirectional planar defects. Phys. B Condes. Matter 2013, 422, 33–35. [Google Scholar] [CrossRef]
- Pan, V.M.; Svechnikov, V.L.; Solovjov, V.F. YBa2Cu3O7- delta single-crystal microstructure related to transport critical current density. Supercond. Sci. Technol. 1992, 5, 707. [Google Scholar] [CrossRef]
- Timusk, T.; Statt, B. The pseudogap in high-temperature superconductors: An experimental survey. Rep. Prog. Phys. 1999, 62, 61–122. [Google Scholar] [CrossRef]
- Aslamazov, L.G.; Larkin, A.I. The influence of fluctuation pairing of electrons on the conductivity of normal metal. Phys. Lett. A 1968, 26, 238–239. [Google Scholar] [CrossRef]
- Lawrence, W.E.; Doniach, S. Theory of layer-structure superconductors. In Proceedings of the 12th International Conference on Low Temperature Physics, Kyoto, Japan, 4–10 September 1970; Kanda, E., Ed.; Keigaku: Tokyo, Japan, 1970; p. 361. [Google Scholar]
- Bieri, J.B.; Maki, K.; Thompson, R.S. Nonlocal effect in magnetoconductivity of high-Tc superconductors. Phys. Rev. B 1991, 44, 4709–4711. [Google Scholar] [CrossRef] [PubMed]
- Vovk, R.V.; Obolenskii, M.A.; Zavgorodniy, A.A.; Goulatis, I.L.; Chroneos, A.; Biletskiy, E.V. Resistive investigation of pseudogap state in non-stoichiometric ReBa2Cu3O7−δ (Re = Y, Ho) single crystals with account for BCS–BEC crossover. J. Alloys Compd. 2009, 485, L21–L23. [Google Scholar] [CrossRef]
- Siegrist, T.; Sunshince, S.; Murphy, D.W.; Cava, R.J.; Zahurak, S.M. Crystal structure of the high-Tc superconductor Ba2YCu3O9−δ. Phys. Rev. B 1987, 35, 7137–7139. [Google Scholar] [CrossRef] [PubMed]
- Bondarenko, A.V.; Prodan, A.A.; Petrusenko, Y.T.; Borisenko, V.N.; Dworschak, F.; Dedek, U. Effect of electron irradiation on vortex dynamics in YBa2Cu3O7−δ single crystals. Phys. Rev. B 2001, 64, 092513. [Google Scholar] [CrossRef]
- Akhavan, M. The question of Pr in HTSC. Phys. B Condes. Matter 2002, 321, 265–282. [Google Scholar] [CrossRef]
- Solovjov, A.L.; Omelchenko, L.V.; Petrenko, E.V.; Vovk, R.V.; Khotkevych, V.V.; Chroneos, A. Peculiarities of pseudogap in Y0.95Pr0.05Ba2Cu3O7−δ single crystals under pressure up to 1.7 GPa. Sci. Rep. 2019, 9, 20424. [Google Scholar] [CrossRef]
- Frishherz, M.C.; Kirk, M.A.; Zhang, G.P.; Weber, H.W. Transmission electron microscopy of defect cascades in YBa2Cu3O7−δ produced by ion irradiation. Philos. Mag. A 1993, 67, 1347–1363. [Google Scholar] [CrossRef]
- Ashkenazi, J. A Theory for the High-T c Cuprates: Anomalous Normal-State and Spectroscopic Properties, Phase Diagram, and Pairing. J. Supercond. Nov. Magn. 2011, 24, 1281–1308. [Google Scholar] [CrossRef][Green Version]
- Vovk, R.V.; Vovk, N.R.; Shekhovtsov, O.V.; Goulatis, I.L.; Chroneos, A. c-axis hopping conductivity in heavily Pr-doped YBCO single crystals. Supercond. Sci. Technol. 2013, 26, 085017. [Google Scholar] [CrossRef]
- Oduleye, O.O.; Penn, S.J.; Alford, N.M.; Lay, L.L.; Beales, T. Thermal cycling, critical current vs. strain, and finite element modelling of 1, 7, 19 and 37 filament Ag/Bi-Sr-Ca-Cu-O (BSCCO) tapes. IEEE Trans. Appl. Supercond. 1999, 9, 2621–2624. [Google Scholar] [CrossRef]
- Wang, Q.; Saunders, G.A.; Liu, H.J.; Acres, M.S.; Almond, D.P. Electrical resistance under pressure in textured Bi2Sr2CaCu2O8+y: Enhancement of the energy gap and thermodynamic fluctuations. Phys. Rev. B 1997, 55, 8529–8543. [Google Scholar] [CrossRef]
- Chroneos, A.I.; Goulatis, I.L.; Vovk, R.V. Atomic Scale Models for RBa2Cu3O6.5 and R1–XPrXBa2Cu3O6.5 Compounds (R=Y and Lanthanides). Acta Chim. Slov. 2007, 54, 179–184. [Google Scholar]
- Chroneos, A.; Kolesnikov, D.D.; Taranova, I.A.; Matsepulin, A.V.; Vovk, R.V. Composition variation and electron irradiation effects on the fluctuation conductivity in Y1–zPrzBa2Cu3O7−δ single crystals. J. Mater. Sci. Mater. Electron. 2020, 31, 19429–19436. [Google Scholar] [CrossRef]
- Khadzhai, G.Y.; Sklyar, V.V.; Vovk, R.V. Suppression of superconductivity in YBa2Cu3O7−δ single crystals upon irradiation with fast electrons. Low Temp. Phys. 2022, 48, 271–273. [Google Scholar] [CrossRef]
- Anderson, P.W.; Zou, Z. “Normal” Tunneling and “Normal” Transport: Diagnostics for the Resonating-Valence-Bond State. Phys. Rev. Lett. 1988, 60, 132–135. [Google Scholar] [CrossRef]
- Stojkovic, B.P.; Pines, D. Theory of the longitudinal and Hall conductivities of the cuprate superconductors. Phys. Rev. B 1997, 55, 8576–8595. [Google Scholar] [CrossRef]
- Valles, J.M., Jr.; White, A.E.; Short, K.T.; Dynes, R.C.; Garno, J.P.; Levi, A.F.J.; Anzlowar, M.; Baldwin, K. Ion-beam-induced metal-insulator transition in YBa2Cu3O7−δ: A mobility edge. Phys. Rev. B 1989, 39, 11599–11602. [Google Scholar] [CrossRef] [PubMed]
- Chryssikos, G.D.; Kamitsos, E.I.; Kapoutsis, J.A.; Patsis, A.P.; Psycharis, V.; Koufoudakis, A.; Mitros, C.; Kallias, G.; Gamari-Seale, E.; Niarchos, D. X-ray diffraction and infrared investigation of RBa2Cu3O7 and R0.5Pr0.5Ba2Cu3O7 compounds (RY and lanthanides). Phys. C Supercond. 1995, 254, 44–62. [Google Scholar] [CrossRef]
- De Gennes, P.G. Superconductivity of Metals and Alloys; W.A. Benjamin, Inc.: New York, NY, USA; Amsterdam, The Netherlands, 1966. [Google Scholar]
- Matthews, A.J.; Kavokin, K.V.; Usher, A.; Portnoi, M.E.; Zhu, M.; Gething, J.D.; Elliot, M.; Herrenden-Harker, W.G.; Phillips, K.; Ritchie, D.A.; et al. Temperature dependence of the breakdown of the quantum Hall effect studied by induced currents. Phys. Rev. B 2004, 70, 075317. [Google Scholar] [CrossRef]
- Adamenko, I.N.; Nemchenko, K.E.; Tsyganok, V.I.; Chervanev, A.I. Interaction of quasiparticles and stationary states of superfluid solutions of helium isotopes. Low Temp. Phys. 1994, 20, 498–504. [Google Scholar]
- Curran, P.G.; Khotkevych, V.V.; Bending, S.J.; Gibbs, A.S.; Lee, S.L.; Mackenzie, A.P. Vortex imaging and vortex lattice transitions in superconducting Sr2RuO4 single crystals. Phys. Rev. B 2011, 84, 104507. [Google Scholar] [CrossRef]
- Randeria, M. Pre-pairing for condensation. Nat. Phys. 2010, 6, 561–562. [Google Scholar] [CrossRef]
- Badoux, S.; Tabis, W.; Laliberte, F.; Grissonnanche, G.; Vignolle, B.; Vignolles, D.; Beard, J.; Bonn, D.A.; Hardy, W.N.; Liang, R.; et al. Change of carrier density at the pseudogap critical point of a cuprate superconductor. Nature 2016, 531, 210–214. [Google Scholar] [CrossRef] [PubMed]
- Kordyuk, A.A. Pseudogap from ARPES experiment: Three gaps in cuprates and topological superconductivity (Review Article). Low Temp. Phys. 2015, 41, 319–341. [Google Scholar] [CrossRef]
- Solovjov, A.L. Chapter 7: Pseudogap and local pairs in high-Tc superconductors. In Superconductors—Materials, Properties and Applications; Gabovich, A.M., Ed.; InTech: Rijeka, Croatia, 2012; pp. 137–170. [Google Scholar]
- He, R.-H.; Hashimoto, M.; Karapetyan, H.; Koralek, J.D.; Hinton, J.P.; Testaud, J.P.; Nathan, V.; Yoshida, Y.; Yao, H.; Tanaka, K.; et al. From a Single-Band Metal to a High-Temperature Superconductor via Two Thermal Phase Transitions. Science 2011, 331, 1579–1583. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.W. The Theory of Superconductivity in the High Cuprates; Princeton University Press: Princeton, NJ, USA, 1997; p. 446. [Google Scholar]
- Emery, V.J.; Kivelson, S.A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 1995, 374, 434–437. [Google Scholar] [CrossRef]
- Corson, J.; Mallozzi, R.; Orenstein, J.; Eckstein, J.N.; Bozovic, I. Vanishing of phase coherence in underdoped Bi2Sr2CaCu2O8+δ. Nature 1999, 398, 221–223. [Google Scholar] [CrossRef]
- Varma, C.M. Theory of the pseudogap state of the cuprates. Phys. Rev. B 2006, 73, 155113. [Google Scholar] [CrossRef]
- Cava, R.J. Structural Chemistry and the Local Charge Picture of Copper Oxide Superconductors. Science 1990, 247, 656–662. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Kosztin, I.; Janko, B.; Levin, K. Pairing Fluctuation Theory of Superconducting Properties in Underdoped to Overdoped Cuprates. Phys. Rev. Lett. 1998, 81, 4708–4711. [Google Scholar] [CrossRef]
- Efetov, K.; Meier, H.; Pépin, C. Pseudogap state near a quantum critical point. Nat. Phys. 2013, 9, 442–446. [Google Scholar] [CrossRef]
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039. [Google Scholar] [CrossRef]
- Suzuki, M.; Watanabe, T. Discriminating the Superconducting Gap from the Pseudogap in Bi2Sr2CaCu2O8+δ by Interlayer Tunneling Spectroscopy. Phys. Rev. Lett. 2000, 85, 4787–4790. [Google Scholar] [CrossRef] [PubMed]
- Habermeier, H.-U. In Proceedings of the ESF International Workshop on Superconductivity in Reduced Dimensions, Sulzburg, Austria, May 2010; p. 33.
- Birgineau, R.J.; Shirane, G. Neutron Scattering Studies of Structural and Magnetic Excitations in Lamellar Copper Oxides. A Review. In Physical Properties of High Temperature Superconductors I; Ginsberg, D.M., Ed.; World Scientific: Singapore, 1989; pp. 152–212. [Google Scholar]
- Gawalek, W.; Schueppel, W.; Hergt, R.; Andra, W.; Fischer, K.; Gornert, P. High critical currents in peritectically grown YBa2Cu3O7-x single crystals. Supercond. Sci. Technol. 1992, 5, S407–S410. [Google Scholar] [CrossRef]
- Ando, Y.; Komiya, S.; Segawa, K.; Ono, S.; Kurita, Y. Electronic Phase Diagram of High-Tc Cuprate Superconductors from a Mapping of the In-Plane Resistivity Curvature. Phys. Rev. Lett. 2004, 93, 267001. [Google Scholar] [CrossRef]
- Fehrenbacher, R.; Rice, T.M. Unusual electronic structure of PrBa2Cu3O7. Phys. Rev. Lett. 1993, 70, 3471–3474. [Google Scholar] [CrossRef]
- Liechtenstein, A.I.; Mazin, I.I. Quantitative model for the superconductivity suppression in R1-xPrxBa2Cu3O7 with different rare earths. Phys. Rev. Lett. 1995, 74, 1000–1003. [Google Scholar] [CrossRef]
- Chu, C.W.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, A.J.; Wang, Y.Q. Evidence for superconductivity above 40 K in the La-Ba-Cu-O compound system. Phys. Rev. Lett. 1988, 58, 405–407. [Google Scholar] [CrossRef]
- Loktev, V.M. Particularities of Superconductivity in 2D Metals: Transition from Cooper Pairing to the Local One. Low Temp. Phys. 1996, 22, 488–491. [Google Scholar]
- Gusynin, P.; Loktev, V.M.; Sharapov, S.G. Phase diagram of a 2D metal system with a variable number of carriers. Sov. ZETF Let. 1997, 65, 182. [Google Scholar] [CrossRef]
- Kondo, T.; Hamaya, Y.; Palczewski, A.D.; Takeuchi, T.; Wen, J.S.; Xu, Z.J.; Gu, G.; Schmalian, J.; Kaminski, A. Disentangling Cooper-pair formation above the transition temperature from the pseudogap state in the cuprates. Nat. Phys. 2011, 7, 21–25. [Google Scholar] [CrossRef]

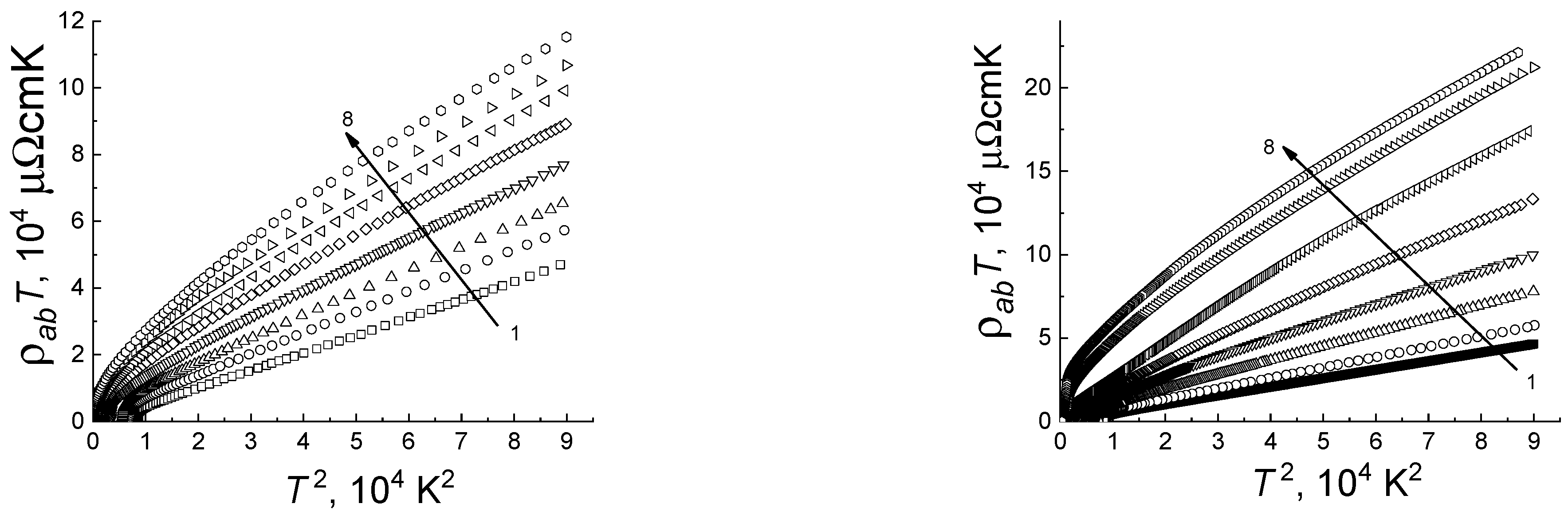
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khadzhai, G.; Goulatis, I.; Chroneos, A.; Feher, A.; Vovk, R. Comparative Analysis of the Irradiation with Medium Fluences of High-Energy Electrons and Pr Doping on the Fluctuation Conductivity of YBa2Cu3O7–δ Single Crystals. Appl. Sci. 2024, 14, 6536. https://doi.org/10.3390/app14156536
Khadzhai G, Goulatis I, Chroneos A, Feher A, Vovk R. Comparative Analysis of the Irradiation with Medium Fluences of High-Energy Electrons and Pr Doping on the Fluctuation Conductivity of YBa2Cu3O7–δ Single Crystals. Applied Sciences. 2024; 14(15):6536. https://doi.org/10.3390/app14156536
Chicago/Turabian StyleKhadzhai, George, Ioannis Goulatis, Alexander Chroneos, Alexander Feher, and Ruslan Vovk. 2024. "Comparative Analysis of the Irradiation with Medium Fluences of High-Energy Electrons and Pr Doping on the Fluctuation Conductivity of YBa2Cu3O7–δ Single Crystals" Applied Sciences 14, no. 15: 6536. https://doi.org/10.3390/app14156536
APA StyleKhadzhai, G., Goulatis, I., Chroneos, A., Feher, A., & Vovk, R. (2024). Comparative Analysis of the Irradiation with Medium Fluences of High-Energy Electrons and Pr Doping on the Fluctuation Conductivity of YBa2Cu3O7–δ Single Crystals. Applied Sciences, 14(15), 6536. https://doi.org/10.3390/app14156536







