Hierarchical Indexing and Compression Method with AI-Enhanced Restoration for Scientific Data Service
Abstract
1. Introduction
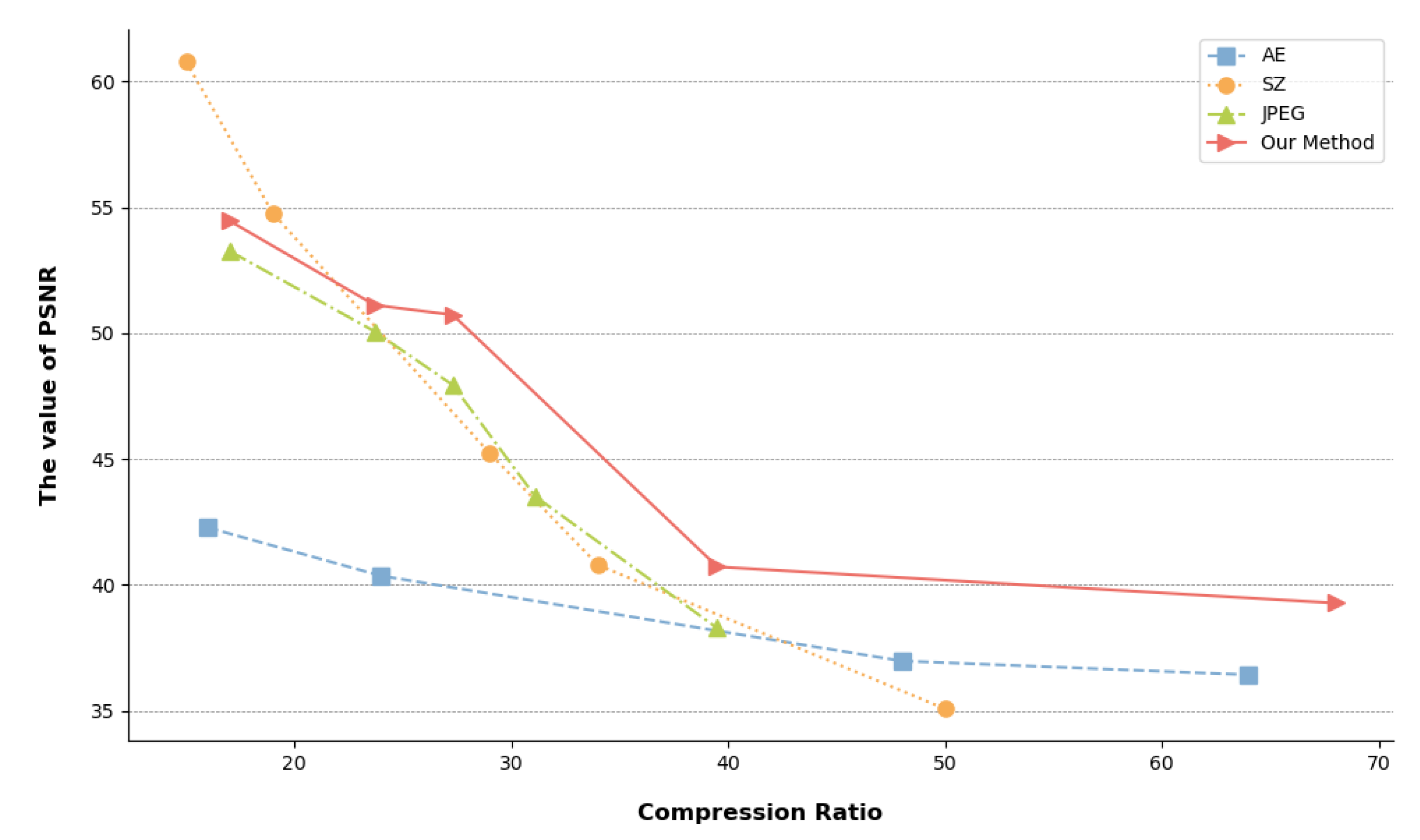
- We achieve comprehensive optimization of scientific data services by combining compression and indexing, achieving loosely coupled error-controlled lossy compression. With data precision guaranteed (PSNR of at least 39 dB), the compression ratio reached 68, which is twice that of SZ.
- We design a multi-level indexing strategy based on a tree structure, which can segment and organize spatiotemporal data at different levels, achieving effective error control. By utilizing the flexibility of quadtrees, we can more effectively manage complex interactions between entities at multiple scales, thereby improving query efficiency.
- We achieve comprehensive optimization for scientific data services by combining compression and indexing. This integration optimizes data storage and retrieval processes, providing more efficient and accurate support for data services.
2. Related Work
2.1. Data Compression Methods
2.2. Tree-Based Data Indexing Methods
3. Proposed Methodology
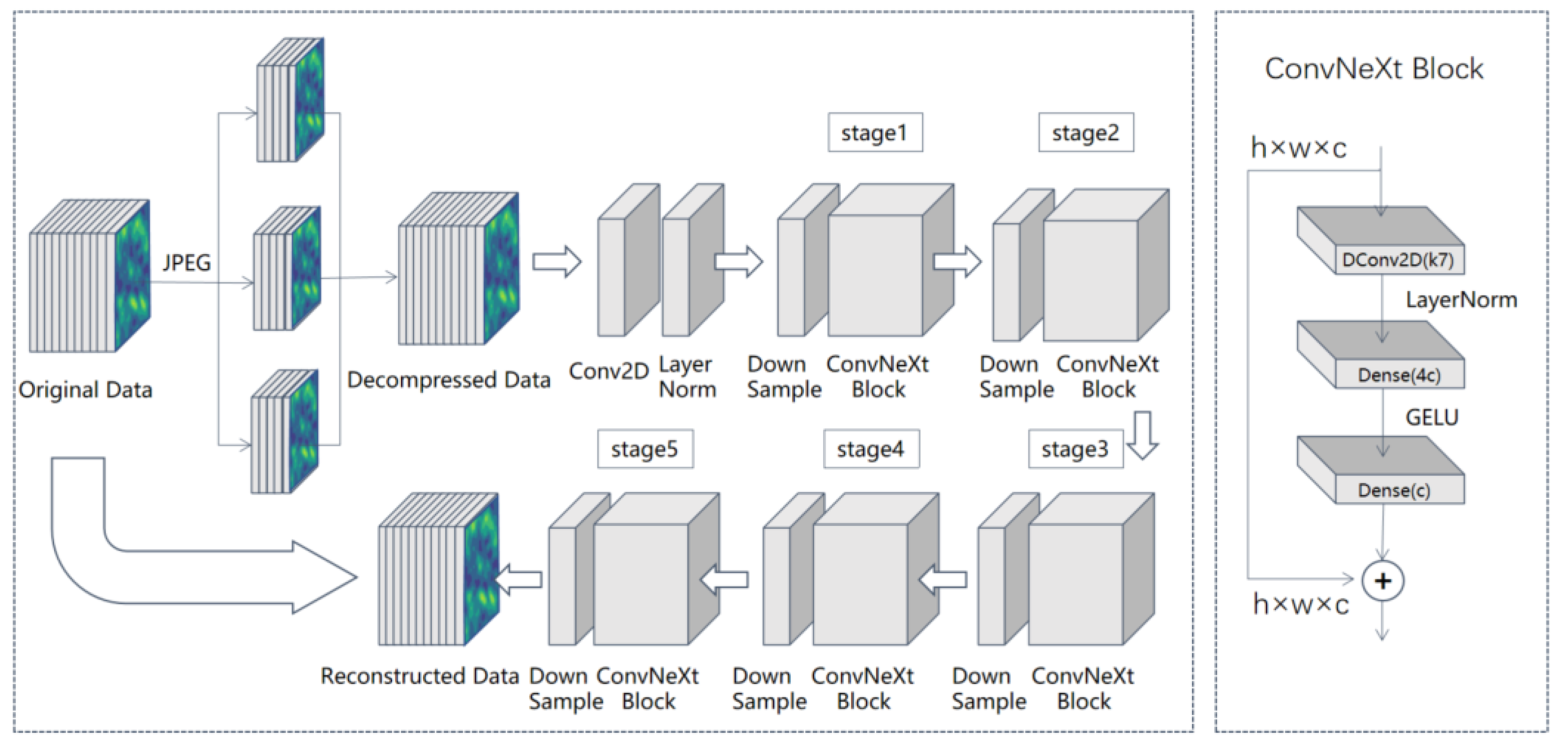
3.1. Multi-Level Compression Based on JPEG
3.2. Indexing Strategy Based on Quadtree
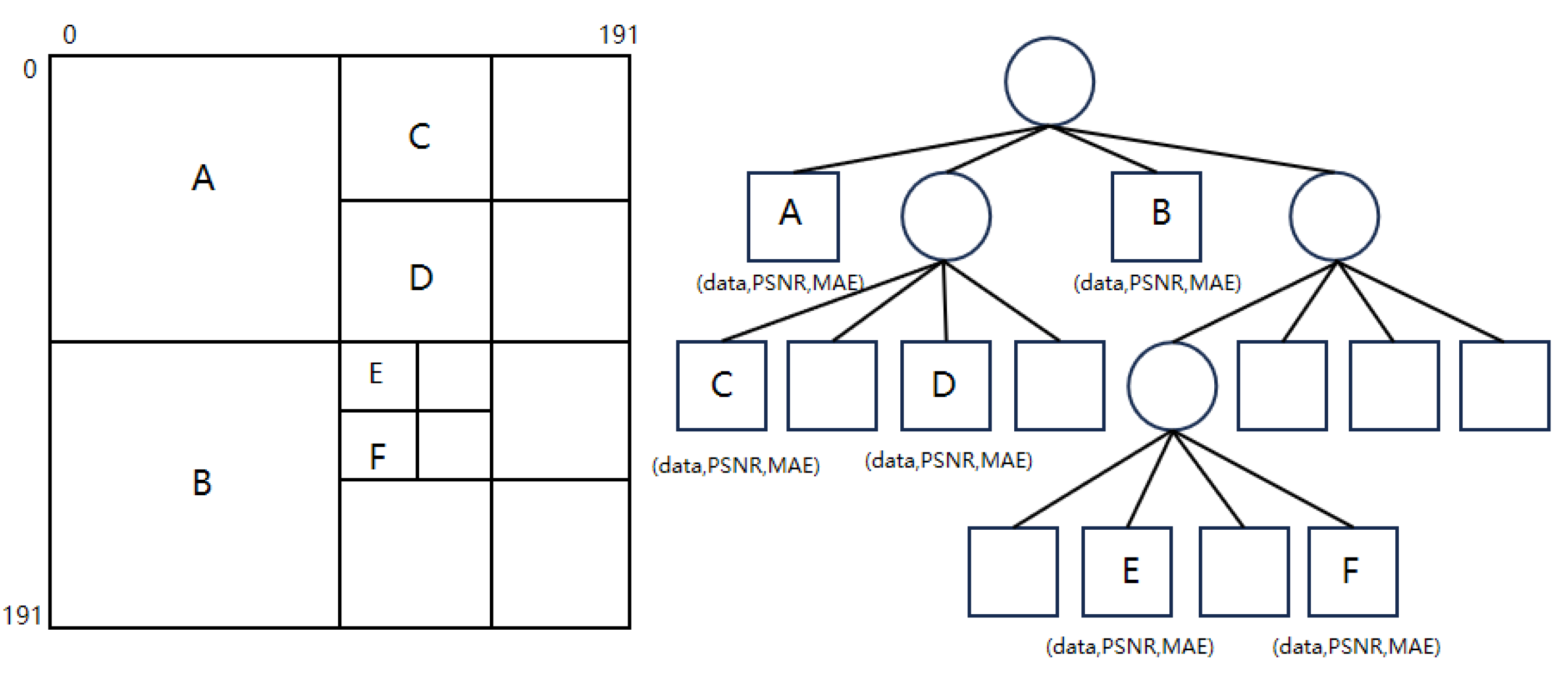
3.2.1. Structure of Quadtree
3.2.2. Indexing Algorithm
| Algorithm 1: build_quadtree |
| Input: spatial data D, x-coordinate of the top left corner lx, y-coordinate of the top left corner ly, x-coordinate of the bottom right corner rx, y-coordinate of the bottom right corner ry, the number of the layers n Output: the root node of the quadtree |
|
| Algorithm 2: range_query |
| Input: the root node of the quadtree node, x-coordinate of the top left corner lx, y-coordinate of the top left corner ly, x-coordinate of the bottom right corner rx, y-coordinate of the bottom right corner ry, condition judgment function F Output: decompressed data |
|
3.2.3. Complexity Analysis
3.3. Data Restoration Enhancement Module
4. Experimentation and Results
4.1. Experimental Setup
4.1.1. Dataset
4.1.2. Metrics
- CR: The compression ratio (CR) is the ratio between the sizes of the original data and their compressed latent representation. The compressed data of our model are outputs of the quantizer in an integer format. We define CR as:
- MAE: Reconstruction quality is measured using traditional error metrics such as the mean squared error (MSE) and the mean absolute error (MAE).
- PSNR: This metric measures the performance of compression schemes. PSNR is defined via the mean squared error (MSE). MSE is given in Equation (11).where and are the original and reconstructed data, respectively.
- PSNR is then defined aswhere is the max value in the dataset and is the min value in the dataset.
- PSNR is inversely proportional to MSE. When the error between input and output data is small, MSE is a small number, which leads to a large PSNR. Therefore, it is desired to maximize PSNR for any compression model.
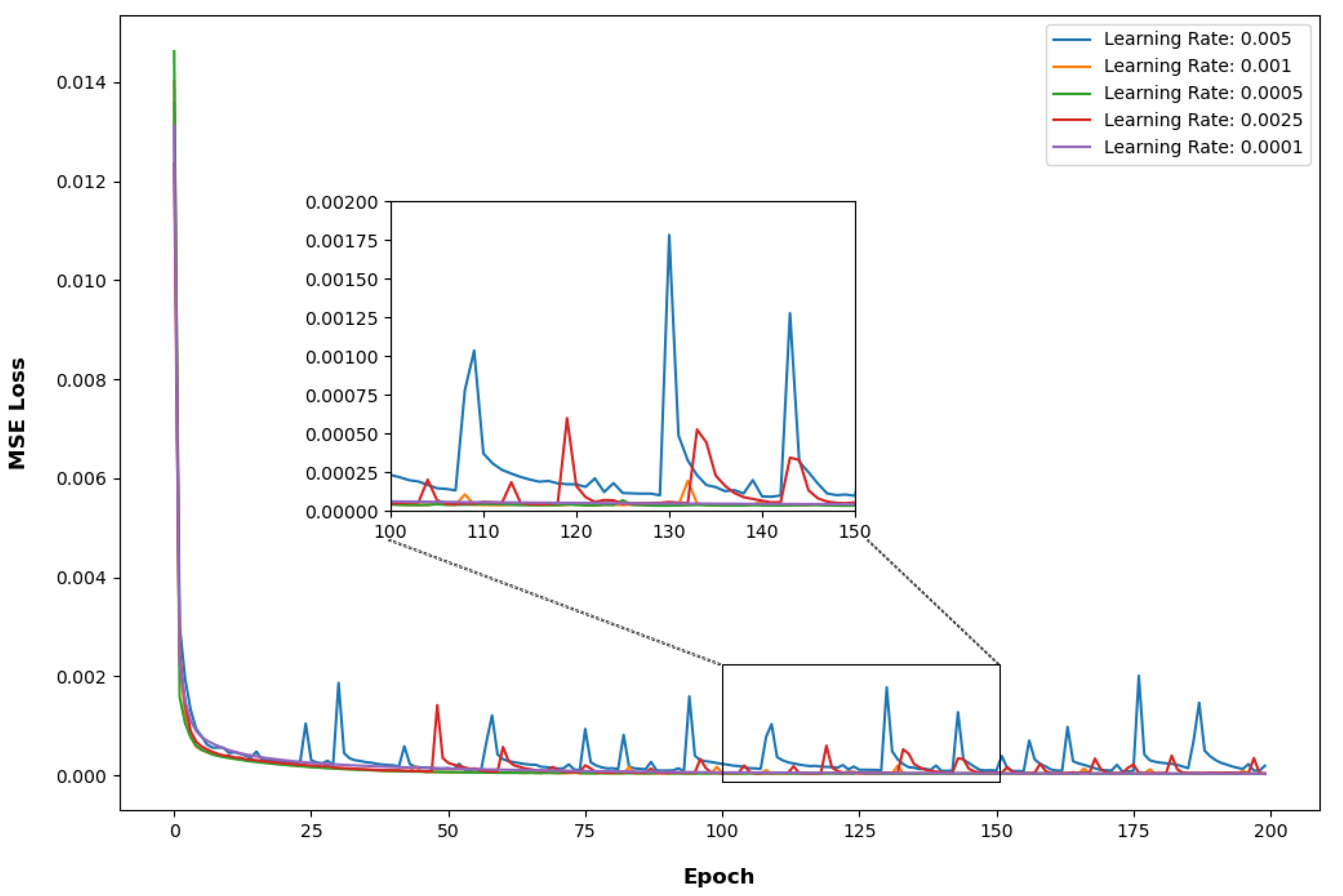
4.1.3. Model Training
4.1.4. Experimental Details
- CPU: 13th Gen Intel(R) Core(TM) i7-13700F 2.10 GHz;
- GPU: NVIDIA GeForce RTX 4090;
- RAM: 64 GB;
- OS: Windows11.
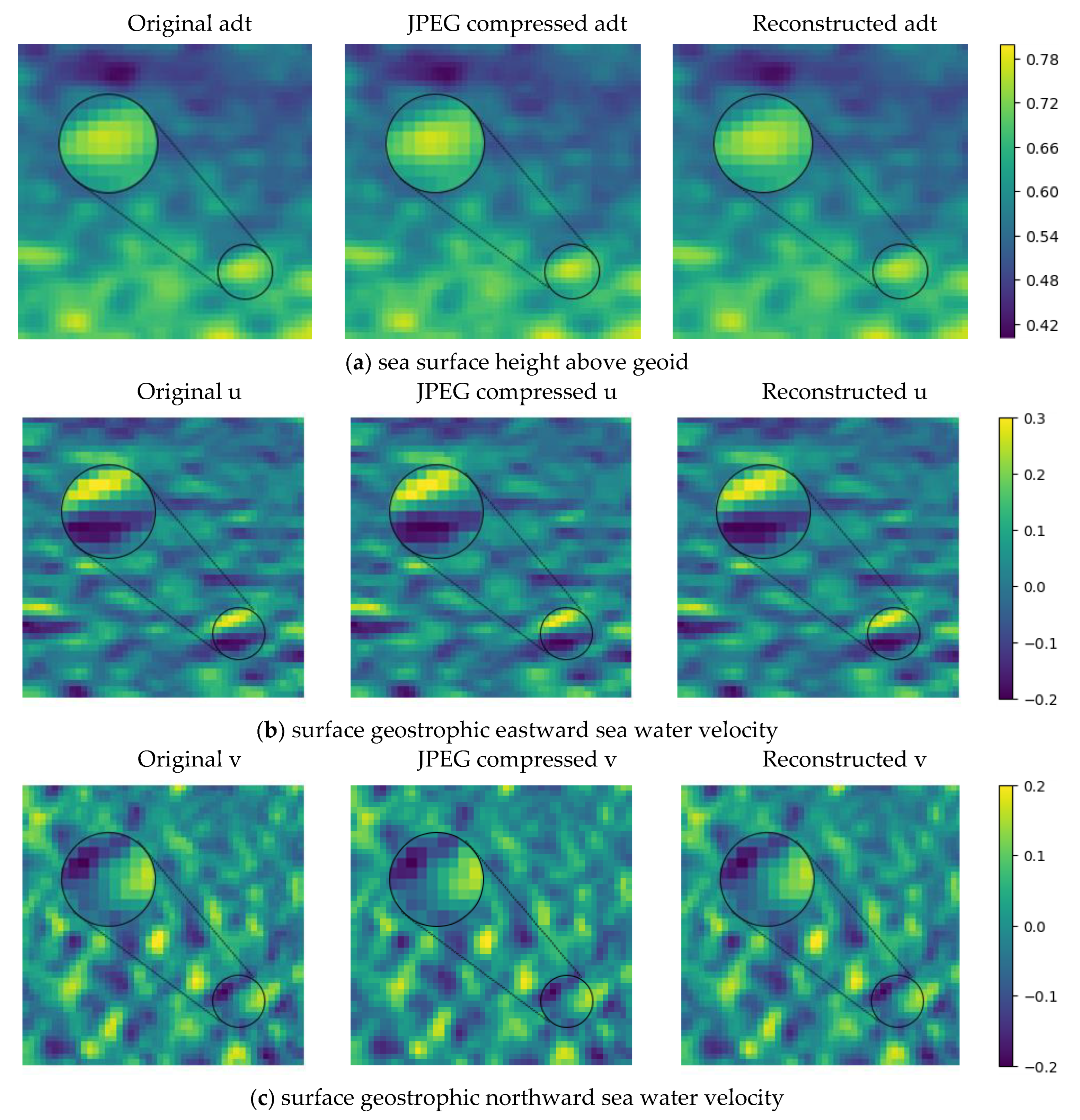
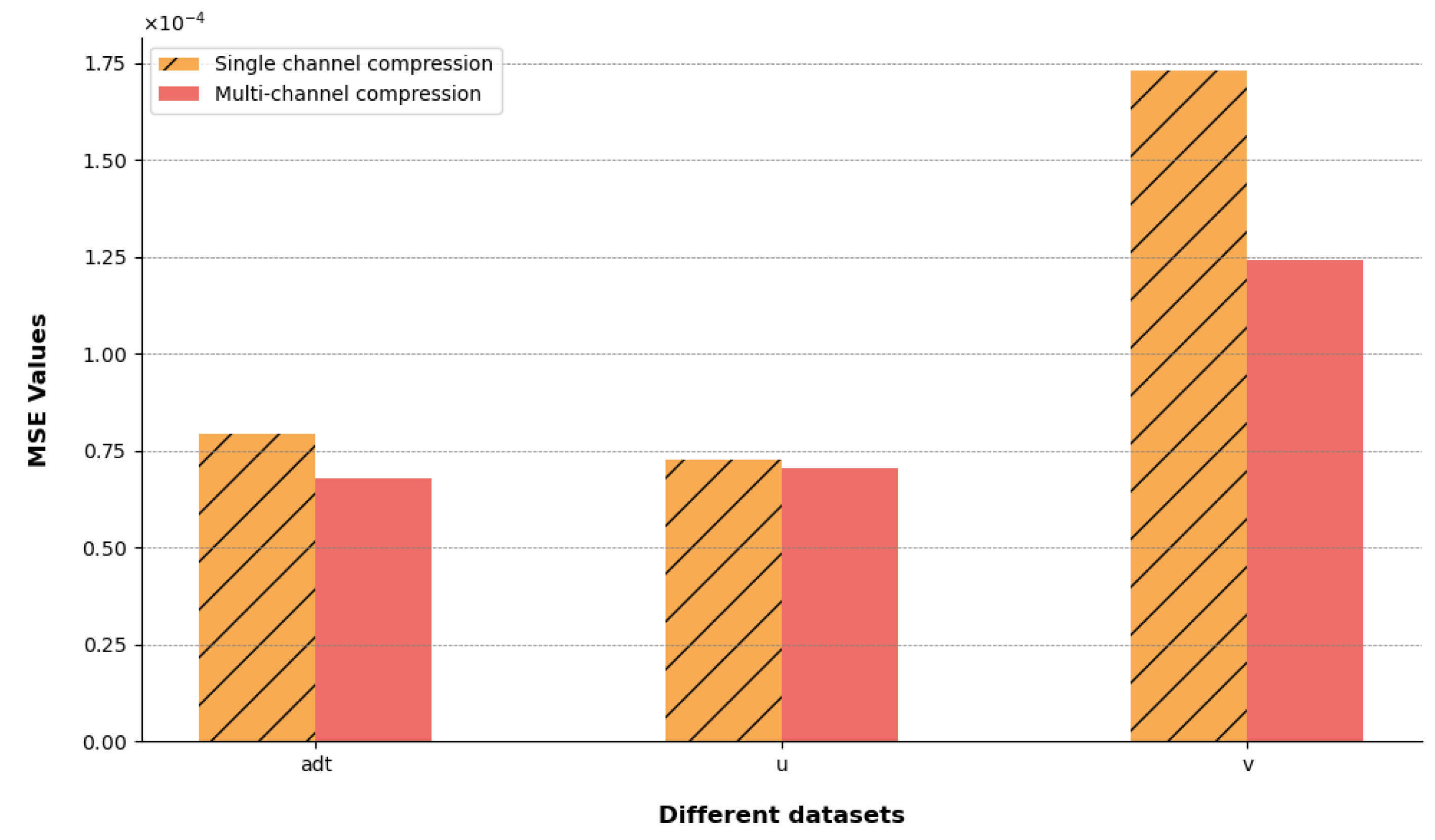
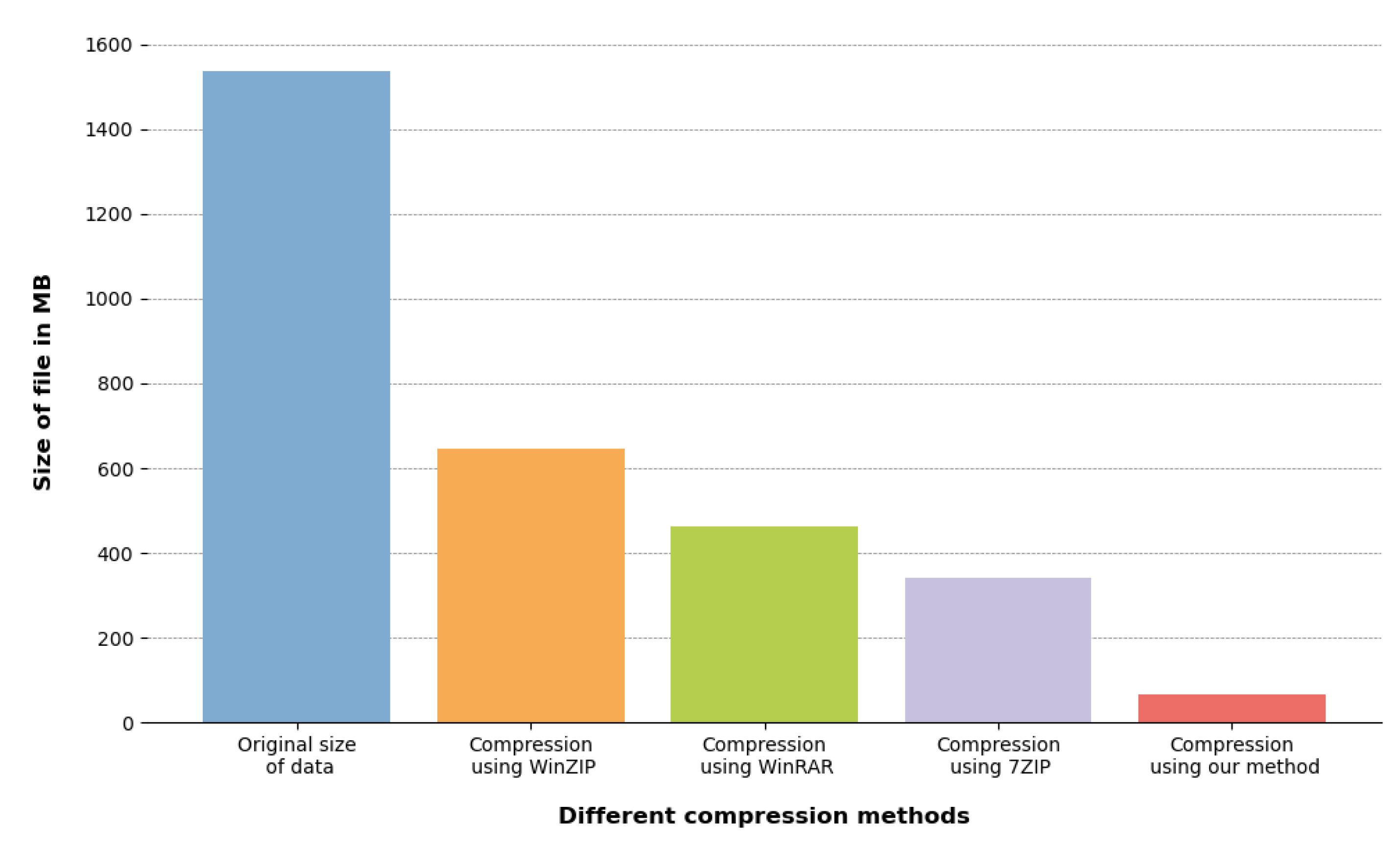
4.2. Visualization of Compression Results
4.3. Comparison of Compression Effects under Different Metrics
4.4. Comparison of Index Construction and Data Query Efficiency
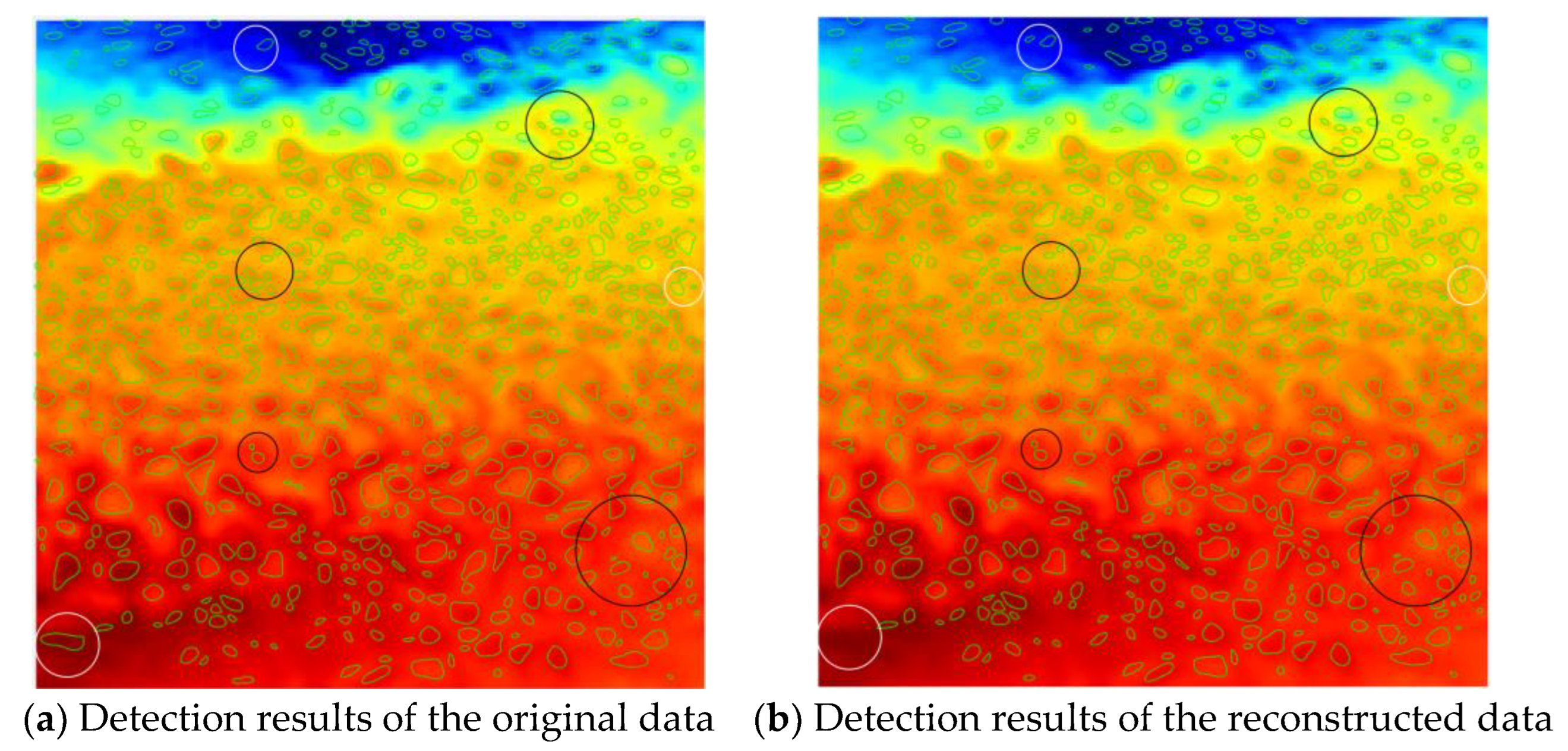
4.5. Case Study of Using Quadtree in Data Analysis
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Di, S.; Zhao, K.; Jin, S.; Tao, D.; Liang, X.; Chen, Z.; Cappello, F. Exploring autoencoder-based error-bounded compression for scientific data. In Proceedings of the 2021 IEEE International Conference on Cluster Computing (CLUSTER), Portland, OR, USA, 7–10 September 2021; pp. 294–306. [Google Scholar]
- Guan, R.; Wang, Z.; Pan, X.; Zhu, R.; Song, B.; Zhang, X. SbMBR Tree—A Spatiotemporal Data Indexing and Compression Algorithm for Data Analysis and Mining. Appl. Sci. 2023, 13, 10562. [Google Scholar] [CrossRef]
- Jayasankar, U.; Thirumal, V.; Ponnurangam, D. A survey on data compression techniques: From the perspective of data quality, coding schemes, data type and applications. J. King Saud Univ.-Comput. Inf. Sci. 2021, 33, 119–140. [Google Scholar] [CrossRef]
- Ballé, J.; Laparra, V.; Simoncelli, E.P. End-to-end optimized image compression. arXiv 2016, arXiv:1611.01704. [Google Scholar]
- Akutsu, H.; Naruko, T. End-to-End Deep ROI Image Compression. IEICE Trans. Inf. Syst. 2020, 103, 1031–1038. [Google Scholar] [CrossRef]
- Theis, L.; Shi, W.; Cunningham, A.; Huszár, F. Lossy image compression with compressive autoencoders. Proceedings of International Conference on Learning Representations, Virtual Event, 25–29 April 2022. [Google Scholar]
- Zhai, J.; Zhang, S.; Chen, J.; He, Q. Autoencoder and its various variants. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 415–419. [Google Scholar]
- Glaws, A.; King, R.; Sprague, M. Deep learning for in situ data compression of large turbulent flow simulations. Phys. Rev. Fluids 2020, 5, 114602. [Google Scholar] [CrossRef]
- Sriram, S.; Dwivedi, A.K.; Chitra, P.; Sankar, V.V.; Abirami, S.; Durai, S.J.R.; Pandey, D.; Khare, M.K. Deepcomp: A hybrid framework for data compression using attention coupled autoencoder. Arab. J. Sci. Eng. 2022, 47, 10395–10410. [Google Scholar] [CrossRef]
- Langdon, G.G. An introduction to arithmetic coding. IBM J. Res. Dev. 1984, 28, 135–149. [Google Scholar] [CrossRef]
- Huffman, D.A. A method for the construction of minimum-redundancy codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Wallace, G.K. The JPEG still picture compression standard. Commun. ACM 1991, 34, 30–44. [Google Scholar] [CrossRef]
- Ziv, J.; Lempel, A. A universal algorithm for sequential data compression. IEEE Trans. Inf. Theory 1977, 23, 337–343. [Google Scholar] [CrossRef]
- Tao, D.; Di, S.; Chen, Z.; Cappello, F. Significantly improving lossy compression for scientific data sets based on multidimensional prediction and error-controlled quantization. In Proceedings of the 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Orlando, FL, USA, 29 May–2 June 2017; pp. 1129–1139. [Google Scholar]
- Lindstrom, P. Fixed-rate compressed floating-point arrays. IEEE Trans. Vis. Comput. Graph. 2014, 20, 2674–2683. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Wang, J.; Liu, Q.; Alibhai, S.; Lu, T.; He, X. High-ratio lossy compression: Exploring the autoencoder to compress scientific data. IEEE Trans. Big Data 2021, 9, 22–36. [Google Scholar] [CrossRef]
- Azri, S.; Ujang, U.; Anton, F.; Mioc, D.; Rahman, A.A. Review of spatial indexing techniques for large urban data management. In Proceedings of the International Symposium & Exhibition on Geoinformation (ISG), Kuala Lumpur, Malaysia, 24–25 September 2013; pp. 24–25. [Google Scholar]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; pp. 47–57. [Google Scholar]
- Sellis, T.; Roussopoulos, N.; Faloutsos, C. The R+-Tree: A Dynamic Index for Multi-Dimensional Objects. In Proceedings of the 13th International Conference on Very Large Data Bases, Brighton, UK, 1–4 September 1987. [Google Scholar]
- Beckmann, N.; Kriegel, H.P.; Schneider, R.; Seeger, B. The R*-tree: An efficient and robust access method for points and rectangles. In Proceedings of the 1990 ACM SIGMOD International Conference on Management of Data, Atlantic, NJ, USA, 23–26 May 1990; pp. 322–331. [Google Scholar]
- Kamel, I.; Faloutsos, C. Parallel R-trees. ACM SIGMOD Rec. 1992, 21, 195–204. [Google Scholar] [CrossRef]
- Kamel, I.; Faloutsos, C. Hilbert r-tree: An improved rtree using fractals. In Proceedings of the 20th International Conference on Very Large Data Bases, Santiago de, Chile, Chile, 12–15 September 1994; Volume 94, pp. 500–509. [Google Scholar]
- Arge, L.; Berg, M.; Haverkort, H.; Yi, K. The priority R-tree: A practically efficient and worst-case optimal R-tree. ACM Trans. Algorithms (TALG) 2008, 4, 1–30. [Google Scholar] [CrossRef]
- Finkel, R.A.; Bentley, J.L. Quad trees a data structure for retrieval on composite keys. Acta Inform. 1974, 4, 1–9. [Google Scholar] [CrossRef]
- Robinson, J.T. The KDB-tree: A search structure for large multidimensional dynamic indexes. In Proceedings of the 1981 ACM SIGMOD International Conference on Management of Data, Ann Arbor, MI, USA, 29 April–1 May 1981; pp. 10–18. [Google Scholar]
- Ke, S.; Gong, J.; Li, S.; Zhu, Q.; Liu, X.; Zhang, Y. A hybrid spatio-temporal data indexing method for trajectory databases. Sensors 2014, 14, 12990–13005. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Han, B.; Chen, H. A hybrid index for multi-dimensional query in HBase. In Proceedings of the 2016 4th International Conference on Cloud Computing and Intelligence Systems (CCIS), Beijing, China, 17–19 August 2016; pp. 332–336. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Le Vu, B.; Stegner, A.; Arsouze, T. Angular momentum eddy detection and tracking algorithm (AMEDA) and its application to coastal eddy formation. J. Atmos. Ocean. Technol. 2018, 35, 739–762. [Google Scholar] [CrossRef]




| Feature | Description | Dimension | Unit |
|---|---|---|---|
| crs | coordinate system description | (0) | - |
| longitude | longitude | (1440, 1) | - |
| latitude | latitude | (720, 1) | - |
| adt | sea surface height above geoid | (1, 720, 1440) | m |
| sla | sea surface height above sea level | (1, 720, 1440) | m |
| ugos | surface geostrophic eastward sea water velocity | (1,720,1440) | m/s |
| vgos | surface geostrophic northward sea water velocity | (1,720,1440) | m/s |
| Quality | CR | MAE | RMSE | PSNR | |||
|---|---|---|---|---|---|---|---|
| JPEG | OURS | JPEG | OURS | JPEG | OURS | ||
| 50 | 27.3 | 0.0169 | 0.0075 | 0.0156 | 0.0104 | 47.94 | 50.73 |
| 70 | 23.7 | 0.0132 | 0.0069 | 0.0123 | 0.0090 | 50.07 | 51.12 |
| 90 | 17.0 | 0.0080 | 0.0053 | 0.0073 | 0.0069 | 53.27 | 54.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, B.; Fang, Y.; Guan, R.; Zhu, R.; Pan, X.; Tian, Y. Hierarchical Indexing and Compression Method with AI-Enhanced Restoration for Scientific Data Service. Appl. Sci. 2024, 14, 5528. https://doi.org/10.3390/app14135528
Song B, Fang Y, Guan R, Zhu R, Pan X, Tian Y. Hierarchical Indexing and Compression Method with AI-Enhanced Restoration for Scientific Data Service. Applied Sciences. 2024; 14(13):5528. https://doi.org/10.3390/app14135528
Chicago/Turabian StyleSong, Biao, Yuyang Fang, Runda Guan, Rongjie Zhu, Xiaokang Pan, and Yuan Tian. 2024. "Hierarchical Indexing and Compression Method with AI-Enhanced Restoration for Scientific Data Service" Applied Sciences 14, no. 13: 5528. https://doi.org/10.3390/app14135528
APA StyleSong, B., Fang, Y., Guan, R., Zhu, R., Pan, X., & Tian, Y. (2024). Hierarchical Indexing and Compression Method with AI-Enhanced Restoration for Scientific Data Service. Applied Sciences, 14(13), 5528. https://doi.org/10.3390/app14135528






