On the Lock-In Phenomena near the Transonic Buffet Onset of a Prescribed Pitching Airfoil
Abstract
1. Introduction
2. Energy Map and Model for Amplitude Growth
3. Numerical Setup and Validation
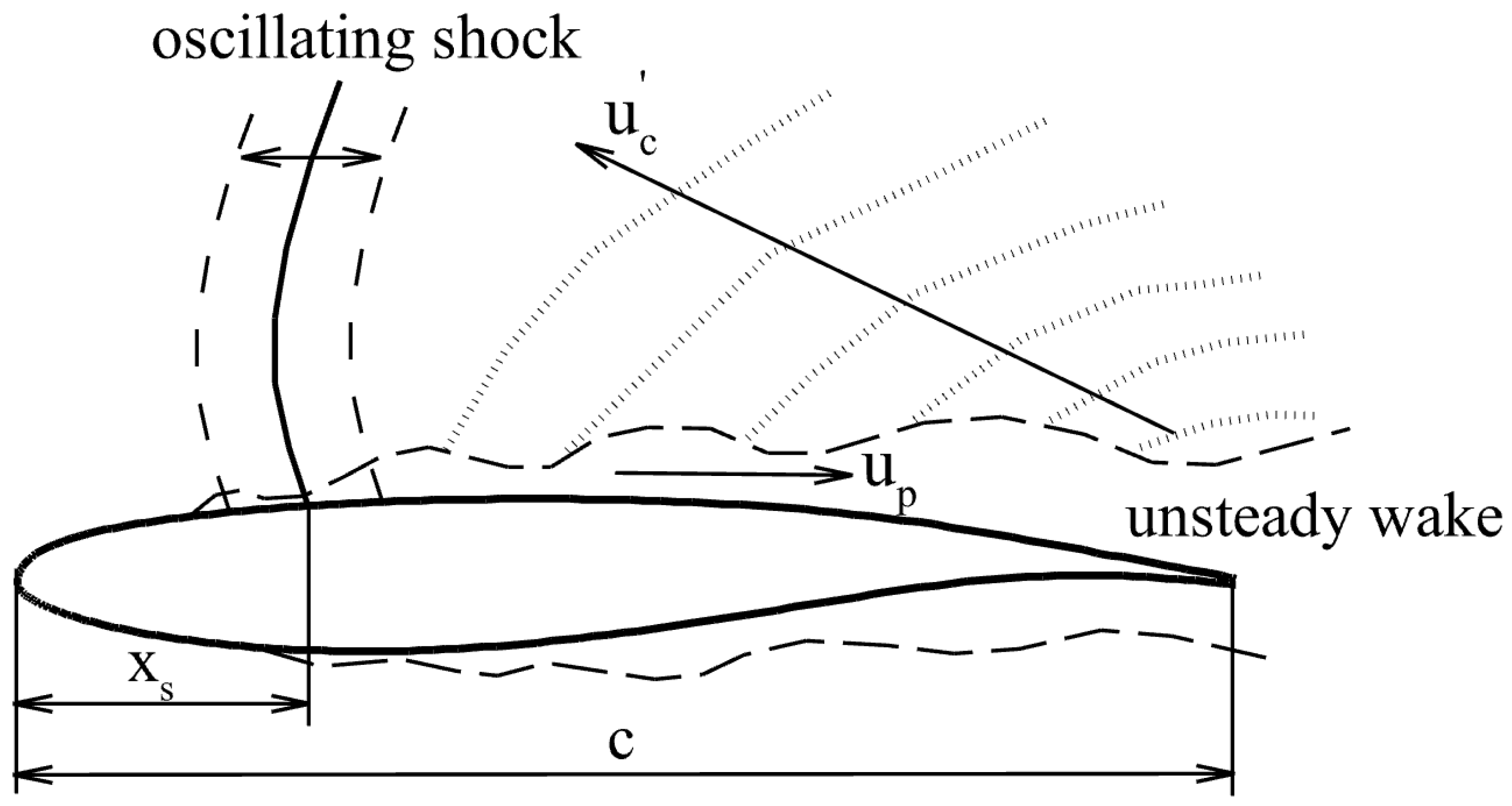
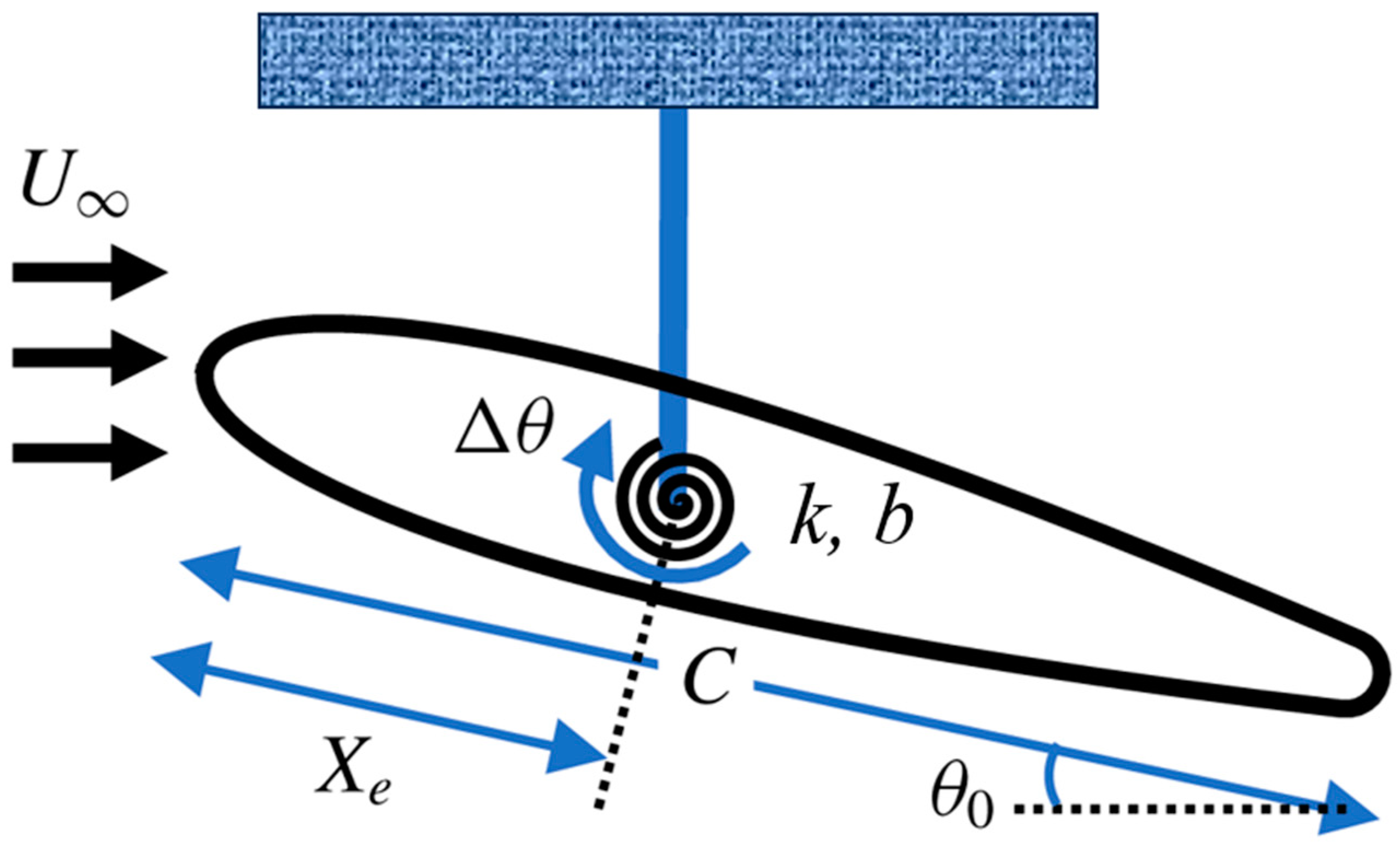
3.1. Test Case Description
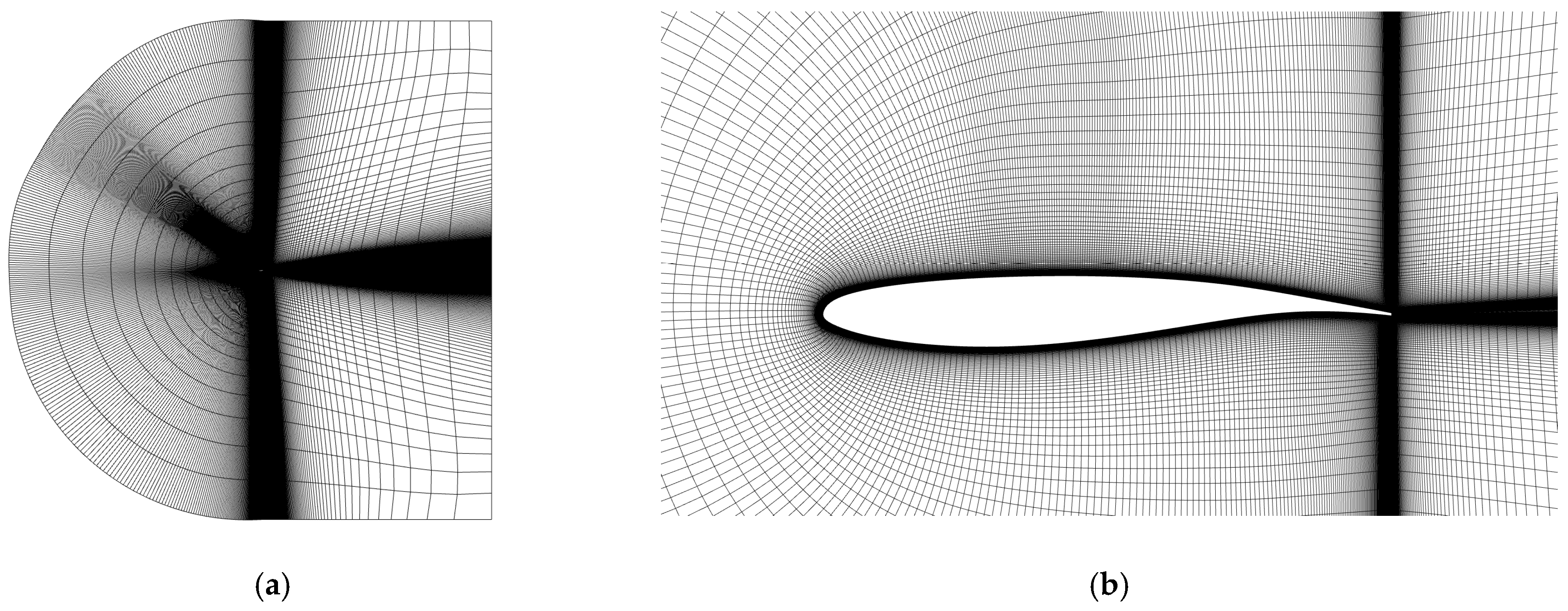
3.2. Numerical Setup
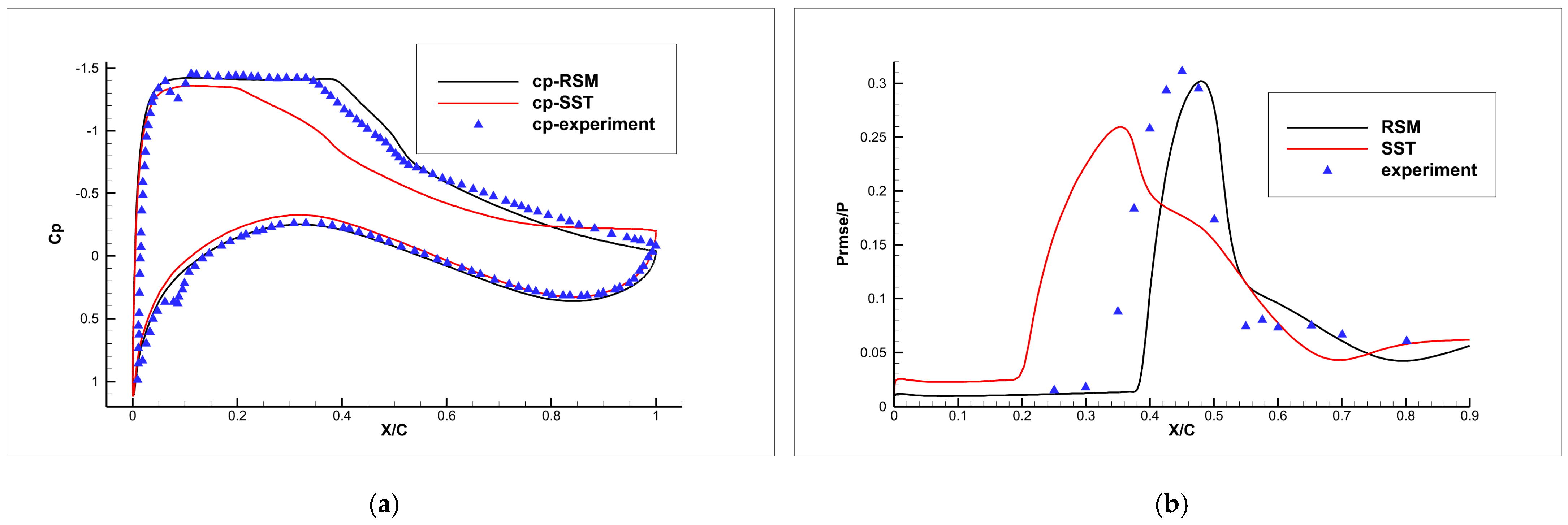
3.3. Numerical Verification
4. Results and Discussions
4.1. Energy Exchange of the Buffet on the Prescribed Pitching Airfoil
4.2. Harmonic Analysis
4.3. Lock-In Boundaries Determination
5. Conclusions
- The modified energy map, which is based on the pitching component of the moment coefficient, fails to indicate the buffet lock-in boundaries for small pitch amplitudes near the buffet onset with the zero-energy transfer index.
- The zero-contour level in the normalized relative phase map of the pitching component of the moment coefficients and the airfoil’s angular velocity generally outlines the buffet lock-in offset as well as the lock-in onset for pitching amplitude less than , indicating that the lock-in phenomena are probably related to the phase shift for small pitch amplitudes near the buffet onset.
- The discrepancy between the lock-in onset and the phase shift for is possibly due to the fact that the instantaneous AoA can be far below the buffet onset (pre-buffet regime), where the shock oscillation vanishes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| K-H | Kelvin–Helmholtz |
| AoA | angle of attack |
| Mach number | |
| Reynolds number | |
| Strouhal number | |
| far-field velocity | |
| density of the air | |
| stagnant pressure | |
| far-field temperature | |
| chord length | |
| dimensional buffet frequency (Hz) | |
| dimensional pitching frequency (Hz) | |
| pressure coefficient | |
| lift coefficient | |
| pitch moment coefficient | |
| component of the moment coefficient corresponding to the prescribed pitch motion frequency | |
| dimensional pitch moment | |
| pitch angle | |
| angular velocity of the pitch motion | |
| initial angle of the pitch motion | |
| amplitude of the pitch motion | |
| amplitude of the FFT component of corresponding to the pitch motion frequency | |
| relative phase between and |
References
- Giannelis, N.F.; Vio, G.A.; Levinski, O. A Review of Recent Developments in the Understanding of Transonic Shock Buffet. Prog. Aerosp. Sci. 2017, 92, 39–84. [Google Scholar] [CrossRef]
- Tijdeman, H. Investigations of the Transonic Flow around Oscillating Airfoils. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1977. [Google Scholar]
- Lee, B.H.K. Oscillatory Shock Motion Caused by Transonic Shock Boundary-Layer Interaction. AIAA J. 1990, 28, 942–944. [Google Scholar] [CrossRef]
- Lee, B.H.K. Self-Sustained Shock Oscillations on Airfoils at Transonic Speeds. Prog. Aerosp. Sci. 2001, 37, 147–196. [Google Scholar] [CrossRef]
- Paladini, E.; Marquet, O.; Sipp, D.; Robinet, J.-C.; Dandois, J. Various Approaches to Determine Active Regions in an Unstable Global Mode: Application to Transonic Buffet. J. Fluid Mech. 2019, 881, 617–647. [Google Scholar] [CrossRef]
- Moise, P.; Zauner, M.; Sandham, N.D. Large-Eddy Simulations and Modal Reconstruction of Laminar Transonic Buffet. J. Fluid Mech. 2022, 944, A16. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidov, D.; Travin, A. Origin of Transonic Buffet on Aerofoils. J. Fluid Mech. 2009, 628, 357–369. [Google Scholar] [CrossRef]
- Crouch, J.D.; Garbaruk, A.; Magidov, D. Predicting the Onset of Flow Unsteadiness Based on Global Instability. J. Comput. Phys. 2007, 224, 924–940. [Google Scholar] [CrossRef]
- Davis, S.S.; Malcolm, G.N. Transonic Shock-Wave/Boundary-Layer Interactions on an Oscillating Airfoil. AIAA J. 1980, 18, 1306–1312. [Google Scholar] [CrossRef][Green Version]
- Despre, C.; Caruana, D.; Mignosi, A.; Reberga, O.; Correge, M. Buffet Active Control-Experimental and Numerical Results. In Proceedings of the Active Control Technology for Enhanced Performance Operational Capabilities of Military Aircraft, Land Vehicles and Sea Vehicles, Braunschweig, Germany, 8–11 May 2000; p. 14. [Google Scholar]
- Raveh, D.E.; Dowell, E.H. Frequency Lock-in Phenomenon for Oscillating Airfoils in Buffeting Flows. J. Fluids Struct. 2011, 27, 89–104. [Google Scholar] [CrossRef]
- Raveh, D.E. Numerical Study of an Oscillating Airfoil in Transonic Buffeting Flows. AIAA J. 2009, 47, 505–515. [Google Scholar] [CrossRef]
- Iovnovich, M.; Raveh, D.E. Transonic Unsteady Aerodynamics in the Vicinity of Shock-Buffet Instability. J. Fluids Struct. 2012, 29, 131–142. [Google Scholar] [CrossRef]
- Raveh, D.E.; Dowell, E.H. Aeroelastic Responses of Elastically Suspended Airfoil Systems in Transonic Buffeting Flows. AIAA J. 2014, 52, 926–934. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, W.; Li, X.; Liu, Y.; Quan, J.; Ye, Z.; Jiang, Y. Mechanism of Frequency Lock-in in Transonic Buffeting Flow. J. Fluid Mech. 2017, 818, 528–561. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, W.; Ye, Z. New Viewpoint on the Mechanism of Transonic Single-Degree-of-Freedom Flutter. Aerosp. Sci. Technol. 2016, 52, 144–156. [Google Scholar] [CrossRef]
- Hartmann, A.; Klaas, M.; Schröder, W. Coupled Airfoil Heave/Pitch Oscillations at Buffet Flow. AIAA J. 2013, 51, 1542–1552. [Google Scholar] [CrossRef]
- Hartmann, A.; Feldhusen, A.; Schröder, W. On the Interaction of Shock Waves and Sound Waves in Transonic Buffet Flow. Phys. Fluids 2013, 25, 026101. [Google Scholar] [CrossRef]
- Feldhusen-Hoffmann, A.; Lagemann, C.; Loosen, S.; Meysonnat, P.; Klaas, M.; Schröder, W. Analysis of Transonic Buffet Using Dynamic Mode Decomposition. Exp. Fluids 2021, 62, 66. [Google Scholar] [CrossRef]
- Feldhusen, A.; Hartmann, A.; Klaas, M.; Schröeder, W. Impact of Alternating Trailing-Edge Noise on Buffet Flows. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar]
- Feldhusen-Hoffmann, A.; Statnikov, V.; Klaas, M.; Schröder, W. Investigation of Shock–Acoustic-Wave Interaction in Transonic Flow. Exp. Fluids 2018, 59, 15. [Google Scholar] [CrossRef]
- Menon, K.; Mittal, R. Flow Physics and Dynamics of Flow-Induced Pitch Oscillations of an Airfoil. J. Fluid Mech. 2019, 877, 582–613. [Google Scholar] [CrossRef]
- Huang, G.; Dai, Y.; Yang, C. Energy Extraction in the Dynamic Modes of Flow for Airfoil’s Laminar Separation Flutter. Phys. Fluids 2022, 34, 083601. [Google Scholar] [CrossRef]
- Turner, J.; Seo, J.H.; Mittal, R. Analysis of the Flow Physics of Transonic Flutter Using Energy Maps. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2023. [Google Scholar]
- Jacquin, L.; Molton, P.; Deck, S.; Maury, B.; Soulevant, D. Experimental Study of Shock Oscillation over a Transonic Supercritical Profile. AIAA J. 2009, 47, 1985–1994. [Google Scholar] [CrossRef]
- Landon, R.H. NACA0012. Oscillatory and Transient Pitching; AGARD R-702, DATA SET 3; Advisory Group for Aerospace Research and Development North Atlantic Treaty Organization: Neuilly sur Seine, France, 1982. [Google Scholar]
- Giannelis, N.F.; Levinski, O.; Vio, G.A. Origins of Atypical Shock Buffet Motions on a Supercritical Aerofoil. Aerosp. Sci. Technol. 2020, 107, 106304. [Google Scholar] [CrossRef]
- Giannelis, N.F.; Levinski, O.; Vio, G.A. Influence of Mach Number and Angle of Attack on the Two-Dimensional Transonic Buffet Phenomenon. Aerosp. Sci. Technol. 2018, 78, 89–101. [Google Scholar] [CrossRef]
- Schulte am Hülse, S.; Lutz, T.; Krämer, E. On the Capability of Unsteady RANS to Predict Transonic Buffet. In Proceedings of the Third Symposium “Simulation of Wing and Nacelle Stall”, Braunschweig, Germany, 21–22 June 2012. [Google Scholar]
- Iovnovich, M.; Raveh, D.E. Reynolds-Averaged Navier-Stokes Study of the Shock-Buffet Instability Mechanism. AIAA J. 2012, 50, 880–890. [Google Scholar] [CrossRef]
- Brunet, V. Computational Study of Buffet Phenomenon with Unsteady RANS Equations. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar]
- Goncalves, E.; Houdeville, R. Turbulence Model and Numerical Scheme Assessment for Buffet Computations. Int. J. Numer. Meth. Fluids 2004, 46, 1127–1152. [Google Scholar] [CrossRef]
- Ortiz-Tarin, J.L.; Nidhan, S.; Sarkar, S. High-Reynolds-Number Wake of a Slender Body. J. Fluid Mech. 2021, 918, A30. [Google Scholar] [CrossRef]
- Brandao, F.L.; Kumar, P.; Mahesh, K. Large-Eddy Simulation of Elliptic Hydrofoil Tip Vortex Cavitation under Incipient Conditions. Int. J. Multiph. Flow 2024, 174, 104795. [Google Scholar] [CrossRef]
- Plasseraud, M.; Kumar, P.; Mahesh, K. Large-Eddy Simulation of Tripping Effects on the Flow over a 6:1 Prolate Spheroid at Angle of Attack. J. Fluid Mech. 2023, 960, A3. [Google Scholar] [CrossRef]
- Govardhan, R.N.; Williamson, C.H.K. Defining the ‘Modified Griffin Plot’ in Vortex-Induced Vibration: Revealing the Effect of Reynolds Number Using Controlled Damping. J. Fluid Mech. 2006, 561, 147. [Google Scholar] [CrossRef]
- Willden RH, J.; Graham JM, R. Three Distinct Response Regimes for the Transverse Vortex-Induced Vibrations of Circular Cylinders at Low Reynolds Numbers. J. Fluids Struct. 2006, 22, 885–895. [Google Scholar] [CrossRef]
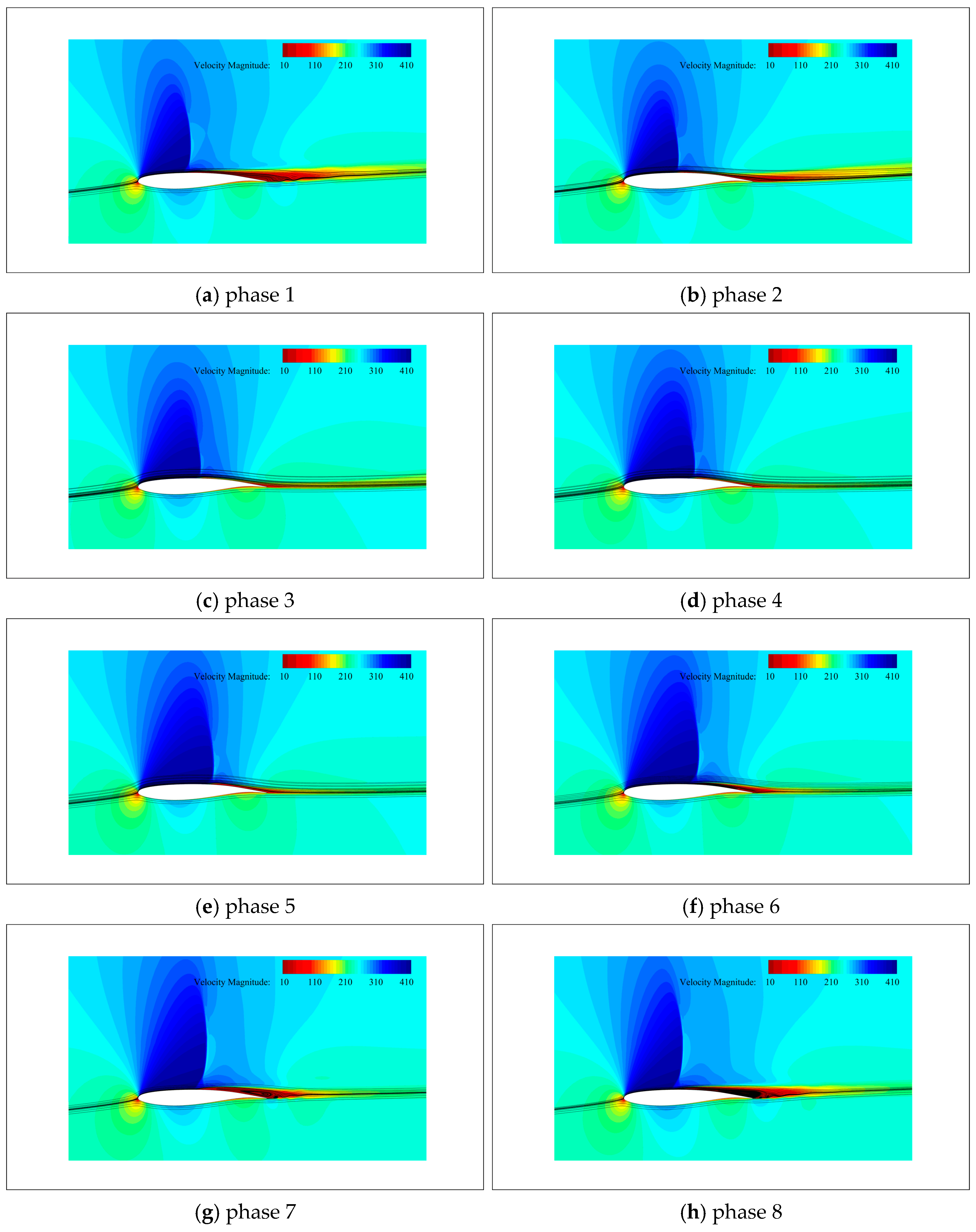
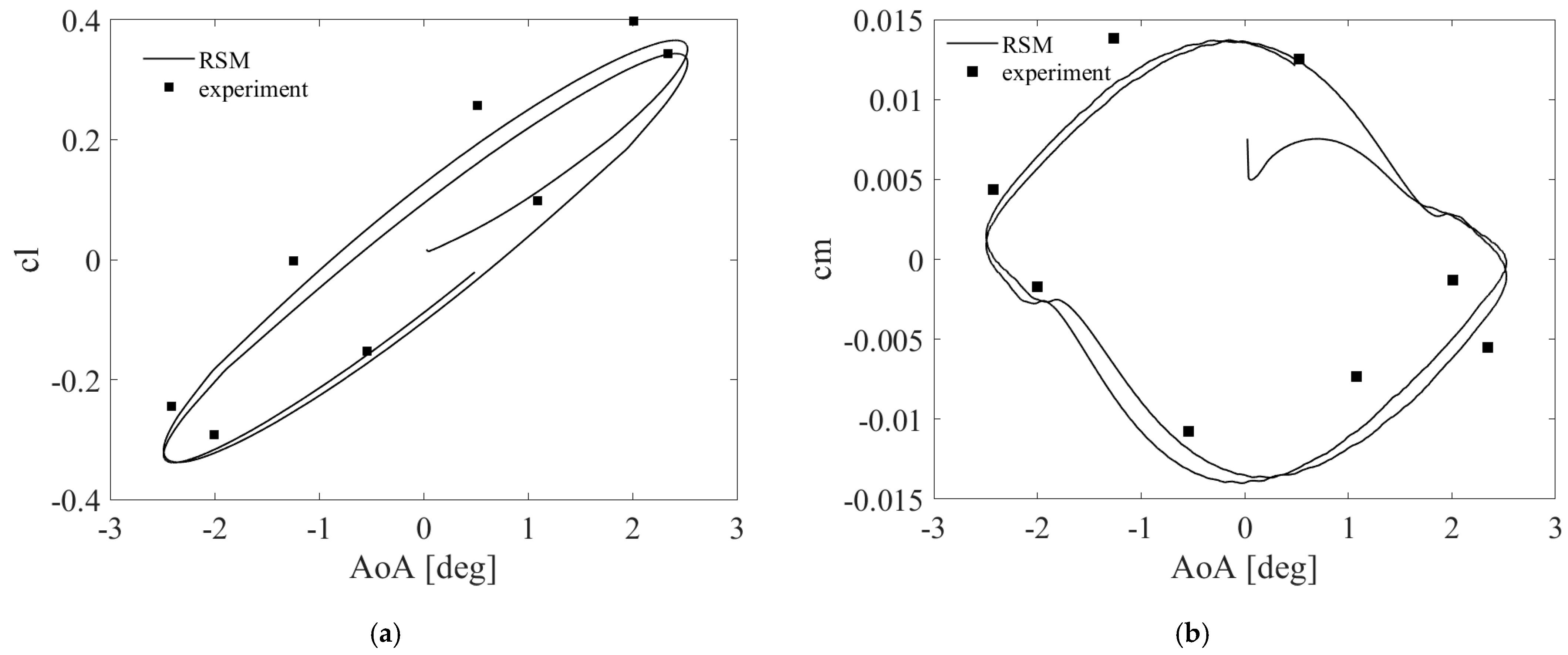


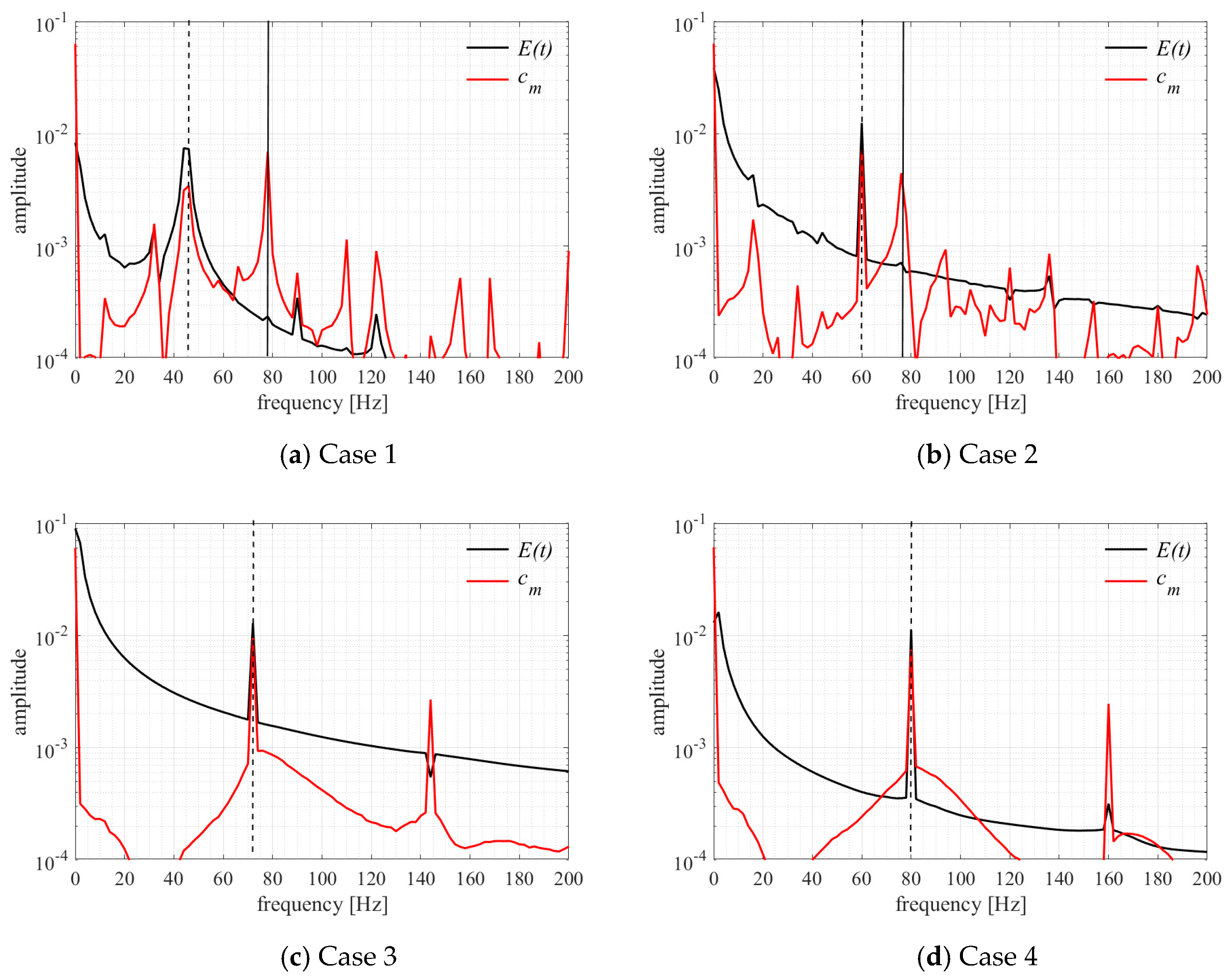
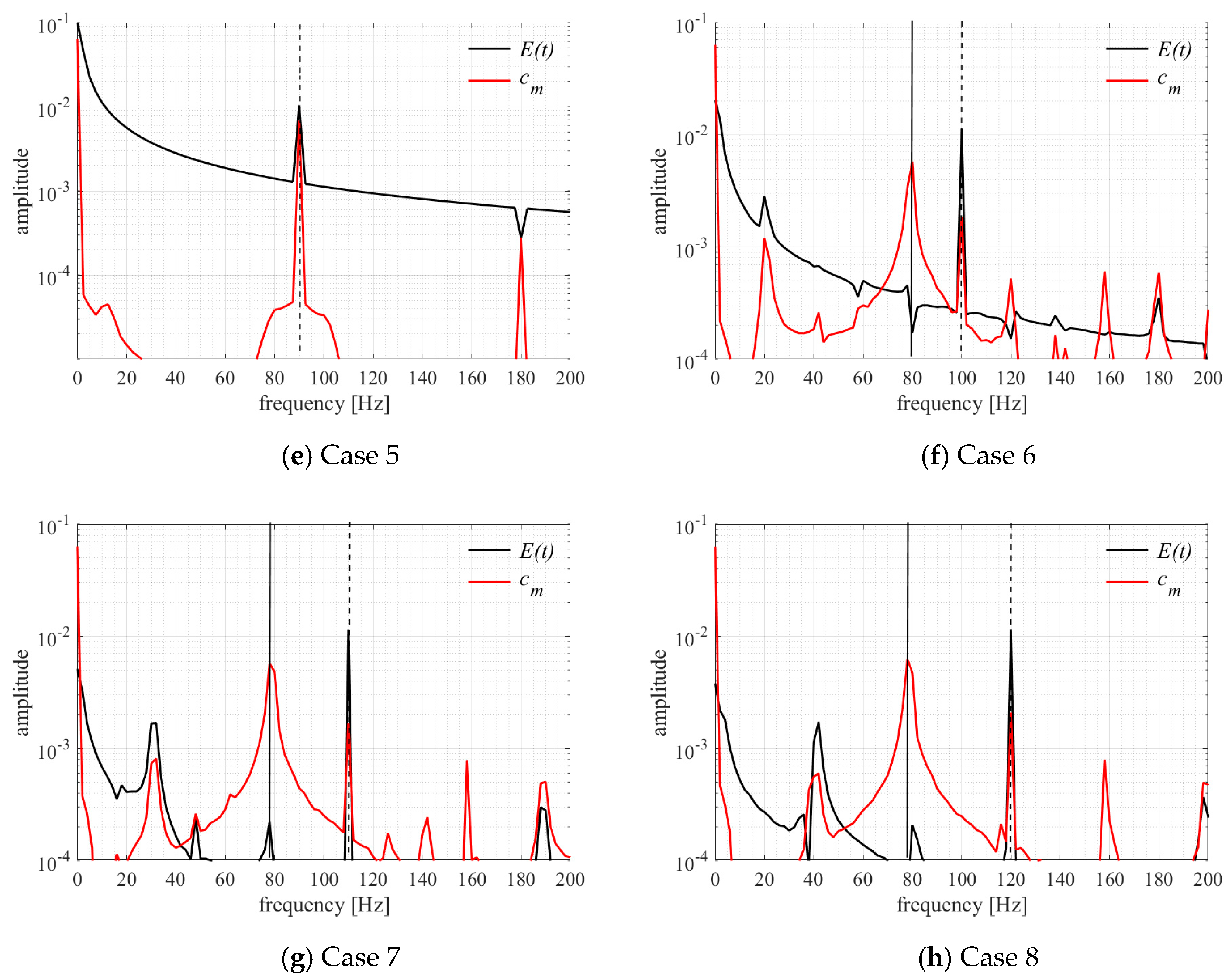
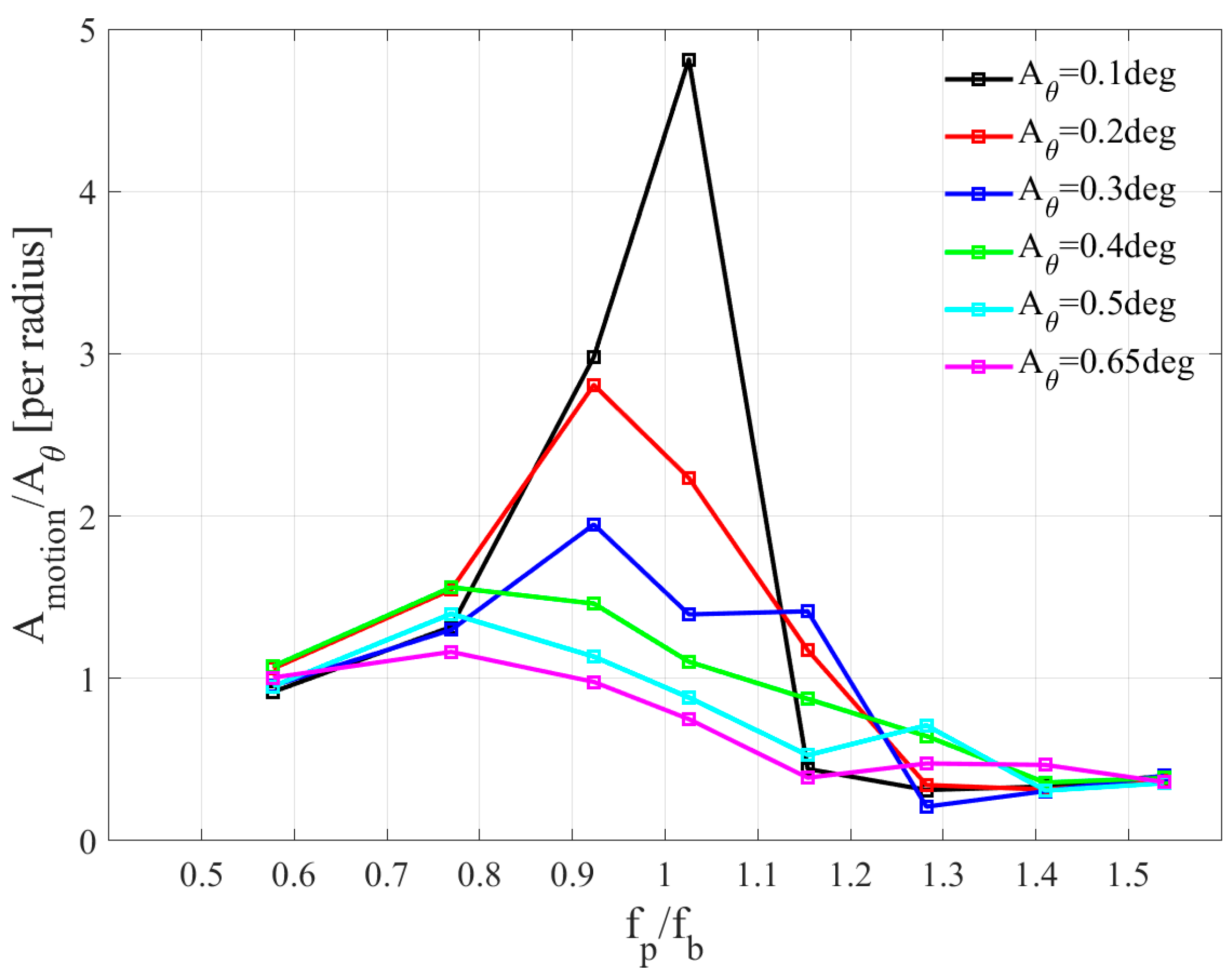
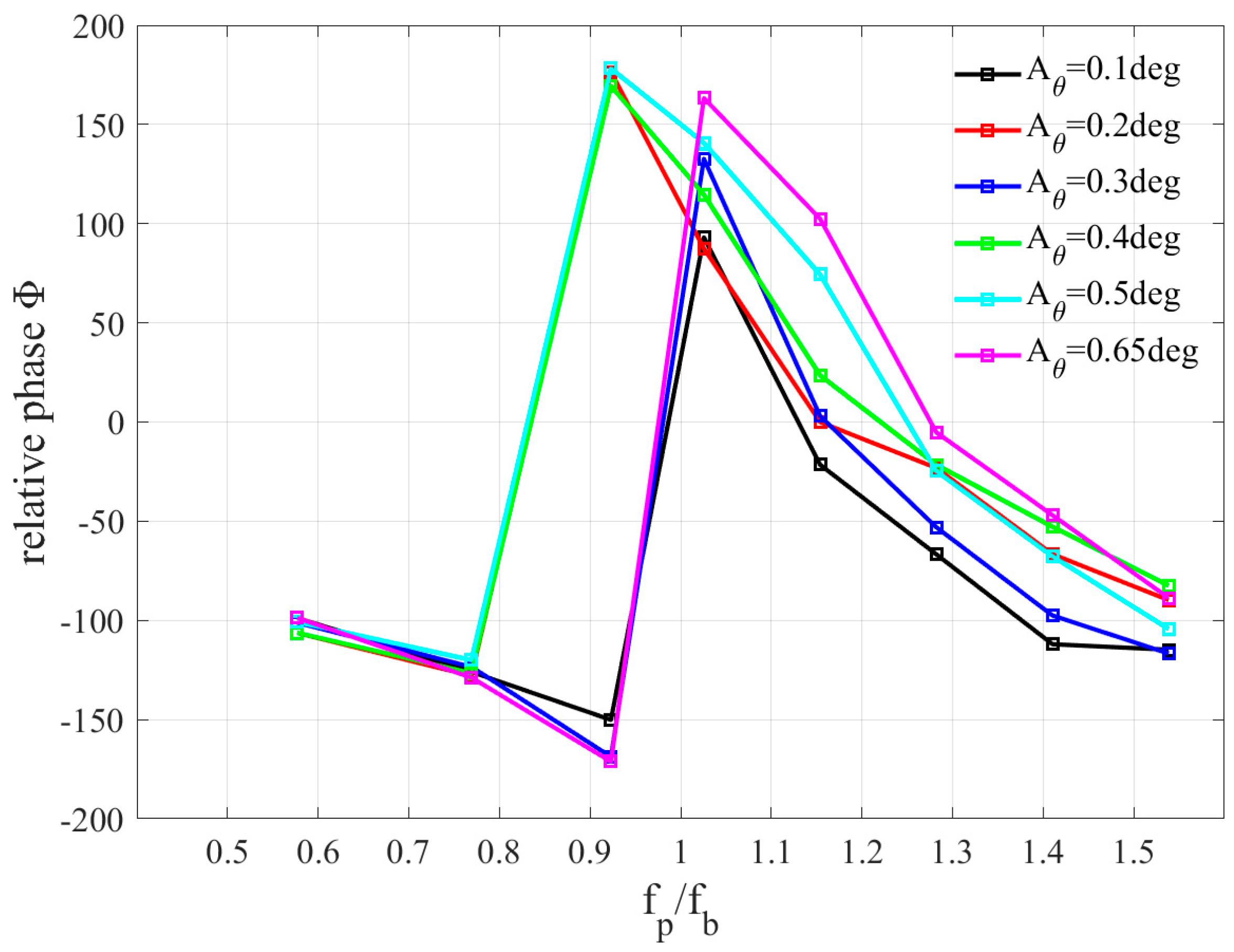
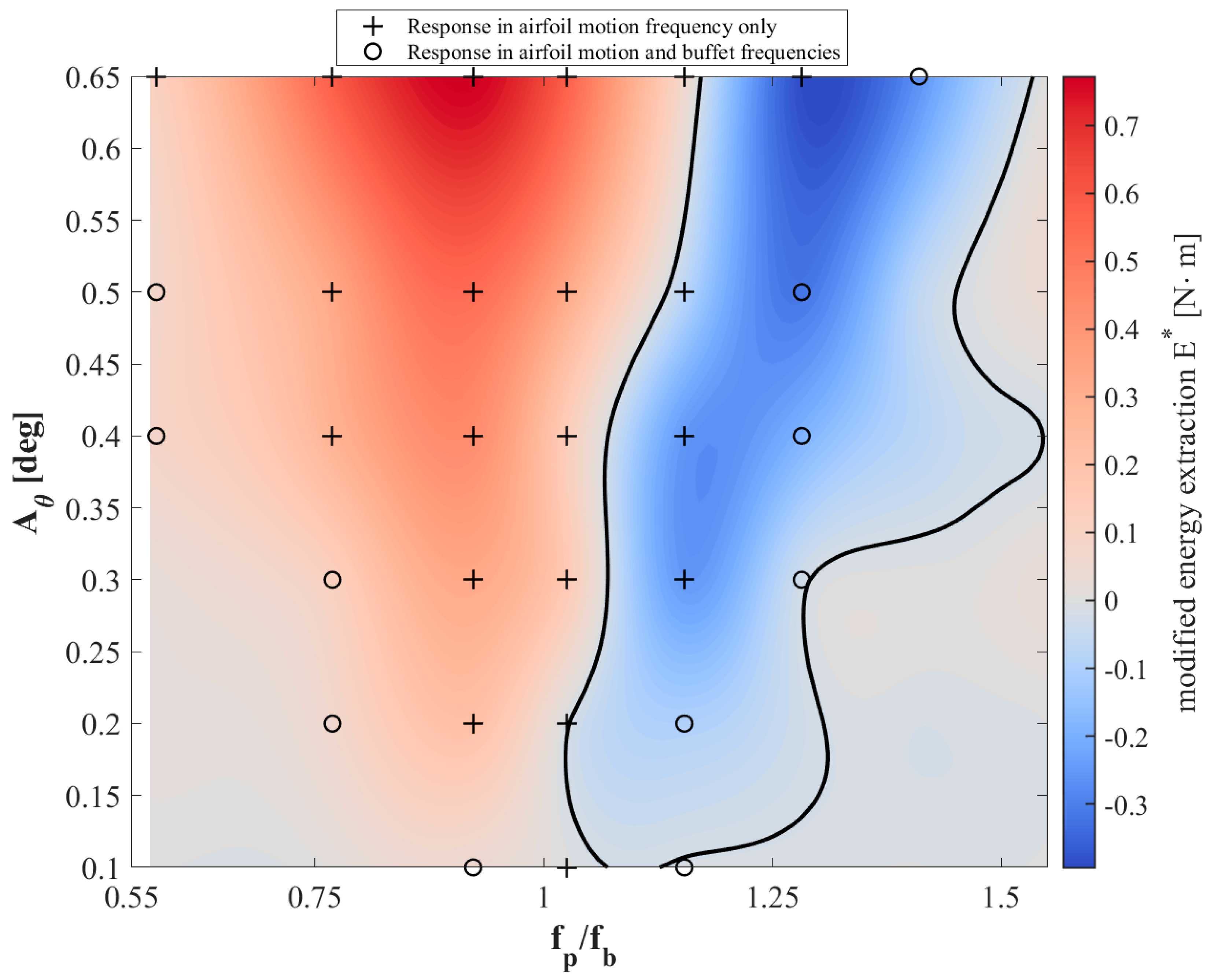

| Grid Size | Number of Layers | Surface Nodes | Total Cells | ||
|---|---|---|---|---|---|
| Coarse | 50 | 449 | 80,360 | 0.075 | 0.163 |
| Medium | 50 | 508 | 110,400 | 0.069 | 0.275 |
| Fine | 60 | 521 | 120,900 | 0.071 | 0.241 |
| [Hz] | ||
|---|---|---|
| Case 1 | 45 | 0.577 |
| Case 2 | 60 | 0.769 |
| Case 3 | 72 | 0.923 |
| Case 4 | 80 | 1.026 |
| Case 5 | 90 | 1.154 |
| Case 6 | 100 | 1.282 |
| Case 7 | 110 | 1.410 |
| Case 8 | 120 | 1.538 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Zheng, G.; Lu, W.; Zhang, Y.; Yang, G. On the Lock-In Phenomena near the Transonic Buffet Onset of a Prescribed Pitching Airfoil. Appl. Sci. 2024, 14, 5463. https://doi.org/10.3390/app14135463
Wei L, Zheng G, Lu W, Zhang Y, Yang G. On the Lock-In Phenomena near the Transonic Buffet Onset of a Prescribed Pitching Airfoil. Applied Sciences. 2024; 14(13):5463. https://doi.org/10.3390/app14135463
Chicago/Turabian StyleWei, Lianyi, Guannan Zheng, Weishuang Lu, Yuchen Zhang, and Guowei Yang. 2024. "On the Lock-In Phenomena near the Transonic Buffet Onset of a Prescribed Pitching Airfoil" Applied Sciences 14, no. 13: 5463. https://doi.org/10.3390/app14135463
APA StyleWei, L., Zheng, G., Lu, W., Zhang, Y., & Yang, G. (2024). On the Lock-In Phenomena near the Transonic Buffet Onset of a Prescribed Pitching Airfoil. Applied Sciences, 14(13), 5463. https://doi.org/10.3390/app14135463






